DOI:10.32604/csse.2021.016748

| Computer Systems Science & Engineering DOI:10.32604/csse.2021.016748 |  |
| Article |
UAV Clustering Scheme for FANETs using Elbow-Hybrid Metaheuristic Techniques
1Department of Electronics and Communication Engineering, National Institute of Technology Patna, Patna, 800005, India
*Corresponding Author: Kundan Kumar. Email: kundan.ec18@nitp.ac.in
Received: 10 January 2021; Accepted: 23 February 2021
Abstract: Great strides have been made to realistically deploy multiple Unmanned Aerial Vehicles (UAVs) within the commercial domain, which demands a proper coordination and reliable communication among the UAVs. UAVs suffer from limited time of flight. Conventional techniques suffer from high delay, low throughput, and early node death due to aerial topology of UAV networks. To deal with these issues, this paper proposes a UAV parameter vector which considers node energy, channel state information and mobility of UAVs. By intelligently estimating the proposed parameter, the state of UAV can be predicted closely. Accordingly, efficient clustering may be achieved by using suitable metaheuristic techniques. In the current work, Elbow method has been used to determine optimal cluster count in the deployed FANET. The proposed UAV parameter vector is then integrated into two popular hybrid metaheuristic algorithms, namely, water cycle-moth flame optimization (WCMFO) and Grey Wolf-Particle Swarm optimization (GWPSO), thereby enhancing the lifespan of the system. A methodology based on the holistic approach of parameter and signal formulation, estimation model for intelligent clustering, and statistical parameters for performance analysis is carried out by the energy consumption of the network and the alive node analysis. Rigorous simulations are run to demonstrate node density variations to validate the theoretical developments for various proportions of network system sizes. The proposed method presents significant improvement over conventional state-of-the-art methods.
Keywords: Clustering; elbow method; hybrid; UAVs; FANETs; energy consumption
UAVs have witnessed widespread application in a varied range of application area. Collaboration of UAVs has been employed for patrolling of borders [1], disaster management [2], rescue and search operations [3], wildfire monitoring [4], remote sensing and agriculture [5], ground and position tracking [6,7], etc. The unique characteristics and advantages of the UAVs such as flexible operation, minimal cost requirements, scalability, flexibility and speed of operation qualify them for the diverse set of applications [8].
With the help of UAVs, a new area of ad-hoc networking is introduced as the Flying Ad-hoc Network. In this network architecture, all the UAVs communicate among each other and at the most one UAV will communicate with the control station for coordination and exchange of information. FANETs face certain challenges owing to the unique features of the UAVs [9]. Most of the design requirements are with respect to these features. The first challenge encountered is the unstable topology due to high mobility of the UAVs [10]. This results in high overhead in routing due to frequent change in positions, unreliable communication and link outage. When the UAVs are very sparsely deployed, the distance over which the communication is taking place is high. Consequently, the energy requirement increases which alleviates the performance of the FANETs as they are equipped with limited battery resources [11].
Clustering is an efficient approach to address the stable topology and energy efficiency requirement of the UAVs [12]. This is by virtue of the scalable and the minimum overhead requirement characteristics of clustering [13]. The clustering process will divide the UAVs in the FANETs into different groups. Based on the performance of the UAVs, one UAV from each group takes up the task of head-node [14]. The head-node aggregates the information of its cluster and forwards it to the destination. This ensures topology maintenance with minimum resource overheads [15] and lowered cost for communication amongst the UAVs. An illustration of UAV clustering is shown in Fig. 1.
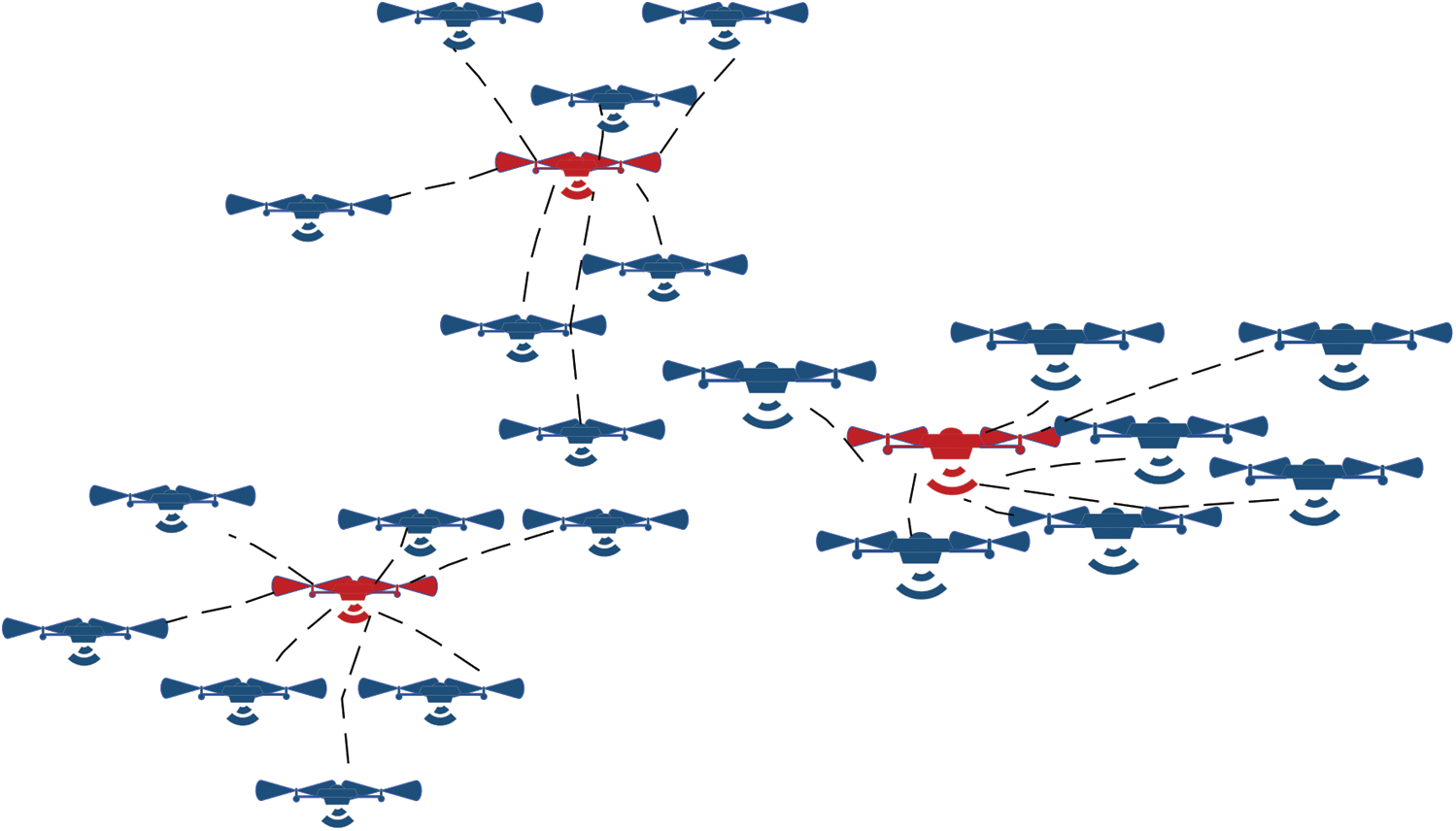
Figure 1: An illustration of UAV Clustering topology; Red ones denote cluster head and blue ones denote cluster members. Dotted lines indicate a cluster
Swarm intelligence has found extensive applications in the field of clustering in ad-hoc networks [16]. Clustering process requires certain benchmarks to achieve the formation of optimal clusters. Further, clustering can also be viewed as an optimization problem [17]. Literature shows the execution of various metaheuristic techniques for clustering in ad-hoc networks. Optimization techniques like Particle Swarm Optimization (PSO) involve position and velocity update for every iteration, and it has been extensively used in mobile ad hoc networks (MANETs) [18]. Ant Colony Optimization (ACO) closely mimics the pheromone-dependent behavior of honeybees popularly used in vehicular ad hoc networks (VANETs) [17]. Glowworm swarm optimization (GSO) is yet another luciferin-based metaheuristic technique amongst many more which are being implemented for clustering in flying ad hoc networks (FANETs) [19].
Various works considering the design restrictions of UAVs and its resulting problems have been carried out in the past. Authors in Zafar et al. [20] proposed a clustering technique to ensure the reliable transmission of data in FANETS. Based on their position, they are divided into clusters. Appointment of head-node is dependent on the signal to noise ratio (SNR). Data transmission can be from either cluster head to cluster head, or from relaying of data to the destination based on the link quality of the cluster heads between which the communications needs to take place. Shi et al. [21] considers both clustering and route maintenance for improving the efficiency in the collaboration of the UAVs. It defines two transmission ranges each, for intra cluster and inter cluster communication. Head nomination is based on the speed, degree, residual energy, and tactical value. The tactical value is defined as the node weightage.
In Zang et al. [22], an algorithm focused on the high mobility of the UAVs based on weighted-clustering technique has been proposed. Several factors such as neighborhood probability of the UAV node, link expiration time and degree of connectivity etc. dominate the selection of the optimal cluster head. Based on these factors, a weightage function is created. Node having the highest weightage is elected as cluster head. Park et al. [23] proposes multiple approaches for cluster head election in UAVs by considering distance between ground control station (GCS) and the UAV, and the residual energy as the primary metrics. The clustering process is controlled by the GCS. The first method works on random election of cluster heads, while the second method selects the cluster heads based on its highest residual energy. Finally, the last method considers both the metrics for election. Addressing the issue of routing and battery resource limitations, a k-means sorted algorithm is proposed in Aadil et al. [11]. The algorithm implements the k-means algorithm which appoints the head-nodes with the highest reservoir of energy, neighborhood, and the distance parameter. It also has a provision for electing different transmission power based on the distance between the two UAVs under communication. Different power levels for different transmission ranges are also defined.
It is evident from literature that metaheuristic techniques are being employed for clustering in FANETs and other ad-hoc networks. Also, implementation of hybrid algorithm is carried out to improve the efficacy of the network. A three phase method based on the combined effect of luciferin attraction of glowworm swarm optimization (GSO) and the marine ecosystem inspired Krill Herd (KH) algorithm is proposed in Khan et al. [8]. The method attempts to improve the energy efficiency of the network, thereby, improving the lifetime of the network. The first phase of the method is the cluster formation, which is carried out by GSO. This is followed by management of the topology by the KH. Finally, the network-maintenance phase monitors the energy and working levels of the UAVs. However, the work lacks intelligent estimation techniques that would have, otherwise, helped in cluster formation. In Khan et al. [19], GSO is implemented as a self-organization based method for clustering. Based on the behavioral nature of GSO, the connectivity and the residual energy of each UAV node, clustering of nodes is carried out. If the connectivity is not there, the node with highest residual energy is elected as the cluster head. The method also includes the management of its topology for stability and improved lifetime. However, it leaves the scope of improvement because of exclusion of channel state information, which is critical to the performance of FANETs because of rapidly changing environment around the UAVs.
A polynomial time algorithm and spiral network discovery for optimal count of UAV to cover the target area is devised in Lyu et al. [24]. UAV clustering may also be optimized by formulation of a constrained mixed integer cost function to deal with high communication cost without data aggregation, as described in Thammawichai et al. [25]. While some works have treated UAVs as static, a more accurate representation is to incorporate dynamic clustering, which would subsequently lower the transmit power as compared to traditional clustering schemes such as k-means clustering. One such approach has been attempted using modified Louvain method [26] and the results are shown to be superior in several aspects. Besides mobility of the UAVs, there are restrictions on cluster size in terms of physical coverage area as well as the number of UAVs per cluster. By considering these constraints, the inefficiency of clustering process may be improved. A game theoretic proposition has been worked out in Xing et al. [27] for coalition framework modelling, and the results have been shown to enhance UAV clustering efficiency under controlled conditions. Since UAV networks suffer from high delay during transmission of data, an intelligent clustering method using block coordinate descent method has been demonstrated to reduce this delay by improving cluster coverage in FANETs. The recent related works on UAVs have been given in Tab. 1.
Table 1: A walkthrough of the recent related works
1.2 Motivations and Applications
UAV has been used extensively by governing bodies to secure hostile [29] terrains by scanning them aerially. Typically, human intervention is nil. UAVs are beneficial in agricultural mapping [30,31] and monitoring. E-commerce is at its nascent stage of delivering goods [32,33] and services with the help of UAVs. The commercial viability has enabled in providing mobile base stations with the help of UAVs to selectively sense and gather data in an on-demand basis.
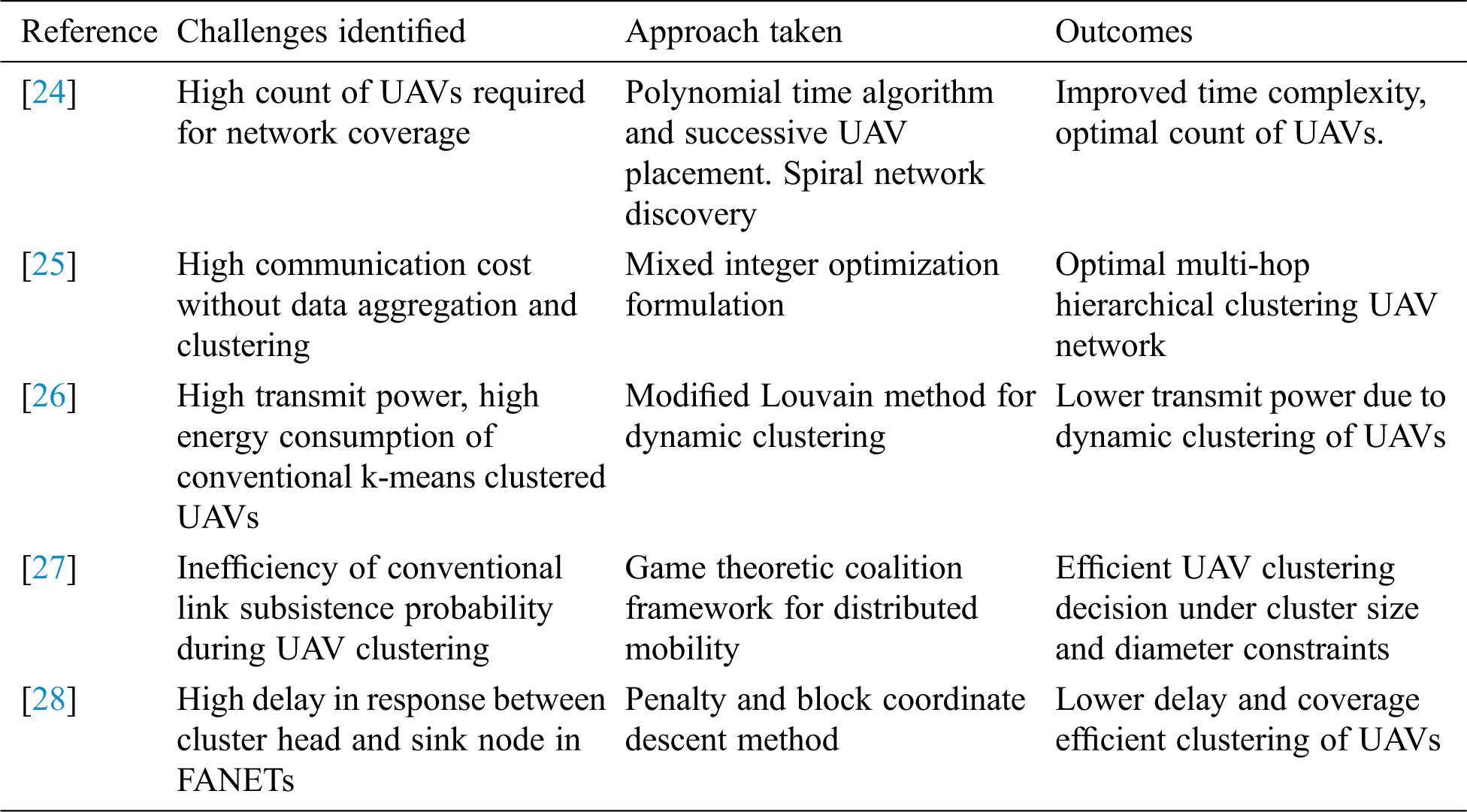
Since most of the works in literature have addressed various parameters of UAV clusters in detail, it is imperative that we consider some of these parameters together to come up with intelligent estimation technique that would determine the clustering behavior of UAVs in FANETs. This is the prime motivation behind current work, and the authors have tried to quantify their findings to the best of their knowledge. A holistic overview of the approach in this paper has been illustrated in Fig. 2. Here, the formulation phase leads to a mathematical implementation phase, followed by a verification phase to come up with lifetime and computation related parameters of the proposed method. Considering the restrictions and the possible approaches, the paper contributes the following:
a) A System Model is presented which highlights parameters of the UAVs critical to clustering and data transmission.
b) An intelligent estimation of UAV-parameters is derived mathematically to be integrated into clustering techniques.
c) Elbow Method is implemented to determine the suitable size of cluster in the deployment scenario of the FANET.
d) Estimated UAV parameter vector is used to modify two popular hybrid metaheuristic algorithms, first, a combined framework of Water Cycle Algorithm (WCA) inspired from the hydrological balance between the three states of water on earth, and the spiral hovering of moth around a light source, named aptly Moth Flame Optimization (MFO). Second, Grey Wolf Optimization (GWO) which mimics the cooperative hunting ability of a pack of wolves, is combined with the swarm behavior of Particle Swarm Optimization (PSO) for performing the clustering and election of cluster heads.
e) To corroborate the theoretical findings, rigorous simulations are run to demonstrate node density variations for various proportions of network system sizes. The results are compared with other techniques to highlight the improvement gained due to intelligent UAV parameter estimation.
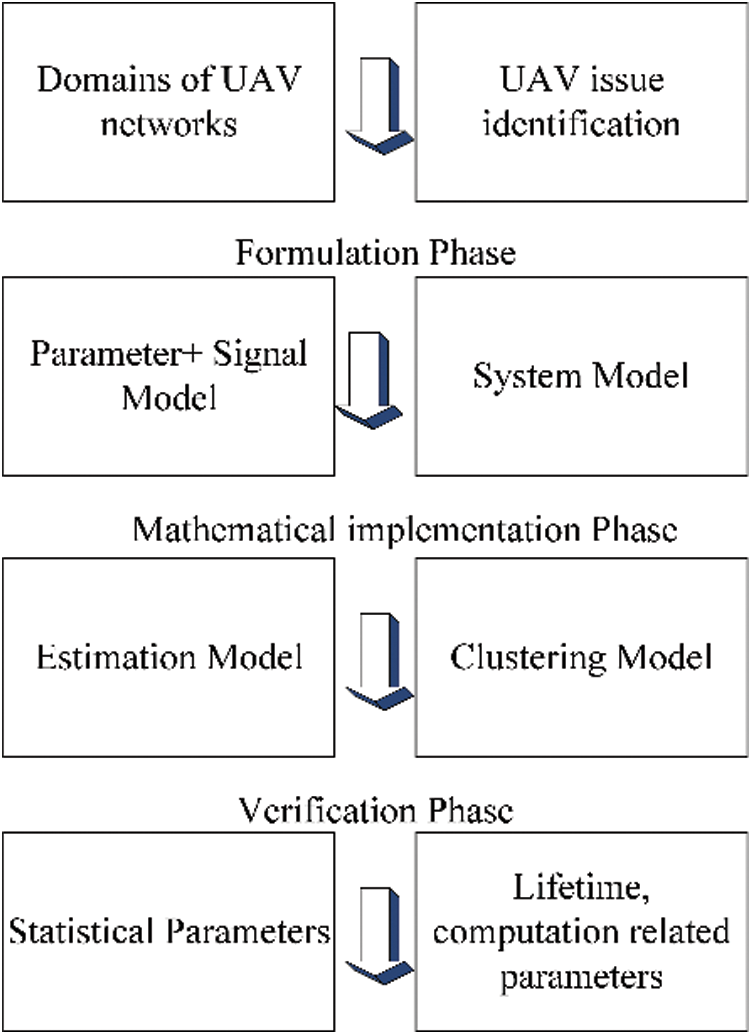
Figure 2: A holistic representation of the approach presented in this paper
To the best of the authors’ knowledge, hybrid metaheuristics with UAV parameter estimation have not been attempted together in the literature for efficient clustering of UAV networks. Therefore, the findings of the current paper are new. The paper has been organized as mentioned: Section 2 describes the Parameter, Signal and System Model of clustering of UAVs. Numerical computations are carried out in Section 3 to validate theoretical findings. Closing remarks are mentioned in Section 4.
UAV nodes in the FANETs have been clustered to address the issues of limited energy and stability in FANETs. The method initially determines the number of clusters required for the deployment scenario. It optimizes the energy consumed in the FANETs as it ensures a tradeoff distance for communication among the head-node and the cluster members. The number of clusters is achieved by the Elbow Method. Further, the network area is partitioned into sub regions based on the number of appropriate clusters to be formed via the k-means algorithm. This is followed by the clustering process and cluster head selection done by the hybrid algorithms, namely, water cycle-moth flame optimization (WCMFO) and Grey Wolf-particle swarm optimization (GWPSO). Cluster heads are elected depending upon the energy level of the UAV nodes and the delay apprehended in the network. Communication amongst the UAVs is carried out via the head UAV which forwards the data towards the control station either directly or via nearest cluster head UAV. Re-clustering is carried out when the head UAV node reaches its threshold condition. The broad outline of clustering approach is presented in Fig. 3. This section provides the network model, details of the hybrid algorithms implemented and the fitness function.
Figure 3: Flowchart of the estimation-based clustering method
We consider a group of multi- energy UAVs where the cluster heads are equipped with the ability to transmit short pulses of higher amplitude. The clusters count of
where,
where,
Proposition 1:
Let a trio of UAV elements
where
Let the minimum mean square estimate (MMSE)
where, the signal model is as follows
where
where,
Thus, the MMSE estimate
where,
The significance of Proposition 1 is that it enables us to monitor UAV health parameters for improved cluster head prediction.
In this paper, FANET is considered over a network area of q×q m2 area deploying ‘K’ UAV nodes having a geographical location of (xk, yk, zk) and an initial energy level of Ek. Fig. 4a depicts the initial deployment scenario. The control station is assumed to be at the boundary of the network area. Since the UAVs are mostly in line of sight (LoS) [9], Free Space Path Loss (FSPL) propagation model is considered. The implementation of the presented method yields ‘N’ clusters with each cluster having a cluster head HN. The scenario after clustering is shown in Fig. 4b. The communication among the UAVs follows the First Order Radio Model as in Aadil et al. [11] where the L2-norm between the UAVs decides the energy consumption during transmission-reception of signals. In view of maintaining a stable topology the Reference Point Group Mobility (RPGM) Model is followed [35]. According to this, the cluster members congregate in tandem with the movement of the head UAV nodes, thus maintaining the topology.
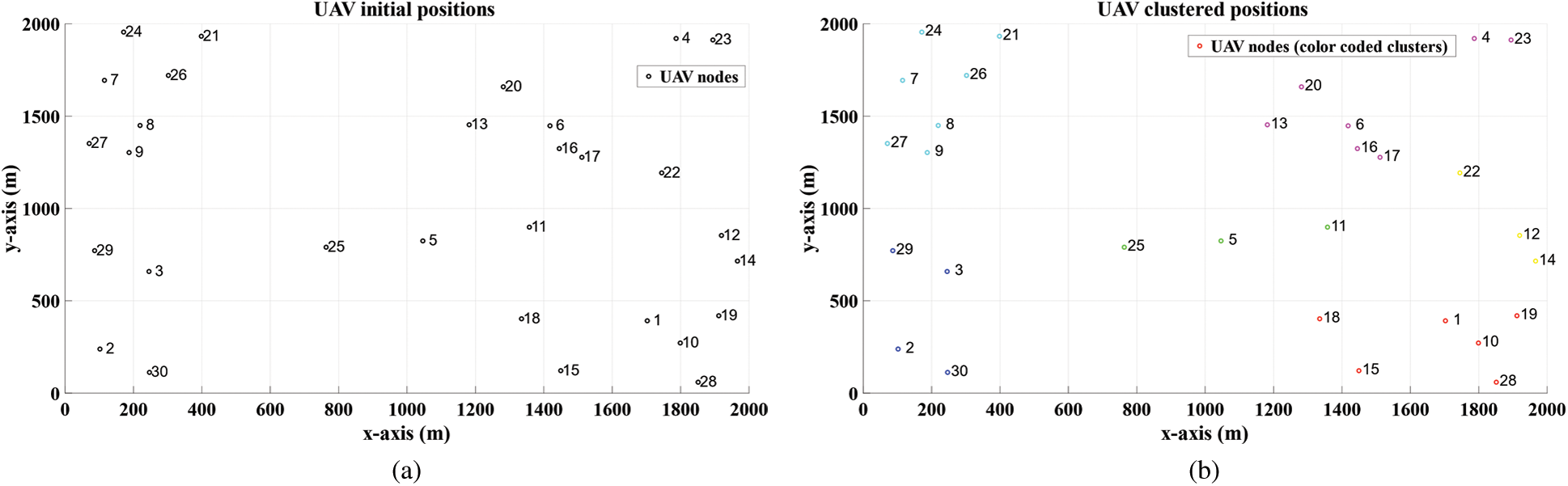
Figure 4: (a) Deployment scenario of FANETs (b) Scenario after clustering of the UAV nodes
A flowchart describing the estimation of parameter- based UAV clustering is shown in Fig. 3. The general framework of any metaheuristic clustering technique requires initialization of UAV positions followed by residual energy calculation of each UAV. If the UAVs require clustering, then first the parameters discussed in section 2.1 are estimated for each UAV. Then, the number of clusters is optimally found by utilizing elbow method. Using K-means technique, an initial set of clusters is created. Based on estimated individual parameter values, a cost function is formulated and subjected to various constraints. The cost function is then solved using emerging hybrid metaheuristic techniques to determine the optimum cluster heads. After every round of transmission, the same technique is evaluated again, till the UAVs have either completed all transmissions, or they deplete their energies completely. The role of estimation-based clustering enables accurate cluster head prediction. This cluster head prediction is possible when the UAV health vector is tuned according to UAV energy, its channel state information and the mobility factor of FANET.
The elbow method is introduced to ensure optimal numbers of clusters for clustering [36]. The method considers the L2-norm between the cluster head and the cluster members to determine the optimal situation. This distance is known as the within cluster sum of squares (WCSS). It tries to deduce the number of clusters wherein there is tradeoff between the WCSS in terms of forming distinct and closed clusters. Considering two network areas of 1000 × 1000 m2 and 2000 × 2000 m2, for a node density of 55, the optimal number of clusters was found to be 6, using the Elbow Method. This is depicted in Fig. 5.
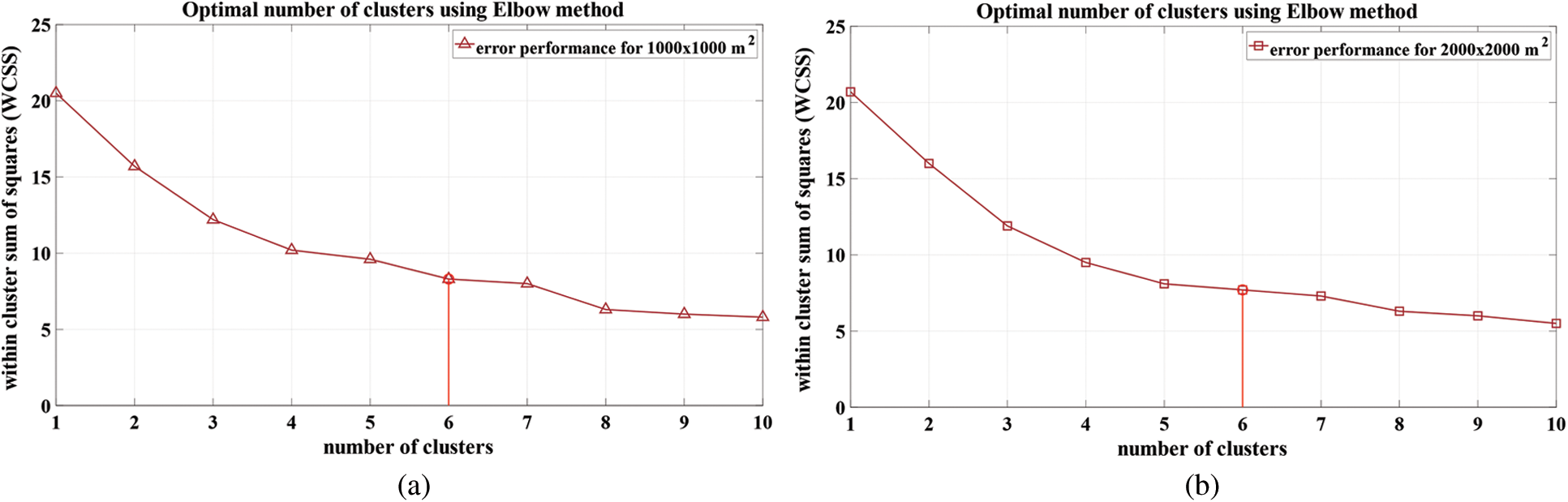
Figure 5: Elbow method implemented for two different network areas of (a) 1000 × 1000 m2 (b) 2000 × 2000 m2
2.4 Clustering by Hybrid Metaheuristics
In this method, after the initial segmentation to ‘N’ sub regions based on the K-means algorithm, a hybrid metaheuristic algorithm is implemented for selecting the optimal cluster heads. The optimal selection depends on certain factors such as energy levels and the delay introduced by it. This section details the hybrid algorithm and the process by which it is being incorporated into the proposed method.
The hybrid algorithm of the Water Cycle Algorithm (WCA) and the Moth Flame Optimization (MFO) is implemented as in Khalilpourazari et al. [37]. The algorithm improves the exploration and exploitation capacity of the WCA. The local search is improved by introducing the spiral movement of the moth, while the randomization by the Levy flight increases the global search ability in the area where the ‘K’ UAV nodes are randomly deployed. The solution for the algorithm is the sea, which is the fittest among ‘M’ streams initialized. Hence, the solution space is ‘M’ streams that contains ‘N’ eligible cluster heads selected from each sub-region. The streams are further segregated to sea, rivers and streams as shown in Eqs. (10) and (11), respectively.
where,
where,
where,
The flowchart of the estimator modified WCMFO algorithm is given in Fig. 6. The network and algorithmic parameters are initialized first, followed by selection of UAVs having energy higher than the threshold. Then the eligible cluster heads are initialized just like rain drops of water cycle algorithm. The UAV parameter vector is then intelligently estimated to determine the future mobility, energy, and channel state information of the UAVs and the network. Based on these parameters, the fitness function of each UAV is computed. Fitness value also determines the classification of water bodies into streams, rivers, and seas. The upcoming position of UAVs is determined by following the spiral movement of moths towards the central flame, and the position of streams using Levy’s flight. Depletion of UAV energy is emulated by evaluating the evaporation condition. Upon completing a finite number of rounds, the process is terminated, and we check for the number of rounds which have been optimally clustered.
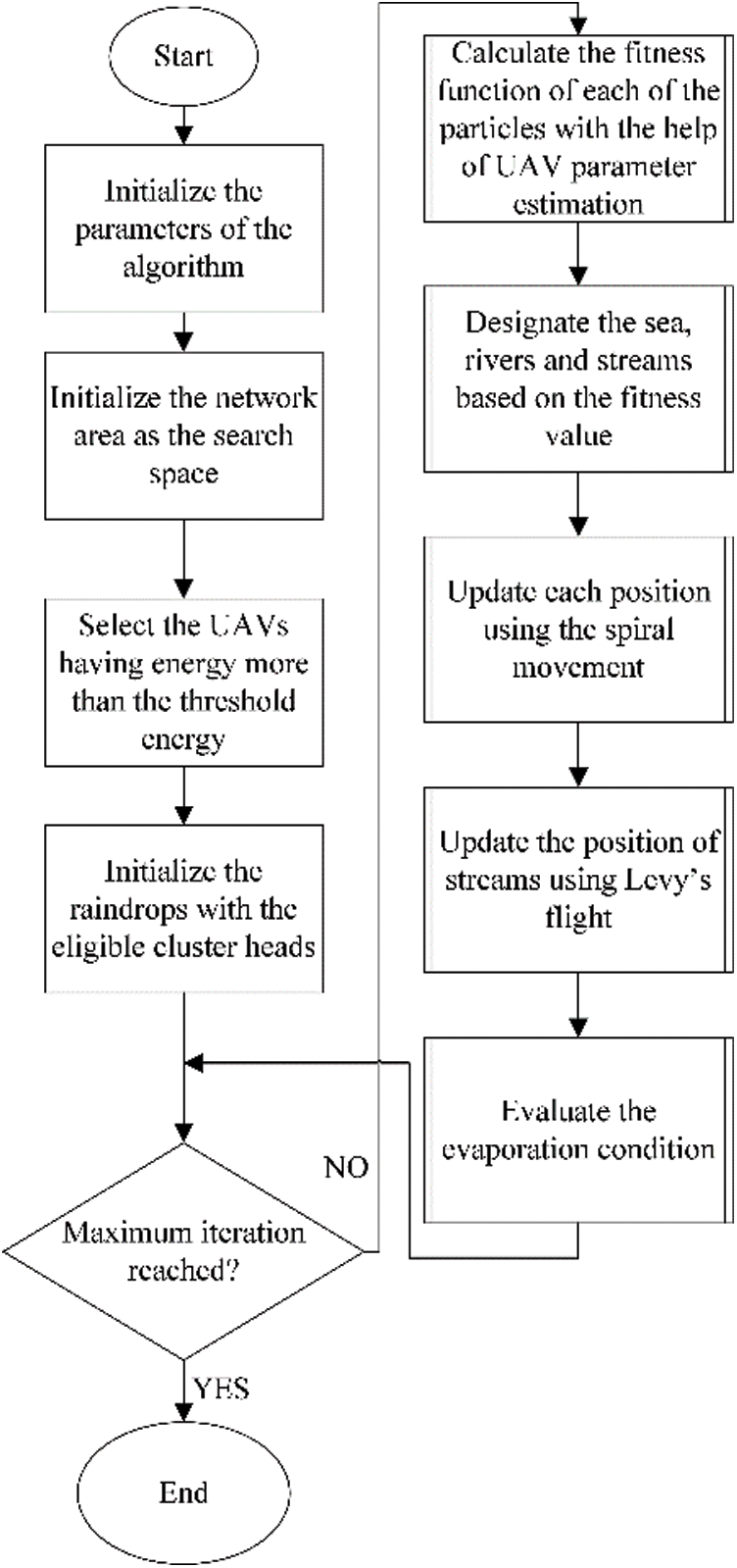
Figure 6: Flowchart of working of the modified WCMFO algorithm
In the implementation of the GWPSO [38], Particle Swarm Optimization (PSO) and the Grey Wolf Optimization (GWO) are incorporated. In this algorithm, the improvement in the local search of PSO is introduced by the global search capabilities of the GWO. The search space for the algorithm is the network area of the FANET with the ‘N’ sub region. A set of ‘M’ particles with ‘N’ cluster heads is initialized as the search space. Based on the fitness these particles are designated as the alpha, beta, and delta particles. An inertia constant value
where,
where,
The flowchart of the intelligent estimator modified GWPSO algorithm is shown in Fig. 7. The first phase involves initialization of set of parameters for the algorithm as well as the UAV network. The UAVs having energy above threshold are selected and cluster heads are eligible for particle initialization. Then the UAV parameter vector is intelligently estimated to determine the next potential UAV energy, mobility, and channel state information of the network. This parameter vector is used to determine the position of three kinds of particles, namely alpha, beta and delta. The position and velocity of UAVs are updated according to the particles of swarm. The convergence constant ‘a’ is computed to check for optimality condition. These steps are iterated till the UAV nodes run out of energy, or successful transmissions are completed.
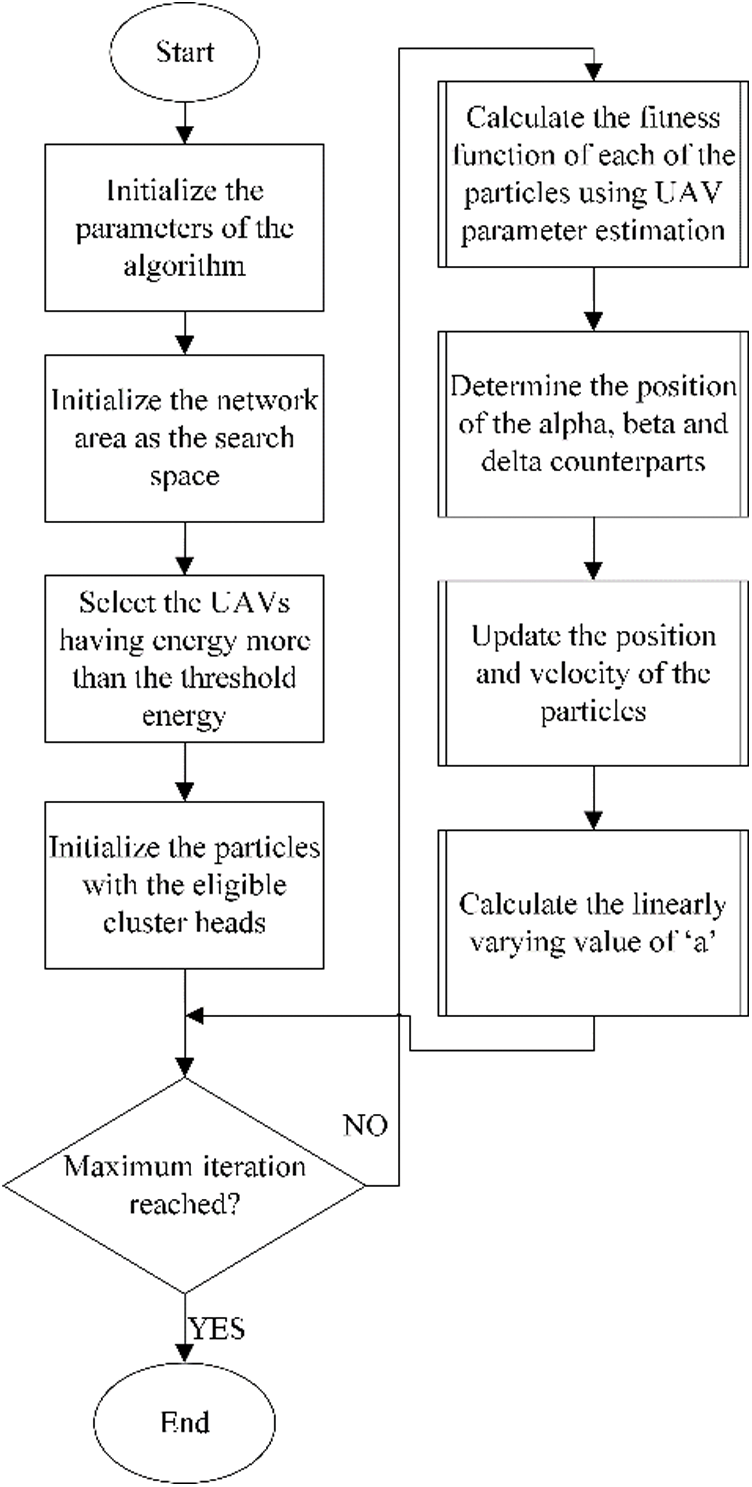
Figure 7: Working Flowchart of the modified GWPSO algorithm
The quality of the cluster head required for the process of clustering is determined by the fitness function. The main function of the optimization approach is to bring about a tradeoff among the objectives to be achieved. The fitness function in this method considers the energy level and the delay as the basis for cluster head election. Energy level is considered to check the survivability of the head nodes, while delay is associated with the reliable and timely transmission of the data. The multi-objective minimization function as shown in Eq. (24).
The functions fa, fb are adapted from [39,40] and incorporated to obtain the optimum situation in the FANETs. They denote the cost functions related to energy requirement and delay associated with each UAV. The Eqs. (25) and (26) govern these factors,
This section briefs the simulation setup and the results obtained based on the parameter evaluation. The parameters considered are the energy consumption and the alive node analysis. Both the parameters give an insight to the lifetime and efficiency of the network. The correlation coefficient between different UAV estimation parameters is crucial because it links charge content of UAV power source with the rate of change of position of UAV, in the presence of a dynamically changing channel state information.
The proposed method is simulated for a FANET setup, where the nodes are randomly deployed. Two network areas, 1000 × 1000 m2 and 2000 × 2000 m2 are considered and the node density is varied from 25 to 55. Simulation parameters are tabulated in Tab. 2. MATLAB is the platform used for the simulations.
The performance of the two hybrid algorithms implemented in the proposed method is compared with respect to network energy consumption and the analysis of the number of alive-nodes. In both the proposed methods, UAV parameter estimation phase is exploited to compute the fitness function to come up with the requisite node analyses. Energy consumption of the proposed method depends on the following constraints: Correlation coefficient between the charge content of UAV power source and the rate of change of position of UAV.
The importance of controlled energy exhaustion is critical due to the limited battery availability of the UAVs. The communication amongst the UAVs are considered using First Order Radio Model. The energy consumption is checked for a stipulated number of transmissions. Fig. 8. depicts the energy consumption of the network for both the network areas. It is evident that WCMFO performs better than the GWPSO, which implies limited energy consumption and a longer network lifetime. With increasing node distance, energy consumption sees an upward growth trend, with the proposed method exhibiting slower growth than the competing models, meaning improved performance.
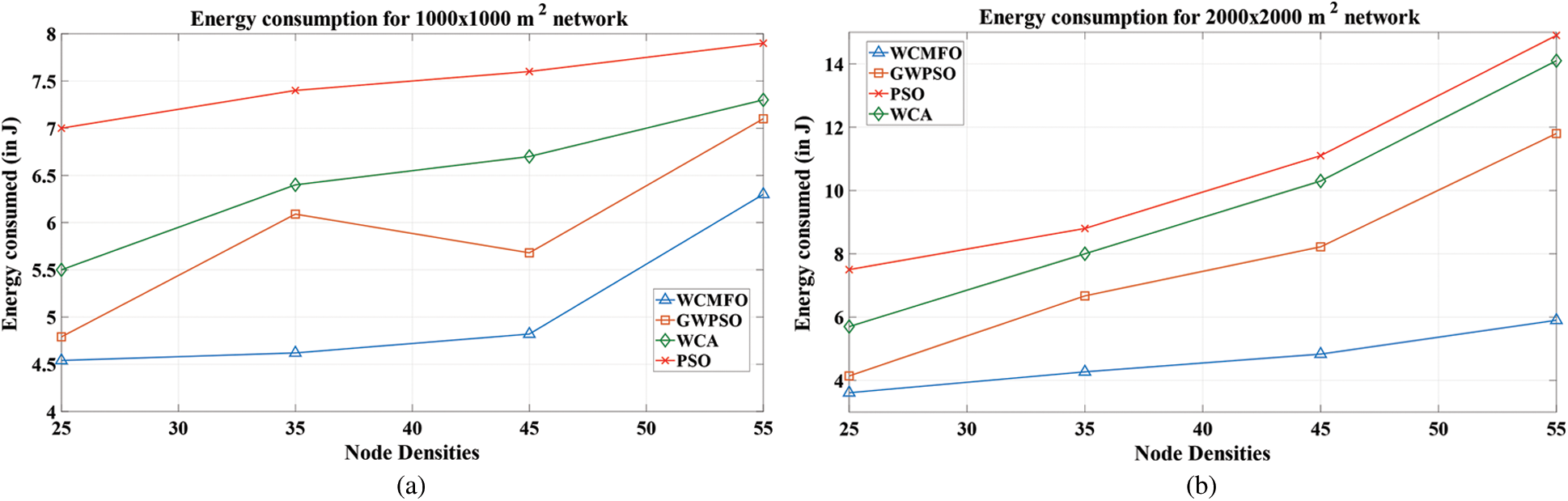
Figure 8: Network energy consumption for a network area of (a) 1000 × 1000 m2 (b) 2000 × 2000 m2
Alive nodes analysis gives an insight of the operational nodes per round of transmission in the network. The lifetime and operation of the network can be determined with the help of alive node analysis. Fig. 9. shows the alive node analysis of the network where the number of nodes operational is checked for the first 5000 rounds. It is carried out for an initial node density of 45. The graphs reveal that WCMFO lifetime is better compared to the GWPSO, hence depicting its efficiency in terms of node lifetime. The number of alive nodes rapidly ceases during the first 3000 rounds in case of competing methods (PSO and WCA).
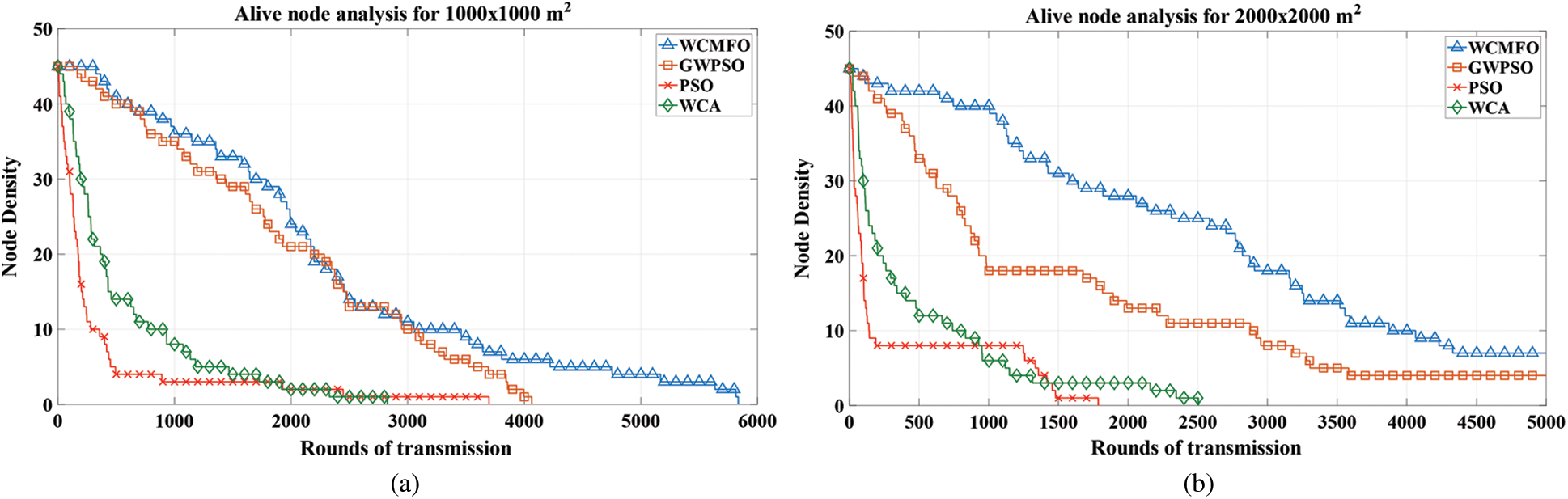
Figure 9: Analysis of the operational nodes per rounds of transmission for an assumed network area of (a) 1000 × 1000 m2 (b) 2000 × 2000 m2 when the node density is 45
Tab. 3 summarizes the comparative results in tabular form.
Table 3: Summary of comparative results
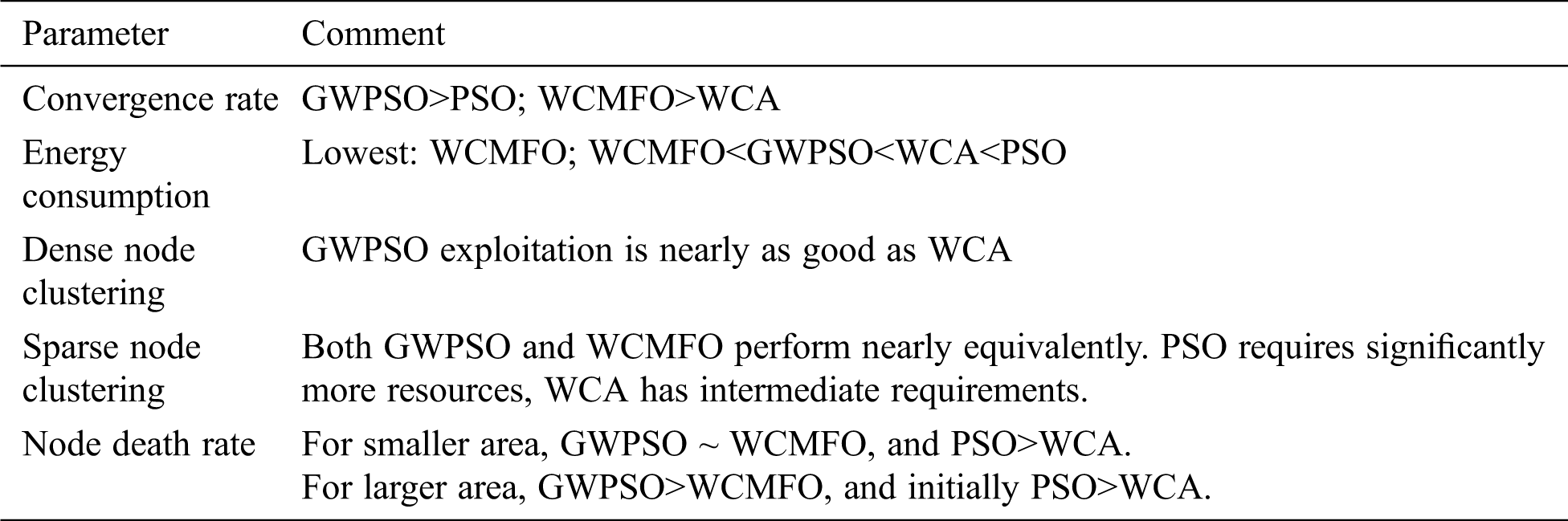
Summarizing the findings of Section 3, the computational analysis included energy consumption and alive node determination for different node deployment sizes. Observing the results, the superiority of the proposed techniques was established with respect to the convergence rate, node density, node death rate etc. In terms of convergence rate, the proposed GWPSO was found to converge faster than conventional PSO, and the proposed WCMFO was found to converge faster than WCA. Energy consumption wise WCMFO was found to be the most efficient, then followed by the proposed GWPSO, while PSO consumed the most energy.
In this paper, the proposed method for clustering in FANETs was presented. It addressed the limited battery availability and unstable topology issues of the UAVs. An intelligent estimation of UAV parameter vector was formulated, and mathematical expression was derived to compute the errors associated with prediction of next state of UAVs. Ideal number of clusters required by the network scenario was then determined by the Elbow Method. Clustering by two emerging hybrid methods WCMFO and GWPSO was implemented by incorporating UAV parameter estimation into the respective fitness functions. Simulations were run for two network areas by varying the node densities. The performances were evaluated based on the energy consumption of the network and the alive nodes to analyze the improvement in the lifetime of the network and to compare with existing schemes. The results demonstrated superior attributes of WCMFO algorithm within the scope of analysis. The better performance of the WCMFO might be attributed to the improvement in the exploration and exploitation phase in the WCA with the inclusion of spiral movement and Levy flight, making it more robust and efficient. The superior performance of modified hybrid techniques over the existing conventional ones highlighted the importance of accurately estimating the UAV parameters and their subsequent inclusion into the cost function to incorporate machine-intelligent UAV clustering in modern-day FANETs.
Funding Statement: The authors received no specific funding for this study.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
1. Z. Sun, P. Wang, M. C. Vuran, M. A. Al-Rodhaan, A. M. Al-Dhelaan et al., “BorderSense: Border patrol through advanced wireless sensor networks,” Ad Hoc Networks, vol. 9, pp. 468–477, 2011. [Google Scholar]
2. I. Maza, F. Caballero, J. Capitán, J. R. Martínez-de-Dios and A. Ollero, “Experimental results in multi-UAV coordination for disaster management and civil security applications,” Journal of Intelligent & Robotic Systems, vol. 61, no. 1–4, pp. 563–585, 2011. [Google Scholar]
3. J. G. Manathara, P. B. Sujit and R. W. Beard, “Multiple UAV coalitions for a search and prosecute mission,” Journal of Intelligent & Robotic Systems, vol. 62, no. 1, pp. 125–158, 2011. [Google Scholar]
4. C. Barrado, R. Meseguer, J. López, E. Pastor, E. Santamaria et al., “Wildfire monitoring using a mixed air-ground mobile network,” IEEE Pervasive Computing, vol. 9, no. 4, pp. 24–32, 2010. [Google Scholar]
5. Xiang H. and Tian L., “Development of a low-cost agricultural remote sensing system based on an autonomous unmanned aerial vehicle (UAV),” Biosystems Engineering, vol. 108, no. 2, pp. 174–190, 2011. [Google Scholar]
6. S. Zhu, D. Wang and C. B. Low, “Ground target tracking using UAV with input constraints,” Journal of Intelligent and Robotic Systems: Theory and Applications, vol. 69, no. 1–4, pp. 417–429, 2013. [Google Scholar]
7. Y. Yuan, L. Cheng, Z. Wang and C. Sun, “Position tracking and attitude control for quadrotors via active disturbance rejection control method,” Science China Information Sciences, vol. 62, no. 1, pp. 1–10, 2019. [Google Scholar]
8. A. Khan, F. Aftab and Z. Zhang, “BICSF: Bio-inspired clustering scheme for FANETs,” IEEE Access, vol. 7, pp. 31446–31456, 2019. [Google Scholar]
9. I. Bekmezci, O. K. Sahingoz and Ş. Temel, “Flying ad-hoc networks (FANETsA survey,” Ad Hoc Networks, vol. 11, no. 3, pp. 1254–1270, 2013. [Google Scholar]
10. M. A. Khan, A. Safi, I. M. Qureshi and I. U. Khan, “Flying ad-hoc networks (FANETsA review of communication architectures, and routing protocols,” in 2017 1st Int. Conf. on Latest Trends in Electrical Engineering and Computing Technologies, INTELLECT 2017, vol. 2018-Janua, pp. 1–9, 2018. [Google Scholar]
11. F. Aadil, A. Raza, M. F. Khan, M. Maqsood, I. Mehmood et al., “Energy aware cluster-based routing in flying ad-hoc networks,” Sensors (Switzerland), vol. 18, no. 5, pp. 1–16, 2018. [Google Scholar]
12. O. K. Sahingoz, “Networking models in flying ad-hoc networks (FANETsConcepts and challenges,” Journal of Intelligent & Robotic Systems, vol. 74, pp. 513–527, 2014. [Google Scholar]
13. M. Y. Arafat and S. Moh, “A survey on cluster-based routing protocols for unmanned aerial vehicle networks,” IEEE Access, vol. 7, pp. 498–516, 2019. [Google Scholar]
14. S. Chinara and S. K. Rath, “A survey on one-hop clustering algorithms in mobile ad hoc networks,” Journal of Network and Systems Management, vol. 17, no. 1–2, pp. 183–207, 2009. [Google Scholar]
15. C. Cooper, D. Franklin, M. Ros, F. Safaei and M. Abolhasan, “A comparative survey of VANET clustering techniques,” IEEE Communications Surveys and Tutorials, vol. 19, no. 1, pp. 657–681, 2017. [Google Scholar]
16. S. Bitam, A. Mellouk and S. Zeadally, “Bio-inspired routing algorithms survey for vehicular ad hoc networks,” IEEE Communications Surveys & Tutorials, vol. 17, no. 2, pp. 843–867, 2015. [Google Scholar]
17. F. Aadil, K. B. Bajwa, S. Khan, N. M. Chaudary and A. Akram, “Caconet: Ant colony optimization (ACO) based clustering algorithm for VANET,” PLoS ONE, vol. 11, no. 5, pp. e0154080, 2016. [Google Scholar]
18. H. Ali, W. Shahzad and F. A. Khan, “Energy-efficient clustering in mobile ad-hoc networks using multi-objective particle swarm optimization,” Applied Soft Computing, vol. 12, no. 7, pp. 1913–1928, 2012. [Google Scholar]
19. A. Khan, F. Aftab and Z. Zhang, “Self-organization based clustering scheme for FANETs using Glowworm Swarm Optimization,” Physical Communication, vol. 36, no. 5, pp. 100769, 2019. [Google Scholar]
20. W. Zafar and B. M. Khan, “A reliable, delay bounded and less complex communication protocol for multicluster FANETs,” Digital Communications and Networks, vol. 3, no. 1, pp. 30–38, 2017. [Google Scholar]
21. N. Shi and X. Luo, “A novel cluster-based location-aided routing protocol for UAV fleet networks,” International Journal of Digital Content Technology and its Applications, vol. 6, no. 18, pp. 376–383, 2012. [Google Scholar]
22. C. Zang and S. Zang, “Mobility prediction clustering algorithm for UAV networking,” 2011 IEEE GLOBECOM Workshops (GC Wkshps), vol. 3, pp. 1158–1161, 2011. [Google Scholar]
23. J. H. Park, S. C. Choi, H. R. Hussen and J. Kim, “Analysis of dynamic cluster head selection for mission-oriented flying ad hoc network,” in Int. Conf. on Ubiquitous and Future Networks, ICUFN, IEEE Computer Society, pp. 21–23, 2017. [Google Scholar]
24. J. Lyu, Y. Zeng, R. Zhang and T. J. Lim, “Placement optimization of UAV-mounted mobile base stations,” IEEE Communications Letters, vol. 21, no. 3, pp. 604–607, 2017. [Google Scholar]
25. M. Thammawichai, S. P. Baliyarasimhuni, E. C. Kerrigan and J. B. Sousa, “Optimizing communication and computation for multi-UAV information gathering applications,” IEEE Transactions on Aerospace and Electronic Systems, vol. 54, no. 2, pp. 601–615, 2018. [Google Scholar]
26. J. Yu, R. Zhang, Y. Gao and L. L. Yang, “Modularity-based dynamic clustering for energy efficient UAVs-aided communications,” IEEE Wireless Communications Letters, vol. 7, no. 5, pp. 728–731, 2018. [Google Scholar]
27. N. Xing, Q. Zong, L. Dou, B. Tian and Q. Wang, “A game theoretic approach for mobility prediction clustering in unmanned aerial vehicle networks,” IEEE Transactions on Vehicular Technology, vol. 68, no. 10, pp. 9963–9973, 2019. [Google Scholar]
28. W. You, C. Dong, X. Cheng, X. Zhu, Q. Wu et al., “Joint optimization of area coverage and mobile edge computing with clustering for FANETs,” IEEE Internet of Things Journal, vol. 8, no. 2, pp. 695–707, 2020. [Google Scholar]
29. A. A. Khuwaja, Y. Chen, N. Zhao, M. S. Alouini and P. Dobbins, “A survey of channel modeling for UAV communications,” IEEE Communications Surveys & Tutorials, vol. 20, no. 4, pp. 2804–2821, 2018. [Google Scholar]
30. M. Bacco, A. Berton, A. Gotta and L. Caviglione, “IEEE 802.15.4 air-ground UAV communications in smart farming scenarios,” IEEE Communications Letters, vol. 22, no. 9, pp. 1910–1913, 2018. [Google Scholar]
31. C. Potena, R. Khanna, J. Nieto, R. Siegwart, D. Nardi et al., “AgriColMap: Aerial-ground collaborative 3D mapping for precision farming,” IEEE Robotics and Automation Letters, vol. 4, no. 2, pp. 1085–1092, 2019. [Google Scholar]
32. H. Huang, A. V. Savkin and C. Huang, “Drone routing in a time-dependent network: Towards low cost and large range parcel delivery,” IEEE Transactions on Industrial Informatics, vol. 17, no. 2, pp. 1526–1534, 2020. [Google Scholar]
33. D. Wang, P. Hu, J. Du, P. Zhou, T. Deng et al., “Routing and scheduling for hybrid truck-drone collaborative parcel delivery with independent and truck-carried drones,” IEEE Internet of Things Journal, vol. 6, no. 6, pp. 10483–10495, 2019. [Google Scholar]
34. S. M. Kay, “Cramer-Rao Lower Bound,” in Fundamentals of Statistical Signal Processing Estimation Theory, 1st ed., vol. 1, Upper Saddle River, NJ, USA: Prentice Hall PTR, pp. 70–73, 1993. [Google Scholar]
35. X. Hong, M. Gerla, G. Pei and C. C. Chiang, “A group mobility model for ad hoc wireless networks,” in Proc. of the 2nd ACM Int. Workshop on Modeling, Analysis and Simulation of Wireless and Mobile Systems, MSWiM 1999, pp. 53–60, 1999. [Google Scholar]
36. F. Liu and Y. Deng, “Determine the number of unknown targets in open world based on elbow method,” IEEE Transactions on Fuzzy Systems, vol. 6706, no. OCTOBER 2018, pp. 1, 2018. [Google Scholar]
37. S. Khalilpourazari and S. Khalilpourazary, “An efficient hybrid algorithm based on water cycle and moth-flame optimization algorithms for solving numerical and constrained engineering optimization problems,” Soft Computing, vol. 23, no. 5, pp. 1699–1722, 2019. [Google Scholar]
38. N. Singh and S. B. Singh, “Hybrid algorithm of particle swarm optimization and grey wolf optimizer for improving convergence performance,” Journal of Applied Mathematics, vol. 2017, no. 1–4, pp. 1–15, 2017. [Google Scholar]
39. R. Kumar and D. Kumar, “Multi-objective fractional artificial bee colony algorithm to energy aware routing protocol in wireless sensor network,” Wireless Networks, vol. 22, no. 5, pp. 1461–1474, 2016. [Google Scholar]
40. G. P. Gupta, “Improved cuckoo search-based clustering protocol for wireless sensor networks,” Procedia Computer Science, vol. 125, no. 4, pp. 234–240, 2018. [Google Scholar]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |