Computer Systems Science & Engineering DOI:10.32604/csse.2022.016007
Article

A Coordinated Search Algorithm for a Lost Target on the Plane

Sundus Naji Al-Aziz1,*, Abd Al-Aziz Hosni El-Bagoury2 and W. Afifi2,3

1Department of Mathematics, College of Science, Princess Nourah bint Abdulrahman University, Riyadh, Saudi Arabia
2Department of Mathematics, Faculty of Science, Tanta University, Tanta, Egypt
3Department of Mathematics and Statistics, College of Science, Taibah University, Yanbu, Saudi Arabia
*Corresponding Author: Sundus Naji Al-Aziz. Email: Sundus.alaziz3@gmail.com
Received: 18 December 2020; Accepted: 20 April 2021

Abstract: Concepts in search theory have developed since World War II. The study of search plans has found considerable interest among searchers due to its wide applications in our life. Searching for lost targets either located or moved is often a time-critical issue, especially when the target is very important . In many commercial and scientific missions at sea, it is of crucial importance to find lost targets underwater. We illustrate a technique known as coordinated search, that completely characterizes the search for a randomly located target on a plane. The idea is to avoid wasting time looking for a missing target. Two searchers or robots start from the center of a circle to search out a lost target, the first searcher looks for the target on the right side of the circular area, and the second one looks for it on the left side. The time taken to detect the target is obtained by assuming the target’s position has a symmetric distribution. The procedures to facilitate the detection of the target are presented as an algorithm and as a flowchart. An application demonstrates the applicability of this search technique and the associated decrease in search cost. Its effectiveness is illustrated by numerical results, which indicates considerable promise.

Keywords: Expected value; sensors; lost target; coordinated search; search algorithm; lost ship

1  Introduction

Search theory rests on the oldest area of operations research. The initial steps made by Koopman in the Anti-submarine Warfare Operations Research Group of the U.S. Navy during World War II for submarine detection are still widely used for this purpose. The theory has also been used by the Navy to search for objects such as the H-bomb lost in the ocean near Palomares, Spain, in 1966, the submarine Scorpion lost in 1968, and numerous lesser-known objects. The U.S. Coast Guard uses the search theory to plan some of its more complicated search and rescue efforts.

To mention some important models of search plans, we should begin with the linear search strategy, which has many life and mission applications, such as searching for a damaged unit in a large linear system (electrical power lines, telephone lines, and gas support lines), whether a linear system is independent or intersecting (see El-Rayes et al. [1], Mohamed [2], Mohamed et al. [3–5], Balkhi [6]). The coordinated search technique has been studied in the case of a linear search. Mohamed et al. [7–9] discussed the coordinated search technique for a target on two intersecting lines, where the target has a symmetric and asymmetric distribution (See Mohamed et al. [10], Afifi et al. [11]). More advanced work applied the coordinated search technique to a moving target on one line as well as on many independent lines. The coordinated search technique in the plane was discussed by Mohamed et al. [12]. El-Hadidy et al. [13,14] proposed a model in 3-D space to find a randomly located target by one or two searchers. Caraballo et al. [15] considered a model in search theory to find a randomly located target in 3-D space. Kassem et al. [16] studied a more sophisticated search model in 3-D space to find a randomly located target. More recently, Teamah et al. [17] obtained an optimal discrete search for randomly moving COVID-19 between several cells in the human body using a monitoring system. Afifi et al. [18] studied the existence of the multi-generalized linear search problem to detect a randomly located target in one of several real lines.

We present a coordinated algorithm, with the important advantage that it avoids wasting time searching for the target. The mission is carried out by two searchers starting from the origin of a known circular area on the sea surface. The first searcher looks for the target on the right side of the circular area, and the second one looks for it on the left side. It is important to note that neither searcher returns to the origin. We use modern means of communication and sign language to save much effort and time.

2  Problem Formulations

On May 19, 2020, maritime authorities announced that they had lost contact with a small ship on its way to the Socotra Archipelago port in the Indian Ocean, carrying two families in addition to the ship’s crew. They suddenly received a call from the missing ship, which enabled them to determine its coordinates. Navy ships were then sent out to search for the missing ship. We present a coordinated algorithm to solve this kind of problem, with the advantage of a detection time saving element, as the probability distribution function of the ship’s location is known to the searchers (sensors).

2.1 Search Framework

Search space: Circular two-dimensional area.

Target: The target is a lost ship randomly located on the sea surface.

Means of search: The search is performed by two searchers on a circular section. They start looking together from the point (0,0) (the center of the circular area), where the region is divided into right and left parts. We also divide the area into concentric circles, as in Fig. 1.

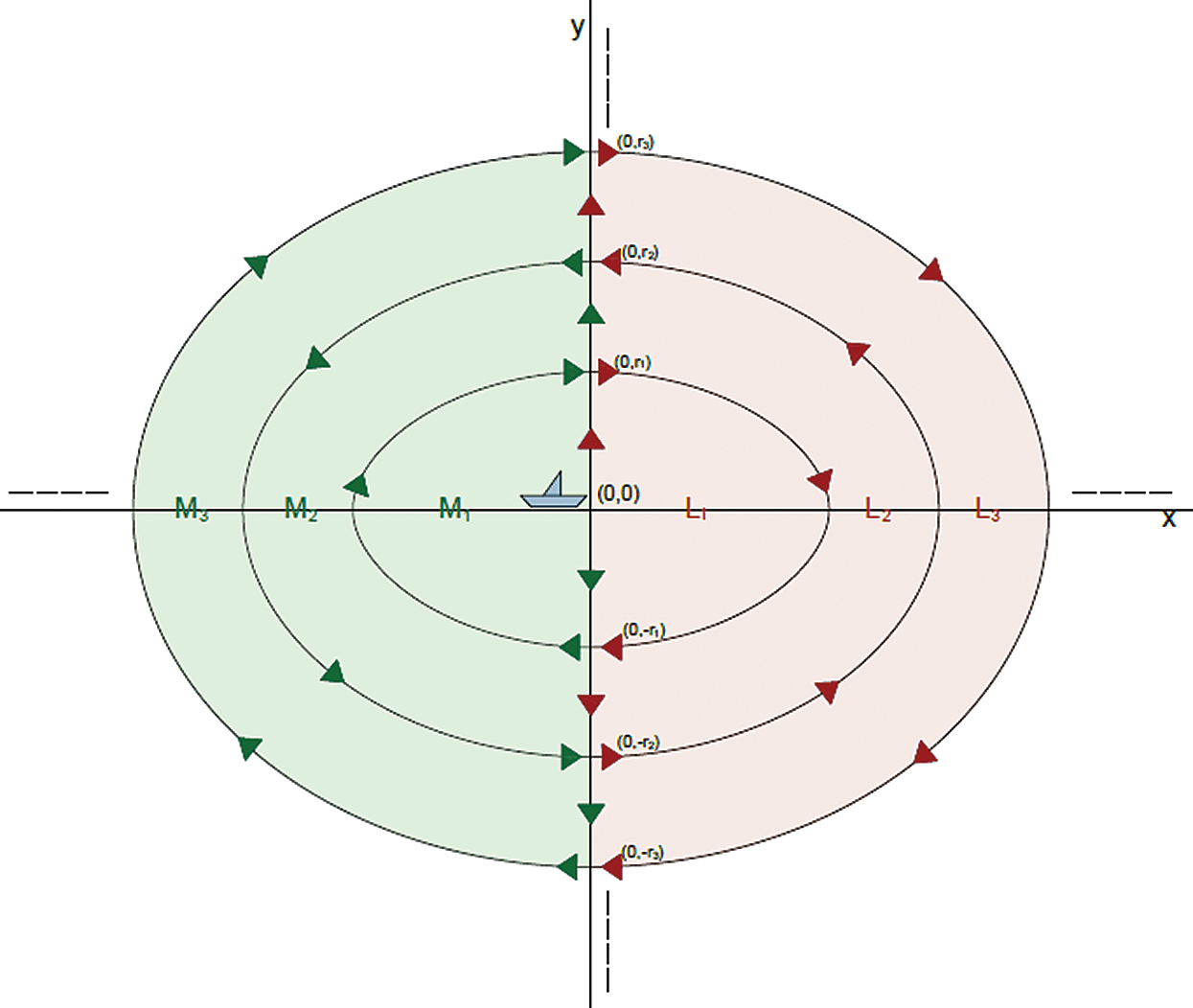
Figure 1: The search path

2.2 The Searching Technique

In this model, the search for the missing ship is carried out according to coordinated movement between the two searchers. After each move, both send signals to a marine ship’s signal reception center by radio telex. There are two types of detection:

1. Perfect detection: One of the searchers detects the lost ship in the specified search section and sends a positive sign.

2. False detection: Neither searcher detects the lost ship in the specified search section, and one or both sends a positive sign.

Let (X, Y) be independent random variables representing the position of the target, with cumulative distribution function (CDF) F(x,y) and probability density function (PDF) f(x,y) .

Searchers s1 and s2 start searching together for the lost ship (target) from the origin (0, 0) with equal speeds ν1=ν2=1 , and they search with a regular speed on the sectors and their tracks. Searcher s1 searches on the right side, and searcher s2 on the left side. Searcher s1 goes through a +ve part y-axis with a distance r1 (radius of the first circle) and starts searching sector L1. After searching sector L1, the searcher reaches the y-axis again but does not return to the origin point and moves toward sector L2 with distance r2−r1 . When it completes the search of sector L2 and does not find the target, it continues searching sector L3, and so on. Simultaneously, searcher s2 searches the opposite area on the left hand-side, goes through a –ve part y-axis with distance r1 , and starts searching sector M1. After searching this sector and not finding the target, it moves to sector M2 with distance r2−r1 . When it completes searching sector M2 and does not find the target, it continues searching sector M3 , and so on. Searchers s1 and s2 search sectors L1 and M1 at the same time. If one of them detects the lost target, it will send a positive sign and the search will end. If both send negative signs, then the two searchers complete their search and move to the next sectors, L2 and M2 , and so on, until one of the searchers detects the lost ship. The searchers do not return to the origin so as to save search time and reduce the expected time to detect the target.

Any track has width ri−ri−1 . The searcher moves on the y-axis +ve and –ve sides until it detects the target. We aim to calculate the expected length of time to detect the target and search the optimal search plan.

Searchers s1 and s2 follow a coordinated search path to find the target. Let Ei and Fi be the search paths of s1 and s2, respectively, i = 1, 2,…, n , and let Li and Mi be their respective search sectors. Let t1 and t2 be the respective times taken by s1 and t2 to search each sector in paths Ei and Fi, respectively.

The search proceeds as follows.

Step 1: The two searchers move from (0,0) to detect the target. Searcher s1 follows search path e1 as follows: Searcher s1 goes to (0, r1) with distance |r1| through a +ve part in y-axis. If the target is not found, it completely searches sector L1 and continues tracking until the point (0, −r1 ). At the same time, searcher s2 goes to (0, −r1) with distance |r1| through a -ve part in x-axis. If the target is not found, it completely searches sector M1 and continues tracking until the point (0, r1 ). At this time, the two searchers send signals to a marine ship’s signal reception center. If one of them sends a positive signal, then the search ends; however, if the two searchers send a negative signal, the searchers will move on to the following step.

Step 2: Searcher s1 completes the search for the lost target and moves to the point (0, r2) with a distance |r2−r1| . The first searcher follows the search path e2 as follows: searcher s1 goes to (0,r2) with distance |r2−r1| through a +ve part on the y-axis. If the target is not found, it completely searches sector L2 and keeps tracking until the point (0,−r2) . At the same time, searcher s2 goes to (0,−r2) with distance |r2−r1| through a -ve part on the x-axis. If the target is not found, it completely searches sector M2 and keeps tracking until the point (0,r2) . At this time, the two searchers send signals to a marine ship’s signal reception center. If one of them sends a positive signal, then the search ends; however, if the two searchers send a negative signal, the searchers will move on to the following step.

Step 3: Searcher s1 completes the search for the lost target and moves to the point (0,r3) with a distance |r3−r2| . The first searcher follows the search path e3 as follows: searcher s1 goes to (0,r3) with distance |r3−r2| through a +ve part on the y-axis. If the target is not found, it completely searches sector L2 and keeps tracking until the point (0,−r2) . At the same time, searcher s2 goes to (0,−r3) with distance |r3−r2| through the -ve part on the x-axis. If the target is not found, it completely searches sector M3 and keeps tracking until the point (0,r3) . At this time, the two searchers send signals to a marine ship’s signal reception center. If one of them sends a positive signal, then the search ends; however, if the two searchers send a negative signal, the searchers will move on to the next sectors, and so on, until one of the two searchers detects the lost ship.

The searchers s1 and s2 follow the search path. Let Ei be the path for the first searcher, where i ≥ 0, t1 is the time for the first searcher, Li is the sector which s1 searches, i = 1, 2, …. , n, and Fi the path of the second searcher, where i ≥ 0, Mi is the sector which s2 searches, i = 1,2,…..n, and the two searchers move from (0,0) to detect the target. The first search path e1 of s1 is as follows: searcher s1 goes to (0, r1) with distance |r1| through a +ve part on the y-axis. If the target is not found, it completely searches sector L1 and keeps tracking until the point (0, −r1 ). The time taken in this step is t1=|r1|+πw1 , and the searcher moves to the point (0, r2) with distance |r2−r1| . It takes time t1=|r2−r1|+πw2 if it does not find the target and moves on to sector L2 while continuing to track. If the target is not found, it moves toward (0,r3) to search sector L3 and keeps tracking until the point (0, −r3 ) with distance |r3−r2| ; it takes time t1=|r3−r2|+πw3 , and so on. The number of circles is i = 1, 2, …. These circles are divided into two equal two sectors, Li and Mi.

Searcher s2 goes to (0, −r1) with distance |r1| through a -ve part on the x-axis. If the target is not found, it completely searches sector M1 and continues tracking until the point (0, r1 ) with time t2=|r1|+πw1 , then moves to the point (0, r2) with distance |r2−r1| and takes time t2=|r2−r1|+πw2 . If the target is not found, it searches sector M2 until the point (0, r2 ). If the target is not found, it moves toward (0,–r3), searches sector M3, and keeps tracking until the point (0, r3 ) with distance |r3−r2| , and so on.

3  Expected Time to Detect Target

Theorem 1: The expected value of the time to detect the target is

E(tϕ)=2[[(|r1|+πw1)∫0π2∫0r1g1(r,θ)rdrdθ]+[(|r2−r1|+πw2)∫0π2∫r1r2g2(r,θ)rdrdθ]+[(|r3−r2|+πw3)∫0π2∫r2r3g3(r,θ)rdrdθ]+⋯⋯+[(|rn−rn−1|+πwn)∫0π2∫rn−1rngn(r,θ)rdrdθ]=2[[(|ri−ri−1|+πwi)∫0π2∫ri−1rigi(r,θ)rdrdθ]] (1)

where i = 1, 2, 3, …, n, r0 = 0.

Proof:

1) For s1:

If the target is in sector L1, then t1=|r1|+πw1 .

If the target is in sector L2, then t1=|r2−r1|+πw2 .

If the target is in sector L3, then t1=|r3−r2|+πw3 , and so on.

2) For s2:

If the target is in sector M1, then t2=|r1|+πw1 .

If the target is in sector M2, then t2=|r2−r1|+πw2 .

If the target is in sector M3, then t2=|r3−r2|+πw3 , and so on.

Then

E(tϕ)=[(|r1|+πw1)∫0π2∫0r1g1(r,θ)rdrdθ]+[(|r2−r1|+πw2)∫0π2∫r1r2g2(r,θ)rdrdθ]+⋯[(|r3−r2|+πw3)∫0π2∫r2r3g3(r,θ)rdrdθ]+⋯⋯+[(|rn−rn−1|+πwn)∫0π2∫rn−1rngn(r,θ)rdrdθ]+[(|r1|+πw1)∫0π2∫0r1g1(r,θ)rdrdθ]+[(|r2−r1|+πw2)∫0π2∫r1r2g2(r,θ)rdrdθ]+[(|r3−r2|+πw3)∫0π2∫r2r3g3(r,θ)rdrdθ]+⋯⋯+[(|rn−rn−1|+πwn)∫0π2∫rn−1rngn(r,θ)rdrdθ]=2[[(|ri−ri−1|+πwi)∫0π2∫ri−1rigi(r,θ)rdrdθ]] .

4  Algorithm and Flowchart

The calculation of the expected value of the time to detect the lost target is described in the following algorithm and flowchart.

5  Application

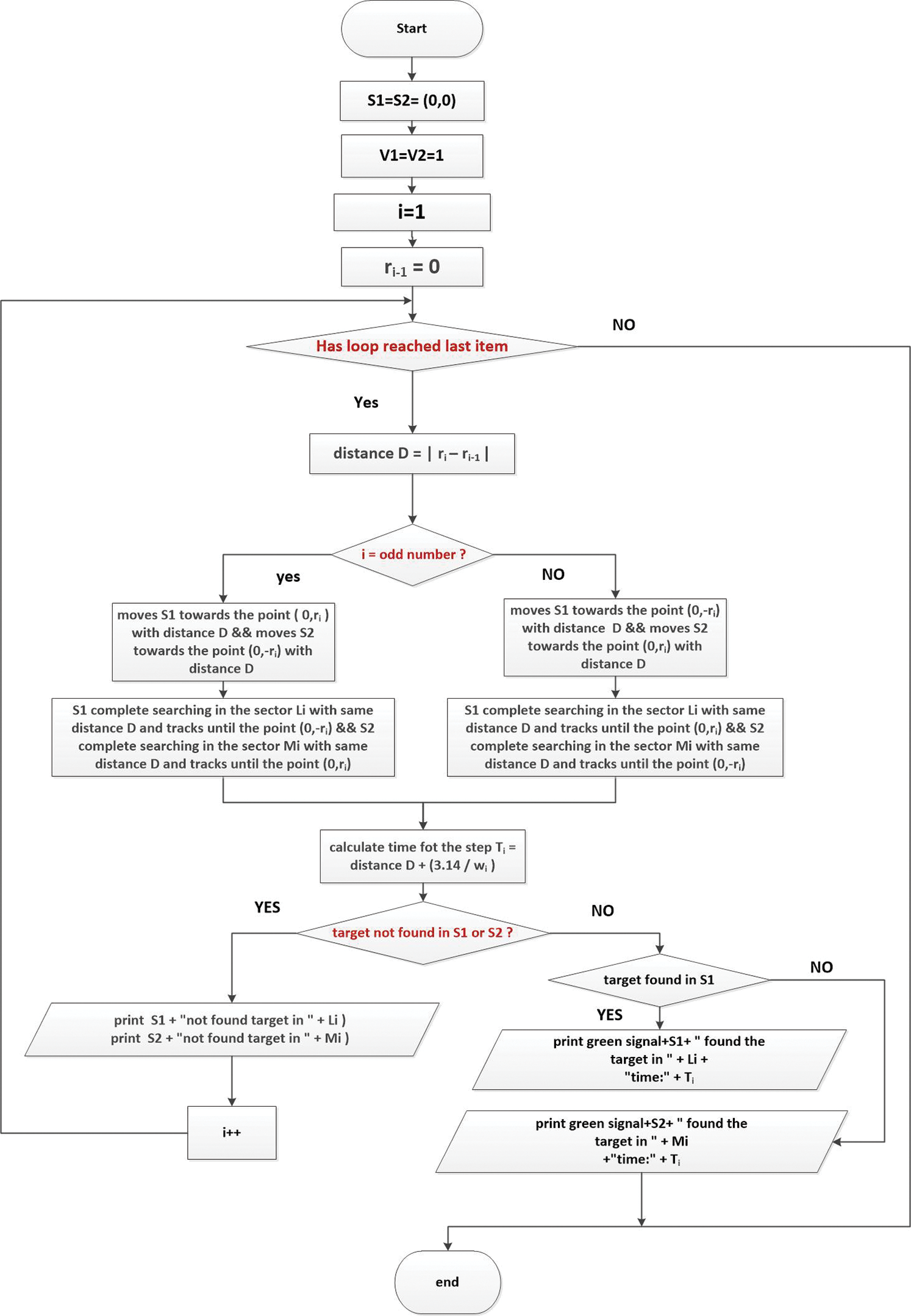
Searchers s1 and s2 have a mission to search for a lost ship on the sea surface. The ship’s location follows a standard bivariate normal distribution for two independent random variables x,y , f(x,y)=12πe−x2+y22 . Changing to polar coordinates x=rcos⁡θ , y=rsin⁡θ , the Jacobian matrix is defined as

So, g(r,θ)=12πe−r22 , and by substituting in Eq. (1), the expected value of the time to detect the target will be

The first search if r: 0 → r1 ; then E(tϕ)=π2[e−r122(πer122erfr12−2r1)2]

The Second search if r: r1 → r2 ; then the expected value will be

E(tϕ)=122[|ri−ri−1|+πwi][−rie−ri22+ri−1e−ri−122+π2(erfri2−erfri−12]. (2)

Special cases:

If r1−r0=r→(3) , where r0 =0, then r2−r1=r→(4) , and r2=2r . Also, r3−r2=r⇒r3=3r .

Hence,

E(tϕ)=122[r+πwi][−rie−ri22+(ri−r)e−(ri−r)22+π2(erfri2−erf(ri−r)2)],E(tϕ)=122[r+πwi][−ire−(ir)22+r(i−1)e−(r(i−r))22+π2(erfir2−erfr(i−1)2)]. (5)

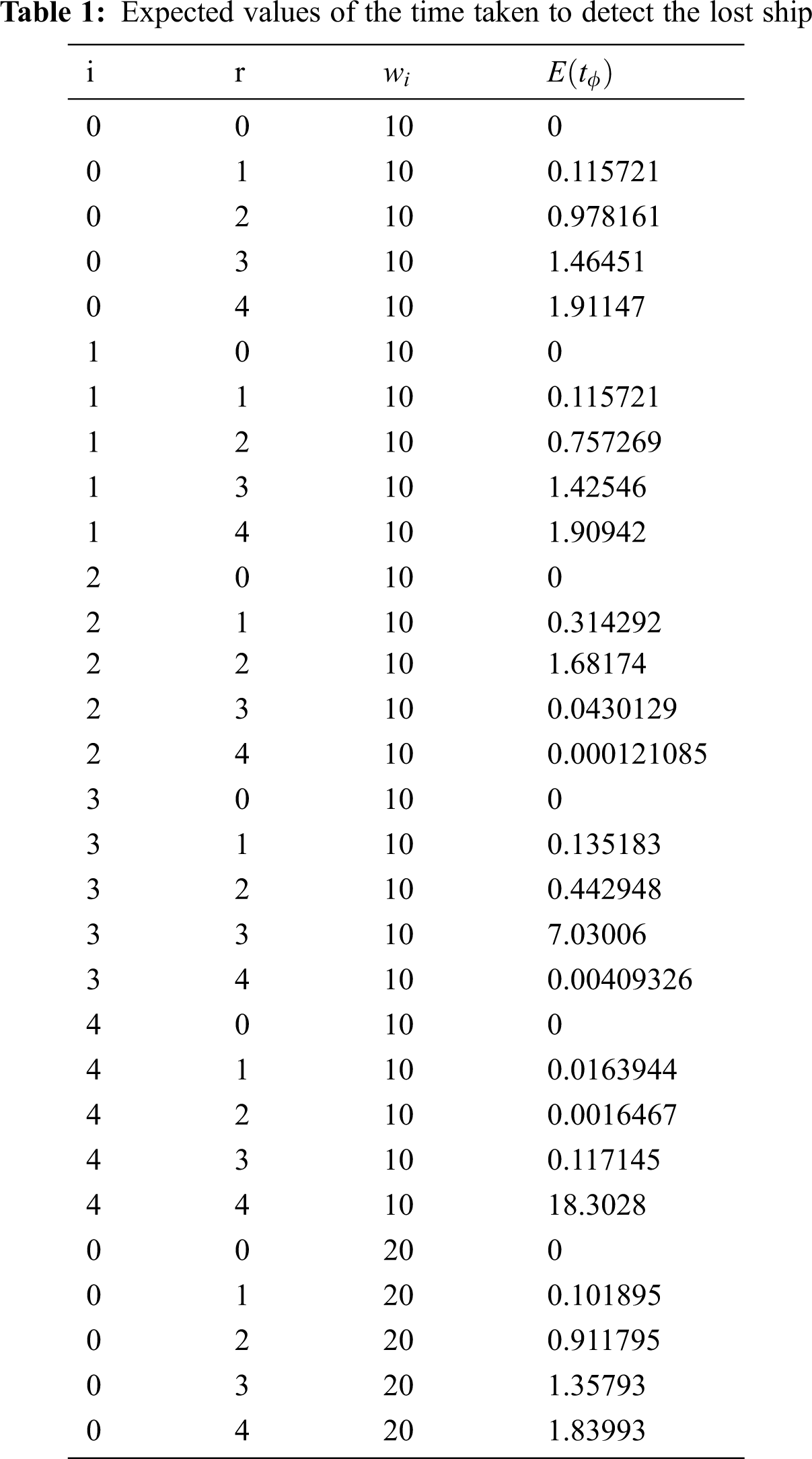
By considering the values of i, r, and wi in Tab. 1 using the Mathematica program, and substituting in Eq. (5), we can obtain the different values of E(tϕ) .

Acknowledgement: We thank the reviewers for careful checking and LetPub (https://www.letpub.com) for its linguistic assistance during the preparation of this manuscript.

Funding Statement: This research was funded by the Deanship of Scientific Research at Princess Nourah bint Abdulrhman University Fast-track Research Funding Program.

Conflict of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  A. B. El-Rayes, A. A. Mohamed and H. Fergani, “On the generalized linear search problem,” Delta Journal, vol. 6, no. 2, pp. 1–10, 1993. [Google Scholar]

 2.  A. A. Mohamed, “The generalized search for one-dimensional random walker,” International Journal of Pure and Applied Mathematics, vol. 19, no. 3, pp. 375–387, 2005. [Google Scholar]

 3.  A. A. Mohamed and M. Abou Gabal, “Generalized optimal search paths for a randomly located target,” in Annual Conf., Cairo, Egypt, pp. 17–29, 2000. [Google Scholar]

 4.  A. A. Mohamed and H. M. Abou Gabal, “Linear search with multiple searchers for a randomly moving target,” in Int. Conf. for Statistics, Computer Science and Its Application, Egypt, pp. 115–124, 2003. [Google Scholar]

 5.  A. A. Mohamed and H. M. Abou Gabal, “Multiplicative linear search problem,” Egyptian Statistical Journal, Cairo University, vol. 48, no. 1, pp. 34–45, 2004. [Google Scholar]

 6.  Z. T. Balkhi, “The generalized optimal search paths for the continuous univariate random variable,” Journal of the Operations Research, vol. 23, no. 1, pp. 67–96, 1989. [Google Scholar]

 7.  A. A. Mohamed, H. M. Abou Gabal and W. A. Afifi, “On the coordinated search problem,” International Journal of Applied Mathematics, vol. 25, no. 5, pp. 627–636, 2007. [Google Scholar]

 8.  A. A. Mohamed, H. M. Abou Gabal and W. A. Afifi, “Coordinated search for a randomly located target,” International Journal of Contemporary Mathematical Sciences, vol. 8, pp. 5–8, 2013. [Google Scholar]

 9.  A. A. Mohamed, H. M. Abou Gabal and W. A. Afifi, “Generalized coordinated search for a randomly located target,” Delta Journal Sciences, vol. 38, pp. 33–42, 2017. [Google Scholar]

10. A. Mohamed and W. A. Afifi, “Quasi-coordinate search for a randomly moving target,” Journal of Mathematics and Physics, vol. 7, no. 8, pp. 1814–1825, 2019. [Google Scholar]

11. W. A. Afifi, A. H. EL-Bagoury and S. N. AL-Aziz, “A novel search algorithm for a multi searchers random walk,” Journal of the Applied Mathematics and Information Science, vol. 14, no. 1, pp. 115–122, 2020. [Google Scholar]

12. A. Mohamed, H. Fergany and M. El-Hadidy, “On the coordinated search problem on the plane,” Journal of the School of Business Administration Istanbul University, vol. 41, no. 1, pp. 80–102, 2012. [Google Scholar]

13. M. El-Hadidy and A. H. EL-Bagoury, “Optimal search strategy for a three dimensional randomly located target,” International Journal of Operational Research, vol. 29, no. 1, pp. 115–126, 2017. [Google Scholar]

14. M. El-Hadidy, A. Teamah and A. H. El-Bagoury, “3-Dimensional coordinated search technique for a randomly located target,” International Journal of Computing Science and Mathematics, vol. 9, no. 3, pp. 258–272, 2018. [Google Scholar]

15. T. Caraballo, A. A. Teamah and H. EL-Bagoury, “Minimizing the expected time to detect a randomly located lost target using 3-dimensional search technique,” Communications in Statistics-Theory and Methods, vol. 49, no. 13, pp. 3313–3328, 2020. [Google Scholar]

16. M. A. Kassem, A. H. EL-Bagoury, W. A. Afifi and S. N. AL-Aziz, “On minimum expected search time algorithm for 3-dimensional randomly located target,” Journal of Statistics Applications & Probability, vol. 10, no. 1, pp. 159–166, 2021. [Google Scholar]

17. A. A. M. Teamah, W. A. Afifi, J. Gani Dar, A. H. EL-Bagoury and S. N. AL-Aziz, “Optimal discrete search for a randomly moving covid19,” Journal of Statistics Applications & Probability, vol. 9, no. 3, pp. 473–481, 2020. [Google Scholar]

18. W. A. Afifi and A. H. EL-Bagoury, “Optimal multiplicative generalized linear search plan for a discrete randomly located target,” Information Sciences Letters, vol. 10, no. 1, pp. 153–158, 2021. [Google Scholar]

This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.