DOI:10.32604/csse.2022.016992

| Computer Systems Science & Engineering DOI:10.32604/csse.2022.016992 |  |
| Article |
Scheduling Flexible Flow Shop in Labeling Companies to Minimize the Makespan
1Department of Industrial Engineering and Management, National Kaohsiung University of Science and Technology, Kaohsiung, 80778, Taiwan
2Department of Supply Chain Management, National Kaohsiung University of Science and Technology, Kaohsiung, 80778, Taiwan
3Department of Marketing and Distribution Management, National Kaohsiung University of Science and Technology, Kaohsiung, 80778, Taiwan
4Faculty of Industrial Engineering and Management, International University, Ho Chi Minh City, 70000, Vietnam
5Faculty of Commerce, Van Lang University, Ho Chi Minh City, 723000, Vietnam
*Corresponding Author: Hsin-Pin Fu. Email: hpfu@nkust.edu.tw
Received: 17 January 2021; Accepted: 14 March 2021
Abstract: In the competitive global marketplace, production scheduling plays a vital role in planning in manufacturing. Scheduling deals directly with the time to output products quickly and with a low production cost. This research examines case study of a Radio-Frequency Identification labeling department at Avery Dennison. The main objective of the company is to have a method that allows for the sequencing and scheduling of a set of jobs so it can be completed on or before the customer’s due date to minimize the number of late orders. This study analyzes the flexible flow shop scheduling problem with a sequence dependent setup by modifying the processing time and setup time to minimize the makespan on multiple machines. Based on the defined mathematical model, this study includes an alternative approach and application of heuristic algorithm with the input being big data. Both optimization programs are used in this study and compared to determine which method can better solve the company’s problems. The proposed algorithm is able to improve machine utilization with large-scale problems.
Keywords: Scheduling; flexible flow shop; sequence dependent setup; just-in-time
Planning and scheduling play a vital role in the supply chain in the manufacturing and service industry. It encompasses allocated, limited resources, as well as the activities that must be accomplished [1–5]. A plan defines what must be done; a schedule specifies both how and when it will be done. The schedule refers to the estimates of the time and resources for each activity, including a set of objectives used to measure the performance of the schedule. The optimal allocation will optimize the objectives of the enterprise, reducing time and costs. Thus, efficient scheduling is critical for the industries to survive in the competitive business market.
There are two types of scheduling environment, flow shop and job shop scheduling. Job shop scheduling means jobs are assigned to resources with a specific time. The flow shop scheduling problem is one of the most popular scheduling environments. The classical flow shop scheduling problem (FSP) involves a set of “n” jobs that need to be processed in a set of “m” machines in series. However, real production systems are rarely applied to a single machine at each stage. Therefore, in many situations, instead of having a series of machines, production has a series of stages of parallel machines to increase capacity and reduce the impact of bottleneck which is called flexible flow shop (FFS) scheduling. In Fig. 1, there are “q” stations, and each station consists of “t” parallel machines and “i” jobs are processed in the series of “q” stations.
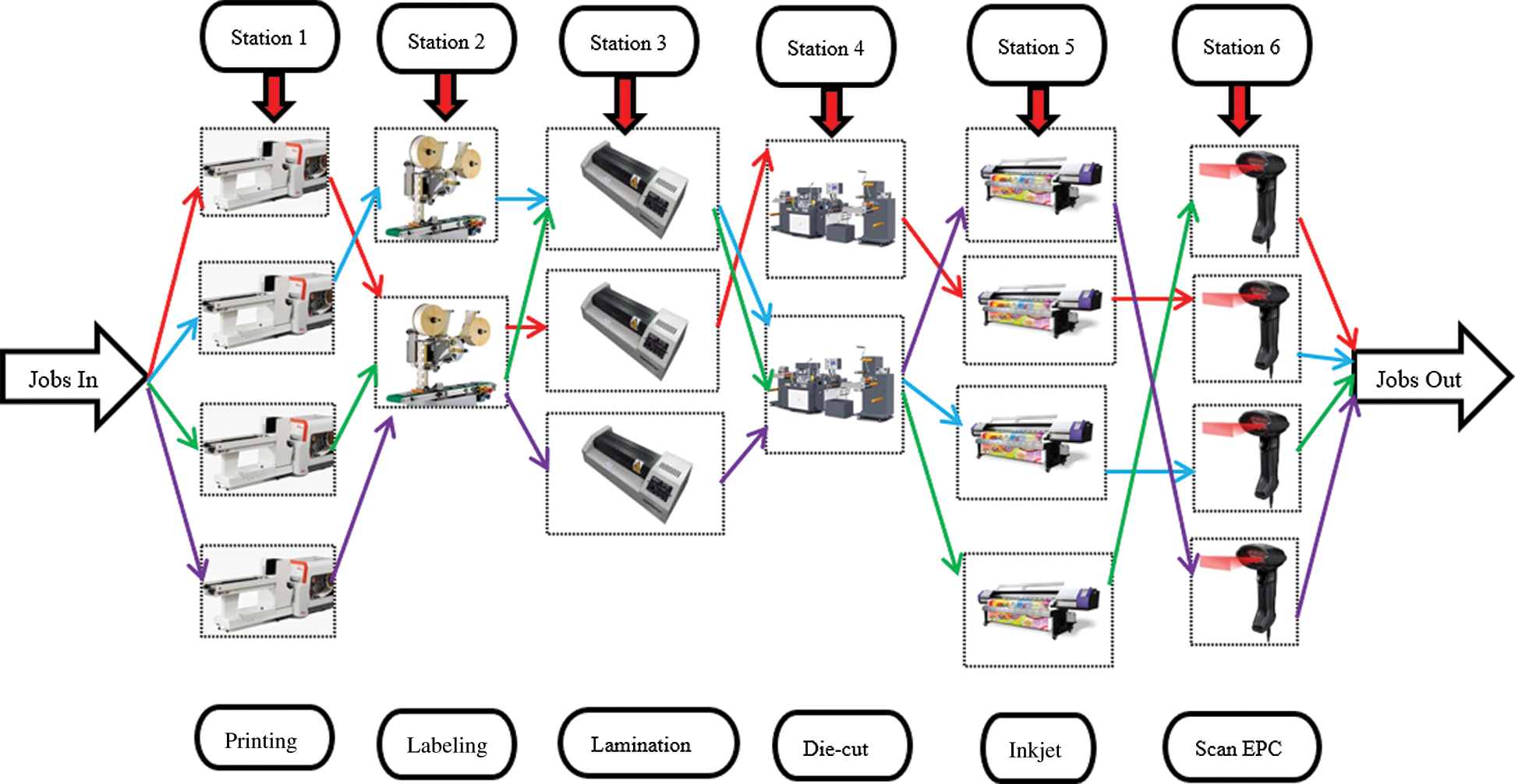
Figure 1: An example of flexible flow shop involves parallel machines
The job shop is a manufacturer’s operation that specializes in low-to medium-volume production and utilizes job or batch processes. By contrast, the flow shop specializes in medium-to high-volume production and utilities line or continuous flow processes. This environment is more suitable and prevalent in Vietnam, particularly in clothing and labeling production. The characteristic of these industries is that product diversity is low, but the volume is high. This research focuses on the scheduling problem for FFS setups.
In manufacturing, production scheduling must be done every day to satisfy the customer’s order. Even though other production parameters, such as operators, maintenance, and inventory, are under control, the manufacturing company may lose its ability to satisfy the planned production volume. If a production line has no optimal production sequence, the completion time of the jobs will be long and variable. This situation can seriously affect the service level with customers. The company should have production back-up plans to overcome unexpected problems in the production environment, such as machine breakdowns. Therefore, optimal production sequences are essential to the success of any manufacturing company. In many industries, such as pharmaceutics, automobile, and printing manufacturing, there are setup times on the equipment between two different jobs. Usually, it is assumed that the setup time is a part of the job processing time. However, in many cases, the production process can consist of several jobs and each job must follow a specific sequence of steps. Each step is processed on a workstation, which includes several different machines, and changing one job to another on a machine can incur considerable setup time. The current problem is how to control setup times effectively that they do not impact the whole process. Furthermore, the complexity of the problem increases when the manufacturing process involves parallel machines in each station (Fig. 1).
This study aims to develop a mathematical model to solve the scheduling problem of the FFS shop manufacturing system with a sequence-dependent setup time and develop a new approach for large size problems using the heuristic algorithm. A comparison of the two approaches is made using a case study to find the optimal solution, as well as the proper use cases of each method. The result of this research can be expanded and applied for similar scheduling problems in FFS manufacturing systems.
2.1 Flexible Flow Shop Scheduling
Cortes et al. [6] proposed multiobjective flow shop scheduling with parallel machines to satisfy industrial scheduling needs. This method basically involves a wide range of objectives and constraints. A multiobjective method was considered on both objective functions: minimizing the manufacturing lead time and resources. The augmented ε-constraint method was selected which was important to prioritize objective functions. The model uses the value of the highest-priority function as a constraint when executing the second-priority objective function. Tran et al. [7] suggested the multiobjective FFS scheduling problem with limited intermediate buffers to minimize the completion time of jobs and the total tardiness time of jobs. They proposed a hybrid water flow algorithm for solving this problem. The Wittrock benchmark was used to test the proposed algorithm, as well as randomly generated instances. Wang et al. [8] considered a two-stage no-wait hybrid flow shop scheduling problem with sequence-dependent setup times at the first stage to minimize the makespan. A branch-and-bound algorithm, a tabu search method and three heuristic methods were proposed to solve the problem.
2.2 Sequence-dependent Setup Times
Setup time can be defined as the time to prepare the necessary resources to perform a task. In a production system, reducing the setup time in flexible machines is an important task for better shop performance. The reduction of setup times cannot be effectively improved without the standardization of the set-up procedures. Allahverdi et al. [9] noted two types of setup times: sequence-dependent and sequence-independent. It is called sequence-independent if the set-up time depends solely on the task to be processed, regardless of its preceding task. In the sequence-dependent type, the set-up time depends on both the task and its preceding task. Sequence-dependent set-up times can be found in various forms of production, where the facility has multipurpose machines. For example, in the printing industry, the set-up time is required to prepare the cleaning machine and setting of the press for processing the next job depending on the color ink, size of paper and type used in the previous job.
Kim et al. [10] investigated the job shop scheduling problems that are complicated by sequence-dependent setup times. They classified and tested scheduling rules by considering whether the setup time and/or due date information is employed. These scheduling rules were evaluated in dynamic scheduling environments defined by due date tightness, setup times, and cost structure. Instead of reducing the flow time alone, this study showed that due date information should be included in the sequencing decision to improve the due date performance. Later, Sun et al. [11] proposed the NP-hard problem of scheduling N independent jobs on a single machine with release dates, due dates, sequence dependent setup times, and no preemption to minimize the weighted sum of squared tardiness. They formulated the sequence-dependent setup times as capacity constraints, which are then relaxed using Lagrangian multipliers. Jiang et al. [12] addressed the energy-efficient permutation flow shop scheduling problem with the sequence-dependent setup time to minimize both the makespan and energy consumption as the green scheduling objective.
2.3 Application of Linear Programming in Manufacturing Scheduling
Linear programming is a mathematical method that is used to determine the best possible outcome or solution from a given set of parameters or list of requirements, which are represented in the form of linear relationships. Other papers have established the mathematical model to cope with the production scheduling problems. Entrup et al. [13] developed mixed-integer linear programming (MILP) models that integrate shelf-life in planning and scheduling in yogurt production. A block planning approach was chosen to guarantee the compactness and computability of the models. Three different MILP models for weekly production planning were presented. First, the model with day bounds (MDB) allows every product to be produced on every production day. Second, to allow overnight production, the MDB was extended to the “model with set-up conservation (MSC)”. Finally, the position-based model (PBM) was developed for increased flexibility, desired for production systems covering a high variety of products. Varmazyar et al. [14] developed a mixed-integer linear programming model with sequence-dependent setup times and minimized the number of tardy jobs. Meng et al. [15] developed more MILP models for hybrid flow shop scheduling problem with unrelated parallel machines to minimize the makespan. Eight MILP models were formulated and compared to obtain the optimal solutions based on different modeling ideas. Zhu et al. [16] presented a mixed integer programming formulation for minimizing total earliness/tardiness in a multimachine scheduling problem. This research allowed setup times to depend on the job-to-job sequence and processing time to depend on the job-machine combination. Although the model could easily provide optimal scheduling, it only involved nine jobs and three or fewer machines. Therefore, it is necessary to develop more efficient computer codes in the future so that the model can solve problems on an industrial scale.
2.4 Application of Heuristic Methods in Manufacturing Scheduling
Heuristic methods do not necessarily need to be perfect. With large problems, they can speed up the process of reaching a satisfactory solution. Heuristics is a flexible technique for making quick decisions, particularly when working with complex data. As a trade-off, heuristics is incapable of finding the optimal or best solution.
In the literature, some studies addressed flow shop scheduling using a heuristic algorithm to minimize the earliness and tardiness costs [17]. We proposed three heuristic algorithms for hybrid flowshop scheduling. The first one allocated different jobs to machines and then converted the hybrid flowshop to solve. The third algorithm, resources leveling was accomplished by comparing the utilized and remaining resources. Wang et al. [18] presented a new efficient hybrid algorithm THNP which integrated a local search method optimizing flowshop production with one-dimensional cutting stock in make-to-order environments. This research aimed to find an integrated schedule to minimize the makespan of the entire manufacturing process. Chen et al. [19] presented the genetic algorithm to design a wide ordering optimization genetic algorithm through coding and genetic operators. Schaller et al. [20] proposed a genetic algorithm for minimizing total earliness and tardiness in permutation for the flow shop without allowing unforced inserted idle time. Wen et al. [21] used the Tabu search method to solve a range of scheduling problems. They developed the algorithms using two heuristics rules to find the starting solutions and two kinds of neighborhood structure, including the pair exchange method and the adjacent exchange method. Bai et al. [22] proposed two new heuristics, the triangular shortest processing time (TSPT) and dynamic triangular shortest processing time (DTSPT), to solve the general m-machine problem to minimize the sum of the completion times. Javadian et al. [23] considered the FFS problem along with the sequence-dependent setup time and machine availability constraints to minimize the total completion time with the modified processing time. Six heuristic algorithms (SMPT, LMPT, Johnson, CDS, Palmer and MNEH) were presented. In addition, two meta-heuristic algorithms, the variable neighborhood search (VNS) algorithm and the genetic algorithm (GA) are applied to solve problems.
The research graph (Fig. 2) shows four necessary stages to carry out the research and show the contributions of this study, including the problems, proposed solutions and a comparison.
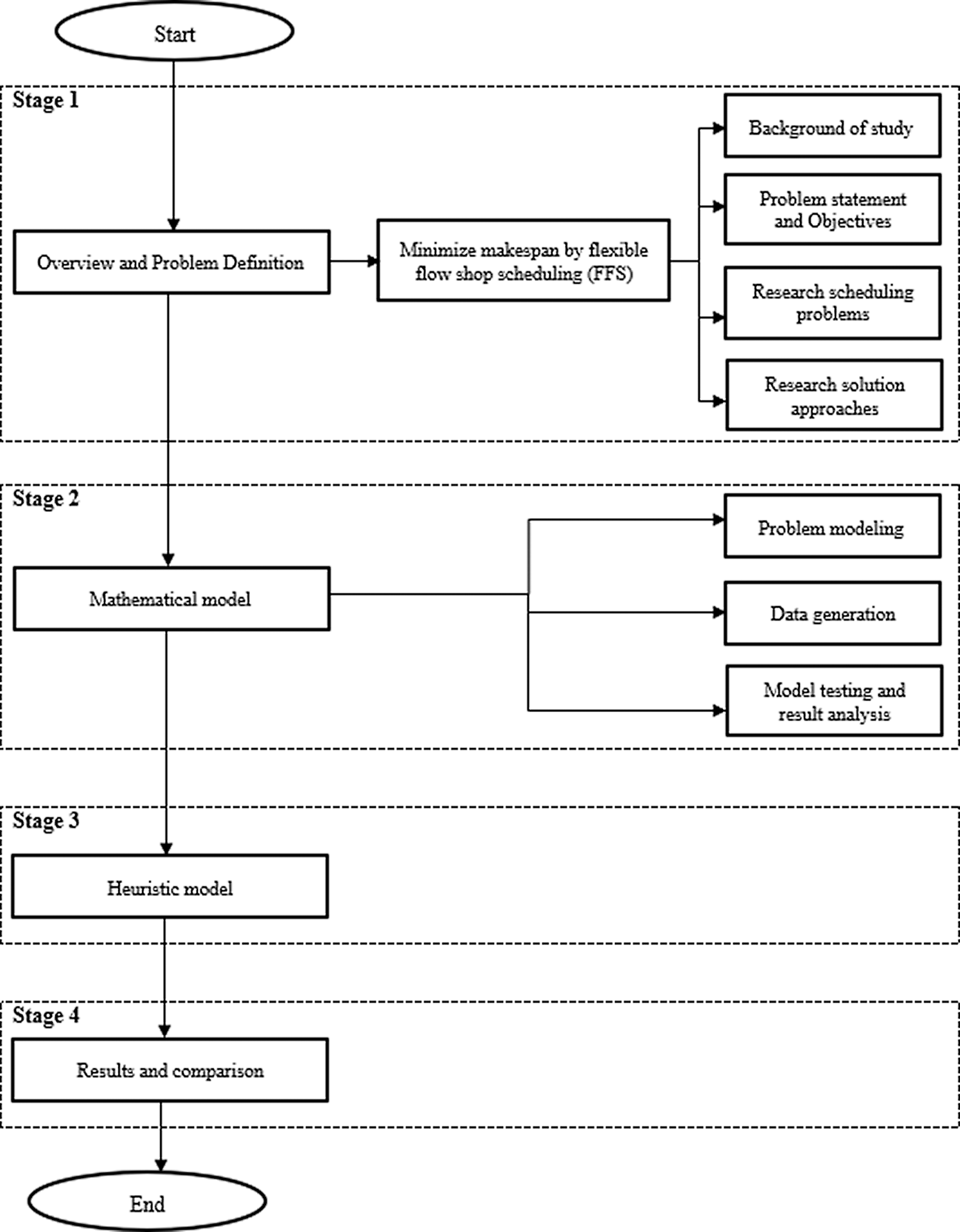
Figure 2: Research flowchart
Stage 1: Overview and Problem Definition
In this stage, the information of the manufacturing process is collected, and the scheduling problem of the process is identified. Then, potential solutions are considered based on the literature.
Stage 2: Mathematical Model
In this stage, a mathematical model of the scheduling problem is developed. CPLEX programming is used to code and run to get the optimal solution. Due to the data problem size, it is challenging to enumerate all of the data. Therefore, in this research, the tuple approach is applied to handle this. As the result is displayed, to check the accuracy and suitability of model, a Gantt chart is defined to check the sequence, setup time, and processing time. From this, we also know which job is late and the gap between each process.
Step 3: Heuristic Model
After testing the mathematical model at the previous stage, the result should satisfy all constraints that fit with the real case study. However, due to the size of data and computational time, the heuristic method should be clarified to give a better solution.
Step 4: Results and Comparison
This step is to show the result of heuristic method after running the model. Then, the results are analyzed, and the two proposed methods compared to recommend a suitable solution for the company.
In a standard mathematical model of FFS scheduling, three indices should be included such as jobs, stations, and machines. The input data to run this model are the setup time, processing time, and due date of jobs. The output of the model is covered by these decision variables, including enabling the job on the machine, the sequence of the job, beginning time, finishing time and total number of late orders.
The indexes notations are as follows:
The set notations are as follows:
The parameter notations are as follows:
The decision variable notations are as follows:
4.2 Flexible Flow Shop Model with Setup Time
The objective is to minimize the makespan to deliver goods to customers just-in-time in production systems.
The general form includes the following assumptions:
• Jobs are independent, and no priorities are assigned to any job type
• All jobs are available for processing at time zero
• Breakdowns are not considered
The formulas are as follows:
Minimize Cmax
Subject to:
With:
• The objective function minimizes the makespan
• Constraint (1) calculates the total late orders
• Constraint (2) defines the makespan which is the time to complete a job.
• Constraint (3) ensures that every job at one station is only assigned once
• Constraint (4) guarantees that the finishing time of job i must be greater than sum of the beginning time and processing time
• Constraint (5) clarifies that for each job, the job must satisfy the workstation sequence constraint. Particularly, the beginning of job k would be after the job before it is done.
• Constraints (6), (7), (8) describe that only one of two job i and j is assigned on machine m and processed before the other.
• Constraint (9) ensures that the beginning of job j would be after that of job i including the processing time and setup time for job i.
• Constraint (10), (11) identify the lateness of order. One order is late if finishing time of job i at station a is larger than its due date.
To validate the FFS model, we used a small sample dataset to test the accuracy of the model of a setup time constraints and processing time constraints. There are three objects that have been taken into consideration for execution, which are the jobs, machines, and stations in process to complete orders. The structure of the data is given in Tab. 1:
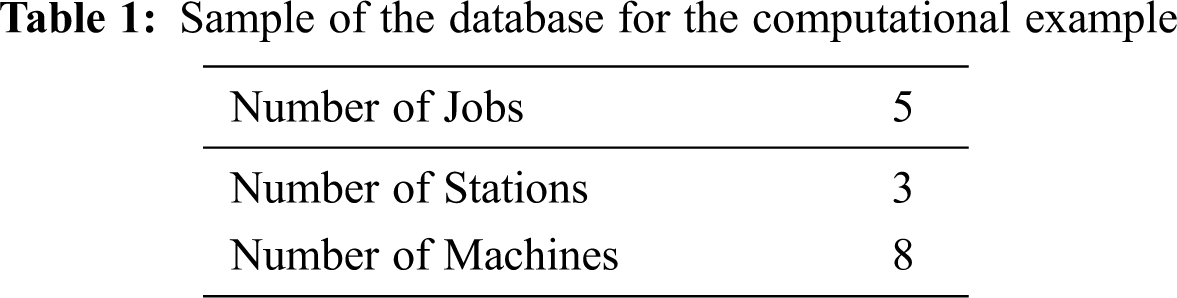
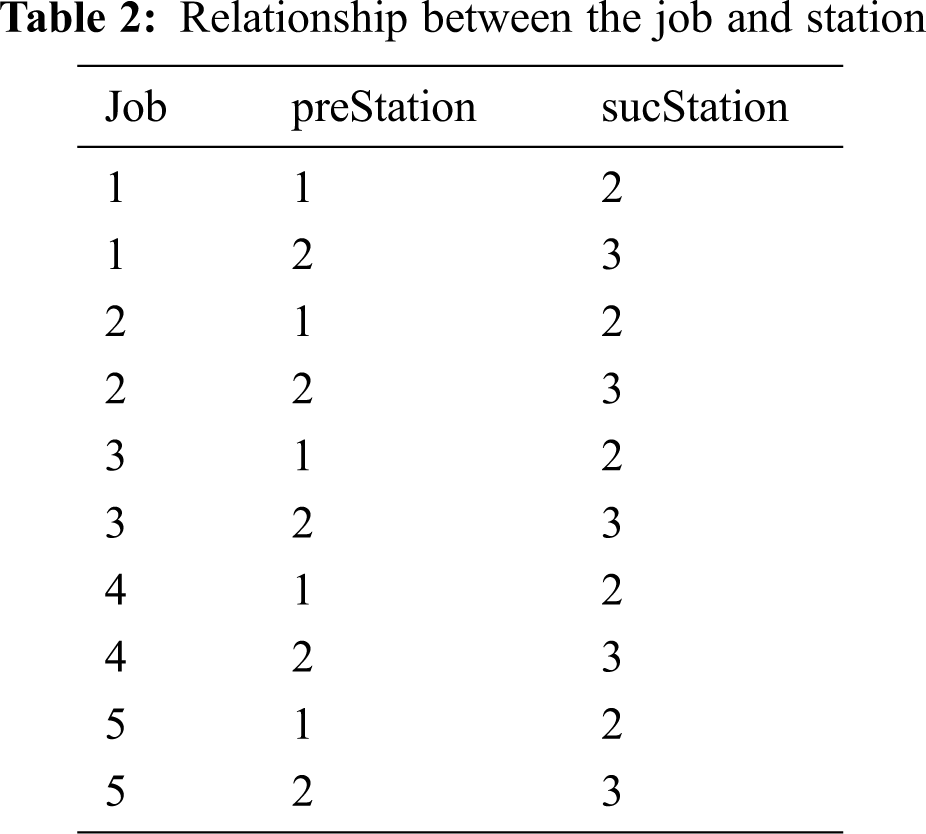
There are five jobs in the system; each job must be processed through all three stations and by sequence to finish task. To be more specific, the relationship of the job and station is defined in NodeSet. The sequence of the job through the station is in ArcSet. preStation is the previous station, sucStation is the next station that the job will be processed continuously. The sequence of each job must be gone through every station in the process. For instance, job 1 needs to arrive at station 1 before passing through station 2, and station 3. This rule is an important constraint in our mathematical model and the feasible solution must be satisfied with this constraint. Tab. 2 shows the relationship between the job and the station:
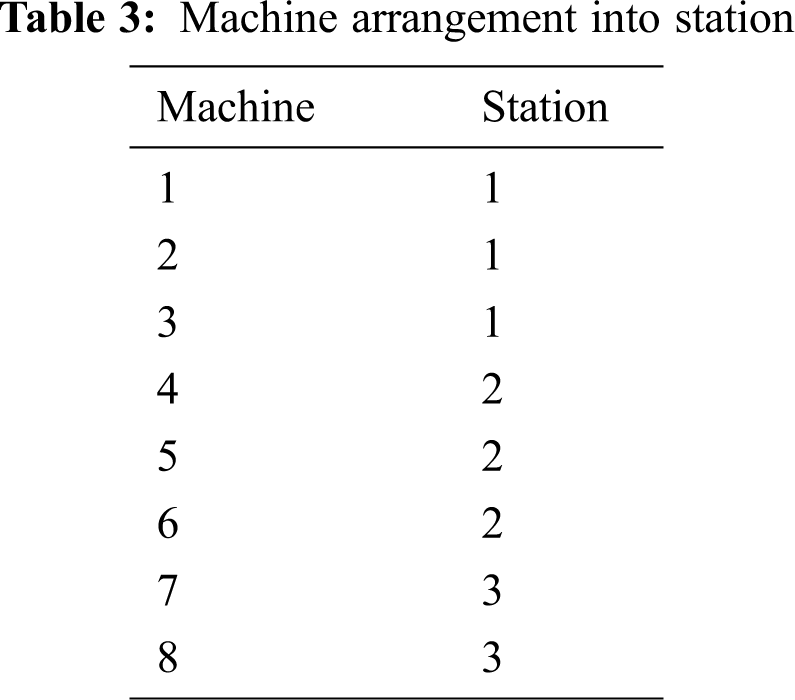
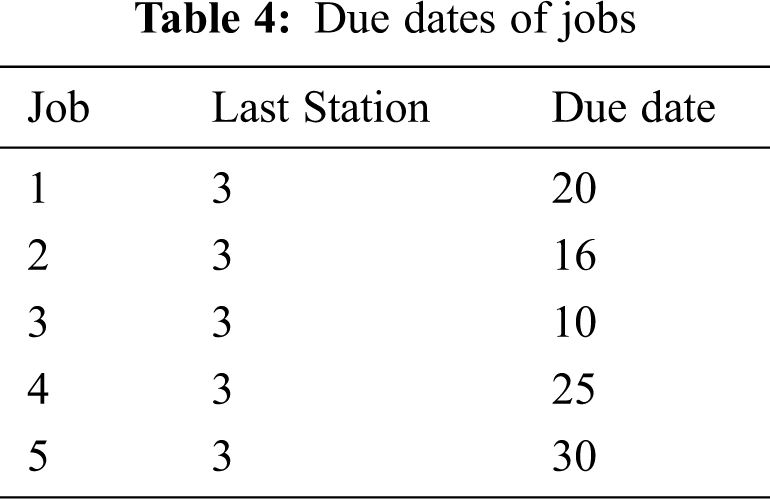
Each workstation has several machines. As shown in Tab. 3, we define machines 1,2, and 3 as being at station 1; machine 4,5, and 6 as being at station 2; and machines 7, and 8 as being at station 3. Moreover, if each job comes to an end process, it will definitely be in the last station (station 3). The proposed method can define whether the job is late based on the due date. The structure of data is illustrated in Tab. 4.
Tab. 5 shows the jobs assigned to the machines with the processing time. As the machines are not identical, it is not necessary for the jobs to be processed in all machines. A job is assigned to a machine depending on the attributes of the products. For example, this label shipment is produced to keep in stock for peak seasons. After the lamination and die-cut process, there is no need to process it on the Inkjet machine to recreate a digital image (Note: Each time slot is 30 min long).

Tab. 6 shows the sequence of jobs assigned to the machines and the setup time of each machine. The job is processed by the machine in certain order, which is similar to what happens at a station. preJob is the previous job of machine. sucJob is the continuous job made by this machine. Since there are different kinds of machines in the workstation, the setup times of the machines are also different from each other (Note: Each time slot is 30 min long).

The data are given in Worksheet with a defined name. CPLEX software was used to solve the flow shop scheduling model for this sample. After running all the data with the appropriate code, the model derived the optimal solution, which satisfied the requirements of the processing time, setup time and sequence constraints. In Tab. 7, X is an index that displays which job is assigned to what machine, otherwise X = 0 (Note: Each time slot is 30 min long).

To check the sequence of jobs on a machine, Y is defined as shown in Tab. 8. Y = 1 if job i is processed before job j on the same machine. The setup time happens when there is a switch between different jobs on the same machine (Note: Each time slot is 30 minutes long).
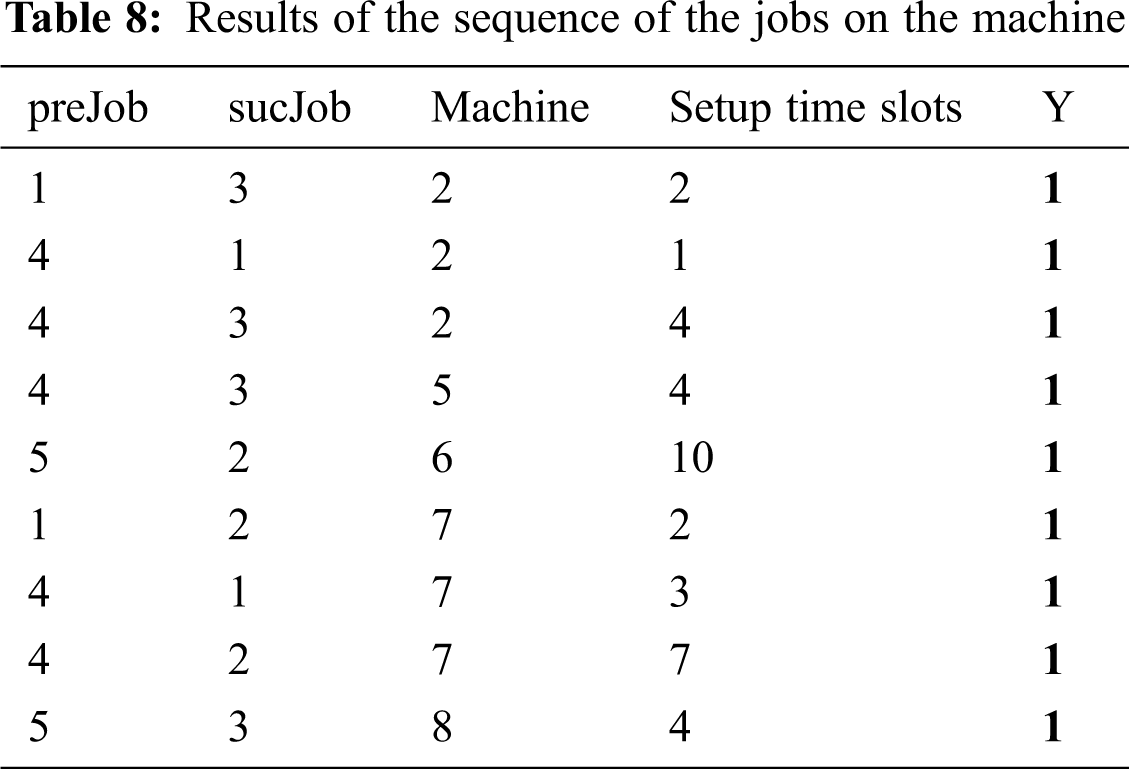
The sequence of job is shown in details:
• Machine 1: Job 2
• Machine 2: Job 4 – Job 1 – Job 3
• Machine 3: Job 5
• Machine 4: Job 1
• Machine 5: Job 4 – Job 3
• Machine 6: Job 5 – Job 2
• Machine 7: Job 4 – Job 1 – Job 2
• Machine 8: Job 5 – Job 3
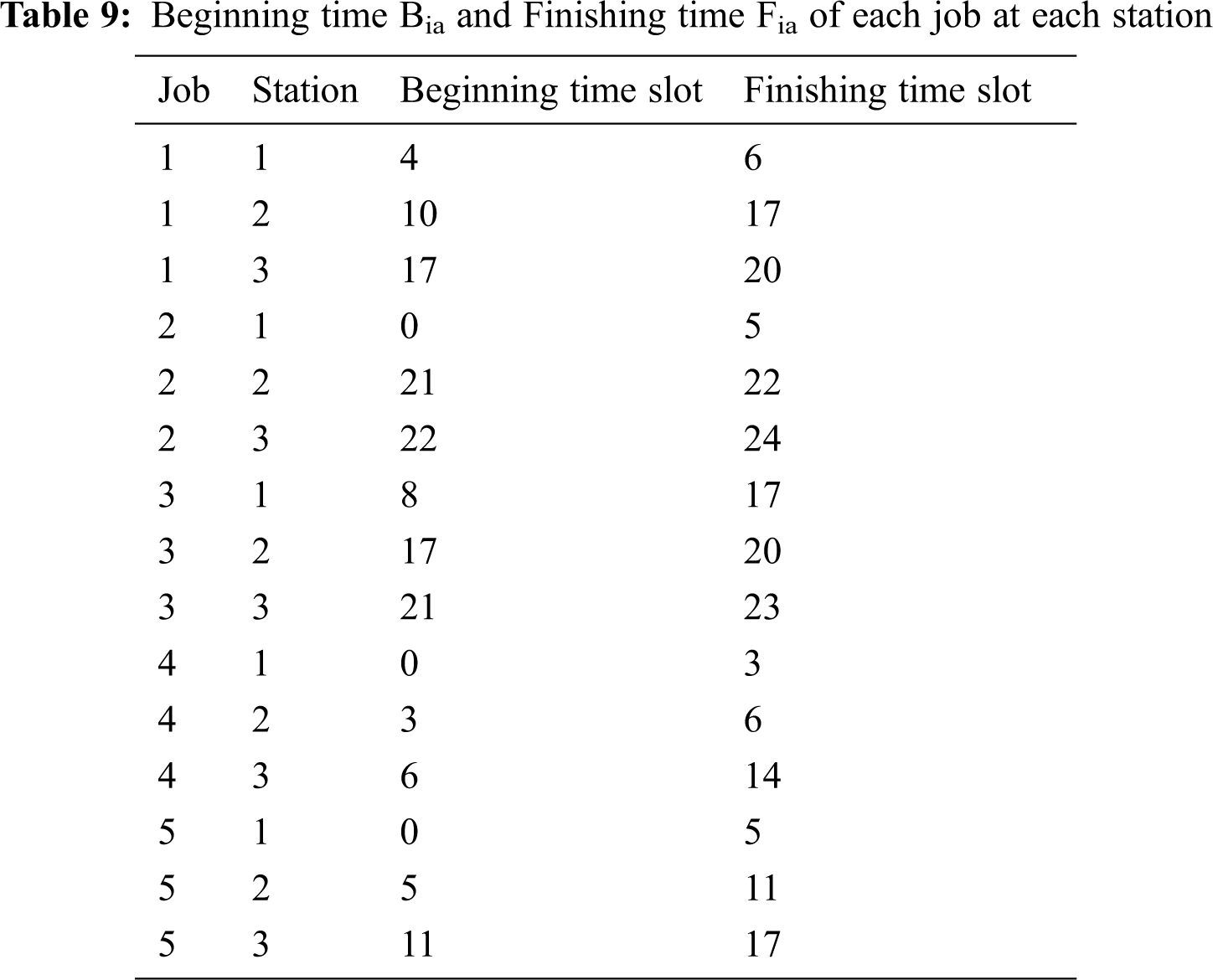
Tab. 9 shows the result of the beginning time and finishing time of each job. Tab. 10 shows the number of late orders. The finishing time is the sum of the beginning time and processing time which is consistent with the data.
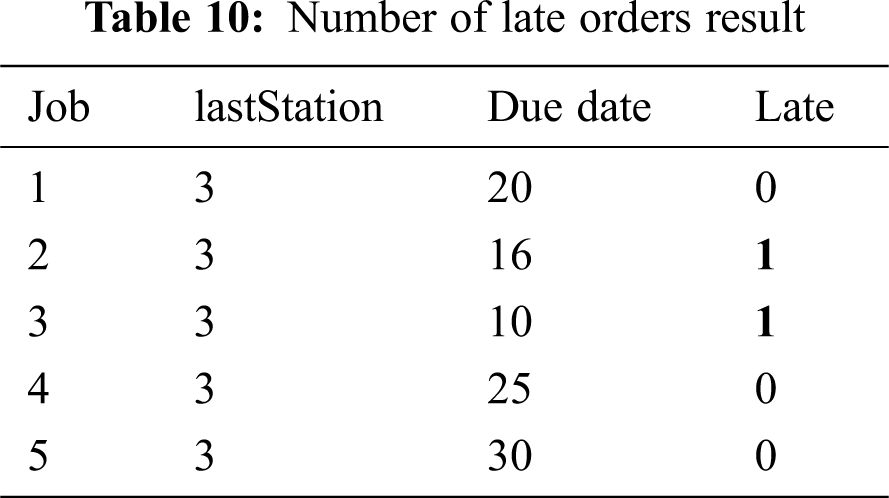
Based on Tabs. 7 and 9, a Gantt Chart (Fig. 3) was drawn to represent the visibility of this problem. A Gantt chart is a visual representation of the schedule’s activities within a defined time interval. It is designed to empower production planners to control and optimize the production plan.
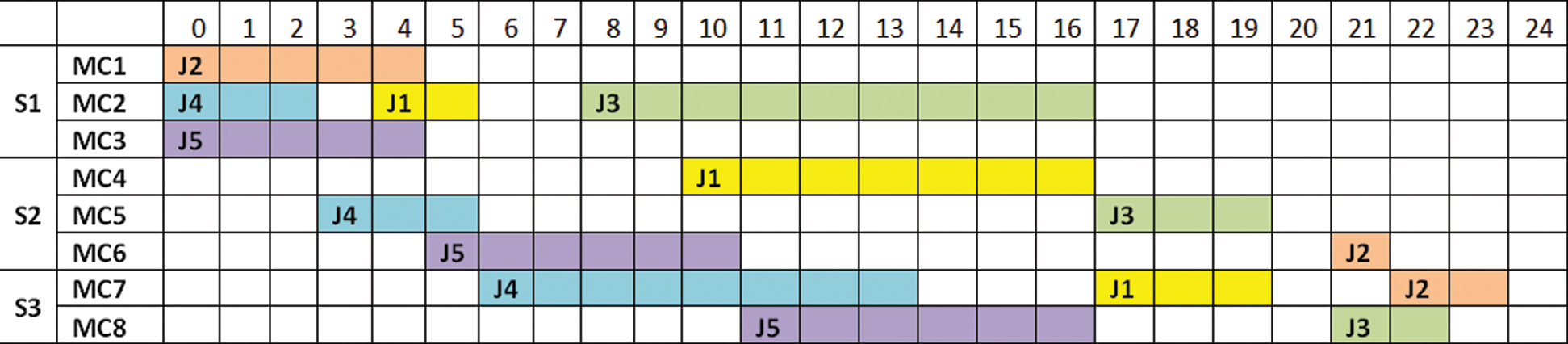
Figure 3: Gantt chart
*Note: Each time slot is 30 minutes long.
After solving the numerical case study, we concluded that the proposed mathematical model is valid for solving the FFS scheduling case, especially for the setup time and non-identical machines. By checking the Gantt chart, setup time, and processing time, the results from the proposed model can provide the optimal solution.
This model was conducted in CPLEX 12.6 and run on Intel® CoreTM i3 running Windows 10. In comparison, Tab. 11 shows the gap between the size of model and the time to solve the optimal solution.

As the number of jobs increases from 5 to 10, the solving time rises relatively with 1.08 – 299.77 seconds. With more than 20 jobs, CPLEX could not give results immediately in a short time. Therefore, an improved method is needed to deliver an accurate solution for large scale data. CPLEX takes a long time to give the optimal solution. Future studies will focus on applying the tuple approach to enumerate all data and reduce the noticeable number of variables.
In this study, the proposed method focuses on solving FFS problem with the optimal solution in an acceptable computational time for larger data. In the future work, many other algorithms like genetic algorithm (GA), and ant colony optimization (ACO), and tabu search could be used for solving this kind of problem. Thus, other algorithms can be used to test and make comparisons. Additionally, a graphical user interface could be implemented to make it easier for users to operate.
Funding Statement: The authors received no specific funding for this study.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
1. W. Shen, “Distributed manufacturing scheduling using intelligent agents,” IEEE Intelligent Systems, vol. 17, no. 1, pp. 88–94, 2002. [Google Scholar]
2. K. Ding, P. Jiang and M. Zheng, “Environmental and economic sustainability-aware resource service scheduling for industrial product service systems,” Journal of Intelligent Manufacturing, vol. 28, no. 6, pp. 1303–1316, 2017. [Google Scholar]
3. K. Lenin, “Hybridization of genetic particle swarm optimization algorithm with symbiotic organisms search algorithm for solving optimal reactive power dispatch problem,” Journal of Applied Science, Engineering, Technology, and Education, vol. 3, no. 1, pp. 12–21, 2021. [Google Scholar]
4. A. Handayani and C. Y. Setyatama, “Analysis of supply chain management performance using SCOR and AHP methods in green avenue apartments of East Bekasi,” Journal of Applied Science, Engineering, Technology, and Education, vol. 1, no. 2, pp. 141–148, 2019. [Google Scholar]
5. N. C. Fertilia and R. Y. A. Adji, “Human resources management planning for increasing precast productivity based on PMBOK at XYZ company,” Quantitative Economics and Management Studies, vol. 1, no. 2, pp. 110–116, 2020. [Google Scholar]
6. B. M. Cortés, J. C. E. Garcia and F. R. Hernández, “Multi-objective flow-shop scheduling with parallel machines,” International Journal of Production Research, vol. 50, no. 10, pp. 2796–2808, 2012. [Google Scholar]
7. T. H. Tran and K. M. Ng, “A hybrid water flow algorithm for multi-objective flexible flow shop scheduling problems,” Engineering Optimization, vol. 45, no. 4, pp. 483–502, 2013. [Google Scholar]
8. S. Wang, X. Wang and L. Yu, “Two-stage no-wait hybrid flow shop scheduling with sequence-dependent setup times,” International Journal of Systems Science. Operations & Logistics, vol. 7, no. 3, pp. 291–307, 2020. [Google Scholar]
9. A. Allahverdi and H. M. Soroush, “The significance of reducing setup times/setup costs,” European Journal of Operational Research, vol. 187, no. 3, pp. 978–984, 2008. [Google Scholar]
10. S. C. Kim and P. M. Bobrowski, “Impact of sequence-dependent setup time on job shop scheduling performance,” International Journal of Production Research, vol. 32, no. 7, pp. 1503–1520, 1994. [Google Scholar]
11. X. Sun, J. S. Noble and C. M. Klein, “Single-machine scheduling with sequence dependent setup to minimize total weighted squared tardiness,” IIE Transactions, vol. 31, no. 2, pp. 113–124, 1999. [Google Scholar]
12. E. Jiang and L. Wang, “An improved multi-objective evolutionary algorithm based on decomposition for energy-efficient permutation flow shop scheduling problem with sequence-dependent setup time,” International Journal of Production Research, vol. 57, no. 6, pp. 1756–1771, 2018. [Google Scholar]
13. M. L. Entrup, H. O. Gunther, P. Van Beek, M. Grunow and T. Seller, “Mixed-integer linear programming approaches to shelf-life-integrated planning and scheduling in yoghurt production,” International Journal of Production Research, vol. 43, no. 23, pp. 5071–5100, 2005. [Google Scholar]
14. M. Varmazyar and N. Salmasi, “Minimizing the number of tardy jobs in flow shop sequence dependent setup times scheduling problem,” Applied Mechanics and Materials, vol. 110-116, pp. 4063–4069, 2011. [Google Scholar]
15. L. Meng, C. Zhang, X. Shao, B. Zhang, Y. Ren et al., “More MILP models for hybrid flow shop scheduling problem and its extended problems,” International Journal of Production Research, vol. 58, no. 13, pp. 3905–3930, 2020. [Google Scholar]
16. Z. Zhu and R. B. Heady, “Minimize the sum of earliness/tardiness in multi-machine scheduling: A mixed integer programming approach,” Computers & Industrial Engineering, vol. 38, no. 2, pp. 297–305, 2000. [Google Scholar]
17. M. B. Fakhrzad and M. Heydari, “A heuristic algorithm for hybrid flow-shop production scheduling to minimize the sum of the earliness and tardiness costs,” Journal of the Chinese Institute of Industrial Engineers, vol. 25, no. 2, pp. 105–115, 2008. [Google Scholar]
18. W. Wang, Z. Shi, L. Shi and Q. Zhao, “Integrated optimisation on flow-shop production with cutting stock,” International Journal of Production Research, vol. 57, no. 19, pp. 5996–6012, 2019. [Google Scholar]
19. T. Chen and G. Zhou, “Modeling production scheduling problem and its solution by genetic algorithm,” Journal of Computers, vol. 8, no. 8, pp. 2126, 2013. [Google Scholar]
20. J. Schaller, “Scheduling a permutation flow shop with family setups to minimise total tardiness,” International Journal of Production Research, vol. 50, no. 8, pp. 2204–2217, 2012. [Google Scholar]
21. U. P. Wen and C. I. Yeh, “Tabu search methods for the flow shop sequencing problem,” Journal of the Chinese Institute of Engineers, vol. 20, no. 4, pp. 465–470, 1997. [Google Scholar]
22. D. Bai and T. Ren, “New approximation algorithms for flow shop total completion time problem,” Engineering Optimization, vol. 45, no. 9, pp. 1091–1105, 2013. [Google Scholar]
23. N. Javadian, M. Amiri-Aref, A. Hadighi, M. Kazemi and A. Moradi, “Flexible flow shop with sequence-dependent setup times and machine availability constraints,” International Journal of Management Science and Engineering Management, vol. 5, no. 3, pp. 219–226, 2013. [Google Scholar]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |