Computer Systems Science & Engineering DOI:10.32604/csse.2022.018227
Article

Vertex-Edge Degree Based Indices of Honey Comb Derived Network

Muhammad Ibrahim1,*, Sadia Husain2, Nida Zahra1 and Ali Ahmad2

1Centre for Advanced Studies in Pure and Applied Mathematics, Bahauddin Zakariya University, Multan, Pakistan
2College of Computer Sciences and Information Technology, Jazan University, Jazan, Saudi Arabia
*Corresponding Author: Muhammad Ibrahim. Email: mibtufail@gmail.com
Received: 01 March 2021; Accepted: 29 April 2021

Abstract: Chemical graph theory is a branch of mathematics which combines graph theory and chemistry. Chemical reaction network theory is a territory of applied mathematics that endeavors to display the conduct of genuine compound frameworks. It pulled the research community due to its applications in theoretical and organic chemistry since 1960. Additionally, it also increases the interest the mathematicians due to the interesting mathematical structures and problems are involved. The structure of an interconnection network can be represented by a graph. In the network, vertices represent the processor nodes and edges represent the links between the processor nodes. Graph invariants play a vital feature in graph theory and distinguish the structural properties of graphs and networks. In this paper, we determined the newly introduced topological indices namely, first ve -degree Zagreb α index, first ve -degree Zagreb β index, second ve -degree Zagreb index, ve -degree Randic index, ve -degree atom-bond connectivity index, ve -degree geometric-arithmetic index, ve -degree harmonic index and ve -degree sum-connectivity index for honey comb derived network. In the analysis of the quantitative structure property relationships (QSPRs) and the quantitative structureactivity relationships (QSARs), graph invariants are important tools to approximate and predicate the properties of the biological and chemical compounds. Also, we give the numerical and graphical representation of our outcomes.

Keywords: Honey comb derived network; ev-degree; topological indices

1  Introduction

A structural molecular diagram is a basic diagram in the study of structural chemical graph theory where atoms are spoken to by nodes and chemical bonds are spoken to by lines. A diagram is associated if there is an association between any pair of nodes. A network is an associated diagram that has no various lines between two nodes and loop. The number of nodes which are associated with a fixed node v is known as the degree of v and is denoted by dv . The collection of all the adjacent nodes to the node v is referred to open neighborhood of v and can be represented by N(v) . The open neighborhood became the closed neighborhood when we include the node v in the collection and is represented by N[v] . The shortest distance between two vertices u,v ∈V(G) is denoted by d(u,v), and the maximum value of d(u,v) in G is called the diameter of G, denoted as diam(G). For basic definition, see West [1].

The relation between the (QSPR) and (QSAR) predict the properties and natural exercises of unstudied material. In these materials, the topological indices and some physico-chemical properties are utilized to anticipate bioactivity for chemical compounds [2–5]. A number represents a topological index in a diagram of a chemical compound, which can be utilized to portray the underlined chemical compound and help to foresee its physio-chemical properties. In 1947 Weiner established the framework of topological index. He was approximated the breaking point of alkanes and presented the Weiner index [6]. In 1975, Milan Randic presented Randic index [7]. In 1998, Bollobas et al. [8] and Amic et al. [9] proposed the general Randic index and has been concentrated by both scientist and mathematicians [10]. The Randic index is one of the most important and generally considered and applied topological index. Numerous surveys, papers and books [11–16] are composed on graph invariant. For detail of different topological indices, see [17–22]. Chellali et al. [23] introduced two novel degree thoughts which they called “ ve -degree and ev -degree”. Horoldagva et al. [24] contributed to the study related to “ ve -degree and ev -degree”. The new style degree base indices have been applied to already existing indices and found the better results in [25–27]. It has been found that the ve -degree Zagreb index has more grounded estimate power than the old-style Zagreb index.

2  The ve -degree and ev -degree Based Topological Indices

Chellali et al. [23] gave the definition of ev -degree of an edge e=uv∈E which is denoted by dev(e) , and is the cardinality of nodes of the union of the closed neighborhoods of u and v . The ve -degree of the node v∈V , denoted by dve(v) , and is the cardinality of lines of different lines that are incident to any node from the closed neighborhood of v . Throughout this paper we consider G is a connected graph, e=uv∈E(G) and v∈V . For some basic definitions regarding “ ev -degree and ve -degree topological indices” [28–30]. The topological indices related to ev -degree are: The ev -degree Zagreb index, ev -degree Randic index, The topological indices related to ev -degree are: The first ve -degree Zagreb α index, first ve -degree Zagreb β index, second ve -degree Zagreb index, ve -degree Randic index, ve -degree atom-bond connectivity index, ve -degree geometric-arithmetic index, ve -degree harmonic index and ve -degree sum-connectivity index.

3  Main Results

In the present section, we determined our computational results for Honey Comb derived network (see Fig. 1), which is a planar graph. The number of nodes and lines in HcDN1(n) are 9n2−3n+1 and 27n2−21n+6 respectively.

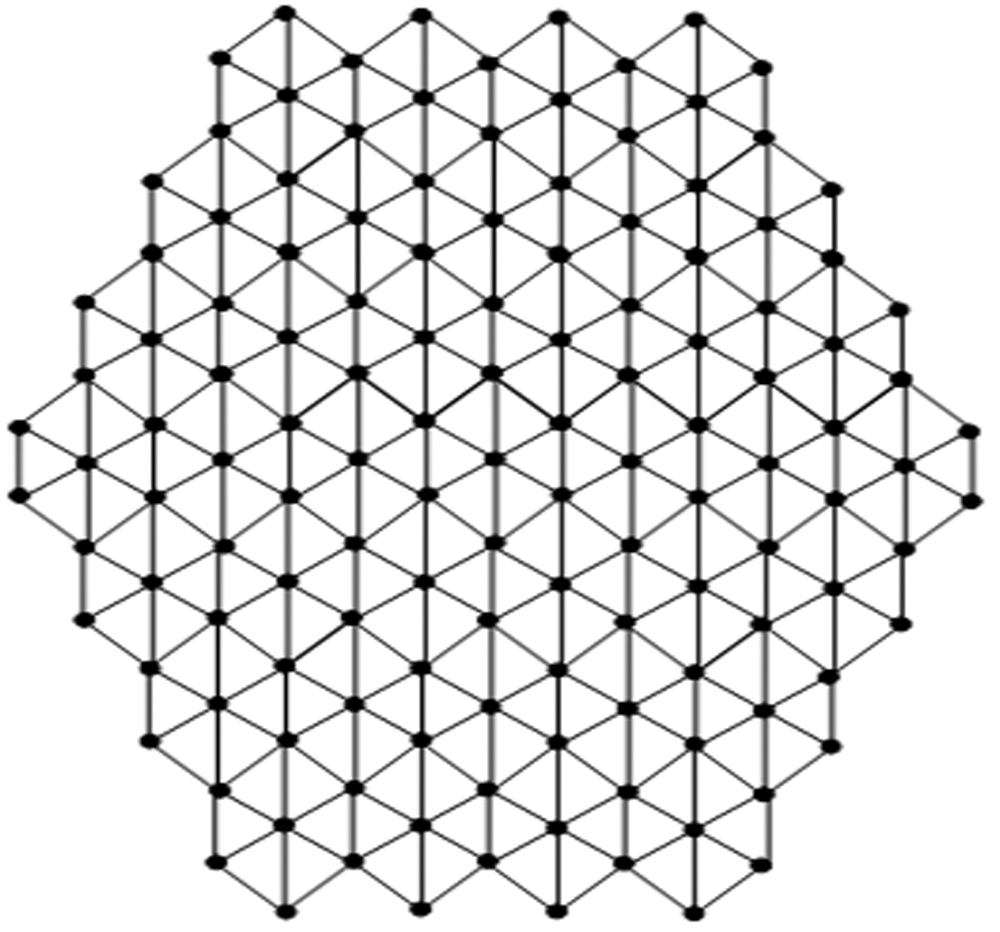
Figure 1: HcDN1(n) network with n=4

There are five types of lines in HcDN1(n) based on degrees of end nodes of each line. Tab. 1 shows line partition of HcDN1(n) . Tab. 2 represents the number of nodes corresponding their degrees.

In Tab. 3, We partition the lines, based on ev -degree of the HcDN1 . In Tabs. 4 and 5, we partition the nodes, based on ve -degree of HcDN1 .

4  Computing Indices for HcDN1 Formulas

In this section, we will calculate ev -degree and ve -degree based indices of the different types of indices which are given as under;

• ev− degree Zagreb Index

Now with the help of Tab. 3, we compute the ev -degree based Zagreb index of HcDN1 as:

• The first ve -degree Zagreb α index

Now with the help of Tab. 4, we compute the first ve -degree Zagreb α index of HcDN1 as:

• The first ve -degree Zagreb β index

Now with the help of Tab. 5, we compute the first ve -degree Zagreb β index of HcDN1 as:

• The second ve-degree Zagreb index

Now with the help of Tab. 5, we compute the second ve -degree based Zagreb index of HcDN1 as:

• The ve -degree Randic index

Now with the help of Tab. 5, we compute the ve -degree Randic index of HcDN1 as:

• The ev -degree Randic index

Now with the help of Tab. 3, we compute the ev -degree based Randic index of HcDN1 as:

• The atom-bond connectivity index

Now with the help of Tab. 5, we compute the atom-bond connectivity index of HcDN1 as:

• The geometric-arithmetic index

Now with the help of Tab. 5, we compute the geometric-arithmetic index of HcDN1 as:

• The harmonic index

Now with the help of Tab. 5, we compute the Harmonic index of HcDN1 as:

• The sum-connectivity index

Now with the help of Tab. 5, we compute the Sum-connectivity index of HcDN1 as:

5  Numerical and Graphical Representation and Discussion

The ve and ev for ten different types od degree base topological descriptors for the HcDN1 are calculated both numerically and graphically. From Fig. 2 it is clearly noted that the behavior of first Zegreb alpha index, first Zagreb beta index and second Zagreb index is almost same in the increasing direction as the value of n increases while ev Zagreb index value has a very rapid increase with the increase value of n . From Fig. 3 it is clearly noted that the behavior of atom bond connectivity index and geometric arithmetic index are almost closely increasing with the increase value of n while ev Randic index value has a very rapid increase with the increase value of n . The numerical representation of HcDN1 is shown in Tabs. 6–8. The graphical representation of HcDN1 are shown in Figs. 2–4.

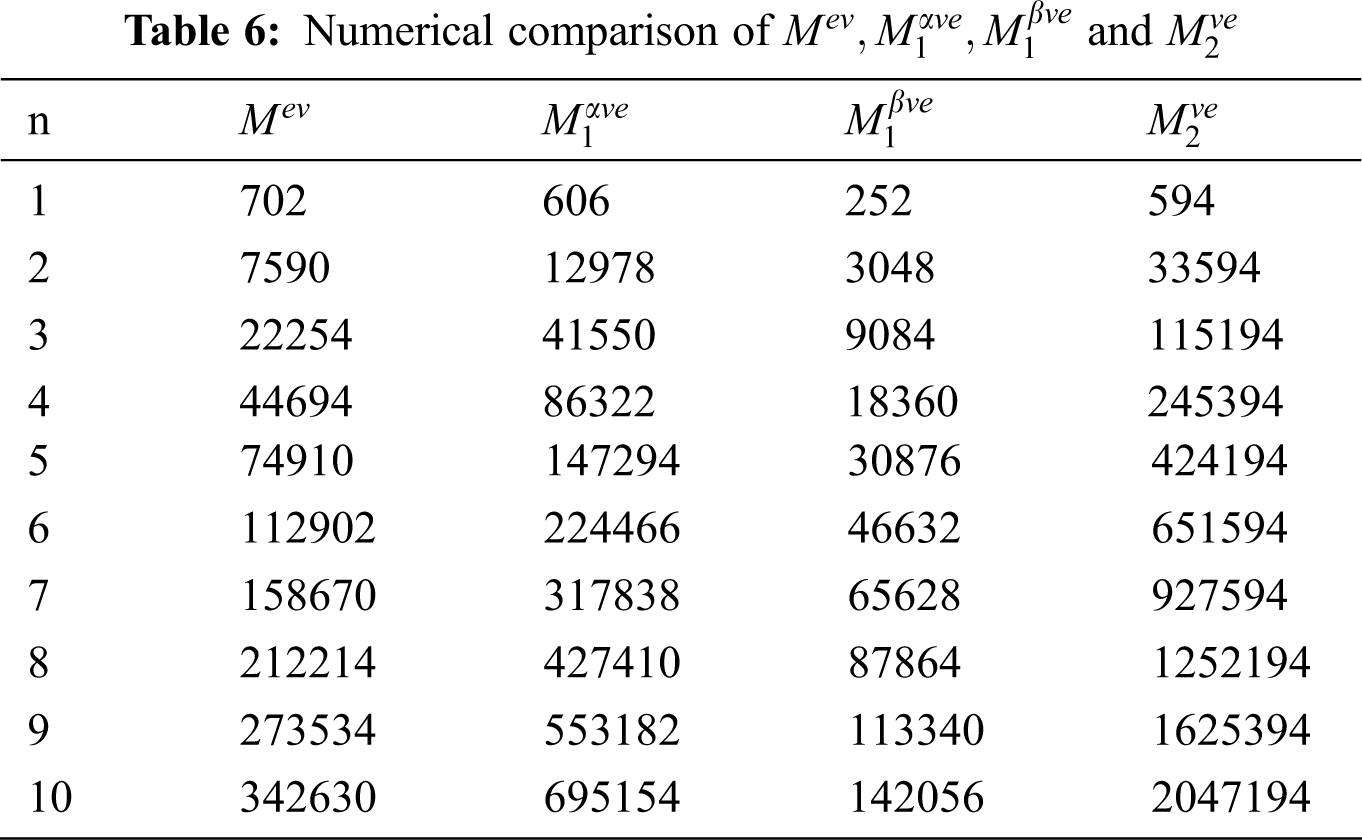
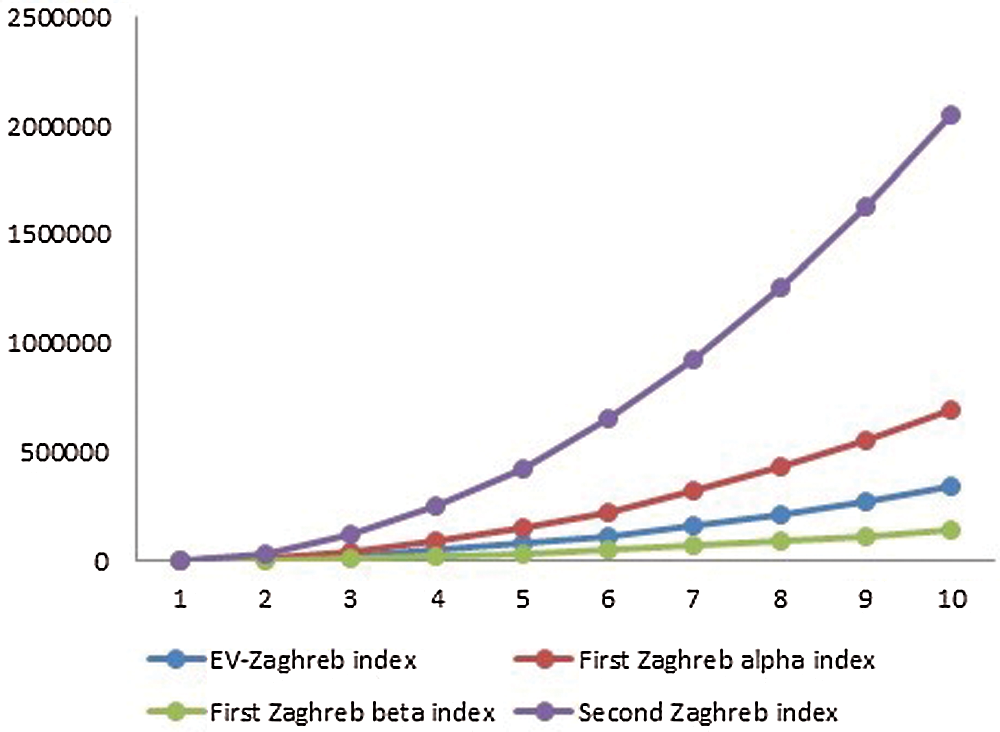
Figure 2: Graphical comparison of Mev , M1αve , M1βve and M2ve

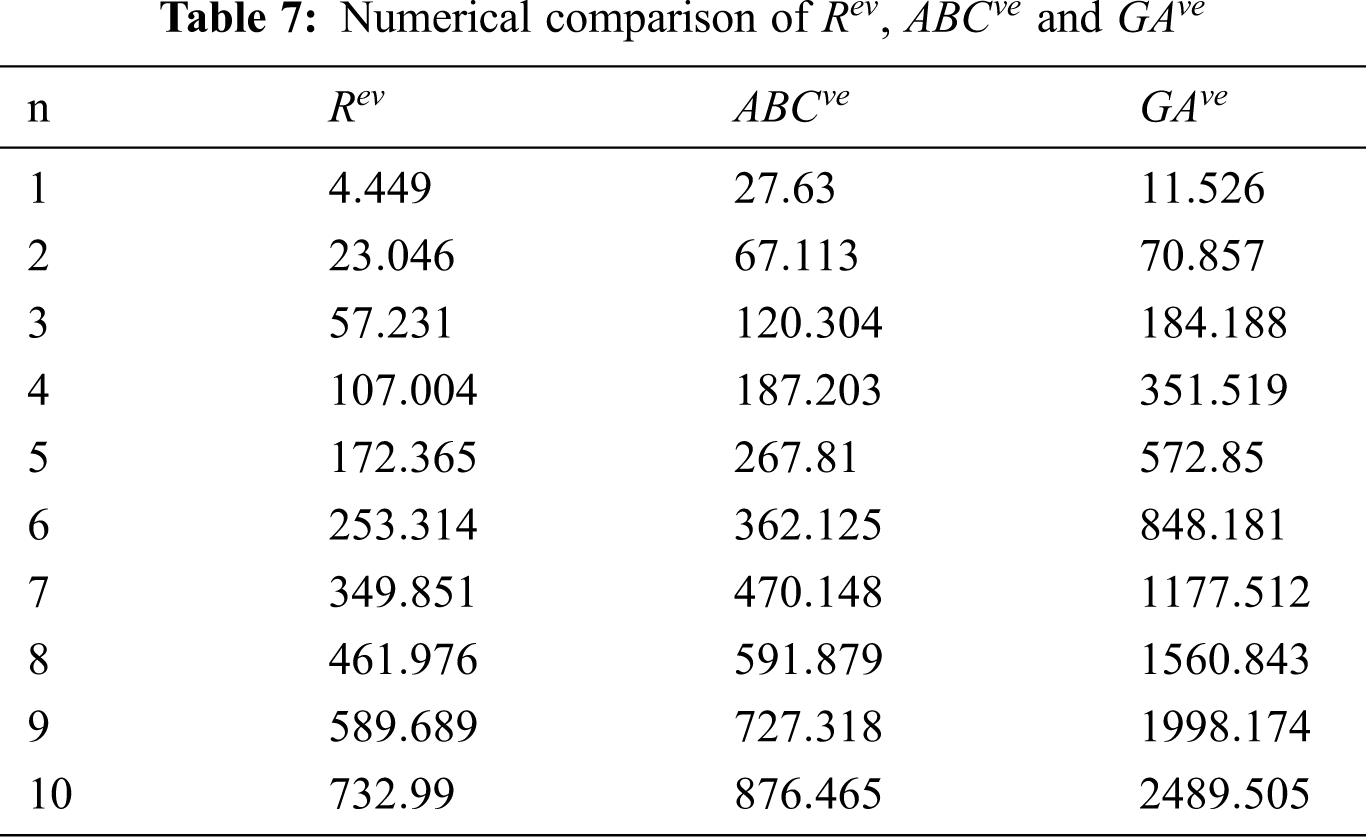
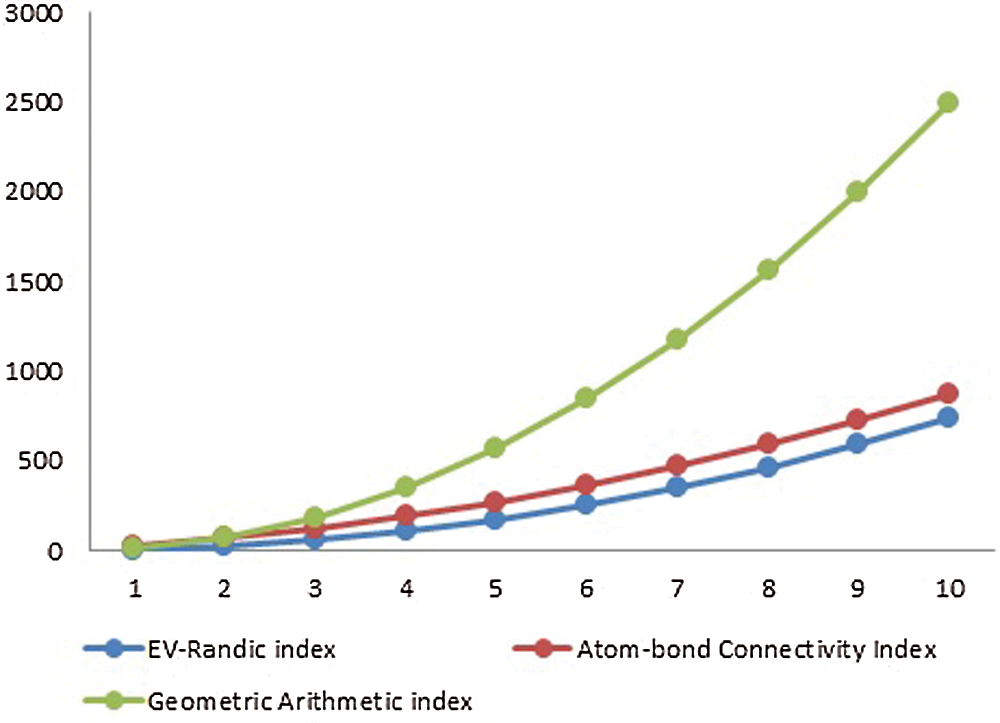
Figure 3: Graphical comparison of Rev , ABCve and GAve

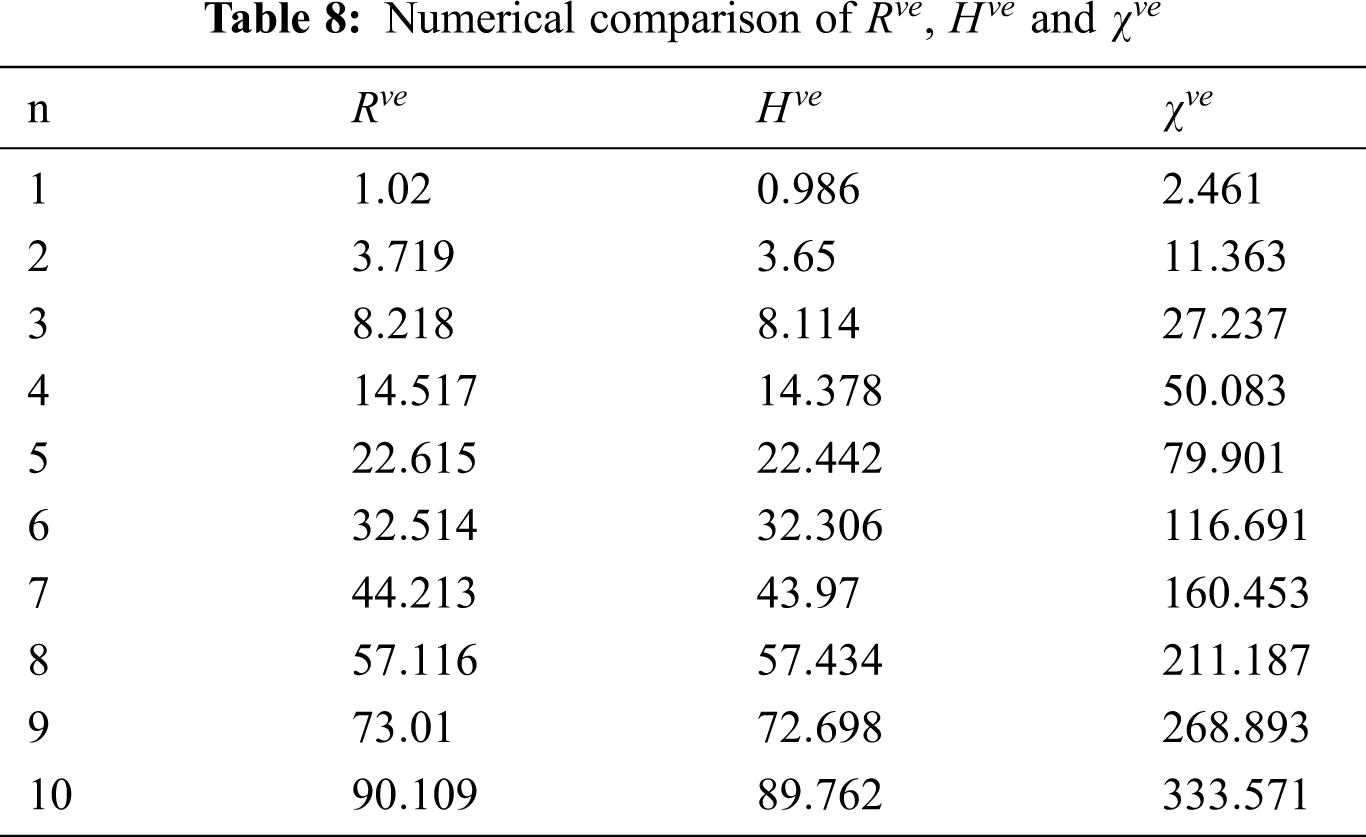
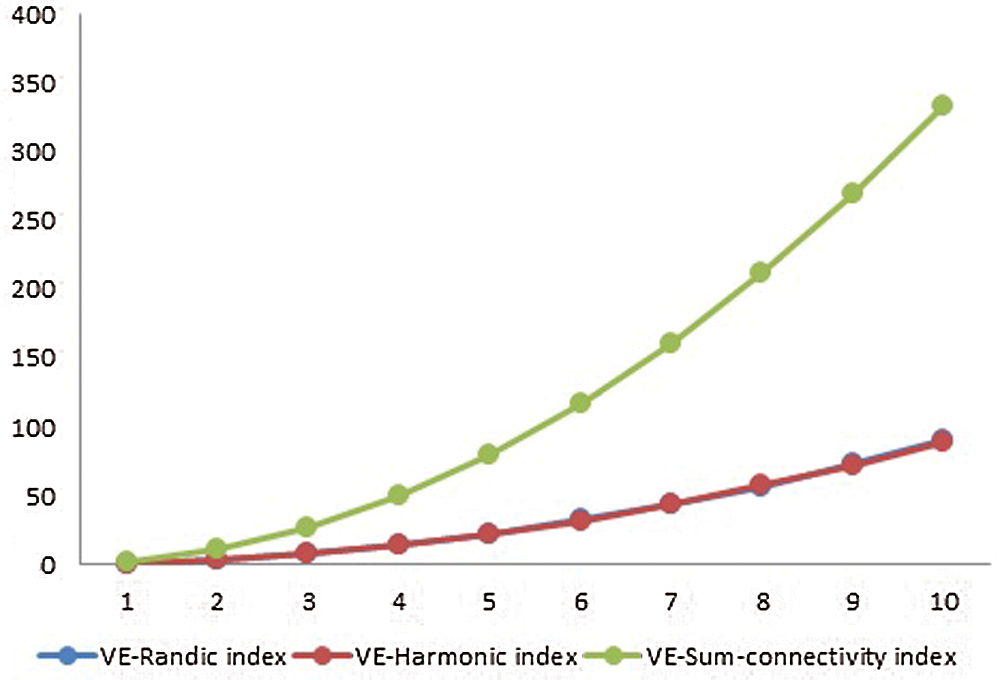
Figure 4: Graphical comparison of Rve , Hve and χve

6  Conclusion

There are many applications of topological descriptors in computer science, networks, agriculture and chemical graph theory etc. These descriptors help in finding the behavior of their structures. We dealt with the honey comb derived network and computed ten different types of topological descriptors which are base on ev and ve degree. We have computed their explicit formulas and then computed their numerical values for different values of n . Further we plotted their graphs for comparison and discussed their behavior. We observe that the values of all descriptors increases with the increase value of n . In the analysis of the quantitative structure property relationships (QSPRs) and the quantitative structureactivity relationships (QSARs), graph invariants are important tools to approximate and predicate the properties of the biological and chemical compounds. In this paper, we study the vertex-edge based topological indices for honey comb derived network.

Funding Statement: The authors received no specific funding for this study.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  D. B. West, Introduction to graph theory, Second Edition. Pearson Education (Singapore) Pte. Ltd., 2002. [Google Scholar]

 2.  G. Rcker and C. Rcker, “On topological indices, boiling points, and cycloalkanes,” Journal of Chemical Information and Computer Sciences, vol. 39, no. 5, pp. 788–802, 1999. [Google Scholar]

 3.  S. Klavzar and I. Gutman, “A comparison of the Schultz molecular topological index with the Wiener index,” Journal of Chemical Information and Computer Sciences, vol. 36, no. 5, pp. 1001–1003, 1996. [Google Scholar]

 4.  F. M. Bruckler, T. Doslic, A. Graovac and I. Gutman, “On a class of distance-based molecular structure descriptors,” Chemical Physics Letters, vol. 503, no. 4–6, pp. 336–338, 2011. [Google Scholar]

 5.  H. Deng, J. Yang and F. Xia, “A general modeling of some vertex-degree based topological indices in benzenoid systems and phenylenes,” Computers and Mathematics with Applications, vol. 61, no. 10, pp. 3017–3023, 2011. [Google Scholar]

 6.  H. Wiener, “Structural determination of paraffin boiling points,” Journal of the American Chemical Society, vol. 69, pp. 17–20, 1947. [Google Scholar]

 7.  M. Randic, “Characterization of molecular branching,” Journal of the American Chemical Society, vol. 97, no. 23, pp. 6609–6615, 1975. [Google Scholar]

 8.  B. Bollobas and P. Erdos, “Graphs of extremal weights,” Ars Combinatoria, vol. 50, pp. 225–233, 1998. [Google Scholar]

 9.  D. Amic, D. Beslo, B. Lucic, S. Nikolic and N. Trinajstic, “The vertex-connectivity index revisited,” Journal of Chemical Information and Computer Sciences, vol. 38, no. 5, pp. 819–822, 1998. [Google Scholar]

10. Y. Hu, X. Li, Y. Shi, T. Xu and I. Gutman, “On molecular graphs with smallest and greatest zeroth-order general Randic index,” MATCH Communication in Mathematical and in Computer Chemistry, vol. 54, no. 2, pp. 425–434, 2005. [Google Scholar]

11. X. Li, I. Gutman and M. Randic, “Mathematical aspects of Randic-type molecular structure descriptors,”University of Kragujevac and Faculty of Science, Kragujevac, 2006. [Google Scholar]

12. M. Randic, “On history of the Randic index and emerging hostility toward chemical graph theory,” MATCH Communication in Mathematical and in Computer Chemistry, vol. 59, pp. 5–124, 2008. [Google Scholar]

13. M. Randic, “The connectivity index 25 years after,” Journal of Molecular Graphics and Modelling, vol. 20, no. 1, pp. 19–35, 2001. [Google Scholar]

14. I. Gutman and B. Furtula, “Recent results in the theory of Randic index,”University of Kragujevac and Faculty of Science, Kragujevac, 2008. [Google Scholar]

15. X. Li and Y. Shi, “A survey on the Randic index,” MATCH Communication in Mathematical and in Computer Chemistry, vol. 59, no. 1, pp. 127–156, 2008. [Google Scholar]

16. S. Nikolic, G. Kovacevic, A. Milicevic and N. Trinajstic, “The Zagreb indices 30 years after,” Croatica Chemica Acta, vol. 76, no. 2, pp. 113–124, 2003. [Google Scholar]

17. I. Gutman and K. C. Das, “The first Zagreb index 30 years after,” MATCH Communication in Mathematical and in Computer Chemistry, vol. 50, no. 1, pp. 83–92, 2004. [Google Scholar]

18. K. C. Das and I. Gutman, “Some properties of the second Zagreb index,” MATCH Communication in Mathematical and in Computer Chemistry, vol. 52, pp. 103–112, 2004. [Google Scholar]

19. I. Gutman, A. Milicevic, S. Nikolic and N. Trinajstic, “About the Zagreb Indices,” Kemija u Industriji, vol. 59, no. 12, pp. 577–589, 2010. [Google Scholar]

20. N. Idrees, R. Khalid, F. B. Farooq and S. Nasir, “Computing topological invariants of triangular chandelier lattice,” CMC-Computers, Materials & Continua, vol. 63, no. 3, pp. 1119–1132, 2020. [Google Scholar]

21. A. Milicevic, S. Nikolic and N. Trinajstic, “On reformulated Zagreb indices,” Molecular Diversity, vol. 8, no. 4, pp. 393–399, 2004. [Google Scholar]

22. A. N. A. Koam, A. Ahmad and M. F. Nadeem, “Comparative study of valency-based topological descriptor for hexagon star network,” Computer Systems Science and Engineering, vol. 36, no. 2, pp. 293–306, 2021. [Google Scholar]

23. M. Chellali, T. W. Haynes, S. T. Hedetniemi and T. M. Lewis, “On degrees and degrees in graphs,” Discrete Mathematics, vol. 340, no. 2, pp. 31–38, 2017. [Google Scholar]

24. B. Horoldagva, K. C. Das and T. A. Selenge, “On ve-degree and ev-degree of graphs,” Discrete Optimization, vol. 31, pp. 1–7, 2019. [Google Scholar]

25. S. Ediz, “A new tool for QSPR researches: ev-degree Randi index,” Celal Bayar University Journal of Science, vol. 13, no. 3, pp. 615–618, 2017. [Google Scholar]

26. B. Sahin and S. Ediz, “On ev-degree and ve-degree topological indices,” Iranian Journal of Mathematical Chemistry, vol. 9, no. 4, pp. 263–277, 2018. [Google Scholar]

27. S. Ediz, “On ve-degree molecular topological properties of silicate and oxygen networks,” International Journal of Computing Science and Mathematics, vol. 9, no. 1, pp. 1–12, 2018. [Google Scholar]

28. M. Cancan, “On ev-degree and ve-degree topological properties of Tickysim spiking neural network,” Computational Intelligence and Neuroscience, Article ID 8429120,2019. [Google Scholar]

29. A. Ahmad, “Comparative study of ve-degree and ev-degree topological descriptors for benzene ring embedded in P-type-surface in 2D network,” Polycyclic Aromatic Compounds, 2020. [Google Scholar]

30. M. Cancan, “On harmonic and ev-degree molecular topological properties of DOX, RTOX and DSL networks,” CMC-Computers, Materials & Continua, vol. 59, no. 3, pp. 777–786, 2019. [Google Scholar]

This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.