DOI:10.32604/csse.2022.019734

| Computer Systems Science & Engineering DOI:10.32604/csse.2022.019734 |  |
| Article |
Symbol Detection Based on Back Tracking Search Algorithm in MIMO-NOMA Systems
Bandirma Onyedi Eylul University, Enginering and Natural Sciences Faculty, Bandirma, 10200, Turkey
*Corresponding Author: M. Nuri Seyman. Email: mseyman@bandirma.edu.tr
Received: 23 April 2021; Accepted: 27 May 2021
Abstract: One of the most important methods used to cope with multipath fading effects, which cause the symbol to be received incorrectly in wireless communication systems, is the use of multiple transceiver antenna structures. By combining the multi-input multi-output (MIMO) antenna structure with non-orthogonal multiple access (NOMA), which is a new multiplexing method, the fading effects of the channels are not only reduced but also high data rate transmission is ensured. However, when the maximum likelihood (ML) algorithm that has high performance on coherent detection, is used as a symbol detector in MIMO NOMA systems, the computational complexity of the system increases due to higher-order constellations and antenna sizes. As a result, the implementation of this algorithm will be impractical. In this study, the backtracking search algorithm (BSA) is proposed to reduce the computational complexity of the symbol detection and have a good bit error performance for MIMO-NOMA systems. To emphasize the efficiency of the proposed algorithm, simulations have been made for the system with various antenna sizes. As can be seen from the obtained results, a considerable reduction in complexity has occurred using BSA compared to the ML algorithm, also the bit error performance of the system is increased compared to other algorithms.
Keywords: MIMO-NOMA; ML algorithm; heuristic; BSA Algorithm
Insufficient frequency spectral resources are the biggest obstacle to high-rate data transmission. Interest in the use of the NOMA technique, which is a kind of multi-carrier system that provides high-rate data transmission by using spectral resources efficiently, has increased considerably in recent years. In addition to providing spectral efficiency of NOMA, its resistance to multipath damping is another important advantage of the system. Therefore, the NOMA technique also forms the basis of 5th generation communication systems [1].
The most significant drawback to being considered in the multiplexing methods is the destructive effects caused by multipath fading. One of the most important ways to deal with these destructive effects is to use a multi-antenna transceiver. By using NOMA combined with multiple antenna structures, not only high-rate data transmission is provided but also the destructive effects caused by fading are minimized [2–7]. However, symbol detection is a crucial process to detect symbols coherently in wireless communication systems [8–21]. Therefore, various algorithms such as zero-forcing (ZF), the vertical Bell Laboratories layered spice-time (VBLAST), and ML are used for symbol detection [8–17]. Although the ML algorithm is the best performing algorithm among these since the computational complexity of this algorithm increase in proportion to the increasing number of antennas, the practicality of this algorithm for the MIMO systems is very low [12]. Therefore, many studies take place in the literature on reducing the computational complexity problem of ML algorithms [13–16]. In the study of [14]; a differential metrics-based ML algorithm that does not require a computational complexity such as the QR decomposition matrix is proposed. In the study [15], an algorithm is for reducing the QR decomposition complexity, which is a pre-processing method for symbol detection, in proportion to the increase in antenna numbers. The authors of [17] in sparse code multiple access systems, modified single tree search scheme is proposed to soft outputs. From these studies, it can be seen that complexity is a serious problem in the detection of data and as a result, the availability of algorithms is restricted.
Many difficult real-time engineering problems have been solved by using heuristic algorithms inspired by the behavior of many events or creatures in nature [18–30]. With the help of heuristic algorithms such as genetic algorithm (GA), particle swarm optimization (PSO), and differential evolution algorithm (DE), ML estimation is computed recursively for optimizing subspace search. Because of ML algorithm needs computation of correlation matrix and matrix inversion, taking advantage of heuristic algorithms we can overcome these computational challenges [18–21]. In [18] GA has been proposed for the ML algorithm in pulse amplitude modulation (PAM) systems. Also, in the studies [19–20], they have obtained the results with less computational complexity close to the ML algorithm, using PSO for spatial multiplexing systems. In the study of [21], it is seen that the complexity of the symbol detector in the MIMO-OFDM system is reduced considerably by utilizing DE. BSA algorithm is a new evolutionary algorithm that provides more efficient solutions with fewer parameters and has recently been used in wide application areas [22]. some studies are using BSA in many areas such as antenna design, medicine, meteorology, Complementary metal oxide semiconductor (CMOS) circuit design, and chemistry [22–29]. When we consider the literature, there is no heuristic-based proposal to eliminate the disadvantages of ML algorithms in MIMO-NOMA systems.
In this study, the BSA is proposed for symbol detection in MIMO-NOMA systems with various transmitter and receiver antennas. To highlight the complexity reduction and bit error rate (BER) efficiency of the proposal, the proposed BSA is compared to the classical algorithms such as ML, ZF and VBLAST and heuristic algorithms such as GA, PSO. The simulation results and complexity analysis demonstrate that our proposal is an effective solution for symbol detection.
This paper is organized as follows, Section 2 introduces the concept of the MIMO-NOMA system and ML scheme. The architecture of the backtracking search algorithm for data detection is described in Section 3. The simulation results and conclusion are drawn in Section 4 and Section 5 respectively.
NOMA combined with MIMO is a new multicarrier modulation system that provides orthogonal access to the users either in frequency, time, space, or code. For this scheme, each user uses the same time and frequency where they are selected considering the power levels. In NOMA, the successive interference cancellation (SIC) is used to reserve the users both in the downlink and uplink [1–7].
When we consider a MIMO-NOMA system consists of N transmitter and M receiver antenna, the signal is transmitted in the same frequency and time domain but various power levels as;
Where
Where
Where
Where
As can be seen from Eq. (6) received signal is a combination of desired and interference signal [2–3]. Interference signals consist of two parts called intra-cluster interference and inter-cluster interference [4]
Channel gains can be presented as follows,
Besides PA coefficients are ordered as
To detect symbol, an ML algorithm can be implemented by maximizing the (9) metric;
Data can be detected by using the Eq. (10) which minimize the squared Euclidian distance to the target vector,
For ML detection
3 Back Tracking Search Algorithm for Symbol Detection
BSA, is a population-based evolutionary algorithm that provides to make the right choice from a variety of ways to reach a goal or search for a value.
BSA is distinct from other similar algorithms in that it has a memory for storing a population from a previous generation, which is then used to create the search-direction matrix for the next iteration. Besides, Since BSA has a basic structure, it is efficient, fast, and capable of solving multidimensional problems. The mix-rate, which is the only control parameter in BSA, decreases the sensitivity of the inceptive values to the algorithm’s parameters greatly. Initialization, selection I, mutation, crossover, and selection II are the five processing stages in BSA [22].
The processing steps of the BSA are given in Fig. 1.

Figure 1: Process steps of BSA
For the symbol detection problem, in the BSA population of the individuals corresponds to the symbols. At the first steps of BSA, the individuals
Where
The population is updated at the beginning of each epoch as follows
Where a and b are uniform real numbers between [0–1] to check whether
BSA alters a randomly selected population from the previous generation as the old population and keeps this old population in memory until it changes.
Population members are shuffled using the permitting function as follows;
The mutation process is then performed using the Eq. (15).
where F is a real number that is used for control of amplification in search space.
The purpose of mutation is to include the experiences of previous generations in the process. In the crossover step, the final version of the trial population
The performance evaluation of the algorithms has been made by considering the systems with 10 MHz bandwidth and 16QAM modulation for various antennas size over the channel. The NOMA system and channel parameters are given in Tabs. 1 and 2 respectively.


Besides the parameters of the proposed heuristic algorithms for data detection are given in Tab. 3.

A comparison between the results of the proposed method to other detectors for a NOMA system with a 2 × 2 antennas array is shown in Fig. 2.
Although it can be observed from Fig. 2 that the ML algorithm is the best performing algorithm, increasing the size of transmitter and receiver antennas makes this algorithm impractical in terms of complexity. Besides, the proposed BSA algorithm has better BER values than not only classical but also heuristic algorithms. At 10−1 BER, the BSA algorithm has a gain of 14 dB better than the worst-performing ZF and 2 dB better than the PSO with the closest performance to it. Also, the difference between BSA and VBLAST at a value of 20 dB signal to noise ratio (SNR) is around 10−1.
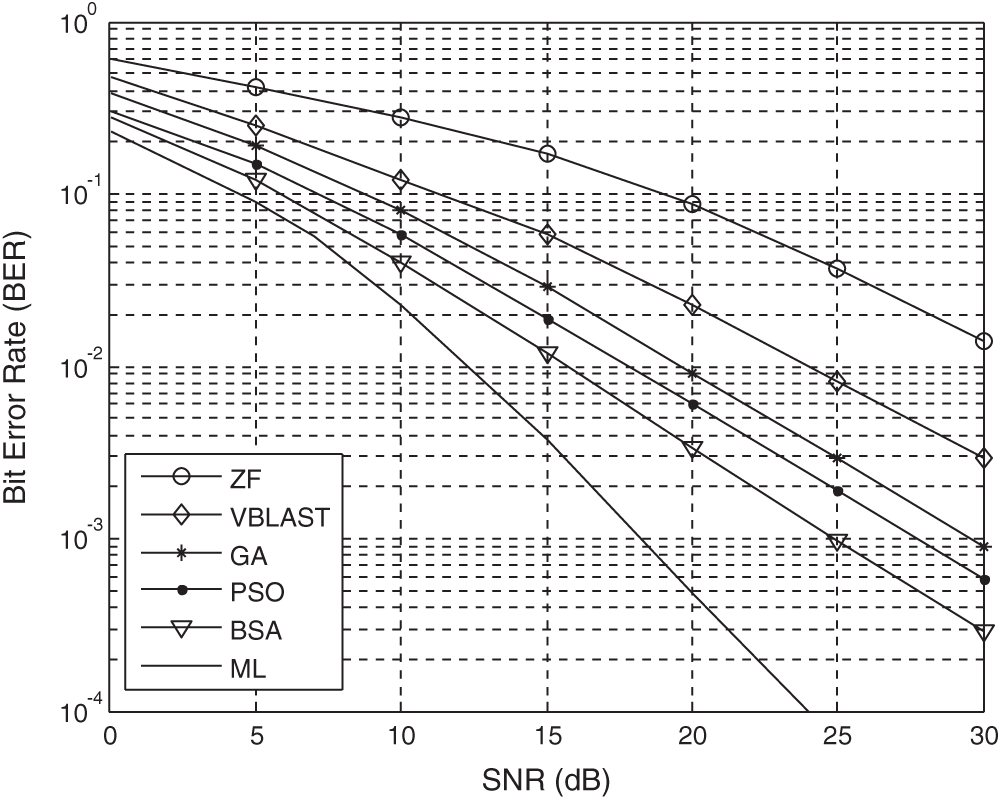
Figure 2: SNR versus BER performance of detectors for 2 × 2 NOMA system
The BER performance of the proposed detector for the systems with 4 × 4 antennas is shown in Fig. 3. It can be seen from Fig. 3 that to have BER = 10−2 GA requires 18 dB, PSO requires 16.5 dB whereas BSA requires 14 dB. Also, at fewer BER values the required SNR value of the proposal is less than the other algorithms.
Finally comparing the performance of the algorithms for the system with 8 × 8 antennas in Fig. 4, we observe that our proposal provides better detection capability not only for few antennas but also for larger antenna arrays. From Fig. 4, it is seen that BSA algorithm needs more than 21 dB of SNR to have BER = 10−3 while PSO and GA need around 23.5 dB and 26 dB of SNR respectively to reach the BER = 10−3. As can be seen from all figures that our proposal offers large SNR improvements compared to other detectors.
Furthermore, to demonstrate the computational complexity benefits of BSA over the ML detector, we can analyze the computational complexity of the detectors in terms of number complex multiplication [19].
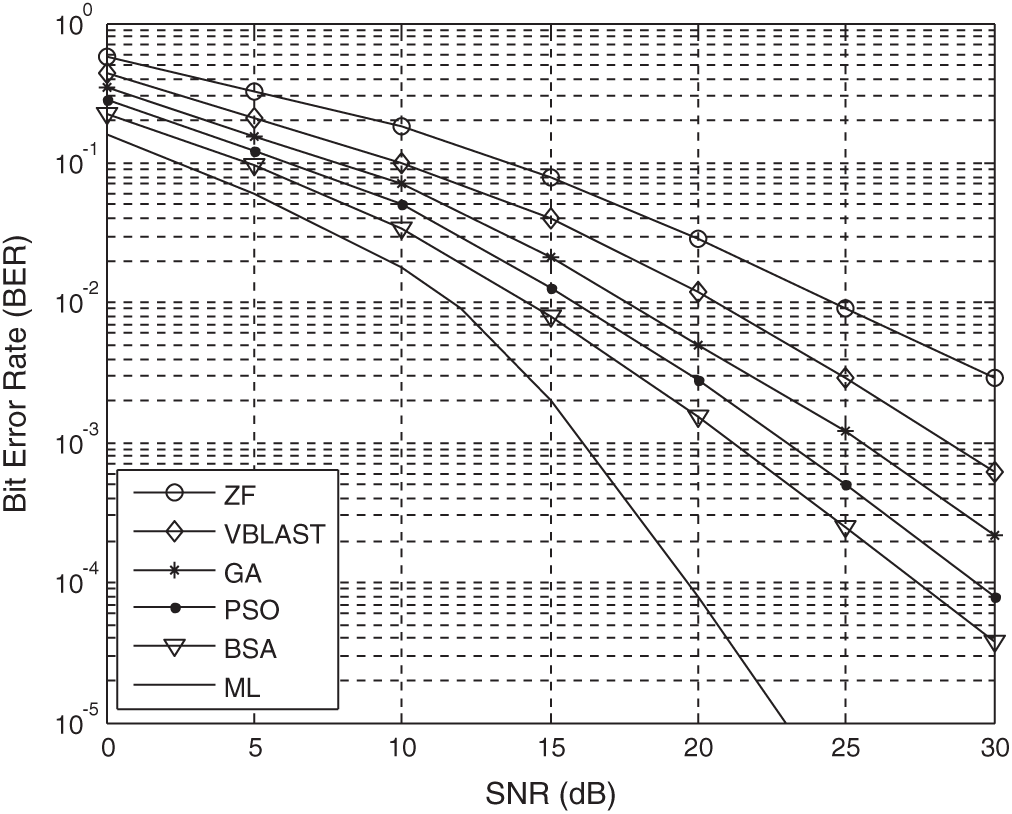
Figure 3: SNR versus BER performance of detectors for 4 × 4 NOMA system
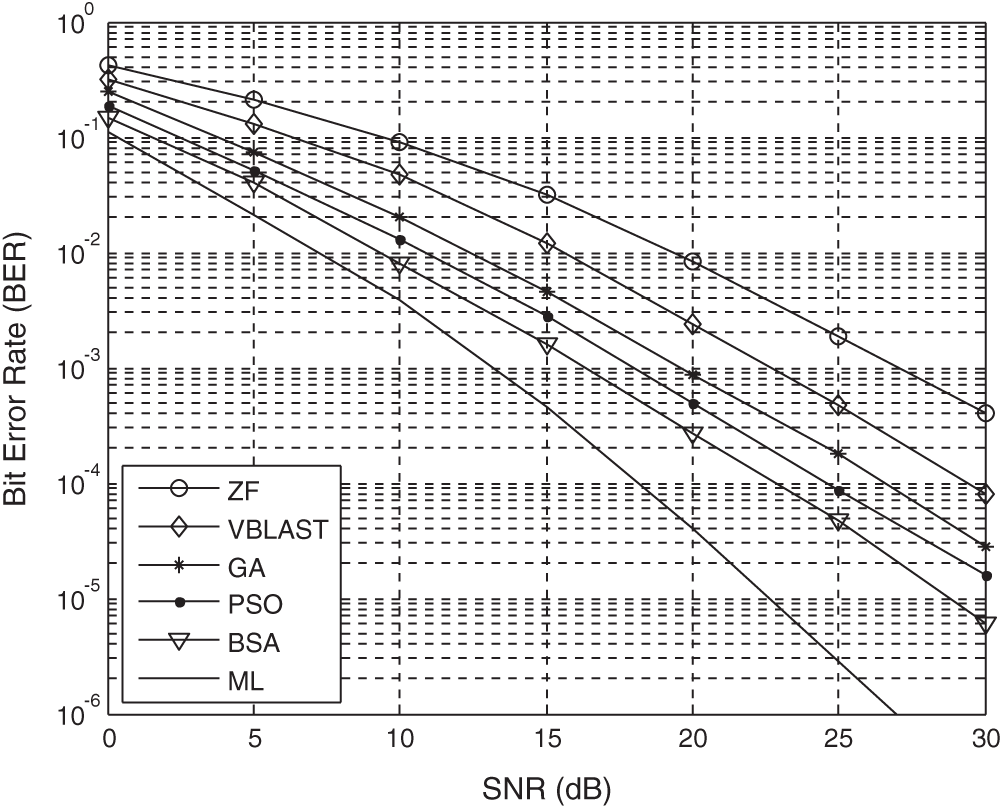
Figure 4: SNR versus BER performance of detectors for 8 × 8 NOMA system
In the ZF algorithm, there are
In the VBLAST algorithm, after the calculation of N times the pseudo-inverse matrix and interference canceling, the complexity can be written as
When we consider the ML algorithm, the number of multiplications required for matrix multiplication and squaring operations are,
Where C is constellation size, in heuristic algorithms, the number of multiplications required to calculate the fitness of each particle in the population are,
After applying the population updating parameters (µ) and Nitr times repetition to convergence to an optimal value, the complexity becomes as
The complexity comparison analysis of the detectors can be found in terms of the number of multiplications in Tab. 4.

As can be seen from this computational complexity analysis, the number of transceiver antennas increases the computational load of each algorithm. However, this amount of load is even higher for the ML detector when the number of antennas increases. For instance, the complexity value of the ML algorithm is 3250 for a 2 × 2 antenna, while the number of antennas is as high as 309 billion in the case of 8 × 8. It can be seen from this analysis that the increase in the number of antennas and modulation index makes the algorithm less practical. Although the complexity of the ZF and VBLAST algorithms is low, their error performance is worse than the heuristic algorithms. Although the value of complexity in heuristic algorithms is similar, the number of iterations required for convergence has a direct effect on the complexity of these algorithms.
To reach optimal solutions for the 4 × 4 NOMA, 8 iterations in the BSA, 10 iterations in the PSO, and 11 iterations in the GA are needed. As a result, BSA, PSO, and GA need 1440, 1800, and 1980 multiplications respectively. Among heuristic algorithms, BSA has the lowest complexity.
Furthermore, BSA provides a 6.25% complexity reduction compared to the ML algorithm 2 × 2 systems. However, it significantly reduces the complexity by 99.59% and 99.9% in 4 × 4 and 8 × 8 systems.
In this study, the use of the BSA algorithm is proposed for data detection in the MIMO-NOMA systems which provide high-rate and quality of service. With this proposed algorithm, computational complexity is reduced in systems where the number of antennas and modulation constellation is large, and BER performance is increased compared to ML algorithm. As can be seen from the simulation results, the BSA algorithm has better values than the other heuristic algorithms in any case; also, it has a close performance to the ML algorithm. Besides, it is better than the classic algorithms such as ZF and VBLAST used for data detection, in terms of BER. So, we can say that the proposed algorithm can be used in a remarkable way for data detection in MIMO-NOMA systems.
Funding Statement: This work was supported by the Scientific Research Projects Coordination Unit of Bandirma Onyedi Eylül University. Project Number BAP-19-MF-1004-005.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
1. Z. Ding, Y. Liu, J. Choi, Q. Sun, M. Elkashlan et al., “Application of non-orthogonal multiple access in LTE and 5G networks,” IEEE Communication Magazine, vol. 55, no. 2, pp. 185–191, 2017. [Google Scholar]
2. Z. Ding, F. Adachi and H. V. Poor, “The application of MIMO to non-orthogonal multiple access,” IEEE Transaction on Wireless Communication, vol. 15, no. 1, pp. 537–552, 2016. [Google Scholar]
3. Y. Liu, G. Pan, H. Zhang and M. Song, “On the capacity comparison between MIMO-NOMA and MIMO-OMA IEEE Access,” Special Selection on Green Communications and Networking for 5G Wireless, vol. 4, pp. 2123–2129, 2016. [Google Scholar]
4. M. Rihan, L. Huang and P. Zhang, “Joint interference alignment and power allocation for NOMA-based multi-user MIMO systems,” EURASIP Journal on Wireless Communications and Networking, vol. 2018, no. 217, pp. 1–13, 2018. [Google Scholar]
5. D. Zhang, Z. Zhou, C. Xu, Y. Zhang, J. Rodriguez et al., “Capacity analysis of non-orthogonal multiple access with mmWave massive MIMO systems,” IEEE Journal on Selected Areas in Communications, vol. 35, no. 7, pp. 1606–1618, 2017. [Google Scholar]
6. Z. Ding, R. Schober and H. Poor, “A general MIMO framework for NOMA downlink and uplink transmission based on signal alignment,” IEEE Transactions on Wireless Communications, vol. 15, no. 6, pp. 4438–4454, 2016. [Google Scholar]
7. A. Akbar, S. Jangsher and F. A. Bhatti, “NOMA and 5G emerging technologies: A survey on issues and solution techniques,” Computer Networks, vol. 190, no. 2021, pp. 1–40, 2021. [Google Scholar]
8. J. Zhang, Y. Zhu, S. Ma, X. Li and K. K. Wong, “Large system analysis of downlink MISO-NOMA system via regularized zero-forcing precoding with imperfect CSIT,” IEEE Communications Letters, vol. 24, no. 11, pp. 2454–2458, 2020. [Google Scholar]
9. S. Ozyurt, E. P. Simon and J. Farah, “NOMA with zero-forcing V-BLAST,” IEEE Communication Letters, vol. 24, no. 9, pp. 2070–2074, 2020. [Google Scholar]
10. L. Xiao, P. Xiao, Z. Liu, W. Yu, H. Haas et al., “A compressive sensing assisted massive SM-VBLAST system: Error probability and capacity analysis,” IEEE Transactions on Wireless Communications, vol. 19, no. 3, pp. 1990–2005, 2020. [Google Scholar]
11. X. Chen, M. Wen and S. Dang, “On the performance of cooperative OFDM-NOMA system with index modulation,” IEEE Communication Letters, vol. 9, no. 9, pp. 1346–1350, 2020. [Google Scholar]
12. M. X. Chang and W. Y. Chang, “Maximum-likelihood detection for MIMO systems based on differential metrics,” IEEE Transactions on Signal Processing, vol. 65, no. 14, pp. 3718–3732, 2017. [Google Scholar]
13. F. Fisher and C. Windpassinger, “Real versus complex-valued equalization in V-BLAST systems,” IET Electronic Letters, vol. 39, no. 5, pp. 470–471, 2003. [Google Scholar]
14. T. H. Kim, “Low complexity sorted QR decomposition for MIMO systems based on pairwise column symmetrization,” IEEE Transactions on Wireless Communications, vol. 13, no. 3, pp. 1388–1396, 2014. [Google Scholar]
15. B. Hassibi and H. Vikalo, “On the sphere-decoding algorithm I. expected complexity,” IEEE Transactions on Signal Processing, vol. 53, no. 8, pp. 2806–2818, 2005. [Google Scholar]
16. M. M. Mansour, S. P. Alex and M. A. Jalloul, “Reduced complexity soft output MIMO sphere detectors-part II, architectural optimizations,” IEEE Transactions on Signal Processing, vol. 62, no. 21, pp. 5506–5520, 2014. [Google Scholar]
17. L. Li, J. Wen, X. Tang and C. Tellambura, “Modified sphere decoding for sparse code multiple access,” IEEE Communication Letters, vol. 22, no. 8, pp. 1544–1547, 2018. [Google Scholar]
18. S. Chen and Y. Wu, “Maximum likelihood channel and data estimation using genetic algorithms,” IEEE Transactions on Signal Processing, vol. 46, pp. 1469–1473, 1998. [Google Scholar]
19. A. A. Khan, S. Bashir, M. Naeem, S. I. Shan and X. Li, “Symbol detection in spatial multiplexing system using particle swarm optimization meta-heuristics,” International Journal of Communication Systems, vol. 21, no. 12, pp. 1239–1257, 2008. [Google Scholar]
20. H. Rehman, S. I. Shah, I. Zaka and J. Ahmad, “An MBER-BLAST algorithm for OFDM-SDMA communication using particle swarm optimization,” International Journal of Communication Systems, vol. 24, no. 2, pp. 185–201, 2011. [Google Scholar]
21. M. N. Seyman and N. Taşpınar, “Symbol detection using differential evolution algorithm in MIMO-OFDM systems,” Turkish Journal of Electrical Engineering & Computer Sciences, vol. 21, no. 2, pp. 373–380, 2013. [Google Scholar]
22. P. Civicioglu, “Backtracking search optimization algorithm for numerical optimization problems,” Applied Mathematics and Computation, vol. 219, no. 15, pp. 8121–8144, 2013. [Google Scholar]
23. H. Wang, Z. Hu, Y. Sun, Q. Su and X. Xia, “Modified backtracking search optimization algorithm inspired by simulated annealing for constrained engineering optimization problems,” Computational Intelligence and Neuroscience, vol. 2018, no. 4, pp. 1–28, 2018. [Google Scholar]
24. S. K. Agarwal, S. Shah and R. Kumar, “Classification of mental tasks from EEG data using backtracking search optimization based neural classifier,” Neurocomputing, vol. 166, pp. 397–403, 2015. [Google Scholar]
25. C. Zhang, J. Zhou, C. Li, W. Fu and T. Peng, “A compound structure of ELM based on feature selection and parameter optimization using hybrid backtracking search algorithm for wind speed forecasting,” Energy Conversion and Management, vol. 143, no. c, pp. 360–376, 2017. [Google Scholar]
26. S. Mallick, R. Kar, D. Mandal and S. P. Ghoshal, “CMOS analog amplifier circuits optimization using hybrid backtracking search algorithm with differential evolution,” Journal of Experimental and Theoretical Artificial Intelligence, vol. 28, no. 4, pp. 1–31, 2015. [Google Scholar]
27. A. Askarzadeh and L. dos Santos Coelho, “A backtracking search algorithm combined with Burger’s chaotic map for parameter estimation of PEMFC electrochemical model,” International Journal of Hydrogen Energy, vol. 39, no. 21, pp. 11165–11174, 2014. [Google Scholar]
28. S. N. A. Latif, J. Shi, H. A. Salman and Y. Tang, “Optimization of demand-response-based intelligent home energy management system with binary backtracking search algorithm,” Information-an International Interdisciplinary Journal, vol. 11, no. 8: 395, pp. 1–18, 2020. [Google Scholar]
29. H. Zhang, S. Xiao and P. Zhou, “Matching pursuit algorithm for backtracking regularization based on energy sorting,” Symmetry, vol. 12, no. 2: 231, pp. 1–12, 2020. [Google Scholar]
30. C. Ocak, I. Tarimer, A. Dalcali and D. Uygun, “Investigation effects of narrowing rotor pole embrace to efficiency and cogging torgue at PM BLDC motor,” TEM Journal, vol. 5, no. 1, pp. 25–31, 2016. [Google Scholar]
31. A. Bishnu and V. Bhatia, “On performance analysis of IEEE 802.22 (PHY) for COST-207 channel models,” in 2015 IEEE Conference on Standards for Communications and Networking (CSCNTokyo, Japan, pp. 229–234, 2015. [Google Scholar]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |