DOI:10.32604/csse.2022.018432

| Computer Systems Science & Engineering DOI:10.32604/csse.2022.018432 |  |
| Article |
A Coordination-Based Algorithm for Dedicated Destination Vehicle Routing in B2B E-Commerce
1Department of Marketing and Distribution Management, National Kaohsiung University of Science and Technology, Taiwan
2Department of Industrial Engineering and Management, Taipei University of Technology, Taiwan
3Department of Enterprise Information and Industrial Engineering, Tunghai University, Taiwan
*Corresponding Author: Hsin-Pin Fu. Email: hpfu@nkust.edu.tw
Received: 09 March 2021; Accepted: 09 May 2021
Abstract: This paper proposes a solution to the open vehicle routing problem with time windows (OVRPTW) considering third-party logistics (3PL). For the typical OVRPTW problem, most researchers consider time windows, capacity, routing limitations, vehicle destination, etc. Most researchers who previously investigated this problem assumed the vehicle would not return to the depot, but did not consider its final destination. However, by considering 3PL in the B2B e-commerce, the vehicle is required back to the nearest 3PL location with available space. This paper formulates the problem as a mixed integer linear programming (MILP) model with the objective of minimizing the total travel distance. A coordinate representation particle swarm optimization (CRPSO) algorithm is developed to obtain the best delivery sequencing and the capacity of each vehicle. Results of the computational study show that the proposed method provides solution within a reasonable amount of time. Finally, the result compared to PSO also indicates that the CRPSO is effective.
Keywords: Third-party logistics; open vehicle routing problem with time windows; dedicated destination
Notations
| t: | Iteration index, t = 1…T |
| i: | Particle index, i = 1…I |
| d: | Dimension index, d = 1…D |
| u: | Uniform random number in the interval [0,1] |
| w(t): | Inertia weight in the tth iteration |
| vid(t): | Velocity of the ith particle at the dth dimension in the tth iteration |
| xid(t): | Position of the ith particle at the dth dimension in the tth iteration |
| Pid: | Personal best position (pbest) of the ith particle in the dth dimension |
| Pgd: | Global best position (gbest) in the dth dimension |
| Cp: | Personal best position acceleration constant |
| Cg: | Global best position acceleration constant |
| Xmax: | Maximum position value |
| Xmin: | Minimum position value |
| Xi: | Vector position of the ith particle, [xi1, xi2, … xiD] |
| Vi: | Vector velocity of the ith particle, [vi1, vi2, … viD] |
| Pi: | Vector personal best position of the ith particle, [Pi1, Pi2, … PiD] |
| Pg: | Vector global best position, [Pg1, Pg2, … PgD] |
| Ri: | Set of vehicle routes corresponding to the ith particle |
| Di: | Set of distances between vehicles and destinations corresponding to ith particle |
| Ψ(Xi): | Fitness value of Xi |
In B2B e-commerce, logistics is viewed as an increasingly important activity. Regardless of industry, most e-businesses rely on logistics management to enhance their competitiveness [1]. Despite the importance of logistics management, e-businesses tend to focus primarily on developing their core abilities (e.g., R&D, product, marketing). Logistics and other non-core activities often are outsourced to other companies [2]. Independent third-party logistics (3PL) companies provide professional, integrated distribution services and information technology to help decrease fixed and variable costs of logistics [3]. With the rapid development of electronic commerce, e-businesses are facing new challenges in the logistics supply chain and are partnering extensively with 3PL firms to deliver products on time, increase customer satisfaction, decrease logistics costs and increase profits.
Logistics professionals must take many constraints into account in order to plan optimal distribution routes that consider customer demand, vehicle routing, vehicle capacity, etc. Together, these constraints associated with delivery logistics are called the vehicle routing problem (VRP) [4]. Ref. [5] solved online pick-to-sort order batching problem for managing frequent arrivals in B2B e-commerce. Ref. [6] applied the meta-heuristic method of ant colony optimization (ACO) to an established set of vehicle routing problems (VRP). The VRP can be divided into two types: the Hamiltonian cycle (traditional VRP, where the vehicle returns to the depot), and the Hamiltonian path (the open vehicle routing problem, or OVRP, where the vehicle does not need to return to the depot). Thus, routing destination is the biggest difference between the VRP and the OVRP.
In this paper, we propose a solution to the open vehicle routing problem with time windows (OVRPTW) considering 3PL. In the problem, a 3PL company leaves its vehicles at its client’s depot until they are loaded. Post-delivery, vehicles do not return to the depot, but to the nearest 3PL company location with available space. In most previous OVRPTW literature that considered 3PL, a vehicle’s final destination was not considered. However, in this research, we not only consider common constraints in OVRPTW such as vehicle capacity, but also a 3PL constraint in which the vehicles must return to a 3PL company location · a limitation of destination. We propose a mixed integer linear programming (MILP) model that considers these practical characteristics. In this research, we use a classical OVRPTW formulation with 3PL considerations to solve an experimental problem set. Due to the computational complexity of the model, we designed a coordinate representation particle swarm optimization (CRPSO) algorithm to obtain the near-optimal vehicle routing plan with the objective of minimizing total travel distance.
The rest of this paper is organized as follows. In Section 2, we review the literature on related VRPs considering 3PL and OVRPTW. In Section 3, we present the proposed MILP model for the problem and the CRPSO algorithm used to obtain the solutions. In Section 4, we present a computational study that demonstrates the excellent performance of the CRPSO algorithm. Finally, in Section 5 we summarize the results of this research and suggest a possible direction for future research.
Many enterprises outsource non-core functions such as distribution logistics to promote competitiveness; in response to this trend, the 3PL sector is growing rapidly [2]. Increasingly, VRP researchers also are considering 3PL. [7] presented a web-based decision support system (DSS) for waste lube oils collection and recycling operations considering cooperation with a 3PL company. Because the logistics function is outsourced to a 3PL company, vehicle routing begins from the depot and ends at a 3PL location. This feature of delivery is similar to our research. In the study, the DSS system enables schedulers to tackle reverse supply chain management problems interactively and can be applied to realistic reverse logistical planning problems [8].
Baykasoglu and Kaplanoglu proposed a multi-agent based load consolidation decision-making approach considering many kinds of logistics mechanisms, including in-house logistics systems and 3PL, so as to improve the logistics efficiency of enterprises [9]. Amorim et al. formulated models for a case of perishable goods with a mix of fixed and loose shelf lives. When the shelf life of product did not match the distribution plan, it would be outsourced to a 3PL company. The results show that the economic benefits derived from using an integrated approach depend greatly on the freshness level of delivered products [10]. Moon et al. extended the VRPTW to the VRPTW with overtime and outsourcing vehicles (VRPTWOV), which allows overtime for drivers and the possibility of using outsourced vehicles. They developed a mixed integer programming model, a genetic algorithm (GA) and a hybrid algorithm based on simulated annealing to demonstrate the efficiency of their solution [11]. In this paper, we extend research in this important area by proposing a solution to an experimental problem set that incorporates 3PL considerations into a classical OVRPTW formulation.
Routing destination is the biggest difference between VRP and OVRP. VRP is called the Hamiltonian cycle, and OVRP is called the Hamiltonian path [12]. All other constraints, such as vehicle capacity, time windows, etc. are the same. OVRP was not as important as VRP in the early 1980s. Schrage was the first to classify routing types and define OVRP with the objective of minimizing the number of routes (i.e., vehicles) and total cost [13].
OVRP is a very common problem in daily life, especially in logistics, transportation and other similar industries. Several scholars have proposed solutions to problems in these contexts. Sariklis and Powell proposed a two-stage model based on a minimum spanning tree to solve a vehicle routing decision problem [14]. Li et al. developed a hybrid ant colony algorithm (ACO) combined with taboo search (TA) to solve OVRP [15]. Fleszar et al. proposed variable neighborhood search (VNS) to determine the customer service sequence [16]. OVRPTW (the focus of this research) extends OVRP by considering the concept of time windows. Recently, researchers have proposed solutions to such problems. Repoussis et al. proposed a comprehensive mathematical model to capture all aspects of OVRPTW, which they solved using a greedy look-ahead route construction heuristic algorithm [7].
In most of the extant literature, researchers solved VRP, VRPTW, OVRP and OVRPTW as individual problems. Unlike previous studies, however, this paper addresses a new topic: OVRPTW considering 3PL. Since OVRPTW is NP-hard, most researchers have solved such problems using heuristic algorithms [16]. However, due to the computational complexity of the model, it was necessary to develop an algorithm based on particle swarm optimization (PSO) to solve the proposed problem. Since a standard PSO algorithm cannot be applied to discrete problems directly, the encoding and decoding methods are critical. Ai and Kachitvichyanukul proposed a PSO algorithm for solving a vehicle routing problem with simultaneous pickup and delivery (VRPSPD) as well as a capacitated vehicle routing problem (CVRP) [17,18]. The solution representation for VRPSPD with n customers and m vehicles is a (n + 2m) dimensional particle. The decoding method starts by transforming the particle into a priority list of customers and a priority matrix of vehicles to serve each customer. The vehicle routes are constructed based on the customer priority list and the vehicle priority matrix. Applying this encoding method, we propose a coordinate representation particle swarm optimization (CRPSO) algorithm to obtain the optimal solution. The designed algorithm with n customers and m vehicles yields (n + 2m + m) dimensions for each particle. The encoding and decoding methods are described in detail in Section 4.
The logistics department at the depot is determining routes for delivery vehicles, and the forwarder will load goods into the vehicles based on customer demand and deliver them following the assigned routes. As shown in Fig. 1, the problem considering 3PL can be described as follows. There is one depot, and the number of vehicles and demand for each customer are known. Many vehicles owned by a 3PL company are parked at the depot and ready to be loaded. All vehicles have the same capacity, and depart the depot to deliver goods to customers with specific demand. Each customer must be served only once by one vehicle within the delivery time window, which is bounded by an earliest start time and latest start time. Since this is an OVRPTW problem considering 3PL, the vehicles do not return to the depot, but to the nearest 3PL company location with available space. Based on these constraints, the objective is to minimize the total travel distance.
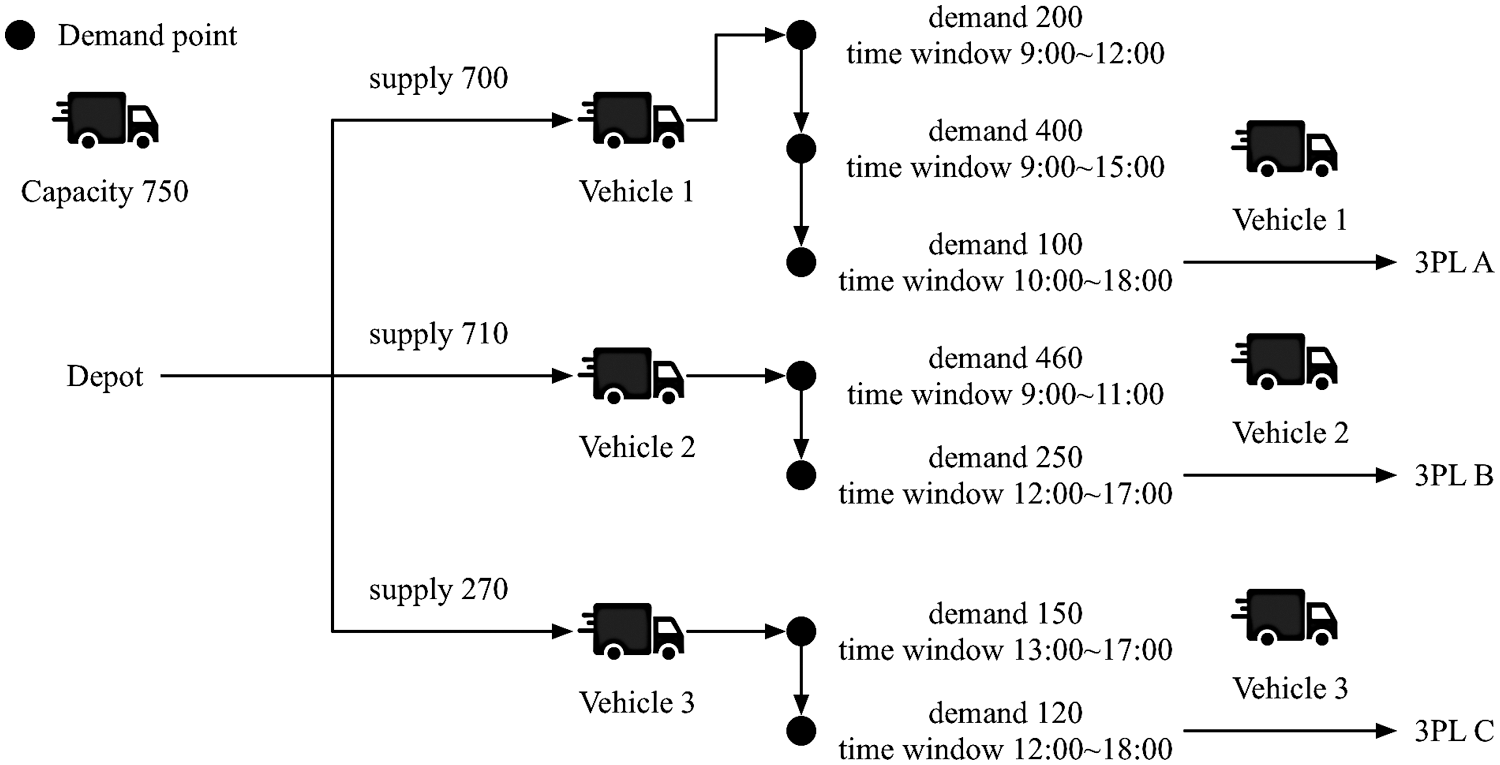
Figure 1: Illustration of delivery logistics
In this section, we formulate the mixed integer linear programming model for the addressed OVRPTW problem considering 3PL. Specifically, we modify Repoussis et al.’s MILP model [7] to incorporate 3PL considerations. Notations are defined as follows:
A. Notations
• Indexes
i, j: the index of the node being used as the demand point, including the depot
k: the service vehicle index
r: the index of 3PL company locations
• Sets
N: the set of customers including node of the depot, where i or j = 1.
V: the set of vehicles
PL: the set of 3PL locations
• Parameters
C: capacity of each vehicle
qi: demand of customer i
cij: the cost from node i to node j, i ≠ j
tij: travel time from node i to node j, i ≠ j
dij: the distance from node i to node j, i ≠ j
wk: fixed cost for the acquisition of vehicle k
[ei,li]: time window, i ∈ N, where
ei: the earliest service start time for customer i
li: the latest service start time for customer i
si: service time of customer i
pi: departure time from customer i
ai: arrival time to customer i
• Variables
C. Mixed integer linear programming model
We formulated a mixed integer linear programming model for the addressed OVRPTW problem considering 3PL. We describe the objective function and constraints below.
Objective function
The objective function is to minimize the total travel distance.
Subject to
Constraints (5) and (6) ensure that exactly one vehicle arrives at and departs from each customer and the depot.
Constraint (7) is relative to x and z variables, ensuring that all customers are visited by active vehicles.
Constraint (8) guarantees the flow continuance for each vehicle route.
Constraint (9) ensures that the total service quantity of each vehicle does not exceed its capacity.
Constraint (10) eliminates sub-tour routes.
Constraints (11) and (12) are related to time windows and ensuring feasible schedules for vehicles. If customers i and j are scheduled consecutively on the route of vehicle k, the arrival time of customer j is equal to the departure time of customer i plus the travel time between these two customers, where M is a large number.
Constraints (13) and (14) insure that the relationships between arrival time, departure time and service time are compatible with customer i’s time window.
Constraint (15) sets the departure time of all vehicles from the depot to be zero.
Lastly, constraints (16) and (17) define variables x and z for each vehicle k. So far, Eqs. (1) to (17) describe the standard VRPTW formulation without considering the “open” routing concept.
Constraints (18) and (19) specify such “open” characteristics. Constraint (18) guarantees that every vehicle will depart from the depot to service a sequence of customers, and constraint (19) ensures that no vehicles will return to the depot. So far, Eqs. (1) to (19) comprise the classical OVRPTW model. In this case, we need the following constraint:
Constraint (20) ensures that the final destination for each vehicle is a 3PL company location. It is worth mentioning the difference between our problem and the original problem solved by [7]. Equation (20) limits the end point of each vehicle’s route to a 3PL company location. That is, when a vehicle finishes making its deliveries, it returns to a specific destination.
We developed a coordinate representation particle swarm optimization algorithm to search for near-optimal solutions of the appropriate customer sequence and determine the feasible capacity of each vehicle based on coordinate dimensions and evolutionary processes. To evaluate the fitness values of the coordinate-coded dimensions obtained from the particle swarm optimization algorithm, we first developed a customer sequencing assignment procedure to determine the customer delivery priorities. Then, we used coordinate representation to generate a vehicle priority matrix and a destination priority matrix. In order to construct vehicle routes, vehicle capacity must be limited. Following the procedures described in the previous section with the associated constraints, the travel distance for each vehicle route can be calculated as the fitness value of each particle dimension. The CRPSO is repeated until the termination condition is satisfied.
Particle swarm optimization was proposed by Eberhart and Kennedy [19]. PSO was first intended to simulate social behavior as a stylized representation of the movement of a group of organisms (e.g., a flock of birds or a school of fish). [20] propose that PSO achieves better specific work output across a range of algorithm control parameters and converges to optimum solution with lower computation cost. [21] implement Particle swarm optimization (PSO) and artificial bee colony (ABC) optimization methods to the histogram stretching technique in parameter selection process. [22] also integrate Particle swarm optimization (PSO) to obtain the optimal parameter combination of the regularization parameter c and the kernel function width coefficient in least squares support vector machine (LSSVM). The newly combined methodology provides better generalization ability, and higher prediction accuracy for highway cost prediction in complex environments. In PSO, a swarm of P particles serves as a searching agent for a specific problem solution. The searching strategy of PSO requires updating the new position and velocity for the next iteration based on the current velocity of each particle (vi), the personal best experience of each particle (xp(i)), and the global best experience of all particles (xg). The procedure of calculating the new velocity and the position of every particle in the next iteration could be shown in the mathematical model. Equation (21) shows that the new velocity of the particle is updated using the current position and the current velocity. Each particle moves the new position in the next iteration according to the Equation (22).
where vid (t) represents the velocity of the dth dimension of the ith particle in the tth iteration. The variable xid(t) represents the position of the dth dimension of the ith particle in the tth iteration. The variable w represents the inertia weight, c1 is the self-cognition acceleration coefficient, and c2 is the social cognition acceleration coefficient, r1 and r2 are two separately generated, uniformly distributed random numbers in the range [0,1].
The CRPSO framework for solving OVRPTW considering 3PL in this paper is based on the Object Library for Evolutionary Techniques [23]. The notations and a description of the algorithm are provided below.
CRPSO Framework
1) Set iteration t = 1. Initialize I particles as a population, generate the ith particle with random position Xi in the range [Xmax, Xmin]. Velocity Vi = 0 and personal best Pi = Xi for i = 1…I.
2) For i = 1…I, decode Xi to a set of vehicle routes Ri and vehicle destination Di (see decoding method in Section 4.3).
3) For i = 1…I, compute the performance measurement of Ri and Di, i.e., the total travel distance for all routes, and set this as the fitness value of Xi, represented byΨ(Xi).
4) Update pbest, for i = 1…I, update Pi = Xi, if Ψ(Xi) < Ψ(Pi).
5) Update gbest, for i = 1…I, update Pg = Pi, if Ψ(Pi) < Ψ(Pg).
6) Update the velocity and the position of each ith particle
If xid (t + 1) > Xmax, then
If xid (t + 1) < Xmin, then
7) If the stopping criterion is met, i.e., t = T, stop. Otherwise, t = t + 1 and return to step 2.
8) Decode Pg as the best set of vehicle routes found, R* + D* with its corresponding performance measurement Ψ(Pg).
3.4 Solution Representation of CRPSO
The solution representation of vehicle routes is one of the key elements for an effective implementation of CRPSO to solve OVRPTW considering 3PL. The solution representation in CRPSO of OVRPTW considering 3PL with n customers and m vehicles consists of (n + 2m + m) dimensional particles, as shown in Fig. 2. Each dimension of a particle is encoded as a real number. Hence, the solution representation is divided into four parts: the customer priority list, the vehicle priority matrix, the 3PL destination priority matrix, and the vehicle capacity matrix. Fig. 2 illustrates an example for eight customers and two vehicles.

Figure 2: Particle dimensions in CRPSO
The first eight dimensions are related to customers, and each dimension represents a single customer. These dimensions are required to create a priority list of customers to be added to the routes. The priority list is determined by sorting the first eight dimensional values. Smaller values indicate higher priority customers. The second and third parts of CRPSO extract the reference points for vehicles. These reference points determine the vehicle priority matrix for routes, which is constructed based on the relative distance between these points and a customer’s location. In other words, a vehicle is defined as a reference point on a Google map. Customers are prioritized to be served by closer vehicles. These reference points also determine the 3PL destination priority matrix based on the distance between these points and 3PL company locations. In the second and third parts, the four dimensions consist of longitude and latitude for each vehicle. Therefore, the representation is called a coordinate representation. The last part, comprised of two dimensions, is associated with the capacity of each vehicle. The value of each dimension is the service limitation for each vehicle. The purpose of this representation is to avoid problems such as exceeding delivery capacity.
In summary, the proposed solution representation consists of three types of dimensional designs, including customer sequencing, vehicle coordinates, and vehicle capacity. The problem with n customers and m vehicles requires (n + 2m + m) dimensions for every particle. Each particle dimension is encoded as a real number. The first n dimensions represent customer priorities, and the values of each dimension are converted into a customer priority list in the decoding procedure. The second 2m dimensions represent the reference points for vehicles. These values are turned into the vehicle priority matrix and the 3PL destination priority matrix. The last m dimensions represent the capacity of each vehicle. An example of the CRPSO solution representation is displayed in Fig. 3.
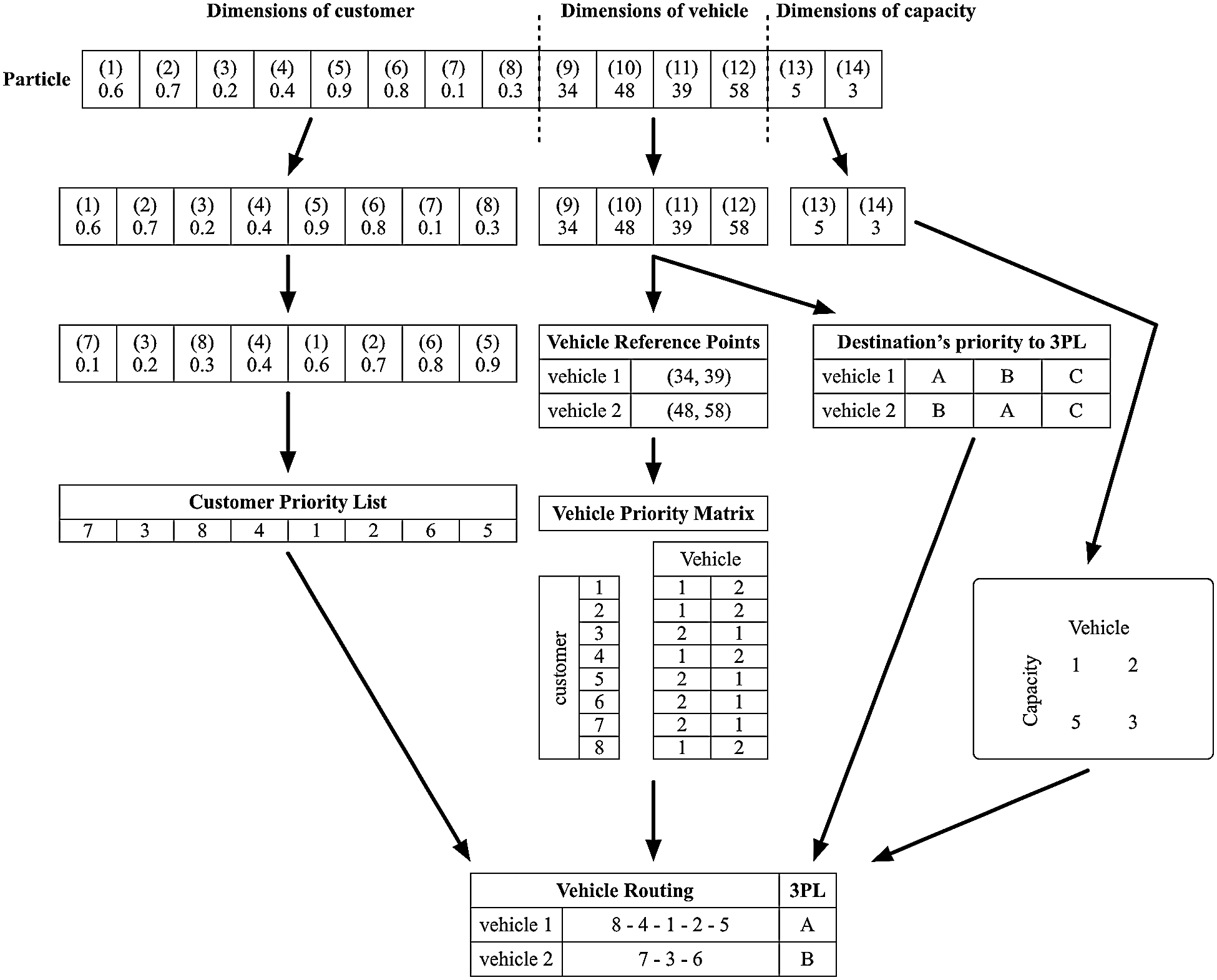
Figure 3: CRPSO solution representation
The decoding method is modified from Ai and Kachitvichyanukul’s decoding method in our CRPSO solution [17]. The notations and decoding procedure are presented below.
Notations
Decoding procedure
1) Construct the priority list of customers (U) and the list of vehicles (L).
i) Build set S = {1, 2, …, n} and
ii) Select c from set S where
iii) Add c to the last position in set U.
iv) Remove c from set S.
v) Repeat step 1, parts b–d until
2) Construct the vehicle priority matrix (V) and the 3PL destination priority matrix (D).
a. Set the vehicle reference position. For j = 1…m, set
b. For each customer k, k = 1…n.
i) For each vehicle j = 1…m, set
ii) Build set S = {1, 2, …, m} and
iii) Select c from set S where
iv) Add c to the last position in set Vk.
v) Remove c from set S.
vi) Repeat step 2b, parts iii–v until
c. For each vehicle j, j = 1…m
i) For each 3PL z = 1…Z, set
ii) Build set S = {1, 2, …, Z} and
iii) Select c from set S where
iv) Add c to the last position in set Dk.
v) Remove c from set S.
vi) Repeat step 2c, parts iii–v until
3) Determine vehicle routes and vehicle 3PL destinations.
a. Set k = 1.
b. Add customers one by one to the route.
i) Set l = Uk and p = 1.
ii) Set j = Vl,q.
iii) Create a new candidate route by inserting customer l into the best sequence in route Rij, which has the smallest additional cost.
iv) Check the capacity and route time constraints of the candidate route.
v) If a feasible solution is reached, update route Rij with the candidate route.
vi) If p = m, go to step 3c. Otherwise, set p = p + 1 and go to step 3b, part ii.
c. If k = n, stop. Otherwise, set k = k + 1 and repeat step 3b.
d. Set j = 1
e. Assign vehicles one by one to a 3PL destination.
i) Set l = Lk and q = 1
ii) Set z = Dl,q.
iii) Create a new candidate destination by assigning vehicle l to the best destination in the 3PL Dij.
iv) If a feasible solution is reached, update the route Dij with the candidate destination.
v) If q = Z, stop. Otherwise, set q = q + 1 and go to step 3e, part ii.
This section compares the performance of the developed CRPSO algorithm to PSO using problems of the same scale, and evaluates the quality of the CRPSO solution by analyzing the computational results. This section consists of three parts: benchmark instances, parameter settings and PSO dimensions, and a comparison table. We tested our research experiments using Solomon’s 56 VRPTW benchmark instances [24] on a computer equipped with an Intel(R) Core(TM) i5-3210M 2.50GHz CPU and 4 GB RAM running the Microsoft Windows 7 operating system.
We tested the proposed heuristic on three different data sets [24]. Solomon’s 56 VRPTW benchmark problems consist of six sets (C1, C2, R1, R2, RC1, RC2), each of which contains between 8 and 12 problems; each data set has 100 nodes. C, R, and RC represent three different types of customer sets. C represents Clustered customers, R indicates randomly (uniformly) distributed customers, and RC represents Semi-clustered customers; that is, a combination of clustered and randomly (uniformly) distributed customers.
Moreover, C, R and RC problems can be further classified into two types: type 1 (C1, R1, RC1) problems have short time windows and small vehicle capacities, and type 2 (C2, R2, RC2) problems have long time windows and large vehicle capacities. However, the proposed problem in this paper is OVRPTW considering 3PL, so the problem set differs from Solomon’s data [24]. Therefore, we divided the original 100 nodes in the experimental problem set into two groups; we assigned the first 90 nodes in each problem to customers, and the remaining 10 nodes to 3PL companies. After a vehicle makes its final delivery, it must return to the nearest 3PL location with available space. Vehicle destinations are limited to the 10 3PL nodes, but the capacity of each 3PL location is limited to three (i.e., only three vehicles can return to each 3PL location). Hence, each vehicle must be assigned to a 3PL location according to the 3PL destination priority matrix. If the nearest 3PL is full, the vehicle will return to the nearest location with available space.
4.2 Parameter Settings and PSO Dimensions
The parameter settings in PSO and CRPSO include population size as 100, iteration as 200, Cp as 2 and Cg as 2. A PSO problem with n customers and m vehicles consists of (n + m) dimensional particles. Each dimension in each particle is encoded as a real number, and the solution representation is divided into two parts. The first part is used to create a customer priority list by sorting the dimensional values. Smaller values indicate higher priority customers. The second part is same as the capacity dimension in CRPSO.
The proposed CRPSO algorithm and PSO was implemented using the Visual Studio C# programming language. Some criteria can be used to evaluate the effectiveness of the developed CRPSO algorithm. One common criterion is the solution gap between the optimal solution of PSO and the best solution found by the CRPSO algorithm. The experiments verify the solution to determine the improvement rate for travel distance. The solution gap is defined as below [25].
where B is the optimal solution obtained from the PSO result, and S is the optimal solution of the CRPSO algorithm.
All 56 data sets from Solomon’s problems [24] are tested and the results are shown in Tab. 1. In the table, TD is travel distance, NV is the number of vehicles used, and CPU is the computational time in seconds. The objective in this research is to minimize the total travel distance, that is, TD is viewed as an indicator of solution quality that enables the PSO and CRPSO solutions to be compared. Overall, the proposed CRPSO algorithm is effective at finding the shortest path to service all customers. Compared to the PSO result, the average travel distances for all three problem types are shorter, as indicated by the solution gap. Beyond the solution gap, NV is another important index to discuss.
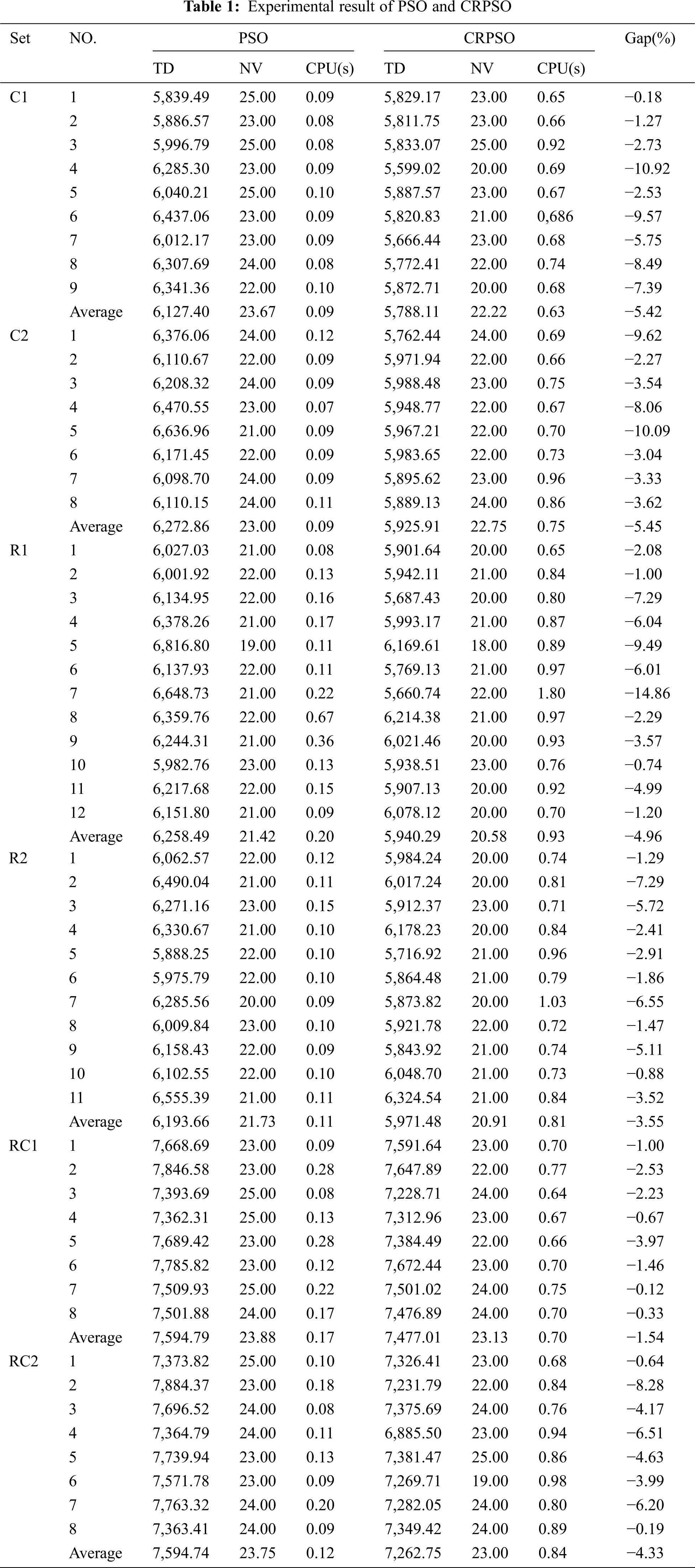
Figs. 4–6 indicate solution quality based on TD and NV. In problem set C, CRPSO is more efficient than PSO for most problems. Although the NV of PSO is less than the NV of CRPSO in problem 5 of subset C2, the total distance is also longer. In this case, routes with a lower NV are not the most appropriate solution. The same situation can be also observed in problem 7 of subset R1. Moreover, PSO and CRPSO have approximately equivalent solving abilities in problem set R compared with the other two problem types.
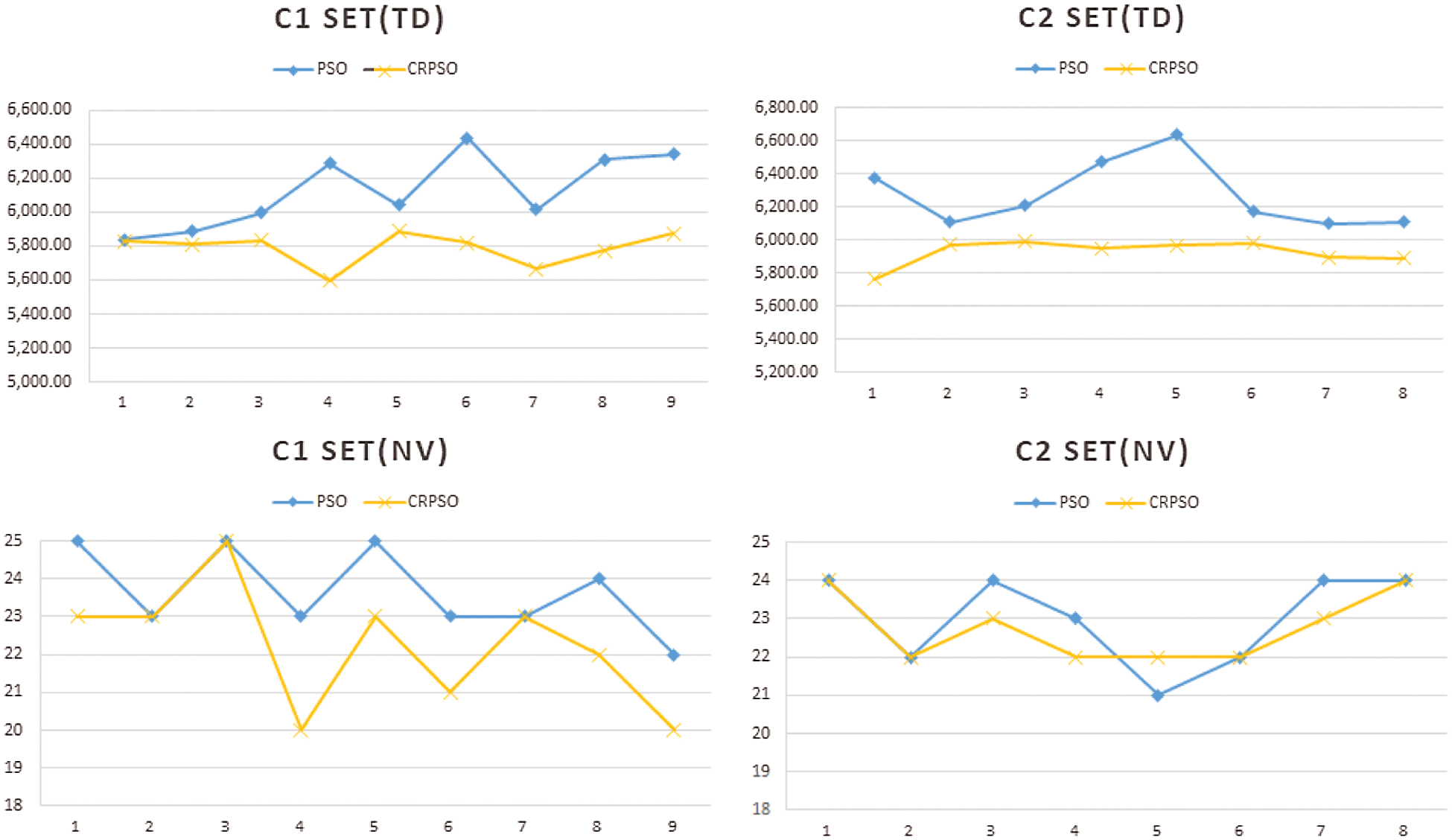
Figure 4: Problem set C
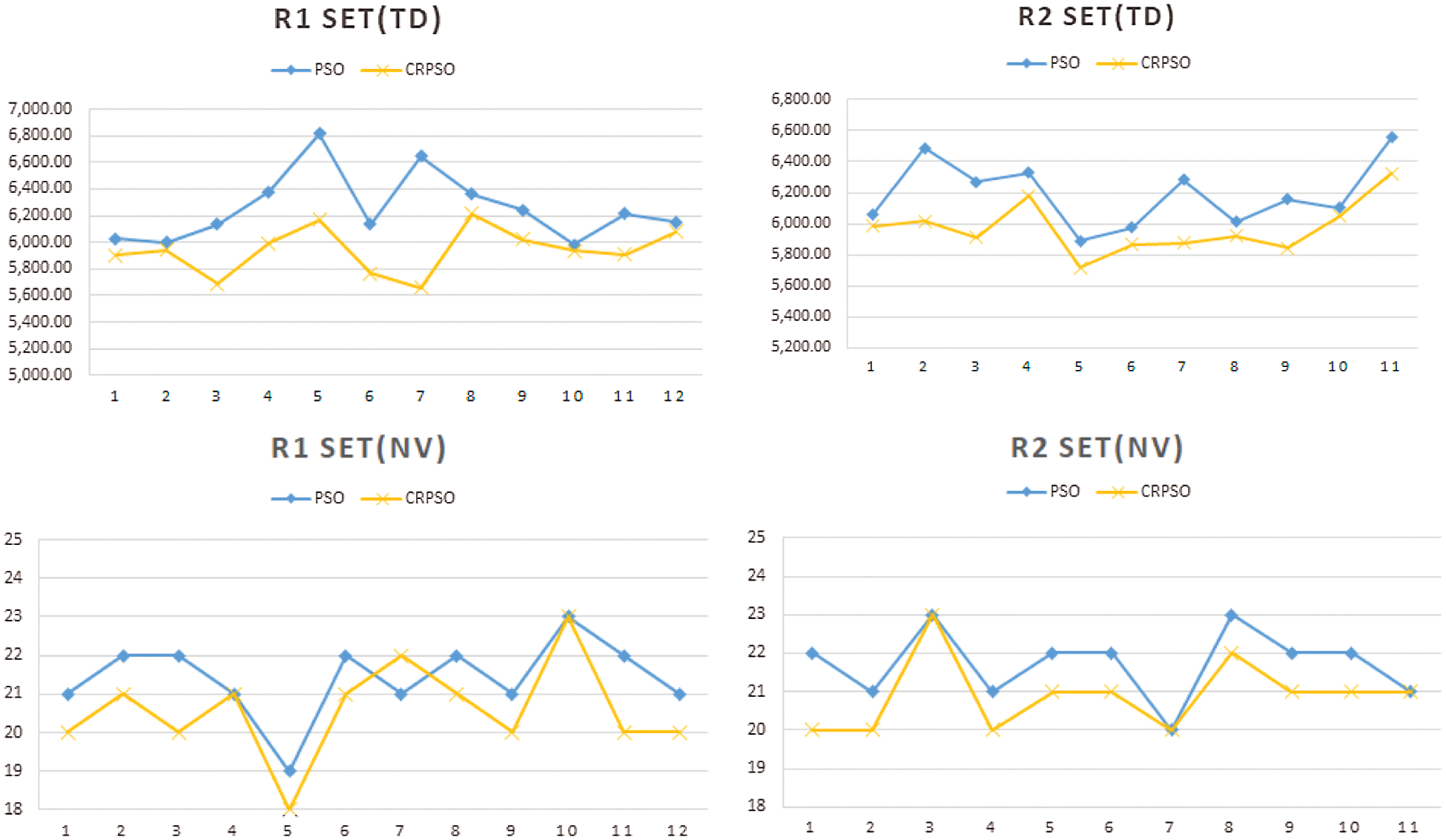
Figure 5: Problem set R
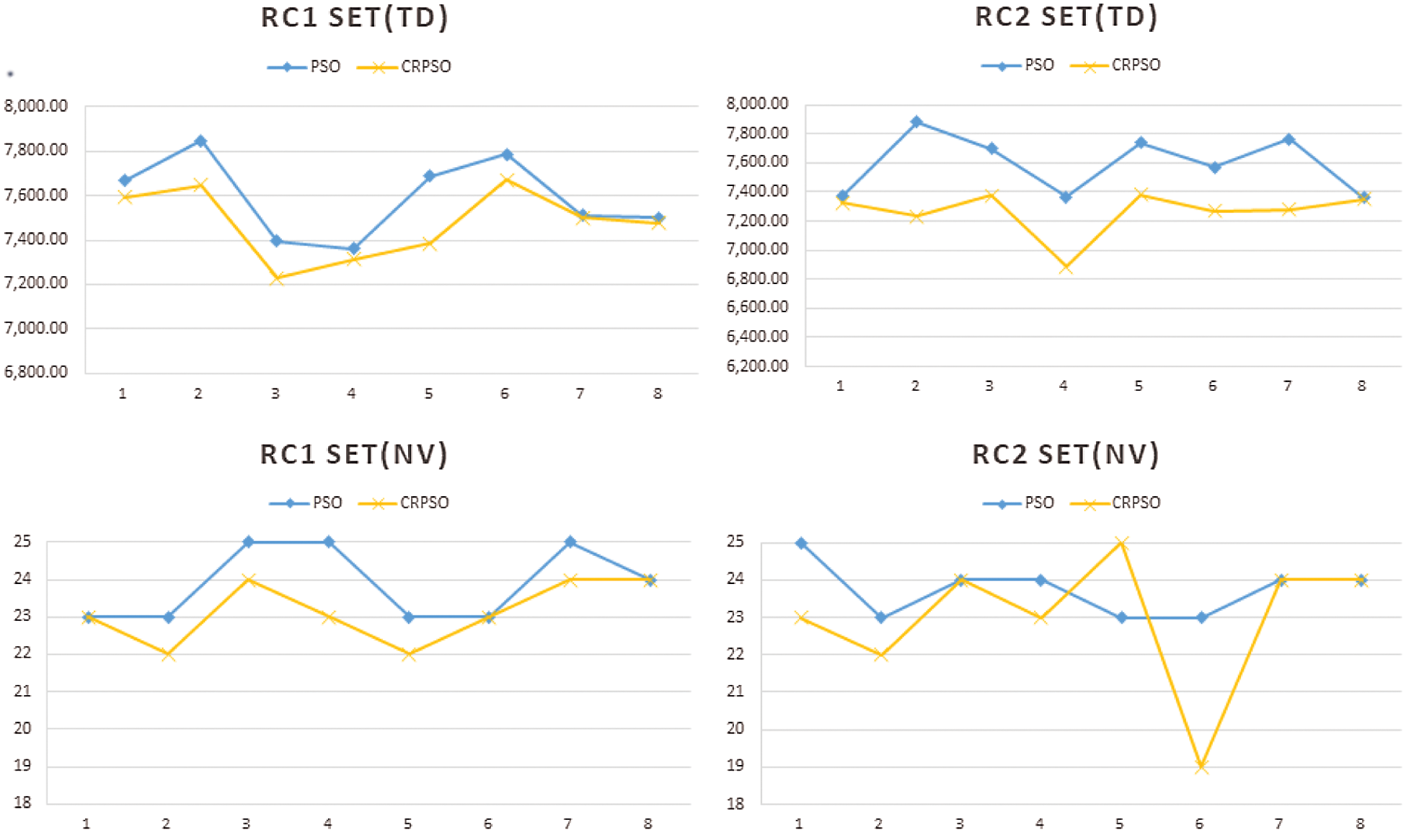
Figure 6: Problem set RC
The experiment in this paper reveals two factors that can be used as comparison criteria to analyze solution quality. As shown in the comparison table, the proposed CRPSO is more feasible for solving OVRPTW considering 3PL. Whether by total travel distance or number of vehicles, CRPSO consistently outperforms PSO with respect to solution quality. Nonetheless, the number of vehicles used is slightly higher in a few problems, as mentioned above. In the tradeoff between travel distance and number of routes, this is a reasonable result. Our approach seems to be a very practical tool that can help 3PL companies effectively schedule their daily routes.
This paper presented a solution to an open vehicle routing problem with time windows considering 3PL. The delivery vehicles are operated by a 3PL company, and return to the nearest 3PL company location with available space once deliveries are complete. This paper modified the mixed integer linear programming model used by Repoussis et al. (2007) considering standard constraints of OVRPTW and 3PL [7]. Due to computational complexity, a CRPSO algorithm to obtain the near-optimal solution is developed. Results of the computational study show that the proposed CRPSO algorithm provides solutions within a reasonable amount of time. The encoding method yields the optimal distribution so that the delivery quantity for each route does not exceed vehicle capacity. Furthermore, the proposed algorithm reduces the number of vehicles used to make deliveries to customers. Finally, the PSO mechanism can generate multiple solutions and continues to iteratively search for the best solution. In terms of future research directions, this research can be expanded to add more locations for each 3PL company so that the vehicle has more destination options. The utility of such an expansion should be investigated.
Funding Statement: All the authors received no specific funding for this study.
Conflicts of Interest: All the authors declare that they have no conflicts of interest to report regarding the present study.
1. S. Hertz and M. Alfredsson, “Strategic development of third-party logistics providers,” Industrial Marketing Management, vol. 32, no. 2, pp. 139–149, 2003. [Google Scholar]
2. J. B. Quinn, “Strategic outsourcing: Leveraging knowledge capabilities,” Sloan Management Review, vol. 40, no. 4, pp. 9–21, 1999. [Google Scholar]
3. M. Christopher, Logistics & supply chain management. New York: Pearson Publishing, 2016. [Google Scholar]
4. G. B. Dantzig and J. H. Ramser, “The truck dispatching problem,” Management Science, vol. 6, no. 1, pp. 80–91, 1959. [Google Scholar]
5. K. H. Leung, C. K. Lee and K. L. Choy, “An integrated online pick-to-sort order batching approach for managing frequent arrivals of B2B e-commerce orders under both fixed and variable time-window batching,” Advanced Engineering Informatics, vol. 45, pp. 101–125, 2020. [Google Scholar]
6. J. E. Bell and P. R. McMullen, “Ant colony optimization techniques for the vehicle routing problem,” Advanced Engineering Informatics, vol. 18, no. 1, pp. 41–48, 2004. [Google Scholar]
7. P. P. Repoussis, C. D. Tarantilis and G. Ioannou, “The open vehicle routing problem with time windows,” Journal of the Operational Research Society, vol. 58, no. 3, pp. 355–367, 2007. [Google Scholar]
8. P. P. Repoussis, D. C. Paraskevopoulos, G. Zobolas, C. D. Tarantilis and G. Ioannou, “A web-based decision support system for waste lube oils collection and recycling,” European Journal of Operational Research, vol. 195, no. 3, pp. 676–700, 2009. [Google Scholar]
9. A. Baykasoglu and V. Kaplanoglu, “A multi-agent approach to load consolidation in transportation,” Advances in Engineering Software, vol. 42, no. 7, pp. 477–490, 2011. [Google Scholar]
10. P. Amorim, H.-O. Günther and B. Almada-Lobo, “Multi-objective integrated production and distribution planning of perishable products,” International Journal of Production Economics, vol. 138, no. 1, pp. 89–101, 2012. [Google Scholar]
11. I. Moon, J.-H. Lee and J. Seong, “Vehicle routing problem with time windows considering overtime and outsourcing vehicles,” Expert Systems with Applications, vol. 39, no. 18, pp. 13202–13213, 2012. [Google Scholar]
12. M. Dorigo, V. Maniezzo and A. Colorni, “Ant system: optimization by a colony of cooperating agents,” IEEE Transactions on Systems, Man, and Cybernetics, Part B: Cybernetics, vol. 26, no. 1, pp. 29–41, 1996. [Google Scholar]
13. L. Schrage, “Formulation and structure of more complex/realistic routing and scheduling problems,” Networks, vol. 11, no. 2, pp. 229–232, 1981. [Google Scholar]
14. D. Sariklis and S. Powell, “A heuristic method for the open vehicle routing problem,” Journal of the Operational Research Society, vol. 51, no. 5, pp. 564–573, 2000. [Google Scholar]
15. X. Li, P. Tian and S. C. Leung, “An ant colony optimization metaheuristic hybridized with tabu search for open vehicle routing problems,” Journal of the Operational Research Society, vol. 60, no. 7, pp. 1012–1025, 2009. [Google Scholar]
16. K. Fleszar, I. H. Osman and K. S. Hindi, “A variable neighbourhood search algorithm for the open vehicle routing problem,” European Journal of Operational Research, vol. 195, no. 3, pp. 803–809, 2009. [Google Scholar]
17. T. J. Ai and V. Kachitvichyanukul, “Particle swarm optimization and two solution representations for solving the capacitated vehicle routing problem,” Computers & Industrial Engineering, vol. 56, no. 1, pp. 380–387, 2009a. [Google Scholar]
18. T. J. Ai and V. Kachitvichyanukul, “A particle swarm optimization for the vehicle routing problem with simultaneous pickup and delivery,” Computers & Operations Research, vol. 36, no. 5, pp. 1693–1702, 2009b. [Google Scholar]
19. R. Eberhart and J. Kennedy, “A new optimizer using particle swarm theory. Paper presented at the MHS’95,” in Proceedings of the Sixth International Symposium on Micro Machine and Human Science, Nagoya, Japan, 1995. [Google Scholar]
20. J. Clarke, L. McLay and J. T. McLeskey Jr, “Comparison of genetic algorithm to particle swarm for constrained simulation-based optimization of a geothermal power plant,” Advanced Engineering Informatics, vol. 28, no. 1, pp. 81–90, 2014. [Google Scholar]
21. A. Elbir, H. İlhan and N. Aydın, “The implementation of optimization methods for contrast enhancement,” Computer Systems Science and Engineering, vol. 34, no. 2, pp. 101–107, 2019. [Google Scholar]
22. X. Wang, S. Liu and L. Zhang, “Highway cost prediction based on LSSVM optimized by initial parameters,” Computer Systems Science and Engineering, vol. 36, no. 1, pp. 259–269, 2021. [Google Scholar]
23. S. Nguyen, T. J. Ai and V. Kachitvichyanukul, Object library for evolutionary techniques ETLib: User’s guide. Thailand: High Performance Computing Group, Asian Institute of Technology, 2010. [Google Scholar]
24. M. M. Solomon, “Algorithms for the vehicle routing and scheduling problems with time window constraints,” Operations Research, vol. 35, no. 2, pp. 254–265, 1987. [Google Scholar]
25. T.-L. Chen, J.-T. Lin and S.-C. Fang, “A shadow-price based heuristic for capacity planning of TFT-LCD manufacturing,” Journal of Industrial and Management Optimization, vol. 6, no. 1, pp. 209–241, 2010. [Google Scholar]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |