DOI:10.32604/csse.2022.019943

| Computer Systems Science & Engineering DOI:10.32604/csse.2022.019943 |  |
| Article |
Software Reliability Assessment Using Hybrid Neuro-Fuzzy Model
1Department of Computer Applications, Manav Rachna International Institute of Research and Studies, Faridabad, 121006, India
2Department of Computer Science, College of Computer Science and Engineering, Taibah University, Madinah, Saudi Arabia
3Department of Computer Applications, Chandigarh Group of Colleges, Landran, 140307, India
4College of Computer Sciences and Information Technology, King Faisal University, Saudi Arabia
5Department of Electronics & Communication Engineering, Birla Institute of Technology, Mesra Jharkhand, India
*Corresponding Author: Surbhi Bhatia. Email: surbhibhatia1988@yahoo.com
Received: 02 May 2021; Accepted: 30 July 2021
Abstract: Software reliability is the primary concern of software development organizations, and the exponentially increasing demand for reliable software requires modeling techniques to be developed in the present era. Small unnoticeable drifts in the software can culminate into a disaster. Early removal of these errors helps the organization improve and enhance the software’s reliability and save money, time, and effort. Many soft computing techniques are available to get solutions for critical problems but selecting the appropriate technique is a big challenge. This paper proposed an efficient algorithm that can be used for the prediction of software reliability. The proposed algorithm is implemented using a hybrid approach named Neuro-Fuzzy Inference System and has also been applied to test data. In this work, a comparison among different techniques of soft computing has been performed. After testing and training the real time data with the reliability prediction in terms of mean relative error and mean absolute relative error as 0.0060 and 0.0121, respectively, the claim has been verified. The results claim that the proposed algorithm predicts attractive outcomes in terms of mean absolute relative error plus mean relative error compared to the other existing models that justify the reliability prediction of the proposed model. Thus, this novel technique intends to make this model as simple as possible to improve the software reliability.
Keywords: Software quality; reliability; neural networks; fuzzy logic; neuro-fuzzy inference system
Reliability is a vital factor of software quality and is an active research area for over a decade. The reliability of software can be interpreted as the probability of performing the failure-free operation in the context of a specified time in a defined environment [1,2]. Checking the reliability of the critical software would cost very higher than conventional software [3]. Certainly, there are no error-free software exits. If the software does not fail, it does not mean it has no fault. There can be hidden faults exist which may cause serious consequences in the case of safety critical applications.
Various researchers have proposed different software reliability models [4]. These traditional software reliability models consider only timing and failure rate as the important factors. Still, this approach is not perfect as various other factors are directly and indirectly associated with reliability [5]. Some of these factors that impact the software’s reliability are Complexity, Changeability and Portability.
The main objective of any organization is to develop the software with less error rate that can only be achieved if the errors can be detected at the very initial stage of developing the software and the cost of achieving the lower error rate will also be minimized if the same can be done at the initial phase of developing the software. Techniques like fuzzy logic, neural network, and neuro-fuzzy show tremendous work in evaluating the software’s reliability [6]. Our main aim in the paper is to predict the reliability of the software using soft computing techniques.
The work is categorized as follows: the second section contains an overview of soft computing techniques. We discuss the proposed algorithm and its framework to evaluate the reliability of the software in the third section. Section four includes results and discussion. It also consists of the comparison among different soft computing techniques. Finally, the paper ends with concluding remarks in section five.
Motivation and Contributions
The research of this paper is motivated by real applications as reliability is one of the vital factors in the development of software. The main purpose of this research is to develop a model that can be used to deal with the data to predict the reliability of the software at an early stage. The faith of the proposed model is due to its hybrid approach; it can predict reliability with more accuracy and efficiency.
The following steps are incorporated for this research:
• Three metrics were identified related to reliability taken as input to design membership function to the proposed fuzzy inference system.
• Fuzzy rules were identified for the three-input membership functions using the Mamdami model
• Use the output of the proposed fuzzy inference system as an input to the proposed Neuro-Fuzzy approach.
• The Proposed model was trained and tested using selected training, and testing data set values and was evaluated on two parameters Mean Relative Error (MRE) and Mean Absolute Relative Error (MARE).
• Analyze the accuracy of the proposed model based on performance parameters MARE and MRE for predicting reliability.
Soft computing comprises various computational methods that comprise Fuzzy logic, Neural Network, Neuro-Fuzzy, probabilistic, and evolutionary computing [2]. These techniques are specially designed to deals with imprecise, uncertain, and difficult problems. This section discussed various existing soft computing methods like Fuzzy Logic, Neural Network, Neuro-Fuzzy Inference System, Genetic algorithm, etc. These techniques are preferred due to their good mapping mechanism with real-time conditions and handling dynamic and complex data. Various related research is mentioned in this section with their findings and observations.
Succi et al. [7] proposed a work design to measure and predict software reliability and prove that it is inevitable in the modern software manufacturing process. He proposed various machine learning techniques to predict and calculate software reliability based on various performance criteria. The Neural Network approach has also successfully solved problems in modeling and recognizing nonlinear systems [8].
Sharma et al. [9] developed the SPI programs to improve the software process for the perspective transformation concerning organization structure, policies and culture, which also helps to improve the overall quality of the software. Authors also compared various quality standard exists in the literature.
Singh et al. [10] proposed various parameters to check the software’s overall maturity and validated the same statistically. The two most popular used fuzzy inference system is Mamdami Fuzzy Inference System and Sugeno Fuzzy Inference System. Fig. 1 shows the functioning of the Fuzzy Inference System.
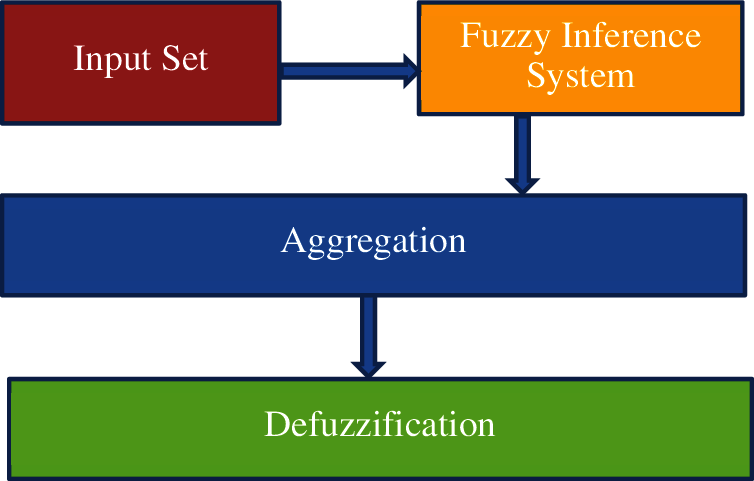
Figure 1: Architecture of fuzzy inference system
Neural Network is a model of a neuron system. Neural Network is a distributed processing system [11] comprised of many neutrally based processing elements. These networks are various areas where pattern recognition, image processing, prediction for the stock market, medicine, reliability, and security. Khoshgoftaar et al. [12] use the neural network to predict the faults’ occurrence and shown static reliability modeling. Jain et al. [13] developed a technique to assess the software reliability of the system that uses different Neural Network frameworks and estimates the component behavior in terms of fault prediction over a cumulative time of execution. Moreover, the fault prediction in software is estimated for the overall system as well.
The Neuro-Fuzzy approach is the combination of concepts based on fuzzy logic and a neural network. The integration of these two paradigms overcomes the limitations of each technique’s isolated concept [14]. The study of the Neuro-Fuzzy Inference Systems begins in the ‘90s, by Jang, Lin and Lee in 1991, Berenji (1992) and Nauck (1993). Various Neuro-Fuzzy systems exist like the cooperative Neuro-Fuzzy’s Inference system, Concurrent Neuro-Fuzzy Inference System, Hybrid Neuro-Fuzzy Inference System [15]. The Neuro-Fuzzy Inference System we will propose in this paper is the hybrid Neuro-Fuzzy System where fuzzy parameters will act as an input parameter to the Neural Network iteratively.
Various authors proposed methods for the prediction of software reliability like bio-inspired hybrid soft computing techniques. In their paper, Sahu et al. [16] also proposed an estimation model using the neural network approach and compared the results with the hybrid Neuro-fuzzy approach.
Sahu et al. [17] proposed Fuzzy AHP-TOPSIS; they take three different alternatives from different databases to predict software reliability, yielding more accurate results than AHP. Sahu et al. [18] emphasize the usability reliability prediction models in the paper as a suggestion to the industry people to enhance the software’s reliability, resulting in a low failure rate and making it cost-effective. Framework for fault prediction was proposed by Juneja in 2019 [19], and the framework was split into various phases; the author identified the applicable metrics for the prediction of software fault in the first phase followed by fuzzy rules and Neuro-Fuzzy classifiers for training and testing of the data for project evaluation. To predict the software’s reliability, Roy et al. [20] in 2019 proposed an ANN-based model using particle swarm optimization (PSO) algorithm. Fault complexity at a different level is evaluated for three different data sets. Also, the proposed model gives better predicting ability than standard PSO. Chan-UkYeom proposed an adaptive Neuro-Fuzzy inference system (ANFIS) with an incremental tree structure based on a context-based fuzzy C-means (CFCM) clustering process in 2020 [21], which shows that ANFIS gives better prediction efficiency than the existing computational approaches.
ANFIS for the time series data was also proposed by Tarno et al. in 2019 [22]. The research objective was to develop the procedure of constructing an Adaptive Neuro-Fuzzy Inference System (ANFIS) model for time series data. The performance of this model was evaluated based on Root Mean Square Error (RMSE) and Mean Absolute Percentage Error (MAPE).
Bharathi used the hidden Markov Model approach; the aim was to improve the software quality at the design level to ensure the reliability of a critical system in a cost-effective manner [23].
3 Performance Measurement Criteria
Different error measurements have been used by various metrics researchers in this study to measure the effectiveness of the proposed model in accessing the software reliability. Two criteria have been considered. MARE is the preferred measure of software reliability and can be calculated given in Eqs. (1) and (2) [24].
where the estimate is the network output for each n is the number of observations. The parameters used in the above equations and their interpretations are shown in Tab. 1.

Combining two concepts of Fuzzy Inference System and Neuro-Fuzzy Inference System to make a hybrid approach is the beauty of the proposed architecture. In the first phase, the metrics mentioned above are used as an input parameter to the Fuzzy Inference System and predict the reliability as an output. Membership functions of all these input and output parameters are designed using MATLAB fuzzy toolbox using Mamdami model after choosing their parameter values. Fuzzy rules are then identified for decision-making and get the correct output. In the second phase, the output of the Fuzzy Inference System is treated as an input to the neuro-fuzzy inference system. The model trained and tested with the help of real time data set. After multiple iterations of training and testing of the data, we get the more accurate value of reliability compared to the other existing models of soft computing.
Software metrics play a vital role in defining the property and characteristics of any software. In this section, identification of reliability-relevant metrics was made. As failure data is not available at the early phase to predict reliability, identified metrics named Complexity, Changeability, and Portability are used to develop a model for the early detection of software reliability [25]. The linguistic values from all these three identified metrics related to reliability were considered input to the proposed model to predict the reliability of the software in the early stage of software development. The selection of these metrics is based on expert opinion. In addition to this, we use the metric set ranked by Masoomeh et al. [24] to find out the most generic set. Fig. 2 gives the details of the proposed model.
• Complexity
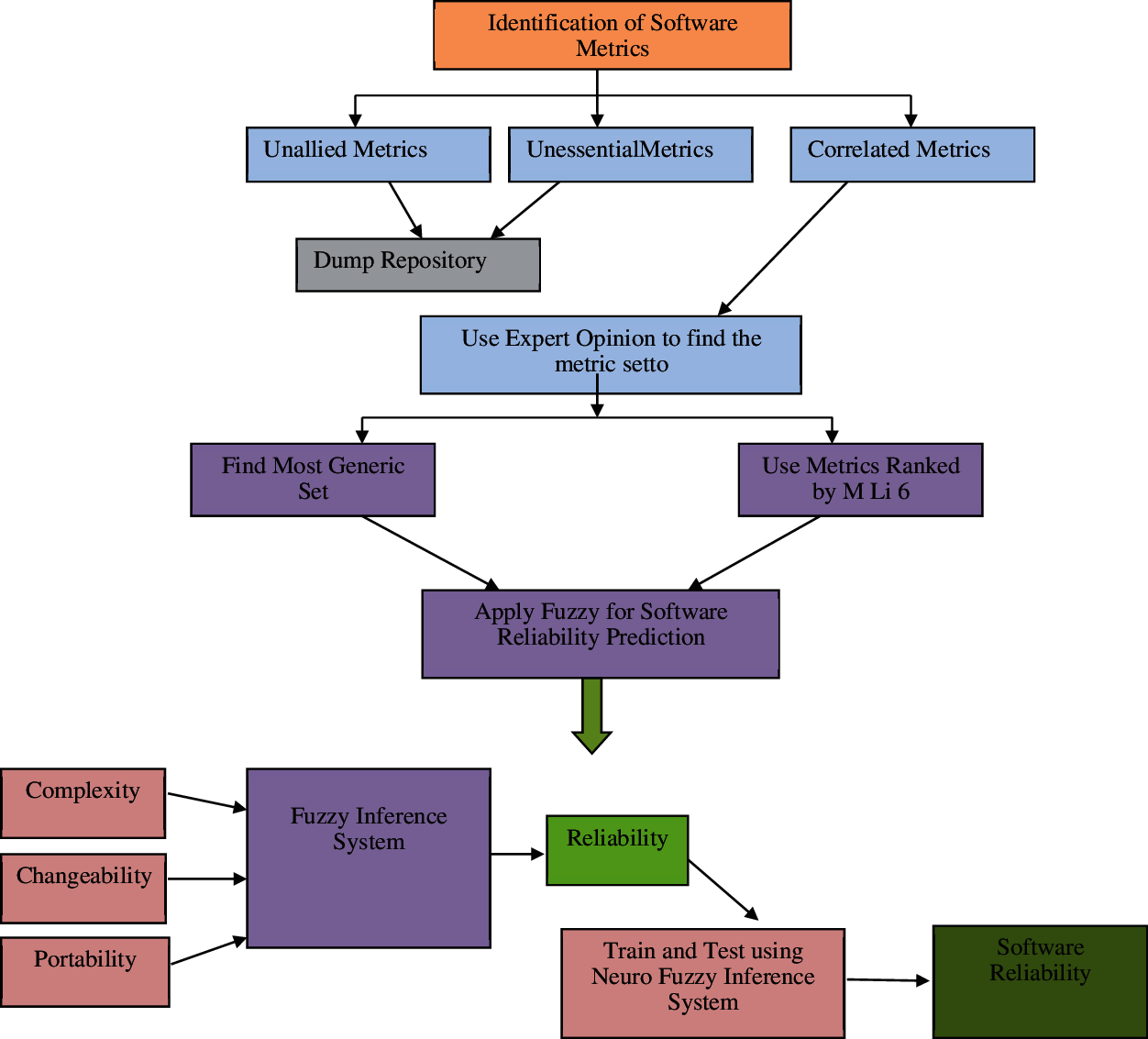
Figure 2: Architecture of proposed model
Complexity is one of the most contributing factors to deciding the level of difficulty in software development. It determines how easy it is to understand the software and is directly related to comprehension. Early prediction of difficulty in terms of complexity is important for smooth software planning and controlling, and clear ones’ knowledge nature of software and finally predicts the product’s reliability.
• Changeability
Changeability refers to the degree of usability and generality; it can be considered one of the characteristics of maintainability, one of the most expensive software development activities. It indicates the effort required to make changes in the software component to adapt to the new platform. It mainly refers to making changes in the program’s data to make it compatible in a new environment. The focus is on the software’s integrity and reliability to perform accurately with different data sets [26]. There is a good correlation between the changeability and complexity of the software.
• Portability
The most desirable software attribute is to measure Portability, indicating how easily a product will run on a different configuration than the existing one. Standard libraries, functions, and subroutines that play a crucial role in portability should be used to make software portable. The use of these standards increases the chance of operating the system in a different environment with an increased rate of success which eventually improves the reliability of the software and makes the system cost-effective to make the system more acceptable in terms of portability; a certain level of abstraction is required from the actual hardware.
4.2 Design of Membership Function for Input and Output Parameters
A membership function is defined as a function that creates a curve to indicate how different points in the input mapped to a value lying between 0 and 1. For a finite set X = {x1, x2, x3,…, xn}, the fuzzy set (X, μ) is denoted by {μ(x1)/x1, μ(x2)/x2, μ(x3)/x3,…,μ(xn)/xn}; where μ: X → [0, 1] is the membership function of x ∈ X. Whereas the membership of elements in a classical set is determined in binary terms either 0 or 1, i.e., either belongs or does not belong to that set. Thus, the fuzzy logic realizes the concept of partial truth value considering linguistic variable. Fuzzy logic constructs ‘if–then’ rule base to formulate the conditional statements. The general form of a simple ‘if-then’ rule is ‘if X is A, then Y is B’, where A and B are the linguistic states of X and Y, respectively. Here, ‘if’ part of the rule is antecedent and ‘then’ part is consequent. In general, the output of each fuzzy rule is a fuzzy set. Here we define the membership function of all three metrics as well as the output parameter. We have used three input and one output parameter, namely Complexity, Changeability, Portability and Reliability, and created the membership functions of all these parameters using the Triangular function given in Fig. 3.

Figure 3: Membership functions for input and output parameters
A fuzzy rule is an expression of “if-then” statements, which indicates the dependencies between the given variables [27]. As the metrics taken has a great impact on the software reliability. To find these metrics’ effect, we used them as an input to fuzzy logic and have designed the fuzzy rules using the rule editor of the Fuzzy Inference System. Fig. 4 shows the Mamdami model for defining fuzzy rules. These are if-then rules and are designed very carefully using expert knowledge as out computational structure is based on the identification of fuzzy rules, which can be edited and seen in the rule editor and viewer of FIS toolbox.
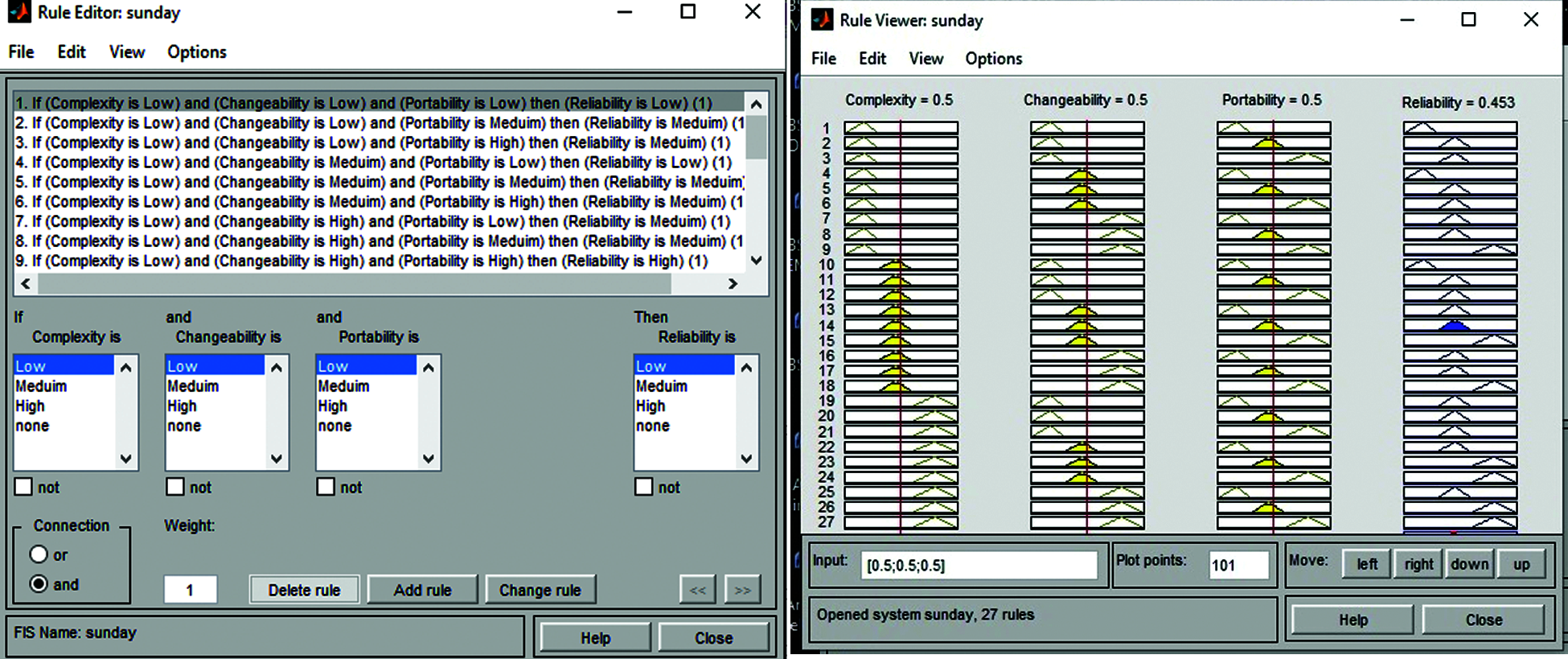
Figure 4: Rule editor and rule viewer
The proposed model is divided into two sections; in the first phase, we proposed a Fuzzy Inference System which was designed using identified metrics as input parameters, namely complexity, changeability and portability. The output of the proposed FIS is in terms of one more parameter name reliability is then given as an input to the proposed model in the second phase. The proposed model also designed with the same identified metrics and trained using selected training data set values and was evaluated on two parameters Mean Relative Error (MRE) and Mean Absolute Relative Error (MARE). After proper training and testing of the proposed architecture, the results show that the proposed hybrid. Neuro-Fuzzy strategy is prepared well and predicts attractive outcomes in terms of MARE and MRE to estimate software reliability.
After implementing the proposed model, we compared the output of the software’s reliability parameter for different input sets of the proposed model with the existing models to check the accuracy and efficiency of the proposed hybrid approach. The comparison shown in Tab. 2 justifies the proposed approach’s results to predict the reliability of any critical software.
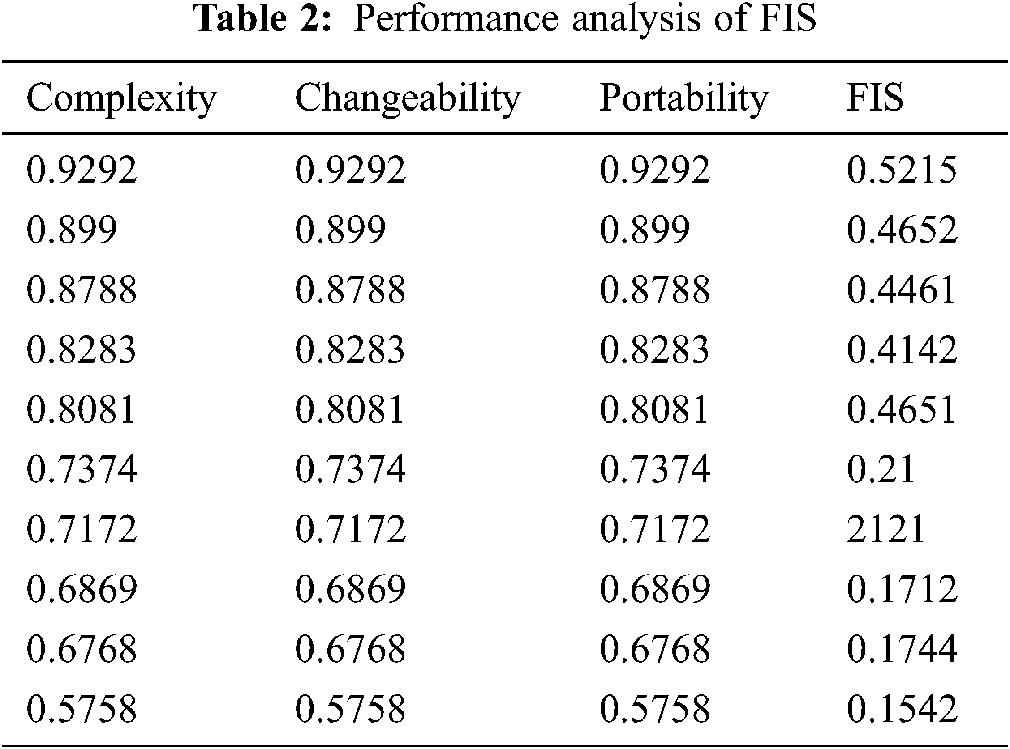
Fuzzy Inference System:
The proposed Fuzzy Inference System results with three input parameters, complexity, changeability and portability and output, are obtained in terms of reliability as shown in Tab. 2. This output is further treated as an input to the neuro Fuzzy Inference System to make the proposed hybrid architecture better results in accuracy and efficiency.
Designing membership functions of all these input parameters and the output have already been explained in the next section. These membership functions are then further evaluated based on fuzzy rules designed for checking the performance of FIS.
Neural Network:
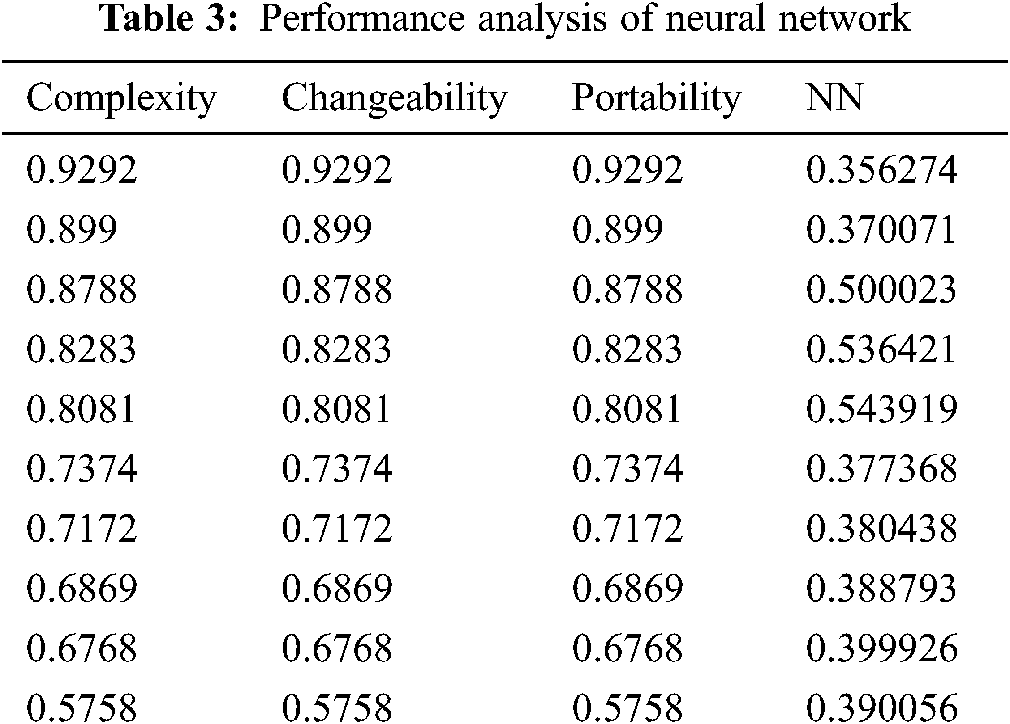
The same data set is then applied on the Neural Network technique of soft computing with the same input parameters to get the output in terms of reliability to check the performance of the proposed model. Tab. 3 shows the performance analysis of Neural Network architecture to predict the reliability of the software.
Adaptive Neuro Fuzzy Inference System:
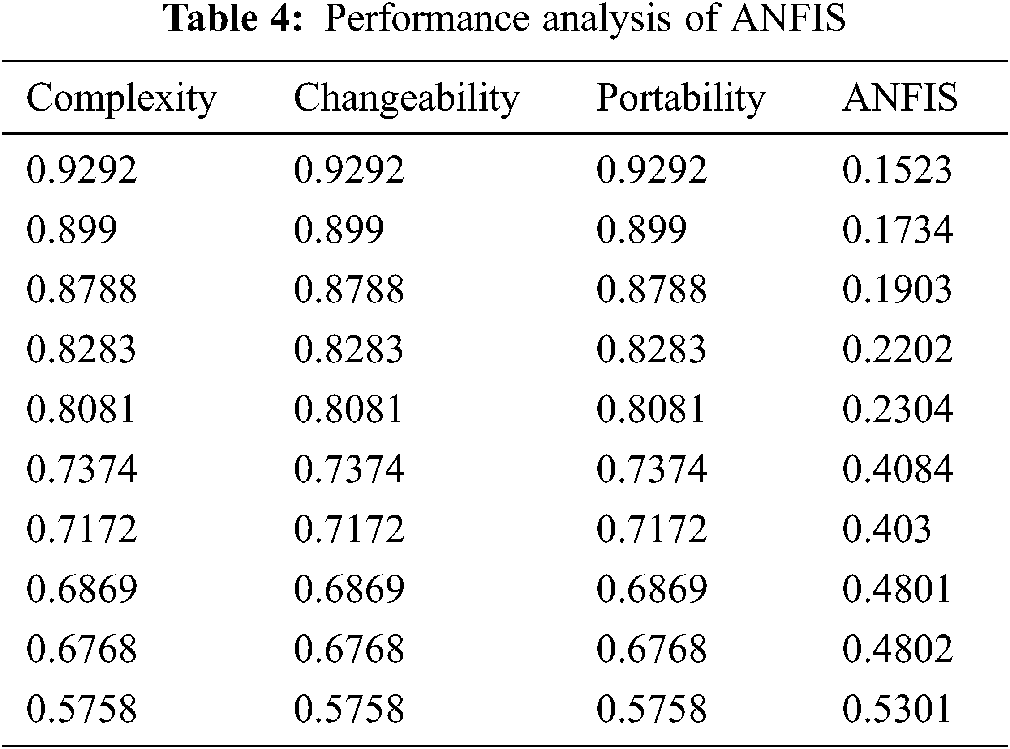
ANFIS with the same input parameters is also trained and tested with the real data set applied on previous approaches to predict the reliability of the software. The results of ANFIS architecture in terms of performance analysis is shown in Tab. 4.
Proposed Neuro-Fuzzy Inference System:
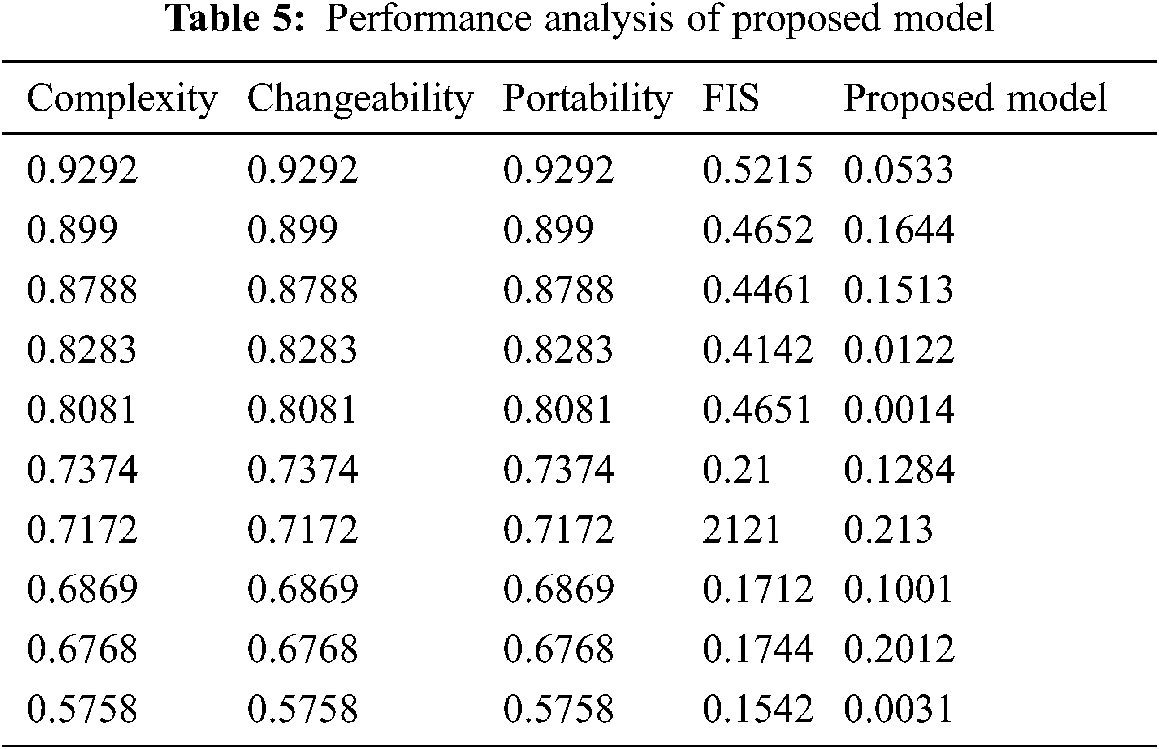
In the proposed system, all the four parameters, complexity, changeability and portability, along with the reliability factor obtained from the proposed fuzzy system, are taken as input; based on these parameters, the system trained and tested with real-time data set and predicted value of reliability is obtained for further decision making in the development of software. Tab. 5 shows the performance analysis of the proposed architecture to predict the reliability of the software. After getting the results of all the existing models trained using the same data sets and same input parameter, we compare their results with the results of the proposed model to justify the results of a hybrid approach. The model was designed with a novel approach. The primary aim is to make this model as simple as possible to improve the software in terms of reliability in a cost-effective manner.
The training statistic set of data is shown in the editor window of the Neuro-Fuzzy toolbox, which clearly shows the evaluation of training and testing data along with the parameters like error tolerance and echoes. The statistics are given in Fig. 5.
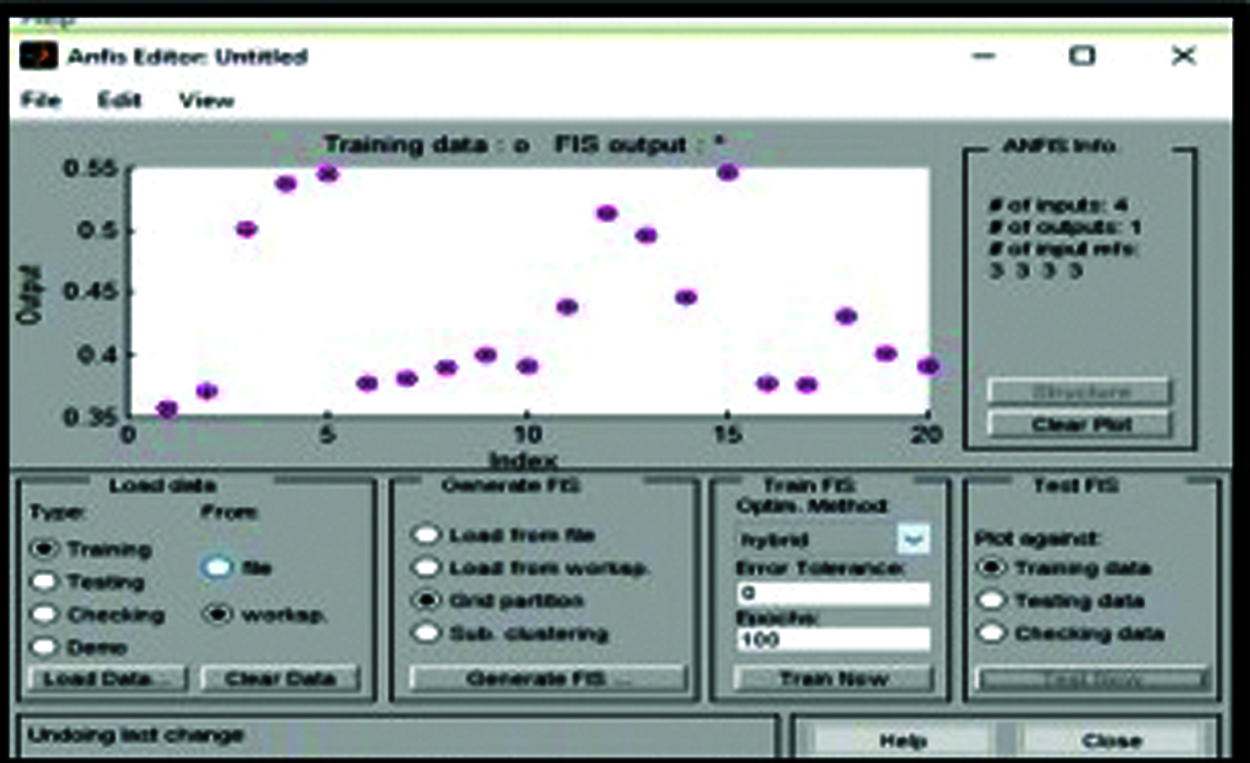
Figure 5: Training statistics set for proposed neuro-fuzzy inference system
Performance analysis of all the existing models and the proposed model is evaluated in MRE and MARE [26,28]. Results show that the performance calculated of the proposed model is 0.0060 and 0.0121, respectively. We also compare the proposed model with other models, as shown in Tab. 6, and the results show that the proposed model gives much better results compared to the other existing models. The power of the soft computation techniques on making predictions on such complex problems is presented in different applications [11]. The results obtained from this study have shown that the hybrid Neuro-Fuzzy Inference System techniques are good for making predictions of the reliability of complex systems due to their ability to handle dynamic problems.

6 Conclusions and Future Scope
Reliability is one of the important factors that affect the selection of software systems. It will improve efficiency and lower the efforts and cost for the development of any software. Our effort discussed soft computing-based techniques, i.e., Fuzzy Inference System, Neural Network and Neuro-Fuzzy Inference System, to estimate the software’s reliability. When discussing developing software, the Neuro-Fuzzy Inference System Technique is steadier and more supportive than the fuzzy model and Neural Network. Software Reliability is an eminent field of research in which remarkable growth can be seen in the future. In this study, we proposed a neuro-fuzzy inference system. The proposed model uses the three important factors related to reliability and uses them as an input to propose a Fuzzy Inference System. The Output of the Fuzzy Inference System then uses input to the proposed Neuro-Fuzzy model to predict the reliability. The model was implemented using the Neuro-Fuzzy tool in Matlab, and results are validated by comparing with the other state-of-art soft computing techniques. The measurement is done based on two performance parameters MRE and MARE. The values of these parameters show that the proposed model’s accuracy is high compared to the other soft computing techniques. The use of a hybrid approach made the model more efficient and accurate. The efforts made will help both the developers and researcher select the best software in terms of Reliability, which ultimately helps to enhance the performance level and amount the efficiency of the overall software system and reflect interesting future research directions.
Funding Statement: The authors received no specific funding for this study.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
1. P. K. Kapur, H. Pham, S. Anand and K. Yadav, “A unified approach for developing software reliability growth models in the presence of imperfect debugging and error generation,” IEEE Transactions on Reliability, vol. 60, no. 1, pp. 331–340, 2011. [Google Scholar]
2. J. D. Musa, “Software reliability engineering: More reliable software, faster development and testing,” New York: McGraw-Hill, 1999. [Google Scholar]
3. J. D. Musa, A. Iannino and K. Komodo, “Software reliability: Measurement, prediction and application,” New York: McGraw-Hill, 1987. [Google Scholar]
4. M. Lee, “Software quality factors and software quality metrics to enhance software quality assurance,” Current Journal of Applied Science and Technology, vol. 4, no. 21, pp. 3069–3075, 2014. [Google Scholar]
5. C. Yamming and X. Shiyi, “Exploration of complexity in software reliability,” Tsinghua Science & Technology, vol. 1, no. 2, pp. 266–269, 2007. [Google Scholar]
6. S. W. A. Rizvi, R. A. Khan and V. K. Singh, “Software reliability prediction using fuzzy inference system: Early stage perspective,” International Journal of Computer Applications, vol. 145, no. 10, pp. 16–23, 2016. [Google Scholar]
7. G. Succi, A. Reznik and V. Ivanov, “Comparing the reliability of software systems: A case study on mobile operating systems,” Information Sciences, vol. 423, pp. 398–411, 2018. [Google Scholar]
8. G. Aggarwal and D. V. Gupta, “Neural network approach to measure reliability of software modules: A review,” International Journal of Advances in Engineering Sciences, vol. 3, no. 2, pp. 1–7, 2013. [Google Scholar]
9. P. Sharma and A. L. Sangal, “Framework for empirical examination and modeling structural dependencies among inhibitors that impact SPI implementation initiatives in software sMEs,” Journal of Software: Evolution and Process, vol. 30, no. 12, pp. 1–20, 2018. [Google Scholar]
10. A. Singh and S. S. Gill, “Measuring the maturity of Indian small and medium enterprises for unofficial readiness for capability maturity model integration-based software process improvement,” Journal of Software: Evolution and Process, vol. 32, no. 9, pp. 1–19, 2020. [Google Scholar]
11. G. G. Tiruneh, A. R. Fayek and V. Sumati, “Neuro-fuzzy systems in construction engineering and management research,”Automation in Construction, vol. 119, no. 2, pp. 225–232, 2020. [Google Scholar]
12. T. M. Khoshgoftaar, R. M. Szabo and P. J. Guasti, “Exploring the behavior of neural-network software quality models,” Software Engineering, vol. 10, no. 3, pp. 89–96, 1995. [Google Scholar]
13. S. K. Jain and M. P. Singh, “Estimation for faults prediction from component based software design using feed forward neural networks,” International Journal of Advanced Research in Computer and Communication Engineering, vol. 2, no. 7, pp. 2631–2660, 2013. [Google Scholar]
14. L. Jing and Y. Tian, “Self-supervised visual feature learning with deep neural networks: A survey,” IEEE Transactions on Pattern Analysis and Machine Intelligence, vol. 117, no. 2, pp. 12–19, 2020. [Google Scholar]
15. E. Czogala and J. Leski, “Neuro-fuzzy intelligent systems, studies in fuzziness and soft computing,” Springer Verlag, pp. 9–14, 2000. [Google Scholar]
16. K. Sahu and R. K. Srivastava, “Predicting software bugs of newly and large datasets through a unified neuro-fuzzy approach: Reliability perspective,” Advances in Mathematics: Scientific Journal, vol. 10, no. 1, pp. 543–555, 2021. [Google Scholar]
17. K. Sahu, F. A. Alzahrani, R. K. Srivastava and R. Kumar, “Evaluating the impact of prediction techniques: Software reliability perspective,” Computers, Materials & Continua, vol. 67, no. 2, pp. 1471–1488, 2021. [Google Scholar]
18. K. Sahu and R. K. Srivastava, “Needs and importance of reliability prediction: An industrial perspective,” Information Sciences Letter, vol. 9, no. 1, pp. 33–37, 2020. [Google Scholar]
19. K. Juneja, “A fuzzy-filtered neuro-fuzzy framework for software fault prediction for inter-version and inter-project evaluation,” Applied Soft Computing, vol. 77, pp. 696–713, 2019. [Google Scholar]
20. P. Roy, G. S. Mahapatra and K. N. Dey, “Novel neural network,” IEEE/CAA Journal of Automatica Sinica, vol. 6, no. 6, pp. 1365–1383, 2019. [Google Scholar]
21. C. Yeom, U. K. Kwak and K. Chang, “Adaptive neuro-fuzzy inference system predictor with an incremental tree structure based on a context-based fuzzy clustering approach,” Applied Sciences, vol. 10, no. 23, pp. 1–15, 2020. [Google Scholar]
22. Tarno, A. Rusgiyonoand and Sugito “Adaptive neuro fuzzy inference system (ANFIS) approach for modeling paddy production data in central java,” in Journal of Physics: Conf. Series, the 8th Int. Seminar on New Paradigm and Innovation on Natural Science and Its Application Central Java, Indonesia, vol. 1217, 2019. [Google Scholar]
23. R. Bharathi and R. Selvarani, “Hidden markov model approach for software reliability estimation with logic error,” International Journal of Automation and Computing, vol. 17, pp. 305–320, 2020. [Google Scholar]
24. Z. Masoomeh, A. G. Chofreh, F. A. Goni and J. J. Klemes, “Air pollution prediction using semi-experimental regression model and adaptive neuro-fuzzy inference system,” Journal of Cleaner Production, vol. 261, no. 2, pp. 234–241, 2020. [Google Scholar]
25. R. K. Sharma and P. Gandhi, “Estimate reliability of component-based software system using modified neuro fuzzy model,” International Journal of Engineering and Technology, vol. 6, no. 2, pp. 45–49, 2017. [Google Scholar]
26. M. Alojail and S. Bhatia, “A novel technique for behavioral analytics using ensemble learning algorithms in e-commerce,” IEEE Access, vol. 8, no. 1, pp. 150072–150080, 2020. [Google Scholar]
27. A. Kishor, C. Chakraborty and W. Jeberson, “A novel fog computing approach for minimization of latency in healthcare using machine learning,” International Journal of Interact Multimedia Artificial Intelligence, vol. 6, no. 6, pp. 10–20, 2021. [Google Scholar]
28. S. S. Kshatri, D. Singh, B. Narain, S. Bhatia, M. T. Quasim et al., “An empirical analysis of machine learning algorithms for crime prediction using stacked generalization: An ensemble approach, IEEE Access, vol. 9, no. 1, pp. 67488–67500, 2021. [Google Scholar]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |