DOI:10.32604/csse.2022.021078

| Computer Systems Science & Engineering DOI:10.32604/csse.2022.021078 |  |
| Article |
A Hybrid Heuristic Algorithm for Solving COVID-19’s Social Distancing at Universities Campus
1Department of Data sciences and Artificial Intelligence, Al-Ahlyyia Amman University, Amman, Jordan
2Department of Software Engineering, Isra University, Amman, Jordan
3Department of CSMIS, Oman college of management and technology, Muscat, Oman
4Faculty of Information Technology and Systems, University of Jordan, Aqaba, Jordan
*Corresponding Author: Issam Alhadid. Email: i.alhadid@ju.edu.jo
Received: 22 June 2021; Accepted: 29 July 2021
Abstract: Social distancing during COVID-19 has become one of the most important measures in reducing the risks of the spread of the virus. Implementing these measures at universities is crucial and directly related to the physical attendance of the populations of students, professors, employees, and other members on campus. This research proposes an automated scheduling approach that can help universities and schools comply with the social distancing regulations by providing assistance in avoiding huge assemblages of people. Furthermore, this paper proposes a novel course timetable-scheduling scheme based on four main constraints. First, a distance of two meters must be maintained between each student inside the classroom. Second, no classrooms should contain more than 20% of their regular capacity. Third, there would be no back-to-back classes. Lastly, no lectures should be held simultaneously in adjacent classrooms. The proposed approach was implemented using a variable neighborhood search (VNS) approach with an adaptive neighborhood structure (AD-NS) to resolve the problem of scheduling course timetables at Al-Ahlyyia Amman University. However, the experimental results show that the proposed techniques outperformed the standard VNS tested on university course timetabling benchmark dataset ITC2007-Track3. Meanwhile, the approach was tested using datasets collected from the faculty of information technology at Al-Ahlyyia Amman University (Jordan). Where the results showed that, the proposed technique could help educational institutes to resume their regular operations while complying with the social distancing guidelines.
Keywords: COVID-19; social distance; variable neighborhood search; adaptive neighborhood structure; university course timetable
In operation research (OR) the problem is modelled quantitatively, whilst in artificial intelligence (AI) it is modelled as a graph (i.e., tree, network or others). After the problem is modelled, we need to solve the problem by exploring different solutions in order to choose the best one among them (search algorithm). The optimality consists of two types of solutions: global and local optimal solutions. The local optimal is the best solution among others within search space region, but not all regions in the search space. Whereas the global optimal is the best solution among all solutions in search space (all regions). In order to find the good local optimal solutions/probably global optimum, an effective search mechanism is needed to help in explore promising regions in the search space. In every search process, there are three common phases: (i) the initial solution (initial start or point); (ii) technique to generate new solutions; (iii) termination criteria. There are three types of search mechanisms [1]:
(i) Analytical Search: It is used a mathematical function as a guide to find the optimal solution if possible (exist). By using this search mechanism there is no greatness to reach the optimal solution in every case, but the local optimum.
(ii) Blind Search: It is also called the unguided search, where the search space is enumerated to search for the optimal solution exhaustively, and there is no guarantee to find the optimal solution.
(iii) Heuristic Search: also called a guided search and there is no guarantee to find the optimal solution same as other search types, but it can produce satisfactory solutions/high quality solutions in most cases. This thesis focuses on heuristic search.
The author in [2] presented that the heuristic search does not guarantee to find the optimal solution but it has procedure to work. Then the work in [3] argued that combining the basic heuristic search methods in high level frameworks can explore the searching space more effectively than basic heuristic, which is called metaheuristic. Moreover, learning approaches are used to organize data in order to identify near-optimal solutions more effectively via an iterative generation process that generates a subordinate heuristic by merging intelligently various conceptions for exploring and exploiting the search region [4].
The work in [5] presented that the Meta-heuristics are “typically high-level strategies which guide an underlying, more problem specific heuristic, to increase their performance”, similar definitions can be found in ([3,6,7]). Metaheuristic starts with one solution or more initial solutions and employ search mechanisms/strategies to search for a better quality solution. There are different ways to categorize the meta-heuristics algorithms. Works in [5,8] categorized the metaheuristic algorithms as follows: Trajectory methods vs. discontinuous methods; one-neighborhood vs. various neighborhood structures; population based vs. single point search; nature inspired vs. non-nature inspiration; dynamic vs. static objective function and memory usage vs. memoryless methods.
Scheduling problem such as university course timetabling (UCTT) is considered as a non-deterministic polynomial (NP) complete problem. Many algorithms were implemented to accomplish scheduling tasks effectively. Reference [9] defined a scheduling algorithm as “the allocation, subject to constraints, of given resources to objects being placed in space-time, in such a way as to satisfy, as nearly as possible, a set of desirable objectives.” Thus, for any scheduling algorithm, a set of objectives needs to be achieved.
According to [10], there are three main timetable problems in the field of education: university timetabling, school examination timetabling, and courses timetabling. Several solutions were suggested to solve the problem of timetable scheduling. Some of those solutions applying high-level strategies included meta-heuristics techniques [11], while others were used to solve similar problems such as the genetic algorithm (GA) [12], Tabu Search (TS) algorithm [13], Simulated Annealing (SA) algorithm [14], and variable neighborhood search (VNS) algorithm [15], among others.
University timetabling, in general, is similar for all universities. For instance, classes reside at the same level and almost identical in sizes. Moreover, each class holds a different group of students as students enroll in different courses and lectures. Work [15] provided a specific definition of timetabling courses in the universities. According to the definition, its mission is room allocating related to assigning timeslots while satisfying hard constraints and minimizing soft constraints. In this approach, the following two rules (hard and soft constraints) must be satisfied and minimized, respectively:
1. Hard constraints: For instance, two or more courses should be scheduled in different classrooms and timeslots.
2. Soft constraints: For example, lecturers with a majority of females are preferred to be assigned morning timeslots.
Roughly, the quality of a timetable is evaluated through such soft constraints and hard constraints. Soft constraints should reach a reasonable satisfaction degree, whereas hard constraints should reach a degree of completeness. For any constraint violation, the design will be penalized. So, the higher the penalties, the lower is the quality of the timetable design. Authors in [16] introduced an interesting abstraction of the problem of courses timetable in a university in terms of representing it properly. The researchers identified three parameters, where C is the courses set, T is the timeslots set, and R is the classrooms set: C = {c1, c2, …, .cn}, T = {t1, t2, …, .tk} and R = {r1, r2, …, ru}. For each course Ci, there are li
All previous works related to timetabling had focused on factors not related to social distance as a critical issue. However, new circumstances developed raised due to the perspective of a disease—COVID-19. COVID-19 is a pandemic that led to the worldwide practice of social distancing to minimize the spread of this virus. Universities and schools are two of the most crowded places, and mass gatherings at those places may cause the virus if social distancing is not maintained. This work provides a new approach to help universities schedule their courses in the manner of keeping students safe as much as possible. For this purpose, a new real-world dataset was collected from the faculty of information technology at Al-Ahlyyia Amman University (AAU). The Faculty of Information Technology has three departments and 12 curricula of students as shown in Tab. 1.

2 Background and Related Works
The problem of course timetabling is a combinatorial optimization problem [21]. Based on constructive heuristics, the heuristic approaches give better results than the other approaches [22]. With this problem, if e events and t timeslots are defined, t checks for positioning the events on the timetable must be done [23]. The constraint-based algorithms such as trees and graphs, “depth-first search,” population-based approaches combined with “backtracking,” and others are used to solve the timetabling problem [24].
Metaheuristics algorithms such as SA, TS, or VNS. However, VNS was used by [25] to deal with many neighborhood structures for switching among them for diversification purposes. The work in [26] defined VNS as “a recent metaheuristic, or framework for building heuristics, which systematically uses the idea of neighborhood change, both in the descent to local minima and in the escape from the valleys which contain them. VNS starts with a shaking procedure to divert the solution to another promising region through the search space; then, the local search methods are applied to optimize the solution quality. Afterwards, the current solution (old) is replaced with a new one [26].

As shown in Tab. 2, each neighborhood has its strengths and weaknesses in terms of searchability and solution quality. For instance, TS performs effectively when the neighborhood structure is small and the landscape is large. Moreover, SA demonstrates an efficient performance, especially when the computational time is sufficient, the neighborhood structure size is large, and the parameters are tuned correctly [31]. However, VNS descent improves the solution quality swiftly by avoiding local optimum solutions.
It is possible to note that there are several neighborhood combinations such as union neighborhood structures [32]. Authors in [33] proposed a combination of neighborhood structures to obtain the VNS by changing between neighborhood structures when the search space is not improving despite some consecutive iterations. The work in [33] shows a new strategy to improve the meta-heuristic robustness in the case of some combinatorial optimization problems called constraint-oriented neighborhood (CON) that consists of different neighborhood structures with a smooth searching process.
Even though the employment of several neighborhoods will produce enhanced results, the computational time might be increased and searching capability may become limited. In this paper, a new VNS is introduced in combination with the adaptive neighborhood structure (AD-NS) that proposed by [34]. The major aim of this combination is to increase the search capability by avoiding the disconnected neighborhoods’ structures and enhancing the solution quality by selecting the suitable neighborhood structure rather than applying many neighborhoods, consuming more computational time.
CBCT is based on scheduling all lectures according to a weekly schedule. Every lecture and a corresponding classroom for it must be set based on a given set of constraints (hard and soft constraints). Therefore, our approach is based on the following entities: weekday, timeslots, and periods. The weekday (day) entity describes five days of the week (Sunday to Friday). The timeslot entity is assigned to the teaching days (Sundays, Tuesdays, and Thursdays) when lectures last for 60 min, whereas lectures last for 90 min for Mondays and Wednesdays. Meanwhile, the algebraic product of timeslots and days generates the total number of scheduling periods, considering that each course has a fixed number of lectures to be scheduled in distinct periods, taught by a specific teacher, and attended by a certain number of students. Furthermore, the lectures of each course must have a minimum number of days to be spread around, considering that there are some periods in which the course cannot be scheduled.
When designing an approach for scheduling a timetable, we need to keep in mind that each room has a capacity that is equal to the total number of seats inside that room. Accordingly, for a large-enough room, all courses can be equally assigned while abiding by the COVID-19 social distance guidelines. In order to enforce social distancing on course scheduling, we need to handle the constraints mentioned in [35] (four hard constraints (H1–H4) and three soft constraints (S1–S3)). Besides, four more soft constraints will be introduced in this work to address the epidemiological situation of the COVID-19. It should be noted that [35] presented a soft constraint called curriculum compactness, where for a given curriculum; a violation is counted if one lecture is not adjacent to any other lecture belonging to the same curriculum on the same day. This means that the students’ agenda should be as compact as possible. On the other hand, this soft constraint contradicts the aim of this research, which is to distribute lectures as much as possible to reduce the crowding among students. Therefore, it will not be adopted within the soft constraints, which we seek to solve (optimize) in this research. It will be replaced by a soft constraint that is concerned only with distributing the courses belonging to the same curriculum in a way that would ensure their distribution in different timeslots and rooms.
As mentioned above, there are four common hard constraints, which are as follows:
H1: For every course, lectures must be scheduled for distinctive periods.
H2: Two lectures cannot be assigned to the same period and the same room.
H3: Lectures of courses in the same curriculum or taught by the same instructor cannot be scheduled in the same period.
H4: If the teacher of a course is not available at a given period, then no lectures of the course can be assigned to that period.
In this section, we will present the seven soft constraints (S1–S7), Tab. 3 contains the soft constraints and their respective explanations and provides the number of violations to be calculated for each constraint and who proposed these soft constraints.

Concerning the violations calculated and determined in Tab. 3, the objective function would be to minimize the soft constraint (S1–S7) violations, i.e., S1 + S2 + S3 + S4 + S5 + S6 + S7.
The VNS starts from the first neighborhood and moves on to the next one in sequence. Many local search methods can be applied within the VNS, including the descent method such as the VND. The VND uses a descent method to move around the neighborhood structures. In this paper, the changing neighborhood structure will be applied adaptively, as per the procedures described as follow [34]:
1. Randomly select one type of soft constraint (i.e., curriculum compactness).
2. Order the lectures according to the selected soft constraint violations in a non-increasing way.
3. Select the lecture with the highest penalties Li, where Li belongs to Crk curricula (Li ∈ Crk).
4. Select another lecture Lj randomly that belongs to different curricula than Li (Lj ∉ Crk).
5. Swap Li and Lj.
The procedures show diverting the search to other solution space and randomly swapping the lectures with the highest penalties with other lectures (free clash).
In this phase, the feasible initial solution is built by satisfying all the hard constraints (H1–H4) using a sequential greedy heuristic.
In this work, the VNS with adaptive neighborhood structure is proposed as shown in Algorithm.1. Thus, the approach starts with a given initial solution (Sol*) using the constructive algorithm; then, we set the initial non-improvement iterations to one (Non_improve = 1) to make sure that the solution avoids being trapped in a local optimum. After that, k neighbors are generated from N neighborhood structures by applying the AD-NS to select the best quality solution (Sol). Then the solution (Sol*) is accepted as the objective value only if its quality is better than the current solution (Sol). Otherwise, the non-improving iterations would be updated.

To achieve the highest fair percentage of comparison and to verify the efficiency of the algorithm, the study compared the proposed algorithm with standard VNS tested on university course timetabling benchmark dataset ITC2007-Track3.
The parameter settings for both (VNS-AD and VNS) are listed in Tab. 4, according to the primary experimentation executed earlier.

Where,
NS1: Moving a lecture from the current period to another free period.
NS2: Swapping lectures randomly.
Tab. 5 shows the statistical results using SPSS obtained by the two approaches; hybrid VNS-ADNS and standard VNS The first column indicates the instances, columns 2–5 and 6–9 and reports the best solution, worst, mean, and standard deviation over 31 runs to each instance for the whole ITC 2007 track3 benchmark datasets.
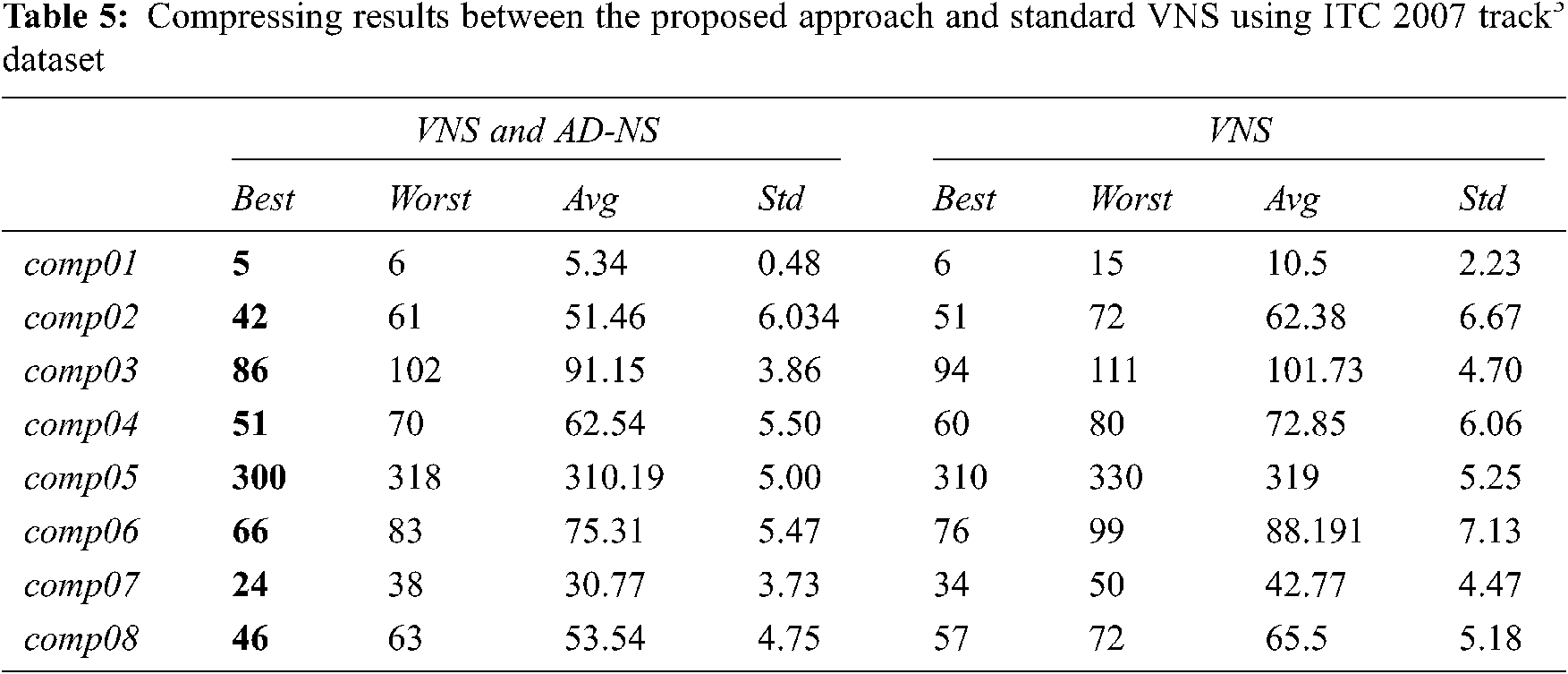
The experimental results in Tab. 4 showed that the proposed VNS improves the solution quality in comparing with standard VNS. Thus, VNS and AD-NS is statistically significant in all instances (ITC2007-Track3) 31 runs for eight instances. Thus, we conclude that hybrid VNS with adaptive neighborhood structure will leads the VNS to improve the solution quality compared to standard VNS.
Furthermore, the proposed approach in this work was tested on the data allocated for the Faculty of Information Technology at Al-Ahliyya Amman University (AAU). The collected dataset is described in Tab. 1. The hybrid VNS-AD approach with the standard VNS with the use of the basic neighborhood structure was compared.
The comparison results between VNS_AD and the standard VNS is shown in Tab. 6, where the first column displays the instances, columns 2–5 and 6–9 report the Best solutions and worst mean, and standard deviation of over 31 runs for both (VNS-AD-NS and VNS), respectively, and column 10 reports P-value of VNS-AD against VNS.

Where,
B: Best result, W: Worst result, M: Mean, STD: Standard deviation.
Tab. 6 shows that the proposed approach performed better and improves the solution quality in comparison with the standard VNS in 31 runs. Moreover, the results (the best and average solution quality) indicated that the proposed approach led the search space to reasonable results and outperformed the standard VNS (See Fig. 1); meanwhile, the VNS-AD-NS results are close to average, and this is illustrated through the small standard deviations. The VNS-AD-NS performance is statically better than that of VNS (P values are less than 0.05). Generally, based on the results, our alternate hypothesis is supported where the VNS with adaptive neighborhood structure strongly improves the VNS performance by guiding the search to a good-quality solution and avoiding the local optimum solution.
The achieved results of the proposed approach are compared with those of the standard VNS and the common soft constraints presented by ITC 2007, which is by given the calculation of social distancing between classrooms, students, and overcrowding buildings during academic lectures through the following proposed measurement as illustrated in Eqs. (1) and (2) for both results hard constraints are satisfied.
S = {x | x is the numbers of students attending lectures at level i in timeslot t}
R = {r | r is the room capacity at level i}
where β is the percentage students’ number per day SDm, which is achieved using our approach in comparison with the actual number of students or actual room capacity R.
Fig. 1 Shows samples of the best solutions in comparison between standard VNS and VNS-AD-NS in 21 runs.
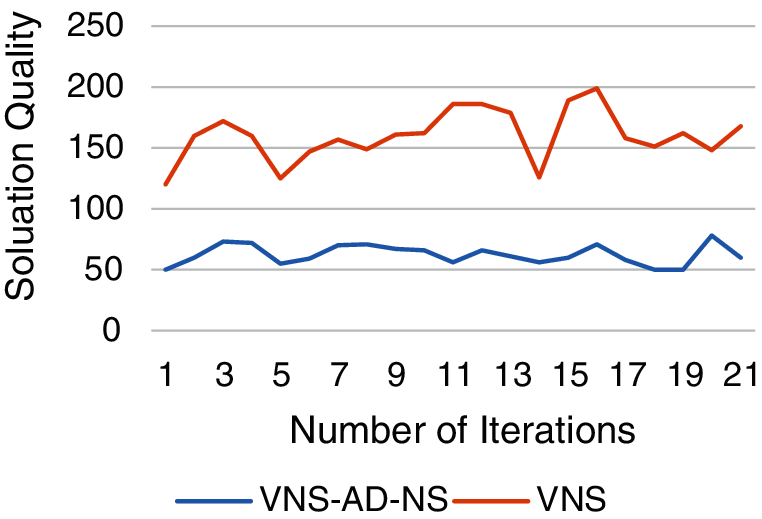
Figure 1: Comparison between VNS-AD-NS and VNS
After 31 runs, the proposed approach shows that the result of ß is equal to 26.2354%, whereas the standard approach achieved 67.2022% in the case of social distancing for the academic schedule during the university day. Tab. 6 shows that the new proposed approach improves the social distancing ratio, ensuring reductions in the rate of coronavirus infection and the students crowding between lectures. Here, ß shows the percentage of students present during lectures inside the buildings for all rooms at the university during the week. Fig. 2 shows the percentage of students present in classrooms during both schedules in 15 attempts.
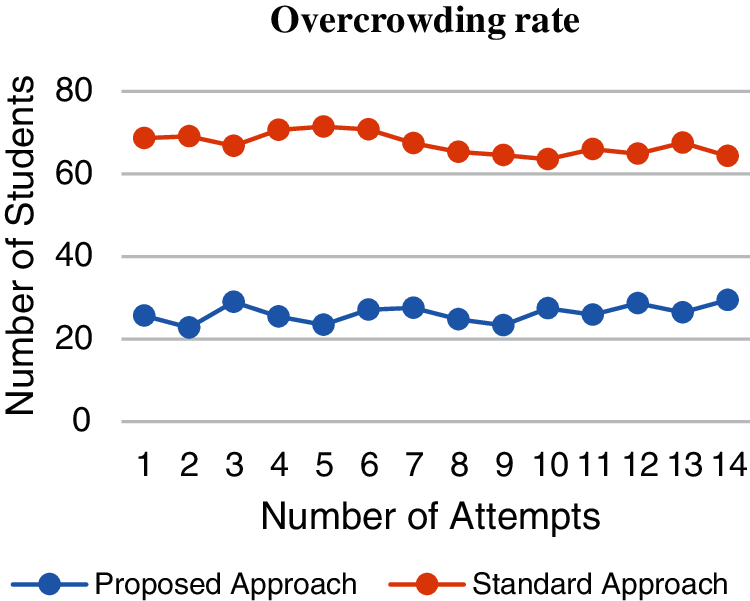
Figure 2: Comparison results between the proposed approach vs. standard approach
Social distancing is the main requirement during the time of COVID-19 for preventing the spread of the afflicting disease. Universities are forced to implement social distancing to prevent the spread of coronavirus among the students, teachers, and other university-related personnel since intensive groupings are one of the most common causes of rapid viral infection transmission. This work presents an approach to distribute lectures and class capacity to reduce massive student gatherings. It proposes new soft and hard constraints that would help reduce the percentage level of students per timeslot to the level suggested by health-care authorities. The soft constraints used in this work enhanced the distribution of students in a manner to avoid the high percentage of student numbers per day. Thus, the proposed approach achieved results that would reduce student crowding as compared to the standard approach, with an occupation of less than 26% of the actual university capacity while assigning timeslots. The present work can be implemented in all faculties and universities in Jordan or elsewhere to meet the conditions proposed by Al-Ahliyya Amman University.
This study guarantees a good result that ensure social distancing between students and employees inside the university campus. This will help to open universities to students and reduce virus infection. However, using Adaptive neighborhood structure will Leeds the VNS to select better neighborhood structure and divert the solution structure to a good promising region.
Acknowledgement: We would like to thank the Al-Ahlyyia Amman University for facilitating and funding this work.
Funding Statement: The authors received no specific funding for this study.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
1. E. Turban, Decision Support and Expert Systems: Management Support Systems. Hoboken, New Jersey: Prentice-Hall, Inc, 1995. [Google Scholar]
2. H. A. Simon, The New Science of Management Decision. Englewood Cliffs, NJ: Prentice-Hall, 1960. [Google Scholar]
3. F. Glover, “Future paths for integer programming and links to artificial intelligence,” Computers & Operations Research, vol. 13, no. 5, pp. 533–549, 1986. [Google Scholar]
4. I. H. Osman and G. Laporte, “Metaheuristics: A bibliography,” Annals of Operations Research, vol. 63, no. 5, pp. 511–623, 1996. [Google Scholar]
5. C. Blum, A. Roli and E. Alba, “An introduction to metaheuristic techniques,” in Parallel Metaheuristics: A New Class of Algorithms , E. Alba (eds.Hoboken: John Wiley & Sons, pp. 3–42, 2005. [Google Scholar]
6. F. Glover and M. Laguna, “Tabu search,” in Handbook of Combinatorial Optimization. Boston, USA: Springer, pp. 2093–2229, 1998. [Google Scholar]
7. I. H. Osman and J. P. Kelly, “Meta-heuristics theory and applications,” Journal of the Operational Research Society, vol. 48, no. 6, pp. 657, 1997. [Google Scholar]
8. M. Birattari, L. Paquete, T. Stützle and K. Varrentrapp, “Classification of metaheuristics and design of experiments for the analysis of components. Germany: FG Intellektik, FB Informatik, Technische Universität Darmstadt, Technical Report AIDA-01-05, 2001. [Google Scholar]
9. A. Wren, “Scheduling, timetabling and rostering—a special relationship?” in Proc. of the Int. Conf. on the Practice and Theory of Automated Timetabling, Edinburgh, UK, pp. 46–75, 1995. [Google Scholar]
10. A. Schaerf, “A survey of automated timetabling,” Artificial Intelligence Review, vol. 13, no. 2, pp. 87–127, 1999. [Google Scholar]
11. C. Blum and A. Roli, “Metaheuristics in combinatorial optimization: Overview and conceptual comparison,” ACM Computing Surveys, vol. 35, no. 3, pp. 268–308, 2003. [Google Scholar]
12. G. Wu, H. Wang, W. Pedrycz, H. Li and L. Wang, “Satellite observation scheduling with a novel adaptive simulated annealing algorithm and a dynamic task clustering strategy,” Computers & Industrial Engineering, vol. 113, no. 14, pp. 576–588, 2017. [Google Scholar]
13. C. H. Aladag, G. Hocaoglu and M. A. Basaran, “The effect of neighbourhood structures on tabu search algorithm in solving course timetabling problem,” Expert Systems with Applications, vol. 36, no. 10, pp. 12349–12356, 2009. [Google Scholar]
14. D. Zhang, Y. Liu, R. M’Hallah and S. C. Leung, “A simulated annealing with a new neighbourhood structure based algorithm for high school timetabling problems,” European Journal of Operational Research, vol. 203, no. 3, pp. 550–558, 2010. [Google Scholar]
15. N. Bol, B. D. Hughes, L. T. Merlot and P. J. Stuckey, “New integer linear programming approaches for course timetabling,” Computers & Operations Research, vol. 35, no. 7, pp. 2209–2233, 2008. [Google Scholar]
16. B. McCollum and N. Ireland, “University timetabling: Bridging the gap between research and practice,” in Proc. of The 6th International Conference on the Practice and Theory of Automated Timetabling, Brno, The Czech Republic, pp. 15–35, 2006. [Google Scholar]
17. Z. Lü and J. K. Hao, “Adaptive tabu search for course timetabling,” European Journal of Operational Research, vol. 200, no. 1, pp. 235–244, 2010. [Google Scholar]
18. A. Alhroob, H. Tarawneh and M. Ayob, “A hybrid simulated annealing with tabu list and allowable solutions memory to solve university course timetabling problem,” European Journal of Scientific Research, vol. 126, no. 1, pp. 84–94, 2014. [Google Scholar]
19. H. Tarawneh, Z. Ahmad and M. Ayob, “A hybrid simulated annealing with solutions memory for curriculum-based course timetabling problem,” Journal of Applied Sciences, vol. 13, no. 2, pp. 262–269, 2013. [Google Scholar]
20. W. Wen-jing, “Improved adaptive genetic algorithm for course scheduling in colleges and universities,” International Journal of Emerging Technologies in Learning , vol. 13, no. 06, pp. 29–42, 2018. [Google Scholar]
21. M. Chen, X. Tang, T. Song, C. Wu, S. Liu et al., “A Tabu search algorithm with controlled randomization for constructing feasible university course timetables,” Computers & Operations Research, vol. 123, pp. 105007, 2020. [Google Scholar]
22. H. Babaei, J. Karimpour and A. Hadidi, “A survey of approaches for university course timetabling problem,” Computers & Industrial Engineering, vol. 86, no. 5, pp. 43–59, 2015. [Google Scholar]
23. R. M. Chen and H. F. Shih, “Solving university course timetabling problems using constriction particle swarm ptimization with local search,” Algorithms, vol. 6, no. 2, pp. 227–244, 2013. [Google Scholar]
24. V. Kralev, R. Kraleva and S. Kumar, “A modified event grouping based algorithm for the university course timetabling problem,” International Journal on Advanced Science, Engineering and Information Technology, vol. 9, no. 1, pp. 229–235, 2019. [Google Scholar]
25. N. Mladenović and P. Hansen, “Variable neighbourhood search,” Computers & Operations Research, vol. 24, no. 11, pp. 1097–1100, 1997. [Google Scholar]
26. P. Hansen and N. Mladenović, “Variable neighbourhood search: Principles and applications,” European Journal of Operational Research, vol. 130, no. 3, pp. 449–467, 2001. [Google Scholar]
27. J. A. M. Pérez, J. M. Moreno-Vega and I. R. Martın, “Variable neighbourhood tabu search and its application to the median cycle problem,” European Journal of Operational Research, vol. 151, no. 2, pp. 365–378, 2003. [Google Scholar]
28. A. Duarte, Á. Sánchez, F. Fernández and R. Cabido, “A low-level hybridization between memetic algorithm and VNS for the max-cut problem,” in Proc. of the 7th Annual Conf. on Genetic and Evolutionary Computation, Washington DC, USA, pp. 999–1006, 2005. [Google Scholar]
29. S. Abdullah, E. K. Burke and B. Mccollum, “An investigation of variable neighbourhood search for university course timetabling,” in Proc. of the 2nd Multidisciplinary Int. Conf. on Scheduling: Theory and Applications, New York, USA, pp. 413–427, 2005. [Google Scholar]
30. E. K. Burke, A. J. Eckersley, B. McCollum, S. Petrovic and R. Qu, “Hybrid variable neighbourhood approaches to university exam timetabling,” European Journal of Operational Research, vol. 206, no. 1, pp. 46–53, 2010. [Google Scholar]
31. G. Wu, H. Wang, W. Pedrycz, H. Li and L. Wang, “Satellite observation scheduling with a novel adaptive simulated annealing algorithm and a dynamic task clustering strategy,” Computers & Industrial Engineering, vol. 113, no. 14, pp. 576–588, 2017. [Google Scholar]
32. L. Di Gaspero and A. Schaerf, “Neighbourhood portfolio approach for local search applied to timetabling problems,” Journal of Mathematical Modelling and Algorithms, vol. 5, no. 1, pp. 65–89, 2006. [Google Scholar]
33. C. Avanthay, A. Hertz and N. Zufferey, “A variable neighbourhood search for graph coloring,” European Journal of Operational Research, vol. 151, no. 2, pp. 379–388, 2003. [Google Scholar]
34. H. Tarawneh and M. Ayob, “Adaptive neighbourhoods structure selection mechanism in simulated annealing for solving university course timetabling problems,” Journal of Applied Sciences, vol. 13, no. 7, pp. 1087–1093, 2013. [Google Scholar]
35. A. Viana, J. P. Sousa and M. A. Matos, Constraint Oriented Neighbourhoods—A New Search Strategy in Metaheuristics. Metaheuristics, Boston, USA: Progress as Real Problem Solvers, pp. 389–414, 2005. [Google Scholar]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |