DOI:10.32604/csse.2022.022758

| Computer Systems Science & Engineering DOI:10.32604/csse.2022.022758 |  |
| Article |
A Prediction Method of Fracture Toughness of Nickel-Based Superalloys
1School of Computer, Beijing Information Science and Technology University, Beijing, 100101, China
2Department of Information Science, University of Arkansas at Little Rock, Arkansas, 72204, USA
*Corresponding Author: Yabin Xu. Email: xyb@bistu.edu.cn
Received: 18 August 2021; Accepted: 24 September 2021
Abstract: Fracture toughness plays a vital role in damage tolerance design of materials and assessment of structural integrity. To solve these problems of complexity, time-consuming, and low accuracy in obtaining the fracture toughness value of nickel-based superalloys through experiments. A combination prediction model is proposed based on the principle of materials genome engineering, the fracture toughness values of nickel-based superalloys at different temperatures, and different compositions can be predicted based on the existing experimental data. First, to solve the problem of insufficient feature extraction based on manual experience, the Deep Belief Network (DBN) is used to extract features, and an attention mechanism module is introduced. To achieve the purpose of strengthening the important features, an attention weight is assigned to each feature according to the importance of the feature. Then, the feature vectors obtained by the DBN module based on the Attention mechanism (A-DBN) are spliced with the original features. Thus, the prediction accuracy of the model is improved by extracting high-order combined features and low-order linear features between input and output data. Finally, the spliced feature vectors are put into the Support Vector Regression (SVR) model to further improve the regression prediction ability of the model. The results of the contrast experiment show that the model can effectively improve the prediction accuracy of the fracture toughness value of nickel-based superalloys.
Keywords: Nickel-based superalloys; fracture toughness; materials genome engineering; deep belief network; attention mechanism; support vector regression
With the continuous development of the aerospace industry, the requirements for the performance and reliability of aero engines continue to increase, and the requirements for the comprehensive performance and temperature-bearing capacity of materials are getting higher [1]. As nickel-based superalloys still have high strength, excellent oxidation, and corrosion resistance under high-temperature conditions, it has become the material of choice for key hot-end components such as modern aero engines, spacecraft, and rocket engines [2].
Fracture toughness is the toughness parameter of material resisting brittle failure, it is the critical value for judging whether the material crack reaches the unstable level, and it plays a vital role in damage tolerance design of materials and assessment of structural integrity [3]. For components that work at high temperatures, the temperature distribution usually has a large gradient, so the fracture toughness values measured at room temperature are far from meeting the design requirements of actual projects. To obtain the law of change of fracture mode with temperature and provide data support for the engineering application of nickel-based superalloys, there is an urgent need for a model that can describe the relationship between fracture toughness and temperature accurately in the design of nickel-based superalloys.
The fracture toughness of superalloys strongly depends on alloy elements and experimental conditions. However, due to its complex and highly nonlinear relationship, it is difficult to use specific mathematical expressions to characterize. Therefore, the diversity and mutual influence of alloy elements are often difficult to determine the appropriate fracture toughness. In the solution to this problem, materials genome engineering technology has shown great potential [4].
Materials genome engineering is a disruptive frontier technology in the field of international material science in recent years. Its basic idea is to integrate high-throughput computing of materials, high-throughput experiments, and big data technology of materials, speeding up the research and development process of materials from discovery, manufacturing to the application through synergistic innovation, and reducing costs [5]. Data + AI (Artificial Intelligence): The core of materials genome engineering, through the application of big data and artificial intelligence technology, realizing the relationship of structure, performance and process of the new material, and solve the process optimization problem, and the performance of the material can be improved.
Based on the principle of materials genome engineering, a prediction model of fracture toughness of nickel-based superalloys based on deep learning is proposed in this paper. Thus, the fracture toughness of nickel-based superalloys of different temperatures and different compositions can be quickly and accurately predicted based on the existing experimental data, reducing the amount and cost of experiments. This method has great theoretical significance and application value for promoting the research and development of nickel-based superalloys technology.
The innovations of this paper are as follows:
1) Aiming at the problem that traditional machine learning methods need to rely on manual experience to extract features, and deep learning is easy to fall into local optima under limited samples. By virtue of the powerful feature extraction capability of deep learning model and the regression prediction capability of SVR, a nickel-based superalloys fracture toughness prediction model that combines A-DBN and SVR is proposed. It can effectively improve the prediction effect of the model.
2) In order to fully reflect the different effects of different features on the prediction results, the attention probability weight is introduced into the DBN, and different weight coefficients are assigned to different features to pay more attention to important features, thereby improved the accuracy of the model.
The direct method to obtain the relationship between fracture toughness and temperature of superalloys is to measure the fracture toughness of standard specimens at different temperatures, and then use empirical models to fit them. However, the applicability of this empirical model is not wide, and it can only be used for the materials under study. Besides, to improve the accuracy of the model, more data under high temperatures are needed, which will cause great time and cost consumption [6].
In order to overcome the limitations of fitting methods based on empirical, some scholars have proposed a master curve method derived from physical meaning [7]. However, this method is only applicable to the ductile-brittle transition temperature range. For ferritic steels, this temperature range is usually lower than 0°C. Obviously, this method is not suitable for nickel-based superalloys that work at high temperature.
Based on the stress-strain curve and the linear expansion coefficient α of superalloys, Li et al. [8] proposed a temperature dependent model to predict the fracture toughness value of superalloys at high temperature. However, this model needs to be based on other mechanical property data, and the accuracy of the predicted data is not high.
To sum up, the physical model based on experience not only consumes a lot of time and cost, but also the accuracy of the prediction is not high.
In recent years, machine learning models have been widely used in predicting the mechanical properties of materials. Mahalle et al. [9] used a feed-forward neural network to predict the mechanical properties (ultimate strength, yield strength, strain hardening exponent, and elongation) of the nickel-based superalloys Inconel 718. Bano et al. [10] used a three-layered feed-forward back propagation neural network to establish an average static fracture energy prediction model for the nickel-based superalloy IN738LC based on experimental data, which reduced the time required for the experiment.
Seibi et al. [11] analyzed the relationship between fracture toughness of 7075-T651 aluminum alloy and crack geometry, load type, and operating temperature using a multilayer feedforward perceptual artificial neural network. Liu et al. [12] used a three-layer BP (Back Propagation) neural network to establish the quantitative relationship between the microstructure and fracture toughness of the niobium-silicon alloy, and optimized the alloy process parameters using an artificial neural network model. Zeng et al. [13] used a three-layer BP neural network to establish a prediction model for the mechanical properties (ultimate tensile strength, tensile yield strength, elongation, reduction of area, and fracture toughness.) of Ti-10 V-2Fe-3Al titanium alloys under deformation temperature, degree of reduction, cooling rate, solution temperature, aging temperature, and other thermal processing parameters and heat treatment regimes. Paul et al. [14] used the double hidden layer BP neural network to establish a fracture toughness prediction model under different alloy compositions and low alloy yield stress, which provided the possibility to design new alloys with higher fracture toughness by modifying the alloy chemical composition.
Qiao et al. [15] used a Generalized Regression Neural Network (GRNN) optimized by Fruit-fly Optimization Algorithm (FOA) to predict the fracture toughness of pearlitic steel to improve the prediction accuracy of a small number of samples. Based on the established model, the influence of alloying elements on fracture toughness was further studied, and the composition parameters of the steel were optimized. Mohanty et al. [16] used artificial neural networks to establish relationships between components and processing parameters and mechanical properties (yield strength, tensile strength, elongation and ductility) of steel plates to find out the importance of different variables. Xiong et al. [17] used five machine learning methods to predict the four mechanical properties of steels—fatigue strength, tensile strength, fracture strength, and hardness—were selected from the Japan National Institute of Material Science Database.
Hamdia et al. [18] used ANN (Artificial Neural Network) and ANFIS (Adaptive Network based Fuzzy Inference Systems) to predict the fracture energy of polymer nanocomposites and compared them with the model of Huang and Kinloch, and three linear regression models. The experimental results show that the prediction effect of ANN and ANFIS is better, and the method of ANFIS is the best. Sun et al. [19] used a three-layer BP neural network to predict the fracture toughness of composite ceramic materials. Ding et al. [20] used a three-layer feedforward neural network to study the influence of the composition, morphology, size, and volume fraction of a single-phase on the fracture toughness of Nb-silicide in-situ composites and used the model to predict the best microstructure that can improve fracture toughness.
The above methods all used a shallow learning model based on machine learning, which has a better prediction effect than an equation or model based on experience, but this shallow learning model needs to rely on prior knowledge of a specific field to extract features, and cannot fully reflect the essential characteristics of the data.
Fu et al. [21] combined deep learning idea with SVR method, and proposed a traffic flow prediction method based on deep learning regression machine. By constructing a multi-layer restricted Boltzmann machine structure, realize the data input of influencing factors and the learning and transformation of layer by layer information, and extract the equivalent key information. After that, the converted equivalent key information is input into the SVR model to achieve short-term traffic flow prediction. Luo et al. [22] proposed a short-term traffic flow prediction method using a DBN model combined with SVR, using the DBN model to learn the feature of traffic flow data in the road network, thereby mining the essential feature of the data. Then use the SVR method to predict the traffic flow. Pan et al. [23] proposed a model that combines Gated Recurrent Unit (GRU) networks and SVR to predict short-term traffic flow. The model uses GRU to extract features from the data and then inputs it into the SVR model at the top of the model to get the final prediction output of the model.
In addition, Xu et al. [24,25] proposed a multi-task learning method and an attention mechanism which applied on deep learning. Zhang et al. [26] proposed a feature representation model combining DBN. Li, et al. [27,28] proposed context learning method and feedback-directed machine learning. These research on the improvement of deep learning models achieved better results and have given us great enlightenment on model design.
Compared with a single SVR model, the advantage of above prediction model that combines deep learning and SVR is that, it can use deep learning model to extract features from data, so as to reduce the dependence of feature extraction on humans. Thus, it can portray the essential characteristics between the data, and improve the prediction accuracy of the model. In addition, compared with a single deep neural network model, this type of combined model can use the nonlinear kernel function of the SVR model to achieve a greater degree of generalization performance on the data, so as to improve the generalization ability of the model.
3.1 Overall Model Architecture
Because of the complexity, high cost, low accuracy, and poor adaptability of experience-based prediction methods, and the traditional machine learning methods that need to extract feature parameters based on experience, they cannot fully reflect the essential characteristics of the data. A combination prediction model of fracture toughness of nickel-based superalloys based on deep learning is proposed as Fig. 1 based on the ideas of materials genome engineering.
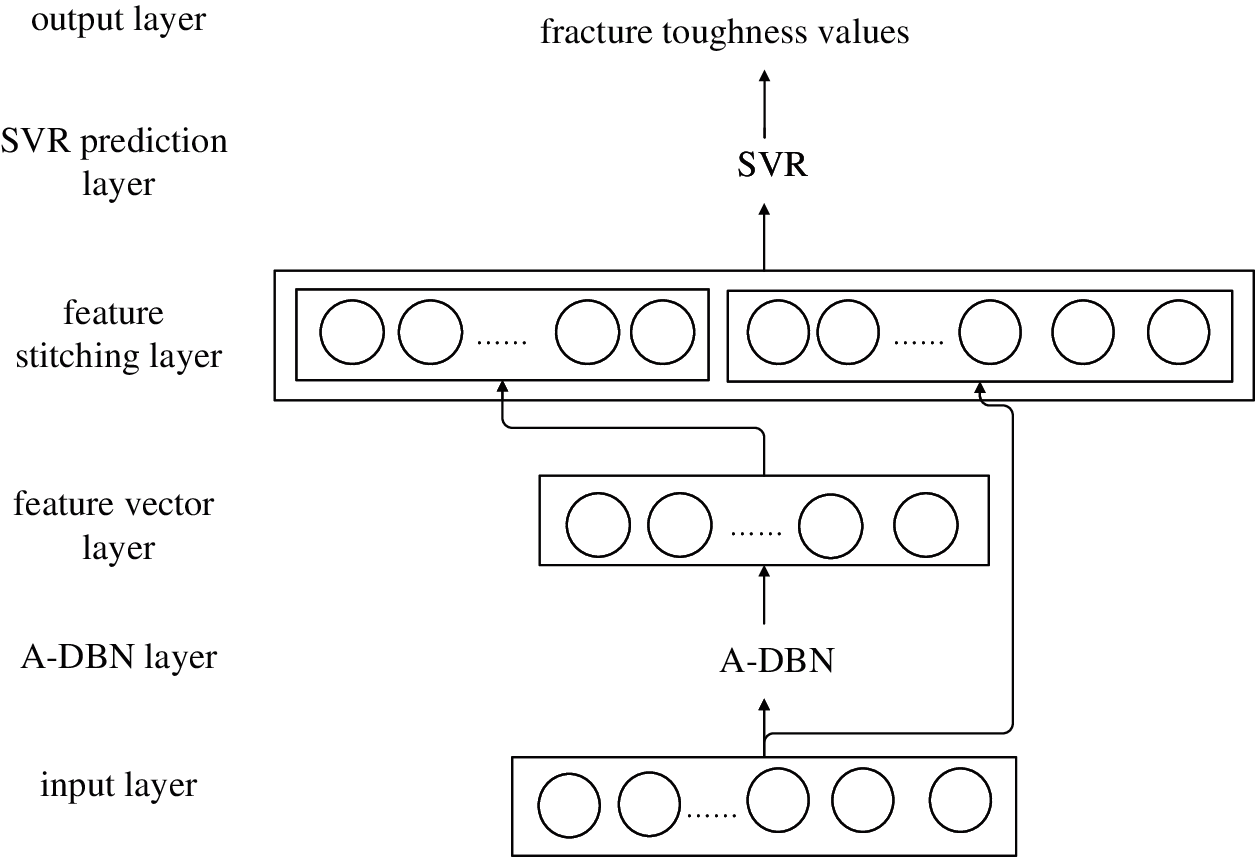
Figure 1: Overall structure of the model
The core idea of the combined model is to combine the A-DBN and SVR to predict the fracture toughness value. First, we use the A-DBN for feature learning and optimization, and splice the original feature vector with the feature vector obtained after A-DBN learning to obtain the low-order linear features and high-order combined features between the input and output data. Then, the spliced feature vectors were input into the SVR layer for the regression prediction of fracture toughness values. The overall structure of the model is shown in Fig. 1, which is mainly divided into an input layer, a DBN layer based on the A-DBN, a feature vector layer, a feature stitching layer, a SVR prediction layer, and a fracture toughness output layer.
The A-DBN layer is composed of DBN and attention mechanism. Where the DBN is a deep neural network composed of two restricted Boltzmann machines and a BP neural network unit. The structure is shown as Fig. 2.
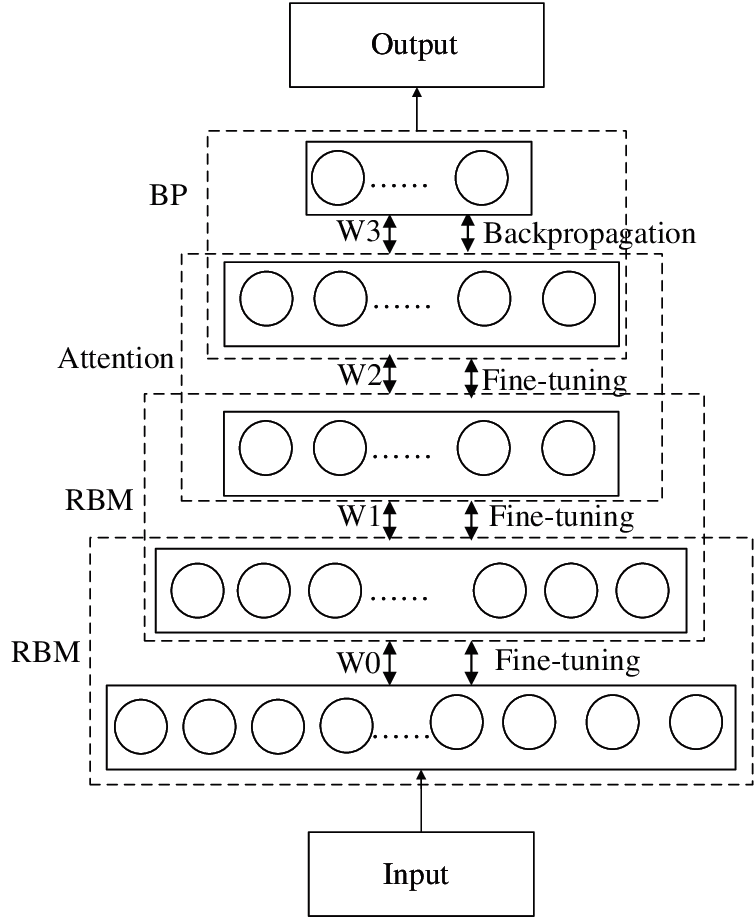
Figure 2: Structure figure of A-DBN
The Restricted Boltzmann Machine (RBM) is a kind of random generative neural network structure, which consists of one visible layer and one hidden layer. The visible layer is composed of visible elements and is used as input training data. The hidden layer is composed of hidden elements and is used as a feature detector. When predicting the fracture toughness of nickel-based superalloys, each layer is trained separately and unsupervised, to ensure that feature information is retained as much as possible when feature vectors are mapped to different feature spaces. Firstly, the characteristic matrix is composed by the content and temperature of each component of nickel-based superalloys, and input into the visible layer of the first RBM network. Then, the output of the previous RBM network is used as the input of the next RBM network. After the two-layer RBM network, the feature vector X of the fracture toughness of the nickel-based superalloys is obtained.
Since each layer of the RBM network can only ensure that the weights in its own layer are optimized for the feature vector mapping of this layer, it is not the best for the feature vector mapping of the entire DBN. So the BP neural network is added to the last layer of the DBN, and train the network model in a supervised manner. In addition, in order to improve the accuracy of model prediction, we introduce an attention mechanism module before the BP neural network. The attention mechanism draws on the processing methods of human vision and focuses attention on key areas. Its essence is to select the information that plays a key role in the task from a variety of information, so as to reduce the complexity of the task and improve the accuracy of the model at the same time. In this module, we input the feature vector X learned through the RBM network into the attention mechanism layer to obtain a new feature vector a. The calculation formula of the new feature vector a is shown in (1).
where, αi is the attention distribution, which indicates the degree of correlation between the ith information in the input information vector X and the query vector Q, when the query vector Q given. The calculation formula is shown in (2) and (3).
where, s(xi, q) is the attention scoring function. W, U and V are weight matrices.
After that, we input the new feature vector into the BP neural network layer and use the backpropagation network to propagate the error information from top to bottom for each layer of RBM, so as to fine-tune the whole A-DBN network. Thus, the feature vector F obtained by the A-DBN network layer is finally obtained.
The SVR algorithm is based on the VC (Vapnik–Chervonenkis) dimension theory and the principle of structural risk minimization. It can fully call the limited sample information and seek the best balance between the complexity of the model and the learning ability to obtain the best generalization ability. Traditional regression models usually calculate the loss directly based on the difference between the model output f(x) and the real output Y. If and only if the two are the same, the loss is zero. In contrast, the SVR hypothesis can tolerate a deviation of at most ε between the two. That is, when the absolute value of the difference between f(x) and Y is greater than ε, the loss is calculated. This is equivalent to taking f(x) as the center and constructing an interval band with a width of 2ε. If the training sample falls into this interval, the prediction is considered as correct. Therefore, the problem of SVR can be transformed into Eq. (4).
In Eq. (4), C is a penalty factor, and ℓε is the ε-insensitive loss function.
SVR maps data from low-dimensional space to high-dimensional space through a suitable kernel function and performs regression in this space to fit a continuous function to minimize the loss function. There are four common kernel functions, which are linear kernel function, polynomial kernel function, radial basis kernel function, and sigmoid kernel function. Since the radial basis kernel function has the advantages of parameter variables, small calculation amount, and high computational efficiency, this paper chooses the radial basis kernel function as the kernel function of SVR, and its mathematical expression is shown in Eq. (5).
In Eq. (5), σ is the width of the radial basis kernel function. C and σ are important parameters related to the generalization performance of the SVR model. This paper uses the K-fold cross-validation method to use the grid search algorithm to optimize the selection of the best combination parameters of the two (C, σ) to ensure the established model has the best performance. The basic principle of K-fold cross-validation is to take turns K times to divide the data set into K parts of the same size, use the K-1 part as the training set, and the remaining 1 part as the verification set, and the average of the accuracy of the K verification results is used as the estimated value of the modeling accuracy.
The basic idea of optimizing the parameters of the SVR model through the grid search algorithm is as follows:
(1) List all possible combinations of parameters and generate a grid.
(2) Carry out SVR modeling for all parameter combinations in turn.
(3) Select the parameter combination with the highest modeling accuracy.
The algorithm steps are as follows:

The time complexity of this algorithm is T(n) = O(n2), which is mainly derived from the double-layer for loop of 1–10 lines.
In summary, about the regression prediction process of the fracture toughness of nickel-based superalloys, we first input the data set into the trained A-DBN model to obtain the feature vector F obtained from the A-DBN model. Then combine the feature vector F and the original features to form a new training set and test set, and input them into the SVR model for training. Finally, use the trained SVR model to predict the fracture toughness value of nickel-based superalloys.
4 Experimental Results and Discussions
4.1 Experimental Data and Preprocessing
First, we download the experimental data of the fracture toughness of nickel-based superalloys from the materials genome engineering database, a total of 877 data. Then integrate the collected data in the order of composition content (C, W, Mo, Nb, Zr, Co, Al, Cr, Ti, Ni), quenching temperature and fracture toughness value to form a two-dimensional matrix of (877, 12). After that, to eliminate the dimensional influence between the indicators, the data is normalized to the maximum value, and all the data is mapped between 0 and 1, as shown in Eq. (6).
where Xscale is the normalized value, X is the original value, Xmax and Xmin are the maximum and minimum values of the original data set, respectively.
Finally, the component content (C, W, Mo, Nb, Zr, Co, Al, Cr, Ti, Ni) and quenching temperature of each piece of data are used as the input vector, and the corresponding fracture toughness value is used as the output vector. And randomly divide the training set and test set according to the ratio of 9:1.
The CPU is Intel(R) Core(TM) i7-7700HQ CPU @ 2.80 GHz, and the memory size is 8GB in this experiment.
In this paper, the Mean Absolute Error (MAE), Root Mean Squared Error (RMSE) and Coefficient of Determination (R2) are selected as the evaluation indicators of this experiment. The calculation methods are shown in Eqs. (7)–(9). Where, the smaller the value of MAE, and RMSE, the better the prediction effect of the model. R2 is used to measure the closeness of the data to the regression line, the value of R2 is closer to 1, the better prediction effect of the model.
where, n represents the total number of samples, Yi represents the true value, and Yip represents the model predicted value.
In order to select the best batch size, we conducted experiments on different batch size (8, 16, 32, 64, 128) under the same experimental environment, and obtained various fracture toughness indexes (MAE, RMSE, R2). The values are shown in Tab. 1.
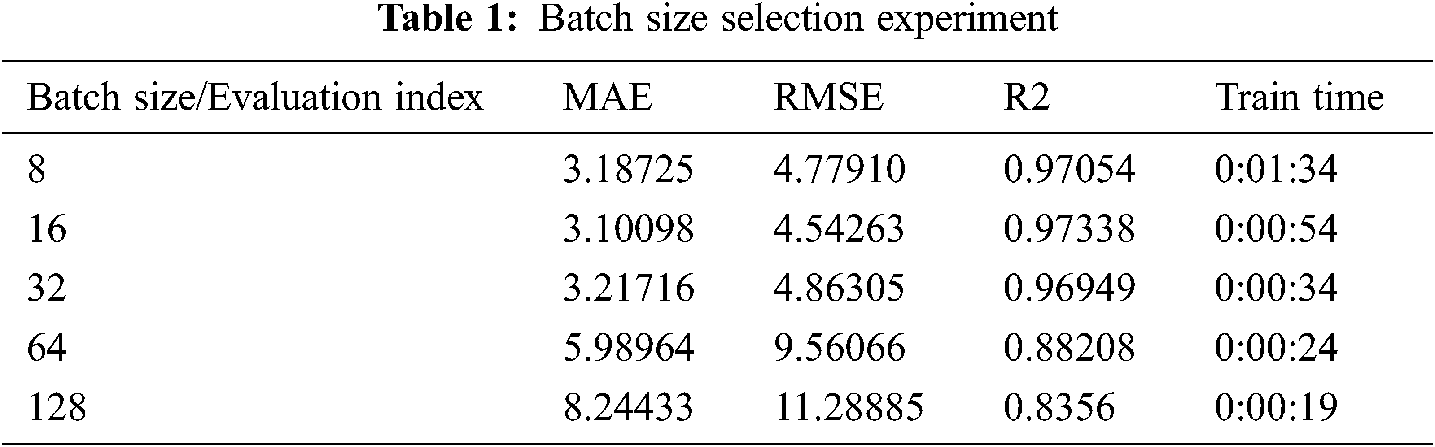
It can be seen from Tab. 1, when the batch size is 16, the overall performance of the model is the best. Therefore, the batch size of the model is selected as 16. Also, use this method to select the optimal training round (Epoch). The experimental results show that when the Epoch of the pre-training stage is 150 and the fine-tuning stage is 300, the entire A-DBN network has the best prediction effect.
In the SVR model, a grid search algorithm combined with cross-validation is used to select the best combination of parameters. The experimental results show that the best parameter combination is: ‘C’ = 10, ‘σ’ = 0.8.
Train the entire model based on the above parameters, and compare the model prediction value and true value after denormalization on the test set to evaluate the prediction effect of the model. The comparison experiment results are shown in Fig. 3.
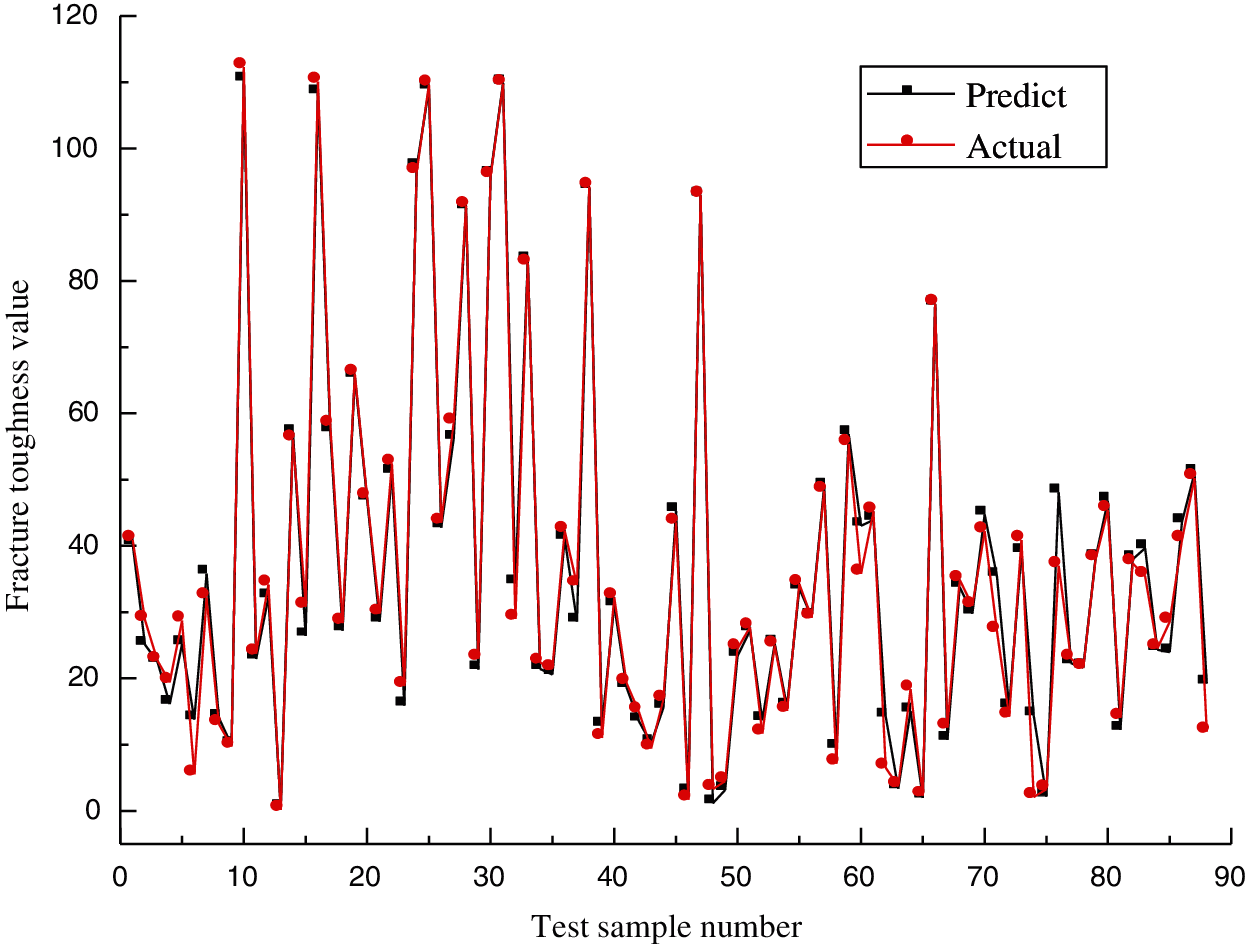
Figure 3: Comparison of prediction value and true value of fracture toughness of nickel-based superalloys
It can be seen from Fig. 3 that the prediction value of the fracture toughness of the nickel-based superalloys can be well fitted with the true value, indicating that the model proposed in this paper has a good prediction effect on the fracture toughness value of nickel-based superalloys.
4.4 Comparison Experiment of Different Prediction Models
To verify the effectiveness of the method in this paper, under the same experimental environment and data, we compare the method in this paper with the commonly used for predicting fracture toughness values: BP neural network, SVR, and basic network structure (DBN, A-DBN, A-DBN + SVR). The comparative experimental results are shown in the Fig. 4.

Figure 4: Comparison of prediction results of fracture toughness models of nickel-based superalloys
It can be seen from Fig. 4 that the combined model based on deep learning proposed in this paper (DBN + Attention + original feature + SVR) has the highest prediction accuracy compared with the traditional machine learning (SVR,BP), DBN, A-DBN, and A-DBN + SVR model. The reasons are as follows: First, the model takes advantage of the excellent feature learning ability of the DBN to overcome the limitation of traditional machine learning methods that rely on artificial experience to extract features. Thus, the learned features have a more essential characterization of the data. Secondly, as the model adds an attention mechanism module to the DBN in the feature learning stage, the model can assign different weights according to the degree of influence of each feature on the fracture toughness of nickel-based superalloys. So that the model can extract features that are more relevant to the fracture toughness value of nickel-based superalloys, improves the prediction performance of the model. Besides, the model combines the feature vectors extracted by the A-DBN module with the original features, and inputs them into the SVR for the regression prediction of fracture toughness value. Thus, not only allows the model to consider both high-order combination features and low-order linear features, but also uses the strong regression prediction ability of SVR, effectively improves the prediction effect of the model.
Through establishing a nickel-based superalloys fracture toughness prediction model that integrates A-DBN and SVR based on the principle of materials genome engineering, we effectively solved the problems of complexity, time-consuming and low accuracy in obtaining the fracture toughness value of nickel-based superalloys by experimental methods. The model uses the DBN to effectively solve the problem of traditional machine learning methods that need to rely on manual experience to extract feature parameters. By adding the attention mechanism to the hidden layer of the network, further optimized the quality of feature extraction. After that, the extracted feature vectors and original features are spliced and input into the SVR model, thus, the model can consider high-order combined features and low-order linear features at the same time, further improved the regression prediction ability of the model.
Funding Statement: This research is supported by Beijing Advanced Innovation Center for Materials Genome Engineering, Beijing Information Science and Technology University, Beijing Key Laboratory of Internet Culture and Digital Dissemination Research (No. ICDDXN004).
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
1. H. Jiang, Y. Guo, Y. Lu and H. Chen, “Tensile properties of a new nickel-based single crystal superalloy,” Journal of Chongqing University, vol. 42, no. 8, pp. 74–78, 2019. [Google Scholar]
2. C. Li, B. Gong, S. Liu, K. Shi, H. Liu et al., “Development of nickel-based super-alloys,” in Proc. CCAW, He Fei, China, pp. 1–5, 2020. [Google Scholar]
3. M. Mu, G. Wang, F. Xuan and S. Tu, “Unified correlation of in-plane and out-of-plane constraints with cleavage fracture toughness,” Theoretical and Applied Fracture Mechanics, vol. 80, no. 2, pp. 121–132, 2015. [Google Scholar]
4. Y. Su, H. Fu, Y. Bai, X. Jiang and J. Xie, “Progress in materials genome engineering in China,” Acta Metallurgica Sinica, vol. 56, no. 10, pp. 1313–1323, 2020. [Google Scholar]
5. H. Wang, X. Xiang and L. Zhang, “Data+AI: The core of materials genomic engineering,” Science & Technology Review, vol. 36, no. 14, pp. 15–21, 2018. [Google Scholar]
6. S. C. Kwon, T. Adachi and W. Araki, “Temperature dependence of fracture toughness of silica/epoxy composites: Related to microstructure of nano- and micro-particles packing,” Composites, Part B Engineering, vol. 39, no. 5, pp. 773–781, 2008. [Google Scholar]
7. K. Wallin, “Irradiation damage effects on the fracture toughness transition curve shape for reactor pressure vessel steels,” International Journal of Pressure Vessels and Piping, vol. 55, no. 1, pp. 61–79, 1993. [Google Scholar]
8. P. Li, L. Cheng, X. Yan, D. Huang, X. Qin et al., “A temperature-dependent model for predicting the fracture toughness of superalloys at elevated temperature,” Theoretical and Applied Fracture Mechanics, vol. 93, no. 1, pp. 311–318, 2018. [Google Scholar]
9. G. Mahalle, O. Salunke, N. Kotkunde, A. K. Gupta and S. K. Singh, “Neural network modeling for anisotropic mechanical properties and work hardening behavior of inconel 718 alloy at elevated temperatures,” Journal of Materials Research and Technology, vol. 8, no. 2, pp. 2130–2140, 2019. [Google Scholar]
10. N. Bano, M. Nganbe and A. Fahim, “Prediction of fracture energy of IN738LC superalloy using neural networks,” in Proc. ICF, Ottawa, Canada, pp. 1–12, 2012. [Google Scholar]
11. A. Seibi and S. M. Al-Alawi, “Prediction of fracture toughness using artificial neural networks (ANNs),” Engineering Fracture Mechanics, vol. 18, no. 3, pp. 311–319, 1997. [Google Scholar]
12. G. Liu, L. Jia, B. Kong, K. Guan and H. Zhang, “Artificial neural network application to study quantitative relationship between silicide and fracture toughness of Nb-si alloys,” Materials & Design, vol. 129, no. 12, pp. 210–218, 2017. [Google Scholar]
13. W. Zeng, Y. Shu and Y. Zhou, “Artificial neural network model for the prediction of mechanical properties of Ti-10 V-2Fe-3Al titanium alloy,” Rare Metal Materials and Engineering, vol. 33, no. 10, pp. 1041–1044, 2004. [Google Scholar]
14. S. Paul and S. Bhattacharjeet, “Modeling and computation by artificial neural network of fracture toughness of low alloy steel to study the effect of alloy composition,” International Journal of Modeling, Simulation, and Scientific Computing, vol. 9, no. 6, pp. 1–14, 2018. [Google Scholar]
15. L. Qiao, Y. Liu and J. Zhu, “Application of generalized regression neural network optimized by fruit fly optimization algorithm for fracture toughness in a pearlitic steel,” Engineering Fracture Mechanics, vol. 235, no. 1, pp. 1–10, 2020. [Google Scholar]
16. I. Mohanty, D. Bhattacharjee and S. Datta, “Designing cold rolled if steel sheets with optimized tensile properties using ANN and GA,” Computational Materials Science, vol. 50, no. 8, pp. 2331–2337, 2011. [Google Scholar]
17. J. Xiong, S. Shi and T. Zhang, “Machine learning of mechanical properties of steels,” Science China Technological Sciences, vol. 63, no. 7, pp. 1247–1255, 2020. [Google Scholar]
18. K. M. Hamdia, T. Lahmer, N. T. Trung and T. Rabczuk, “Predicting the fracture toughness of PNCs: A stochastic approach based on ANN and ANFIS,” Computational Materials Science, vol. 102, no. 1, pp. 304–313, 2015. [Google Scholar]
19. D. Sun, L. Liu, H. Shi, X. Ma, C. Zhang et al., “Prediction of composite ceramics’ fracture toughness based on BP neural network,” Materials Science and Technology, vol. 13, no. 5, pp. 10–12, 2005. [Google Scholar]
20. F. Ding, J. Weng, X. Chen, L. Jia, H. Zhang et al., “Improvement of fracture toughness of directionally solidified Nb-silicide in situ composites using artificial neural network,” Materials Science and Engineering A, vol. 605, no. 1, pp. 65–72, 2014. [Google Scholar]
21. C. Fu, S. Yang and Y. Zhang, “Promoted short-term traffic flow prediction model based on deep learning and support vector regression,” Transportation Systems Engineering and Information, vol. 19, no. 4, pp. 130–134 + 148, 2019. [Google Scholar]
22. X. Luo, Q. Jiao, L. Niu and Z. Sun, “Short-term traffic flow prediction based on deep learning,” Application Research of Computers, vol. 34, no. 1, pp. 91–93 + 97, 2017. [Google Scholar]
23. W. Pan and D. Chen, “Research on short-term traffic flow prediction based on GRU-sVR,” Computer Technology and Development, vol. 29, no. 10, pp. 11–14, 2019. [Google Scholar]
24. Y. Xu, X. Meng, Y. Li and X. Xu, “Research on privacy disclosure detection method in social networks based on multi-dimensional deep learning,” Computers, Materials & Continua, vol. 62, no. 1, pp. 137–155, 2020. [Google Scholar]
25. K. Yang, Y. Wang, W. Zhang, J. Yao and Y. Le, “Keyphrase generation based on self-attention mechanism,” Computers, Materials & Continua, vol. 61, no. 2, pp. 569–581, 2019. [Google Scholar]
26. C. Zhang, J. Cheng, X. Tang, V. Sheng and Z. Dong, “Novel DDoS feature representation model combining deep belief network and canonical correlation analysis,” Computers, Materials & Continua, vol. 61, no. 2, pp. 657–675, 2019. [Google Scholar]
27. Z. Li, J. Zhang, K. Zhang and Z. Li, “Visual tracking with weighted adaptive local sparse appearance model via spatio-temporal context learning,” IEEE Transactions on Image Processing, vol. 27, no. 9, pp. 4478–4489, 2018. [Google Scholar]
28. Z. Li, W. Li, F. Lin, Y. Sun, M. Yang et al., “Hybrid malware detection approach with feedback-directed machine learning,” Science China (Information Sciences), vol. 63, no. 3, pp. 235–245, 2020. [Google Scholar]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |