DOI:10.32604/csse.2022.022899

| Computer Systems Science & Engineering DOI:10.32604/csse.2022.022899 |  |
| Article |
PAPR Reduction Using Advanced Partial Transmission Scheme for 5G Waveforms
1Department of Electronics and Communication Engineering, JECRC University, Jaipur, 303905, INDIA
2Department of Electrical and Computer Engineering, Kennesaw State University, GA, USA
3Electronics and Communication Engineering, CMR Institute of Technology, Bangalore, INDIA
4Department of Computer Science, College of Computers and Information Technology, Taif University, 11099, Saudi Arabia
*Corresponding Author: Mehedi Masaud. Email: mmasud@tu.edu.sa
Received: 21 August 2021; Accepted: 22 September 2021
Abstract: The implementation of Peak Average to Power Ratio (PAPR) reduction technologies will play an important role in the regularization of Fifth Generation (5G) radio communication. PAPR reduction in the advanced waveform will be the key part of designing a 5G network for different applications. This work introduces the simulation of an Advanced Partial Transmission Sequence (A-PTS) reduction techniques for Orthogonal Frequency Division Multiplexing (OFDM) and Filter Bank Multi-Carrier (FBMC) transmission schemes. In the projected A-PTS, the FBMC signals are mapped into the number of sub-blocks and Inverse Fast Fourier transform (IFFT) is performed to estimate the high peak power in the time domain. The FBMC sub-blocks are multiplied with the phase elements to achieve an optimal PAPR value. A MATLAB 2014v simulation is used to estimate the PAPR, Bit Error Rate (BER), Error Vector Magnitude (EVM), and Modulation Error Rate (MER) performance of the proposed reduction schemes. The simulated result reveals that the performance of the projected algorithm is better than the conventional algorithms.
Keywords: PAPR; PTS; OFDM; FBMC; 5G
Due to the increase in requirement of high data speed, low latency, efficient spectral accessing, and connectivity with a large number of machines, it has become essential to investigate an advanced multi-carrier technique [1]. It is predicted that the data consumption will increase to 30% by 2021, which cannot be handled by the current used waveform method known as OFDM. The schematic of OFDM is given in Fig. 1. OFDM is currently utilized in Fourth Generation (4G) radio and it has several applications [2]. In OFDM, a cyclic prefix (CP) is introduced to overcome the Inter Symbol Interference (ISI), which was regarded as a serious problem in the Third Generation (3G) radio system. However, the addition of CP results in the 11% wastage of bandwidth. PAPR, spectrum leakage due to the large side lobes, bad performance in Cognitive Radio (Cr) scenario, and sensitivity to frequency and time scattering are few concerns of the OFDM structure [3]. Several studies [4–6] suggested that OFDM is not a suitable candidate for the forthcoming 5G radio system. Hence, it is necessary to look out for an alternate of OFDM waveform.
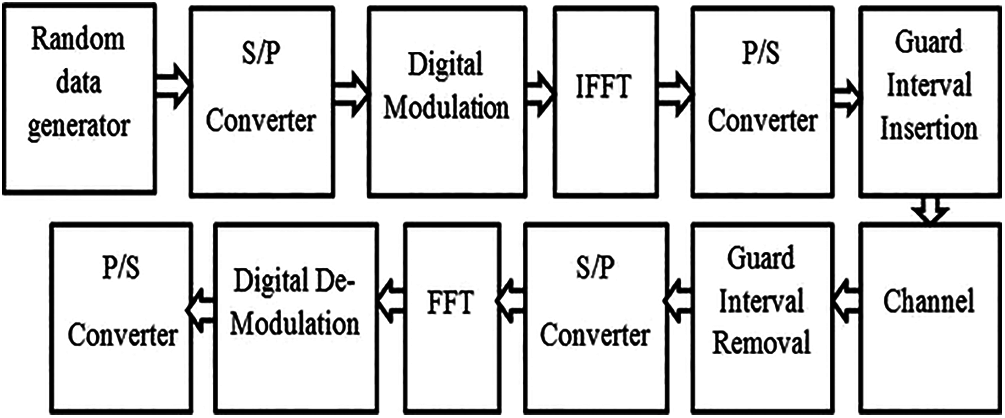
Figure 1: Block diagram of OFDM
The structure of FBMC is shown in Fig. 2. FBMC is regarded as an appropriate competitor for the 5G framework. FBMC is implemented by utilizing a cluster of filters at the transmitter and the receiver part of the structure followed by Fourier transforms. The use of filters boosts the throughput of the structure as well as also mitigates the concerns related to ISI. Hence, in FBMC, ISI can be overcome without inserting the CP. It is also seen that the FBMC has spectrum accessing performance than the OFDM structure [7]. Many studies confirmed that the FBMC is better suited for the CR than the OFDM as its efficiency is high in the fading environment. Thus, makes it suitable for several applications such as Digital Subscribers Lines (DSL), PLC, and similar function [8,9]. However, the enactment of FBMC degrades with the combination of Multiple Inputs and Multiple Outputs (MIMO) system and the complexity is high due to increase in filter size [10,11]. PAPR is a key imperative delinquent in OFDM and FBMC structure. Several PAPR methods have been investigated for OFDM [12]. However, the PAPR algorithms designed for OFDM cannot be applied to FBMC due to their disparate structure arrangement [13].
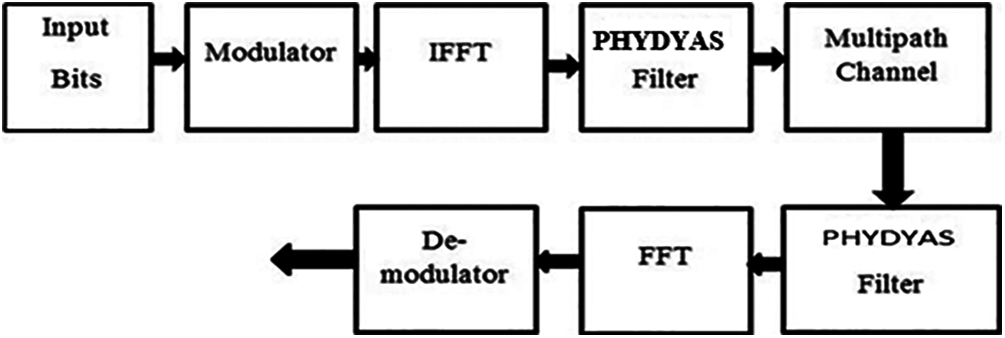
Figure 2: Schematic of FBMC
PAPR occurs when the amplitude of the sub-carriers is increased due to the constructive interference. In [14], PAPR reduction is applied to the NOMA system by using a bacteria foraging algorithm and it increased the complexity due to the number of phase searches for an optimal PAPR. However, in the proposed work, the phase search is not increasing the complexity. In recent years, there are numerous PAPR algorithms like A-and Mu law [15], clipping [16], Selective Mapping (SLM) [17], PTS [18], hybrid [19] which have been investigated on the FBMC structure. In [20], the SLM-Circulation Transform (SLM-CT) algorithm was introduced to mitigate the peak power of the FBMC arrangement. It is observed that the SLM lowers down the high amplitude power of FBMC and CT reduces the complexity of the structure. A-Law and Mu-Law have also been applied to decrease the PAPR of the FBMC waveform. It was shown that Mu-law accomplished a gain of 2 dB better than the A-law [21]. The authors introduced a clipping method to minimize the maximum peak power of the FBMC. The outcome of the study revealed that the suggested clipping algorithm efficiently lowered the PAPR of the FBMC structure as compared with PAPR of the OFDM [22]. In [19], a hybrid algorithm is designed to mitigate the amplitude power of the FBMC system. It was shown that its efficiency and throughput performance of the FBMC is superior to OFDM based k-hybrid algorithm. Recently, PAPR algorithms such as Tone Reservation (TR) and hybrid PAPR algorithms were applied on FBMC and OFDM waveform. It is seen that the proposed algorithms generated a gain of 3 dB for FBMC in comparison to OFDM [23]. In [24], the authors investigate the effect of PAPR on multi-carrier waveforms. Several power reductions based PAPR algorithms were tested on multicarrier waveforms. It is seen that the algorithm gave superior performance on FBMC and NOMA as compared with OFDM. The authors also compared the performance of FBMC and Universal Filter Multi Carrier (UFMC) framework. It is seen that UFMC gives a better performance than FBMC or OFDM but has more complexity which is a major issue for the applicability of UFMC [25].
The contributions of the article are as follows:
• We propose a novel modified A-PTS PAPR minimization algorithm for beyond 5G candidate waveforms.
• The throughput of the proposed system is vastly improved as compared with the existing method, without significant increase of complexity.
• It is seen that the spectrum leakage of the FBMC is significantly reduced on applying the A-PTS algorithm.
The key concept of OFDM is to split the single carrier into the number of orthogonal sub-carriers. The OFDM symbol is given as [26]:
T is the total period. The OFDM signal with m sub-carriers is given as:
where L is the OFDM symbol index, P(t) is the response of the filter,
The PAPR of the OFDM signal is given as:
where E is the Expectation operator.
The key aspect of FBMC is to split the transmission channel into several sub-channels. The sub-channels in the FBMC structure are orthogonal. The orthogonality between the sub-channels helps to exploit the entire spectrum of the system. The FBMC signals can be denoted as [27]:
From Eq. (8), it is observed that the filter is applied to the individual sub-carriers.
The PAPR of the FBMC signals is given by:
The PAPR in dB is given by:
The CCDF of the FBMC signal is estimated as:
2.3 A-PTS (Advanced Partial Transmission Sequence)
PTS is one of the most efficient methods used for minimizing the peak power of the signal and is schematically shown in Fig. 3. The modulated FBMC signals are separated into the number of sub-blocks and Inverse Fast Fourier Transform (IFFT) is carried out to estimate the PAPR of the signals. The optimal phase elements vectors are searched for each FBMC sub-blocks. Following the algorithm, the FBMC sub-blocks are multiplied by the phase vectors, which thereby optimizes the PAPR [28].
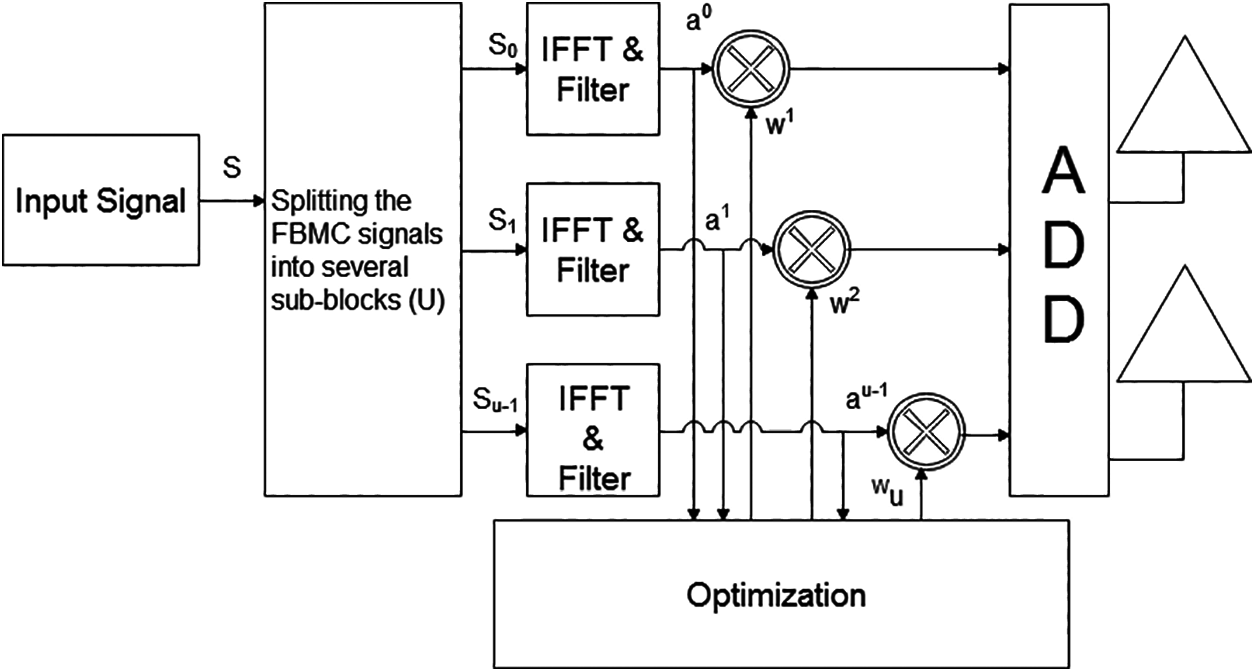
Figure 3: Advanced PTS
Let us consider a FBMC sub-blocks given as:
The FBMC sub-blocks
where W is the angle vectors restricted to the set
The IFFT is carried out to estimate the amplitude peak power given as:
The PAPR is estimated as:
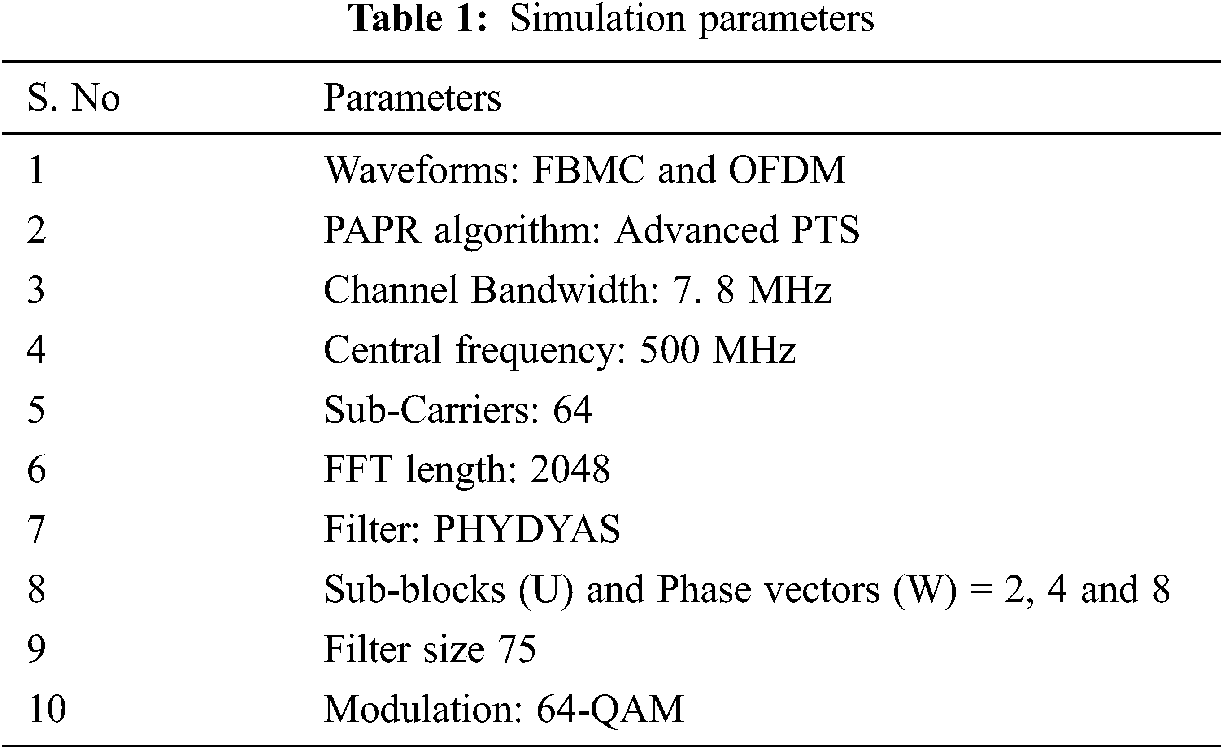
The work is implemented by using a Matlab-2013 software. The simulation parameters used are given in Tab. 1.
The proposed A-PTS is applied to FBMC by varying the number of sub-blocks (U) and phase element vector (W), as shown in Fig. 4. At the CCDF of 10−5, the peak power is lower to 7.9 dB (PTS U = 8 W = 2), 8.3 dB (PTS U = 8 W = 4), 8.6 dB (PTS U = 8 W = 8), and 9.1 dB (PTS) as compared to the original PAPR of FBMC (12 dB).

Figure 4: PAPR analysis for U and W = 2
The PAPR curves are analyzed for the proposed method (W = 4 and U = 2, 4, and 8). At the Complementary Cumulative Distribution Function (CCDF) of 10−5, peak power is minimized to 6.6 dB, 6.9 dB, 7.6 dB, and 9 dB. It is observed that the PTS (W = 4, U = 8) generated a gain of 0.3, 1, 2.4, and 5.4 dB as compared with the other comparable methods, as shown in Fig. 5.

Figure 5: PAPR analysis for U and W = 4
In Fig. 6, the peak power is estimated for W = 8 and U = 2, 4, and 8. It is observed that by increasing the number of U and W, the ideal PAPR can be accomplished. At the CCDF of 10−5, the PTS (U = 8 W = 8) achieved the best performance by decreasing the peak power to 4.1 dB as compared with other comparable algorithms.

Figure 6: PAPR analysis for U and W = 8
The throughput of the system is analyzed by estimating the BER of the projected algorithms on FBMC structure shown in Fig. 7. It is observed that for a large number of sub-blocks and phase vectors, efficient performance is accomplished. The BER of 10−5 is obtained at the SNR of 4.4, 5.1, 6.4, 7.1, and 8.8 dB as compared to the PAPR of FBMC structure (12 dB).

Figure 7: BER analysis for U and W
In Fig. 8, we have estimated the PAPR performance. The proposed PTS algorithm is implemented at the transmitter f FBMC and OFDM structure. It is seen that the projected PTS-FBMC (U = 8, W = 8) obtained a gain of 3.2 and 7.8 dB as compared with PTS-OFDM (PTS U = 8 W = 2), PTS-FBMC, and PTS-OFDM techniques.

Figure 8: PAPR of OFDM and FBMC
In this work, we have considered athematic operations such as additions and multiplications and IFFT as the complexity of the PAPR algorithm. The complexity of the proposed algorithm and Conventional PTS [29] is given as:
The constellation diagram of the proposed PAPR reduction techniques is indicated in Fig. 9. It shows all the possible symbols used by the system to transmit the data. Error Vector Magnitude (EVM) and Modulation Error Rate (MER) are figures of merit of transmission accuracy. They compute the performance and efficiency of transmission. It takes into accounts the phase and peak distortions as well as interference and provides an inclusive figure of merit for calculating the effectiveness of a system. The EVM and MER of the proposed PAPR reduction schemes is 0.83 dB and MER = 0.705 dB

Figure 9: EVM and MER
The collaboration within the 5G network and these by reduction of the PAPR is essential condition for the deployment of the 5G in cellular communication. The main objective of the proposed work is to design a PAPR technique for advanced waveform techniques and to optimize the 5G output. A new modified PTS-FBMC is implemented and proposed for the upcoming 5G radio framework. The proposed algorithm is analyzed and estimated for FBMC and OFDM structure in MATLAB 2014. The advanced PTS is obtained by changing the number of sub-blocks (U) and Phase vectors (W) to decrease the PAPR. According to the assessments and investigation, the proposed PTS-FBMC transmission scheme out-performs the typical PTS-OFDM structure. The design complexity of the novel transmission methods is moderate, and can be even further reduced by using the fewer number of FFTs and limiting the count of sub-carriers. The significant advantage of the suggested scheme over the OFDM is an enhancement of PAPR and BER performance due to the modified PTS at the transmitting. It is concluded therefore that FBMC is an ideal contender for the 5G network, particularly when aided by the proposed PAPR reduction scheme.
Acknowledgement: The authors would like to thank for the support from Taif University Researchers Supporting Project number (TURSP-2020/73), Taif University, Taif, Saudi Arabia.
Funding Statement: This work was supported by Taif University Researchers Supporting Projects (TURSP). Under number (TURSP-2020/73), Taif University, Taif, Saudi Arabia.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
1. S. Mattisson, “An overview of 5G requirements and future wireless networks: Accommodating scaling technology,” IEEE Solid-State Circuits Magazine, vol. 10, no. 3, pp. 54–60, 2018. [Google Scholar]
2. M. Mounir, M. B. EI. Mashade, S. Berra, G. S. Gaba, M. Masud et al., “A novel hybrid precoding-companding technique for peak-to-average power ratio reduction in 5G and beyond,” Sensors, vol. 21, no. 4, pp. 1–21, 2021. [Google Scholar]
3. A. K. Bairagi, Md S. Munir, M. Alsenwi, N. H. Tran, S. S. Alshamrani et al., “Coexistence mechanism between eMBB and uRLLC in 5G wireless networks,” IEEE Transactions on Communications, vol. 69, no. 3, pp. 1736–1749, 2021. [Google Scholar]
4. R. W. Bauml, R. F. Fischer and J. B. Huber, “Reducing the peak-to-average power ratio of multicarrier modulation by selected mapping,” Electronics Letters, vol. 32, no. 22, pp. 2056–2057, 1996. [Google Scholar]
5. J. G. Andrews, S. Buzzi, W. Cho, V. S. Hanly, A. Lozano et al., “What will 5G be,” IEEE Journal on Selected Areas in Communications, vol. 32, no. 6, pp. 1065–1082, 2014. [Google Scholar]
6. X. Zhang, L. Chen, J. Qiu and J. Abdoli, “On the waveform for 5G,” IEEE Communications Magazine, vol. 54, no. 11, pp. 74–80, 2016. [Google Scholar]
7. J. Kim, Y. Park, S. Weon, J. Jeong, S. Choi et al., “A new filter-bank multicarrier system: The linearly processed FBMC system,” IEEE Transactions on Wireless Communications, vol. 17, no. 7, pp. 4888–4898, 2018. [Google Scholar]
8. A. Hammoodi, L. Audah and M. A. Taher, “Green coexistence for 5G waveform candidates: A review,” IEEE Access, vol. 7, pp. 10103–10126, 2019. [Google Scholar]
9. D. Mattera, M. Tanda and M. Bellanger, “Analysis of an FBMC/OQAM scheme for asynchronous access in wireless communications,” EURASIP Journal on Advances in Signal Processing, vol. 2015, no. 1, pp. 64, 2015. [Google Scholar]
10. R. Arjun, I. Bhadauria, H. Shah, V. Sangwan and V. M. Gadre, “Filter bank multicarrier-QAM for MIMO systems,” in 2017 Twenty-third National Conf. on Communications (NCC), Chennai, pp. 1–6, 2017. [Google Scholar]
11. A. Farhan, N. Marchetti, L. E. Doyle and B. F. Boroujeny, “Filter bank multicarrier for massive MIMO,” in 2014 IEEE 80th Vehicular Technology Conf. (VTC2014-Fall), Vancouver, British Columbia, Canada, pp. 1–7, 2014. [Google Scholar]
12. F. B. Ogunkoya, W. O. Popoola, A. Shahrabi and S. Sinanović, “Performance evaluation of pilot-assisted PAPR reduction technique in optical OFDM systems,” IEEE Photonics Technology Letters, vol. 27, no. 10, pp. 1088–1091, 2015. [Google Scholar]
13. H. Rathore and A. Kumar, “Reduction of peak average power ratio for FBMC waveform with P-PTS technique,” Int. Journal of Sensors, Wireless Communications and Control, vol. 10, no. 1, pp. 47–54, 2020. [Google Scholar]
14. A. Kumar, M. Gupta, D. Le and A. A. Aly, “PTS-PAPR reduction technique for 5G advanced waveforms using BFO algorithm,” Intelligent Automation & Soft Computing, vol. 27, no. 3, pp. 713–722, 2021. [Google Scholar]
15. A. Hasan, M. Zeeshan, M. A. Mumtaz and M. W. Khan, “PAPR reduction of FBMC-OQAM using A-law and Mu-law companding,” in 2018 ELEKTRO, Mikulov, Czech Republic, pp. 1–4, 2018. [Google Scholar]
16. J. Moon, Y. Nam and J. Kim, “PAPR reduction in the FBMC-OQAM system via segment-based optimization,” IEEE Access, vol. 6, pp. 4994–5002, 2018. [Google Scholar]
17. A. Kumar and H. Rathore, “Modified DSLM technique for PAPR reduction in FBMC system,” Radioelectronics and Communications Systems, vol. 62, no. 8, pp. 416–421, 2019. [Google Scholar]
18. Z. He, L. Zhou, Y. Chen and X. Ling, “Low-complexity PTS scheme for PAPR reduction in FBMC-OQAM systems,” IEEE Communications Letters, vol. 22, no. 11, pp. 2322–2325, 2018. [Google Scholar]
19. A. Kumar, “PAPR reduction of FBMC using hybrid and k-hybrid techniques,” Radioelectronics Communication System, vol. 62, no. 10, pp. 501–509, 2019. [Google Scholar]
20. A. Kumar and M. Gupta, “A comprehensive study of PAPR reduction techniques: Design of DSLM-CT joint reduction technique for advanced waveform,” Soft Computing, vol. 24, no. 16, pp. 11893–11907, 2020. [Google Scholar]
21. I. A. Shaheena, A. Zekrya, F. Newagya and R. Ibrahimb, “Performance evaluation of PAPR reduction in FBMC system using nonlinear companding transform,” ICT Express, vol. 5, no. 1, pp. 41–46, 2019. [Google Scholar]
22. Z. Kollar and P. Horvath, “PAPR reduction of FBMC by clipping and its iterative compensation,” Journal of Computer Networks and Communications, vol. 2012, no. 4, pp. 1–11, 2012. [Google Scholar]
23. M. Laabidi, R. Zayani, D. Roviras and R. Bouallegue, “PAPR reduction in FBMC/OQAM systems using active constellation extension and tone reservation approaches,” in 2015 IEEE Sym. on Computers and Communication (ISCC), Larnaca, Cyprus, pp. 657–662, 2015. [Google Scholar]
24. A. Kumar, “A novel hybrid PAPR reduction technique for NOMA and FBMC system and its impact in power amplifiers,” IETE Journal of Research, vol. 5, no. 1, pp. 1–17, 2019. [Google Scholar]
25. S. Sidiq, F. Mustafa, J. A. Sheikh and B. A. Malik, “FBMC and UFMC: The modulation techniques for 5G,” in 2019 Int. Conf. on Power Electronics, Control and Automation (ICPECA), New Delhi, India, pp. 1–5, 2019. [Google Scholar]
26. D. W. Lim, S. J. Heo, J. S. No and H. Chung, “A new PTS OFDM scheme with low complexity for PAPR reduction,” IEEE Transactions on Broadcasting, vol. 52, no. 1, pp. 77–82, 2006. [Google Scholar]
27. F. Sandoval, G. Poitau and F. Gagnon, “Hybrid peak-to-average power ratio reduction techniques: Review and performance comparison,” IEEE Access, vol. 5, pp. 27145–27161, 2017. [Google Scholar]
28. A. Kumar, S. Ambigapathy, M. Masud, E. S. Jaha, S. Chakravarty et al., “An efficient hybrid PAPR reduction for 5G NOMA-FBMC waveforms,” Computers, Materials & Continua, vol. 69, no. 3, pp. 2967–2981, 2021. [Google Scholar]
29. A. Kumar, M. A. Albreem, M. H. Alsharif, A. Jahid, P. Uthansakul et al., “An efficient genetic hybrid PAPR technique for 5G waveforms,” Computers, Materials & Continua, vol. 67, no. 3, pp. 3283–3292, 2021. [Google Scholar]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |