DOI:10.32604/csse.2022.023018

| Computer Systems Science & Engineering DOI:10.32604/csse.2022.023018 |  |
| Article |
Roosters Algorithm: A Novel Nature-Inspired Optimization Algorithm
1Ardahan University, Ardahan, 75003, Turkey
2Cukurova University, Adana, 01330, Turkey
*Corresponding Author: Mashar Gencal. Email: masharcenkgencal@ardahan.edu.tr
Received: 25 August 2021; Accepted: 27 September 2021
Abstract: Some species of females, e.g., chicken, bird, fish etc., might mate with more than one males. In the mating of these polygamous creatures, there is competition between males as well as among their offspring. Thus, male reproductive success depends on both male competition and sperm rivalry. Inspired by this type of sexual life of roosters with chickens, a novel nature-inspired optimization algorithm called Roosters Algorithm (RA) is proposed. The algorithm was modelled and implemented based on the sexual behavior of roosters. 13 well-known benchmark optimization functions and 10 IEEE CEC 2018 test functions are utilized to compare the performance of RA with the performance of well-known algorithms; Standard Genetic Algorithm (SGA), Differential Evolution (DE), Particle Swarm Optimization (PSO), Cuckoo Search (CS) and Grey Wolf Optimizer (GWO). Also, non-parametric statistical tests, Friedman and Wilcoxon Signed Rank Tests, were performed to demonstrate the significance of the results. In 20 of the 23 functions that were tested, RA either offered the best results or offered similar results to other compared algorithms. Thus, in this paper, we not only present a novel nature-inspired algorithm, but also offer an alternative method to the well-known algorithms commonly used in the literature, at least as effective as them.
Keywords: Evolutionary computation; meta-heuristics; optimization; roosters algorithm
Nowadays, researchers have begun to get more inspiration from nature in order to model optimization algorithms. Thus, these stochastic algorithms, which are also called meta-heuristics, have become popular for some reasons:
Generally, meta-heuristics are based on a simple idea such as an evolutionary process, a behavior of an animal or a plant, a physical event etc. Such ideas allow researchers to simply model and implement an algorithm. Thus, researchers will quickly compare the performance of the algorithm with the performance of other meta-heuristics.
On the other hand, meta-heuristics can solve an optimization problem efficiently. They can certainly handle problems such as getting stuck in local optima or premature convergence, where former methods often encounter [1–4]. Thanks to their stochastic natures, meta-heuristics can avoid this type of problems, and explore the search space efficiently. Therefore, they can be accomplished in challenging problems.
Another important reason is that meta-heuristic algorithms can find the optimum point(s) without taking derivatives. As known, in mathematics, values that make the first derivative of a function zero give the optimum point(s). However, when the number of variables is large, it will be challenging to perform this operation. Meta-heuristic algorithms offer a straightforward technique that uses random solutions to arrive at optimum points, rather than taking derivations. This makes meta-heuristics extremely suitable for types of problems that are difficult to derive.
Meta-heuristic algorithms generally initiate with randomly creating the potential solutions, called initial population. After the initial population is generated, they proceed by evaluating fitness values (via a fitness function) of individuals in the population. Afterwards, their nature-inspired searching steps starts. Next, they return to the beginning of the process and repeat it until the termination criteria are met; either the optimum solution is found or maximum number of generations are reached.

Figure 1: The taxonomy of well-known meta-heuristic algorithms
In the literature of meta-heuristics, algorithms can be classified in four main groups [5,6]: Evolutionary Algorithms (EAs), Swarm-based, Physics/Chemistry-based and Human-based algorithms, see Fig. 1.
EAs employ intelligent strategies, which are selection, recombination (also called crossover), and mutation. By using these strategies, EAs iteratively improve the initial solution to produce new solutions. The most popular EAs are Genetic Algorithms (GAs) [1], Differential Evolution (DE) [7] and Biogeography-Based Optimizer (BBO) [8].
Swarm-based algorithms (SBA) inspire by living creatures as swarm, flocks or herds. One of the most well-known SBA is Particle Swarm Optimization (PSO) [9]. Essentially, PSO was designed to simulate social behavior of bird flock and fish swarm. However, it was comprehended that PSO actually performs optimization. Unlike to GAs, each potential solution (particle) also includes a velocity to move around in the search space. Other famous SBA are Ant Colony Optimization (ACO) [10], Cuckoo Search (CS) [11], Artificial Bee Colony (ABC) [12], Firefly Algorithm (FA) [13] and Grey Wolf Optimizer (GWO) [14].
Another group of meta-heuristics are Physics/Chemistry-based algorithms, which are inspired by the physical or chemical laws. Some common ones are Simulated Annealing (SA) [15], Big-Bang Big-Crunch (BBBC) [16], Gravitational Search (GS) [17] and Black Hole (BH) [18].
In addition the meta-heuristics mentioned above, there are also some algorithms that inspired from human behaviors: Tabu Search (TS) [19], Harmony Search (HS) [20], Imperialist Competitive Algorithm (ICA) [21], Teaching Learning Based Optimization (TLBO) [22] and Fireworks Algorithm (FA) [23].
However, one main problem of meta-heuristics is the lack of adjusting the balance between exploration and exploitation, which directly affects the genetic diversity of the population.
Exploration is an activity that discovers information or resources while exploitation refers researching a limited (but promising) area of the search space (owing to hope developing the promising solution). The traditional technique that using large population sizes to make exploration efficiently is inadequate since it causes to increase the computational budget. On the other hand, giving priority to good solutions is the common way for exploitation. However, this technique might bring about losing genetic diversity as the average and poor solutions are generally overlooked.
The aim of this paper is to create an algorithm to solve the main problem of meta-heuristics that mentioned in the above paragraphs. For this purpose, we have designed a new algorithm called Roosters Algorithm (RA). Owing to the step of RA, which benefits from the average and poor solution, it can control the genetic diversity better than other meta-heuristics that were tested.
Based on the No Free Lunch (NFL) theorem [24], a single algorithm cannot perform well in every optimization problem. This theorem allows researchers to present new algorithms to solve different problems in the related fields, which also encouraged us to propose RA.
In this paper, the performance of RA was compared with the performance of the distinguished meta-heuristic algorithms: Standard GA (SGA), DE, PSO, CS and GWO. In addition to utilizing thirteen basic benchmarks, ten IEEE CEC 2018 test functions (shifted, rotated, expanded etc.) were also employed for the comparison. Furthermore, non-parametric statistical tests, Friedman and Wilcoxon Signed Rank, were performed to demonstrate the significance of the tests results.
According to the obtained results, RA performs better than other meta-heuristics that compared in this paper. Thus, besides presenting a novel algorithm, we also offer an alternative method to the well-known meta-heuristics, which is at least as effective as they are.
The rest of paper is organized as follow: Section 2 explains inspiration of RA besides to introducing it. While Section 3 describes the tests, Section 4 discusses the results from these tests. Finally, Section 5 concludes the paper.
Female creatures might mate with more than one males [25]. In the mating of these polygamous creatures, the reproductive success of a male is based on the quality of his sperms, according to “sperm competition” theory [25]. Since chickens are these type of creatures, they can mate more than one roosters, especially attractive ones.
As in humans, the sexual life of roosters with chickens begins with flirting [26]. First of all, a rooster presents some foods to a chicken, and shows his dancing skills to engage her. If she is impressed by him, then they can mate.
However, the rooster may want to mate a chicken without her permission. In this scenario, even if he ejaculates his sperms to her ova, she nervously sprinkle them.
On the other hand, the age of the rooster is another important factor for mating [26]. For instance, chickens do not want to mate with senior roosters as their proportions of fertilizing an egg is very low.
When mating procedure is completed, the sperm competition starts if the chicken has more than one male. The VSL value, the most common estimator of sperm cell velocity, is significantly important in the competition of sperms [25]. If the VSL of a male’s sperm is higher than others, he is more likely to outstrip his opponents in the manner of fertilizing the egg.
Furthermore, if the chicken has fears about her life or she has a disease, it directly affects the formation of her egg [26], i.e., disrupts the DNA of the egg.

Inspired by the sexual life of roosters with chickens, a novel natured-inspired optimization algorithm called RA, whose complexity is O (n) (where n is the population size), is proposed. Initially, the rooster size, which is the number of roosters that desire to mate, is determined. Then, the algorithm sustains its procedure by creating the initial population, as other meta-heuristics do. In RA, roosters and their offspring are accepted as the candidate solution for the problem.
After stochastically identifying roosters and chickens, the attractive chicken is determined among chickens by looking at their fitness values which are acquired by the fitness function that needs to be optimized. The age of a rooster, which means the number of existences of the rooster during its life cycle, shows how effectively he dances. On the other hand, the fitness value also refers whether the rooster is accomplished to find food resources. For instance, the rooster having better fitness value can present adequate foods for a chicken.
If a rooster impresses the chicken by dancing or presenting food, he can mate with her. Otherwise, he may try to mate by force, which is randomly determined. However, in this case, the chicken kills sperms of the rooster by sprinkling them.
When the attractive chicken may have more than one male, the competition occurs among the sperms of males. In this case, the sperm quality of males is identified by VSL value, which is obtained by the fitness function. The offspring who has better VSL value than others gets a chance to fertilize an egg. If the chicken has only one male, then his offspring fertilizes the egg.
Furthermore, if the chicken has fears about her life or she has a disease, then the offspring is mutated. Random Mutation, which randomly select gene(s) by replacing any value within the range of corresponding dimension(s), has been utilized for the mutation.
The process of RA is repeated until the termination criteria are met; either the optimum solution is found or maximum number of generations are reached, shown in Algorithm 1.
In the field of meta-heuristics, researchers have generally employed benchmarks as test functions. On the other hand, with the advancement of technology, the number of proposed algorithms in meta-heuristics has increased; therefore, different types of functions has been needed to test them. To do that, researchers has created new test functions by shifting, rotating, expanding and hybridizing the well-known benchmarks.
These functions are grouped into two classes; unimodal and multimodal. Unimodal class comprises sensitive functions that accomplish to converge slowly to the global extremum. Multimodal class includes functions having more than one local extremum.
In addition to utilizing thirteen well known benchmarks in the field of meta-heuristics [27,28], ten IEEE CEC 2018 test functions [29] were also operated to test the performance of the compared algorithms, see Tab. 1.
Hypothesis testing has been commonly used in order to infer the comparison of the algorithms [30]. However, the null hypothesis, H0, and the alternative hypothesis, H1, are supposed to be defined in order to make inferences. The null hypothesis is a proposition that generally refers no differences between compared algorithms. Conversely, the alternative hypothesis is an expression of the differences. In our case;
H0: There is no difference between compared algorithms
H1: There is difference between compared algorithms
Moreover, the probability value of a statistical test, α, decides which hypothesis should be rejected. For our test, α is accepted as 0.05.
In this paper, Friedman and Wilcoxon Signed Rank tests were performed to demonstrate the significance of the results. While IBM SPSS Statistics 22 was utilized to obtain the results of the Friedman test, the signrank function of Matlab 2019a was used to get the results of the Wilcoxon Signed Rank test.
The Friedman test, introduced by Friedman [31,32], is a non-parametric statistical test. It has been utilized to specify differences in behaviour of more than one algorithm. In the Friedman test, test cases are represented in rows and results of compared algorithms takes places in columns.
The test initiates its procedure by giving rank to each row based on the values of columns in the row, then, it computes the total rank values for each column. The significance of the test is determined by
where k means number of columns, n refers number of rows and
3.2.2 Wilcoxon Signed Rank Test
Wilcoxon signed rank test is another non-parametric statistical test that has been used to state the differences between two samples or algorithms [34]. As a common way, the test initially takes differences between the results of the two algorithms whose sizes are N*1 (where N means the number of tests) in order to obtain the difference vector. Then, it ranks to each row of the vector from 1 to N, i.e., min. value is ranked 1. Afterwards, it computes
All algorithms were implemented by using Matlab 2019a, except CS and GWO. The Matlab codes of CS and GWO were taken from [35] and [36] respectively.
The tests were repeated with 30 runs that have 30 different random seeds in order to minimize the effects of randomization. The results were achieved by utilizing default parameter settings of algorithms. All algorithms were analyzed where population sizes are equal to 50, 100 and 200. As expected, all algorithms show their best performance when population size is 200. Therefore, population size is taken as 200 throughout tests. Furthermore the number of iteration is accepted as 100. The results in the following tables are acquired based on the best results of algorithms. On the other hand, rooster size, which is an experimental value, was accepted as 4 during the tests.
4.1 Results of the Test Functions
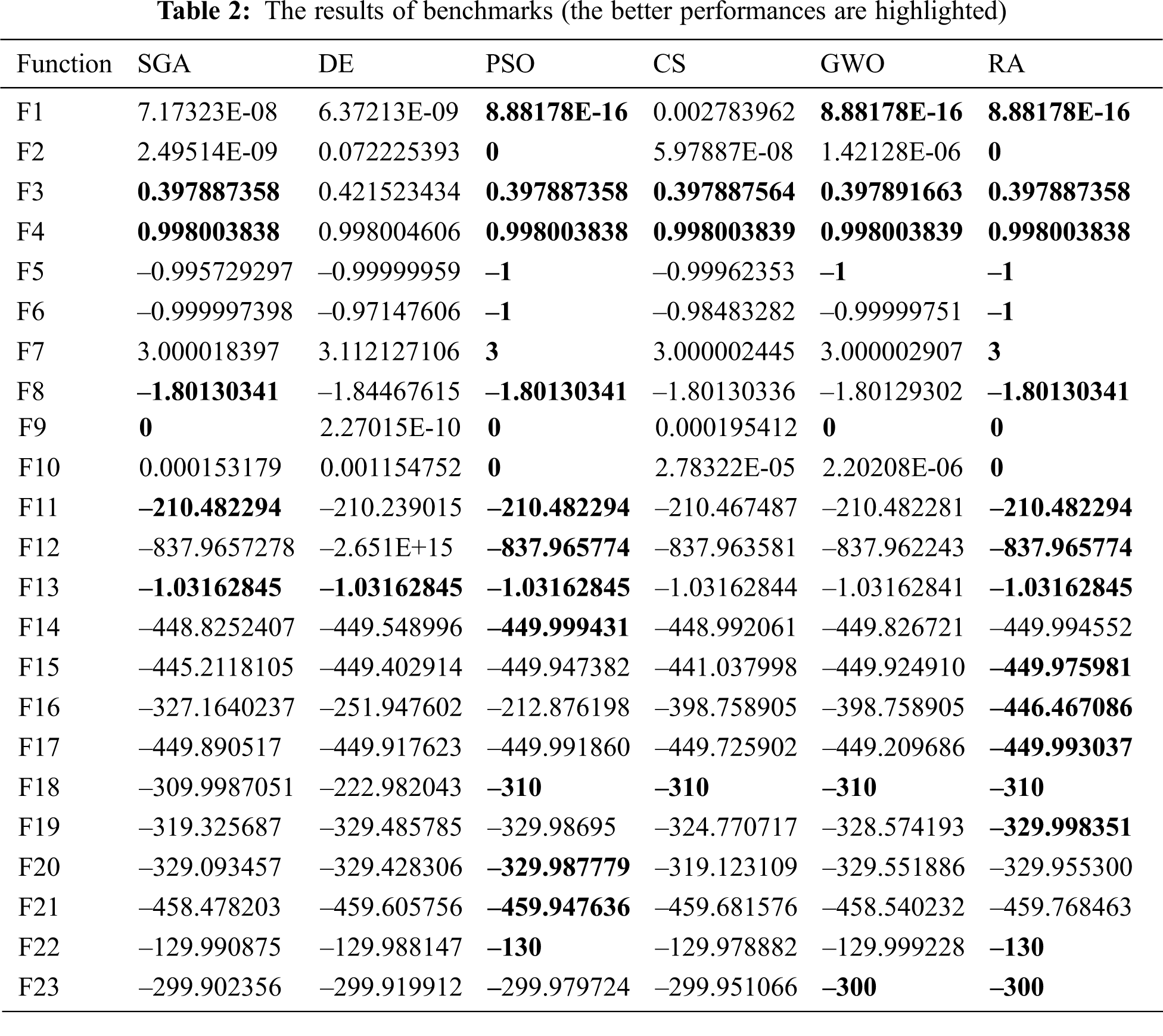
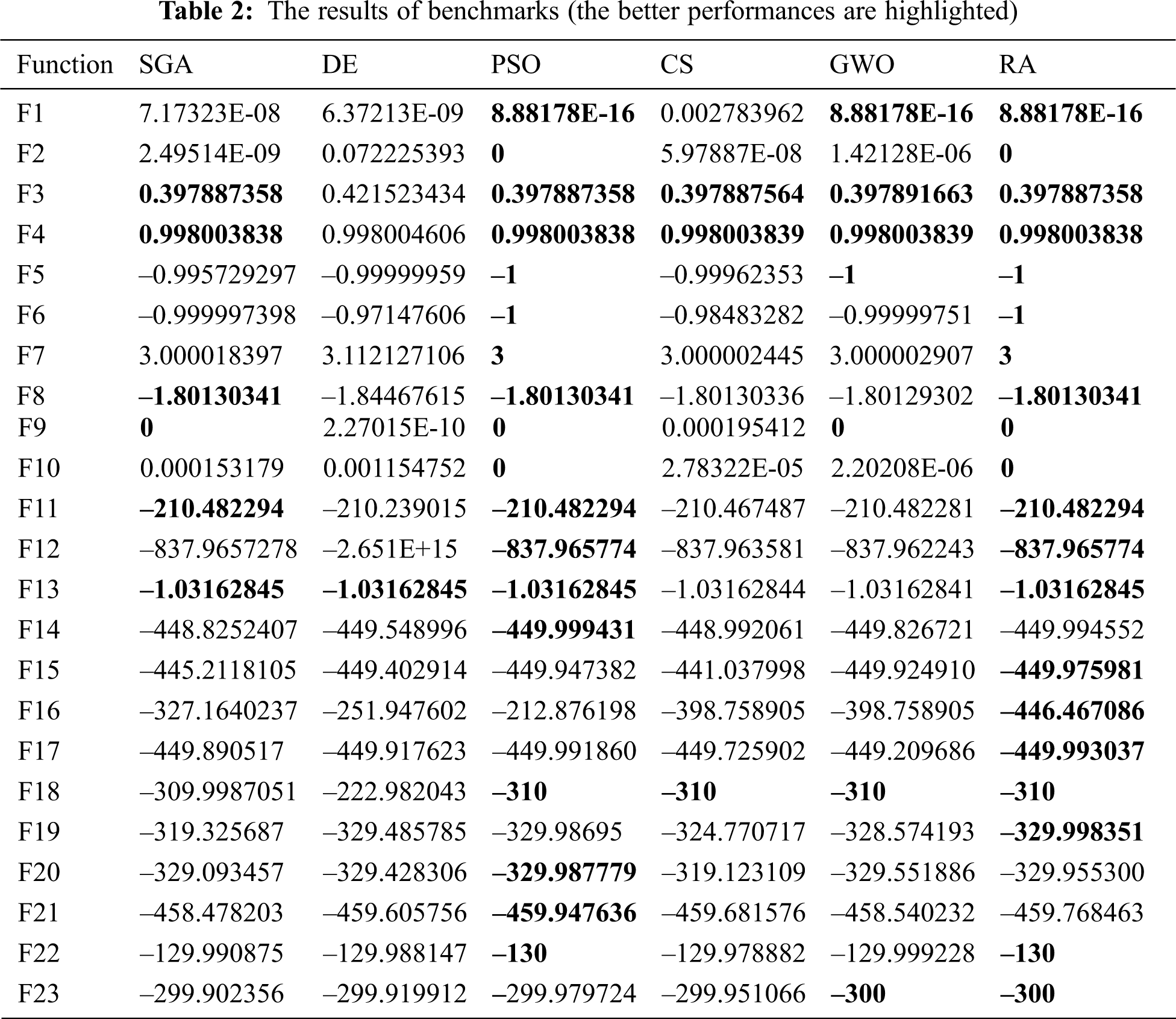
According to Tab. 2, RA offers better performance than the compared algorithms, albeit with small differences. In all basic benchmark functions (from F1-F13), RA offers the best performance in all cases. Moreover, in IEEE CEC 2018 functions (except F14, F20 and F21), RA is either only the winner or there is a tie between some of compared algorithms.
Moreover, PSO is the second algorithm that present the best performance. It achieves global values in all basic benchmark functions. However, it is not as successful as RA in IEEE CEC 2018 functions.
Even though RA proved its effectiveness on the test functions, non-parametric statistical tests should be applied in order to show the significance of obtained results.
It is obvious to clarify which algorithm is more successful by looking at Tab. 3. An algorithm having minimum rank value means that the algorithm has better performance comparing to other. According to Tab. 3, RA presents better performance in all test functions.


In addition to having probability values that are less than α = 0.05,
4.3 Results of Wilcoxon Signed Rank Test

p values describe the significant differences between the compared algorithms. These values must be less than α = 0.05 to reject null hypothesis. Otherwise, it is required to accept it, which means that compared algorithms have similarity in terms of performance.
Based on the results in Tab. 5, the performance of RA is only similar to the performance of PSO since the p value is 0.08984375. On the other hand, CS and SGA behaves similarly in the terms of the performance.
In this paper, a novel nature-inspired optimization algorithm called RA has been introduced. The algorithm is modelled by inspiring the sexual behaviour of roosters with chickens.
In order test its performance in 23 test functions (13 basic benchmarks, 10 IEEE CEC 2018), it was compared with well-known algorithms; SGA, DE, PSO, CS and GWO. Furthermore, non-parametric statistical tests, Friedman and Wilcoxon Signed Rank, were utilized to make sense of the obtained results.
To summarize all the test results that have been made, RA has presented successful results in both unimodal and multimodal functions, thanks to its step that takes advantage of average and potentially poor results. However, although PSO performed very close to RA, it was the second best method among the compared methods.
On the other hand, the statistical results not only confirms the test results, but also approve that RA offers the best performance comparing the other algorithms that were tested.
Considering the results that were acquired, the following remarks can be made:
• Besides to simple test functions, compelling test functions such as IEEE CEC’18 should be also used to observe the performance of an algorithm.
• RA is accomplished in either basic or challenging (shifted, rotated, hybrid and expanded) functions.
• It does not exist an algorithm that solve all optimization problem, according to the NFL theorem. As the performance of RA is reasonable, it can be considered as an alternate optimizer.
As a future work, testing the performance of RA in real world engineering optimization problems can be recommended.
Funding Statement: The authors received no specific funding for this study.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
1. J. H. Holland, Adaptation in natural and artificial systems: An introductory analysis with applications to biology. In: Control and Artificial Intelligence. A Bradford Book, London, England: MIT Press, 1992. [Google Scholar]
2. J. E. Baker, “Reducing bias and inefficiency in the selection algorithm,” in Proc. of the Second Int. Conf. on Genetic Algorithms, vol. 206, pp. 14–21, 1987. [Google Scholar]
3. J. J. Greffenstette and J. E. Baker, “How genetic algorithms work: A critical look at implicit parallelism,” in Proc. of the 3rd Int. Conf. on Genetic Algorithms, pp. 20–27, 1989. [Google Scholar]
4. D. Whitley and J. Kauth, “Genitor: A different genetic algorithm,” in Proc. of the Rocky Mountain Conf. on Artificial Intelligence, pp. 118–130, 1988. [Google Scholar]
5. A. A. Heidari, S. Mirjalili, H. Faris, I. Aljarah, M. Mafarja et al., “Harris hawks optimization: Algorithm and applications,” Future Generation Computer Systems, vol. 97, pp. 849–872, 2019. [Google Scholar]
6. G. Dhiman and Vijay Kumar, “Emperor penguin optimizer: A bio-inspired algorithm for engineering problems,” Knowledge-Based Systems, vol. 159, no. 2, pp. 20–50, 2018. [Google Scholar]
7. R. Storn and K. Price, “Differential evolution-a simple and efficient heuristic for global optimization over continuous spaces,” Journal of Global Optimization, vol. 11, no. 4, pp. 341–359, 1997. [Google Scholar]
8. D. Simon, “Biogeography-based optimization,” IEEE Transactions on Evolutionary Computation, vol. 12, no. 6, pp. 702–713, 2008. [Google Scholar]
9. J. Kennedy and R. Eberhart, “Particle swarm optimization,” in Proc. of ICNN’95-International Conference on Neural Networks, vol. 4, pp. 1942–1948, 1995. [Google Scholar]
10. M. Dorigo and G. Di Caro, “Ant colony optimization: A new meta-heuristic,” in Proc. of the Congress on Evolutionary Computation-CEC99, vol. 2, pp. 1470–1477, 1999. [Google Scholar]
11. A. H. Gandomi, X. S. Yang and A. H. Alavi, “Cuckoo search algorithm: A metaheuristic approach to solve structural optimization problems,” Engineering with Computers, vol. 29, no. 1, pp. 17–35, 2013. [Google Scholar]
12. D. Karaboga and B. Akay, “A comparative study of Artificial Bee Colony algorithm,” Applied Mathematics and Computation, vol. 214, no. 1, pp. 108–132, 2009. [Google Scholar]
13. X. S. Yang, “Firefly algorithms for multimodal optimization,” in Int. Symp. on Stochastic Algorithms, Springer, pp. 169–178, 2009. [Google Scholar]
14. S. Mirjalili, S. M. Mirjalili and A. Lewis, “Grey wolf optimizer,” Advances in Engineering Software, vol. 69, pp. 46–61, 2014. [Google Scholar]
15. S. Kirkpatrick, C. D. Gelatt and M. P. Vecchi, “Optimization by simulated annealing,” Science, vol. 220, no. 4598, pp. 671–680, 1983. [Google Scholar]
16. O. K. Erol and I. Eksin, “A new optimization method: Big Bang-Big Crunch,” Advances in Engineering Software, vol. 37, no. 2, pp. 106–111, 2006. [Google Scholar]
17. E. Rashedi, H. Nezamabadi-Pour and S. Saryazdi, “Gsa: A gravitational search algorithm,” Information Sciences, vol. 179, no. 13, pp. 2232–2248, 2009. [Google Scholar]
18. A. Hatamlou, “Black hole: A new heuristic optimization approach for data clustering,” Information Sciences, vol. 222, pp. 175–184, 2013. [Google Scholar]
19. F. Glover, “Tabu search-part I,” ORSA Journal on Computing, vol. 1, no. 3, pp. 190–206, 1989. [Google Scholar]
20. Z. W. Geem, J. H. Kim and G. V. Loganathan, “A new heuristic optimization algorithm: Harmony search,” Simulation, vol. 76, no. 2, pp. 60–68, 2001. [Google Scholar]
21. E. Atashpaz-Gargari and C. Lucas, “Imperialist competitive algorithm: An algorithm for optimization inspired by imperialistic competition,” IEEE Congress on Evolutionary Computation, pp. 4661–4667, 2007. [Google Scholar]
22. R. V. Rao, V. J. Savsani and D. Vakharia, “Teaching-learning-based optimization: An optimization method for continuous non-linear large scale problems,” Information Sciences, vol. 183, no. 1, pp. 1–15, 2012. [Google Scholar]
23. Y. Tan and Y. Zhu, “Fireworks algorithm for optimization,” in International Conference in Swarm Intelligence, Springer, pp. 355–364, 2010. [Google Scholar]
24. D. H. Wolpert and W. G. Macready, “No free lunch theorems for optimization,” IEEE Transactions on Evolutionary Computation, vol. 1, no. 1, pp. 67–82, 1997. [Google Scholar]
25. J. Santiago-Moreno, M. Esteso, C. Castano, A. Toledano-Diaz and A. Lopez-Sebastian, “Post-coital sperm competence in polygamous animals: The role of sperm traits in species-specific strategies,” Andrology S1, vol. 3, pp. 2167–2250, 2015. [Google Scholar]
26. N. Vougiouklis, “Sex and the chicken,” 2016. [Online]. Available: https://www.slideshare.net/NikitasVougiouklis/sex-and-the-chicken. [Google Scholar]
27. M. Molga and C. Smutnicki, “Test functions for optimization needs” vol. 101, pp. 48, 2005. [Google Scholar]
28. S. Surjanovic and D. Bingham, “Virtual library of simulation experiments: Test functions and datasets,” 2013. [Online]. Available: http://www.sfu.ca/{~}ssurjano. [Google Scholar]
29. J. L. Rueda and I. Erlich, “Hybrid single parent-offspring MVMO for solving CEC2018 computationally expensive problems,” IEEE Congress on Evolutionary Computation (CEC), pp. 1–8, 2018. [Google Scholar]
30. W. J. Conover, “Practical nonparametric statistics,” In: Applied Probability and Statistics, 3rd ed., vol. 350. NY, USA: John Wiley & Sons, 1998. [Google Scholar]
31. M. Friedman, “The use of ranks to avoid the assumption of normality implicit in the analysis of variance,” Journal of the American Statistical Association, vol. 32, no. 200, pp. 675–701, 1937. [Google Scholar]
32. M. Friedman, “A comparison of alternative tests of significance for the problem of m rankings,” Annals of Mathematical Statistics, vol. 11, no. 1, pp. 86–92, 1940. [Google Scholar]
33. D. J. Sheskin, Handbook of parametric and nonparametric statistical procedures, 3rd ed., London, England: Chapman & Hall/CRC Press, 2003. [Google Scholar]
34. F. Wilcoxon, “Individual comparisons of grouped data by ranking methods,” Journal of Economic Entomology, vol. 39, no. 2, pp. 269–270, 1946. [Google Scholar]
35. X. Yang, “Cuckoo search algorithm (CS),” 2021. [Online]. Available: https://www.mathworks.com/matlabcentral/fileexchange/29809-cuckoo-search-cs-algorithm. [Google Scholar]
36. S. Mirjalili, “Grey wolf optimizer (GWO),” 2021. [Online]. Available: https://www.mathworks.com/matlabcentral/fileexchange/44974-grey-wolf-optimizer-gwo. [Google Scholar]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |