DOI:10.32604/csse.2022.023136

| Computer Systems Science & Engineering DOI:10.32604/csse.2022.023136 |  |
| Article |
Modelling of the Slope Solute Loss Based on Fuzzy Neural Network Model
1School of Hydrology and Water Resources, Nanjing University of Information Science & Technology, Nanjing, 210044, China
2Water Resources Research Institute, China Institute of Water Resources and Hydropower Research, Beijing, 100044, China
3Department of Geography and Environmental Sustainability, University of Oklahoma, Norman, 73071, USA
4Wuxi Research Institute, Nanjing University of Information Science & Technology, Wuxi, 214100, China
*Corresponding Author: Xiaona Zhang. Email: nanaxiao86@163.com
Received: 29 August 2021; Accepted: 03 November 2021
Abstract: In regards to soil macropores, the solute loss carried by overland flow is a very complex process. In this study, a fuzzy neural network (FNN) model was used to analyze the solute loss on slopes, taking into account the soil macropores. An artificial rainfall simulation experiment was conducted in indoor experimental tanks, and the verification of the model was based on the results. The characteristic scale of the macropores, the rainfall intensity and duration, the slope and the adsorption coefficient of ions, were chosen as the input variables to the Sugeno FNN model. The cumulative solute loss quantity on the slope was adopted as the output variable of the Sugeno FNN model. There were three membership functions, and the type of membership function was gbellmf (generalized bell membership function). The hybrid learning algorithm, which combines the back propagation algorithm with a least square method, was applied to train and optimize the network parameters, and the optimal network parameters were determined. The simulation results showed that the simulated values were consistent with the measured values.
Keywords: Slope solute loss; soil macropores; fuzzy neural network
Soil solute including soil organic matter, pesticide and chemical fertilizers is indispensable in most agricultural systems. Understanding solute transport in soils is essential in the agriculture field. However, the existence of soil macropores formed by root channels, earthworm burrows and cracks or fissures, conduct soil solute rapidly moves to the deeper profile without interaction with other soil bodies [1]. Although soil macropores accounts for only about 0.1% of the entire soil volume, it has dramatic effects on solute transport. The importance of the soil macropores for solute transport has been repeatedly demonstrated, either in the laboratory, or in situ utilizing breakthrough experiments on small undisturbed soil columns [2–12].
Previous studies have been more concerned about the macropore structure description using computed tomography scans, the solute movement in soil considering macropores, and the solute exchange mechanisms between the soil matrix region and the macropore region [13–24]. The solute transport and loss processes on slopes with soil macropores have been considered in a few research papers.
When the rainfall intensity is greater than the surface infiltration rate, the overland flow appears on the slope and it carries the solute to transport. This process is very complex [25–28]. So it is difficult to describe this complex process with a model with clear physical concepts [29]. Many studies have used soil mixing layer theory to estimate the loss [30–32]. It has been reported that the soil mixing layer models may significantly underestimate solute concentration in surface runoff [31]. The dual-permeability model is usually to describe the solute transport process in soils considering soil macropores [33]. But the number of the parameters in this model is relatively more and the value is difficult to determine. To strengthen research in the aspect of solute transport and loss processes on slopes with soil macropores, a solute transport experiment on pervious slopes with soil macropores is conducted. And then choose a suitable method to descript this process.
The rest of this study is organized as follows: Section 2 discusses study area and the experimental design. Section 3 focuses on the design idea for modeling the solute transport and loss processes on slopes with soil macropore. The results and discussions are presented in Section 4. The conclusion will be discussed with the implications of this study.
Experiments were carried out on the Loess Plateau, located in the Yangling District in the Shanxi Province of China. Yangling (E107°59′–108°08′, N34°14′–34°20′) (Fig. 1) is located in the west of the Guanzhong Plain, north of the Wei River. The Yangling area slopes downward from north to south and can be divided into five different terrain types: a slope in the north, with three terraces below, and the Wei River beach at the bottom in the south. The highest elevation is 530.1 m and the lowest is 403.2 m. Its climate is suitable for the growth of many crops. The region can be described as warm temperate with a semi-humid monsoon climate. The average annual temperature is 13.0°C. The average temperatures of January and July are –2°C and 26.7°C, respectively. The accumulated temperature (≥10°C) ranges from 4300°C to 4500°C, and the frost-free period is more than 200 days. The average hours of sunlight range from 23 to 29 hours per day. The average annual rainfall and the mean annual evaporation are 636.6 mm and 884.0 mm, respectively.
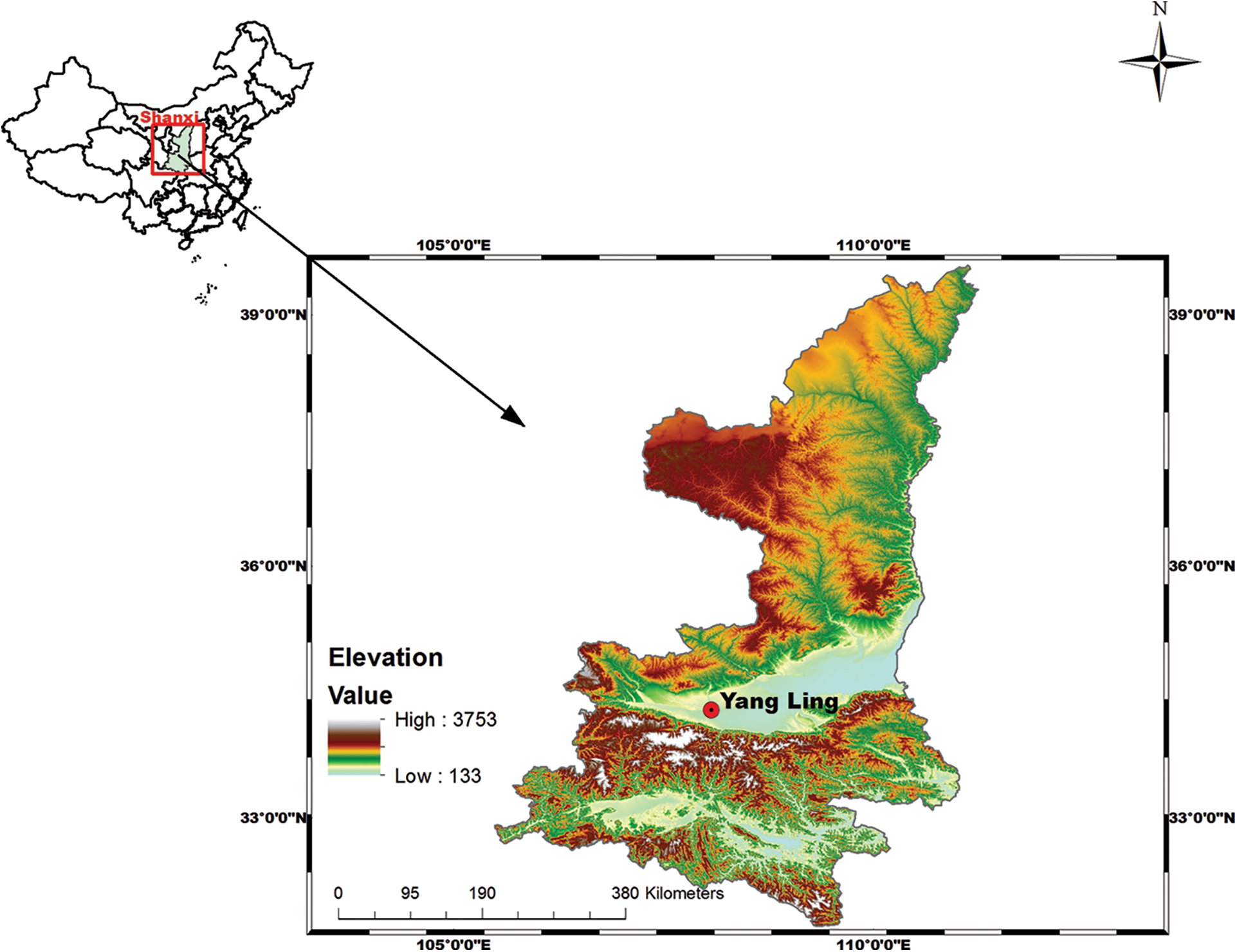
Figure 1: Yangling district, Shanxi province of China
To simulate actual field conditions, a stratified earth method is used in the borrowing and filling process. 0–0.15 m is the first layer and 0.15–0.30 m is the second layer. The saturated hydraulic conductivity of the first layer and the second layer is 1.62 10–6 m/s and 1.33 10–6 m/s respectively. The porosity is 42.1% and 35.1% respectively. According to the USDA, the soil is classified as the heavy loam.
Three different experimental tanks with variable slopes are used. The length of the experimental tanks is 2.0 m, the width of the experimental tanks is 0.55 m and the depth of the experimental tanks is 0.30 m. The outlets of the groundwater runoff the interflow runoff and the surface runoff, located in 0 m, 0.00175 m, and 0.0035 m, respectively, from the experimental tank bottom. The difference among the three experimental tanks is the underlying surfaces (Tab. 1). The distribution of the soil macropores in tank 2 is shown in Fig. 2.
The automatic rainfall simulation system, in the lateral jet zone of the state key laboratory of soil erosion and dryland farming on the Loess Plateau, is adapted.

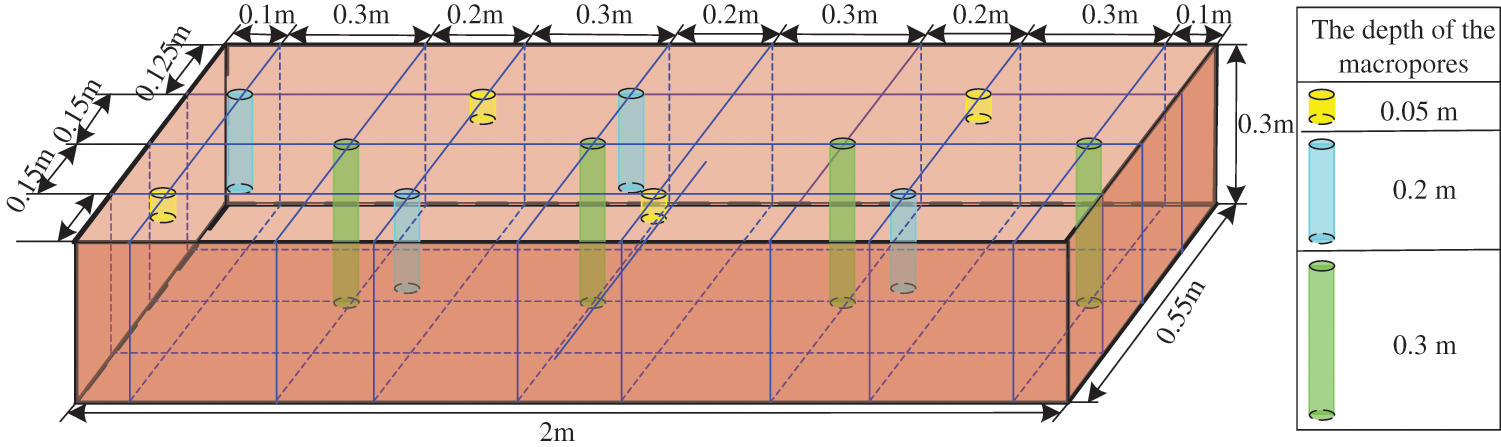
Figure 2: The distribution of the soil macropores in the experimental tank
Different tests are conducted. Before each rainfall, the mixed solvent with 1.7 g KBr and 1000 mL water is evenly dispersed into the three experimental tanks. The gravimetric method is used to measure the surface runoff, the interflow runoff, and the groundwater runoff. The negative pressure meter method is adapted to measure the soil volumetric water content. The colorimetry method is used to measure the Br-concentration in the water samples.
3 The Design Idea of the FNN Model for Slope Solute Loss Considering Soil Macropores
Based on the measured experimental data, the FNN not only makes full use of the human experience, but also has a self-learning ability [34–41]. The FNN model does not to analyze the internal specific process. After the FNN model is trained, using the measurement input and output data, a slope solute loss model equivalent to the actual physical process is established.
3.1 FNN Structure and Learning Algorithm
Using the learning ability and nonlinear mapping ability of neural network, the FNN is mainly based on fuzzy control theory, to make the fuzzy controller have better stability and carry out information processing. The core of fuzzy control lies in the fuzzy controller, which mainly includes three links: fuzzification, fuzzy inference and defuzzification. Among them, fuzzy inference is the key. As a typical fuzzy inference model, the rule of the Takagi-Sugeno FNN model is
If
where,
If
If
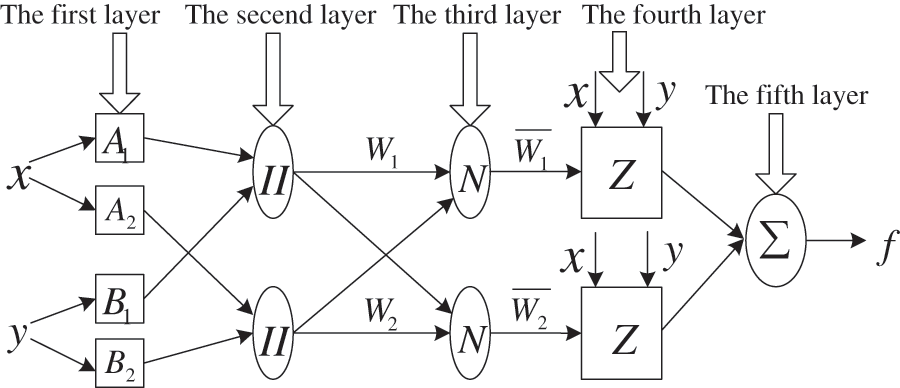
Figure 3: The FNN structure
As a fuzzy layer, the role of the first layer is the fuzzification of input parameters. Each node in this layer has an adaptive function. The membership function of the fuzzy set
where,
where,
As a fuzzy rule layer, the role of the second layer is to use the algebraic operation of multiplication to obtain the output of each node of the layer.
where,
As a defuzzification layer, the role of the third layer is to perform normalization processing through calculating the ratio between
where,
The output of node
where,
As the output layer, the role of the fifth layer is to calculating the total sum of all former layer parameters
The FNN prediction model and its fuzzy inference system, are established by given input and output data sets. The FNN is an organic combination of fuzzy theory and neural network, and its nonlinear mapping ability and self-learning adaptability are strong. It can effectively obtain the optimal parameters of the membership function and then determine the solute loss on the slope. Based on the hybrid learning algorithm training and optimizing its membership function parameters, combined with the least square method and the back propagation algorithm, the optimal network parameters are finally determined. According to the model input parameters and these optimized network parameters, the cumulative slope solute loss can be predicted.
3.2 The Solute Loss FNN Model Considering Soil Macropores
According to the slope solute loss considering soil macropores, five variables including rainfall intensity, rainfall duration, slope, the characteristic scale of the soil macropores and the adsorption coefficient of ion are selected as input parameters. Since each variable corresponds to three fuzzy sets, there are 5 × 3 = 15 nodes in the first layer. With the combination of the fuzzy sets of the input variables, two hundred forty-three fuzzy training rules are generated. Therefore, there are two hundred forty-three nodes in the second, third and fourth layers are all two hundred forty. There is only one node that represents cumulative slope solute loss in the fifth layer, which is the fusion result of the two hundred forty-three nodes in the fourth layer. The FNN model structure of the cumulative solute loss on the slope is shown in Fig. 4.
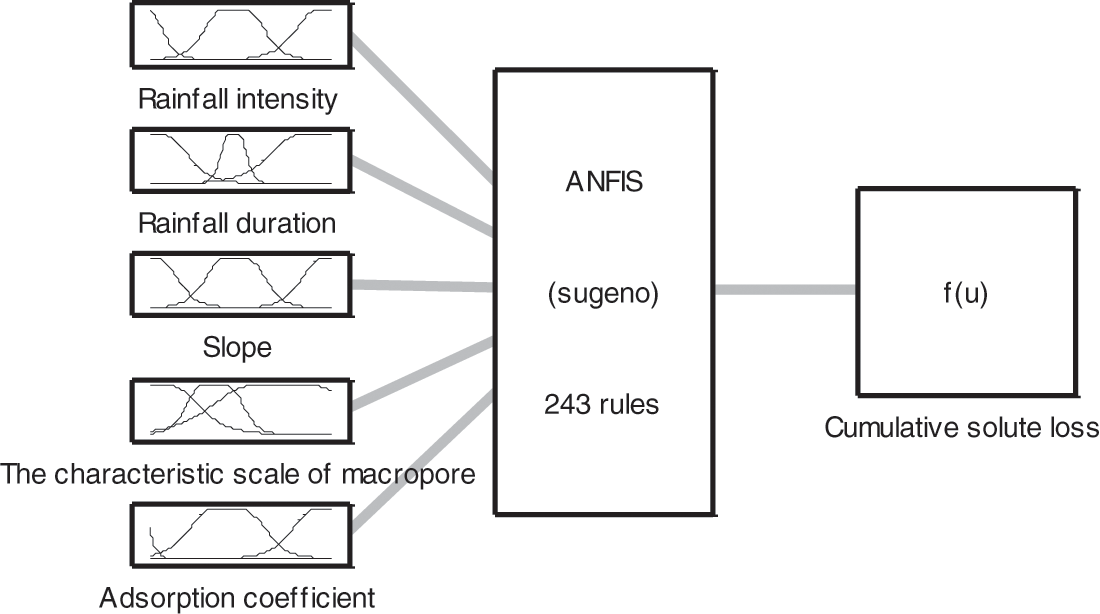
Figure 4: The structure of the slope solute loss FNN model
As the input variables, the rainfall intensity and the rain duration can be directly obtained from the automatic rainfall simulation system, the adsorption coefficient of ions is obtained by solving adsorption isotherms based on adsorption experiments and the characteristic scale of the soil macropores can be acquired based on the improved VIMAC model [42,43]. The slope can be gained by the following formula:
where,
In the infiltration simulation, it is assumed that the distribution of the alfalfa roots is uniform. The distribution of the soil macropores in experimental tank 1 is uniform. The artificial macropores are only considered in experimental tank 2. The soil in experimental tank 3 is regarded as homogeneous soil without considering the soil macropores. In order to run the improved VIMAC model, the infiltration parameters in the matrix flow domain are determined by the measured data of experimental tank 3. The measured data of experimental tank 1 is used to calculate the infiltration parameters in the macropores flow domain and the horizontal infiltration. The measured data of experimental tank 2 is used to verify the infiltration model. Zhang provided the solution method of the improved VIMAC model, and determined the estimation methods of the model parameters. The optimal fitting for the undersurface runoff process is as a standard of the verification and parameter calibration of the infiltration model. The membership function type of the input variables is gbellmf, and the number of the membership functions is three. The output variable of the FNN model is the cumulative solute loss on the slope. The slope cumulative solute loss
where,
A hybrid learning algorithm is applied to train the model. The Sugeno model is selected as the fuzzy reasoning model. The running data system is determined by the learning network to adjust and update the network weights. After completing the learning network weight adjustment, the weights enter into a decision network. Then, the values of the cumulative slope solute loss are gained by fuzzy computing.
To verify the effectiveness of the proposed cumulative FNN model on solute loss on slopes considering the soil macropores, the data of the solute cumulative loss with nine rainfalls and twenty-seven slopes are measured. The number of selected training samples and checking samples of cumulative solute loss FNN model is reasonable. The experimental data is divided into one hundred and forty-three sets of training samples and twenty-six sets of checking samples. The cumulative solute loss FNN model is established using the sample data. The model has good generalization performance for the new data. The input data of the cumulative slope solute loss FNN model is shown in Fig. 5.
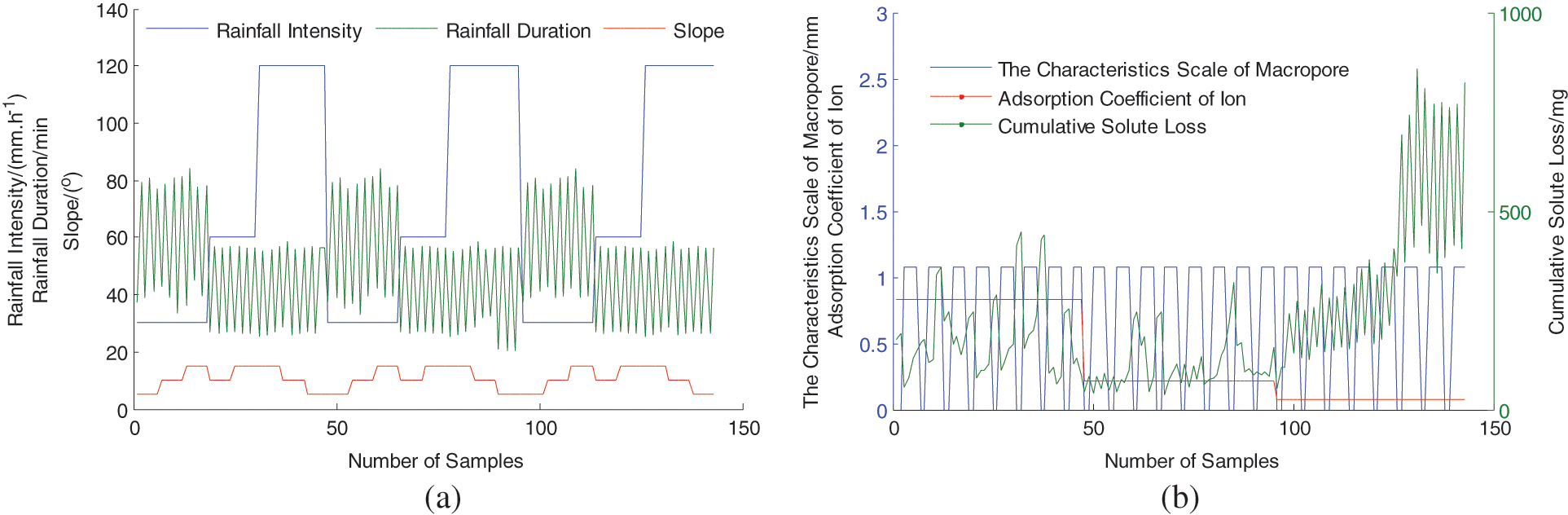
Figure 5: The input data of the slope solute loss FNN model: (a) experiment results of rainfall intensity, rainfall duration and slope; (b) experiment results of the characteristics scale of macropore, adsorption coefficient and cumulative solute loss
After the measured experiment data are normalized, the slope cumulative solute loss FNN model is trained by normalized data. In the process of training, the maximum number of training is eighty. The maximum training error is 0.001. The combination of back propagation algorithm with the least-square method is selected. The comparison between the simulation results and the experiment results of the cumulative solute loss is shown in Fig. 6. The training and checking error change curve during the training process is shown in Fig. 7. As can be seen from Fig. 6, the simulation cumulative solute loss using the proposed method has a good consistency with that of the experiment, which shows the effectiveness of the proposed method. It can be seen from Fig. 7, that the training error and checking error decrease with the increase of the number of steps. The maximum root mean square error of the training data is 0.25. The results therefore show that the established model is valid.
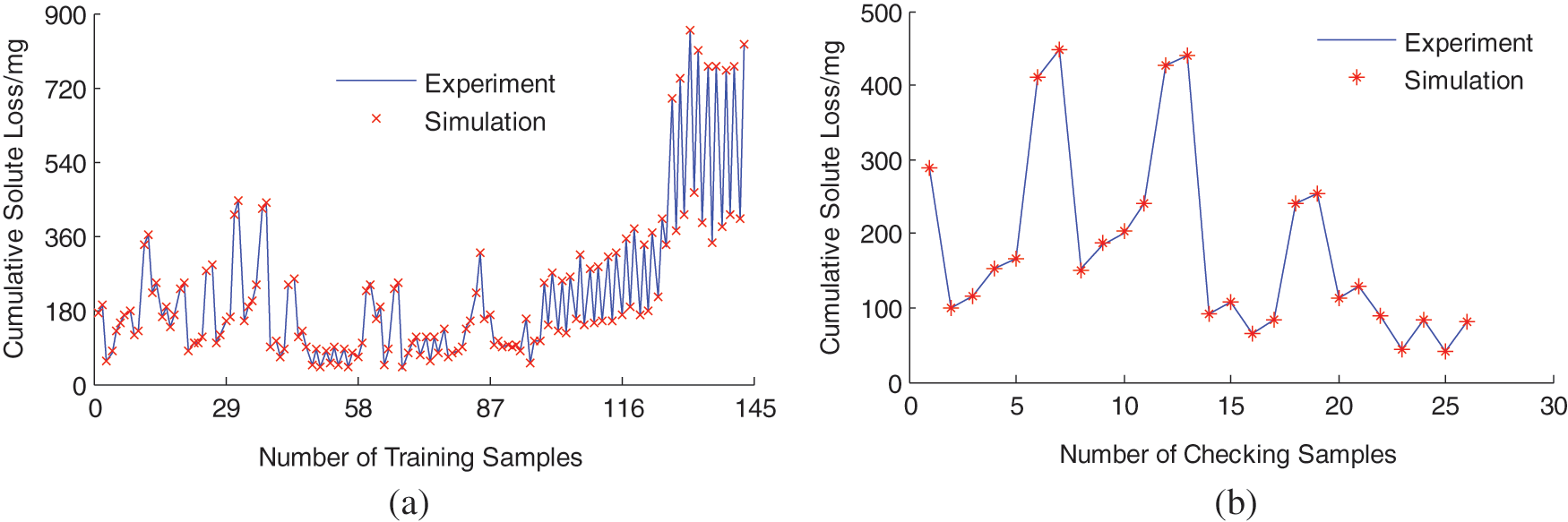
Figure 6: The comparison of the slope cumulative solute loss: (a) training samples; (b) checking samples
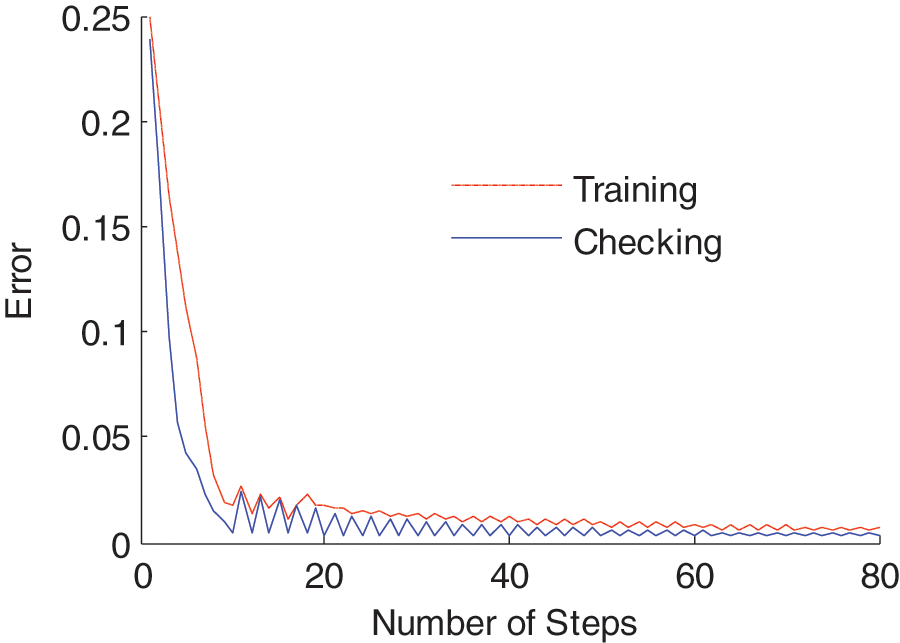
Figure 7: The error change curve during the training process
The comparison of cumulative solute loss between the simulation and the experiment is shown in Fig. 8. The absolute error between simulation slope cumulative solute loss and measured slope cumulative solute loss is shown in Fig. 9. As can be seen from Figs. 8 and 9, the simulation values of the cumulative solute loss are nearly consistent with the experimental values of the cumulative solute loss under various conditions. The maximum error of the FNN cumulative solute loss is ±2 mg. The proposed method can achieve the prediction of cumulative solute loss on slopes under different experimental conditions. Therefore, the effectiveness of the proposed method in this study is again verified.
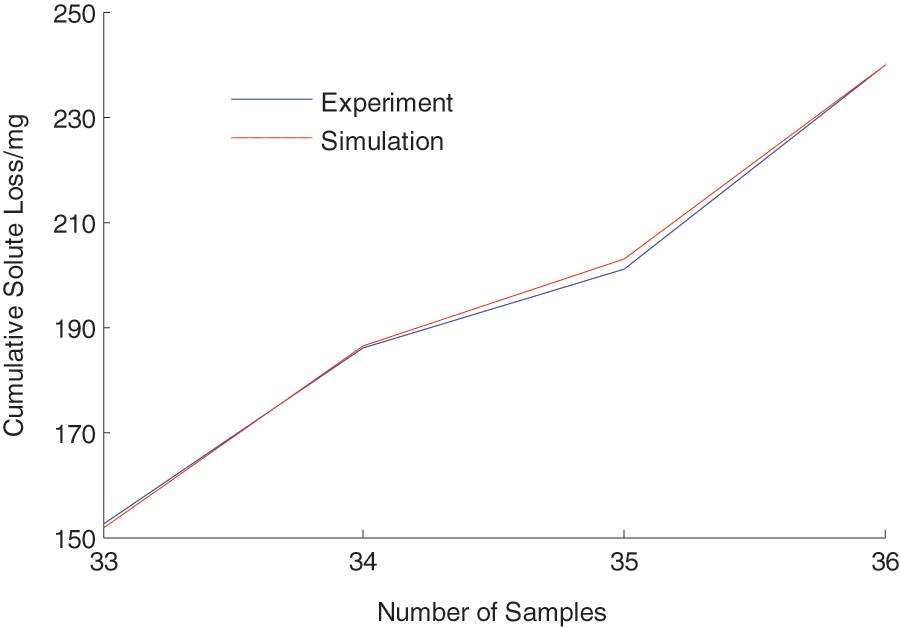
Figure 8: The partial comparison curve of the slope cumulative solute loss
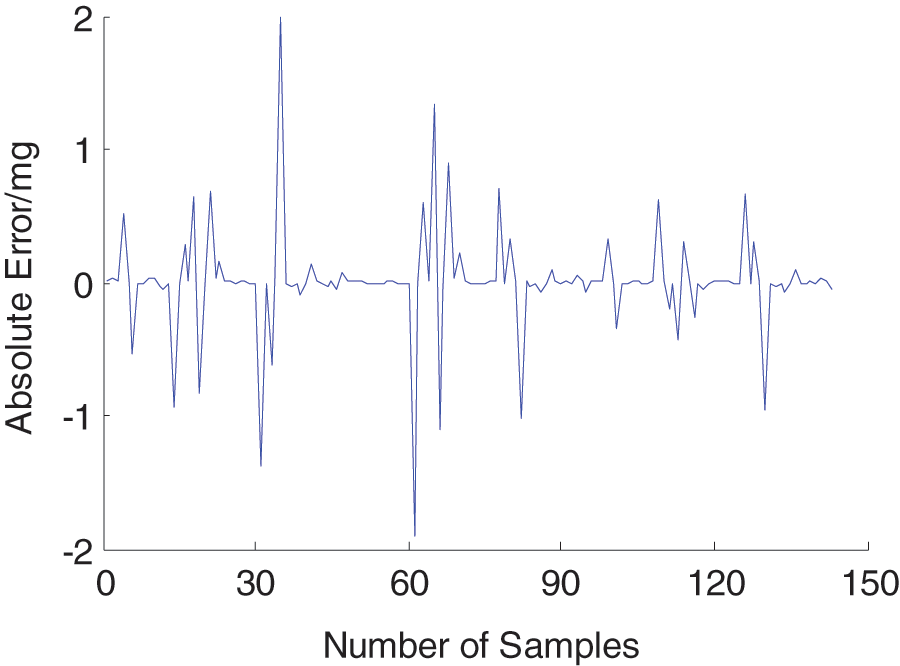
Figure 9: The absolute error curve of the slope cumulative solute loss
This study of slope solute loss modelling considering soil macropores, is significant to the agricultural management of non-point source pollution and nutrient loss. In this study, a new model calculating the cumulative solute loss on slopes considering soil macropores, is proposed based on the FNN. The input variables include: rainfall intensity; rainfall duration; slope; the characteristic scale of the soil macropores and the adsorption coefficient of ion. The output variable is the cumulative solute loss on the slope. The rainfall intensity and duration are directly obtained from the automatic rainfall simulation system. The slope is obtained by measuring the elevation of the experimental tank, as well as, the length of the experimental tank. The adsorption coefficient of ion is obtained by adsorption experiments and the relevant references. The characteristic scale of the soil macropores is obtained by the calculation of the improved VIMAC model simulation. In order to test the feasibility of this model, artificial rainfall simulation experiments are conducted in indoor experimental tanks. The results demonstrate, that the results of the simulations show that slope cumulative solute loss is consistent with the measurement results.
The new model is subject to the following limitations: (1) as an input variable, the characteristic scale of the soil macropores is obtained by the improved VIMAC model; (2) if different sizes of experimental tanks are used, the results may vary. This limitation may be resolved by further developing this fuzzy neural network model. For example, the factor characterizing scale can be considered.
Funding Statement: This research was financially supported by the National Natural Science Foundation of China (No. 41301037), the Natural Science Foundation of Jiangsu Province (BK20201136, BK20191401), the Natural Science Foundation of the Jiangsu Higher Education Institutions of China (No. 11KJB170008) and Innovation and Entrepreneurship Training Program for College Students in Jiangsu Province (No. 201910300106Y). For the help in carrying out the experiments, I wish to thank for Professor Rui Xiaofang, Hohai University, China.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
1. K. Beven and P. Germann, “Macropores and water flow in soils,” Water Resource Research, vol. 18, no. 5, pp. 1311–1325, 1982. [Google Scholar]
2. N. W. Haws, P. S. C. Rao, J. Simunek and I. C. Poyer, “Single-porosity and dual porosity modeling of water flow and solute transport in subsurface-drained fields using effective field-scale parameters,” Journal of Hydrology, vol. 313, no. 3–4, pp. 257–273, 2005. [Google Scholar]
3. E. Lamy, L. Lassabatere, B. Bechet and H. Andrieu, “Modeling the influence of an artificial macropore in sandy columns on flow and solute transfer,” Journal of Hydrology, vol. 376, no. 3–4, pp. 392–402, 2009. [Google Scholar]
4. A. Elci and F. Molz, “Identification of lateral macropore flow in a forested riparian wetland through numerical simulation of a subsurface tracer experiment,” Water Air Soil Pollution, vol. 197, no. 1–4, pp. 149–164, 2009. [Google Scholar]
5. S. Katuwal, T. Norgaard, P. Moldrup, M. Lamandé, D. Wildenschild et al., “Linking air and water transport in intact soils to macropore characteristics inferred from X-ray computed tomography,” Geoderma, vol. 237–238, no. 7, pp. 9–20, 2015. [Google Scholar]
6. S. K. Frey, H. T. Hwang, Y. J. Park, S. I. Hussain, N. Gottschall et al., “Dual permeability modeling of tile drain management influences on hydrologic and nutrient transport characteristics in macroporous soil,” Journal of Hydrology, vol. 535, no. 3–4, pp. 392–406, 2016. [Google Scholar]
7. S. Batany, P. E. Peyneau, L. Lassabatere, B. Bechet, P. Faure et al., “Interplay between molecular diffusion and advection during solute transport in macroporous media,” Vadose Zone Journal, vol. 18, no. 1, pp. 1–15, 2019. [Google Scholar]
8. H. Hlavacikova, L. Holko, M. Danko and V. Novak, “Estimation of macropore flow characteristics in stony soils of a small mountain catchment,” Journal of Hydrology, vol. 574, no. 7, pp. 1176–1187, 2019. [Google Scholar]
9. N. J. Jarvis, “A review of non-equilibrium water flow and solute transport in soil macropores: Principles, controlling factors and consequences for water quality,” European Journal of Soil Science, vol. 71, no. 3, pp. 279–302, 2020. [Google Scholar]
10. A. Sternagel, R. Loritz, J. Klaus, B. Berkowitz and E. Zehe, “Simulation of reactive solute transport in the critical zone: A Lagrangian model for transient flow and preferential transport,” Hydrology and Earth System Sciences, vol. 25, no. 3, pp. 1483–1508, 2021. [Google Scholar]
11. A. Ilek, J. Kucza and W. Witek, “Using undisturbed soil samples to study how rock fragments and soil macropores affect the hydraulic conductivity of forest stony soils: Some methodological aspects,” Journal of Hydrology, vol. 570, no. 3, pp. 132–140, 2019. [Google Scholar]
12. T. Z. Zhou, P. Xin, L. Li, D. A. Barry and J. Simunek, “Effects of large macropores on soil evaporation in salt marshes,” Journal of Hydrology, vol. 584, no. 5, pp. 1–10, 2020. [Google Scholar]
13. F. Abbasi, J. Feyen and M. Van Genuchten, “Two-dimensional simulation of water flow and solute transport below furrows: Model calibration and validation,” Journal of Hydrology, vol. 290, no. 1–2, pp. 63–79, 2004. [Google Scholar]
14. L. F. Luo, H. Lin and S. C. Li, “Quantification of 3-D soil macropore networks in different soil types and land uses using computed tomography,” Journal of Hydrology, vol. 393, no. 1–2, pp. 53–64, 2010. [Google Scholar]
15. F. S. J. Martínez, M. A. Martín, F. J. Caniego, M. Tuller, A. Guber et al., “Multifractal analysis of discretized X-ray CT images for the characterization of soil macropore structures,” Geoderma, vol. 156, no. 1–2, pp. 32–42, 2010. [Google Scholar]
16. A. Tiktak, R. F. A. Hendriks, J. J. T. I. Boesten and A. M. A. Linden, “A spatially distributed model of pesticide movement in Dutch macroporous soils,” Journal of Hydrology, vol. 471, no. 11, pp. 316–327, 2012. [Google Scholar]
17. S. Feng, H. H. Liu, K. Wang, R. D. Zhang and Z. H. Tang, “Investigation into preferential flow in natural unsaturated soils with field multiple-tracer infiltration experiments and the active region model,” Journal of Hydrology, vol. 508, no. 1–2, pp. 137–146, 2014. [Google Scholar]
18. Z. B. Zhang, X. Peng, H. Zhou, H. Lin and H. Sun, “Characterizing preferential flow in cracked paddy soils using computed tomography and breakthrough curve,” Soil and Tillage Research, vol. 146, pp. 53–65, 2015. [Google Scholar]
19. P. Xin, X. Yu, C. Lu and L. Li, “Effects of macro-pores on water flow in coastal subsurface drainage systems,” Advances in Water Resources, vol. 87, pp. 56–67, 2016. [Google Scholar]
20. K. Muller, S. Katuwal, I. Young, M. McLeod, P. Moldrup et al., “Characterising and linking X-ray CT derived macroporosity parameters to infiltration in soils with contrasting structures,” Geoderma, vol. 313, no. 3, pp. 82–91, 2018. [Google Scholar]
21. Z. C. Li, X. Hu, X. Y. Li, Y. M. Huang, X. C. Wu et al., “Quantification of soil macropores at different slope positions under alpine meadow using computed tomography in the Qinghai lake watershed, NE Qinghai-Tibet,” Eurasian Soil Science, vol. 52, no. 11, pp. 1391–1401, 2019. [Google Scholar]
22. F. Pittman, A. Mohammed and E. Cey, “Effects of antecedent moisture and macroporosity on infiltration and water flow in frozen soil,” Hydrological Processes, vol. 34, no. 3, pp. 795–809, 2020. [Google Scholar]
23. X. Y. Min, H. Jiao and X. J. Li, “Characterizing effects of mechanical compaction on macropores of reclaimed soil using computed tomography scanning,” Canadian Journal of Soil Science, vol. 100, no. 2, pp. 150–161, 2020. [Google Scholar]
24. A. Marquart, D. J. Eldridge, K. Geissler, C. Lobas and N. Blaum, “Interconnected effects of shrubs, invertebrate-derived macropores and soil texture on water infiltration in a semi-arid Savanna rangeland,” Land Degradation & Development, vol. 31, no. 16, pp. 2307–2318, 2020. [Google Scholar]
25. L. R. Ahuja, A. N. Sharpley and O. R. Lehman, “Effect of soil slope and rainfall characteristics on phosphorus in runoff,” Journal of Environmental Quality, vol. 11, no. 1, pp. 9–13, 1982. [Google Scholar]
26. R. S. Walton, R. E. Volker, K. L. Bristow and K. R. J. Smettem, “Experimental examination of solute transport by surface runoff from low-angle slopes,” Journal of Hydrology, vol. 233, no. 1–4, pp. 19–36, 2000. [Google Scholar]
27. B. Gao, M. T. Walter, T. S. Steenhuis, J. Y. Parlange, B. K. Richards et al., “Investigating raindrop effects on transport of sediment and non-sorbed chemicals from soil to surface runoff,” Journal of Hydrology, vol. 308, no. 1–4, pp. 313–320, 2005. [Google Scholar]
28. C. R. Yu, B. Gao, R. Muñoz-Carpena, Y. Tian, L. Wu et al., “A laboratory study of colloid and solute transport in surface runoff on saturated soil,” Journal of Hydrology, vol. 402, no. 1–2, pp. 159–164, 2011. [Google Scholar]
29. L. Lu, J. C. Wu and J. J. Wang, “Monte Carlo modeling of solute transport in a porous medium with multi-scale heterogeneity,” Advances in Water Science, vol. 19, no. 3, pp. 333–338, 2008. [Google Scholar]
30. T. Yang, Q. Wang, L. Wu, G. Zhao, Y. Liu et al., “A mathematical model for soil solute transfer into surface runoff as influenced by rainfall detachment,” Science of the Total Environment, vol. 558, no. 1, pp. 590–600, 2016. [Google Scholar]
31. J. Tong, B. X. Hu, J. Yang and Y. Zhu, “Using a hybrid model to predict solute transfer from initially saturated soil into surface runoff with controlled drainage water,” Environmental Science & Pollution Research, vol. 23, no. 12, pp. 12444–12455, 2016. [Google Scholar]
32. J. Tong and M. Ye, “A new soil mixing layer model for simulating conservative solute loss from initially saturated soil to surface runoff,” Journal of Hydrology, vol. 590, no. 1, pp. 125514, 2020. [Google Scholar]
33. X. Shuang, W. Zhang and J. Hamza, “A new model approach for reactive solute transport in dual-permeability media with depth-dependent reaction coefficients,” Journal of Hydrology, vol. 577, no. 10, pp. 123946, 2019. [Google Scholar]
34. T. H. Ricardo, A. M. C. Jesus, A. M. Samuel, H. C. Tonatiuh and S. C. Lizbeth, “Tuning of a TS fuzzy output regulator using the steepest descent approach and ANFIS,” Mathematical Problems in Engineering, vol. 2013, pp. 14–26, 2013. [Google Scholar]
35. R. H. Abiyev, “Credit rating using type-2 fuzzy neural networks,” Mathematical Problems in Engineering, vol. 2014, no. 2, pp. 1–8, 2014. [Google Scholar]
36. K. Zheng, Q. Zhang, Y. Hu and B. Wu, “Design of fuzzy system-fuzzy neural network-backstepping control for complex robot system—ScienceDirect,” Information Sciences, vol. 546, pp. 1230–1255, 2020. [Google Scholar]
37. W. Hung, W. L. Mao and H. Y. Huang, “Modified PSO algorithm on recurrent fuzzy neural network for system identification,” Intelligent Automation & Soft Computing, vol. 25, no. 2, pp. 329–341, 2019. [Google Scholar]
38. W. Sun, G. Zhang, X. Zhang, X. Zhang and N. Ge, “Fine-grained vehicle type classification using lightweight convolutional neural network with feature optimization and joint learning strategy,” Multimedia Tools and Applications, vol. 2020, pp. 1–14, 2020. [Google Scholar]
39. X. Zhang, X. Yu, W. Sun and A. Song, “Soft tissue deformation model based on Marquardt algorithm and enrichment function,” Computer Modeling in Engineering & Sciences, vol. 124, no. 3, pp. 1131–1147, 2020. [Google Scholar]
40. S. Liu and W. Zhang, “Application of the fuzzy neural network algorithm in the exploration of the agricultural products e-commerce path,” Intelligent Automation & Soft Computing, vol. 26, no. 3, pp. 569–575, 2020. [Google Scholar]
41. C. Anitescu, E. Atroshchenko, N. Alajlan and T. Rabczuk, “Artificial neural network methods for the solution of second order boundary value problems,” Computers Materials & Continua, vol. 59, no. 1, pp. 345–359, 2019. [Google Scholar]
42. X. Zhang, “Study on runoff yield and concentration model and solute loss model in macroporous soils and experiment verification,” Ph.D. dissertation. Hohai University, Nanjing, Jiangsu, China, 2010. [Google Scholar]
43. G. Roberto, “Preferential flow in macroporous swelling soil with internal catchment: Model development and applications,” Journal of Hydrology, vol. 269, no. 3–4, pp. 150–168, 2002. [Google Scholar]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |