DOI:10.32604/csse.2022.021590

| Computer Systems Science & Engineering DOI:10.32604/csse.2022.021590 |  |
| Article |
Enhanced Route Optimization for Wireless Networks Using Meta-Heuristic Engineering
1Department of Electronics and Communication Engineering, SACS MAVMM Engineering College, Madurai, India
2Department of Computer Science and Engineering, SACS MAVMM Engineering College, Madurai, India
3Department of Computer Science, Cihan University-Duhok, Kurdistan Region, Iraq
4Department of Computer Science and Engineering Bapatla Engineering College, Bapatla, Andhra Pradesh, India
5Department of Computer Application, National Institute of Technology, Thiruchirapalli, India
6School of Computer Science and Engineering, Vellore Institute of Technology, Chennai, India
7Department of Computer Science and Engineering, M.I.E.T Engineering College, Trichy, India
*Corresponding Author: P. Sundara Vadivel. Email: sundar.me2009@gmail.com
Received: 07 July 2021; Accepted: 12 August 2021
Abstract: Wireless Sensor Networks (WSN) are commonly used to observe and monitor precise environments. WSNs consist of a large number of inexpensive sensor nodes that have been separated and distributed in different environments. The base station received the amount of data collected by the numerous sensors. The current developments designate that the attentFgion in applications of WSNs has been increased and extended to a very large scale. The Trust-Based Adaptive Acknowledgement (TRAACK) Intrusion-Detection System for Wireless Sensor Networks (WSN) is described based on the number of active positive deliveries and The Kalman filter used in Modified Particle Swarm Optimization (MPSO) has been proposed to predict knot confidence. Simulations were run for non-malicious networks (0% malicious) and different percentages of malicious nodes were discussed. The findings suggest that the proposed method TRAACK Modified Particle Swarm Optimization (MPSO) packet delivery rate outperforms TRAACKPSO by 3.3% with 0% malicious nodes. Similarly, the packet delivery rate of TRAACKMPSO is 30% malicious, 3.5% better than TRAACKPSO in WSN.
Keywords: Trust-based adaptive acknowledgment (TRAACK); modified particle swarm optimization (MPSO); intrusion detection system (IDS); kalman filter
The process of optimization entails looking for vectors in functions that produce the best results. In optimization, all feasible values are termed potential solutions, and one extreme value is known as the optimum solution. The two types of optimization algorithms are deterministic and stochastic algorithms. If the cycles start with one initial point, the deterministic technique uses gradients like hill-climbing, which have strict motions and create the same set of solutions [1]. Even with the same starting point, stochastic methods do not use gradients and produce variable solutions. But final values, although mildly varying, will converge to one optimal solution within a particular accuracy. There are two types of stochastic protocol: one is known as heuristic and the other is known as metaheuristic. Currently, bio-inspired metaheuristic protocols are powerful and effective in solving modern nonlinear numerical global optimization problems. To a certain extent, meta-heuristic protocols attempt to balance between global and local searches. Optimization problems with several objective functions are common in practically all fields or areas of study. Regarding the challenges, the purposes to be improved usually conflict, implying that there is no single solution to the problem. Rather, the purpose is to develop great trade-off solutions that indicate a possible compromise between the goals. Particle Swarm Optimization (PSO) is a heuristic search strategy based on an evolutionary protocol [2] that replicates a swarm of birds searching for food. PSO is a logical candidate for multi-objective optimization because of its simplicity and population-based strategy.
1.1 Particle Swarm Optimization (PSO)
PSO is a swarm intelligence technique that approximates swarm social behaviour [3]. PSO shares numerous traits with EA that have aided in its adaptation to multi-objective settings [4]. Though some concepts from EAs can be easily applied to PSO, particular elements that distinguish PSO from them, such as directed mutation, population representations, and operators, must be measured when developing tactics that take advantage of PSO’s efficacy.
PSO can deal with both continuous and discrete parameter problems. PSO’s execution is straightforward, requiring only a small amount of code. It is also low-cost in terms of memory and speed. It works well with multi-objective optimization. PSO has the following advantages: (1) because it is based on intelligence, it may be used in a variety of sectors, including engineering and scientific study. (2) PSO does not compute overlaps or mutations. Searches can be carried out at the particle’s speed. Only the optimal particle was capable of communicating information to other particles during the growth of various generations, and research was carried out at a quick pace. (3) PSO’s computations are quite basic. When compared to other development computations, they have a far higher optimization potential and may be completed quickly. (4) PSO supports real number codes, and the solution is directly defined. The solution’s constant [5] is the same as the dimension quantity. The following are some of PSO’s flaws: (1) PSO is susceptible to incomplete optimization, which results in less precision when regulating speed and direction. (2) PSO is incapable of resolving handful and optimization difficulties. (3) PSO will address the challenges of the uncoordinated system such as the rules of the motion or a method for resolving particle energy fields.
1.2 Multi-Objective Particle Swarm Optimization (MO-PSO)
MOPSO is an optimization technique that was inspired by flocks of birds and has recently attracted a lot of attention due to its superb conjunction promptness. MO topics include several goals that are necessary to address solutions at the same time. These problems arise in different applications where two or more possible offsets must be reduced at the same time [6]. Pareto optimization gives you the choice to redesign the optimization for issues with several criteria. Unlike single-goal optimization, multi-goal problems are classified based on commitments. The multiple objective problems were investigated based on Pareto optimal solutions with the different environments. An example of this is the optimization of the form, in which the different properties are taken into account with the same aptitude of the different structures. It is imperative to discover the most possible number of results with their different properties. The researchers are motivated to expand the Multi-objective optimization using a bio-inspired technique after realizing the PSO algorithm is the problem of single-objective optimization. It was a sort of optimization issue in which resolutions might be judged based on more than two contradicting or incompatible goals. These types of optimization problems differ from traditional optimization problems in that the final result is not a set of substitutes but rather the best solution and in which no single member of the final result set is completely better than another and when no single solution is superior than the others.
Hybrid optimization is one of the most recent heuristic optimization methods. For a single optimization, these optimization types assume that two or more protocols are executing. Heuristics are used in hybrid optimizations to select the optimum protocol for the given situation. Because hybrid log maps are created by combining two log map methods, graph colours and linear scans are employed [7]. The benefits of stochastic and deterministic optimization are combined in a hybrid optimization strategy. The Evolutionary Algorithm (EA) is the foundation for a stochastic optimization approach in which the best linkage [8] is found through extensive experimentation. The local optimization techniques are used in the deterministic method which helps to reduce the high CPU time. Developmental Algorithms have been widely utilized for finding a different solution with multi-objective optimization issues. Due to the nature of the size, the computational cost will increase. The complexity of the problem and the number of optimum function evaluations required in the method may be too expensive. As a result, there is a need to increase MOPSO’s accuracy, particularly in high-dimensional problems.
The optimization question by presenting two distinct functions corresponding to the two declared objectives. A deployment protocol based on Multi-Objective Particle Swarm Optimization with Non-Dominated Relative Crowding Distance (MOPSO-NRCD) is presented to address the two primary problems of applying Multi-objective Particle Swarm Optimization (MOPSO) in the resolution of the suggested optimization issue. A new selection strategy with non-dominated relative crowding distance was proposed for the problem with different values. To address particle allocation, MO-multi-swarm PSO’s architecture was suggested. Finally, simulations are run to demonstrate the benefits and correctness of the proposed deployment strategy. It has been demonstrated that the MOPSO-NRCD protocol outperforms the classic Multi-Objective Particle Swarm Optimization with Crowding Distance when an equal number of units are used (MOPSO-CD) [9]. A discrete PSO model is proposed for the resolution of network clustering challenges, based on which a multi-objective discrete PSO is recommended. The process of breakdown is used. For a problem-specific population, a population initialization technique based on label propagation and the turbulence operator was presented. Kernel K-Means and the Ratio were reduced as objectives [10]. Multiple pathways from sources to destinations can be found in graphs. Among these, finding the best path is a difficult task to tackle. Finding a path through a graph is an NP-hard problem. Particle Swarm Optimization (PSO) is a technique for resolving the routing problem by generating an optimal path from a graph. PSO encoded particles using discrete mathematics, which divides the search space into smaller search spaces and solves discrete optimizations [11]. A unique approach for MPR selection was devised using particle swarm optimization sigmoid increasing inertia weight (PSOSIIW) to increase the attainment of the OLSR [12]. PSO benefits significantly from the sigmoid growing inertia weight in terms of simple and quick convergence on ideal solutions. The packet delay of all nodes and supporting MPR selection in OLSR for the fitness function, the degree of willingness is proposed. NS−2 is used to investigate the throughputs, packet losses, and end-to-end delays of the suggested techniques. In comparison to normal OLSR and OLSR-PSO, the OLSR-PSOSIIW showed superior performance, particularly in terms of throughput and end-to-end delays. An innovative PSO-based On-Demand Multi-cast Routing Protocol improves message transmitting performance [13]. It is appropriate for MANETs with frequent topological changes and limited power. The protocol has been tested in a variety of realistic scenarios.
Swarm Intelligence methods are vastly utilized in science and engineering domains like Mobile AdHoc Networks (MANETs) and Wireless Sensor Networks (WSNs). The new and encouraging domain with a focus on adapting group behaviour of several animal species such as ants, birds or bees. A huge quantity of routing algorithms for Wireless Sensor Networks (WSN) has been formulated by simulating the foraging activity of the animals. The typical principals of the Swarm Intelligence were reviewed in the past literature also available on the SI algorithms as per several encouraging meta-heuristics. The termite colony optimization characteristics and the fission-fusion social structure based spider monkey optimization characteristics based clustering concerning the wireless sensor networks was explained [14]. A Vehicle Routing Problem (VRP) used a time-space to account for production and pollution route difficulties (PPRP-TW). It’s an NP-hard problem that focuses on optimizing routing concerns over a specific period. A fleet of comparable vehicles is dispatched from the production facility to a set of clients in various places. The transportation component of the PPRP-TW is primarily concerned with carbon footprints. As a result, a multi-objective multi-vehicle PPRP-TW (MMPPRP-TW) was created with the goals of lowering overall operational costs and lowering total emissions The Hybrid Self-Learning Particle Swarm Optimization (SLPSO) methodology is employed in the multi-objective model for MMPPRP-TW [15].
Swarm Intelligence (SI) is a natural-inspired technique of evolution and it has been used to solve several difficult optimization problems. Under the umbrella of SI, two basic approaches are used. The first is PSO, and the second is Ant Colony Optimization (ACO). The swarming activity is spoken concerning social insects such as bees, ants or wasps. An insect nest is made up of hundreds or thousands of individual insects. Even though a single insect isn’t exceptionally brilliant, the social group as a whole has collective intelligence, this implies that ants can gather food effectively, bees can manage the temperature in their hives, and so on. Individual insects are reactive agents that accidentally react to local incitements. A protocol that simulates flocks of birds, called PSO. In this process, individuals in the flock are driven by personal and global bests. The behaviours converge rapidly into a near-optimal geographical position for each person [16]. PSO starts with an arbitrary beginning population moving at an arbitrary speed. Particle transport takes place in a problem space. The particles all have memory, and they remember their previous best position and fitness. The variable pbest represents the swarm’s previous best position, whereas gbest represents the swarm’s best overall location. The essential idea of PSO is to push all particles toward pbest and gbest at every time step. The velocity and position of each particle are altered in Eq. (1).
The particle’s velocity is represented by Vid and ith particle with d dimensions represented by X id
where W denote the weight of inertia and the cognition and social components are denotes as c1 and c2 respectively.
MO-PSO begins with population Po of N arbitrarily created CH vectors T that possess unique IDs in the network. All vectors T cover the entire network for communications. It is significant to note that all particles possess the features given below: completeness, as well as uniqueness. This implies that all particles cover the entire network and the unique CHs. For all solutions, objectives are computed through the usage of corresponding equations. First, neighbours of CHs are found which are at the first position in the CH vector T, compute power utilization of the CH, mobility and communication range. Similarly, objectives for all CHs are computed. Degree difference is computed for all CHs through = |d − 1| wherein is degree difference, d refers to the total quantity of CH neighbour’s while 1 is a pre-defined threshold. Similarly, Objectives are determined for all CHs in a single population solution. After that, all meanings of all CH targets are summarized. The summation is the population’s cumulative objective values of a single solution. Likewise, goals are calculated for all populations [17]. Kalman filtering part can be utilized to register the probability utilizing assessed neighbourhood data [18]. This estimation can be utilized to gauge the trusted segment to accomplish the plan objective. The advantage of the segments being used in conjunction with other frameworks for updating trust is the trust figure based on Kalman. External components can be employed with weights, making them more versatile. Fig. 3. 2 describes the Common Kalman filter procedure. It is noted that rather than Minimum Mean Square Error (MMSE), the neighbourhood appraisals are sat back shifting trust-sensitive filters [19]. The hello message of each routing protocol hub produces the standardized time-varying trust esteems w (I; j) [n]. The hello message of each routing protocol hub yields the standardized time-varying trust esteems w (I; j) [n] [20]. Mono-dimensional structures with states controlled by the following are used to ease presentation:
The state of method at time t + 1 is determined by the state of the time t setting and the discretionary procedure. Wt. Bringing out sporadic objective facts yt of the system, such as in (3):
Observations are dependent on the current state of the system and the arbitrary term Wt.
Discrete faith lit levels, an only assessment Ts, t∈ [0, 1], this represents a node’s overall trustworthiness degree and is determined by combining utilities from various attributes in (4):
where wi weights given to the service attributes are implied. Ts, t is 0 for untrusted nodes and 1 for nodes that realistically forecast service quality [21]. The overall level of trust is useful in reputation structures to spread B’s credibility as Ts, t (B), where B is an intermediate node [22]. Fig. 1. Depicts the adaptive Acknowledgment scheme.

Figure 1: Adaptive acknowledgement scheme
A node-level strategy has resorted to a timing window technique where the amount of trust is expected [23]. Using the confidence values calculated in a specific time range and discarding older entries.
AACK is an ACK-based network layer approach that is thought to be a combination of TACK and ACK [24]. AACK reduces network overheads while maintaining the same network speed as TACK. AACK packets are sent in TRAACK based on trust requirements in (5):
AACKs are not delivered if nodes are relatively stable across the path, lowering control packet overheads. When it comes to trust levels that are in between high and low, AACKs are sent out in a random order to guarantee that packets do not get lost on the way [25]. If the confidence on the route is very small, AACKs will be used for measures of route use trust values to pick router.
Simulations were performed using MS-MAC as the MAC layer protocol, and a simple steering flood portion. AACK and TRAACK suggested a total of five runs. In the second period of the examination, vindictive hubs were presented. Five runs were directed for every situation and the normal results acquired were estimated [26]. Figs. 2 and 4 shows the network’s control packet overhead, Packet Delivery Ratio and end-to-end delay in the presence and absence of malicious nodes. Total network area (Circular area 2 km diameter), Maliciousness (0%, 10%, 20%, and 30%), Mobility (Random waypoint), the Transmission range of node (100 m), Radio propagation model (Free space), Traffic for simulation (Constant Bit Rate), QoS parameters including PDR, Overhead routing, and end-to-end latency are all evaluated using simulation. Simulation results of Proposed TRAACK-MPSO for WSN.

Figure 2: Packet delivery ratio for proposed PSO technique
It is observed from Tab. 1 and Fig. 2 that At 0% malicious, TRAACK-MPSO performs 3.3% better than TRAACK-PSO in terms of packet delivery ratio. Similarly, at 30% malicious, TRAACK-packet MPSO’s delivery ratio exceeds TRAACK-PSO by 3.5%. The MPSO develops solutions based on several parameters, resulting in greater outcomes.

It is observed from Tab. 2 and Fig. 3 that the control packet overhead of TRAACK-MPSO is lower by 4.1% than TRAACK-PSO at 0% malicious. Similarly, at 30% malicious, the control packet overhead of TRAACK-MPSO is lower by 3.6% than TRAACK-PSO.

Figure 3: Control packet overhead for proposed PSO technique

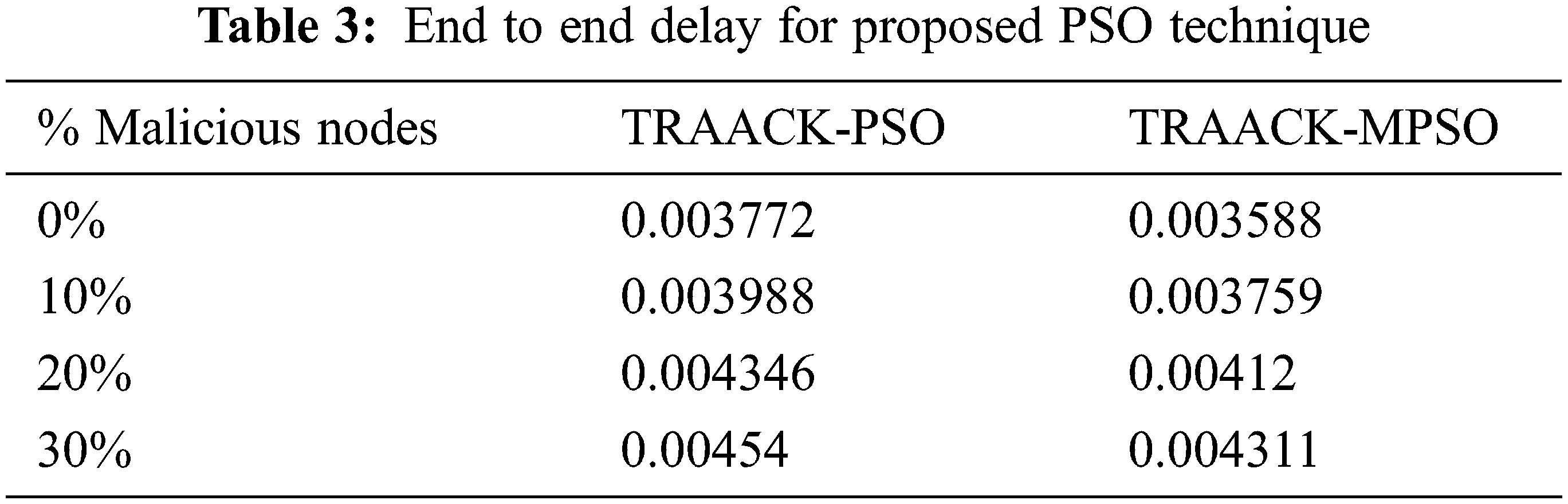
Tab. 3 and Fig. 4 show that the end-to-end delay of TRAACK-MPSO is 5% less than that of TRAACK-PSO, which is 0% malicious. Similarly, TRAACK-MPSO has a 5.2% lower end-to-end delay than TRAACK-PSO at 30% malicious.

Figure 4: End to end delay for proposed PSO technique
WSN’s open mode makes it defenceless against various attacks. Different strategies are joined to relieve the malignant hubs from the system. ACK based directing understands vague crashes, recipient impacts, and restricted transmission power. Trust is an effective component used to enhance remote system security. In this work, a Kalman filter-based TRACK IDS for WSN is proposed to anticipate trust in the hub. The investigation setup comprises 30 nodes spread out over a two-kilometer area. A simulation of the absence and different percentages of malicious nodes on the network was performed. The results indicate that TRAACKMPSO’s packet delivery rate is 3.3% better than the malicious 0% of TRAACKPSO. Similarly, the packet delivery rate of TRAACKMPSO is 30% malicious, 3.5% better than TRAACKPSO in WSN.
Acknowledgement: We show gratitude to anonymous referees for their useful ideas.
Funding Statement: The authors received no specific funding for this study.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
1. G. Wang and L. Guo, “A novel hybrid bat algorithm with harmony search for global numerical optimization,” Journal of Applied Mathematics, vol. 2013, pp. 1–22, 2013. [Google Scholar]
2. M. Reyes-Sierra and C. C. Coello, “Multi-objective particle swarm optimizers: A survey of the state-of-the-art,” International Journal of Computational Intelligence Research, vol. 2, no. 3, pp. 287–308, 2016. [Google Scholar]
3. J. Kennedy, R. C. Eberhart and Y. Shi, Swarm Intelligence, San Francisco: Morgan Kaufmann, pp. 1–544, 2001. [Online]. Available: https://www.elsevier.com/books/swarm-intelligence/eberhart/978-1-55860-595-4. [Google Scholar]
4. V. Selvi and R. Umarani, “Comparative analysis of ant colony and particle swarm optimization techniques,” International Journal of Computer Applications, vol. 5, no. 4, pp. 1–6, 2010. [Google Scholar]
5. D. D. Patil and B. D. Dangewar, “Multi-objective particle swarm optimization (MOPSO) based on pareto dominance approach,” International Journal of Computer Applications, vol. 107, no. 4, pp. 1–11, 2014. [Google Scholar]
6. J. Cavazos, J. E. B. Moss and M. F. O’Boyle, “Hybrid optimizations: which optimization algorithm to use?” in Int. Conf. on Compiler Construction, Berlin Heidelberg, pp. 124–138, 2006. [Google Scholar]
7. Y. Yang, T. Zhang, W. Yi, L. Kong, X. Li et al., “Optimal deployment of multistatic radar system using multi-objective particle swarm optimization,” Information Theory, vol. 12, no. 5, pp. 1–12, 2016. [Google Scholar]
8. M. Gong, Q. Cai, X. Chen and L. Ma, “Complex network clustering by multiobjective discrete particle warm optimization based on decomposition,” IEEE Transactions on Evolutionary Computation, vol. 18, no. 1, pp. 82–97, 2013. [Google Scholar]
9. A. Toofani, “Solving routing problem using particle swarm optimization,” International Journal of Computer Applications, vol. 52, no. 18, pp. 16–18, 2012. [Google Scholar]
10. R. F. Malik, T. A. Rahman and R. Ngah, “The new multipoint relays selection in OLSR using particle swarm optimization,” Telkomnika, vol. 10, no. 2, pp. 343–352, 2012. [Google Scholar]
11. E. Baburaj and V. Vasudevan, “An intelligent mesh based multicast routing algorithm for MANETs using particle swarm optimization,” International Journal of Computer Science and Network Security, vol. 8, no. 5, pp. 214–218, 2008. [Google Scholar]
12. T. Gui, C. Ma, F. Wang and D. E. Wilkins, “Survey on swarm intelligence based routing protocols for wireless sensor networks: an extensive study,” in Int. Conf. on Industrial Technology (ICIT), Taipei, Taiwan, pp. 1944–1949, 2016. [Google Scholar]
13. N. Jiang, F. Li, T. Wan and L. Liu, “Poisson dynamics in fitness evolution model for wireless sensor networks,” Journal of Ambient Intelligence and Humanized Computing, vol. 5, no. 6, pp. 919–927, 2014. [Google Scholar]
14. A. S. H. Abdul-Qawy and T. Srinivasulu, “SEES: A scalable and energy-efficient scheme for green IoT-based heterogeneous wireless nodes,” Journal of Ambient Intelligence and Humanized Computing, vol. 10, no. 4, pp. 1571–1596, 2019. [Google Scholar]
15. R. S. Kumar, K. Kondapaneni, V. Dixit, A. Goswami, L. S. Thakur et al., “Multi-objective modeling of production and pollution routing problem with time window: A self-learning particle swarm optimization approach,” Computers & Industrial Engineering, vol. 85, pp. 29–40, 2016. [Google Scholar]
16. J. Kennedy and R. Eberhart, “Particle swarm optimization,” Proc. of ICNN’95-Int. Conf. on Neural Networks,” Perth, WA, Australia, pp. 1942–1948, 1995. [Google Scholar]
17. H. Ali, W. Shahzad and F. A. Khan, “Energy-efficient clustering in mobile ad-hoc networks using multi-objective particle swarm optimization,” Applied Soft Computing, vol. 12, no. 7, pp. 1913–1928, 2012. [Google Scholar]
18. K. K. Somasundaram and J. S. Baras, “Performance improvements in distributed estimation and fusion induced by a trusted core,” in Int. Conf. on Information Fusion, Seattle, WA, USA, pp. 1942–1949, 2009. [Google Scholar]
19. J. Muñoz, R. González, A. Otero, L. Gazca, M. Huerta et al., “A flooding routing algorithm for a wireless sensor network for seismic events,” in Int. Conf. on Computing Systems and Telematics (ICCSAT), Xalapa, Mexico, pp. 1–6, 2015. [Google Scholar]
20. F. Ishmanov, S. W. Kim and S. Y. Nam, “A robust trust establishment scheme for wireless sensor networks,” Sensors, vol. 15, no. 3, pp. 7040–7061, 2015. [Google Scholar]
21. S. Shanmuga Priya, A. Valarmathi and D. Yuvaraj, “The personal authentication service and security enhancement for optimal strong password,” Concurrency and Computation: Practice and Experience, vol. 31, no. 14, pp. 1–7, 2019. [Google Scholar]
22. D. Yuvaraj and M. Sivaram, “Nature inspired evolutionary algorithm (ACO) for efficient detection of DDoS attacks on networks,” International Journal of Advanced Trends in Computer Science and Engineering, vol. 8, no. 1.4, pp. 44–50, 2019. [Google Scholar]
23. M. Sivaram, A. S. Mohammed, D. Yuvaraj,V. Porkodi, V. Manikandan et al., “An advanced expert system using particle swarm optimization based adaptive network-based fuzzy inference system to diagnose the physical constitution of the human body,” in Int. Conf. on Emerging Technologies in Computer Engineering, Springer, Singapore, pp. 349–362, 2019. [Google Scholar]
24. D. Yuvaraj, M. Sivaram and S. Navaneetha Krishnan, “Intelligent detection of untrusted data transmission to optimize energy in sensor networks,” Journal of Information and Optimization Sciences, vol. 41, no. 3, pp. 799–811, 2020. [Google Scholar]
25. P. Sudhakaran, S. Swaminathan, D. Yuvaraj and S. S.Priya, “Load predicting model of mobile cloud computing based on glowworm swarm optimization LSTM network,” International Journal of Interactive Mobile Technologies, vol. 14, no. 5, 2020. [Google Scholar]
26. B. B. Ahamed and D. Yuvaraj, “Dynamic secure power management system in mobile wireless sensor network,” in Int. Conf. on Intelligent Computing & Optimization, Thailand, pp. 549–558, 2019. [Google Scholar]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |