DOI:10.32604/csse.2022.022402

| Computer Systems Science & Engineering DOI:10.32604/csse.2022.022402 |  |
| Article |
MRI Brain Tumor Segmentation with Intuitionist Possibilistic Fuzzy Clustering and Morphological Operations
Department of Information Technology, Sri Ramakrishna Engineering College, Coimbatore, 641022, India
*Corresponding Author: J. Anitha. Email: anitha.j@srec.ac.in
Received: 06 August 2021; Accepted: 01 November 2021
Abstract: Digital Image Processing (DIP) is a well-developed field in the biological sciences which involves classification and detection of tumour. In medical science, automatic brain tumor diagnosis is an important phase. Brain tumor detection is performed by Computer-Aided Diagnosis (CAD) systems. The human image creation is greatly achieved by an approach namely medical imaging which is exploited for medical and research purposes. Recently Automatic brain tumor detection from MRI images has become the emerging research area of medical research. Brain tumor diagnosis mainly performed for obtaining exact location, orientation and area of abnormal tissues. Cancer and edema regions inference from brain magnetic resonance imaging (MRI) information is considered to be great challenge due to brain tumors complex structure, blurred borders, besides exterior features like noise. The noise compassion is mainly reduced along with segmentation stability by suggesting efficient hybrid clustering method merged with morphological process for brain cancer segmentation. Combined form of Median Modified Wiener filter (CMMWF) is chiefly deployed for denoising, and morphological operations which in turn eliminate nonbrain tissue, efficiently dropping technique’s sensitivity to noise. The proposed system contains the main phases such as preprocessing, brain tumor extraction and post processing. Image segmentation is greatly achieved by presenting Intuitionist Possibilistic Fuzzy Clustering (IPFC) algorithm. The algorithm’s stability is greatly enhanced by this clustering along with clustering parameters sensitivity reduction. Then, the post processing of images are done through morphological operations along with Hybrid Median filtering (HMF) for attaining exact tumors representations. Additionally, suggested algorithm is substantiated by comparing with other existing segmentation algorithms. The outcomes reveal that suggested algorithm achieves improved outcomes pertaining to accuracy, sensitivity, specificity, and recall.
Keywords: Morphological Image Processing (MIP); Magnetic Resonance Imaging (MRI); brain tumor; clustering; K-means clustering; image segmentation; Fuzzy-C-Means (FCM)
The process involved in digital image partitioning into multiple regions is generally referred as image segmentation. The main segmentation aim is changing an image representation into more significant and at ease in analysis. It is greatly utilized for locating objects and boundaries in images. A group of areas that cooperatively shields the complete image is considered to be the image segmentation outcome [1]. Consequently, medical diagnosis greatly necessitates medical image segmentation which is regarded as challenging task for the reason of reduced contrasts, diverse categories of noise, incomplete/ diffusive borders [2]. Brain structure scanning might be greatly achieved through Magnetic Resonance Imaging (MRI) / computed tomography (CT) scans. Diagnosis is performed at ease by MRI scan when compared to CT scan. Human body does not get affected since there is no radiation involved and mainly depends on magnetic field in addition to radio waves [3]. Conversely, brain cancer is considered to be the major cause of mortality amid people. The early stage detection might increase the survival probability which is substantiated through evidence. Mostly, treatments for strokes are provided by physician apart from tumor treatment and hence tumor identification is greatly necessitated for treatment. The early brain tumor detection might help in increasing the person lifetime [4]. Hence there is a great necessity for a capable medical image segmentation technique with certain chosen attributes like rapid computation, minimum client communication, precise, as well as vigorous segmentation results [5].
Conversely, two fundamental image strength data properties: discontinuity as well as resemblance are considered to be key component in image segmentation algorithms [6]. The segmentation approach mainly depends on processed image partitioning on basis of variations in intensity, for instance edges and corners in case of formal category. The second choice is on basis of an image partitioning into areas that are alike owing to a predefined criteria group. Consequently, various segmentation techniques such as artificial neural network based segmentation approaches, histogram based approaches, physical method dependent methods, edge-related approaches, area-based approaches (region split, rising, and integration), with clustering approaches (K-means, Fuzzy C-means, Mean Shift, anticipation increase) [7–9].
The unified methodology development is considered to be a great challenge which can be greatly utilized for all images and applications categories. Also, desired approach choice for specific image category is yet another issue. Consequently, no widespread recognized method does exist for image segmentation. It is considered to be an open challenge in image processing and computer vision arenas [10]. The clustering problem is yet another challenge in determining pixels in an image belong together most applicably. Various researches have been carried out for performing image segmentation on basis of clustering techniques. These approaches achieve clustering either through partitioning or grouping pixels. Certain criteria are used for entire image partitioning into regions that are ‘‘good’’. But in grouping, pixel grouping is done on basis of certain assumptions for determining the groups rather [11]. Various clustering algorithms like hard clustering or K-means clusters, Fuzzy clustering are greatly utilized in in image segmentation process. Also clustering is yet a great challenging area which is utilized as a unique tool for gaining intuition into data distribution in diverse clusters for additional examination. Cluster analysis functions as pre-processing stage for another methods, like categorization which will then function on identified groups [12].
For enhancing unsteadiness clustering as well as mitigating its sensitivity to noise, efficient clustering segmentation method is suggested in research. Key research hand-outs are presented below:
i) Initially, combined form of median modified Wiener filter (CMMWF) is greatly exploited for denoising the Brain tumor images.
ii) A hybrid clustering algorithm on basis of Intuitionist Possibilistic Fuzzy Clustering (IPFC) is suggested.
iii) IPFC algorithm is employed for initializing the clustering center, which significantly enhances algorithm stability and also increases sensitivity to noise.
iv) Suggested technique is integrated with morphological process for pre-processing and post processing, that additionally enhances segmentation correctness.
Consequently, image segmentation accuracy is considerably enhanced. The Paper structure is given below: Related paper survey is given in Section 2. Suggested technique is elucidated in Section 3. Experimentation outcomes and evaluation are presented in Section 4. Lastly, inferences and unresolved concerns are enumerated in Section 5.
Kalaiselvi and Somasundaram [13] performed brain tissue images segmentation by utilizing fuzzy C-means (FCM) which is considered to be computationally more effectual as a result of seed point’s initialization by means of image histogram data. Nonetheless, the technique yet doesn’t discourse sensitivity to noise as well as intensity inhomogeneity (IIH).
Noreen et al. [14] suggested an approach namely hybrid MR segmentation for inhomogeneity elimination on basis of DWT and FCM. It greatly utilizes DWT to contribute MR image for attaining 4 sub-bands; at that moment, inverse discrete wavelet transform (IDWT) is functional for obtaining a high-quality image. Lastly, FCM grouping is deployed for image segmentation. While this method discourses only sensitivity issue of intensity nonuniformity, data space information uncertainty is not taken into account.
Christe et al. [15] suggested an approach by integrating K-means with fuzzy C-means which clearly defines total groups, vagueness, distance, ending criterion. The overlapping intensities is easily managed, however evidently tissue boundaries are not described.
Wilson and Dhas [16] utilized K-means, FCM for iron detection in brain SWI. Evaluated by comparing two methods. It is thereby substantiated that FCM algorithm offers better outcomes for identifying iron-containing areas than K-means.
Abdel-Maksoud et al. [17] utilized K-means, FCM clustering by considering the techniques merits and demerits. It is validated that K-means algorithm might achieve faster brain cancer detection than FCM method, whereas FCM method might identify cancer which is not identified via K-means. This approach integrates K-means clustering along with FCM for segmentation. It is thereby validated that 2 methods combination is highly beneficial than separate methods. Their seed points selection is done arbitrarily ensuing in overfitting which is considered as a drawback.
In [18], a methodology is suggested brain cancer categorization on basis of SVM with fuzzy c-means. This hybrid technique is greatly utilized for brain tumor prediction. Image enhancement is attained through is similarity enhancement and mid-range draw out. Also, skull stripping is attained through double thresholding as well as morphological procedures. Tumor detection is greatly achieved by Fuzzy C means via segmentation. Also, feature extraction is attained via Grey level run length matrix (GLRLM) following which SVM is deployed for tumor classification. This hybrid approach offers accurate outcomes for brain tumor detection.
Tao Wang et al. [19] suggested a methodology on basis of Normalized Gaussian Bayesian categorization with novel 3D Fluid Vector Flow method for automatic brain cancer identification and segmentation. There are two major contributions. One is Normalized Gaussian Mixture Model for modelling a healthy brain tissue and the other is extended 2D Fluid Vector Flow to 3D space deployed for tumor segmentation.
Though, noise sensitivity is greatly reduced to certain extent by present medical image segmentation algorithm, challenge lies in segmentation stability. Hybrid algorithm is greatly suggested for mitigating clustering algorithm noise sensitivity and enhancing clustering algorithm stability. The benefits of both the algorithm are mainly utilized by proposing hybrid algorithm. Additionally, preprocessing and post processing are done by utilizing morphological operations and thereby enhancing segmentation accuracy further and thereby substantiated. Tab. 1 shows the comparative table for existing methods.

Segmentation method suggested in the research is primarily fragmented to three portions which is presented in Fig. 1. First step is that preprocessing and accomplishing brain surface extortion (BSE). Actual noisy brain MR image denoising is done by deploying combined form of median modified Wiener filter (CMMWF) and morphological operations which in turn eliminate nonbrain tissue for obtaining brain parenchyma denoised image 0. Step 2 (Tumor image clustering and extraction). Image segmentation is greatly achieved by presenting Intuitionist Possibilistic Fuzzy Clustering (IPFC) algorithm. On the basis of threshold, tumor region extraction is done based on threshold. Step 3 (post processing). Extracted tumor images post processing are done through morphological operations and Hybrid median filtering (HMF) for attaining exact brain tumors representations.

Figure 1: Proposed flow diagram
3.1 Preprocessing Using Combined Form of Median Modified Wiener Filter (CMMWF)
The lesions segmentation and patients’ conditions diagnosis are greatly affected if the medical images are noisy quite often. Wiener filtering is greatly utilized for removing noise in MRI brain images which in turn helps ineffective elimination of Gaussian noise, while protecting original image texture.
A. Median and Wiener Filters
Generally, corrupted images restoring which are susceptible to noise is done by a proper method like filtering. The mathematical formulation is given below [20]:
where
where
where
(a) Combined form of MMWF (CMMWF)Technique
MMWF technique is greatly utilized for noise distribution reduction in degraded images and this designing is done by Cannistraci et al. [22]. Main objective of the method is enhancing feature through without noising background area of corrupted image by means of median filter. Additionally, edge signal is maintained by this method by Wiener filter. This approach is mainly on basis of Wiener filter, replacing mask matrix pixel values with median values, thus achieving noise reduction in corrupted image. Average data
MMWF method advantage is degraded images enhancement is done as follows: Due to drop-off-effect, edge signal is well-maintained before related with median and Wiener filter methods. MMWF method might achieve significantly well than traditional filters pertaining to denoising effect; additionally, it might concurrently preserve edge signal and eliminate background noise signal [23]. Fig. 2 displays an image with Gaussian noise (noise variance, 0.02) with conforming without noise image attained by combined form of median modified Wiener filter (CMMWF).

Figure 2: Denoising of the image by adding noise as well as filtering CMMWF (a) MR image (b) Image with noise (c) Denoised image
Besides, MR brain data mainly comprise nonbrain tissues images like skull and exterior membrane, revealed in red Fig. 2. For computing complex reduction besides segmentation improvement morphological process are greatly involved for non-brain tissue elimination. Morphological procedures are employed for borders identification as well as objects skeletons in an image [24]. Expansion and corrosion are the two main common morphological operations. Expansion helps in image’s edges enlarging, filling target edges or its interior hopelessness. Corrosion performs image borders erosion [25]; the main target is erosion of final image’s borders saw tooth. Starting process corresponds to growth plus corrosion process extension, wherever etching is executed initially after which similar structural factors are deployed for development [26]; the process is represented by
where X represents brain image, Y denotes structural element, “
Let us take an arbitrary MR image, where Gaussian noise (variance, 0.02) is provided, revealed in Fig. 3b. By previously mentioned preprocessing phases, noise plus non-brain designs are efficiently eliminated, despite the fact that simultaneously MR image texture features are also preserved. The preprocessing outcomes is presented in Fig. 3c.

Figure 3: Sample of combining gaussian noise (variance, 0.02) to MR image for removing noise and ensuing image acquired following preprocessing (a) MR image (b) Noisy image (c) Pre processed image
3.2 Clustering Using Intuitionist Possibilistic Fuzzy Clustering (IPFC) Algorithm
Various fuzzy clustering algorithms is conferred in the section. Input database represented via ‘
Possibilistic clustering methods estimate typicality each data point and, unlike the membership values are not constrained to sum-to-one across clusters. When the typicality of a data point is close to zero for a particular cluster, it indicates that the data point is an outlier with respect to cluster. A data point is an outlier in all clusters (i.e., sufficiently far from all cluster centers) will have a low typicality value in all clusters. Thus, the estimated typicality values identify the outliers in an input data set and prevent them from influencing cluster estimation and biasing the resulting cluster representative values.
A. Fuzzy Clustering
The clustering technique established by Dunn, was FCM, which was improved by Bezdek [27]. The notion in this algorithm is that number of clusters, ‘c’, is predetermined for specified dataset as well as objective function is:
where,
The degree of membership for (1) is found as follows:
where, m represents fuzzy index (constant) and center vector
But, FCM is extremely ineffective in distinguishing accurate centroids when noise and outliers exists in [28].
B. Possibilistic Fuzzy C-Mean (PFCM)
In excess of k-mean outputs, FCM clustering outcomes are better nonetheless further noise receptive. single constraint is that every membership degrees for every data point are integrated cluster-wise to single, owing to irregular points being cluster data. FCM restrictions were mitigated by Possibilistic method along fuzzy c-mean hybridization, plus that methodology was termed Possibilistic fuzzy clustering (PFCM). Formula (4) signifies Possibilistic fuzzy c-mean methodology as:
The membership degree and positive number play a vital role in Eqs. (5) and (6) as follows:
In Eq. (6), W represents an modifiable weight that is characteristically fixed to 1. FCM (by formula (3)) attains feasible result for centroid revamping. By formula (4), PFCM reduces when ever entire groups are concurrent groups. Membership value depends mainly on space amid information in addition to specific cluster deprived of any consideration of other clusters.
C. Intuitionist Fuzzy C-Mean (IFCM)
Due to Intuitionist fuzzy clustering method, another enhanced fuzzy clustering is presented in this research. Accordingly, intuitionist fuzzy sets are used to update the conventional approach of fuzzy c-mean. Due to the modification of cluster centers, the integration of intuitionist properties with fuzzy c-mean method is enabled. Intuitionist fuzzy sets [29] are suggested and the occurrence of hesitation degree is conferred by Atanassov. As conferred by the author, it cannot always be valid that membership as well as non-membership degree summation is one. Since the hesitation degree may occur, hesitation level was described 1 subtracting the overall degrees of membership as well as non-membership. Following Eq. (14) expresses the degree of hesitation.
By using Eq. (8), the degree of hesitation is estimated initially. Subsequently, values of Intuitionist fuzzy membership are acquired as expressed by the following equation,
In which, intuitionistic fuzzy membership of mth data in lth class is signified by
In context of Eq. (9), the updation of cluster center along with membership matrix is carried out concurrently. For tumor classification, numerous medical image segmentation systems use traditional k-mean clustering technique suggested by various authors.
D. Proposed Intuitionist Possibilistic Fuzzy Clustering (IPFC) for Tumour Segmentation
On the basis of segmentation part, amalgamating likelihood fuzzy c-mean with Intuitionist fuzzy c-mean and reducing total repetitions to minimize the running period is the core concept behind the proposed study.
Algorithm 1: IPFC
1. Initialization
2. Estimate PFCM
3. Determine Hesitation degree is initially
4. Attain Intuitionistic fuzzy membership value by:
5. Switch Eq. (13) by Eq. (11) to identify IPFC.
The improved cluster center will be:
and cluster midpoint was restructured besides instantly connection matrix is streamlined.
6. Complete the iteration. Patronize the convergence standard.
7. If convergence take extended time, stop the iteration, or else go back to Step 2.
As depicted in Fig. 4c, segmented images achieved through mentioned clustering algorithm might feature small holes/over segmentation because of different factors, like intensity non-uniformity and noise.

Figure 4: Segmentation results after post processing: (a) MRI data, (b) truth of ground, (c) cancer region extorted with no post processing, (d) cancer region acquired then post processing
For post processing, Hybrid median filtering (HMF) and hole-filling can be utilized, through which the segmentation accuracy can be improved. In extracted tumor areas, the small holes are filled and a few missegmented areas filtering is done, once post-processing is completed. In Fig. 4d, the segmentation algorithm’s results are depicted, which is obtained after post processing. Besides, the original MR image is presented in Fig. 4a, and ground truth image is depicted in Fig. 4b.
Based on various modalities of brain MR images collected from the open-access image library called BRATS 2012 (http://www.slicer.org/pages/ Special: Slicer Downloads), the proposed algorithm is tested. The overall implementation of proposed approach is carried out under Matlab R2016a simulator that runs on the configuration of Intel Core i5 CPU 2.5 GHz, 8 GB RAM. For segmenting FLAIR images in BRATS 2012, the method proposed in this study is predominantly utilized [30]. Besides, the segmentation algorithm is tested through 100 MR images pairs associated to twenty dissimilar tumor patients.
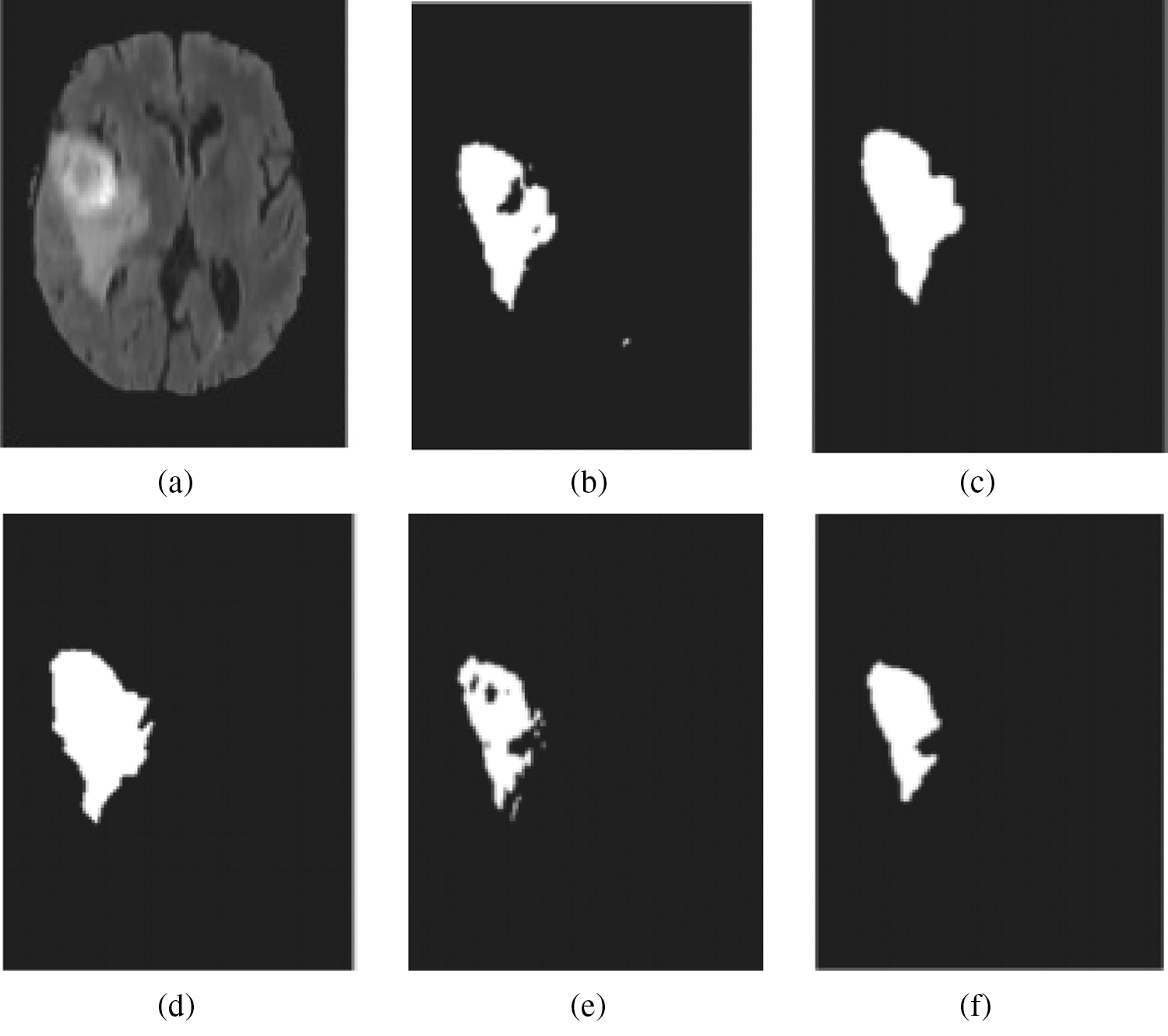
Figure 5: Generation of two unstable outcomes from Intuitionist Possibilistic Fuzzy Clustering (IPFC) (a) MRI data (b) cancer area extorted from initial outcome (c) cancer area then post processing extorted from initial outcome (d) image with ground truth (e) cancer area extorted from next outcome (f) cancer area then post processing extorted from next outcome
In this work, application of Intuitionist Possibilistic Fuzzy Clustering (IPFC) is proposed to accomplish the deterministic initialization task, through which the segmentation algorithm’s stability is greatly improved. In addition, empirical findings also reveal the optimal stability of the proposed approach is referred in Fig. 5.
A. Comparison with Some Recently Proposed Clustering Algorithms
The anticipated method efficacy is assessed through comparison of various contemporary clustering algorithms. For analysis purpose, the random selection of tree brain MR images is performed. The suggested algorithm clustering efficiency and its performance comparison with regard to FCM, K-means group are depicted in Fig. 6. Accordingly, clearly exhibited algorithm proposed in this study has high accuracy than other algorithms in terms of texture details handling.
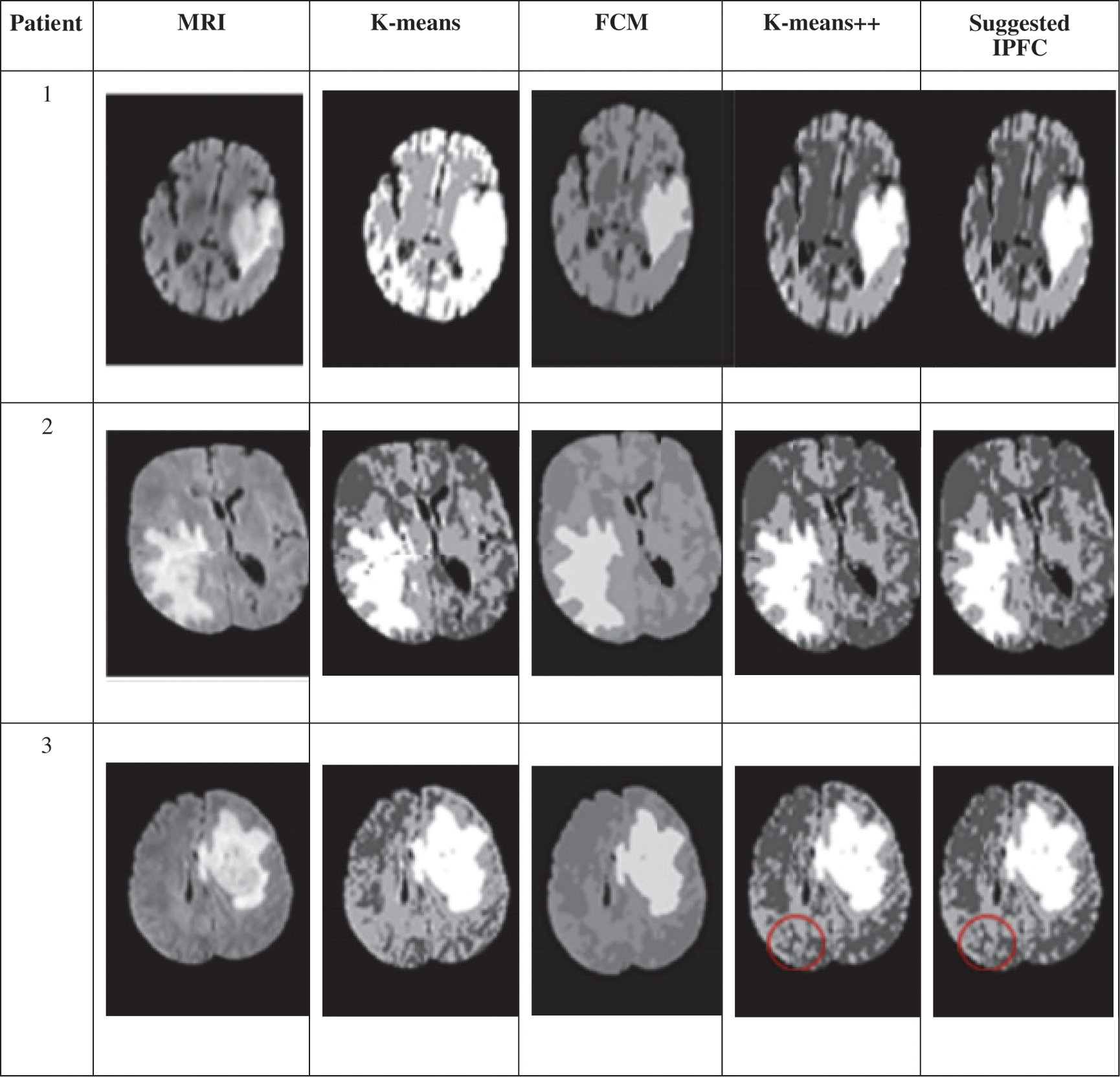
Figure 6: Clustering outcomes of K-means, FCM, K-means++methods, suggested IPFC clustering method
Moreover, segmentation quality is evaluated through four performance parameters, namely Dice or Accuracy, Sensitivity, Specificity, and Recall to assess proposed algorithm’s efficiency. Among the parameters taken, the Accuracy rate is often considered as a significant evaluation index that signifies ratio of area, in which 2 objects interconnect to the overall region. To appropriate partition, the value of Dice is taken as 1. Besides, the quantification of true positive (TP) count by the pixels that are appropriately detected as belongs to the region of interest is named as Sensitivity, based on which the maximum number of true positives denotes maximum accuracy. Whereas, the quantification of the number of false positive (FP) by the pixels that are not actually belong to region of interest, nevertheless are wrongly categorized as belong to the region of interest is called Specificity, in which the maximum number of FPs reduces the Specificity. Finally, a proportion of TPs with overall positives, that total number of TPs plus false negatives (FNs) is referred to as Recall [20]. Estimation of these parameters are given by,
In the above equations, the definition of TP, TN, FP, and FN are given below,
i) TP indicates the existence of tumor and appropriate detection of it.
ii) TN signifies the non-existence of tumor and it is not detected.
iii) FP denotes the non-existence of tumor but it is detected inappropriately.
iv) FN indicates the existence of tumor, but it is not identified.
For instance, individual brain images belongs to three different patients have been considered in this study as samples. Consequently, recommended IPFC algorithm comparison is done with three different clustering algorithms, namely K-means, FCM and K-means++ algorithms, which is depicted in Tab. 2 The numerical outcomes represent that suggested algorithm has maximum values with regards to Dice, Sensitivity, and Specificity parameters.
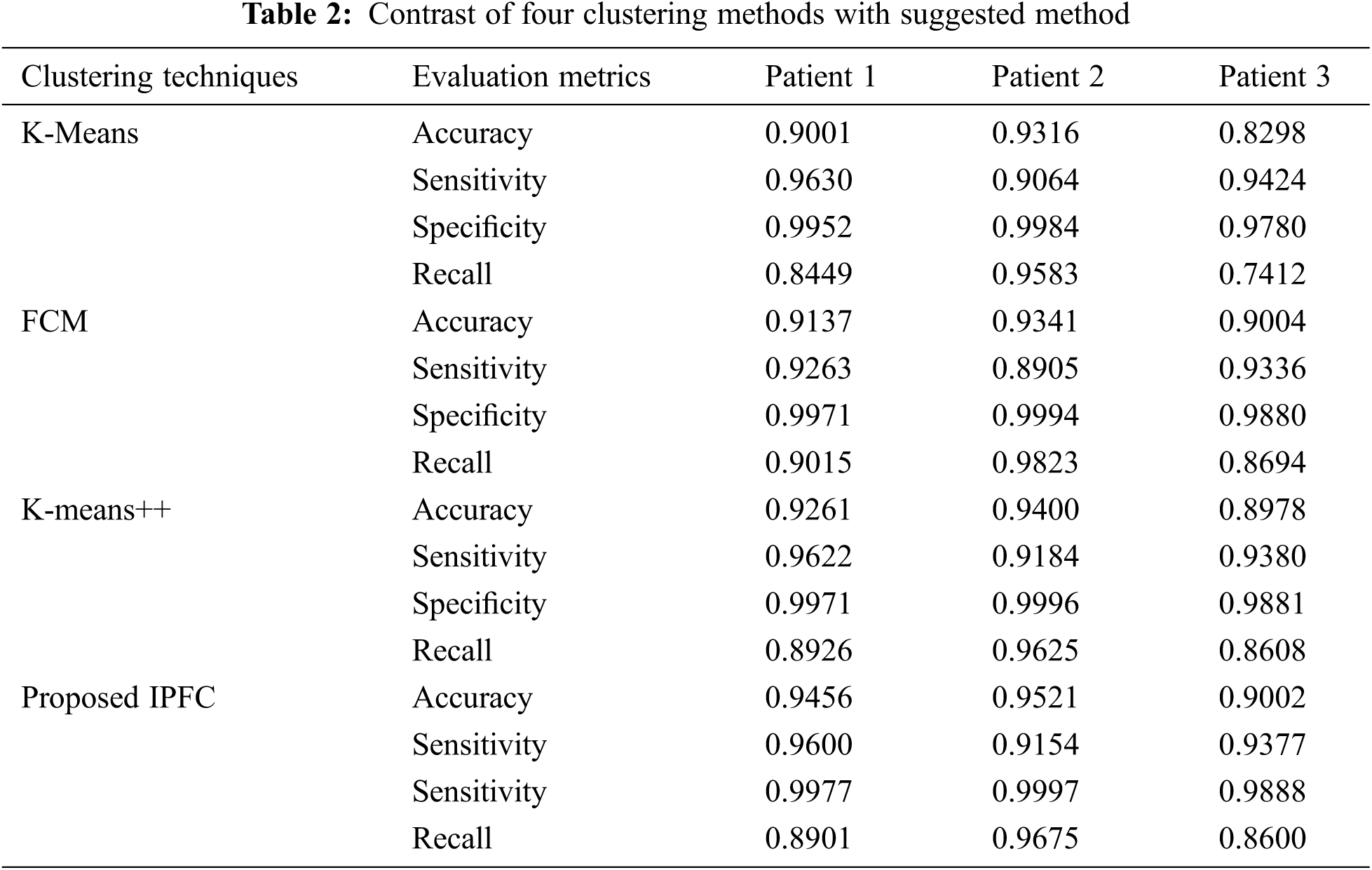
As depicted in Tab. 3, the numerical results obtain through the implementation on 100 images substantiate that suggested IPFC is efficient than other prevailing algorithms.
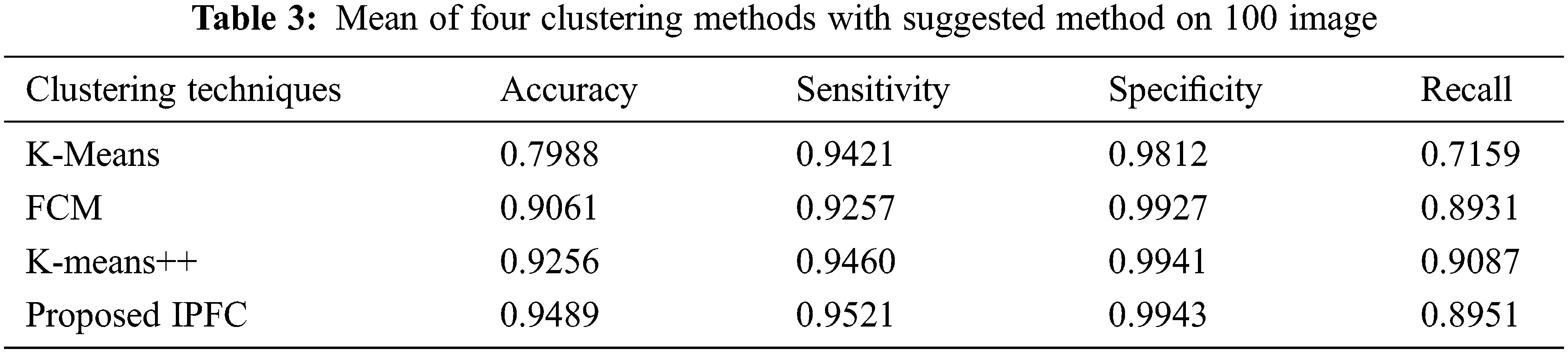
In Fig. 7, the accuracy values individually obtained by suggested and prevailing algorithms are compared as regards Brain tumor segmentation process. Accordingly, suggested IPFC algorithm outclasses prevailing algorithms by obtaining 94% accuracy rate, since K-Means, FCM and K-Means++ algorithms solely obtain 79%, 90%, and 92%, respectively.
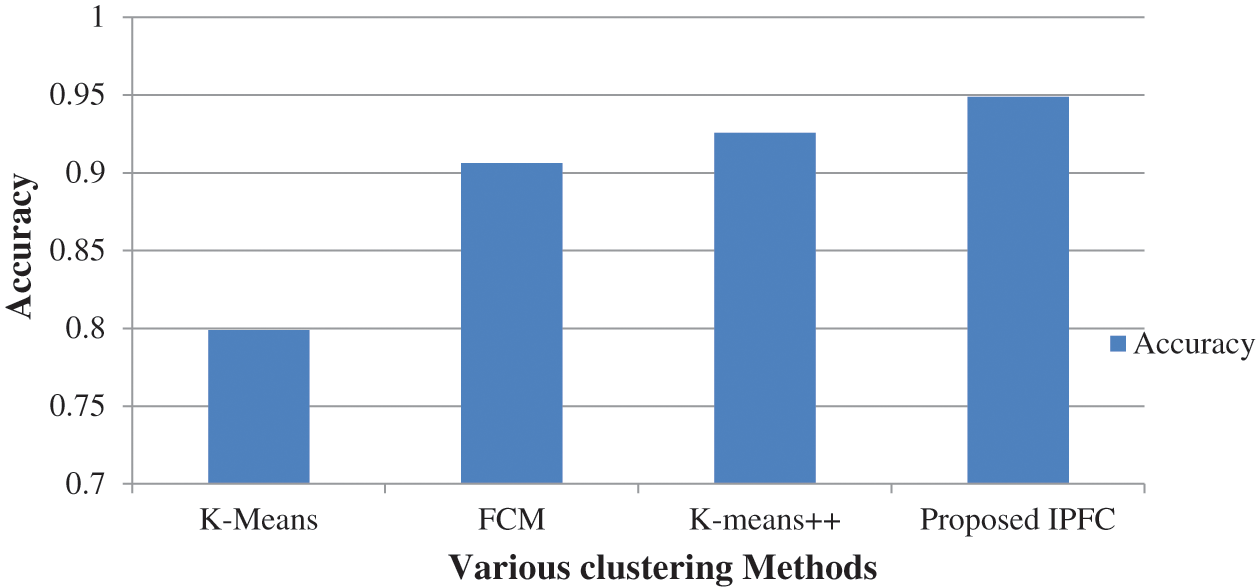
Figure 7: Accuracy comparison
Fig. 8 compares suggested and prevailing algorithms sensitivity values obtained during Brain tumor segmentation process. Accordingly, recommended IPFC algorithm outclasses prevailing algorithms by obtaining 0.9521 sensitivity value. Because, K-Means, FCM and K-Means++ algorithms solely obtain 0.9421, 0.9927, and 0.9460, correspondingly, which are lower than the proposed algorithm.
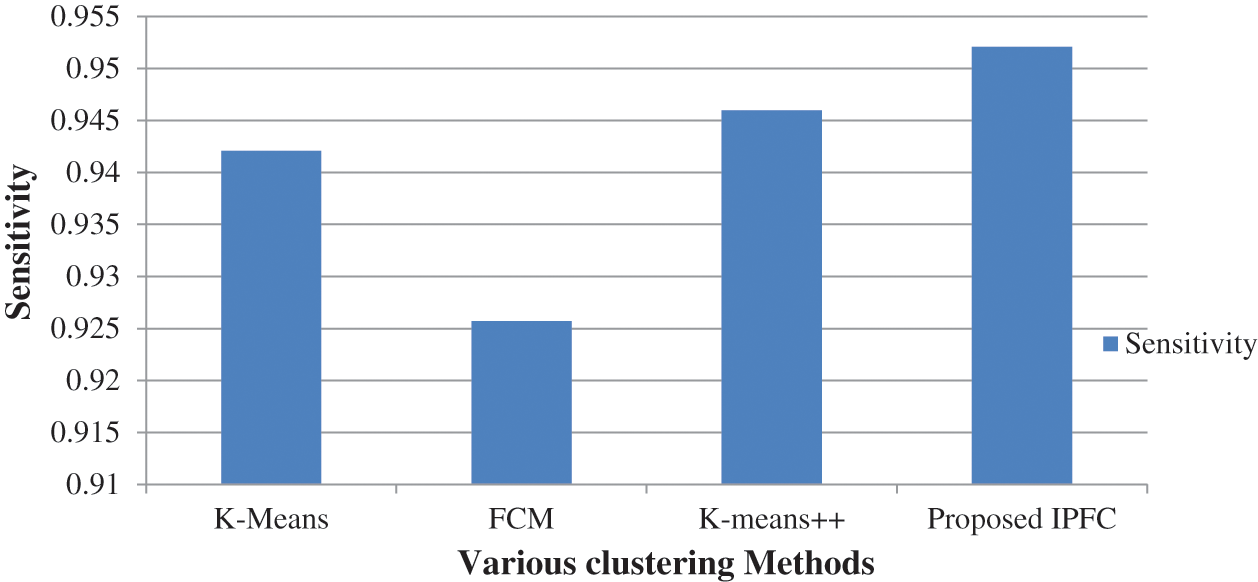
Figure 8: Sensitivity comparison
In Fig. 9, the Specificity values individually attained through suggested and prevailing algorithms are compared as regards Brain tumor segmentation process. Through the results, it is depicted that suggested IPFC algorithm is capable of outperforming prevailing algorithms by obtaining 0.9943 Specificity value, since K-Means, FCM and K-Means++ algorithms solely obtain lesser Specificity as follows, i.e., 0.9812, 0.9257, and 0.9941, respectively.
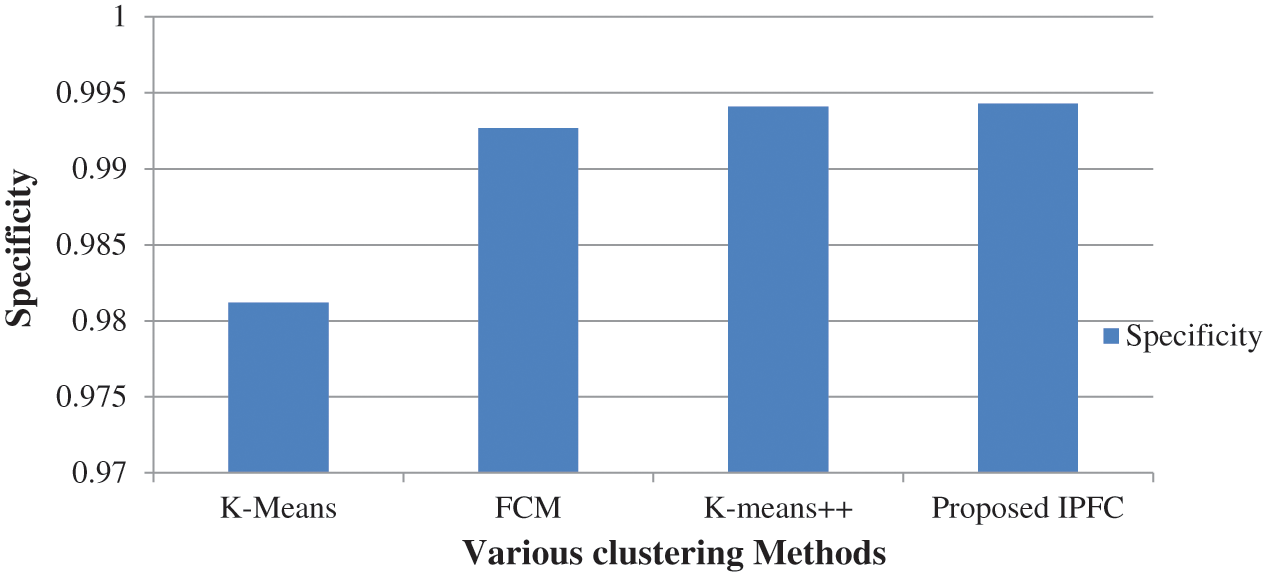
Figure 9: Specificity comparison
Fig. 10 compares anticipated and prevailing algorithms recall rates obtained during Brain tumor segmentation process. Subsequently, suggested IPFC algorithm outclasses prevailing algorithms by attaining 0.8951 Recall rate. Because, K-Means, FCM and K-Means++ algorithms solely obtain 0.7159, 0.8931, and 0.9087, correspondingly, which are lesser than the proposed algorithm.
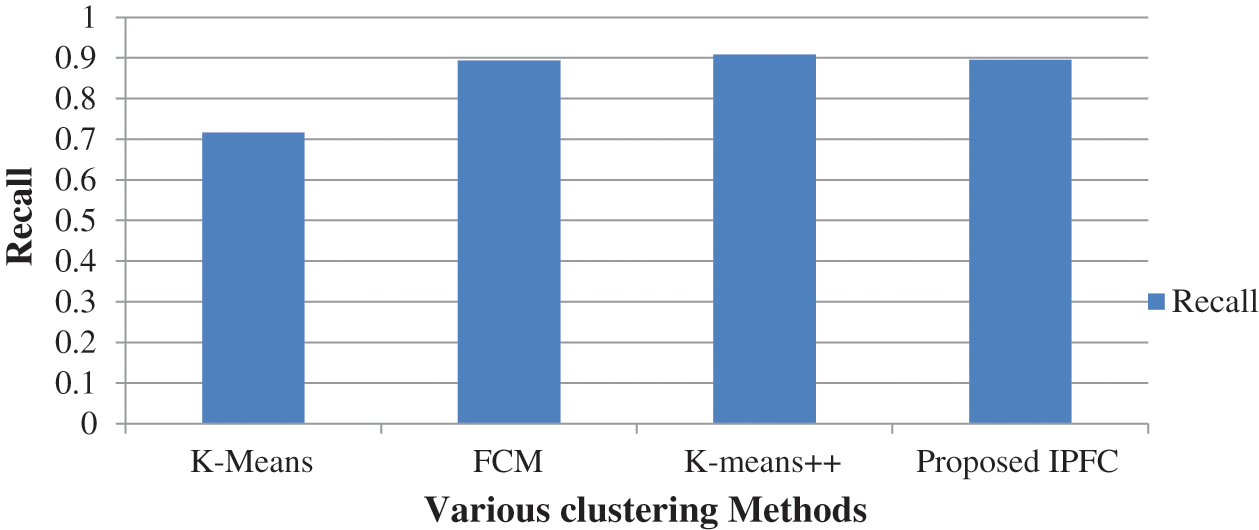
Figure 10: Recall comparison
This study proposes the combination of hybrid clustering algorithm and morphological operations for achieving segmentation process with brain tumor images. During this algorithm process, the outer membrane is removed using morphological operations, through which the computational complexity and clustering iteration count can significantly be reduced. The centroids of clusters are initialized through IPFC clustering algorithm during the clustering stage. Besides, this approach is efficient in resolving the issue of unstable clustering that emerges from the uncertainty corresponding to the cluster centroids initialization, thereby a stable clustering outcomes are generated by all clusters. Moreover, the overfitting is greatly prevented through the proposed approach. Based on Gaussian kernel framework, a fuzzy C-means clustering is further exploited by the algorithm. The proposed IPFC algorithm is focused to improve the MRI brain tumor segmentation accuracy results prominently. For the given database, the proposed IPFC algorithm achieves 94% accuracy rate whereas K-Means, FCM and K-Means++ algorithms obtain lower accuracy 79%, 90%, and 92% respectively. For suggested algorithm, algorithm robustness is enhanced further, since sensitivity to the clustering factors is prominently diminished. As a post processing, lastly morphological operations and Hybrid median filtering are utilizied, through which segmentation accuracy is significantly improved.
Acknowledgement: We show gratitude to anonymous referees for their useful ideas.
Funding Statement: The authors received no specific funding for this study.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
1. V. Janani and P. Meena, “Image segmentation for tumor detection using fuzzy inference system,” International Journal of Computer Science and Mobile Computing (IJCSMC), vol. 2, no. 5, pp. 244–248, 2013. [Google Scholar]
2. B. Dong, A. Chien and Z. Shen, “Frame based segmentation for medical images,” Communications in Mathematical Sciences, vol. 32, no. 4, pp. 1724–1739, 2010. [Google Scholar]
3. J. Patel and K. Doshi, “A study of segmentation methods for detection of tumor in brain MRI,” Advance in Electronic and Electric Engineering, vol. 4, no. 3, pp. 279–284, 2014. [Google Scholar]
4. R. S. Kabade and M. S. Gaikwad, “Segmentation of brain tumour and its area calculation in brain MR images using K-mean clustering and fuzzy C-mean algorithm,” International Journal of Computer Science & Engineering Technology, vol. 4, no. 5, pp. 524–531, 2013. [Google Scholar]
5. H. A. Aslam, T. Ramashri and M. I. A. Ahsan, “A new approach to image segmentation for brain tumor detection using pillar K-means algorithm,” International Journal of Advanced Research in Computer and Communication Engineering, vol. 2, no. 3, pp. 1429–1436, 2013. [Google Scholar]
6. J. Acharya, S. Gadhiya and K. Raviya, “Segmentation techniques for image analysis: A review,” International Journal of Computer Science and Management Research, vol. 2, no. 1, pp. 1218–1221, 2013. [Google Scholar]
7. D. Naik and P. Shah, “A review on image segmentation clustering algorithms,” International Journal of Computer Science and Information Technologies, vol. 5, no. 3, pp. 3289–3293, 2014. [Google Scholar]
8. S. A. Christe, K. Malathy and A. Kandaswamy, “Improved hybrid segmentation of brain MRI tissue and tumor using statistical features,” ICTACT Journal on Image and Video Processing, vol. 1, no. 1, pp. 43–49, 2010. [Google Scholar]
9. G. K. Seerha and R. Kaur, “Review on recent image segmentation techniques,” International Journal on Computer Science and Engineering, vol. 5, no. 2, pp. 109–112, 2013. [Google Scholar]
10. R. Dass and D. S. Priyanka, “Image segmentation techniques,” International Journal of Electronics & Communication Technology, vol. 3, no. 1, pp. 66–70, 2012. [Google Scholar]
11. J. Kaur, S. Agrawal and R. Vig, “Integration of clustering, optimization and partial differential equation method for improved image segmentation,” International Journal of Image, Graphics and Signal Processing, vol. 4, no. 11, pp. 26–33, 2012. [Google Scholar]
12. M. Panda and M. R. Patra, “Some clustering algorithms to enhance the performance of the network intrusion detection system,” Journal of Theoretical and Applied Information Technology, vol. 4, no. 8, pp. 795–801, 2008. [Google Scholar]
13. T. Kalaiselvi and K. Somasundaram, “Fuzzy c-means technique with histogram based centroid initialization for brain tissue segmentation in MRI of head scans,” in Int. Sym. on Humanities, Science and Engineering Research, Kuala Lumpur, Malaysia, pp. 149–154, 2011. [Google Scholar]
14. N. Noreen, K. Hayat and S. A. Madani, “MRI segmentation through wavelets and fuzzy C-means,” World Applied Sciences Journal, vol. 13, pp. 34–39, 2011. [Google Scholar]
15. S. A. Christe, K. Malathy and A. Kandaswamy, “Improved hybrid segmentation of brain MRI tissue and tumor using statistical features,” ICTACT Journal on Image and Video Processing, vol. 1, no. 1, pp. 43–49, 2010. [Google Scholar]
16. B. Wilson and J. P. M. Dhas, “An experimental analysis of Fuzzy C-means and K-means segmentation algorithm for iron detection in brain SWI using Matlab,” International Journal of Computer Applications, vol. 104, no. 15, pp. 36–38, 2014. [Google Scholar]
17. E. Abdel-Maksoud, M. Elmogy and R. Al-Awadi, “Brain tumor segmentation based on a hybrid clustering technique,” Egyptian Informatics Journal, vol. 16, no. 1, pp. 71–81, 2015. [Google Scholar]
18. A. Singh, “Detection of brain tumor in MRI images, using combination of fuzzy c-means and SVM,” in 2nd Int. Conf. on Signal Processing and Integrated Networks (SPIN), Noida, India, pp. 98–102, 2015. [Google Scholar]
19. T. Wang, I. Cheng and A. Basu, “Fully automatic brain tumor segmentation using a normalized Gaussian Bayesian classifier and 3D fluid vector flow,” in IEEE Int. Conf. on Image Processing, Hong Kong, China, pp. 2553–2556, 2010. [Google Scholar]
20. A. Sharma and J. Singh, “Image denoising using spatial domain filters: A quantitative study,” in 6th Int. Congress on Image and Signal Processing (CISP), Hangzhou, China, pp. 293–298, 2013. [Google Scholar]
21. S. Esakkirajan, T. Veerakumar, A. N. Subramanyam and C. H. Prem Chand, “Removal of high-density salt and pepper noise through modified decision based unsymmetric trimmed median filter,” IEEE Signal Processing Letters, vol. 18, no. 5, pp. 287–290, 2011. [Google Scholar]
22. C. V. Cannistraci, F. M. Montevecchi and M. Alessio, “Median-modified Wiener filter provides efficient denoising, preserving spot edge and morphology in 2-DE image processing,” Proteomics, vol. 9, no. 21, pp. 4908–4919, 2009. [Google Scholar]
23. C. V. Cannistraci, A. Abbas and X. Gao, “Median Modified Wiener Filter for nonlinear adaptive spatial denoising of protein NMR multidimensional spectra,” Scientific Reports, vol. 5, no. 1, pp. 603, 2015. [Google Scholar]
24. U. Ilhan and A. Ilhan, “Brain tumor segmentation based on a new threshold approach,” Procedia Computer Science, vol. 120, no. 1.-II, pp. 580–587, 2017. [Google Scholar]
25. R. Radha and B. Lakshman, “Retinal image analysis using morphological process and clustering technique,” Signal & Image Processing, vol. 4, no. 6, pp. 55–69, 2013. [Google Scholar]
26. A. M. Raid, W. M. Khedr, M. A. El-Dosuky and M. Aoud, “Image restoration based on morphological operations,” International Journal of Computer Science, Engineering and Information Technology (IJCSEIT), vol. 4, no. 3, pp. 9–21, 2014. [Google Scholar]
27. J. C. Bezdek, R. Ehrlich and W. Full, “FCM: The fuzzy c-means clustering algorithm,” Computers & Geosciences, vol. 10, no. 2-3, pp. 191–203, 1984. [Google Scholar]
28. A. Gosain and S. Dahiya, “Performance analysis of various fuzzy clustering algorithms: A review,” Procedia Computer Science, vol. 79, no. 2, pp. 100–111, 2016. [Google Scholar]
29. K. T. Atanassov, “On intuitionistic fuzzy sets theory,” Berlin, Heidelberg: Springer, pp. 1–16, 2012. [Online]. Available: https://link.springer.com/chapter/10.1007/978-3-642-29127-2_1. [Google Scholar]
30. C. Zhang, X. Shen, H. Cheng and Q. Qian, “Brain tumor segmentation based on hybrid clustering and morphological operations,” International Journal of Biomedical Imaging, vol. 2019, no. 3, pp. 1–11, 2019. [Google Scholar]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |