DOI:10.32604/csse.2022.021932

| Computer Systems Science & Engineering DOI:10.32604/csse.2022.021932 |  |
| Article |
Cognitive Radio Networks Using Intelligent Reflecting Surfaces
Information Technology Department, Saudi Electronic University, Riaydh, Kingdom of Saudi Arabia
*Corresponding Author: Raed Alhamad. Email: ralhamad@seu.edu.sa
Received: 20 July 2021; Accepted: 26 September 2021
Abstract: In this article, we optimize harvesting and sensing duration for Cognitive Radio Networks (CRN) using Intelligent Reflecting Surfaces (IRS). The secondary source harvests energy using the received signal from node A. Then, it performs spectrum sensing to detect Primary Source PS activity. When PS activity is not detected, The Secondary Source SS transmits data to Secondary Destination SD where all reflected signals on IRS are in phase at SD. We show that IRS offers 14, 20, 26, 32, 38, 44, 50 dB enhancement in throughput using M = 8, 16, 32, 64, 128, 256, 512 reflectors with respect to CRN without IRS. We also suggested to add a second IRS between A and SS to increase the harvested energy. The use of 2 IRS with M1 = 8 reflectors in the first IRS and M2 = 8 reflectors in the second IRS offers 18 dB gain (respectively 32 dB) gain with respect to a single IRS with M2 = 8 reflectors (respectively without IRS). The use of 2 IRS with M1 = 16 reflectors in the first IRS and M2 = 8 reflectors in the second IRS offers 28 dB gain (respectively 42 dB) gain with respect to a single IRS with M2 = 8 reflectors (respectively without IRS). Our results are valid for Nakagami channels of fading figure m. We also provide the throughput of IRS with energy harvesting. We have studied packet waiting time and total delay in the presence and absence or IRS. At Signal to Noise Ratio (SNR) per bit equal to 0 dB, packet waiting time is 0.9 ms when there is no IRS and 0.5 ms when there is an IRS with M = 8 reflector. At SNR per bit equal to 0 dB, total transmission delay is 54 ms when there is no IRS and 1.5 ms when there is an IRS with M = 8 reflectors. We show that the energy efficiency is larger when both harvesting and sensing durations are optimized. The maximum of energy efficiency is 260 Mbit/s/Hz/J when harvesting and sensing durations are optimized while the maximum is 80 Mbit/s/Hz/J when harvesting and sensing durations are not optimized.
Keywords: Cognitive radio networks; energy harvesting; spectrum sensing; throughput analysis
Intelligent Reflecting Surfaces (IRS) are able to enhance significantly the throughput of wireless systems [1–5]. The phase shift of each IRS reflector is optimized so that reflections are in phase at the destination [6–8]. IRS is placed between the source and the destination so that all reflections have the same phase at the destination [9,10]. The number of reflectors has been varied and takes values M = 8, 16, 32, 64, 128, 256, 512 and the throughput increases as M increases [11–13]. Asymptotic performance analysis of wireless systems using IRS was discussed in [14–16]. Antenna design and measurement results were discussed in [17]. Machine and deep learning algorithms were applied to wireless communications using IRS [18,19].
In this paper, we suggest to optimize harvesting and sensing duration for CRN using IRS. The Secondary Source SS harvests energy during a T seconds where T is frame duration and 0 < a < 1 is the harvesting duration. Then SS performs spectrum sensing using the energy detector over (1-a)bT seconds to detect Primary Source PS activity where 0 < b < 1 provides the sensing duration. When PS activity is not detected, SS transmits data to the Secondary Destination SD during (1-a)(1-b)T. We show that IRS offers 14, 20, 26, 32, 38, 44, 50 dB enhancement in throughput using M = 8, 16, 32, 64, 128, 256, 512 reflectors with respect to CRN without IRS [20]. We also suggested to add a second IRS between A and SS to increase the harvested energy. The use of 2 IRS with M1 = 8 reflectors in the first IRS and M2 = 8 reflectors in the second IRS offers 18 dB gain (respectively 32 dB) gain with respect to a single IRS with M2 = 8 reflectors (respectively without IRS [20]). The use of 2 IRS with M1 = 16 reflectors in the first IRS and M2 = 8 reflectors in the second IRS offers 28 dB gain (respectively 42 dB) gain with respect to a single IRS with M2 = 8 reflectors (respectively without IRS [20]). We also derive the Probability Density Function (PDF), the Cumulative Distribution Function (CDF) of SNR and the throughput of CRN using IRS where the secondary source harvests energy. Beamforming allows increasing the harvested energy as suggested in [21,22]. The weighting coefficient of different antennas can be optimized to maximize the harvested energy. Beamforming requires multiple antennas as proposed in [21,22]. In this paper, a single antenna is used at the secondary source.
Next section optimizes the throughput when there is a single IRS. Section 3 proposes the use of a second IRS to increase the harvested energy. Section 4 describes the numerical results and Section 5 concludes the paper.
The system model of Fig. 1 contains a Primary Source and a Primary Destination PS and PD, a Secondary Source and Destination SS and SD, node A and IRS. SS harvests energy over a T seconds. T is frame duration and 0 < a < 1 is the harvesting duration. Then, SS performs spectrum sensing to detect PS activity during (1-a)bT seconds where 0 < b < 1 provides the sensing duration. When PS activity is not detected, SS transmits a packet of symbols to SD over (1-a)(1-b)T seconds. A Nakagami channel of fading figure m is assumed.
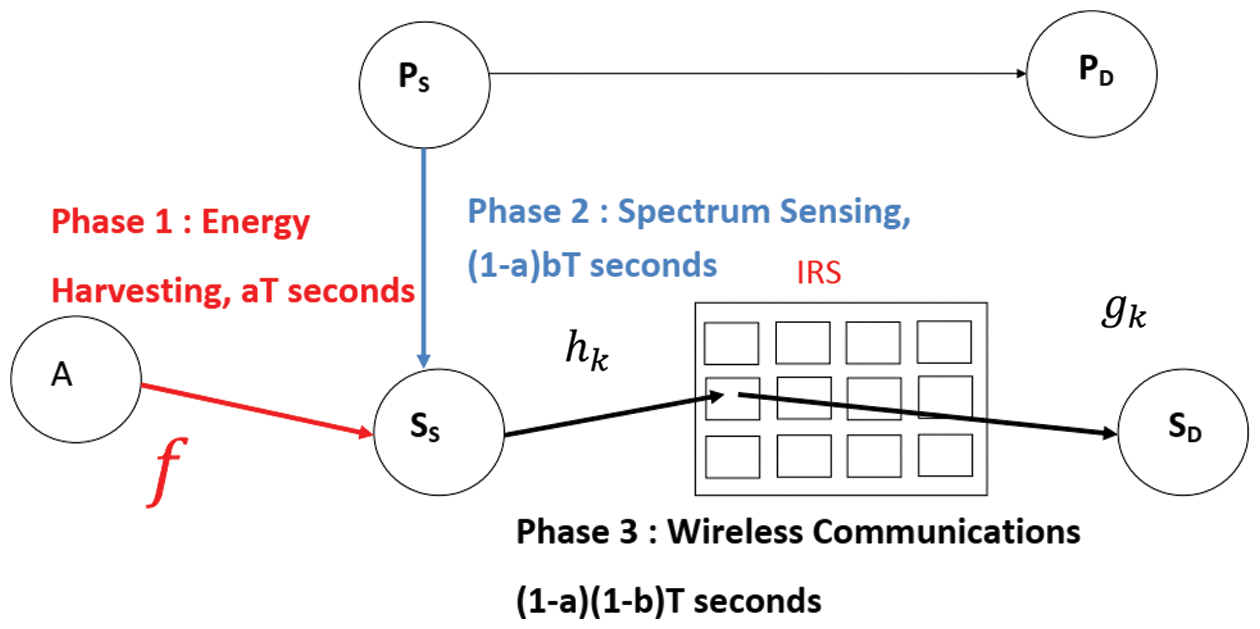
Figure 1: System model
The harvested energy at SS is equal to
where δ is the efficiency of energy conversion process, Ts is symbol duration, PA = EA/Ts is the power of A, f is channel gain between A and SS. We have E(|f|2) = 1/D1PLE where D1 is the distance between A and PS, E(.) is the expectation operator and PLE is the Path Loss Exponent.
The symbol energy of SS is computed as:
Let hq the channel gain between SS and q-th reflector of IRS. Let gq the channel gain between q-th reflector of IRS and SD. We have: E(|hq|2) = 1/D2PLE where D2 is the distance between SS and IRS. E(|gq|2) = 1/D3PLE where D3 is the distance between IRS and SD.
We have hq = aqe−jbq where a_q = |h_q| and bq is the phase of hq: E(aq) = Γ(m + 0.5)/(Γ(m)*
The phase of q-th IRS reflector is given by [1]
The received signal at SD is given by
where sp is the p-th symbol and np is a Gaussian noise of variance N0.
Using (3), we have
The SNR at SD is computed as [1]
where
Using (2), we deduce
X has a Gaussian distribution with mean and variance
Therefore, X2 has a non central chisquare distribution with one degree of freedom. For Nakagami channels, |f|2 has a central chi-square distribution with 2 m degrees of freedom. The SNR is the product of a non central chisquare r.v. X2 and f|2 has a central chi-square distribution with 2 m degrees of freedom. The CDF of SNR at SD is given by [23,24]
when Gn,mp,l(x) is the Meijer G-function.
The Packet Error Probability (PEP) at SD can be computed as [25]
where
and pep(u) is the PEP for Quadrature Amplitude Modulation (QAM) of size Q [26]
where PL is packet length in symbols.
The throughput at SD is computed as
where B is the used bandwidth, Pf(a, b) is the false alarm probability written as
μ is the energy detector threshold and
Harvesting duration a and sensing duration b are optimized to maximize the throughput:
In Fig. 2, IRS1 is placed between A and SS to increase the harvested energy while IRS2 is located between SS and SD so that all reflected signals are in phase at SD.
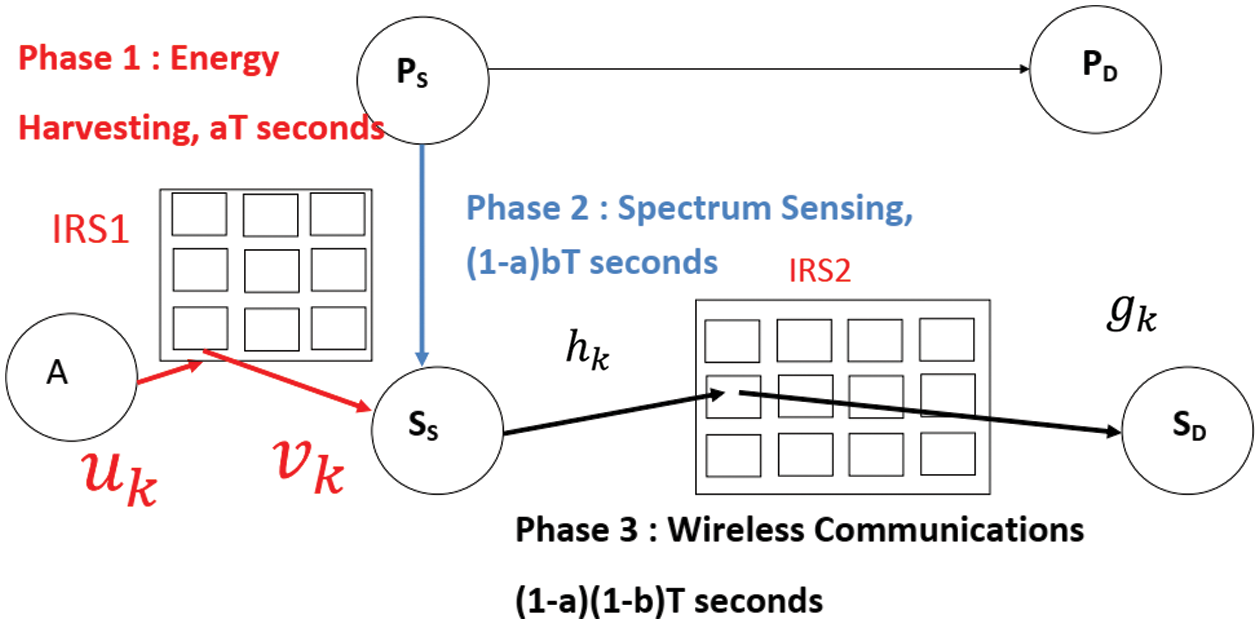
Figure 2: IRS to increase the harvested energy
When energy harvesting uses IRS, the harvested energy is expressed as
where
M1 is the number of reflectors of the first IRS, δq = |uq|, uq is the channel gain between A and IRS1 and ρq = |vq|, vq is the channel gain between IRS1 and SS.
Z has a Gaussian distribution with mean and variance
D4 is the distance between A and IRS1 and D5 is the distance between IRS1 and SS.
We deduce
The SNR at SD is equal to
where X is defined in (7).
The CDF of SNR at SD is equal to [23,24]
The throughput is computed and optimized using (10)–(16).
Figs. 3–5 depict the throughput for Quadrature Phase Shift Keying (QPSK) modulation, 16 and 64 QAM modulations, m = 2, μ = 1, EA = 1, D1 = 1.1, D2 = 1.2, D3 = 1.4, PLE = 3. A single IRS with M = 8 reflectors was used. The distance between SS and PS is 2. We plotted the theoretical throughput and the computer simulations (sim). We observe that optimal a b offers more than 4 dB gain with respect to a = 1/3 and optimal b. The proposed optimal a and b offers up to 20 dB gain with respect to optimal a and b = 1/2. A significant throughput enhancement is observed when optimizing a and b with respect to a = 1/3 and b = 1/2 where harvesting, sensing and data transmission are performed over the same durations.
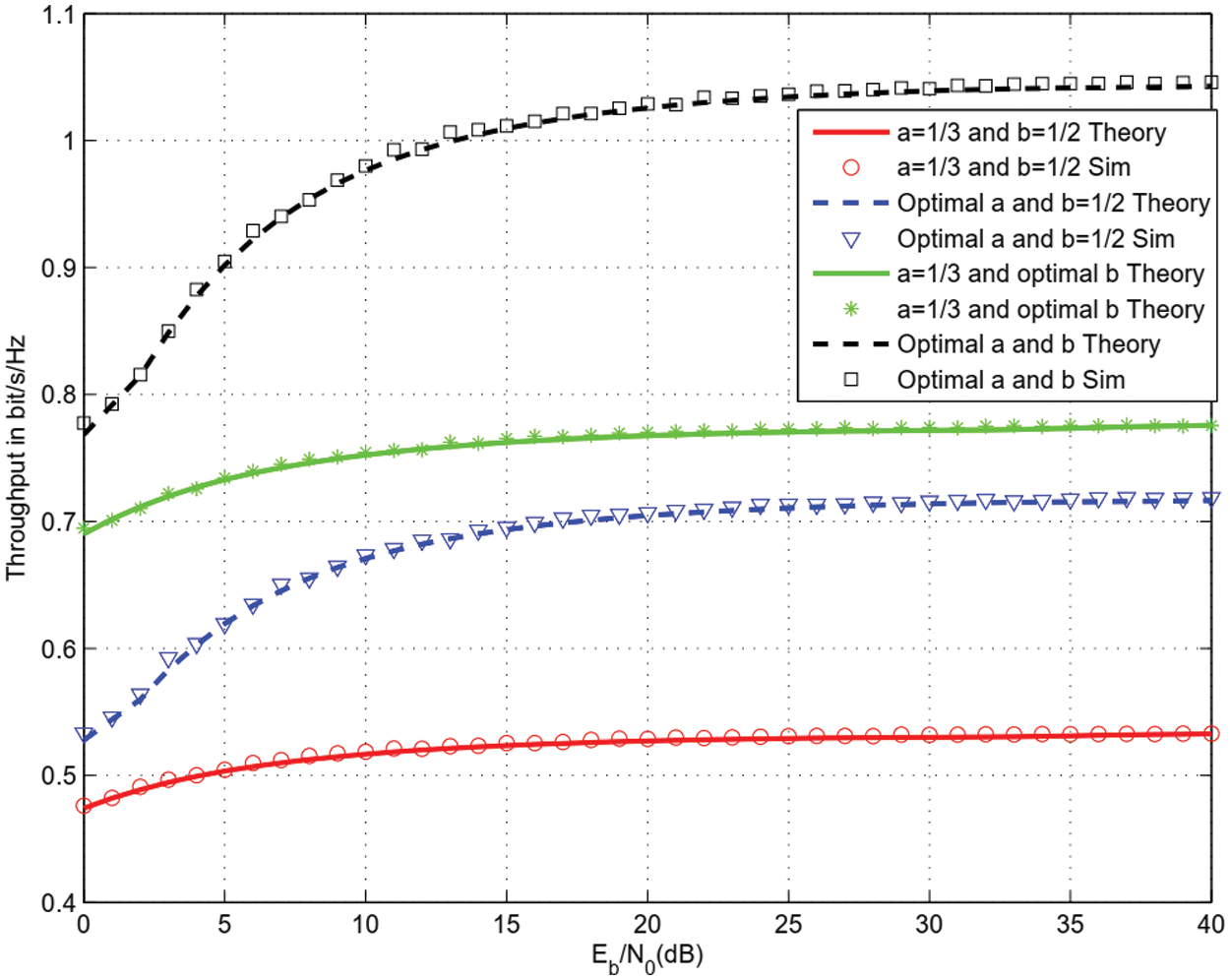
Figure 3: Throughput for QPSK and M = 8
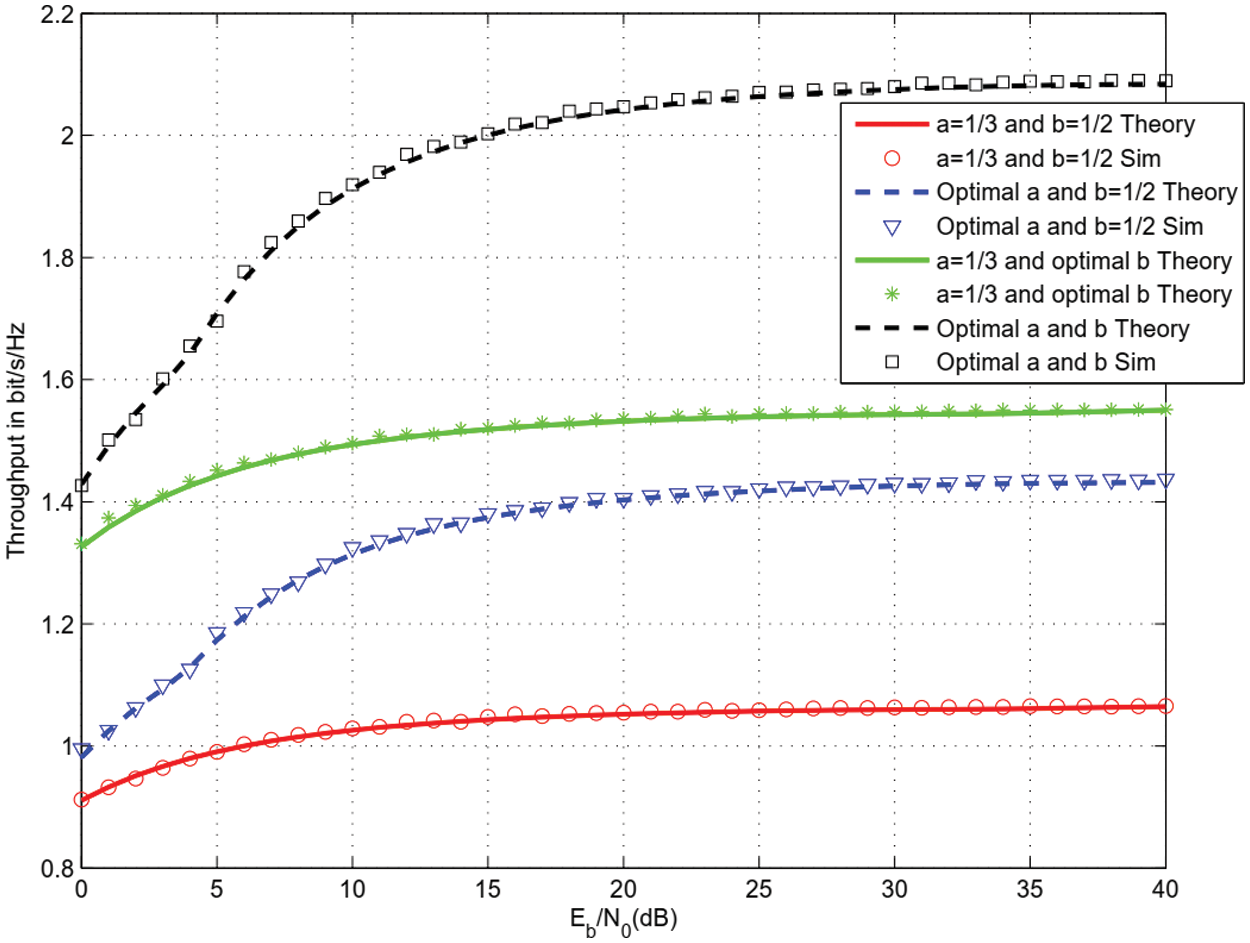
Figure 4: Throughput for 16 QAM and M = 8
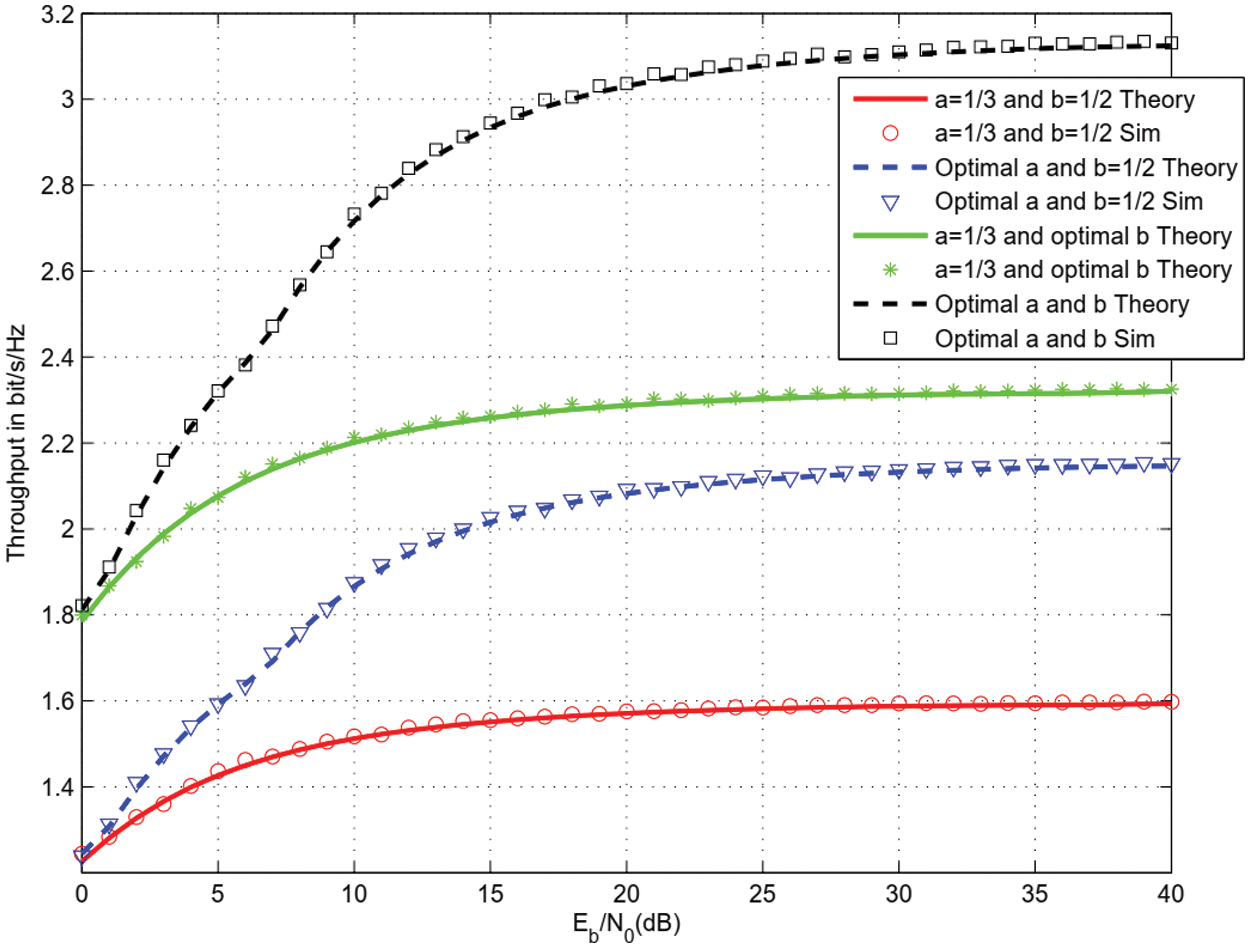
Figure 5: Throughput for 64 QAM and M = 8
For the same parameters as Figs. 3–5, Figs. 6 and 7 depict the throughput for 16 and 64 QAM modulation and different number of reflecting surfaces M = 8, 16, 32, 64, 128, 256, 512. Sensing and harvesting duration were optimized in Figs. 6 and 7. We observe 14, 20, 26, 32, 38, 44, 50 dB enhancement in throughput using M = 8, 16, 32, 64, 128, 256, 51 reflectors with respect to CRN without IRS [20].
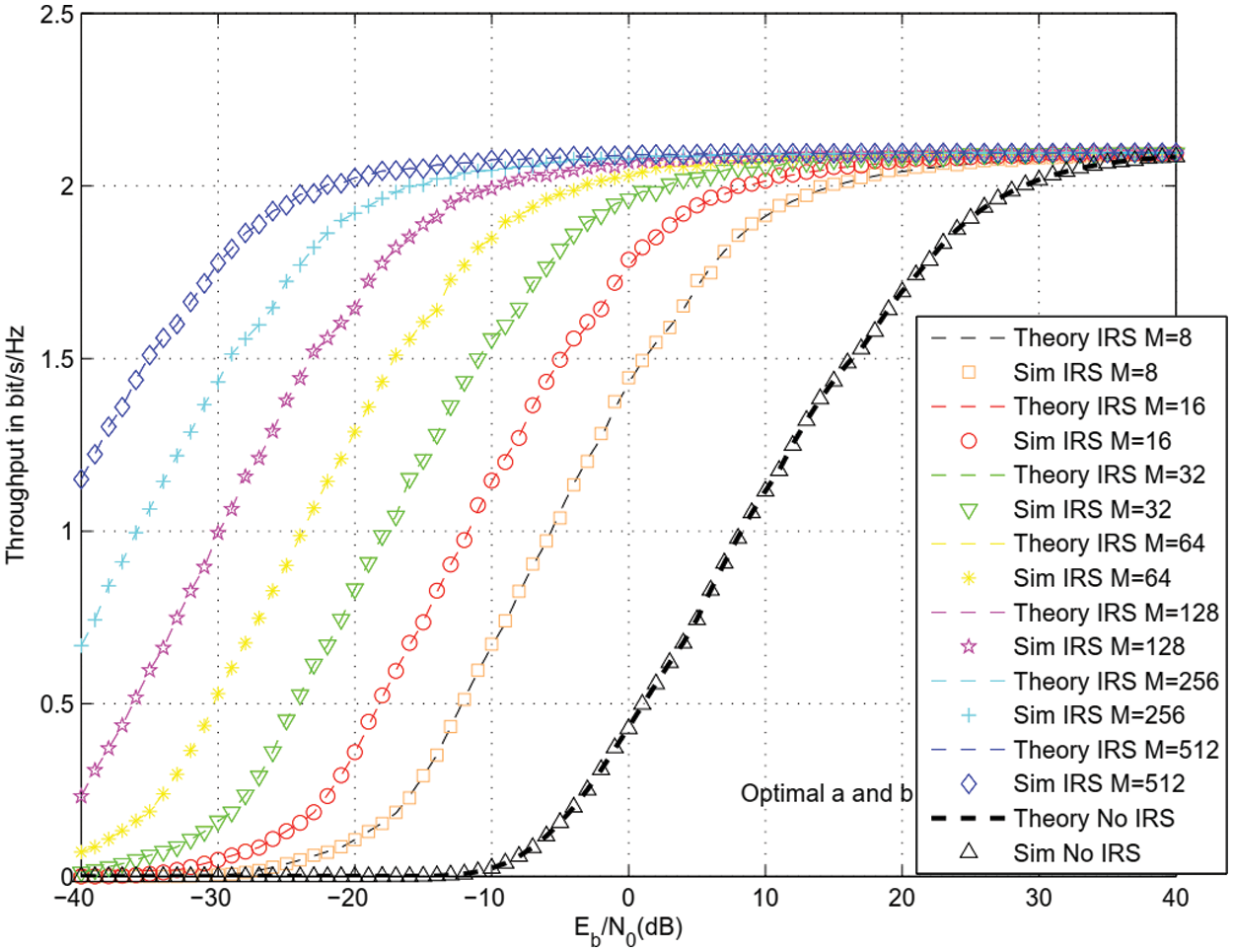
Figure 6: Throughput for 16 QAM and different values of M
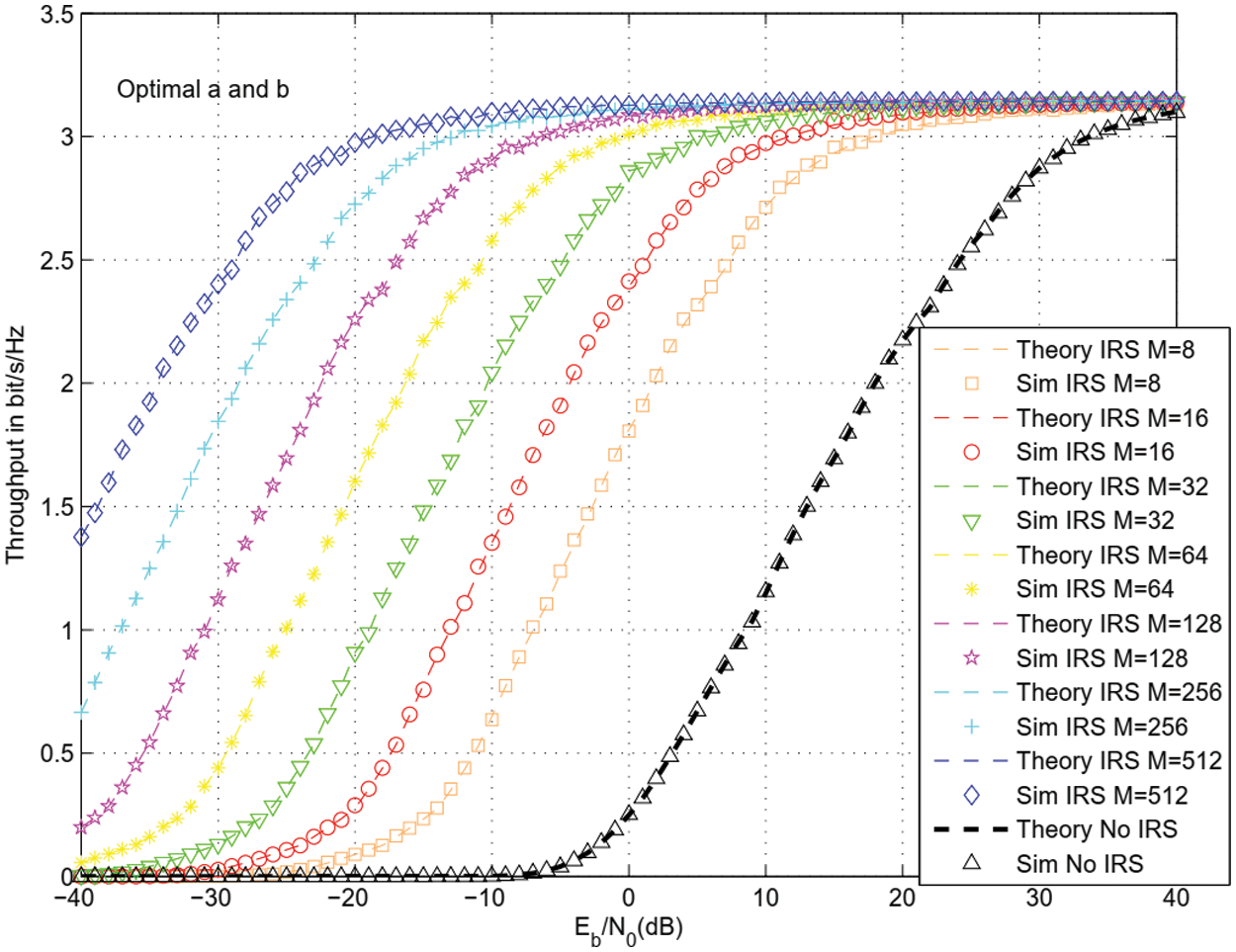
Figure 7: Throughput for 64 QAM and different values of M
Fig. 8 shows the throughput of 16 QAM modulation for the same parameters as Figs. 3–5 and when there are 2 IRS for D4 = 1.1 and D5 = 1.2. The use of 2 IRS with M1 = M2 = 8 reflectors offers 18 dB gain (respectively 32 dB) gain with respect to a single IRS with M2 = 8 reflectors (respectively without IRS [20]). The use of 2 IRS with M1 = 16 reflectors in the first IRS and M2 = 8 reflectors in the second IRS offers 28 dB gain (respectively 42 dB) gain with respect to a single IRS with M2 = 8 reflectors (respectively without IRS [20]).
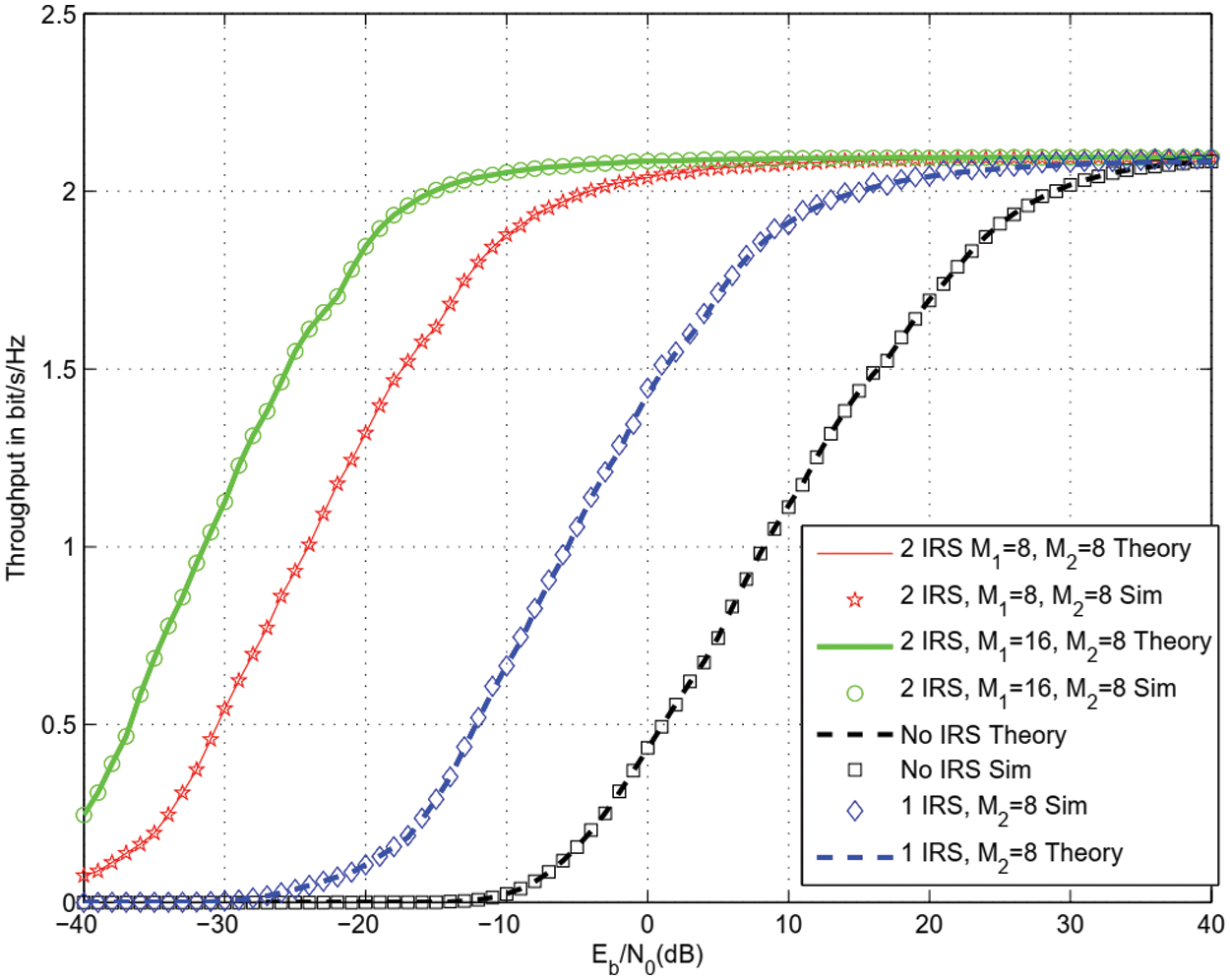
Figure 8: Throughput for 16 QAM with 2 IRS and m = 2
Fig. 9 shows the effects of fading figure m = 1, 2, 3 on throughput of 64 QAM modulation for the same parameters as Figs. 3–5. There are M = 8 reflectors in a single IRS. We observe a throughput enhancement as m increases. Note that m = 1 corresponds to Rayleigh channels.
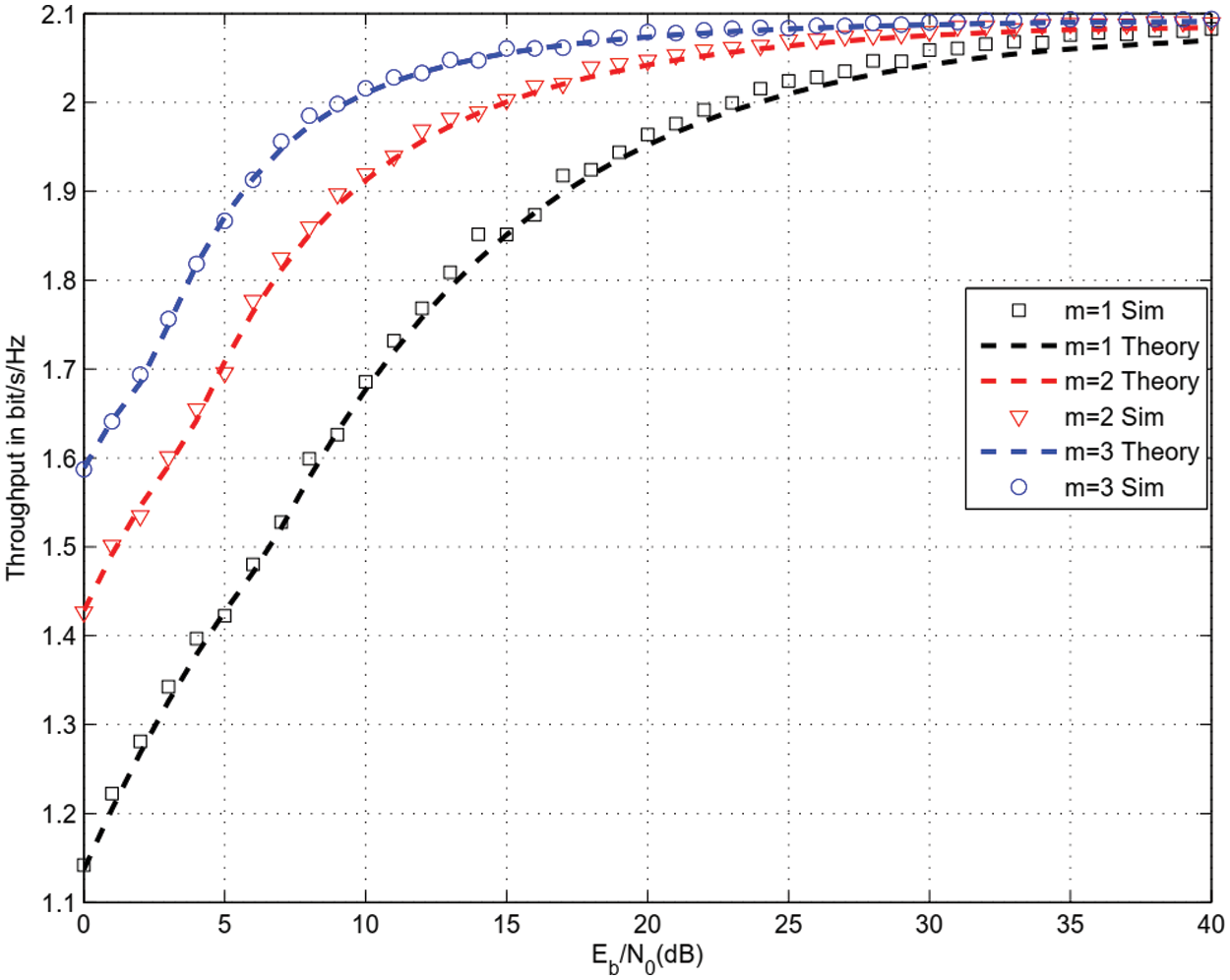
Figure 9: Effects of fading figure m on throughput for 16 QAM modulation
Figs. 10 and 11 depict the throughput for 8 Phase Shift Keying (8-PSK) and 32 Amplitude Shift Keying (ASK) modulations. There is a single IRS with M = 8 reflectors. Optimal harvesting and sensing durations offers the largest throughput for all modulations studied.
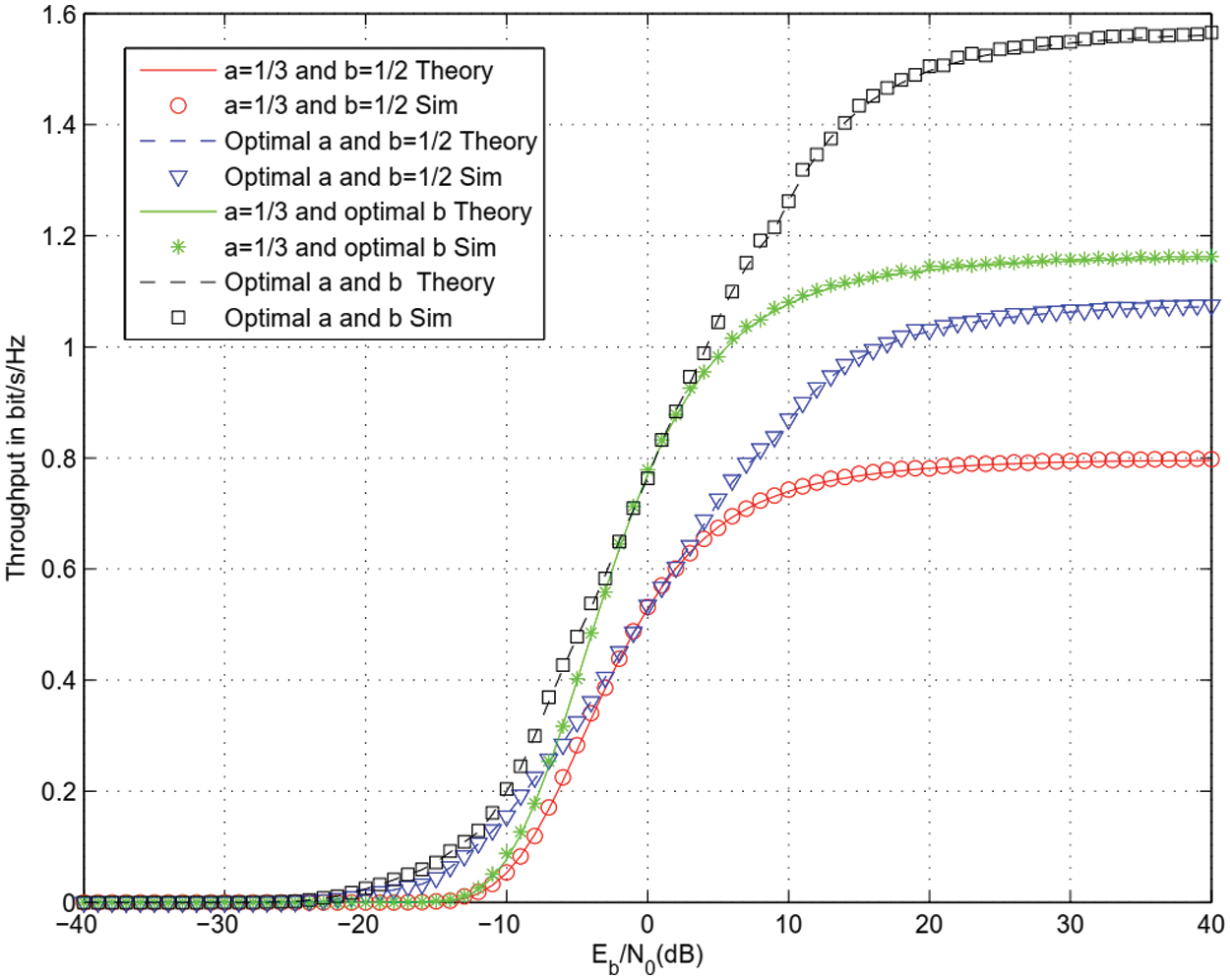
Figure 10: Throughput for 8 PSK modulation and M = 8
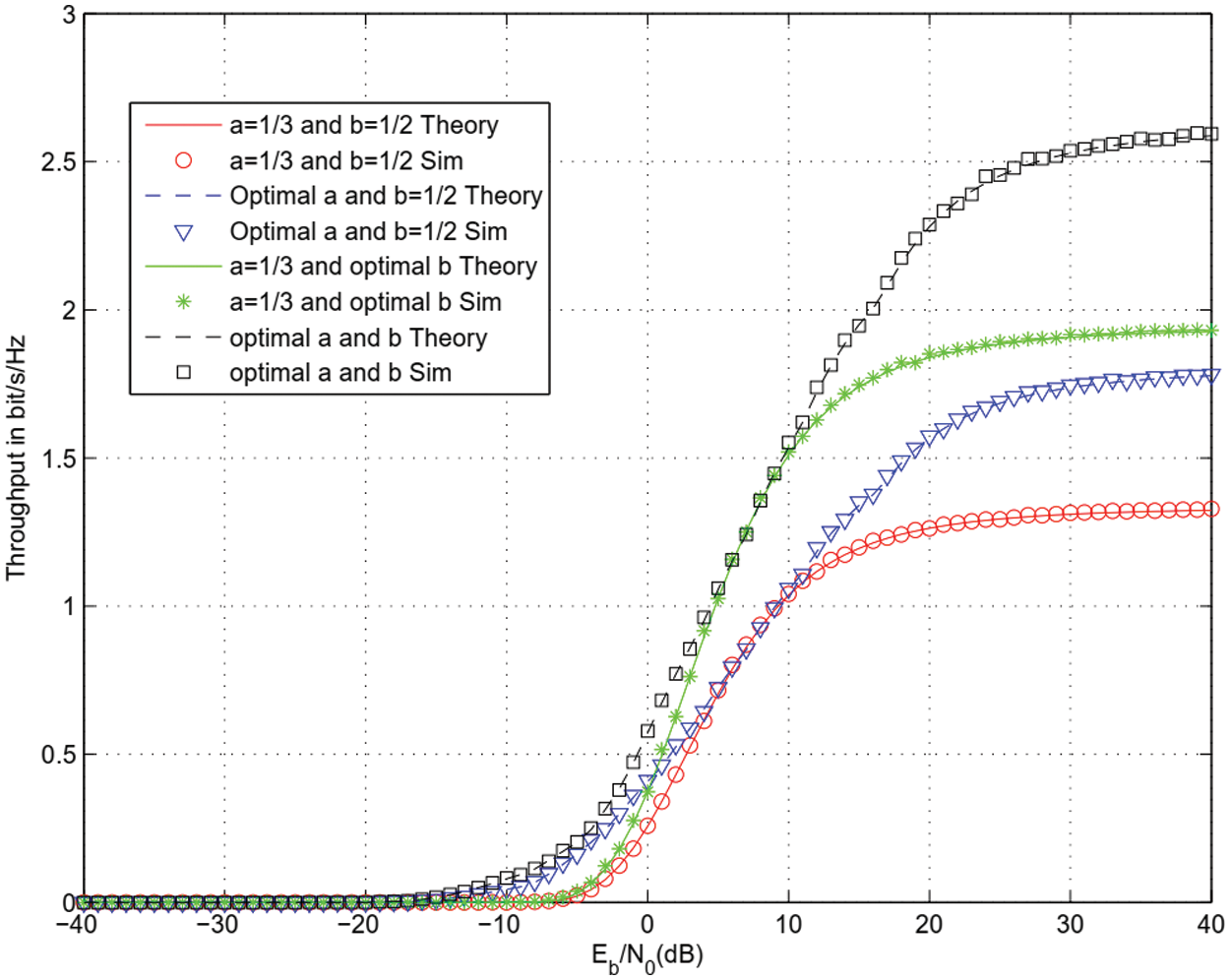
Figure 11: Throughput for 32 ASK modulation and M = 8
Fig. 12 depicts the energy efficiency vs. the throughput. The energy efficiency is defined as the throughput in bit/s/Hz divided by the spent energy in J. It is observed that the proposed optimal harvesting and sensing durations offers the largest energy efficiency. The maximum of energy efficiency is 260 Mbit/s/Hz/J when harvesting and sensing durations are optimized while the maximum is 80 Mbit/s/Hz/J when harvesting and sensing durations are not optimized.
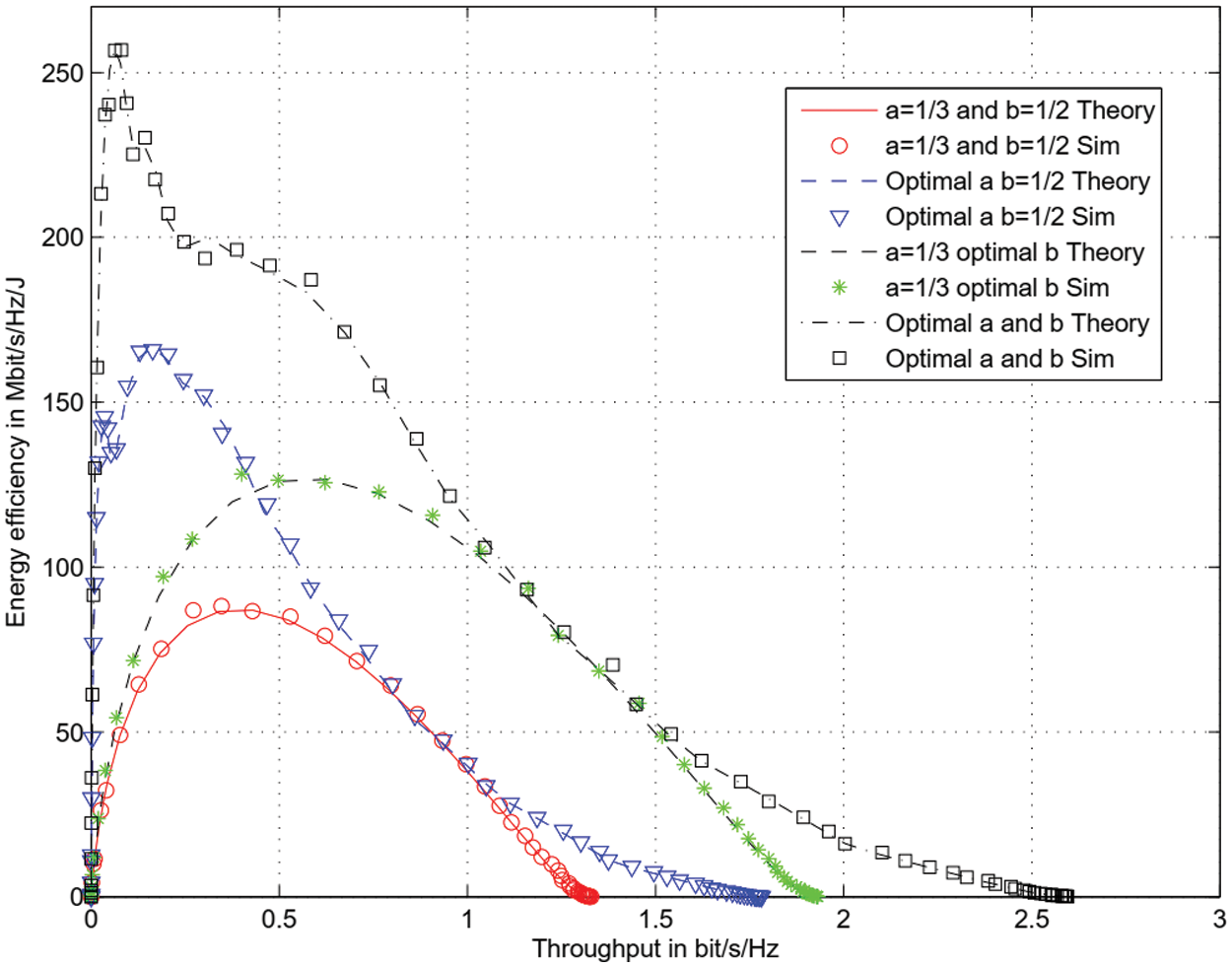
Figure 12: Energy efficiency for 32 ASK modulation and M = 8
Figs. 13–16 show packet waiting time and total delay in the presence and absence or IRS. Packet arrival rate is 0.01 and frame duration 1 ms. At SNR per bit equal to 0 dB, packet waiting time is 0.9 ms when there is no IRS and 0.5 ms when there is an IRS with M = 8 reflector. At SNR per bit equal to 0 dB, total transmission delay is 54 ms when there is no IRS and 1.5 ms when there is an IRS with M = 8 reflectors and optimized harvesting and sensing durations.
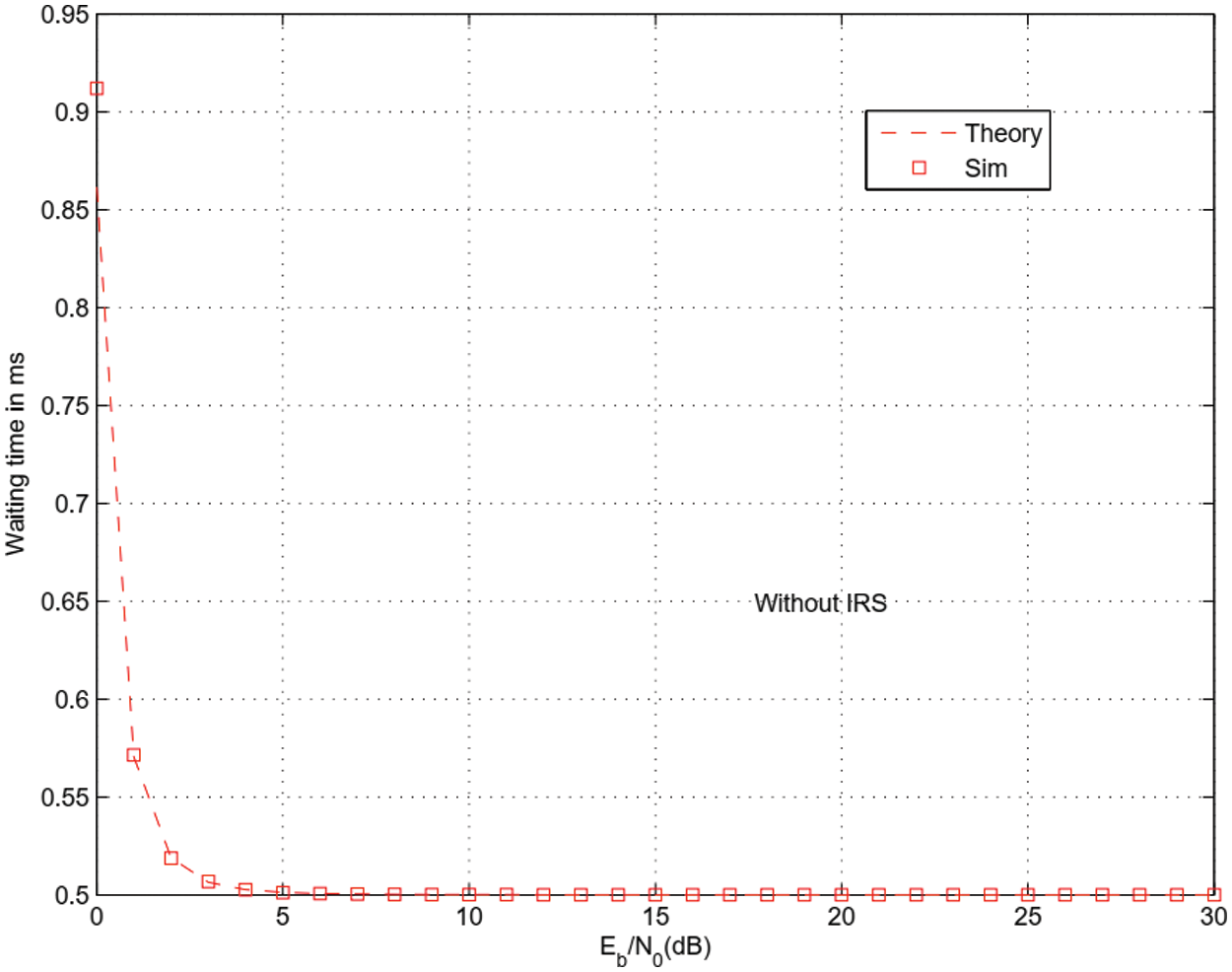
Figure 13: Packet’s waiting time without IRS
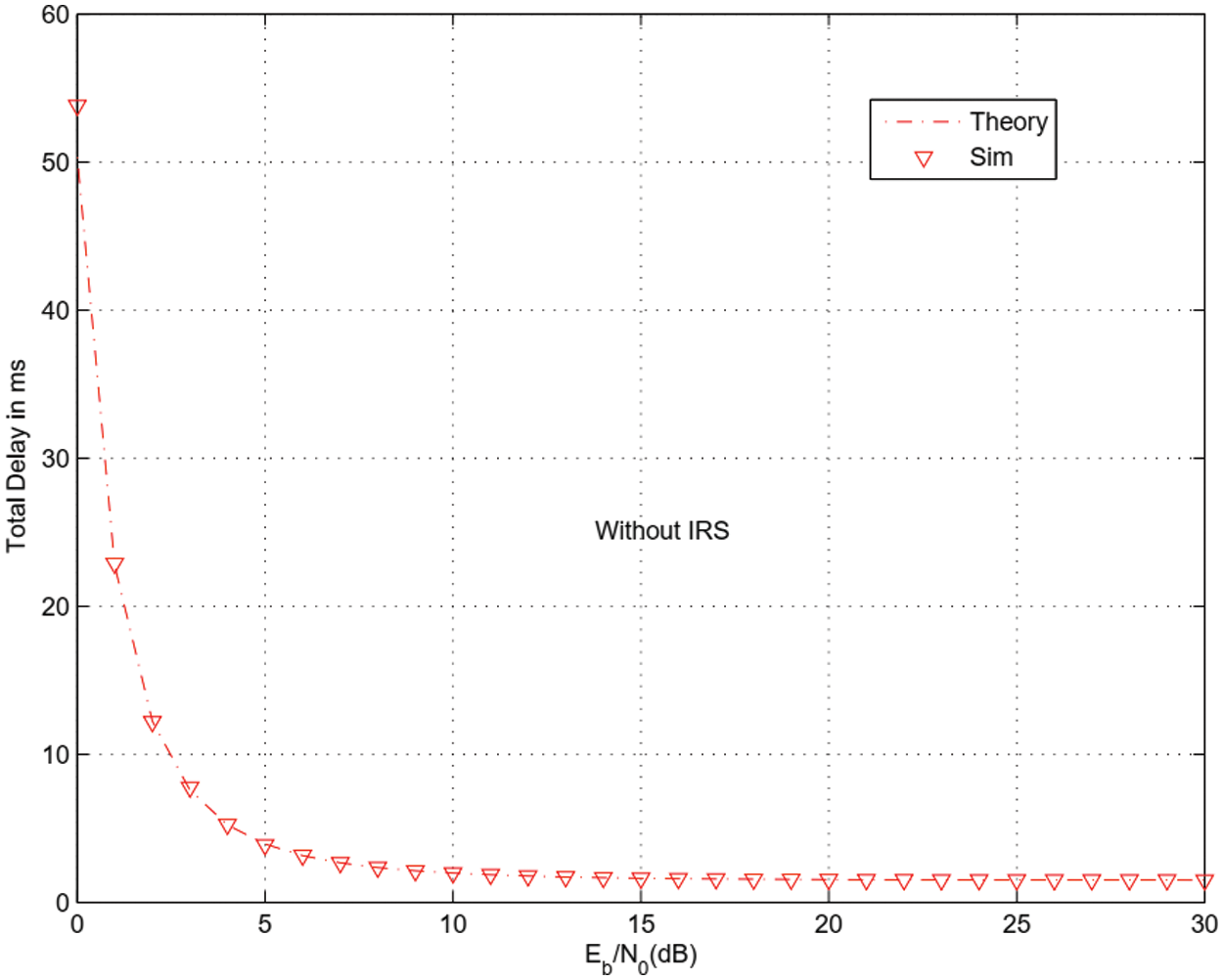
Figure 14: Total delay without IRS
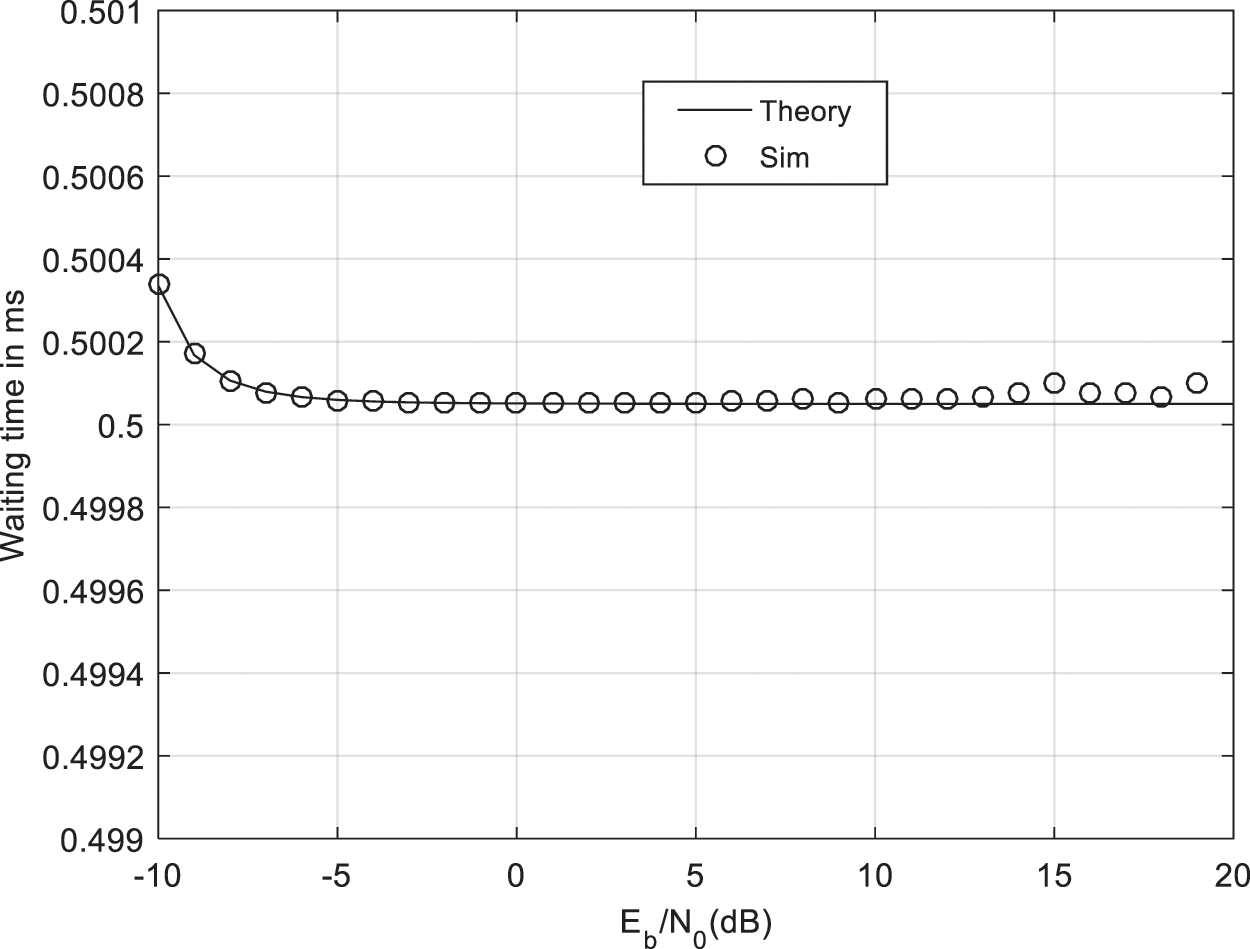
Figure 15: Waiting time with IRS and M = 8 reflectors
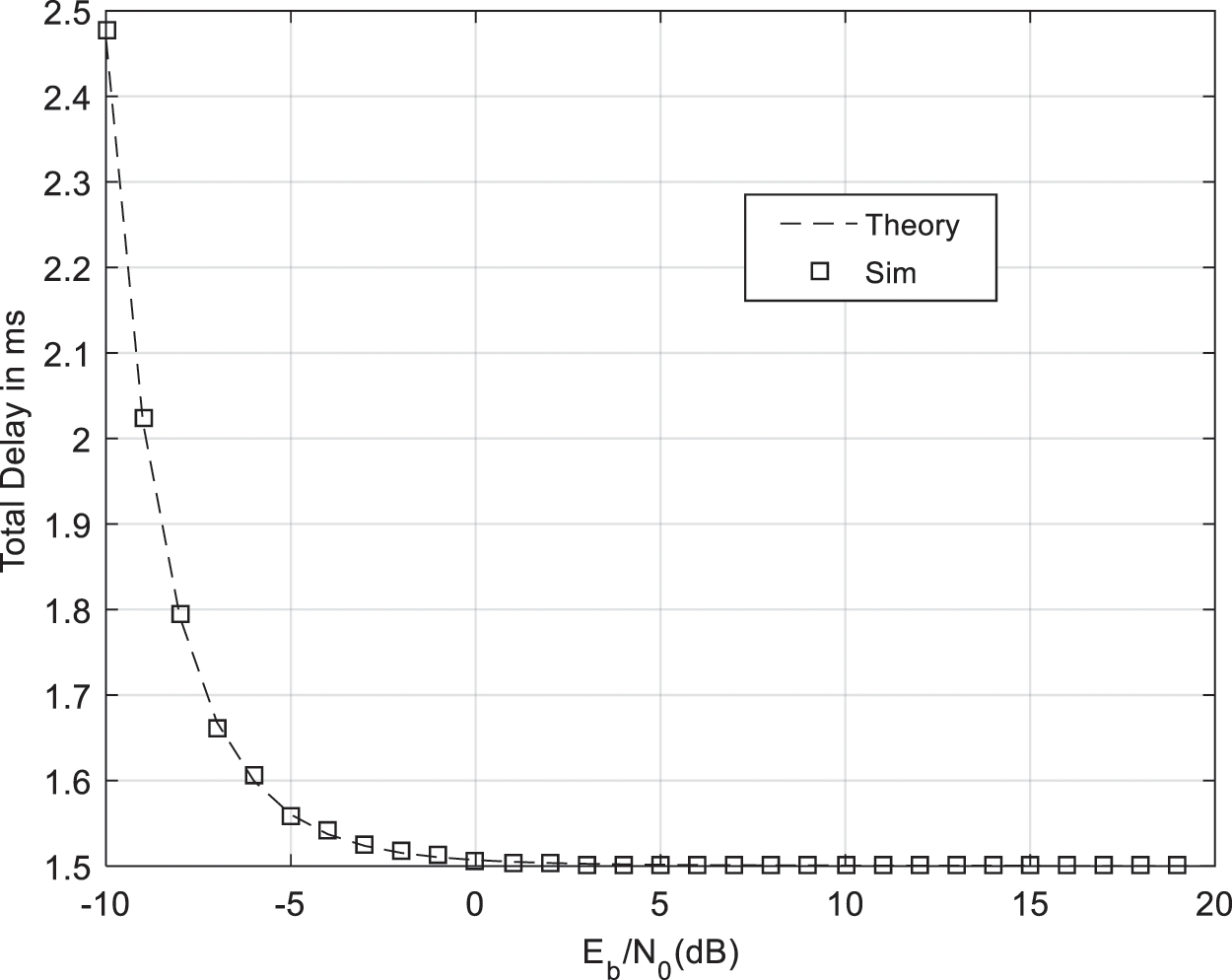
Figure 16: Total delay with IRS and M = 8 reflectors
In this paper, we optimized harvesting and sensing duration for CRN using Intelligent Reflecting Surfaces (IRS). SS performs spectrum sensing to detect primary activity. When primary source activity is not detected, SS sends data to Secondary Destination SD where all reflected signals on IRS are in phase at SD. We observed 14, 20, 26, 32, 38, 44, 50 dB enhancement in throughput using M = 8, 16, 32, 64, 128, 256, 512 reflectors with respect to CRN without IRS [20]. We also suggested to add a second IRS between A and SS to increase the harvested energy. The use of 2 IRS with M1 = M2 = 8 reflectors offers 18 dB gain (respectively 32 dB) gain with respect to a single IRS with M2 = 8 reflectors (respectively without IRS [20]). The use of 2 IRS with M1 = 16 reflectors in the first IRS and M2 = 8 reflectors in the second IRS offers 28 dB gain (respectively 42 dB) gain with respect to a single IRS with M2 = 8 reflectors (respectively without IRS [20]). As a perspective, we can optimize harvesting and sensing durations for CRN using Non Orthogonal Multiple Access (NOMA). As a perspective, we can increase the harvested energy using beamforming when the secondary source has multiple transmit antennas.
Funding Statement: The author received no specific funding for this study.
Conflicts of Interest: The author declares that he has no conflicts of interest to report regarding the present study.
1. E. Basar, M. Renzo, J. Rosny, M. Debbah, M. S. Alouini et al., “Wireless communications through reconfigurable intelligent surfaces,” IEEE Access, vol. 7, no. 2, pp. 116753–116773, 2019. [Google Scholar]
2. H. Zhang, B. Di, L. Song and Z. Han, “Reconfigurable intelligent surfaces assisted communications with limited phase shifts: How many phase shifts are enough?,” IEEE Transactions on Vehicular Technology, vol. 69, no. 4, pp. 4498–4502, 2020. [Google Scholar]
3. M. Renzo, “6G wireless: Wireless networks empowered by reconfigurable intelligent surfaces,” in 25th Asia-Pacific Conf. on Communications, Ho Chi Minh City, Vietnam, vol. 1, no. 1, pp. 12–13, 2019. [Google Scholar]
4. E. Basar, “Reconfigurable intelligent surface-based index modulation: A new beyond MIMO paradigm for 6G,” IEEE Transactions on Communications, vol. 68, no. 5, pp. 3187–3196, 2020. [Google Scholar]
5. Q. Wu and R. Zhang, “Towards smart and reconfigurable environment: Intelligent reflecting surface aided wireless network,” IEEE Communications Magazine, vol. 58, no. 1, pp. 106–112, 2020. [Google Scholar]
6. C. Huang, A. Zappone, G. Alexandropoulos, M. Debbah and C. Yuen, “Reconfigurable intelligent surfaces for energy efficiency in wireless communication,” IEEE Transactions on Wireless Communications, vol. 18, no. 8, pp. 4157–4170, 2019. [Google Scholar]
7. G. C. Alexandropoulos and E. Vlachos, “A hardware architecture for reconfigurable intelligent surfaces with minimal active elements for explicit channel estimation,” in 2020 IEEE Int. Conf. on Acoustics, Speech and Signal Processing, Barcelona, Spain, vol. 1, no. 1, pp. 9175–9179, 2020. [Google Scholar]
8. H. Guo, Y. Liang, J. Chen and E. Larsson, “Weighted sum-rate maximization for reconfigurable intelligent surface aided wireless networks,” IEEE Transactions on Wireless Communications, vol. 19, no. 5, pp. 3064–3076, 2020. [Google Scholar]
9. V. Thirumavalavan and T. Jayaraman, “BER analysis of reconfigurable intelligent surface assisted downlink power domain NOMA system,” in 2020 Int. Conf. on Communication Systems and Networks, Bangalore, India, vol. 1, no. 2, pp. 519–522, 2020. [Google Scholar]
10. C. Pradhan, A. Li, L. Song, B. Vucetic and Y. Li, “Hybrid precoding design for reconfigurable intelligent surface aided mmwave communication systems,” IEEE Wireless Communications Letters, vol. 9, no. 7, pp. 1041–1045, 2020. [Google Scholar]
11. K. Ying, Z. Gao, S. Lyu, Y. Wu, H. Wang et al., “GMD-Based hybrid beamforming for large reconfigurable intelligent surface assisted millimeter-wave massive MIMO,” IEEE Access, vol. 8, no. 2, pp. 19530–19539, 2020. [Google Scholar]
12. L. Yang, W. Guo and I. Ansari, “Mixed dual-hop FSO-RF communication systems through reconfigurable intelligent surface,” IEEE Communications Letters, vol. 24, no. 7, pp. 1558–1562, 2020. [Google Scholar]
13. B. Di, H. Zhang, L. Li, L. Song, Y. Li et al., “Practical hybrid beamforming with finite-resolution phase shifters for reconfigurable intelligent surface based multi-user communications,” IEEE Transactions on Vehicular Technology, vol. 69, no. 4, pp. 4565–4570, 2020. [Google Scholar]
14. Q. Nadeem, A. Kammoun, A. Chaaban, M. Debbah and M. Alouini, “Asymptotic max-min SINR analysis of reconfigurable intelligent surface assisted MISO systems,” IEEE Transactions on Wireless Communications, vol. 19, no. 12, pp. 7748–7764, 2020. [Google Scholar]
15. W. Zhao, G. Wang, S. Atapattu, T. Tsiftsis and C. Tellambura, “Is backscatter link stronger than direct link in reconfigurable intelligent surface-assisted system?,” IEEE Communications Letters, vol. 24, no. 6, pp. 1342–1346, 2020. [Google Scholar]
16. S. Li, B. Duo, X. Yuan, Y. Liang and M. Renzo, “Reconfigurable intelligent surface assisted UAV communication: Joint trajectory design and passive beamforming,” IEEE Wireless Communications Letters, vol. 9, no. 5, pp. 716–720, 2020. [Google Scholar]
17. L. Dai, B. Wang, M. Wang, X. Yang, J. Tan et al., “Reconfigurable intelligent surface-based wireless communications: Antenna design, prototyping, and experimental results,” IEEE Access, vol. 8, no. 3, pp. 45913–45923, 2020. [Google Scholar]
18. S. Hua and Y. Shi, “Reconfigurable intelligent surface for green edge inference in machine learning,” in IEEE Global Communication Conf. Workshops, Waikoloa, HI, USA, vol. 2, no. 3, pp. 10–15, 2019. [Google Scholar]
19. C. Huang, G. Alexandropoulos, C. Yuen and M. Debbah, “Indoor signal focusing with deep learning designed reconfigurable intelligent surfaces,” in IEEE 20th Int. Workshop on Signal Processing Advances in Wireless Communications, Cannes France, vol. 3, no. 4, pp. 11–14, 2019. [Google Scholar]
20. R. Alhamad and H. Boujemaa, “Optimal harvesting and sensing durations for cognitive radio networks,” Signal Image Video Processing, vol. 14, no. 7, pp. 1397–1404, 2020. [Google Scholar]
21. Y. Alsaba, S. K. A. Rahim and C. Y. Leow, “Beamforming in wireless energy harvesting communications systems: A survey,” IEEE Communications Surveys & Tutorial, vol. 20, no. 2, SECOND QUARTER, pp. 1329, 2018. [Google Scholar]
22. Y. Alsaba, C. Y. Leow and S. K. A. Rahim, “Full-duplex cooperative non-orthogonal multiple access with beamforming and energy harvesting,” IEEE Access, vol. 6, pp. 19726–19738, 2018. [Google Scholar]
23. M. Najafi, V. Jamali, P. D. Diamantoulakis, G. Karagiannidis and R. Schobert, “Non-orthogonal multiple access for FSO backhauling,” in IEEE Wireless Communications and Networking Conf., vol. 1, no. 1, pp. 21–24, Barcelona, 2018. [Google Scholar]
24. W. Wells, R. Anderson and J. Cell, “The distribution of the product of two central or non-central chi-square variates,” The Annals of Mathematical Statistics, vol. 33, no. 3, pp. 1016–1020, 1962. [Google Scholar]
25. X. Burr, A. Wei, J. Ben and D. Grace, “A general upper bound to evaluate packet error rate over quasi-static fading channels,” IEEE Transactions on Wireless Communications, vol. 10, no. 5, pp. 1373–1377, 2011. [Google Scholar]
26. J. Proakis, Digital Communications. 5th ed, vol. 1. USA: Mac Graw-Hill, 2007. [Google Scholar]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |