DOI:10.32604/csse.2022.024695

| Computer Systems Science & Engineering DOI:10.32604/csse.2022.024695 |  |
| Article |
A Novel Optimizer in Deep Neural Network for Diabetic Retinopathy Classification
1Department of Computer Science and Engineering, Velammal Institute of Technology, Chennai, 601204, Tamilnadu, India
2Department of Computer Science and Engineering, Saveetha Engineering College, Chennai, 602105, Tamilnadu, India
*Corresponding Author: Pranamita Nanda. Email: pranamitananda.cse@velammalitech.edu.in
Received: 27 October 2021; Accepted: 10 December 2021
Abstract: In severe cases, diabetic retinopathy can lead to blindness. For decades, automatic classification of diabetic retinopathy images has been a challenge. Medical image processing has benefited from advances in deep learning systems. To enhance the accuracy of image classification driven by Convolutional Neural Network (CNN), balanced dataset is generated by data augmentation method followed by an optimized algorithm. Deep neural networks (DNN) are frequently optimized using gradient (GD) based techniques. Vanishing gradient is the main drawback of GD algorithms. In this paper, we suggest an innovative algorithm, to solve the above problem, Hypergradient Descent learning rate based Quasi hyperbolic (HDQH) gradient descent to optimize the weights and biases. The algorithms only use first order gradients, which reduces computation time and storage space requirements. The algorithms do not require more tuning of the learning rates as the learning rate tunes itself by means of gradients. We present empirical evaluation of our algorithm on two public retinal image datasets such as Messidor and DDR by using Resnet18 and Inception V3 architectures. The findings of the experiment show that the efficiency and accuracy of our algorithm outperforms the other cutting-edge algorithms. HDQHAdam shows the highest accuracy of 97.5 on Resnet18 and 95.7 on Inception V3 models respectively.
Keywords: CNN; diabetic retinopathy; data augmentation; gradient descent; deep learning; optimization
Diabetic retinopathy (DR) is the most common complication of diabetes. It is the major cause of permanent blindness in people in their working years [1]. Inflammation and retinal neurodegeneration, in addition to microvascular alterations, may contribute to diabetic retinal damage in the early stages of DR. DR affects about 100 million people worldwide and is expected to become a growing burden, with estimates showing that DR-related visual impairment and blindness increased by 64 percent and 27 percent, respectively, between 1990 and 2010 [2]. Mild Non-Proliferative Diabetic Retinopathy (NPDR), moderate NPDR, severe NPDR, and PDR are the four phases of DR in terms of severity. Therefore, an early diagnosis of DR saves the patient from any complications or vision loss. The different classes of DR images are given in Fig. 1.
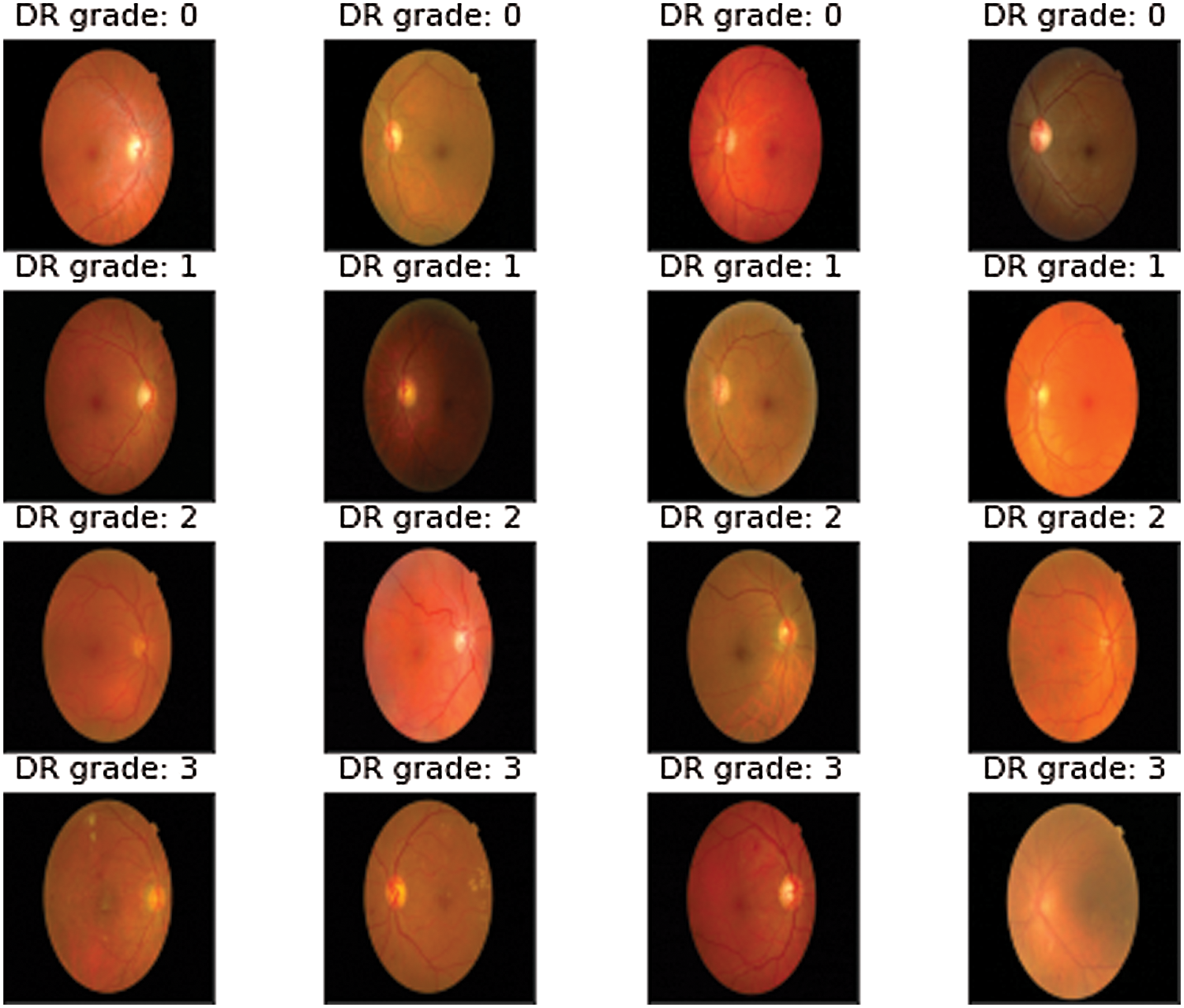
Figure 1: Sample retinal images of different DR grades from Messidor dataset
The image processing steps to classify DR images using CNN have been proven a powerful tool such as a Deep learning-based system for predicting DR development. Complex features like aneurysms, exudate and hemorrhages on the retina were used for classification by using CNN architecture with data augmentation [3]. The CNN model designed by [4] prevents the gradient diffusion, and improves accuracy of detection. Through the categorization of retinal pictures, multi-scale shallow CNNs with performance integration were employed to diagnose Diabetic Retinopathy early [5]. Large data sets are not available in the medical image analysis application sector. A data-space approach to the problem of data scarcity is Data augmentations, which covers the techniques that enlarge and improve the amount and quality of the training dataset to make them enable to be fed to any Deep learning algorithm [6]. Data augmentations avoids the problem of overfitting as well as imbalanced data set by extracting more information from the original data set. Datasets that are unbalanced can be dangerous as they bias the system towards majority class prediction [7].
Along with the increasing complexity of deep neural network architectures, selecting a proper optimizer for training a DNN is very important to get a fast convergence speed with generalized solution. Gradient based optimizers have been used extensively in DNNs to optimize the loss function and improve the performance. Most widely used adaptive optimization algorithms include Adam and Adaptive Gradient [8] often lead to worse generalization performance than gradient descent algorithms. For bridging the gap between adaptive algorithms and gradient descent algorithms methods like Quasi Hyperbolic Adam (QHAdam) have been proposed. There is no agreement on which optimization strategies should be used for DNNs. As a result, the user’s decision on the best optimization algorithm is based on their preferences.
We suggest a novel optimized convolutional neural network with hypergradient learning rate for better accuracy. Before applying the input to the proposed optimized CNN the input images are preprocessed. The images are resized and then data augmentation is done.
Several techniques have been proposed in the last few years for the purpose of early detection of Diabetic retinopathy diseases using DNN. In this section, we discuss the related researches in DR image classification, data augmentations and the optimization methods in deep neural network.
2.1 Diabetic Retinopathy Classification
For diabetic retinopathy detection, [9] proposed an integrated lesion identification system with Laplacian of Gaussian and Matched Filters, as well as post-processing techniques. To uncover the latent structure of microaneurysm data, a constrained Principal Component Analysis is used. The hybrid graph convolutional network for retinal image categorization [10] eliminates the requirement for time-consuming annotation. The cross-disease attention network [11] jointly grades DR and Diabetic macular edema as well as their internal interaction. Category attention block and Global attention block [12] explored the region-wise features for each DR grade and also detailed small lesion information. By adopting a hierarchical structure, the casual association between DR related variables and DR severity levels was incorporated [13].
A heuristic-based approach for creating Neovessel like structures [14] was designed which relied on the common location and shape of the structures. Reference [15] Constructed the data mixture model by mixing up the training samples and their labels. The image augmentation algorithms had been based on geometric transformations, kernel filters, color space augmentations, combining different images, feature space augmentations, adversarial training, neural style transfer, meta learning and generative adversarial networks. Random image cropping and patching was proposed by [16], in which four images were randomly cropped and patched to generate a new training image.
2.3 Optimizations in Deep Learning
The most frequently encountered optimization in deep learning is Stochastic Gradient Descent (SGD), which attains small generalization error [17]. Adam which is a hybrid optimization approach combining the benefits of two popular optimization methods: Adaptive Gradient (AdaGrad) for sparse gradients and Root Mean Squared Propagation (RMSProp) for non-stationary targets. AdaGrad adjusts the learning rate according to the parameters, with bigger updates for infrequent features and lower updates for those that occur frequently. Adaptive gradient method with data-dependent bound (AdaDB) [18] has a data-dependent learning rate bound that is restricted between a lower bound which is constant and changing upper bound. Quasi-Hyperbolic Momentum (QHM) algorithm is an alteration of momentum SGD and QHAdam a variation to Adam. The convergence rate was improved by dynamically updating the learning rate by using the gradient with respect to the learning rate. Normalized direction preserving Adam had been designed for improving generalization performance by enabling more precise direction and step size control while updating weights and biases. The optimization algorithm which is based on gradient and hyperplane called as Evolved Gradient direction Optimizer (EVGO) avoids vanishing gradient problem in optimizations [19].
The proposed system is developed in three phases which include preprocessing of images, data augmentation and optimizing the CNN by using the proposed algorithm and classifying the dataset. The flow diagram of the entire process is given in Fig. 2.
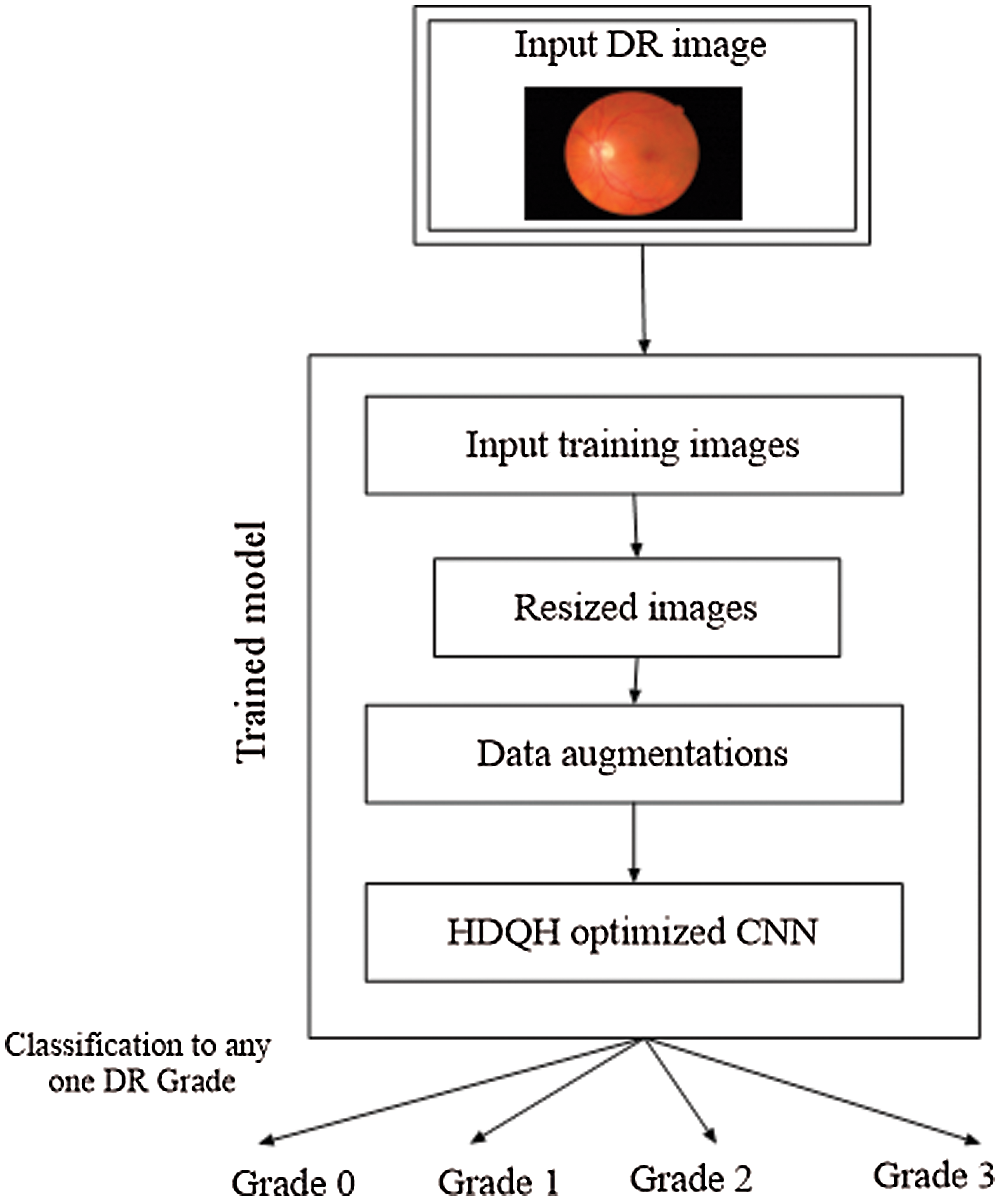
Figure 2: Flow diagram of the process
The main motivation of this article is on increasing the performance and reducing the dependency on hyperparameter tuning. Learning rate is the important hyperparameter in DNN and it needs to be tuned always. The following recursive formula (1) describes the most frequent gradient descent method:
where, θ represents the DNN parameters such as weights and biases,
In this part, we introduce a novel optimization technique that outperforms previous cutting-edge methods by a large margin. Hypergradient descent learning rate combined with Quasi Hyperbolic momentum (QHM) and also with Quasi Hyperbolic Adam (QHAdam) to produce better optimized algorithm called as Hypergradient descent based Quasi Hyperbolic Momentum (HDQHM) or Hypergradient descent based Quasi Hyperbolic Adam (HDQHAdam). Both of the algorithms are motivated by introducing the learning rate as a vector instead of a scalar. The update rule for the learning rate μ is derived by using its value in the previous step. For this the partial derivative of
The update rule for the learning rate μ is
The update rule of HDQHM is given by
The adaptive gradient descent algorithm (Adam) is given by Eq. (5).
QHAdam, which is an improvement to Adam provides superior optimization. Both QHM and QHAdam lacks the learning rate adaptation technique. Hence in this article, both the algorithms are empowered with hypergradient learning rate. The update rule for HDQHAdam is
The hypergradient descent of learning rate is
The parameters φ1, φ2 ∈ [0, 1), v1,v2 ∈ R and


The efficiency of our suggested method is evaluated on retinal image classification task. Here we have used publicly available retinal image datasets called MESSIDOR dataset [20] and DDR dataset [21].
a) MESSIDOR dataset
A color video was used to collect the data from three ophthalmologic departments. At 1440∗960, 2240∗1488, or 2304∗1536 pixels, images were taken with 8 bits per color pane. Out of total 1200 images in the dataset, 800 were captured with pupil dilation and 400 were captured without dilation. Each image is provided with 2 diagnosis retinopathy grade and risk of macular edema. Here the dataset is used for retinopathy grade classification. Totally there are four classes of images 0, 1, 2 and 3. From the 1200 images, 75% of the dataset is used for training and validation and 25% of the data is used for testing. Out of the training and validation dataset, 75% is used for training and 25% used for validation.
b) DDR dataset
DDR dataset contains 13673 images, out of which 6835 are training images, 2733 validation images and 4105 test images. Totally there are 6 classes of images such as 0, 1, 2, 3, 4 and ungradable. The ungradable DR is not taken into consideration in our experiment because of their poor quality. Therefore, our task is a five class classification task with 6320 training, 2503 validation and 3759 test images.
The input images are preprocessed to remove the unwanted noise by using Gaussian filter. Removing Gaussian noise includes smoothing inside the regions of an image without losing sharpness of the edges [22], which is shown in Fig. 3.

Figure 3: Image denoising applied on Messidor dataset
The images are of different size and color as those have come from different sources. As the Fig. 4 shows, the number of images in training dataset in each class varies. Hence to avoid this imbalanced dataset, data augmentation is applied. Data augmentation is also applied to avoid overfitting. There are two types of augmentations: Data wrapping augmentations and Oversampling augmentations. The labels of the images are preserved only in Data wrapping augmentations. It incorporates augmentations like random erasing, neural style transfer, geometric and color changes, and adversarial training. Artificial instances are manufactured and added to the training set in oversampling augmentations.

Figure 4: DR grade class counts of Messidor dataset
Here we have applied Data wrapping augmentations to avoid imbalanced data as well as varying size and color of the images. The Fig. 5 shows sample images before and after applying augmentations.

Figure 5: Original vs. augmented images
The experiments are performed by using Pytorch framework on both Messidor and DDR datasets. The performance of our proposed algorithm is shown by using ResNet18 and InceptionV3. For both the models we have used a batch size of 32. The hypergradient learning rate β is set to 0.005. The ResNet18 and InceptionV3 models were trained for 100 epochs. After each epoch the models were evaluated on the test set. Tab. 1 gives the best accuracy on the test set for the different optimizers on Messidor dataset. Similarly, Figs. 6 and 7 show the performance prediction on the test set for different epochs while running on Resnet18 and Inception V3 models with ReLu activation function. The training and validation loss of HDQHM and HDQHAdam are given in Figs. 8 and 9 respectively, which shows the convergence of the proposed algorithms.

Figure 6: Prediction performance on test set (Resnet18) (Messidor dataset)

Figure 7: Prediction performance on test set on Inceptionv3 (Messidor dataset)

Figure 8: Train loss and validation loss for HDQHM on Resnet18 (Messidor dataset)

Figure 9: Train loss and validation loss for HDQHAdam on Resnet18 (Messidor dataset)

It’s worth noting that the proposed HDQH algorithms produce substantially better outcomes than other methods. HDQHAdam shows the highest accuracy of 97.5 and 95.7 on Resnet18 and Inception V3 models respectively. The algorithm HDQHM also performs better than the other algorithms with a test accuracy of 89.9 and 84.5 on Resnet18 and Inception V3 respectively.
Similar experiments are carried out on DDR dataset. The prediction performance on test set is shown in Fig. 10. The comparison of proposed algorithm with the existing algorithms for DDR dataset is given in Tab. 2.

Figure 10: Prediction performance on test set (Resnet18) for DDR dataset

In this article, we present a better optimization algorithm for classification of DR fundus images. The algorithm has updates for the learning rate itself based on the previous gradients instead of taking a constant learning rate. The Quasi hyperbolic algorithms are improved by introducing an update rule for the learning rate. Experimental results on Messidor and DDR datasets shows that HDQHM and HDQHAdam outpaces the other cutting-edge algorithms Adam, SGD etc. in terms of their test accuracy and loss value in classifying the DR images.
Funding Statement: The authors received no specific funding for this study.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
1. W. Wang and A. C. Y. Lo, “Diabetic retinopathy: Pathophysiology and treatments,” International Journal of Molecular Sciences, vol. 19, no. 6, pp. 1816–1830, 2018. [Google Scholar]
2. J. L. Leasher, R. R. Bourne, S. R. Flaxman, J. B. Jonas, J. Keeffe et al., “Global estimates on the number of people blind or visually impaired by diabetic retinopathy: A meta-analysis from 1990 to 2010,” Diabetes Care, vol. 39, no. 9, pp. 1643–1649, 2016. [Google Scholar]
3. H. Pratt, F. Coenen, D. M. Broadbent, S. P. Harding and Y. Zheng, “Convolutional neural networks for diabetic retinopathy,” Procedia Computer Science, vol. 90, no. 1, pp. 200–205, 2016. [Google Scholar]
4. Y. Sun, “The neural network of one-dimensional convolution-an example of the diagnosis of diabetic retinopath,” IEEE Access, vol. 7, no. 1, pp. 69657–69666, 2019. [Google Scholar]
5. W. Chen, B. Yang, J. Li and J. Wang, “An approach to detecting diabetic retinopathy based on integrated shallow convolutional neural networks,” IEEE Access, vol. 8, no. 1, pp. 178552–178562, 2020. [Google Scholar]
6. C. Shorten and T. M. Khoshgoftaar, “A survey on image data augmentation for deep learning,” Journl of Big Data, vol. 6, no. 60, pp. 1–48, 2019. [Google Scholar]
7. M. Buda, A. Maki and M. A. Mazurowski, “A systematic study of the class imbalance problem in convolutional neural networks,” Neural Networks, vol. 106, no. 1, pp. 249–259, 2018. [Google Scholar]
8. J. Duchi, E. Hazan and Y. Singer, “Adaptive subgradient methods for online learning and stochastic optimization,” Journal of Machine Learning Research, vol. 12, no. 61, pp. 2121–2159, 2011. [Google Scholar]
9. L. Qiao, Y. Zhu and H. Zhou, “Diabetic retinopathy detection using prognosis of microaneurysm and early diagnosis system for non-proliferative diabetic retinopathy based on deep learning algorithms,” IEEE Access, vol. 8, no. 1, pp. 104292–104302, 2020. [Google Scholar]
10. G. Zhang, J. Pan, Z. Zhang, H. Zhang, C. Xing et al., “Hybrid graph convolutional network for semi-supervised retinal image classification,” IEEE Access, vol. 9, no. 1, pp. 35778–35789, 2021. [Google Scholar]
11. X. Li, X. Hu, L. Yu, L. Zhu, C. W. Fu et al., “CANet: Cross-disease attention network for joint diabetic retinopathy and diabetic macular edema grading,” IEEE Transctions on Medical Imaging, vol. 39, no. 5, pp. 1483–1493, 2019. [Google Scholar]
12. A. He, T. Li, N. Li, K. Wang and H. Fu, “CABNet: Category attention block for imbalanced diabetic retinopathy grading,” IEEE Transactions on Medical Imaging, vol. 40, no. 1, pp. 143–153, 2021. [Google Scholar]
13. J. Wang, Y. Bai and B. Xia, “Simultaneous diagnosis of deverity and features of diabetic retinopathy in fundus photography using deep learning,” IEEE Journal of Biomedical and Health Informatics, vol. 24, no. 12, pp. 3397–3407, 2020. [Google Scholar]
14. T. Araújo, G. Aresta, L. Mendonça, S. Penas, C. Maia et al., “Data augmentation for improving proliferative diabetic retinopathy detection in eye fundus images,” IEEE ACCESS, vol. 8, no. 1, pp. 182462–182474, 2020. [Google Scholar]
15. C. Wang, L. Zhang, W. Wei and Y. Zhang, “Hyperspectral image classification with data augmentation and classifier fusion,” IEEE Geoscience and Remote Sensing Letters, vol. 17, no. 8, pp. 1420–1424, 2020. [Google Scholar]
16. R. Takahashi, T. Matsubara and K. Uehara, “Data augmentation using random image cropping and patching for deep CNNs,” IEEE Transactions on Circuits and Systems for Video Technology, vol. 30, no. 9, pp. 2917–2931, 2020. [Google Scholar]
17. M. Hardt, B. Recht and Y. Singer, “Train faster, generalize better: Stability of stochastic gradient descent,” in Proc. of the Thirty Third Int. Conf. on Int. Conf. on Machine Learning (ICML 16), New York City, NY, USA, vol. 48, no. 1, pp. 1225–1234, 2016. [Google Scholar]
18. L. Yang and D. Cai, “AdaDB: An adaptive gradient method with data-dependent bound,” Neurocomputing, vol. 419, no. 1, pp. 183–189, 2021. [Google Scholar]
19. I. Karabayir, O. Akbilgic and N. Tas, “A novel learning algorithm to optimize deep neural networks: Evolved gradient direction optimizer (EVGO),” IEEE Transactions on Neural Networks and Learning Systems, vol. 32, no. 2, pp. 685–694, 2020. [Google Scholar]
20. E. Decencière, X. Zhang, G. Cazuguel, B. Lay, B. Cochener et al., “Feedback on a publicly distributed image database: The messidor database,” Image Analysis & Stereology, vol. 33, no. 3, pp. 231–234, 2014. [Google Scholar]
21. T. Li, Y. Gao, K. Wang, S. Guo, H. Liu et al., “Diagnostic assessment of deep learning algorithms for diabetic retinopathy screening,” Information Sciences, vol. 501, no. 1, pp. 511–522, 2019. [Google Scholar]
22. R. Garnett, T. Huegerich, C. Chui and W. He, “A universal noise removal algorithm with an impulse detector,” IEEE Transactions on Image Processing, vol. 14, no. 11, pp. 1747–1754, 2005. [Google Scholar]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |