Computer Systems Science & Engineering DOI:10.32604/csse.2023.026046
Article

A Steganography Based on Optimal Multi-Threshold Block Labeling

Shuying Xu1, Chin-Chen Chang1 and Ji-Hwei Horng2,*

1Department of Information Engineering and Computer Science, Feng Chia University, Taichung, 407, Taiwan
2Department of Electronic Engineering, National Quemoy University, Kinmen, 892, Taiwan
*Corresponding Author: Ji-Hwei Horng. Email: horng@email.nqu.edu.tw
Received: 14 December 2021; Accepted: 25 January 2022

Abstract: Hiding secret data in digital images is one of the major research fields in information security. Recently, reversible data hiding in encrypted images has attracted extensive attention due to the emergence of cloud services. This paper proposes a novel reversible data hiding method in encrypted images based on an optimal multi-threshold block labeling technique (OMTBL-RDHEI). In our scheme, the content owner encrypts the cover image with block permutation, pixel permutation, and stream cipher, which preserve the in-block correlation of pixel values. After uploading to the cloud service, the data hider applies the prediction error rearrangement (PER), the optimal threshold selection (OTS), and the multi-threshold labeling (MTL) methods to obtain a compressed version of the encrypted image and embed secret data into the vacated room. The receiver can extract the secret, restore the cover image, or do both according to his/her granted authority. The proposed MTL labels blocks of the encrypted image with a list of threshold values which is optimized with OTS based on the features of the current image. Experimental results show that labeling image blocks with the optimized threshold list can efficiently enlarge the amount of vacated room and thus improve the embedding capacity of an encrypted cover image. Security level of the proposed scheme is analyzed and the embedding capacity is compared with state-of-the-art schemes. Both are concluded with satisfactory performance.

Keywords: Reversible data hiding; encryption image; prediction error compression; multi-threshold block labeling

1  Introduction

With the rapid development of digital multimedia, the information security of multimedia becomes a tremendous challenge. As a fundamental form of multimedia, the information security of digital images has drawn much attention. Therefore, many technologies have been developed to increase image security, such as watermark [1,2], secret sharing [3,4], and data hiding [5–26]. As a crucial branch of the image security field, the data hiding technology hides secret information in a cover image while preserving its visual appearance. Thus, it is widely applied in copyright protection, integrity verification, and access control. During the last decades, there are multitudinous data hiding methods have been proposed, which are classified into reversible data hiding (RDH) [5–7] and irreversible data hiding [8–10]. The irreversible data hiding causes permanent damage to the carrier image, which is not applicable to the applications that cannot tolerate any distortion, such as law forensics and medical images. On the contrary, reversible data hiding recovers the carrier image without any distortion after extracting the secret data, so it has wider use. According to the different operation domains of the RDH, which can be further divided into four classes: the spatial domain-based RDH [3–8], the frequency domain-based RDH [11–13], the compressed domain based-RDH [14,15], and the encryption domain-based RDH [16–27] approaches.

Since the continuous improvement of hardware computing efficiency and network transmission speed, the images from the sensitive applications such as secure remote sensing and medical services are uploaded to the cloud. The cloud service provider embeds additional data to the unloaded images. However, consider the confidentiality of those images, some privacy protection techniques must take to prevent the exposure of the original image. Thus, the reversible data hiding in encrypted images (RDHEI) aroused heated discussions in the security field. In this application context, the RDHEI method consists of three participants, the content owner, the data hider, and the recipient. On the content owner’s side, the cover image is encrypted before uploading to the cloud. On the data hider’s side, the secret data is embedded into the obtained encrypted image. On the recipient’s side, extracts the secret data, restores the cover image, or executes both activities according to his/her specific permissions. Based on the order of image encryption and vacating room for data embedding, the existing RDHEI schemes are classified into two types, reserving room before encryption (RRBE) [16–20] and vacating room after encryption (VRAE) [21–27].

In the RRBE methods, the content owner reserves room for data embedding before image encryption. In 2013, the first RRBE based scheme is proposed by Ma et al. [16], which divides the cover image into smooth regions and complex regions according to the texture characteristics. After that, the LSBs in the smooth regions are replaced with the secret data in the data hiding side. In 2019, Chen et al. [17] proposed a novel RDHEI method that compresses the bit-planes of the original image by bit-plane rearrangement (BPR) and the extended run-length coding (ERLC) to vacate the room for data embedding. In [18], based on adaptive prediction-error labeling (APL), a high-capacity and secure RDHEI method is proposed by Wu et al., which takes advantage of the Laplacian-like distribution of prediction errors to increase the reserved room before encryption. In Xu et al. method [19], an RDHEI method based on vector quantization (VQ) prediction and parametric binary tree labeling (PBTL) is proposed, which adaptively sets the labeling parameters to maximize the vacating room for data embedding. Later, based on the hierarchical quad-tree coding and bit-plane compression, Liu et al. [20] proposed an RDHEI method which minimizes image file size and improves the embedding capacity. Although the relationship between adjacent pixels is fully utilized to embed secret data in the RRBE methods, the exposed label bits may leak information of the cover image.

In the VRAE methods, the content owner encrypts the cover image without any preprocessing. In short, the spare room is vacated on the data hider side, which is more secure for the carrier image. In 2014, a VRAE based RDHEI method is proposed by Wu et al. [21], pixels inside the image are classified into the qualified set or the forbidden set like a chessboard, where the qualified pixels are exploits for data embedding while the forbidden pixels are not. In 2015, based on the idea of cross-division and additive homomorphism, Li et al. [22] propose an RDHEI method, which has better embedding performance. In Xiao et al. method [23], a separable RDHEI method based on pixel value ordering (PVO) is proposed, where the additive homomorphism ensures that the performance of PVO in encrypted domain is close to that in plain domain. In 2018, Qin et al. [24] proposed an adaptive reversible data hiding scheme, which classifies encrypted blocks into two sets corresponding to smooth and complex regions and embeds more bits into the smooth blocks. Based on the most significant bit (MSB) prediction, Puteaux et al. [25] proposed an RDHEI method, which exploits the MSB of pixels in the available block for data hiding, while the MSB of pixels in the unavailable block are adopted to record the prediction error location. Later, according to the characteristics of the image block, the method proposed by Bhardwaj et al. [26] further divides blocks into sub-image blocks to increase the embedding capacity. In 2020, Chen [27] proposed a novel method, which is based on the compression of pixel differences, where the prediction errors are recorded by the Huffman coding.

We propose an efficient reversible data hiding scheme in encrypted images based on an optimal multi-threshold block labeling, which provides a high capacity for data embedding. Our contributions can be summarized as follow.

(1)   The in-block pixel correlation is preserved, while image privacy is protected by encryption.

(2)   The PER, OTS, and MTL methods are exploited to compress the bit-planes of prediction error and thus maximize embedding capacity. Experimental results show that the embedding capacity of our scheme outperforms state-of-the-art schemes.

(3)   Data extraction and image recovery processes are separable. The authorities can be granted with different keys.

The remaining parts of the scheme are organized as follows. The details of our scheme are introduced in Section 2. Section 3 expounds on the experimental results. In the end, the conclusions of this scheme are obtained in Section 4.

2  The Proposed Method

In this section, the details of the proposed scheme are described as follows. Fig. 1 shows the framework of the scheme. In our scheme, there are three participants, namely content owner, data hider, and receiver. The content owner encrypts the original image by block permutation, pixel permutation, and block-based stream cipher processes. Then, the data hider exploits the prediction error rearrangement (PER), the optimal parametric selection (OPS), and the multi-threshold labeling (MTL) to vacate the room and embeds the secret data into the spare space. The receiver extracts the secret data using the data hiding key, restores the original image using the image encryption key, or do both according to its authority.

Figure 1: The framework of the proposed OMTBL-RDHEI scheme

2.1 Encrypted Image Generating

To protect the privacy of image content, the content owner encrypts the original image before transmitting it. The image encryption of the proposed scheme consists of block permutation, pixel permutation, and block-wise stream cipher procedures. Thus, the image encryption key that used in the encryption operation contains three sub-keys {KeB,KeP,KeR} .

Consider that the original image Io sized M × N is divided into k non-overlapping 2 × 2 blocks B1,B2,…,Bk at first. The total number k of image blocks can be computed by Eq. (1). Note that, there are residual pixels when M or N is odd. In practical applications, the residual pixels are merely encrypted with the standard stream cipher at the pixel level, while the regular blocks are applied to embed secret data after the encryption procedures.

k=⌊M2⌋×⌊N2⌋ (1)

After partitioning into blocks, these blocks are scrambled using the block permutation key KeB , where KeB is a random-ordered sequence of distinct integers from 1 to k. The blocks B1,B2,…,Bk are permuted into B1′,B2′,…,Bk′ according to the sequence KeB . To reinforce the effect of permutation encryption, pixels p1,1(t),p1,2(t),p2,1(t),p2,2(t) inside the block Bt′(1≤t≤k) are scrambled into p′1,1(t),p′1,2(t),p′2,1(t),p′2,2(t) using the pixel permutation key KeP , which is a random-ordered sequence of distinct integers from 1 to 2 × 2.

An image encryption result is shown in Fig. 2, where Fig. 2a is a standard grayscale test image of ‘Lena’; Figs. 2b–2d are the encryption results of difference phases. The histograms of Figs. 2a–2d are given in Figs. 2e–2h. As shown in Fig. 2c, the image content has been greatly damaged after the block permutation and pixel permutation. However, the histogram is still preserved as shown in Fig. 2g, which exposes the information of image. To improve security, the block-based stream cipher is conducted to further encrypt the image. For each permutated image block Bt′(1≤t≤k), decompose the pixels pi,j(t) inside the block into the eight binary bits as Eq. (2), where (i, j) represent the coordinates of pixels in the block and γ indicates the γ-th bit of each pixel.

pi,jγ,(t)=⌊pi,j(t)28−γ⌋mod2,γ=1,2,…,8 (2)

Figure 2: The example of the image encryption for ‘Lena’. (a) Original ‘Lena’ image, (b) ‘Lena’ image after blocks permutation, (c) ‘Lena’ image after blocks permutation and pixels permutation, (d) final encrypted image, (e-h) histograms of (a-d)

Next, the block encryption key KeR is applied to generate a pseudo random matrix R with the size of ⌊M2⌋×⌊N2⌋ to perform the block-based stream cipher operation by Eq. (3), where Rγ,(t) denotes the γ-th bit of the t-th number in the pseudo random matrix. Note that the pixels of a block are encrypted with the same 8-bit pseudo random number. In the end, the encrypted bits are assembled into decimal form using Eq. (4) to obtain the encrypted image E.

ei,jγ,(t)=pi,jγ,(t)⊕Rγ,(t) (3)

ei,j(t)=∑γ=18⁡ei,jγ,(t)×28−γ (4)

In practical applications, the block permutation stream, the pixel permutation stream and the block-wise stream cipher is generated by an encryption key Ke. After the encryption procedures, the content owner uploads the encrypted image E to the cloud.

The image content is completely unreadable for the encrypted image shown in Fig. 2d, and the pixel-values are uniformly distributed as shown in Fig. 2h. This is, after our encryption process, the privacy of the cover image is well guaranteed. More details of security analysis are demonstrated in Section 3.1.

2.2 Prediction Error Rearrangement

After receiving the encrypted image E, the data hider decomposes it into 2 × 2 blocks B1′,B2′,…,Bk′. For each image block Bt′(1≤t≤k), the pixel located at (i, j) = (1, 1) is assigned as the reference pixel, while the others are treated as replaceable pixels and predicted by the reference pixel as shown in Fig. 3. Then, the prediction errors are calculated as Eq. (5). where (i,j)∈{(1,2),(2,1),(2,2)}. Then, we collect the prediction errors {d1,2(1),d2,1(1),d2,2(1),d1,2(2),…,d1,2(k),d2,1(k),d2,2(k)} from blocks in the encrypted image. Fig. 4 shows the collected prediction errors of image ‘Lena’ and ‘Airplane’, which are highly concentrated in the vicinity of 0. In theory, the range of di,j(t) is within [−255, 255]. However, since the correlation inside each block is retained by the encryption method above, the actual pixel values in a block are very close to each other. Inspired by concentrated distribution of the prediction errors, we reasonably infer that there is much redundant space inside the prediction errors that can be vacated for data embedding.

di,j(t)=ei,j(t)−e1,1(t) (5)

Figure 3: The reference pixel and reconfigurable pixels

Figure 4: The histogram of the prediction errors. (a) Lena (b) Airplane

To compress the redundant space, we decompose the absolute prediction errors |di,j(t)| into the prediction error stream di,jl,(t),l=1,2,…,8 using Eq. (6). In addition, the signs of prediction errors di,j(t) are recorded by Eq. (7). Recall that the prediction errors di,j(t) are distributed in the vicinity of 0. Thus, the first few bits of each prediction error stream di,jl,(t) are dominated by zeros. For most conventional data compression methods, a long stream of repeated zeros or ones is easier to compress. A prediction error rearrangement (PER) method is proposed to rearrange the prediction error stream di,jl,(t) of each block. In the proposed PER method, the bit order l is applied as the primary key and the spatial indices (i, j) are applied as the secondary key to sort the prediction error stream of each block. Specifically, the prediction error streams are rearranged into d1,21,(t),d2,11,(t),d2,21,(t),d1,22,(t),…,d1,28,(t),d2,18,(t),d2,28,(t). After performing PER, the concatenated streams for all blocks are generated, each stream Sc(t) starts with a long repeating zero. An illustrative example is given in Fig. 5, where the concatenated stream Sc(t) is generated, in the order indicated by the arrow lines, as “000 000 000 000 000 001 111 010”.

di,jl,(t)=⌊|di,j(t)|2l−1⌋,l=1,2,…,8 (6)

si,j(t)={0,di,j(t)≤01,di,j(t)>0 (7)

Figure 5: The example of PER

To verify the effect of our PER method, the number n0(t) of repeated zeros in the concatenated stream Sc(t) of images ‘Lena’ and ‘Airplane’ are counted as shown in Fig. 6. It can be seen that the peak bin of n0(t) is located at a high value for both cases. There is a considerable amount of redundant space to be vacated.

Figure 6: The histogram for no. (a) Lena (b) Airplane

2.3 Multi-Threshold Labeling

In this processing phase, we propose a novel block labeling method, called multi-threshold labeling (MTL), which vacates room from the encrypted image E using multiple thresholds {θ0,θ1,…,θ2δ−1} , where 1 ≤ δ ≤ 4. In our MTL method, the leading zeros of each block are abbreviated by using an appropriate threshold θj,0≤j≤2δ−1 selected from the given list.

For an encrypted image E, the number of leading zeros n0(t) for the concatenated stream Sc(t) of all blocks are counted first. Then, the given threshold list is applied to classify and label each block. The number of leading zeros n0(t) ranges from 0 to 24 bits. By applying the list of 2δ thresholds, we can divide this range into 2δ+1 segments. The blocks with n0(t)<θ0 are classified into non-embeddable blocks, while the blocks with n0(t) located at the remaining segments are classified as embeddable blocks and labeled with a threshold indicator for each. A floor operation ⌊⋅⌋θ is defined to assign a corresponding threshold for each block. The number n0(t)θ is the greatest threshold value θj less than or equal to n0(t) . Based on the floor operation, the leading zeros of a block can be abbreviated by a threshold indicator followed by the remaining zeros.

In the Fig. 7, we take two encrypted image blocks from “Lena” image to illustrate the procedure of the proposed MTL, where the applied threshold list is {θ0,θ1,…,θ3}={5,10,15,20}.

Figure 7: Illustration of the proposed MTL method

For the block in Fig. 7a, the replaceable pixels are predicted using the reference pixel, and the prediction errors are obtained by Eq. (5). Then, use Eqs. (6) and (7) to obtain the prediction error streams and the sign bits. Next, the prediction error rearrangement (PER) is applied to rearrange the prediction error streams into a concatenated stream Sc(t)=“000000000000000001111010” . Since the n0(t)=18 for the current block, it is embeddable n0(t)>θ0=5 and its corresponding threshold is ⌊n0(t)⌋θ=θ2=15 . Therefore, this block is labeled with a concatenation of eight bits for reference pixel value, one flag bit ‘1’, two indicator bits ‘10’, three sign bits ‘100’, and the remaining segment of Sc(t) as illustrated in the figure. Note that the vacated room is left unchanged.

For the block in Fig. 7b, the replaceable pixel values are predicted and rearranged as demonstrated in the figure. Since n0(t)=4<θ0 , the whole block is kept unchanged except for the replacement of a non-embeddable flag bit. The substituted bit is recorded into the additional information stream.

2.4 Optimal Threshold Selection

In the MTL proposed in the previous subsection, we randomly select a set of four equally spaced thresholds to label the example block. To maximize the total vacated room of a given image, the number of indicator bits and the values of thresholds can be adjusted according to the image features. An optimal threshold selection (OTS) algorithm is proposed to optimize the threshold settings.

As shown in Algorithm 1, we fully try the possible length of indicator bits δ from 1 to 4 bits and evaluate the vacated room for all (242δ) possible combinations of threshold values. According to our MTL method, a block of n0(t) leading zeros is abbreviated by ⌊θj=n0(t)⌋θ in δ bits. Thus, the vacated room can be calculated by EC = θj − 1 − 3 − δ bits, where 1 is the length of flag bit and 3 is the length of sign bits. A block of leading zeros less than θ0 is not embeddable and an additional bit replaced by the flag bit should be recorded. Its effective embedding capacity is − 1 bit. The overall algorithm is summarized as follows.

After obtaining the optimal threshold list, the data hider is ready to hide secret data into the encrypted image. In order to demonstrate the data hiding procedure, Fig. 8 applies the optimal threshold list {θopt0,θopt1,⋯,θopt3}={9,12,15,18} of the image “Lena” as an example. As shown in the figure, the optimal multi-threshold labeling vacates more room than the case applying fixed threshold list in Fig. 7a. Then, the vacated room is filled with encrypted secret data stream to complete the data hiding procedure. In order to verify the superiority of the OTS, we further conducted experiments as shown in Section 3.2.

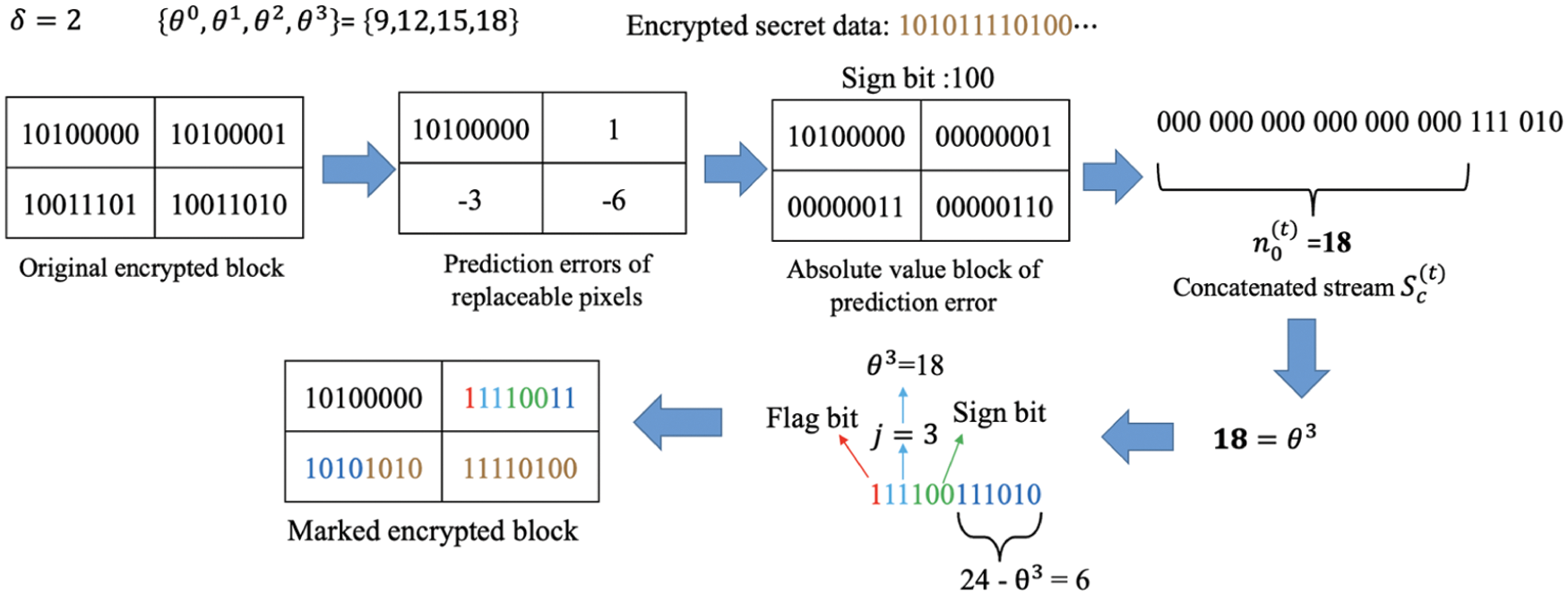
Figure 8: Illustration of the optimal multi-threshold labeling and data hiding

The optimal threshold list should be shared with the receiver to exactly decrypt image and secret data. The proposed solution is to record the required information with a fixed threshold list for a least number of leading blocks. Besides, instead of recording the complete optimal threshold list, we record the optimal parameters δopt and iopt obtained in the optimization algorithm. The complete list can be recovered with simple manipulations based on the two parameters. The least number of leading blocks which can provided (2+⌈ log2(242δopt) ⌉) bits of vacated room are labeled with the fixed threshold list. After recording the optimal parameters, the remaining blocks are treated as regular blocks and processed with the optimal multi-threshold labeling method. The whole procedure is summarized as Algorithm 2.

2.5 Data Extraction and Image Recovery

A recipient of the marked encrypted image can extract the secret data, restore the cover image, or do both according to his/her authorization. The data extraction and image recovery are in the reverse order of the encryption and embedding procedure.

When the recipient holds the data-hiding key Kh, he/she can accurately extract the secret data. The procedure is shown as the Algorithm 3. In our method, the marked encrypted image E^ is decomposed into blocks Bt′′ at first. In addition, we assume that the recipient knows the fixed parametric δfix and ifix in advance, which is used to provide (2+⌈ log2(242δopt) ⌉) bits of vacated room for recording δopt and iopt in the fix block.

When the recipient holds the encryption key Ke, he/she can losslessly restore the original image. The procedure is shown as the Algorithm 4. Note that, the data extraction is exploited to obtain the δopt and iopt in fix blocks and Da in regular blocks. In addition, the reverse order of the PER means that the bits of Sc(t) are sequentially recorded back to the replaceable pixels inside the block. As shown in Fig. 9, we read the concatenated stream “000 000 000 000 000 001 111 010” and sequentially record them into replaceable pixel e1,1(t), e2,1(t), and e2,2(t) in the order as, indicated by the arrow lines, defined in the PER method.

Figure 9: The reverse order of PER

Fig. 10 shows the example of data extraction and image recovery for the marked regular image block with the optimal threshold list {θ14330, θ14331, θ14332, θi3opt} = {9, 12, 15, 18} of the ‘Lena’ image.

Figure 10: Data extraction and image recovery for marked regular encrypted block

As shown in Fig. 10a, when the recipient holds the data-hiding key Kh, he/she read the flag bit ‘1’ at first. Then, connect the bit stream of replaceable pixels into a refactor stream “111100111010101011110100”. Next, read δ = 2 indicator bits “11” and convert it into a decimal value “3”. After that, extracts the θ3−1−3−δ LSBs encrypted secret data “101011110100”. In the end, the data-hiding key Kh is exploited to decrypts the encrypted secret data.

As shown in Fig. 10b, when the recipient holds the encryption key Ke, he/she read the flag bit ‘1’ at first. Then, connect the bit stream of replaceable pixels into a refactor stream “111100111010101011110100”. Next, read δ = 2 indicator bits “11” and convert it into a decimal value “3”. After that, read the 3 sign bits “110”, the (24- θ14333 ) bits unchanged stream “111010” immediately then. Generate θ14333 repeating zeros and connect it with the (24- θij ) bits unchanged stream “111011” to obtain the concatenated stream Sc(t) “000000000000000000111011”. The inverse order of the PER method is used to recover the prediction error streams “00000001”, “00000011”, “00000110”. According to the sign bits “110”and the prediction error block, the original encrypted block is restructured. In the end, the encryption key Ke is exploited to decrypt the encrypted image.

3  Experimental Result and Discussions

To evaluate the performance of the proposed scheme, the experiments including security analysis, embedding capacity and comparison are conducted. For these experiments, we select six standard gray-scale images as test images: Airplane, F16, Lena, Peppers, Barbara, and Elaine as shown in Fig. 11. Moreover, the databases BOWS-2 [28] and BOSSbase [29] are applied to further verify the generality of the scheme.

Figure 11: The test images of the proposed scheme

3.1 Security Analysis

As shown in Fig. 2h, the pixel values in the encrypted image are even and chaotic. In order to further test the pixel distribution of the image generated in different phases, we conduct Lena as an example to present the corresponding experiment results as shown in Fig. 12.

Figure 12: Results in different phases for ‘Lena’. (a1) Original ‘Lena’ image, (b1) encrypted ‘Lena’ image, (c1) embedded encrypted ‘Lena’ image (d1) recovered ‘Lena’ image, (a2-d2) histograms of images a1-d1, (a3-d3) pixel distributions of the images a1-d1

In the Fig. 12, the original image (a1) and the recovered image (d1) are the same, which mean that the proposed scheme can recover the original image losslessly. In additional, as we can see, the pixel distribution of encrypted image and embedded encrypted image are even and chaotic that is difference from the distribution of original image. Thus, we can conclude that it is almost impossible to obtain the information of the original image from the encrypted image by statistical attack.

To further explore the security of the proposed scheme, we applied the information entropy to measure the randomness of the images in different phases. The information entropy can be obtained by Eq. (8), where s represents the gray level of image pixels, p(si) represents the relative probability of a particular gray level si in an image, and 2n represents the total number of gray levels. The theoretical maximum value of information entropy is 8, which means that the image has a high degree of randomness. The information entropy of test image in different phases are listed in Tab. 1. As we can see, the entropy of encrypted image and embedded encrypted image are almost equal to 8, which means that the proposed scheme has stronger security.

H(s)=−∑i=02n−1⁡p(si)⋅log2⁡(p(si)) (8)

3.2 Embedding Capacity

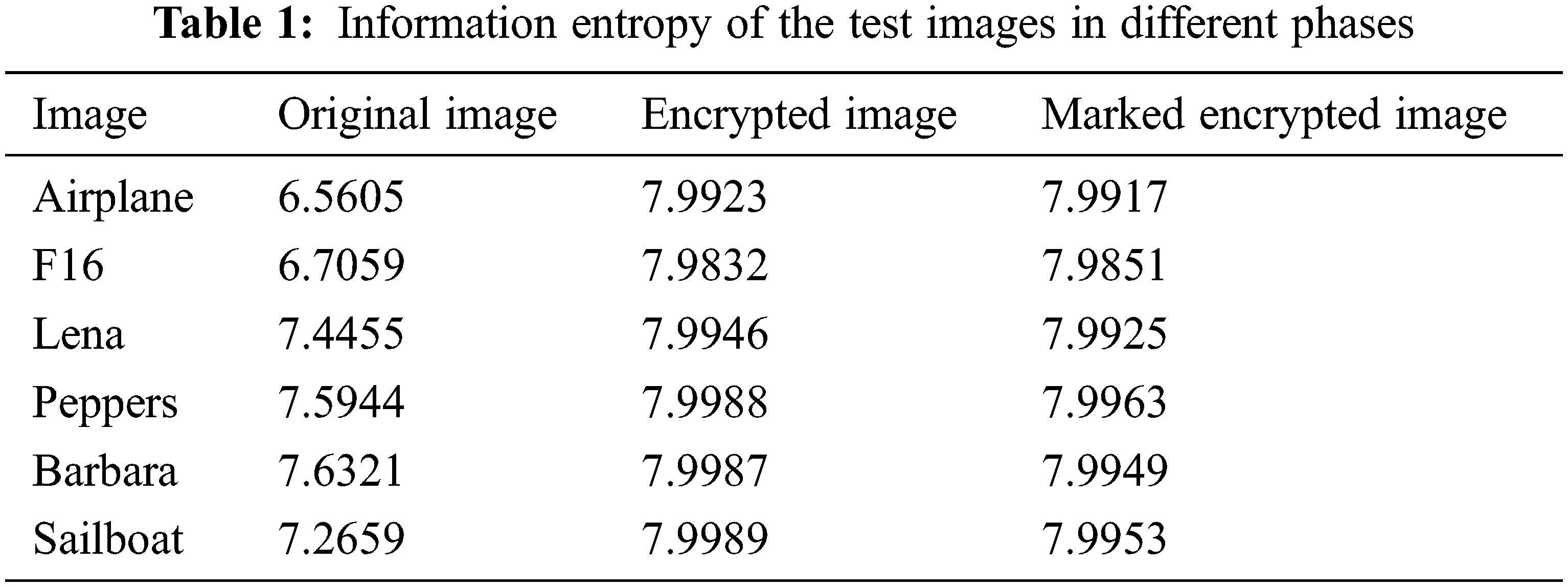
To evaluate the embedding capacity of the proposed scheme, some experiments are conducted in this section. A comparison with state-of-the-art schemes is also presented. The embedding capacity of a cover image is measured with the embedding rate Cbr in bits per pixel defined by

Cbr=N/n(I)(bpp), (9)

where N is the amount of embedded data in bits and n(I) is the number of pixels in the cover image.

We first verify the effectiveness of the OTS method. A random threshold list, a fixed equidistant threshold list, and the optimal threshold list obtained by our method are applied to the image ‘Lena’, with δ = 2 and δ = 3, the corresponding embedding rates are listed in Tab. 2. As shown in the table, the optimal threshold list obtain by our OTS method significantly outperforms the random selected and the fixed equidistant lists.

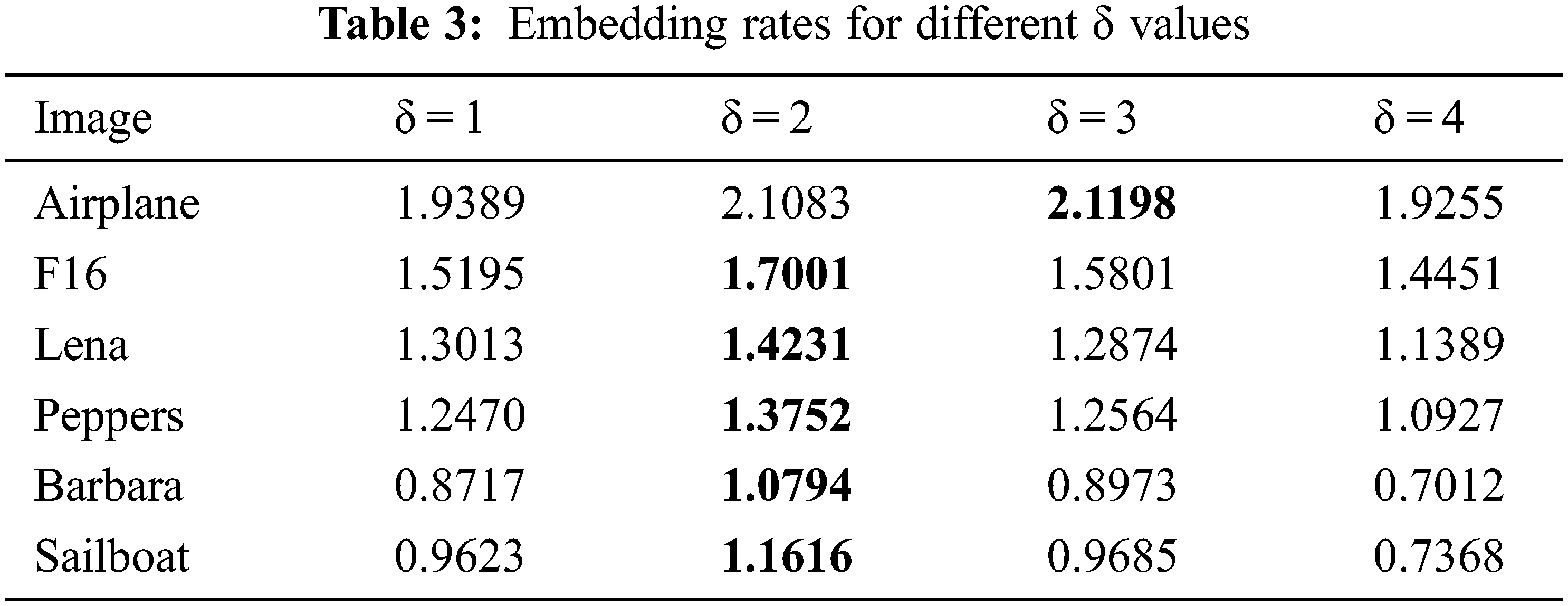
The embedding rates of the proposed scheme for different δ values are listed in Tab. 3. The embedding rate at δ = 2 is the best for most of the test images and exceeds 1 bpp for all. The only exceptional case is the image ‘Airplane’, whose best value occurs at δ = 3. An image with a smooth variation of pixel values has a larger dynamic range of prediction error. More threshold levels can improve its compression ratio of prediction error.

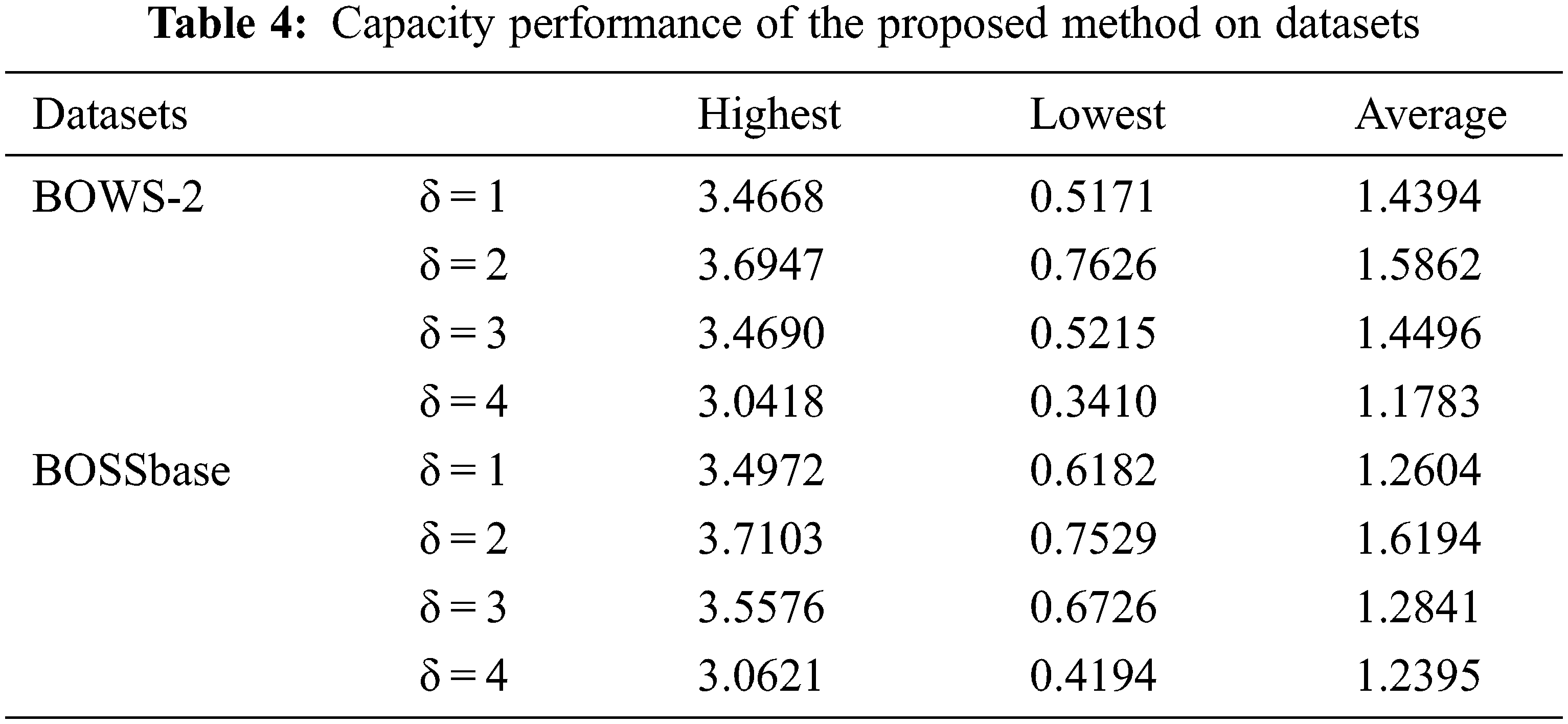
Next, to verify the generality of our scheme, the databases BOWS-2 [28] and BOSSbase [29] are applied to measure the embedding rate. Tab. 4 demonstrate the embedding capacity performance of the proposed method on the BOW-2 and BOSSbase database. Through observation, we can find that the highest embedding rate achieve 3.6947 bpp for BOWS-2 and 3.7103 bpp for BOSSbase, and the average embedding rate achieve 1.5862 bpp for BOWS-2 and 1.6194 bpp for BOSSbase when δ = 2.

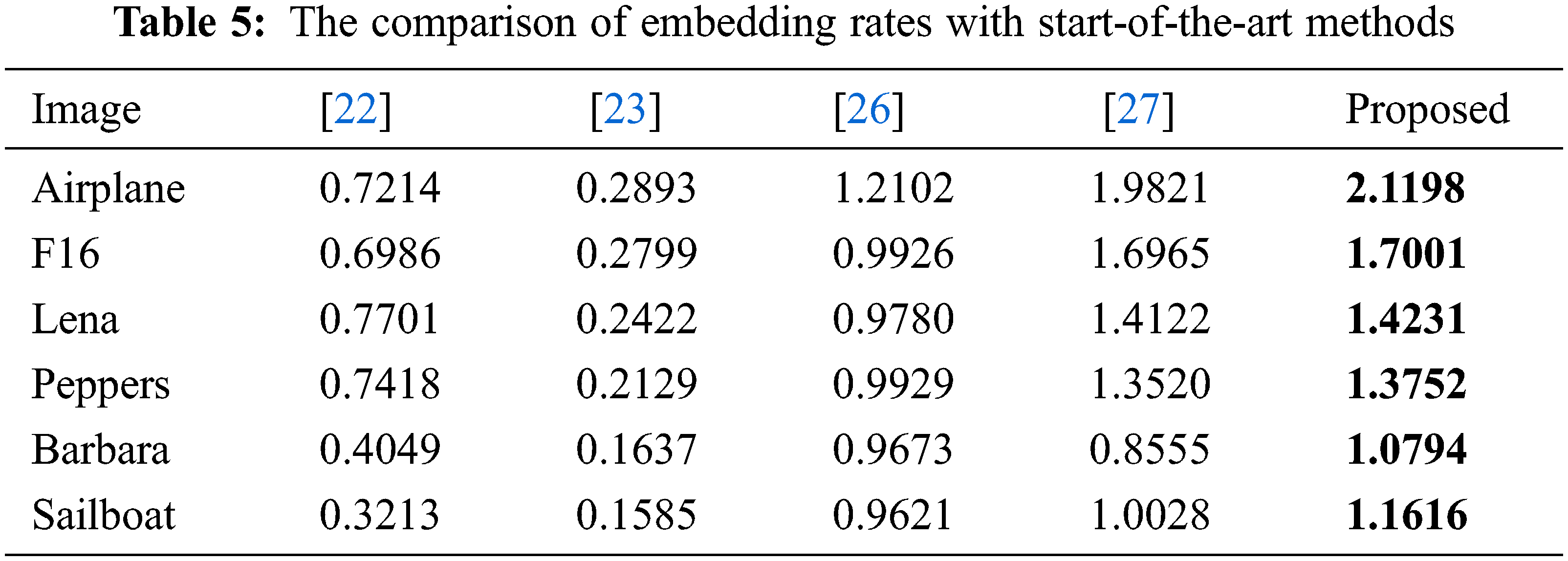
To further investigate the performance of our scheme, the proposed scheme is compared with five state-of-the-art schemes, including the Li et al. [22], the Xiao et al. [23], the Bhardwaj et al. [26], and the Chen’s [27] schemes. The comparison for the six test images is listed in Tab. 5. As shown in the table, the embedding capacity of our scheme for smooth images such as ‘Airplane’ and ‘F16’ exceeds 1.7 bpp, which is a significant improvement. In addition, the embedding capacity for complex images such as ‘Barbara’ and ‘Sailboat’ can exceed 1 bpp. A visualized bar chart corresponding to Tab. 5 is given in Fig. 13.

Figure 13: The comparison of embedding rates in bar chart

4  Conclusions

We propose a novel OMTBL-RDHEI scheme. In our scheme, the cover image is first processed by the content owner with a block-level encryption, including a block permutation, a pixel permutation, and a block-based stream cipher, which retains the in-block spatial correlation of the original image. The data hider exploits the PER method to rearrange the in-block perdition errors and obtain the concatenation streams. Then, the OPS method is applied to select the optimal threshold list. In the end, the ABL method labels all image blocks with the optimal list. The receiver extracts the embedded secret data and restores the original image without any distortion. Experiments show that the proposed scheme improves the average embedding rate to 1.5862 bpp for BOWS-2 dataset and 1.6194 bpp for BOSSbase dataset. In addition, the proposed scheme ensures a good security level. In the future, we plan to seek a more efficient image compression approach that can further increase the data embedding capacity.

Funding Statement: This research was funded by the Ministry of Science and Technology of Taiwan, Grant Number MOST 110-2221-E-507-003.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  C. -C. Chang, C. -T. Li and Y. Q. Shi, “Privacy-aware reversible watermarking in cloud computing environments,” IEEE Access, vol. 6, pp. 70720–70733, 2018. [Google Scholar]

 2.  C. Qin, P. Ji, C. -C. Chang, J. Dong and X. Sun, “Non-uniform watermark sharing based on optimal iterative BTC for image tampering recovery,” IEEE Multimedia, vol. 25, no. 3, pp. 36–48, 2018. [Google Scholar]

 3.  C. Qin, C. Jiang, Q. Mo, H. Yao and C. -C. Chang, “Reversible data hiding in encrypted image via secret sharing based on GF(p) and GF(2^8),” IEEE Transactions on Circuits and Systems for Video Technology, 2021. http://dx.doi.org/10.1109/TCSVT.2021.3091319. [Google Scholar]

 4.  C. -C. Chang and C. -T. Li, “Algebraic secret sharing using privacy homomorphisms for IoT-based healthcare systems,” Mathematical Biosciences and Engineering, vol. 16, no. 4, pp. 3367–3381, 2020. [Google Scholar]

 5.  S. Yi and Y. Zhou, “Binary-block embedding for reversible data hiding in encrypted images,” Signal Processing, vol. 133, pp. 40–51, 2017. [Google Scholar]

 6.  C. -C. Chang, “Neural reversible steganography with long short-term memory,” Security and Communication Networks, vol. 2021, pp. 14, 2021. [Google Scholar]

 7.  C. -C. Chang, “Cryptospace invertible steganography with conditional generative adversarial networks,” Security and Communication Networks, vol. 2021, pp. 14, 2021. [Google Scholar]

 8.  J. -H. Horng, S. Y. Xu, C. -C. Chang and C. -C. Chang, “An efficient data-hiding scheme based on multidimensional mini-SuDoKu,” Sensors, vol. 20, no. 9, pp. 2739, 2020. [Google Scholar]

 9.  J. -H. Horng, J. Lin, Y. J. Liu and C. -C. Chang, “3D multilayered turtle shell models for image steganography,” Computer Modeling in Engineering & Sciences, vol. 125, no. 2, pp. 879–906, 2020. [Google Scholar]

10. C. -C. Chang, Y. J. Liu and T. S. Nguyen, “A novel turtle shell-based scheme for data hiding,” in 2014 Int. Conf. on Intelligent Information Hiding and Multimedia Signal Processing, Kita Kyushu, Japan, pp. 89–93, 2014. [Google Scholar]

11. C. -Y. Yang and W. -C. Hu, “Reversible data hiding in the spatial and frequency domains,” International Journal of Image Processing, vol. 3, no. 6, pp. 373–384, 2010. [Google Scholar]

12. H. Zhang and L. T. Hu, “A data hiding scheme based on multidirectional line encoding and integer wavelet transform,” Signal Processing: Image Communication, vol. 78, pp. 331–334, 2019. [Google Scholar]

13. F. Li, Q. Mao and C. -C. Chang, “A reversible data hiding scheme based on IWT and the sudoku method,” International Journal of Network Security, vol. 18, no. 3, pp. 410–419, 2014. [Google Scholar]

14. F. J. Huang, X. C. Qu, H. J. Kim and J. W. Huang, “Reversible data hiding in JPEG images,” IEEE Transactions on Circuits Systems for Video Technology, vol. 26, no. 9, pp. 1610–1621, 2016. [Google Scholar]

15. X. Wang, C. -C. Chang and C. -C. Lin, “Adaptive reversible data hiding scheme for AMBTC compressed images,” Multimedia Tools and Applications, vol. 79, pp. 6547–6568, 2020. [Google Scholar]

16. K. Ma, W. Zhang, X. Zhao, N. Yu and F. Li, “Reversible data hiding in encrypted images by reserving room before encryption,” IEEE Transactions on Information Forensics and Security, vol. 8, no. 3, pp. 553–562, 2013. [Google Scholar]

17. K. Chen and C. -C. Chang, “High-capacity reversible data hiding in encrypted images based on extended run-length coding and block-based MSB plane rearrangement,” Journal of Visual Communication and Image Representation, vol. 58, pp. 334–344, 2019. [Google Scholar]

18. X. Wu, T. Qiao, M. Xu and N. Zheng, “Secure reversible data hiding in encrypted images based on adaptive prediction-error labeling,” Signal Processing, vol. 188, pp. 108200, 2021. [Google Scholar]

19. S. Y. Xu, J. -H. Horng and C. -C. Chang, “Reversible data hiding scheme based on VQ prediction and adaptive parametric binary tree labeling for encrypted images,” IEEE Access, vol. 9, pp. 55191–55204, 2021. [Google Scholar]

20. Y. Liu, G. Feng, C. Qin, H. Lu and C. -C. Chang, “High-capacity reversible data hiding in encrypted images based on hierarchical quad-tree coding and multi-msb prediction,” Electronics, vol. 10, no. 6, pp. 664, 2021. [Google Scholar]

21. X. Wu and S. Wei, “High-capacity reversible data hiding in encrypted images by prediction error,” Signal Processing, vol. 104, no. 6, pp. 387–400, 2014. [Google Scholar]

22. M. Li, D. Xiao, Y. Zhang and H. Nan, “Reversible data hiding in encrypted images using cross division and additive homomorphism,” Signal Processing: Image Communication, vol. 39, pp. 234–248, 2015. [Google Scholar]

23. D. Xiao, Y. Xiang, H. Zheng and Y. Wang, “Separable reversible data hiding in encrypted image based on pixel value ordering and additive homomorphism,” Journal of Visual Communication and Image Representation, vol. 45, pp. 1–10, 2017. [Google Scholar]

24. C. Qin, W. Zhang, F. Cao, X. Zhang and C. -C. Chang, “Separable reversible data hiding in encrypted images via adaptive embedding strategy with block selection,” Signal Processing, vol. 153, pp. 109–122, 2018. [Google Scholar]

25. P. Puteaux and W. Puech, “An efficient msb prediction-based method for high-capacity reversible data hiding in encrypted images,” IEEE Transactions on Information Forensics and Security, vol. 13, no. 7, pp. 1670–1681, 2018. [Google Scholar]

26. R. Bhardwaj and A. Aggarwal, “An improved block based joint reversible data hiding in encrypted images by symmetric cryptosystem,” Pattern Recognition Letters, vol. 139, pp. 60–68, 2020. [Google Scholar]

27. K. Chen, “High capacity reversible data hiding based on the compression of pixel differences,” Mathematics, vol. 8, no. 9, pp. 1435, 2020. [Google Scholar]

28. P. Bas and T. Furon, “Image database of BOWS-2,” Accessed: Jun. 22, 2019. [Online]. Available: http://bows2.ec-lille.fr/. [Google Scholar]

29. P. Bas, T. Filler and T. Pevný, “Break our steganographic system—The ins and outs of organizing BOSS,” in Int. Workshop on Information Hiding, Berlin, Heidelberg, Springer, pp. 59–70, 2011. [Online]. Available: http://dde.binghamton.edu/download/. [Google Scholar]

This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.