DOI:10.32604/csse.2023.030646

| Computer Systems Science & Engineering DOI:10.32604/csse.2023.030646 |  |
| Article |
Distributed Timestamp Mechanism Based on Verifiable Delay Functions
1Engineering Research Center of Digital Forensics of Ministry of Education, School of Computer Science, Nanjing University of Information Science and Technology, Nanjing, 210044, China
2Nanjing University of Aeronautics and Astronautics, Nanjing, 210008, China
3Department of Cyber Security at VaporVM, Abu Dhabi, 999041, United Arab Emirates
*Corresponding Author: Yongjun Ren. Email: renyj100@126.com
Received: 30 March 2022; Accepted: 12 May 2022
Abstract: In the data communication system, the real-time information interaction of communication device increases the risk of privacy sensitive data being tampered with. Therefore, maintaining data security is one of the most important issues in network data communication. Because the timestamp is the most important way to authenticate data in information interaction, it is very necessary to provide timestamp service in the data communication system. However, the existing centralized timestamp mechanism is difficult to provide credible timestamp service, and users can conspire with timestamping servers to forge timestamps. Therefore, this paper designs a distributed timestamp mechanism based on continuous verifiable delay functions. It utilizes multiple independent timestamp servers to provide timestamp services in a distributed model and appends the timestamp to the data once the data is generated. Thus, it can prove that the data already exists at a certain time and ensure the accuracy of the timestamp. Moreover, a digital blind signature based on elliptic curve cryptography is utilized to solve the problem of timestamp forgery in timestamp service. Finally, the security analysis of the scheme ensures the data security of data communication system and the concurrency rate of timestamp. The experimental results also show that the scheme greatly improves the efficiency of digital signatures.
Keywords: Timestamp; verifiable delay functions; blockchain
With the rapid transformation of the traditional manufacturing industry to the intelligent industry, productivity efficiency has been greatly improved. However, ensuring the security of data information has also become one of the concerns of industry and academia [1]. Malicious users may tamper with or falsify data in communication devices. Generally, trusted third party is an important mechanism to provide data security and the public key infrastructure (PKI) [2] can establish the trust relationship in the digital society. And information hiding technology [3,4] can also hide secret data in public media information to ensure the secure transmission and storage of data. However, it is also necessary to ensure that the communication data has existed before a certain time to prevent the data information from being tampered with.
Timestamps have more advantages over traditional techniques. The timestamp is formed by adding time information to a digital signature. It can correctly provide the time of data generation and prove the identity of the data owner. The existing schemes utilized a trusted timestamp server (TSS) to embed timestamps for the data. The data is transmitted to the TSS once it is created. And the TSS responds to the data owner with an attached timestamp.
However, there are also some problems with the existing timestamp mechanism. The existing centralized timestamp service model assumes that TSS is secure and trusted. However, providing timestamps for data through a single TSS may lead to collusion between users and TSS. The recorded timestamps can be tampered or forged arbitrarily, and the security of these schemes is damaged. As such, TSS becomes a single point of failure in the systems. In addition, the existing distributed scheme also needs to provide timestamps through a group of voluntary issuers. That is, users must interact with all issuers in real-time to protect their outsourced data. Consequently, users should not only bear the additional communication burden, but also bear the additional cost of all issuers.
In order to solve the problems of single point of failure and user burden, this paper designs a distributed TSS mechanism to improve the secure storage architecture based on blockchain [5]. In this framework, the timestamp services supplied by the TSS mechanism and the blockchain provides second timestamp services and storage services [6]. When the distributed TSS receives the timestamp request from the user or devices, it executes a random algorithm [7] to select a primary TSS to provide a timestamp for the data. Then, it conducts a transaction that integrates the timestamped data on a public blockchain [8]. After the transaction is recorded in a block of the blockchain, the data is timestamped for the second time. Moreover, this paper is linking computational work to the elapsed time, which avoids that the TSS interact with the validator. So, non-interactive proofs are generated via verifiable delay functions (VDF) random oracles. The ability to create forged proofs completely depends on the corruption period and the ability of the adversary to computer VDF in a shorter time. Thus, it can only be realized through a faster VDF core. The specific contributions of this paper are as follows.
1. According to the security requirements of the TSS for timestamping data, a distributed TSS structure is constructed, which can effectively prevent a single TSS from colluding with users to tamper with data.
2. In the process of generating hash chains structure with distributed timestamps, this paper builds timestamps based on a continuous VDF (cVDF) [9] for a new block that need to be timestamped, which can implement the function of work proof in a relatively low cost and sustainable way.
3. In the block generation process of the hash chain structure, the timestamped data is transferred to the block for storage [10] and the timestamp is generated for the block itself when the block is generated. At this time, the timestamp can not only be the timestamp of the block itself, but also equivalent to the second timestamp of the data, which improves the data security and ensures the immutability of blocks.
4. The timestamp can be constructed by adding the date to a digital signature, where it uses a digital blind signature based on elliptic curve cryptography (ECC) [11]. It can well protect the data information privacy of users, and has high security performance, short information length and low storage space requirements.
2.1 Verifiable Delay Functions
A VDF is closely related to time-lock puzzles. The VDF requires a specified number of sequential steps to evaluate and will produce a function with a unique output that can be validated effectively and publicly. In 2018, Boneh et al. [12] give some application scenarios for VDF as well as formal models, security analysis and general construction methods. However, these candidate constructions do not fully satisfy all the essential properties of VDF. Subsequently, Wesolowski [13] and Pietrzak [14] both used the method of successive square operations in a finite group of unknown order to construct VDF, differing in the construction of their generating proofs. But this approach does not meet the desired efficiency of verifiability. In particular, even if the VDF could quickly verify each call, it would still be necessary to store all proofs of intermediate values in order to verify the final output of the iterative function, so the proof size and verification time grow linearly with the number of calls. Therefore, Ephraim et al. [9] first proposed a continuous VDF based on a tree structure to achieve successive iterations, so that the output of each intermediate iteration can be effectively verified, and the final computed proofs can be efficiently aggregated.
In 2019, De-Feo et al. [15] proposed a new VDF based on the assumption of ECC and instantiated this framework using super singular elliptic curves and bilinear pairs. The structure of this VDF is non-interactive in nature, and the output is validly validated without additional proof. However, the only safe way to instantiate a VDF is to require a trusted setup to perform a random homologous traversal. In fact, this setup needs to start with a super singular elliptic curve with an unknown automorphic ring. In the same year, Döttling et al. [16] obtain a simple construction of a tight VDF from any SNARGs combined with repeated hash. Landerreche et al. [17] proposed for the first time to study non-interactive cryptographic timestamps based on VDF using random oracle model under the framework of universal composability. In 2020, Song and Zhu et al. [18,19] argue that VDF is a core function of next generation blockchain systems that involve square operations on many complex operations (such as large number divisions and multiplication operations) that account for a large proportion of the computation of VDF. Schindler et al. [20] proposed a random beacon protocol, which has a unique set of guarantees that target realistic system models. Gritti [21] was the first to propose a publicly verifiable proof of retrievability and reliability using VDF, combining the publicly verifiable proof of retrievability scheme [22,23] with an exponentially VDF scheme in a finite group proposed. Rotem [24] combines a VDF candidate structure based on the correct exponential proof of the repeat square function to produce a VDF with batch validation.
The timestamp authenticates the time when the data is generated by certain technical means, so as to verify whether the data has been tampered with after it is generated. Simple timestamp protocol is based on trusted third party. However, it may introduce time delay issues, especially when users make frequent timestamp requests. In 1991, Haber and Stornetta proposed their linear chaining scheme [25], which forces a potentially untrustworthy TSS to produce true relative timestamps. The tree linking scheme [26] and binary linking scheme [27,28] further improve linear linking scheme. But such protocols only provide relative timestamps, which cannot satisfy some applications. In 2005, Bonnecaze Alexis proposed a distributed timestamping scheme [29], which provides absolute timestamps. With a multi-server architecture, it is difficult for users to collude with these signers to generate fake timestamps. Unfortunately, this scheme is based on a network of servers managed by an administratively independent entity, which is difficult to construct in a local area network, so its reliability may be severely compromised.
In 2011, Ting et al. [30] propose to implement a delegated timestamping mechanism through a forward secure proxy signature scheme [31] to provide digital timestamps with enhanced validity guarantees and national standard-compliant digital time traceability [32]. In 2019, Zhang et al. [33] propose two accurate blockchain-based timestamping schemes that solves the single point of failure problem. To make this scheme well compatible with cloud storage services, the log server is constrained by the cloud service provider to maintain outsourced files and their timestamps.
For the sake of ensuring data security, this paper propose a blockchain [34] based data security storage architecture. As shown in Fig. 1, the architecture is mainly divided into three layers: user layer, distributed TSS layer and blockchain layer. This describes the key components of each layer and the process of timestamping data through a distributed TSS mechanism is described in detail.
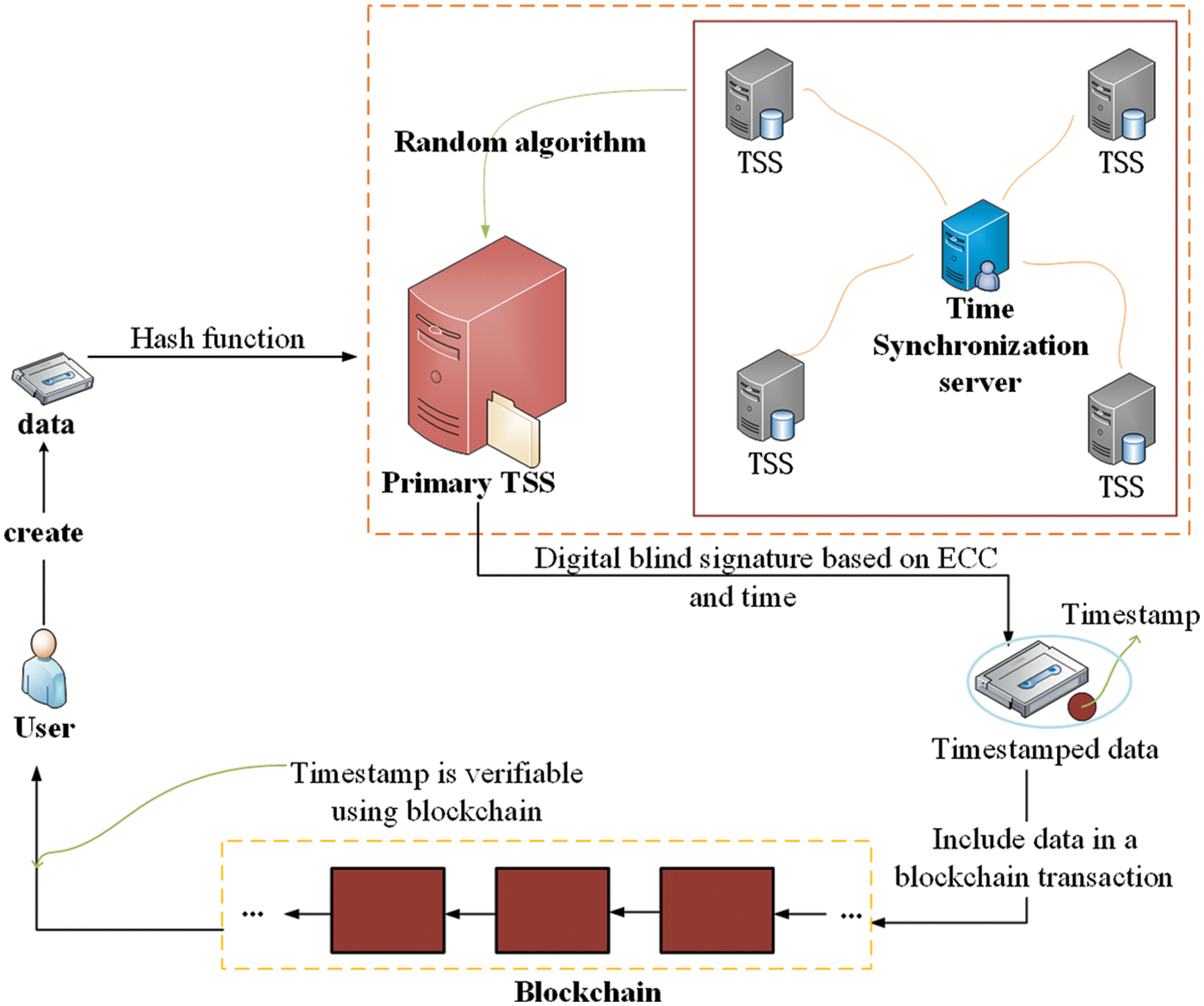
Figure 1: The system model of providing timestamp for data by distributed TSS
Users: The user is the owner of the data, and she/he creates a new data. The user computers the hash value of the data information through a hash algorithm. Then, the hash value is transferred to the distributed TSS mechanism, and a primary TSS is randomly selected through a random algorithm.
Distributed TSS: TSS is a timestamp authority system based on the PKI technology, which provides accurate and reliable timestamp services for everyone. The solution of providing timestamps for data through a single TSS maybe lead to collusion between the users and the TSS, which cannot fully ensure the data security. A distributed TSS mechanism is designed in this article that maintains the same time source through time synchronization server [35]. The distributed hash link TSS uses accurate time source, high strength and standard security mechanism to confirm the existence of system processing data at a certain time and the time order of related operations. And it provides basic services for time non-repudiation and anti-tampering in information system.
Blockchain: Blockchain is conducive to improving the efficiency of data storage and ensuring data privacy and security. It is a distributed ledger database based on multiple technologies such as peer-to-peer (P2P) network [36], consensus mechanism [37], cryptography technology [38] and smart contract [39]. Its multi integrated technical architecture gives itself technical characteristics such as decentralization and programmability. Therefore, the use of blockchain is sufficient to ensure that all timestamped data information stored in its system is secure. And it can output a timestamp of a specific data to device, which indicates the physical time of data storage.
4.1 Modelling Verifiable Delay Functions
In order to build a distributed TSS mechanism, the following related concepts are explained with reference [17]. Here a cryptographic hash function is used to link the VDF-proof sequences to form a distributed TSS, which is modeled as the originally proposed random oracle sequence. By adding VDF to these sequences, it can enhance the constructions and maintain the property that dictates that such sequences can only be built in a sequential manner, so as to preserve the security from our previous construction.
Public-key signatures. Assume EU-CMA signature scheme with security parameter λ. For consistency, we represent the computations related to this scheme as interaction with a signature oracle Σ in the following way:
– Each participant has a public/secret key pair (pk, sk) known to Σ.
– On query Σ.sig(sk, msg):
A signature sig
– On query Σ.verify(pk, msg, sig):
If (sk, msg, sig) is in the memory of Σ and (pk, sk) is a valid keypair, return accept. Otherwise, return reject.
It assumes that the probability that any polynomial probability time (PPT) adversary forges a signature without knowledge of the corresponding secret key is negligible in λ.
Sequence. This denotes a sequences of n elements from a set X as S = <xi | xi
AVL Trees. Binary trees are a finite set of n nodes, or it consists of a root node and two disjoint left and right subtrees called the root respectively. The absolute value of the balance factor of the left and right subtrees is not more than 1, and both the left and right subtrees are balanced binary trees.
1. AVL.root(S): It computers the root hash value of the AVL tree for some ordered finite sequence S.
2. AVL.path(S, v): It outputs the AVL path of the string sequence S.
3. AVL.verify(T): It given an input sequence T, if T is a valid AVL tree path, then output accept. Otherwise, it outputs reject.
The Sloth structure of Wesolowski [40] uses iterative modular square root and binary permutation function, which just meets our notion of a VDF. Unfortunately, this construction only has a logarithmic usability. In [13], it clearly proposed that Wesolowski’s effective VDF can also satisfy the candidate structure. Because its output consists of only two field elements, and the succinctness of the proof minimizes overhead of generating timestamp.
Ephraim et al. proposed cVDF with the same properties. It can not only perform fast verification, but also satisfy fast computation iterations. Although Wesolowski’s VDF can aggregate these intermediate proofs to obtain a single short proof, the verification time still grows linearly with t. In contrast, cVDF allows continuous iteration of a function, and the output of multiple iterations can be effectively verified in a time without much correlation. Moreover, cVDF can verify each intermediate state without recalculation, and the output of each step is publicly verifiable. Most importantly, cVDF supports multiple iterations of hyper-polynomials.
Landerreche believes that a VDF V = (VDF.gen, VDF.verify, VDF.extend) has security parameters λ and parameters g, v
VDF.gen(x, s)→(s, p) is a slow cryptographic algorithm that takes an input x
VDF.verify(x, s, p)→{accept, reject} is a fast cryptographic algorithm, in which the algorithm inputs x, p and strengths, and verifies in up to s·v time steps. If (s, p) = VDF.gen(x, s), output accept; Otherwise output reject;
VDF.extend() is a slow cryptographic algorithm, in which the algorithm inputs x, (s, p) = VDF.gen(x, s) and strength s* and extend in s·g parallel time steps.
In the evaluation algorithm, an output value and a proof are generated. The output value is computed through the specified sequence time steps, but the calculation of the proof is not obtained through the given sequence steps. Therefore, the calculation of the proof should not take too long compared with the output value of the function. This paper treats two outputs as one output value, and assume that the construction is effective and immediate. This method shows in Wesolowski’s VDF that the calculation of the proof can be regarded as a part of the whole calculation, because the proof can usually be generated by parallelization without significantly affecting the calculation time. If it is not assumed that the calculation of the proof is immediate, the extended VDF waste multiple calculation proofs (more than one calculation). It can reduce the efficiency of the extended VDF and the security properties are not affected by allowing VDF extension.

This links each party’s cVDF-rate to the global clock and model it as a read-only global oracle, which returns increasing time receipts. This allows us to generate a non-interactive proof that proves that a certain amount of time has passed since the prover recorded the message. As shown in Algorithm 1, refer to [17] to use the functionality
Participants can only interact with the random oracle cVDF through the function
4.2 Block Generation and Chain Structure
After the data is stored, the distributed TSS randomly selects an edge node [41] of the device to generate a new block. If this new block is the first block, then its previous block hash is set to zero [42]. Our prover maintains a list of blocks, each block contains a cVDF certificate, a record to be timestamped, and additional information. These blocks are linked by using a hash function [43], and each block contains the hash of the previous block.
The two important functions of the hash chain are the construction of blocks and chains. The block forming is used to form a block from a set of events, and the chain forming is to link the generated blocks together to form a hash chain structure similar to a blockchain. Next, this have to define the concept of block and chain.
Block. This defines a block for a party P with public key pk as a tuple B = (num, prev, vp, vo, t, e) and the relevant explanation is as follows.
1. num is the serial number of the block.
2. prve is the root hash of the previous block. For the initial block, and it sets the hash of the public key pk to the hash of its previous block. That is, when num = 0, prev = H(pk).
3. vp is a (time receipt, signature)-pair.
4. vo = (s, p) is a cVDF output.
5. t is a time receipt of the creation of the block.
6. e is the data information to be timestamped.
It assumes that there is a credible distributed timestamp synchronization system to ensure that the time and date of the timestamp provided by the distributed hash link TSS for each data message are highly consistent, so as to effectively ensure the accuracy and reliability of the block timestamp. Each element of the sequence of the string sequence must be composed of the output of cVDF(p) preceded by a time receipt(t). Additionally, we have prev and c are leaves. These assumptions allow to easily describe the connection between these instances and the next cVDF input.
Chain. This defines a block for a party P with public key pk as a sequence of blocks C = Bi where for all 0 ≤ i ≤ k.
1. The sequence number of the i-th block is i, that is, Bi.num = i.
2. The hash value of the previous block of the i-th block is AVL.root(Bi−1). For the initial block, it sets the hash of the public key pk to the hash of its previous block. That is, when i = 0, Bi.prev = H(pk).
3. The output of the i-th block is the output of cVDF in this block, that is, Bi.p = cVDF(Bi.t || Bi.prev || Bi.sig, Bi.s) for i ≥ 1.
4. Σ.verify(pk, Bi.t || Bi.prev, Bi.sig) = accept.
5. The time receipt of block Bj is greater than the time of the block before it. That is, Bi.t, Bj.t for all i<j≤ k.
Finally, each node compares its own data with the blockchain and updates the blockchain. In order to save the storage space of each node, after the edge node of the device uploads these blocks to the server, the data stored in each node can be periodically cleared.
4.3 Distributed Hash Link TSS Scheme
Through the timestamp security protocol, this paper proposes a timestamp scheme that combines the distributed protocol and the linear link protocol to construct a distributed hash link protocol. The construction idea is as follows.
1. The k random signers required in the distributed protocol are replaced with k TSS to reduce the burden of users.
2. The request of N users at the same time required in the linear link protocol is changed to k TSS and the TSS is randomly selected to timestamp the data, so as to avoid the risk of collusion between users and TSS.
3. In the process of timestamp service, the status of the TSS as a third party or notary is crucial. Our digital signature algorithm adopts the distributed hash link TSS scheme of ECC blind signature.
The prover maintains a block list, and stores the cVDF proof, timestamp records and additional information in the block. All blocks are linked by the cryptographic hash function, and each block contains the hash value of the previous block, forming the first proposed timestamp paper by Hubble and Stornata hash chain structure, which is similar to the chain structure of blockchain. In order to improve the security and efficiency of the structure, we can use the structure of k TSS linear chains to adopt a distributed balanced binary tree structure (e.g., Merkle tree [44]) with a primary TSS and k − 1 auxiliary TSS, and put all TSS signature pairs. In the same block, the output information of each block represents a timestamp. Next, the specific steps of the distributed hash link timestamp scheme are as follows.
1. The user sends the data y and the logo ID of the data y that need to be timestamped to k distributed TSS mechanisms, namely (y, ID);
2. Randomly select the TSS as the primary TSS through the random algorithm, while other k − 1 TSS are regarded as auxiliary servers;
3. The k-TSS sign the data (y, ID), and each generates a timestamp signature pair. Then, they generate k signature pairs Vm: Vm = sigm(tm, IDm, ym) {m = 1, 2, …, k}, where tm is the time and date when the m-th TSS signed the data, and then k − 1 auxiliary TSS respectively send Vm to the primary TSS;
4. The primary TSS stores the data signatures sent by k − 1 auxiliary TSS and the Vm generated by itself into a block and establishes a binary tree structure according to the sequence of the signature time of each. Here default the m-th TSS as the primary service provider, and set Vm as the timestamp pairing of the leftmost node of the binary tree structure;
5. The primary TSS outputs the root information of the binary tree as the timestamp of y, and stores the data and the timestamp in the block.
In the chain structure, Bi.prev = AVL.root(Bi−1) allows us to generate an AVL tree for the entire chain by linking the AVL tree through prev. We use the root of the previous block as part of our cVDF input, so it can make a similar AVL tree connection through the poke cVDF input. This structure starts from any element in a block and ends at the end of the chain, passing through every VDF proof and including every time receipt.
This section discusses the security properties of distributed TSS. It assumes that the electronic signature system used by TSS is secure and reliable, and its key has not been cracked. If an attacker wants to tamper with data information, an incorrect timestamp is required instead of the real timestamp in a distributed TSS structure. First, the attacker needs to collude with the primary TSS, and also needs to obtain information about other TSS in the distributed TSS structure in order to collude. Secondly, it is also necessary to ensure that the hash values generated by the hash function between linked blocks are consistent. Next, the steps taken by the attacker to tamper with the data are analyzed.
1. Attackers colludes with the primary TSS to obtain the signatures Vm of all TSS;
2. Attackers colludes with any TSS and replaces the correct (y, IDn) with the wrong (
3. Attackers must also replace the real Ln+1 with a fake
Since the hash chain is sequence numbered by each time information, and it adds cVDF-proof to each block to enhance the strength of the hash chain and timestamp, it is impossible for an attacker to add other information to the hash chain and tamper with it. First of all, the choice of the primary TSS is randomly selected through a random algorithm. As long as the random algorithm is designed well, it becomes very difficult for the attacker and the primary TSS to collude with each other. At the same time, the attacker cannot obtain the information of other TSS, making it impossible to replace the correct (y, IDn) with the wrong (
As long as the hash function for linking the block is designed well enough, it can ensure that the hash value of the block will not be affected. To be exact, the distributed TSS model is secure by ensuring that not all TSS is colluding with attackers. Meanwhile, preventing malicious TSS from colluding with attackers can also be prevented by realistic management system.
6.1 Comparison of Timestamp Protocols
This section compares our protocol with other protocols. For this reason, several mature timestamping protocols are selected here as benchmarks. The specific comparison results are shown in Tab. 1. First of all, the distributed protocol transfers the dependence on TSS trust to the dependence on user cooperation. The more users participating, the safer the timestamp, but the pressure on the user load will increase exponentially. Secondly, the linear link protocol is not much different from distributed protocol in terms of terminal and transport requirements. But when the validator challenges the linear link protocol, complete verification is equivalent to recalculating the entire link. Therefore, as long as the number of TSS participants is well controlled, our distributed hash link protocol is a relatively secure solution.

Calculation. Since the timestamp protocol must hash the data that the user needs to authenticate, all timestamp protocols must perform at least one hash function calculation. At the same time, both plain timestamp protocols and linear timestamp protocols are constructed by adding time information to digital signatures, so they all need to verify the data signature. The tree timestamp protocol decomposes the timestamp into many rounds, and only one timestamp verification is required for each round. However, in order to prevent the time stamp from being forged, both the distributed time stamp protocol and the time stamp protocol in this paper use the random generation algorithm to select the issuer and the main time stamp server respectively for digital signature.
Storage. Both plain timestamp protocols and linear timestamp protocols need to store signatures that provide timestamp services for data. In addition, the linear timestamp protocol also needs to store the identity information ID of the n-th and (n + 1)-th users to form a linear link structure. The tree timestamp protocol can generate timestamps in the process of each round, so it needs to store the timestamps of each round to avoid the loss of timestamps. However, the distributed timestamp protocol and our timestamp protocol need k issuers or servers to provide signatures, so they store k signatures to ensure the accuracy of the final timestamp.
TSS/Users. The whole process of timestamp service depends on either TSS or the user itself. Both plain timestamp protocols and linear timestamp protocols rely completely on TSS. The tree timestamp protocol relies on cooperation between TSS and users. The distributed timestamp protocol rely completely on user. However, these protocols either increase the additional burden on TSS or users. Our protocol proposes to use a random algorithm to select one of k servers, so that the entire timestamp service process relies only on the randomly selected primary server.
6.2 Concurrency Rate of Distributed TSS Mechanism
The concurrency capability of the timestamp mechanism refers to the rate at which the timestamp mechanism can process timestamp requests concurrently. In the simulation experiment of concurrency rate of distributed timestamp mechanism, when the distributed TSS is started, the main control process starts 10 Apache HTTP server sub-processes, and each sub-process has 30 threads. The minimum number of threads allowed by the main control process is 150 and the maximum number of idle processes is 1200. The main control process can start up to 105 processes. At the same time, 3000 clients are allowed to access at the same time. Under the condition that the length of the signature key of the TSS is 1024 bits, the client simulates the user to obtain the timestamp through HTTP/HTTPS.
Fig. 2 shows the experimental results of the concurrency rate of the TSS. The abscissa represents the number of concurrent accesses to the TSS N, and the ordinate represents the average number of requests that the TSS can handle per second under a certain value of N. It can be seen from the experimental results that when N = 2500, the average timestamp request value that the TSS can handle per second reaches the maximum (around 1200 and 1600). when N > 2500, the timestamp processed by the TSS are gradually decreasing.
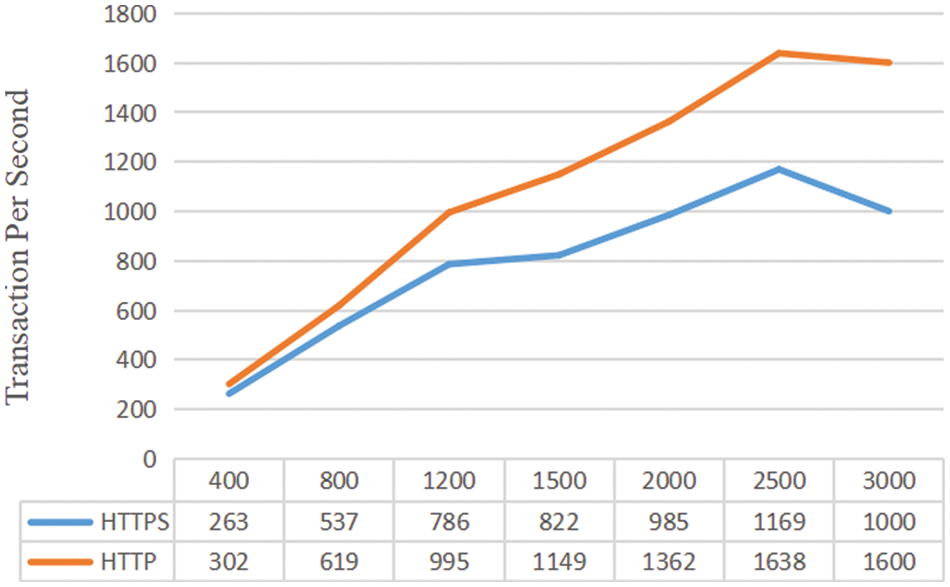
Figure 2: Overview of the concurrency rate of distributed timestamp
6.3 Ciphertext Length of Distributed TSS Mechanism
For ECC signature encryption algorithm and RSA encryption algorithm, their key lengths are shown in Tab. 2. Obviously, ECC signature encryption uses a 160 bits key to achieve the same security effect as RSA signature encryption with a 1024 bits key.

The length of the key actually refers to the length of the public key modulo n. Theoretically, the larger the n, the higher the security strength of the algorithm. For ECC signature encryption algorithm based on discrete logarithm calculation on elliptic curve and RSA encryption algorithm based on large integer factorization problem, the security strength of ECC is higher than that of RSA. In other words, if you need to provide the same security strength, the key length required by ECC is much lower than that of RSA. This effectively solves the problem of improving the security strength by increasing the key length.
The ciphertext lengths of ECC signature encryption and RSA signature encryption with different security levels are experimentally tested here. As shown in Fig. 3, when signing and encrypting the data information of 200 bits at the encryption level of 80 bits, the ciphertext length of RSA is 128 bytes, while the ciphertext length of ECC is 40 bytes, which is not very different from each other. At the security level of 256 bits, RSA encryption algorithms have a redaction length of 1920 bytes, while ECC has a redaction length of only 64 bytes. In terms of ciphertext length, ECC doesn’t change significantly with the increase of security level, while RSA increases significantly with the increase of security level. It can be seen that the storage space occupied by ECC signature encryption algorithm is far less than that of RSA signature encryption.
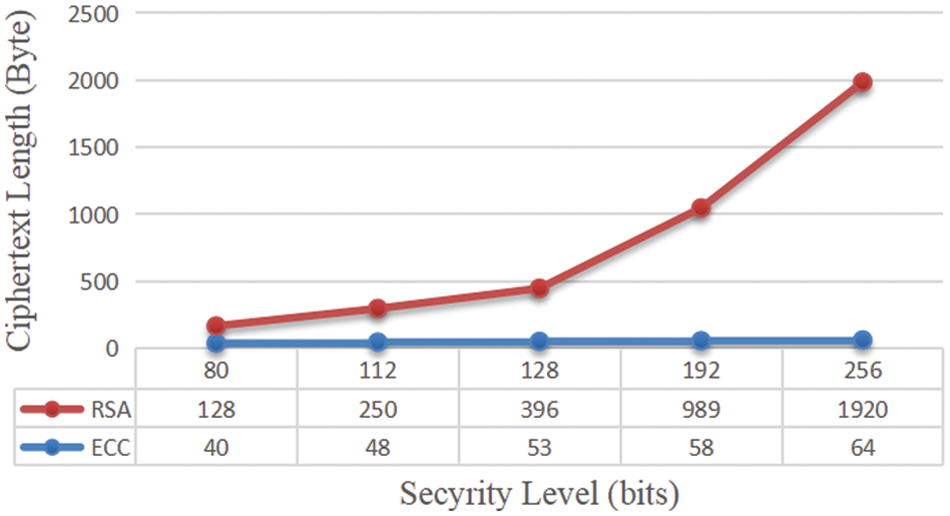
Figure 3: Comparison of ciphertext length between ECC and RSA signature encryption
Next, this section selects data with a size of about 2 M to conduct 5 sets of experimental tests to compare RSA and ECC signature encryption to data information encryption. In Fig. 4, although the two types of encryption signature time exceed 2 mins, it is obvious that the ECC signature is about 30s faster than the RSA signature on average.
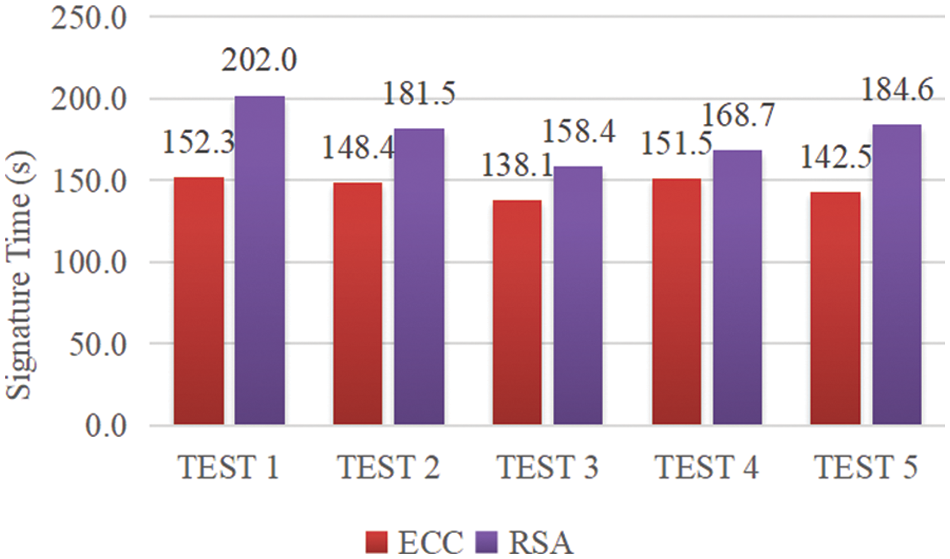
Figure 4: Comparison of ECC and RSA encryption time
The ECC encryption algorithm has a small amount of computation and fast processing speed. With the same computing resources, although RSA can improve the speed of encryption and signature verification by selecting smaller public keys, RSA’s private key decryption is completely incomparable with ECC. At the same time, ECC’s key generation speed is more than 100 times faster than RSA. For example, for a 160 bits ECC and a 1024 bits RSA, the signature time of ECC is 3.0 ms and the key pair generation time is 3.8 ms, but the RSA encryption algorithm is as high as 228.4 and 4708.3 ms, respectively, so under the same conditions, ECC has higher encryption performance.
This paper proposes a secure storage architecture based on blockchain to meet the requirements of data security. Moreover, this paper uses timestamp technology to solve the security problem that data may be forged and tampered with. And a distributed model with multiple TSS is proposed to provide timestamp services, which improves the reliability and accuracy of timestamps. The time synchronization services are provided for distributed TSS mechanism. In addition, this paper utilizes blind signature encryption algorithm of ECC based on discrete logarithm calculation on elliptic curve to improve security of the signature in distributed TSS, and blockchain technology is applied to provide secure storage services and secondary timestamp services for data. Meanwhile, the data reliability and availability are also improved by using a distributed timestamp and the blockchain.
Funding Statement: This work was supported by National Key R&D Program of China (Grant Nos. 2021YF B2700503, 2020YF B1005900). Zhaoyang Han received the grant and the URLs to sponsors’ websites is https://service.most.gov.cn/. This work was also supported by the National Natural Science Foundation of China (No. 62072249), Yongjun Ren received the grant and the URLs to sponsors’ websites is https://www.nsfc.gov.cn/.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
1. B. Bajic, A. Rikalovic, N. Suzic and V. Piuri, “Industry 4.0 implementation challenges and opportunities: A managerial perspective,” IEEE Systems Journal, vol. 15, no. 1, pp. 546–559, 2021. [Google Scholar]
2. D. Díaz-Sánchez, A. Marín-Lopez, F. A. Mendoza, P. A. Cabarcos and R. S. Sherratt, “TLS/PKI challenges and certificate pinning techniques for IoT and M2M secure communications,” IEEE Communications Surveys Tutorials, vol. 21, no. 4, pp. 3502–3531, 2019. [Google Scholar]
3. L. Liu, L. Meng, L. Zheng, Y. Peng and X. Wang, “A novel high-capacity information hiding scheme based on improved U-Net,” Security & Communication Networks, vol. 2022, no. 1, pp. 1–12, 2022. [Google Scholar]
4. H. T. Wu, T. Zhou, Z. Zhuang and C. Xian, “Reversible transformation of tetrahedral mesh models for data protection and information hiding,” Journal of Information Security and Applications, vol. 66, no. 6, pp. 1–10, 2022. [Google Scholar]
5. Y. J. Ren, Y. Leng, J. Qi, K. S. Pradip and J. Wang, “Multiple cloud storage mechanism based on blockchain in smart homes,” Future Generation Computer Systems, vol. 115, no. 3, pp. 304–313, 2021. [Google Scholar]
6. Y. J. Ren, F. Zhu, J. Wang, P. Sharma and U. Ghosh, “Novel vote scheme for decision-making feedback based on blockchain in internet of vehicles,” IEEE Transactions on Intelligent Transportation Systems, vol. 23, no. 2, pp. 1639–1648, 2022. [Google Scholar]
7. J. G. Chen, K. Li, T. Zhuo, K. Bilal, S. Yu et al., “A parallel random forest algorithm for big data in a spark cloud computing environment,” IEEE Transactions on Parallel & Distributed Systems, vol. 28, no. 4, pp. 919–933, 2017. [Google Scholar]
8. W. Liang, M. Tang, J. Long, X. Peng, J. Xu et al., “A secure FaBric blockchain-based data transmission technique for industrial Internet-of-Things,” IEEE Transactions on Industrial Informatics, vol. 15, no. 6, pp. 3582–3592, 2019. [Google Scholar]
9. N. Ephraim, C. Freitag, I. Komargodski and R. Pass, “Continuous verifiable delay functions,” in Proc. 39th Annual Int. Conf. on the Theory & Applications of Cryptographic Techniques, Zagreb, Croatia, pp. 125–154, 2020. [Google Scholar]
10. C. P. Ge, W. Susilo, Z. Liu, J. Y. Xia and L. M. Fang, “Secure keyword search and data sharing mechanism for cloud computing,” IEEE Transactions on Dependable & Secure Computing, vol. 18, no. 6, pp. 2787–2800, 2021. [Google Scholar]
11. G. Culot, F. Fattori, M. Podrecca and M. Sartor, “Addressing industry 4.0 cybersecurity challenges,” IEEE Engineering Management Review, vol. 47, no. 3, pp. 79–86, 2019. [Google Scholar]
12. D. Boneh, J. Bonneau, B. Bünz and B. Fisch, “Verifiable delay functions,” in Proc. Annual Int. Cryptology Conf., Santa Barbara, CA, USA, pp. 757–788, 2018. [Google Scholar]
13. B. Wesolowski, “Efficient verifiable delay functions,” Journal of Cryptology, vol. 33, no. 4, pp. 2113–2147, 2020. [Google Scholar]
14. K. Pietrzak, “Simple verifiable delay functions,” in Proc. 10th Innovations in Theoretical Computer Science Conf., San Diego, CA, US, pp. 1–15, 2019. [Google Scholar]
15. L. De-Feo, S. Masson, C. Petit and A. Sanso, “Verifiable delay functions from supersingular isogenies and pairings,” in Proc. Int. Conf. on the Theory & Application of Cryptology & Information Security, Kobe, Japan, pp. 248–277, 2019. [Google Scholar]
16. N. Dttling, S. Garg, G. Malavolta and P. Vasudevan, “Tight verifiable delay functions,” in Proc. Int. Conf. on Security & Cryptography for Networks, Amalfi, Italy, pp. 65–84, 2020. [Google Scholar]
17. E. Landerreche, M. Stevens and C. Schaffner, “Non-interactive cryptographic timestamping based on verifiable delay functions,” in Proc. 24th Int. Conf. on Financial Cryptography & Data Security, Kota Kinabalu, Malaysia, pp. 541–558, 2020. [Google Scholar]
18. D. Zhu, Y. F. Song, J. Tian, Z. F. Wang and H. B. Yu, “An efficient accelerator of the squaring for the verifiable delay function over a class group,” in Proc. 2020 IEEE Asia Pacific Conf. on Circuits & Systems, Ha Long, Vietnam, pp. 137–140, 2020. [Google Scholar]
19. Y. F. Song, D. Y. Zhu, J. Tian and Z. F. Wang, “A high-speed architecture for the reduction in VDF based on a class group,” in Proc. 2020 IEEE 33rd Int. System-on-Chip Conf., Las Vegas, NV, USA, pp. 147–152, 2020. [Google Scholar]
20. P. Schindler, A. Judmayer, M. Hittmeir, N. Stifter and E. Weippl, “RandRunner: Distributed randomness from trapdoor VDFs with strong uniqueness,” in Proc. 2020 Network & Distributed System Security Symp. Conf., San Diego, CA, USA, pp. 21–25, 2020. [Google Scholar]
21. C. Gritti, “Publicly verifiable proofs of data replication and retrievability for cloud storage,” in Proc. 2020 Int. Computer Symp. Conf., Tainan, Taiwan, pp. 431–436, 2020. [Google Scholar]
22. R. Chen, Y. Li, Y. Yu, H. Li, X. Chen et al., “Blockchain-based dynamic provable data possession for smart cities,” IEEE Internet of Things Journal, vol. 7, no. 5, pp. 4143–4154, 2020. [Google Scholar]
23. H. Wang, “Proxy provable data possession in public clouds,” IEEE Transactions on Services Computing, vol. 6, no. 4, pp. 551–559, 2013. [Google Scholar]
24. L. Rotem, “Simple and efficient batch verification techniques for verifiable delay functions,” in Proc. Theory of Cryptography Conf., Raleigh, NC, USA, pp. 382–414, 2021. [Google Scholar]
25. S. Haber and W. S. Stornetta, “How to time-stamping of digital documents,” Journal of Cryptology, vol. 3, no. 2, pp. 99–112, 1991. [Google Scholar]
26. Y. Kim, J. Jo and S. Lee, “ADS-B vulnerabilities and a security solution with a timestamp,” IEEE Aerospace & Electronic Systems Magazine, vol. 32, no. 11, pp. 52–61, 2017. [Google Scholar]
27. Y. Z. Liu, F. Yang, K. Gao, W. J. Dong and J. Song, “A zero-watermarking scheme with embedding timestamp in vector maps for big data computing,” Cluster Computing, vol. 20, no. 4, pp. 3667–3675, 2017. [Google Scholar]
28. G. Hua, J. Goh and V. L. L. Thing, “A dynamic matching algorithm for audio timestamp identification using the ENF criterion,” IEEE Transactions on Information Forensics & Security, vol. 9, no. 7, pp. 1045–1055, 2014. [Google Scholar]
29. W. Yu, W. Yao, X. Deng, Y. Zhao and Y. Liu, “Timestamp shift detection for synchrophasor data based on similarity analysis between relative phase angle and frequency,” IEEE Transactions on Power Delivery, vol. 35, no. 3, pp. 1588–1591, 2020. [Google Scholar]
30. P. Y. Ting, F. D. Chu, C. S. Liao and H. T. Lin, “A digital standard time dissemination architecture for trustworthy time stamping,” IEEE Transactions on Instrumentation & Measurement, vol. 60, no. 7, pp. 2584–2589, 2011. [Google Scholar]
31. C. P. Ge, W. Susilo, J. Baek, Z. Liu and J. Y. Xia, “A verifiable and fair attribute-based proxy re-encryption scheme for data sharing in clouds,” IEEE Transactions on Dependable & Secure Computing, vol. 21, no. 7, pp. 1–12, 2021. [Google Scholar]
32. Y. J. Ren, K. Zhu, Y. Q. Gao, J. Y. Xia, S. Zhou et al., “Long-term preservation of electronic record based on digital continuity in smart cities,” Computers, Materials & Continua, vol. 66, no. 3, pp. 3271–3287, 2021. [Google Scholar]
33. Y. Zhang, C. Xu, N. Cheng, H. Li, H. Yang et al., “Chronos+: An accurate blockchain-based time-stamping scheme for cloud storage,” IEEE Transactions on Services Computing, vol. 13, no. 2, pp. 216–229, 2020. [Google Scholar]
34. Y. J. Ren, F. J. Zhu, S. P. Kumar, T. Wang, J. Wang et al., “Data query mechanism based on hash computing power of blockchain in Internet of Things,” Sensors, vol. 20, no. 1, pp. 1–22, 2020. [Google Scholar]
35. D. C. Mazur, R. A. Entzminger, J. A. Kay and P. A. Morell, “Time synchronization mechanisms for the industrial marketplace,” IEEE Transactions on Industry Applications, vol. 53, no. 1, pp. 39–46, 2017. [Google Scholar]
36. X. R. Zhang, X. Sun, W. Sun, T. Xu and P. P. Wang, “Deformation expression of soft tissue based on BP neural network,” Intelligent Automation & Soft Computing, vol. 32, no. 2, pp. 1041–1053, 2022. [Google Scholar]
37. Y. J. Ren, J. Qi, Y. P. Liu, J. Wang and G. Kim, “Integrity verification mechanism of sensor data based on bilinear map accumulator,” ACM Transactions on Internet Technology, vol. 21, no. 1, pp. 1–20, 2021. [Google Scholar]
38. X. R. Zhang, W. F. Zhang, W. Sun, X. M. Sun and S. K. Jha, “A robust 3-D medical watermarking based on wavelet transform for data protection,” Computer Systems Science & Engineering, vol. 41, no. 3, pp. 1043–1056, 2022. [Google Scholar]
39. Y. J. Ren, J. Qi, Y. P. Cheng, J. Wang and O. Alfarraj, “Digital continuity guarantee approach of electronic record based on data quality theory,” Computers, Materials & Continua, vol. 63, no. 3, pp. 1471–1483, 2020. [Google Scholar]
40. A. Lenstra and B. Wesolowski, “Trustworthy public randomness with sloth, unicorn, and TRX,” International Journal of Applied Cryptography, vol. 3, no. 4, pp. 330–343, 2017. [Google Scholar]
41. T. Li, Q. Qian, Y. J. Ren, Y. Z. Ren and J. Y. Xia, “Privacy-preserving recommendation based on kernel method in cloud computing,” Computers, Materials & Continua, vol. 66, no. 1, pp. 779–791, 2021. [Google Scholar]
42. L. M. Fang, M. H. Li, Z. Liu, C. T. Lin, S. L. Ji et al., “A secure and authenticated mobile payment protocol against off-site attack strategy,” IEEE Transactions on Dependable & Secure Computing, vol. 21, no. 2, pp. 1–12, 2021. [Google Scholar]
43. C. P. Ge, W. Susilo, J. Baek, Z. Liu, J. Y. Xia et al., “Revocable attribute-based encryption with data integrity in clouds,” IEEE Transactions on Dependable & Secure Computing, vol. 99, pp. 1, 2021. [Google Scholar]
44. Y. Z. Wang, Y. L. Shen, H. Wang, J. L. Cao and X. H. Jiang, “MtMR: Ensuring MapReduce computation integrity with Merkle tree-based verifications,” IEEE Transactions on Big Data, vol. 4, no. 3, pp. 418–431, 2018. [Google Scholar]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |