DOI:10.32604/csse.2023.026238

| Computer Systems Science & Engineering DOI:10.32604/csse.2023.026238 |  |
| Article |
Algorithms for Pre-Compiling Programs by Parallel Compilers
Department of Computer Science and Information, College of Science, Majmaah University, Al-Majmaah, 11952, Saudi Arabia
*Corresponding Author: Fayez AlFayez. Email: f.alfayez@mu.edu.sa
Received: 19 December 2021; Accepted: 10 March 2022
Abstract: The paper addresses the challenge of transmitting a big number of files stored in a data center (DC), encrypting them by compilers, and sending them through a network at an acceptable time. Face to the big number of files, only one compiler may not be sufficient to encrypt data in an acceptable time. In this paper, we consider the problem of several compilers and the objective is to find an algorithm that can give an efficient schedule for the given files to be compiled by the compilers. The main objective of the work is to minimize the gap in the total size of assigned files between compilers. This minimization ensures the fair distribution of files to different compilers. This problem is considered to be a very hard problem. This paper presents two research axes. The first axis is related to architecture. We propose a novel pre-compiler architecture in this context. The second axis is algorithmic development. We develop six algorithms to solve the problem, in this context. These algorithms are based on the dispatching rules method, decomposition method, and an iterative approach. These algorithms give approximate solutions for the studied problem. An experimental result is implemented to show the performance of algorithms. Several indicators are used to measure the performance of the proposed algorithms. In addition, five classes are proposed to test the algorithms with a total of 2350 instances. A comparison between the proposed algorithms is presented in different tables discussed to show the performance of each algorithm. The result showed that the best algorithm is the Iterative-mixed Smallest-Longest- Heuristic (ISL) with a percentage equal to 97.7% and an average running time equal to 0.148 s. All other algorithms did not exceed 22% as a percentage. The best algorithm excluding ISL is Iterative-mixed Longest-Smallest Heuristic (ILS) with a percentage equal to 21,4% and an average running time equal to 0.150 s.
Keywords: Compiler; encryption; scheduling; big data; algorithms
This work addressess the time challenge of transmitting a big number of encrypted files through a network. Sending several data at the same time by activating the encryption mode is a challenging task. Indeed, compiler data encryption requires time to process data. Faced with huge data we will end up facing a problem of assignment otherwise a problem of waiting will appear and can lead to problems and delay sending data.
Authors in [1], proposed a technique utilizing the scheduling algorithms for memory-bank management, register allocation, and intermediate-code optimizations. The objective was the minimization of the overhead of trace scheduling and the Multi-flow compiler was described. The trace scheduling compiler using the VLIW architecture was examined and investigated in [2–6].
In [7], authors proposed compiler-assisted techniques for operating system services to ensure sufficient energy consumption. The simulation shows the effectiveness of the proposed techniques to achieve better results using dynamic management systems.
A recent study in [8] presented a manner to perform the whole-program transfer scheduling on accelerator data transfers seeking to reduce the number of bytes transferred and enhanced program performance and efficiency.
Other studies such as [9–12] investigate the register allocation and instruction assignment.
A novel domain-specific language and compiler were developed to target FPGAs and CGRAs from common source code in [13]. Authors prove that applications written in spatial are, on average, 42% shorter and achieve a mean speedup of 2.9x over SDAccel HLS.
Several patents were developed regarding the allocation compiler code generation and scheduling, such as in [14,15]. Parallel architectures such as multiprocessors are still difficult to exploit in the presence of compilers [16].
Several authors treated the fair load balancing into computer [17–19]. Other domains that others treated the load blanching are the projects assignment and gas turbines aircraft engines [20–25]. Recently, a novel research work to fight COVID-19 using load balancing algorithm is developed in [26]. Other works treated the scheduling algorithms and the load balancing are [27,28].
The aim of this work is to introduce a novel architecture manipulating the transmission of data through network guaranteeing the effectiveness of encryption. This paper introduces a novel architecture to show the necessity of security into a network. The proposed control aims to ensure a fair distribution of the set of files to different compilers which are responsible for the encryption. To the best of authors knowledge, this problem has never been studied in the literature. Several interesting papers in the literature deal with trace scheduling compiler [29–32].
This paper is organized as the following in Section 2, we begin with an overall presentation of the novel proposed architecture. The studied problem is described in Section 3. The proposed algorithms solving the studied problems are developed in Section 4. Section 5, presents experimental results to show the performance of the proposed algorithms. A conclusion is presented in Section 6.
In this paper, we propose a new architecture for the data transmission process that requires several security processes. Authors in this project discovered the need of fare distributing that appears when there are files need to be encrypted using compilers before being sent through the network. In presence of big data, we must impose appropriate algorithm that organize the manner of transmission of the files among compilers to guarantee the optimum usage of recourses by distributing the files among compilers for encryption process taking into account the file size. In order to do that, we propose to add a new component into network architecture. This component will be known as “scheduler” that responsible to give a good planning of the dispatching files to different compilers to guarantee time efficiency in the encryption tasks.
The novel architecture proposed in this paper is described in Fig. 1. The component “reception process” is represented by “Scheduler r” and “decrypter” in Fig. 2. This architecture is decomposed into 7 components. These components are given as following:
• Data center: this component is responsible to collect all files that need to be sent through the network. The collection of files must be done in a secure place.
• scheduler s: is the scheduler responsible to give an appropriate distribution of files that need to be encrypted by the compiler before sending the files through routers.
• Encrypter: this component is responsible to encrypt files. The encrypter contain different compilers that are responsible of executing the encryption algorithm.
• Routers: Scheduler r: scheduler that responsible to receive files from routers and apply the appropriate algorithm to assign files to compilers (see Fig. 3).
• Decrypter: this component applies the algorithm that can decrypt files to be readable by the receiver.
• Terminal server: the receiver accounts.
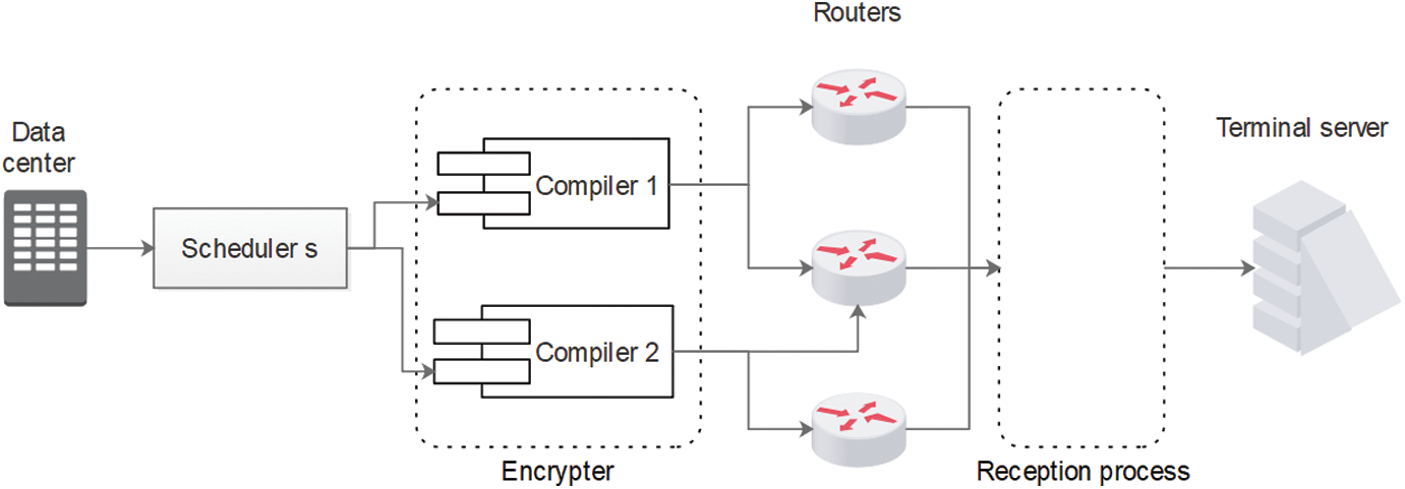
Figure 1: Data sent process
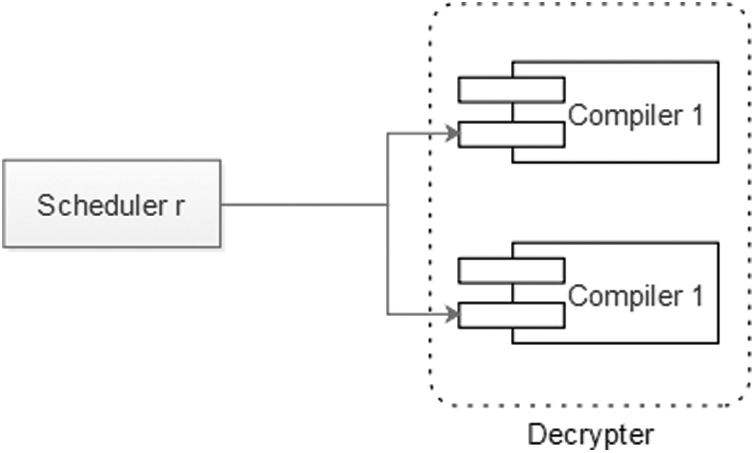
Figure 2: The reception process component
In a specific network, any data breach can impact directly to national security, therefore, enforcing a strong encryption system is very important. A strong security system must be applied for any confidential national data to guarantee security and avoid any data leaks.
This section describes the proposed new network architecture that focused on the scheduler component. Assuming that big data saved in
Before we give the solution to the scheduling problem, we must give some notation as follows.
Denoting by
Example 1
We consider a given instance, with two compilers

We chose an algorithm to schedule files on compilers. The algorithm will give the schedule shown in Fig. 3. It is clear to see that compiler 1 execute the encryption program for files {2,3,4}. Contrariwise, for compiler 2, files {1,5} are picked. Based on Fig. 3, the compiler 1 has a total executed size 6790. However, compiler 2 has a total size of 6012. The size gap between compiler 1 and compiler 2 is
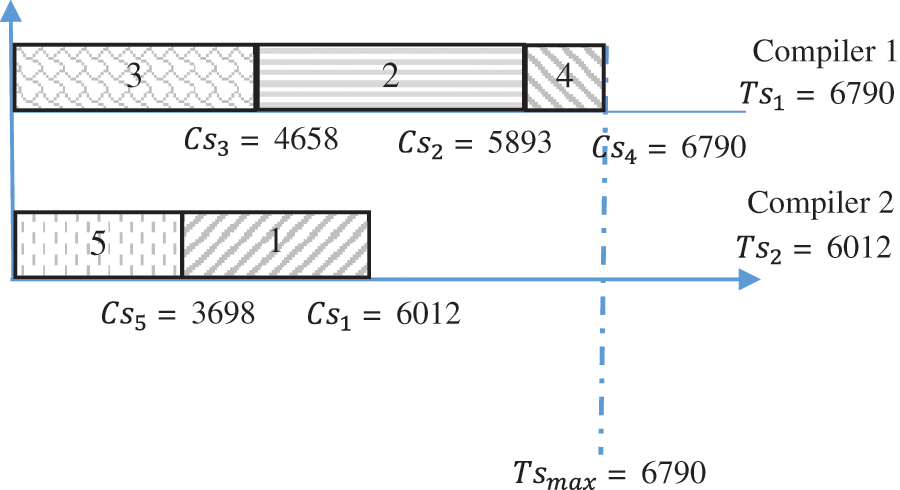
Figure 3: Files-compilers dispatching for example 1
We need some indicators to evaluate the performance of different algorithms and the impact of the chosen algorithm on the reducing of the calculated gap. In this paper, we propose to follow the indicator that calculate the difference between all compilers executed sizes and the compiler having the minimum total size. For Example, 1, the indicator is
Hereafter, let
In this section, we present several approximate solutions to solve the problem. We develop algorithms that return results within a good timing. The proposed heuristics are based essentially on the longest and smallest sizes dispatching rules with some variants. We choose the dispatching rules because the running time of those algorithms is more suitable.
4.1 Longest Size Heuristic (
The files are sorted in non-increasing order of their sizes. After that, we schedule the files on the compiler which has the minimum total size at this time.
4.2 Smallest Size Heuristic (
The files are sorted in increasing order of their sizes. After that, we schedule the files which on the compiler that has the minimum total size at this time.
4.3 Half-mixed Longest-Smallest Heuristic (
This heuristic is the moderation between the
The algorithm of the

4.4 Half-mixed Smallest-Longest Heuristic (
This heuristic is the moderation between the
4.5 Iterative-mixed Longest-Smallest Heuristic (
For this heuristic, instead of scheduling half of the larger files, we iterated over larger

4.6 Iterative-mixed Smallest-Longest- Heuristic (
For this heuristic, we adopt the same idea developed for
In this section, we adopt and examine several classes that gives different manner of generation of instances in order to discuss the results and examine the assessment of the proposed algorithms.
All developed algorithms are coded with Microsoft Visual C++ (Version 2013). The proposed algorithms were coded and executed on an Intel(R) Core (TM) i5-3337U CPU @ 1.8 GHz and 8 GB RAM. The operating system utilized throughout the research work is windows 10 with 64 bits. these algorithms were examined on five different types of sets of instances. We generate the size
• Class 1:
• Class 2:
• Class 3:
• Class 4:
• Class 5:
The triple
The pair (

Tab. 2 have in total 2350 instances. Different variables are selected to measure the performance assessment of the proposed algorithms. These variables are:
•
•
•
•
•
An overall of results, present
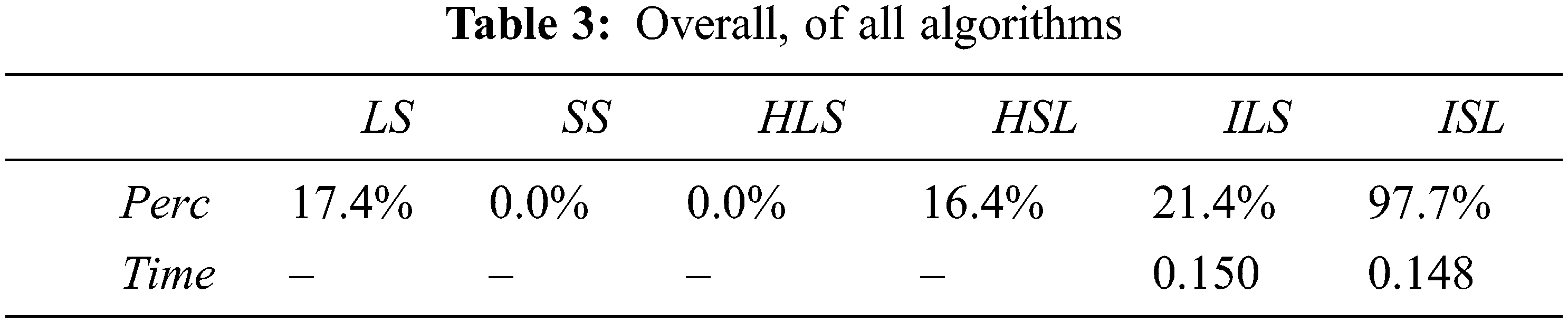
Tab. 3 shows that the algorithm that conduct the best value is
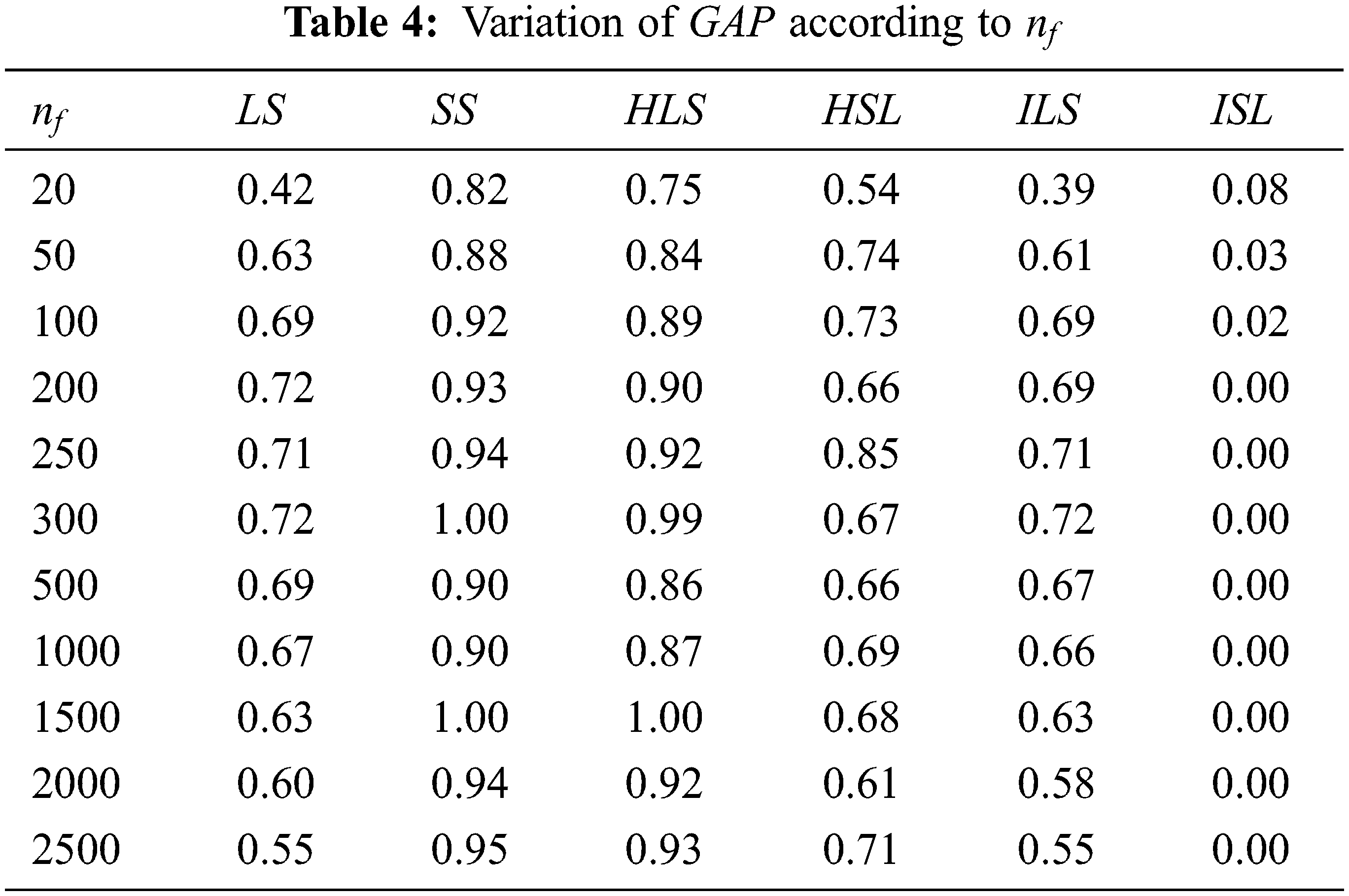
For algorithms [
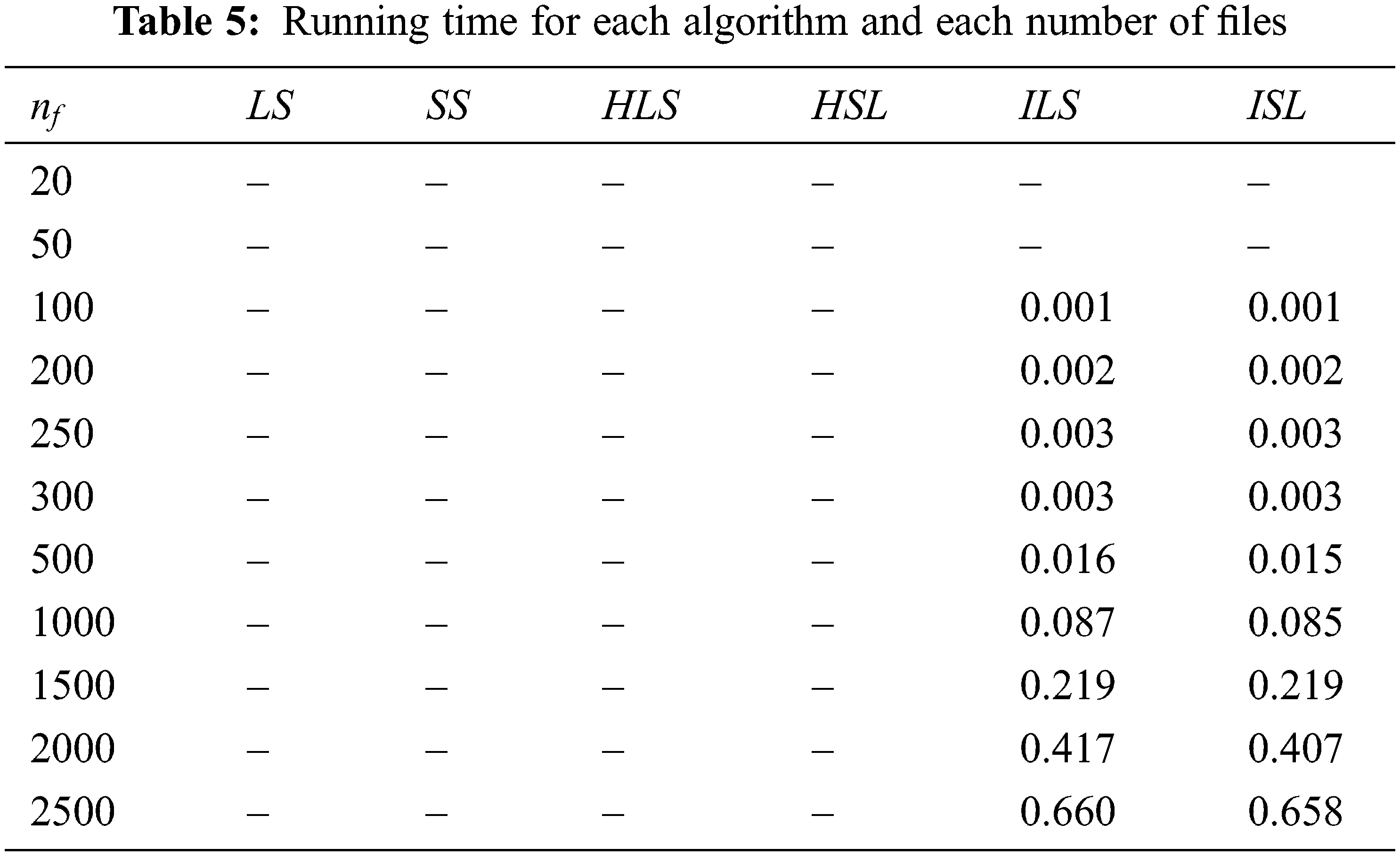
Tab. 5 shows that running time increase when the number of files increase for
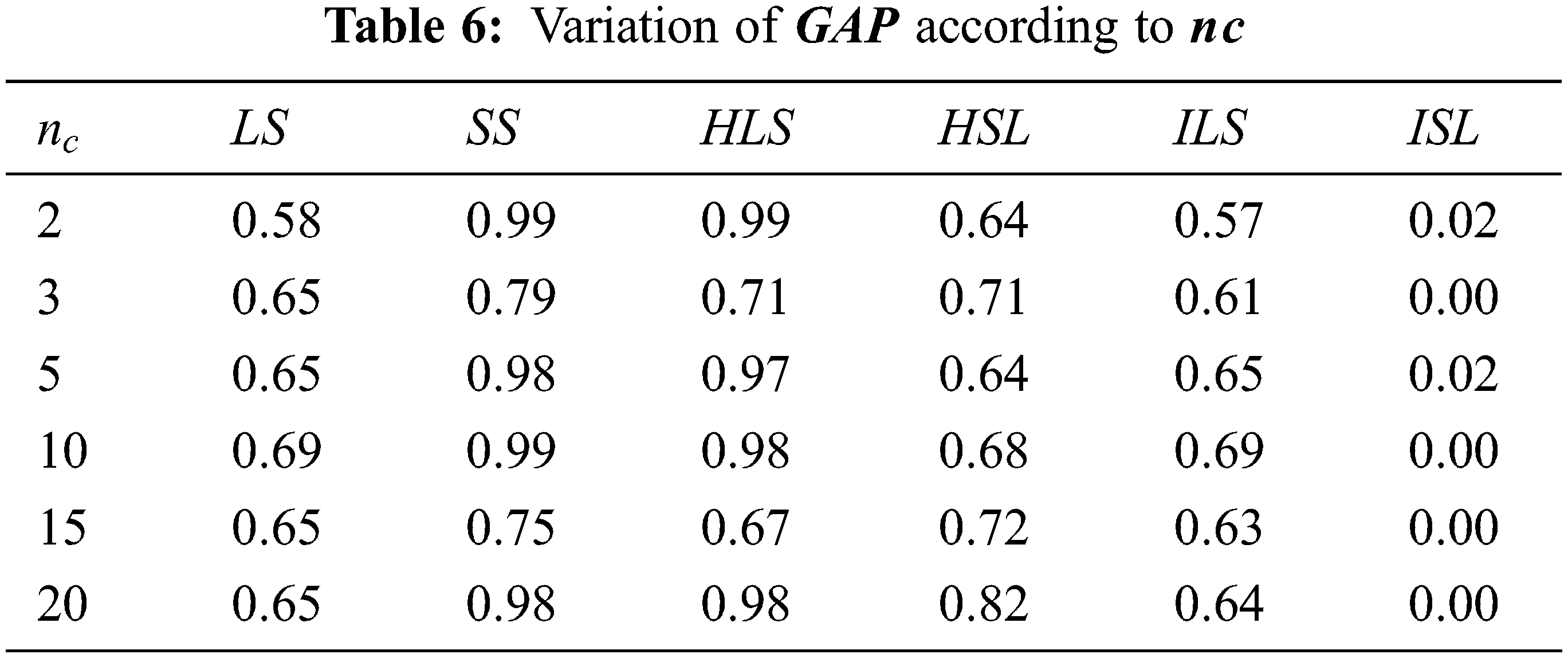
The corresponding running times for algorithms detailed in Tab. 6 are given in Tab. 7 below. Tab. 7 shows that running time increase when the number of files increases for ILS and ISL. For other algorithms, the time is less than 0.001 s.

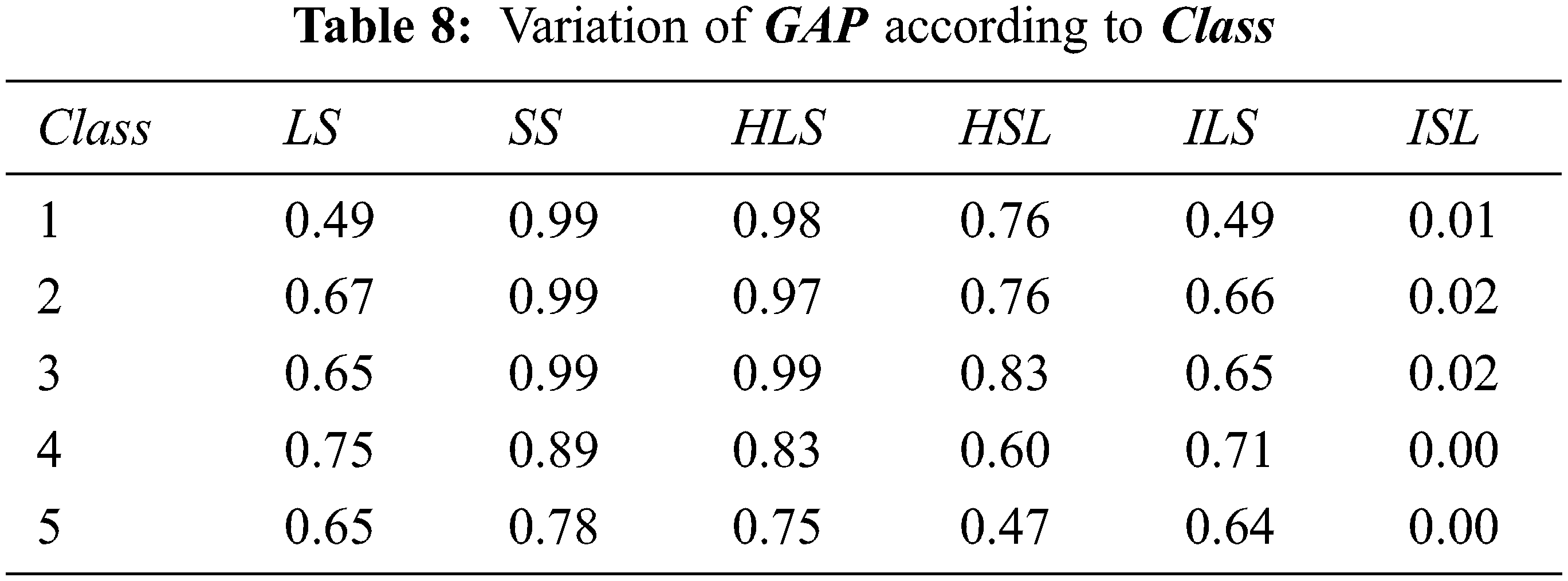
The behavior of the average gap according to different classes is showed in Tab. 8. This last table shows that there is not any correlation between the different classes and average gap. Thus, all classes having the same difficulty because the average gap differed slightly between class and other one.
The corresponding running times for algorithms detailed in Tab. 8 are given in Tab. 9 below.
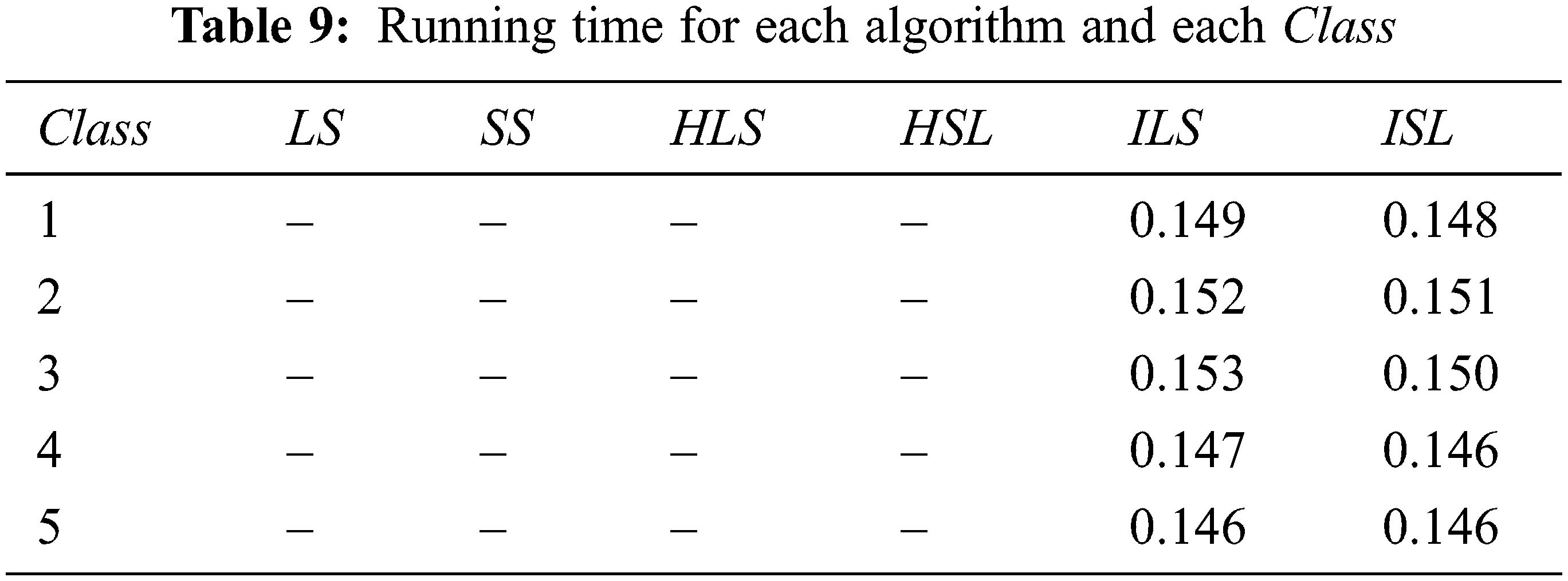
Tab. 9 shows that the algorithms
This work mainly focused on the fair distribution problem of files before the encryption process in compilers. The main contribution of this paper is based essentially on two approaches. Firstly, the proposal of a novel architecture regarding the transmission of different files in the presence of big data into the network using encryption process for files before transmitting to a network. Secondly, scheduling problem of assigning fair file loads to compilers in order to ensure timely compilation process. The problem studied in this paper is an NP-hard problem. In order to assure a fair distribution of files among different compilers, this work gives several solutions and approaches. These approaches improve the network performance and allow sending the maximum data in remarkable time. Several algorithms are proposed to solve the current challenge. The experimental results show that no dominance between algorithms and time is very interesting. The proposed heuristics can be used in the future to compare with other algorithms and develop an exact method to solve the problem.
Acknowledgement: The author would like to thank the Deanship of Scientific Research at Majmaah University for supporting this work under Project Number No. R-2022-85.
Funding Statement: The author received Funding for this study from Majmaah University.
Conflicts of Interest: The author declare that they have no conflicts of interest to report regarding the present study.
1. P. G. Lowney, S. M. Freudenberger, T. J. Karzes, W. Lichtenstein, R. P. Nix et al., “The multiflow trace scheduling compiler,” The Springer International Series in Engineering and Computer Science, vol. 234, pp. 51–142, 1993. [Google Scholar]
2. R. P. Colwell, R. P. Nix, J. J. O’Donnell, D. B. Papworth and P. K. Rodman, “A VLIW architecture for a trace scheduling compiler,” IEEE Transactions on Computers, vol. 37, no. 8, pp. 967–979, 1988. [Google Scholar]
3. R. P. Colwell, R. P. Nix, J. J. O’donnell, D. B. Papworth and P. K. Rodman, “A VLIW architecture for a trace scheduling compiler,” ACM SIGARCH Computer Architecture News, vol. 15, no. 5, pp. 180–192, 1987. [Google Scholar]
4. J. R. Ellis, “Bulldog: A compiler for VLIW architectures,” Ph.D. dissertation, Yale Univ., New Haven, CT (USA1985. [Google Scholar]
5. O. Mutlu, S. Mahlke, T. Conte and W.-m Hwu, “Iterative modulo scheduling,” IEEE Micro, vol. 38, no. 1, pp. 115–117, 2018. [Google Scholar]
6. C. Six, S. Boulmé and D. Monniaux, Certified compiler backends for VLIW processors highly modular postpass-scheduling in the compcert certified compiler, France, hal, 2019. [Google Scholar]
7. D. Mosse, H. Aydin, B. Childers and R. Melhem, “Compiler-assisted dynamic power-aware scheduling for real-time applications,” in Workshop on Compilers and Operating Systems for Low Power, Louisiana, USA, 2000. [Google Scholar]
8. M. B. Ashcraft, A. Lemon, D. A. Penry and Q. Snell, “Compiler optimization of accelerator data transfers,” International Journal of Parallel Programming, vol. 47, no. 1, pp. 39–58, 2019. [Google Scholar]
9. R. C. Lozano and C. Schulte, “Survey on combinatorial register allocation and instruction scheduling,” ACM Computing Surveys (CSUR), vol. 52, pp. 1–50, 2019. [Google Scholar]
10. R. C. Lozano, M. Carlsson, G. H. Blindell and C. Schulte, “Combinatorial register allocation and instruction scheduling,” ACM Transactions on Programming Languages and Systems (TOPLAS), vol. 41, pp. 1–53, 2019. [Google Scholar]
11. Ł. Domagała, D. van Amstel, F. Rastello and P. Sadayappan, “Register allocation and promotion through combined instruction scheduling and loop unrolling,” in Proc. of the 25th Int. Conf. on Compiler Construction, Barcelona Spain, pp. 143–151, 2016. [Google Scholar]
12. P. S. Rawat, F. Rastello, A. Sukumaran-Rajam, L.-N. Pouchet, A. Rountev et al., “Register optimizations for stencils on GPUs,” in Proc. of the 23rd ACM SIGPLAN Symp. on Principles and Practice of Parallel Programming, Vienna Austria, pp. 168–182, 2018. [Google Scholar]
13. D. Koeplinger, M. Feldman, R. Prabhakar, Y. Zhang and S. Hadjis, “Spatial: A language and compiler for application accelerators,” in Proc. of the 39th ACM SIGPLAN Conf. on Programming Language Design and Implementation, Philadelphia PA USA, pp. 296–311, 2018. [Google Scholar]
14. H. M. Jacobson, R. Nair, J. K. O'brien and Z. N. Sura, “Power-constrained compiler code generation and scheduling of work in a heterogeneous processing system,” Google Patents, 2015. [Google Scholar]
15. A. F. Glew, D. A. Gerrity and C. T. Tegreene, “Entitlement vector for library usage in managing resource allocation and scheduling based on usage and priority,” Google Patents, 2016. [Google Scholar]
16. J. A. Fisher, J. R. Ellis, J. C. Ruttenberg and A. Nicolau, “Parallel processing: A smart compiler and a dumb machine,” in Proc. of the 1984 SIGPLAN Symp. on Compiler Construction, Montreal Canada, pp. 37–47, 1984. [Google Scholar]
17. M. Jemmali and H. Alquhayz, “Equity data distribution algorithms on identical routers,” in Int. Conf. on Innovative Computing and Communications, Ostrava, Czech Republic, pp. 297–305, 2020. [Google Scholar]
18. H. Alquhayz, M. Jemmali and M. M. Otoom, “Dispatching-rule variants algorithms for used spaces of storage supports,” Discrete Dynamics in Nature and Society, vol. 2020, pp. 1–9, 2020. [Google Scholar]
19. H. Alquhayz and M. Jemmali, “Max-min processors scheduling,” Information Technology and Control, vol. 50, pp. 5–12, 2021. [Google Scholar]
20. M. Alharbi and M. Jemmali, “Algorithms for investment project distribution on regions,” Computational Intelligence and Neuroscience, vol. 2020, pp. 1–13, 2020. [Google Scholar]
21. M. Jemmali, “An optimal solution for the budgets assignment problem,” RAIRO—Operations Research, vol. 55, pp. 873–897, 2021. [Google Scholar]
22. M. Jemmali, “Budgets balancing algorithms for the projects assignment,” International Journal of Advanced Computer Science and Applications (IJACSA), vol. 10, pp. 574–578, 2019. [Google Scholar]
23. M. Jemmali, L. K. B. Melhim, S. O. B. Alharbi and A. S. Bajahzar, “Lower bounds for gas turbines aircraft engines,” Communications in Mathematics and Applications, vol. 10, no. 3, pp. 637–642, 2019. [Google Scholar]
24. M. Jemmali, “Projects distribution algorithms for regional development,” ADCAIJ: Advances in Distributed Computing and Artificial Intelligence Journal, vol. 10, no. 3, pp. 293–305, 2021. [Google Scholar]
25. M. Jemmali, L. K. B. Melhim and M. Alharbi, “Randomized-variants lower bounds for gas turbines aircraft engines,” in World Congress on Global Optimization. Metz, France, 949–956, 2019. [Google Scholar]
26. M. Jemmali, “Intelligent algorithms and complex system for a smart parking for vaccine delivery center of COVID-19,” Complex & Intelligent Systems, Vol. 8, pp. 597–609, 2021. [Google Scholar]
27. M. Jemmali, M. M. Otoom and F. AlFayez, “AlFayez Max-min probabilistic algorithms for parallel machines,” in Int. Conf. on Industrial Engineering and Industrial Management, Paris, France, pp. 19–24, 2020. [Google Scholar]
28. M. Jemmali and A. Alourani, “Mathematical model bounds for maximizing the minimum completion time problem,” Journal of Applied Mathematics and Computational Mechanics, vol. 20, no. 4, pp. 43–50, 2022. [Google Scholar]
29. S. M. Freudenberger, T. R. Gross and P. G. Lowney, “Avoidance and suppression of compensation code in a trace scheduling compiler,” ACM Transactions on Programming Languages and Systems (TOPLAS), vol. 16, no. 4, pp. 1156–1214, 1994. [Google Scholar]
30. G. Shobaki, K. Wilken and M. Heffernan, “Optimal trace scheduling using enumeration,” ACM Transactions on Architecture and Code Optimization (TACO), vol. 5, no. 4, pp. 1–32, 2009. [Google Scholar]
31. J. Eisl, D. Leopoldseder and H. Mössenböck, “Parallel trace register allocation,” in Proc. of the 15th Int. Conf. on Managed Languages & Runtimes, Linz Austria, pp. 1–7, 2018. [Google Scholar]
32. J. Eisl, Divide and allocate: The trace register allocation framework, San Francisico, CA, USA, ACM, 2018. [Google Scholar]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |