Computer Systems Science & Engineering DOI:10.32604/csse.2023.026461
Article

Colliding Bodies Optimization with Machine Learning Based Parkinson’s Disease Diagnosis

Ashit Kumar Dutta1,*, Nazik M. A. Zakari2, Yasser Albagory3 and Abdul Rahaman Wahab Sait4

1Department of Computer Science and Information Systems, College of Applied Sciences, AlMaarefa University, Ad Diriyah, Riyadh, 13713, Kingdom of Saudi Arabia
2Department of Nursing, College of Applied Sciences, AlMaarefa University, Ad Diriyah, Riyadh, 13713, Kingdom of Saudi Arabia
3Department of Computer Engineering, College of Computers and Information Technology, Taif University, Taif, 21944, Kingdom of Saudi Arabia
4Department of Archives and Communication, King Faisal University, Al Ahsa, Hofuf, 31982, Kingdom of Saudi Arabia
*Corresponding Author: Ashit Kumar Dutta. Email: adotta@mcst.edu.sa
Received: 27 December 2021; Accepted: 30 March 2022

Abstract: Parkinson’s disease (PD) is one of the primary vital degenerative diseases that affect the Central Nervous System among elderly patients. It affect their quality of life drastically and millions of seniors are diagnosed with PD every year worldwide. Several models have been presented earlier to detect the PD using various types of measurement data like speech, gait patterns, etc. Early identification of PD is important owing to the fact that the patient can offer important details which helps in slowing down the progress of PD. The recently-emerging Deep Learning (DL) models can leverage the past data to detect and classify PD. With this motivation, the current study develops a novel Colliding Bodies Optimization Algorithm with Optimal Kernel Extreme Learning Machine (CBO-OKELM) for diagnosis and classification of PD. The goal of the proposed CBO-OKELM technique is to identify whether PD exists or not. CBO-OKELM technique involves the design of Colliding Bodies Optimization-based Feature Selection (CBO-FS) technique for optimal subset of features. In addition, Water Strider Algorithm (WSA) with Kernel Extreme Learning Machine (KELM) model is also developed for the classification of PD. CBO algorithm is used to elect the optimal set of features whereas WSA is utilized for parameter tuning of KELM model which altogether helps in accomplishing the maximum PD diagnostic performance. The experimental analysis was conducted for CBO-OKELM technique against four benchmark datasets and the model portrayed better performance such as 95.68%, 96.34%, 92.49%, and 92.36% on Speech PD, Voice PD, Hand PD Meander, and Hand PD Spiral datasets respectively.

Keywords: Parkinson’s disease; colliding bodies optimization algorithm; feature selection; metaheuristics; classification; kelm model

1  Introduction

World Health Organization (WHO) reports that neurological diseases like multiple sclerosis, Parkinson’s disease (PD), shingles, epilepsy, Alzheimer’s disease, and stroke affect the Nervous Systems that is inclusive of nerves, brain, and the spine that connects them. An approximate of 16 out of 60 persons suffer from neurological disorders globally [1]. PD, a term initially coined by Parkinson [2], is a degenerative disorder of Central Nervous System that is closely related to a progressive movement-oriented chronic disorder [3]. According to PD Foundation, 4% of the global population before the age of 50 are diagnosed with PD while 7–10 million people around the world are affected with this disease. PD researches, in computational fields, are focused mainly on disease diagnosis. The studies conducted earlier were aimed at recognizing the patient’s degree of severity and diagnosing whether the PD is present or not. These studies focused on extracting features from handwriting exams amongst others [4]. Several researchers used signal during examination to diagnose the disease. But researches associated with handwriting-based examination (handwriting examination-based quality of patient tracing result could be employed to analyze the presence of PD) is very limited [5].

Early and accurate diagnosis of PD is indispensable, owing to its capacity to offer important data that can reduce the progression of the disease. In the recent past, several data-driven methodologies have been proposed to optimize the diagnosis of PD. Unlike method-based diagnosis systems, previous accessibility of analytical method is needed, whereas, in data-driven approaches, the availability of historical information is required. In recent times, Machine Learning (ML) has evolved as a promising area of study in diagnosing PD in both academia and healthcare industry [6,7]. Owing to its data-driven approach, ML methods introduced a paradigm shift in the way how pertinent data are analyzed and extracted in PD biomarkers. Moreover, ML technique offers relevant data-based insights which provide guidance associated with PD diagnosis and classification that in turn accelerates the decision making process [8]. Different ML approaches have been employed in the literature to overcome PD diagnosis problems. For example, in [9,10], dysphonia measurement was applied among healthy people to diagnose PD in them. Support vector machine (SVM) model was employed to only four dysphonic characteristics to PD classification because of their capacity in extracting non-linearity by utilizing non-linear kernel.

Kaur et al. [11] proposed an architecture-based grid search optimization to improve the deep learning (DL) method to predict the earlier onset of PD. In this method, numerous hyperparameters are to be tuned and set for the assessment of data using DL technique. The presented methodology includes hyperparameter, performance, and the optimization of DL approach. Mohammed et al. [12] aimed at analyzing the PD via voice dataset feature. The researchers proposed a Multiagent Feature Filter (MAFT) model to select the optimal features from voice data. MAFT approach was developed to select a subset of features so as to enhance the entire performance of prediction model and avoid overfitting as a result of extreme reduction of the features. Furthermore, this approach focused on reducing the difficulty of the predictions, speeding up the training phase, and constructing strong training models.

Gao et al. [13] employed a multi-disciplinary model to investigate PD patient falls using neuroimaging, clinical, and data demographics from two independent initiatives. With this ML approach, the authors created a prediction system for distinguishing non-fallers and fallers. With the help of controlled feature selection (FS) method, the authors detected the primary predictor of patient’s fall which includes Yahr stage, gait speed and Hoehn, gait difficulty-related measurements, and postural instability. For method-free analytical and method-based approaches, the researchers applied logistic regression (LR), random forest (RF), SVM, and extreme gradient boosting (XGboost). Rahman et al. [14] presented a PD diagnosis method through the extraction of cepstral features from voice signal, gathered from healthy ones and PD patients. In order to categorize the extracted feature, the authors utilized classification via SVM and reduction dimension via linear discriminant analysis (LDA). Olivares et al. [15] introduced an enhanced extreme learning machine (ELM) method by utilizing bat algorithm (BA) model that boosts the training stage of ML technique to either keep or reduce the loss and increase the accuracy in the learning stage. In order to evaluate the presented model, PD audio database was used.

The current study develops a new Colliding Bodies Optimization Algorithm with Optimal Kernel Extreme Learning Machine (CBO-OKELM) for diagnosis and classification of PD. The goal of the proposed CBO-OKELM technique is to identify whether PD exists or not in an individual. CBO-OKELM technique involves the designing of Colliding Bodies Optimization based Feature Selection (CBO-FS) technique for optimal subset of features. In addition, Water Strider Algorithm (WSA) with Kernel Extreme Learning Machine (KELM) model is developed for the classification of PD. The simulation analysis was conducted for CBO-OKELM technique against four benchmark datasets and the results were investigated under varying aspects. In short, the contributions of the paper are given herewith.

•   A new Colliding Bodies Optimization Algorithm with Optimal Kernel Extreme Learning Machine (CBO-OKELM) is developed for diagnosis and classification of PD

•   Colliding Bodies Optimization based Feature Selection (CBO-FS) technique is derived for optimal subset of features

•   Water Strider Algorithm (WSA) is introduced along with Kernel Extreme Learning Machine (KELM) model for classification process

•   The performance of the proposed CBO-OKELM model on four benchmark four was validated to highlight the betterment of the model.

2  The Proposed Model

In current study, a new CBO-OKELM technique is presented for diagnosis and classification of PD. The presented CBO-OKELM technique intends to determine whether PD exists or not in an individual. CBO-OKELM technique encompasses three major processes namely CBO-FS based feature selection, KELM-based classification, and WSA-based parameter tuning. The utilization of CBO algorithm, to elect the optimal set of features, and WSA, for parameter tuning of KELM model, help in accomplishing the maximum PD diagnostic performance.

2.1 Design of CBO-FS Technique

At the initial stage, CBO technique is utilized to choose an optimum subset of features. All the search agents are demonstrated as ‘bodies’ with mass as well as velocity. The primary place of ith body is arbitrarily given from j dimension search space, set by the user.

xij=xj,min+rand⋅(xj,max−xj,min), (1)

where rand implies an arbitrary number between zero and one. The collision takes place between two bodies, and in their places, the effect is upgraded dependent upon 1D collision laws [16]. To provide the body Xk (is also named as particle or object), their mass is determined as follows

mk=1/Jk1/∑i=1n⁡(1/Ji),k=1,…,n (2)

where Jk refers to the cost function value of kth particle and n can be an even number, denotes the entire amount of bodies utilized during the optimization procedure (population size). The n Colliding Body (CB) is arranged as to increasing the series based on its main purpose values. Afterwards, it is separated into two equivalent groups such as Stationary Objects (SO) and Moving Objects (MO). The objects of MO group collide against the member of SO group to improve its place and push the stationary objects near optimum places. To be specific, the colliding pairs are introduced based on the increasing order in terms of main function. Therefore, an optimum moving particle collides with an optimum stationary one. The velocity of the body, before the collision, is allocated as follows

Stationarybodies:vi=0,i=1,n2, (3)

Movingbodies:vj=xi−(n/2)−xi,i=n2+1,…,n. (4)

In other meta-heuristic techniques, the velocities are not determined as a derivative of place in terms of time. However, it can be written as a displacement under search space. Based on colliding bodies’ method, the collision velocity is computed as follows.

Stationarybodies:vi′=(mi+(n/2)+ϵmi+(n/2))vi+(n/2)mi+mi+(n/2),i=1,…n2, (5)

Movingbodies:vi′=(mi−ϵmi−(n/2))vimi+mi−(n/2),i=n2+1,…n, (6)

where ɛ refers to Coefficient of Restitution which is determined as a ratio of comparative velocity between two bodies after and before the collision.

ϵ=|vi+1′−vi′||vi+1−vi|. (7)

Fig. 1 illustrates the flowchart of CBO technique. This coefficient considers the diversity linearly between one and zero under the optimization procedure [17] to ensure the balance between exploration as well as exploitation stages. After the computation of displacement, it is feasible to determine the novel places of stationary and moving bodies as follows.

Stationarybodies:xinew=xj+rand.vi′,i=1,n2, (8)

Movingbodies:xinew=xi−(n/2)+rand.vi′,i=n2+1,…n, (9)

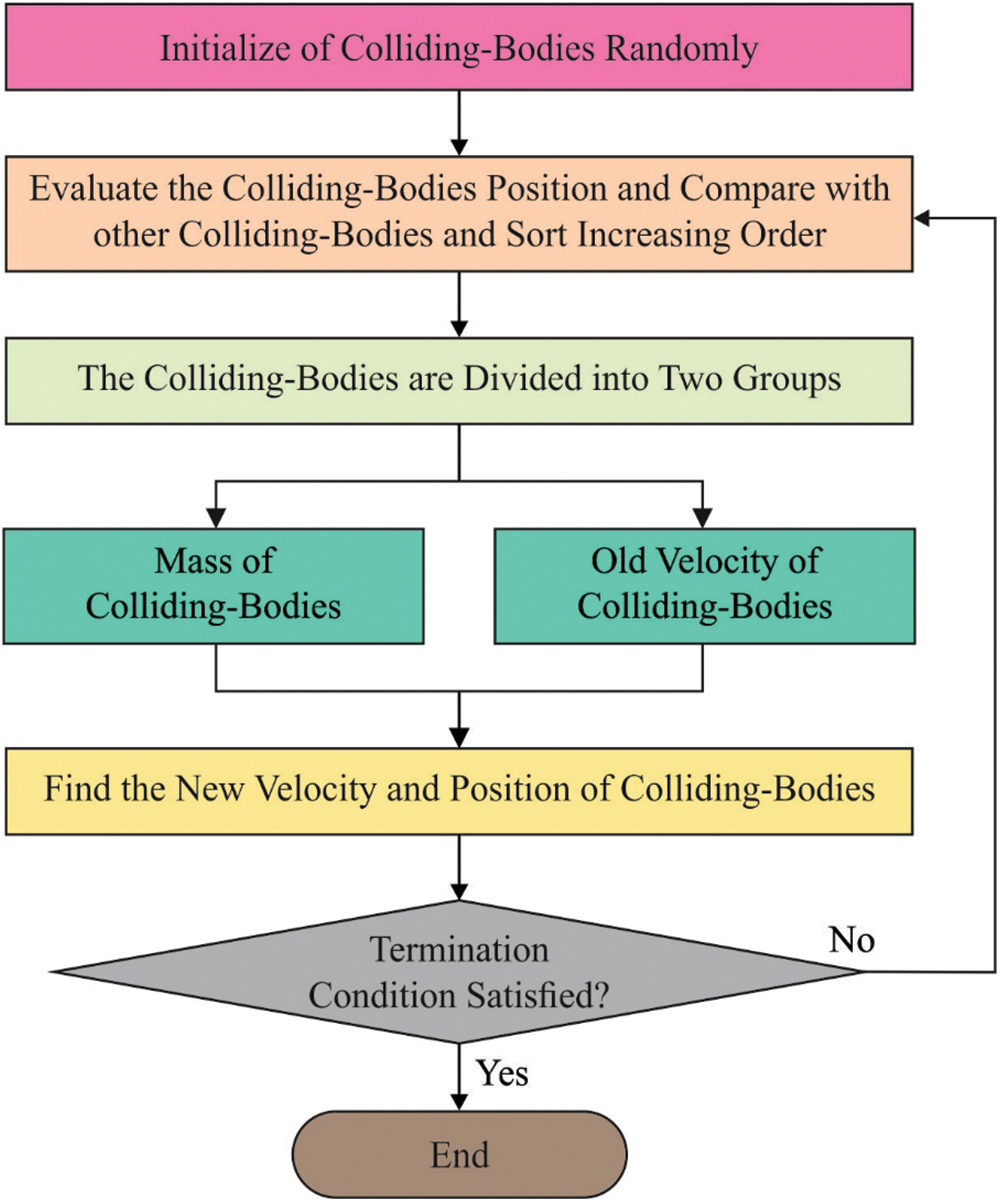
Figure 1: Flowchart of CBO

where rand implies the uniformly-distributed arbitrary vector in the range of −1 and 1. This iteration method is implemented on every particle during all the rounds and is repeated until it satisfies the end condition. The pseudocode 1 of CBO is reported herewith. In FS, once the size of feature vector is denoted as N, the amount of distinct feature sets is often considered to be 2N. This is an enormous space for detailed exploration. The presented hybrid technique was utilized to achieve this goal so as to find the feature space dynamically and consider the right group of features. The FS falls under multi-objective issues, as it needs to fulfil the exceeding one purpose to take an optimum solution that minimizes the subset of FS. Simultaneously, it should also maximize the accuracy of the outcome to the provided classifier.

For the results, the fitness function of the CBO is to define the solution from the situation created to achieve a balance between two purposes as given in Eq. (10).

fitness=αΔR(D)+β|Y||T| (10)

where ΔR(D) being the classifier error rate. |Y| refers to the size of subset which the technique chooses and |T| represents the entire amount of features comprised of present data set. α implies the parameter ∈ [0, 1] compared with the weight of error rate of classifier correspondingly and β = 1 − α indicates the importance of feande reduction. The classifier accuracy is considered as an important and weight parameter before counting the FS. If the estimation function is only accounted for calculating the accuracy of classifier, then the result is exclusive of the solutions, similar to accuracy. However, it takes the minimum chosen features which serve as an important feature to decrease the size of the challenge.

2.2 Design of OKELM Technique

During classification process, the chosen features are received by KELM model to classify the features as whether PD exists or not. ELM has the ability to learn fast and it involves only less number of tunable parameters. With a few alteration parameters, it doesn’t offer the selection of input weights and confidential conditions as new learning algae to feed forward neural network (FFNN) from a single hidden state. Fig. 2 depicts the framework of KELM. A novel model to ELM in the kernel is newly extended [18]. The subsequent section provides a brief outline for KELM technique.

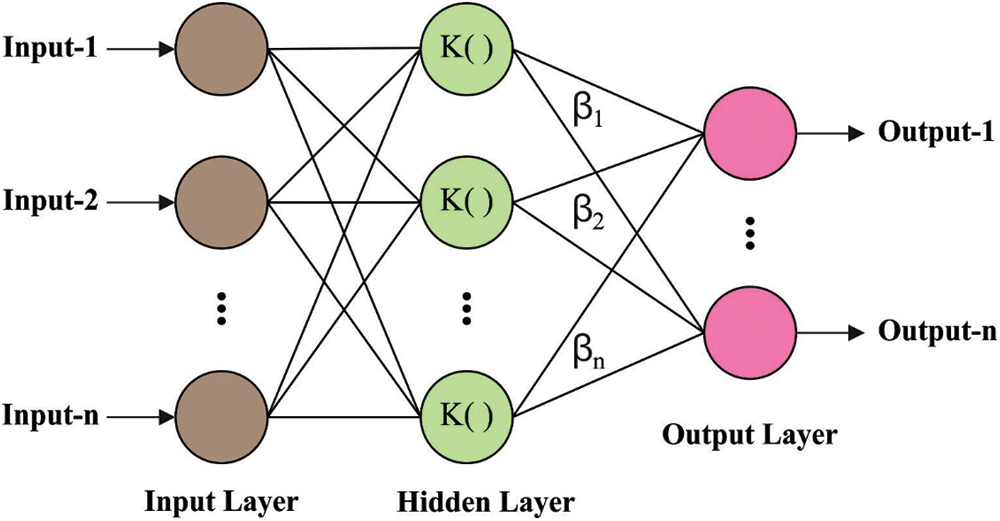
Figure 2: Structure of KELM

In the trained set, A={(xi,ti)|xi∈Rn,ti∈Rm,k=1,2,…,N} is provided, where n × 1 the input feature vector of xi and m × 1 of ti target vectors. The activation function h(x) is demonstrated as follows.

∑i=1N~⁡βih(wi⋅xj+bi)=0j,j=1,2,…,N (11)

wi stands for the weighted vector between the hidden state of ith and input state, and the individuality amongst the hidden state of ith is named after bi, the weighted vector amongst ith and resultant state is βi; oj refers to the target vector of jth input data. wi ⋅ xj defines the result of wi and xj internal products. N~ refers to the amount of hidden state nodes. In order to assess these instances correctly, ∑jN⁡‖0j−tj‖=0 is provided and ∑i=1N~⁡βih(wi⋅xj+bi)=tj,j=1,2,…,N with βi,wi,bi that is provided as Hβ = T,

where

H(w1,…,wN~,b1,…,bN~,x1,…,xN)=(h(w⋅xl+b1)⋯h(wN~⋅x1+bN~⋮⋱⋮h(w⋅xN+b1)⋯h(wN~⋅xN+bN~))N×N~ (12)

β=[βlT⋮βTN]N~×m,T=[tlT⋮tNT]N×m (13)

H signifies the outcome matrix of hidden state with ith column of H being ith hidden output neurons in terms of x1, x2, ⋅ ⋅ ⋅ , xN. An enter weight and vector confidential state bias require not to be modified. In that framework, the resultant weight of linear systems Hβ = T is provided as mathematical equation with the least square solution, β^ :

|H(w1,…,wN~,b1,…,bN~)β^−T‖=minβ‖H(w1,…,wN~,b1,…,bN~)β−T‖ (14)

Based on Moore-Penrose (MP) generalization inverse and kernel learning model, the resultant purpose of KELM is demonstrated as follows

F(x)=hβ=h(x)H†(1C+HH†)−1T={K(x,x1)⋮K(x,xN)}(1C+ΩELM)−1T (15)

Generally, RBF kernel is utilized from these techniques as (x,xi)=exp(−γ‖x−xi||2) , the penalty parameter C and gamma kernel μ are the two important parameters that depend upon the previous explanations. An initial parameter C is optimum for the minimization of appropriate error and difficulty of method. The second parameter γ defines the non-linear prediction under input region to huge space.

In order to adjust the parameters involved in KELM model optimally, WSA is used. WSA is a new population-based SI optimization technique simulated based on Water Strider (WS) life process. WSA simulates based on intelligent ripple transmission, succession, mating style, territorial performance, and WSs feeding processes. These approaches are executed with an effort to utilize mathematically-easy designs that signify the life processes of WS. Due to the hydrophobic leg of WS and surface tension of water, this set of animals possess a natural capability to live on top of the water [19]. The striders establish a territory for itself, while in case of a female WS, it makes so to defend its food resource, and in case of a male strider, it is to protect the mating partner. All the territories are generally occupied by a couple of female striders and one male is referred to as a ‘keystone’ strider. By oscillating its leg on top surface of the water, the strider takes ripples with distinct amplitudes, durations, and frequencies, thereby it can transmit distinct kinds of signals with one another.

According to this feature, the signals convey a distinct kind of data such as prevention of an invader, locating a prey, and courtship. Incoming signals are obtained with sensory receptor organ on its leg. This organ differentiates the signal too which is created by trapping the prey insects on the surface of water. The pre-copulatory calling signal, sent by male insects, are returned by negative/positive messages by the female insects. According to this feedback, the strider updates its places as provided in Eq. (16):

WSit+1=WSit+R. rand; Positive response WSit+1=WSit+R.(1+rand); negative response  (16)

where WSit refers to the place of ith WS from tth cycle and rand signifies the arbitrary number between zero and one. Besides,

R=WSFt−1−WSit−1    (17)

Convergence, exploratory, local optimum avoidance, exploitative, and the other presented technique features were analyzed by implementing the method on huge amount of multimodal, biased, unimodal shifted, and composite functions.

3  Experimental Validation

The proposed model was simulated using Python 3.6.5 tool. The performance validation of the proposed CBO-OKELM technique was done using benchmark datasets such as HandPD Spiral, HandPD Meander, Speech PD, and Voice PD.

Tab. 1 provides the number of features chosen by CBO-FS technique against other methods. Fig. 3 shows the features selected by CBO-OKELM technique on test datasets. It is evident that the proposed CBO-OKELM technique selected 3, 4, 7, and 6 on HandPD Spiral, HandPD Meander, Speech PD, and Voice PD datasets respectively.

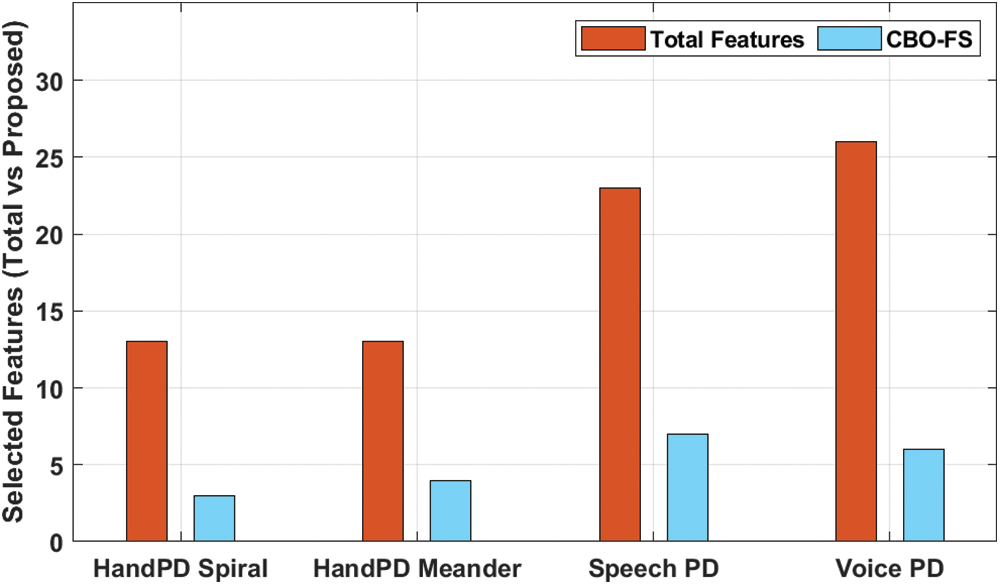
Figure 3: Number of FS analysis of CBO-FS technique

Fig. 4 illustrates the results, accomplished from comparative analysis, of CBO-FS technique against existing techniques. The results show that the proposed CBO-OKELM technique selected the least number of features compared to other techniques. For instance, with HandPD Spiral dataset, CBO-OKELM technique selected three features whereas modified grasshopper optimization algorithm (MGOA), modified grey wolf optimizer (MGWO), and Optimal Cuttlefish Algorithm (OCFA) techniques selected 5, 7, and 8 features respectively. Moreover, with voice PD dataset, the proposed CBO-OKELM method opted for 6 features, whereas MGOA, MGWO, and OCFA techniques selected 8, 9, and 17 features correspondingly.

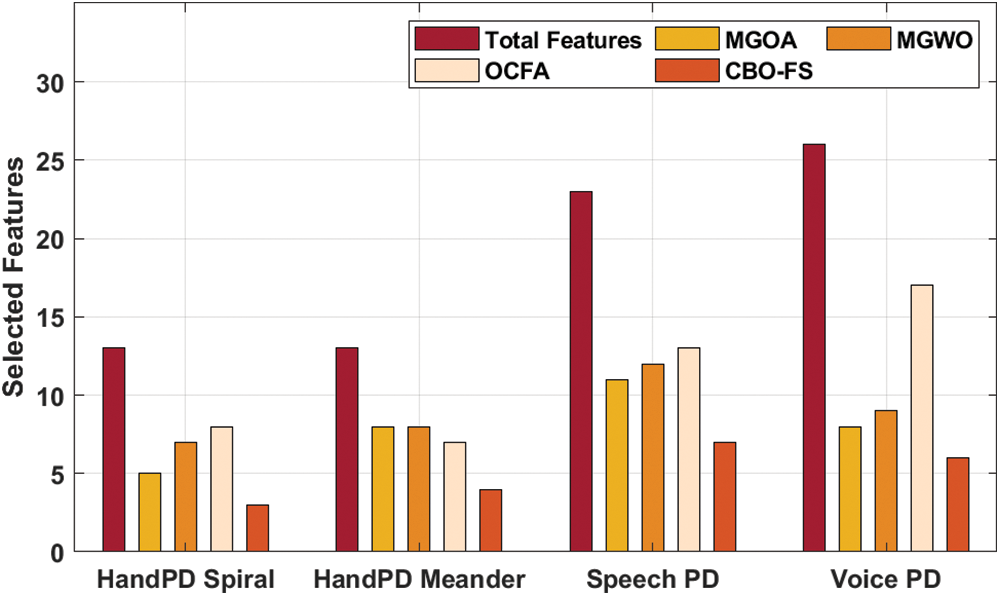
Figure 4: FS analysis of CBO-FS approach

Tab. 2 and Fig. 5 provide the results for accuracy analysis accomplished by CBO-OKELM technique against recent techniques on test datasets. The results exhibit that the proposed CBO-OKELM technique achieved high accuracy values on test dataset.

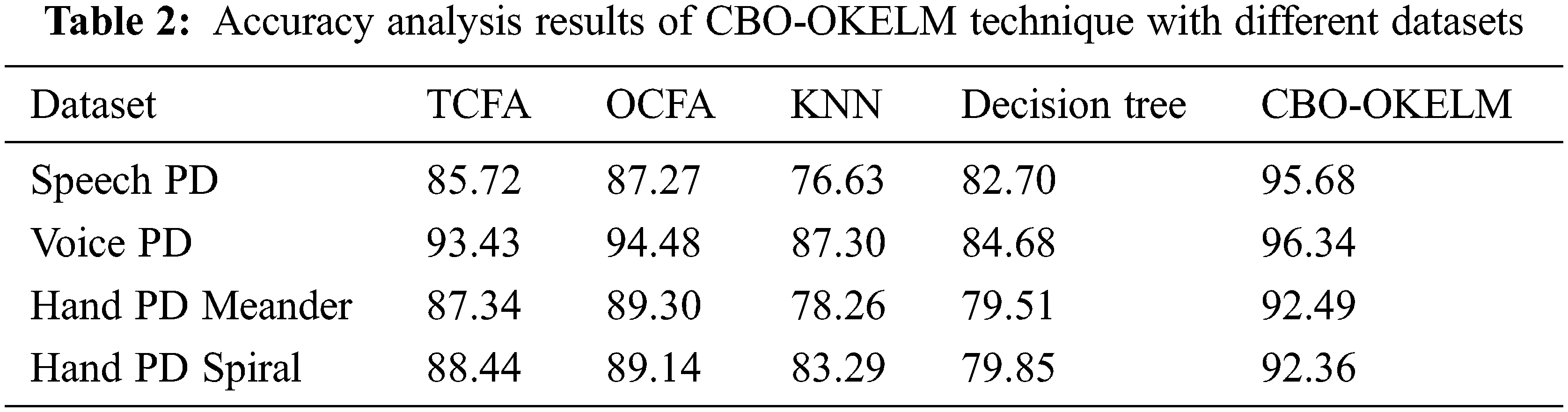
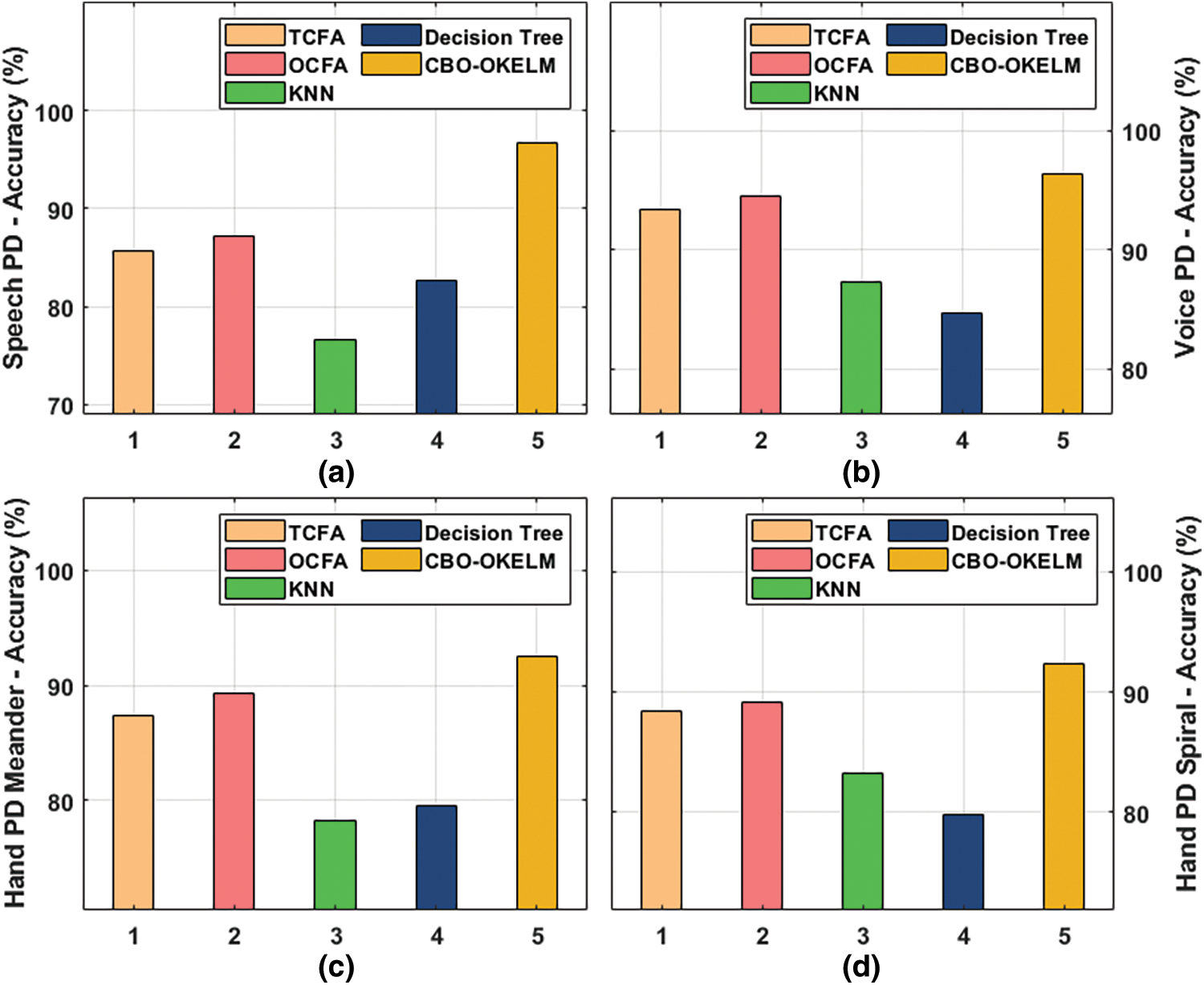
Figure 5: Accuracy analysis of CBO-OKELM technique

For instance, on speech PD dataset, the proposed CBO-OKELM technique gained a high accuracy of 95.68%, whereas total clock face area (TCFA), OCFA, k-nearest neighbor (KNN), and decision tree (DT) models obtained the least accuracy values namely, 85.72%, 87.27%, 76.63%, and 82.70%. Along with that, on voice PD dataset, the presented CBO-OKELM method attained a superior accuracy of 96.34%, whereas TCFA, OCFA, KNN, and DT algorithms obtained minimal accuracy values such as 93.43%, 94.48%, 87.30%, and 84.68% correspondingly. Eventually, on hand PD meander dataset, CBO-OKELM system reached a superior accuracy of 92.49%, whereas other techniques such as TCFA, OCFA, KNN, and DT approaches attained the least accuracy values namely, 87.34%, 89.30%, 78.26%, and 79.51%. Meanwhile, on hand PD spiral dataset, the proposed CBO-OKELM methodology achieved an increased accuracy of 92.36%, whereas TCFA, OCFA, KNN, and DT methods attained the least accuracy values such as 88.44%, 89.14%, 83.29%, and 79.85% correspondingly. Then, Fig. 6 shows the results for overall accuracy analysis of CBO-OKELM model.

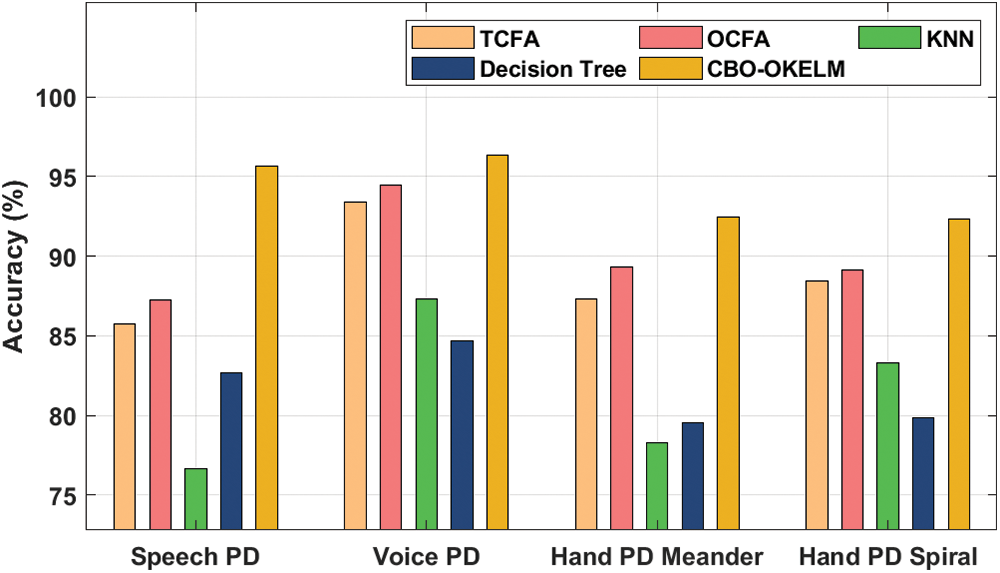
Figure 6: Overall accuracy analysis of CBO-OKELM technique

Fig. 7 illustrates the ROC analysis results attained by the proposed CBO-OKELM approach on test dataset. The figure exposes that the presented CBO-OKELM method reached improved outcomes with a minimal ROC of 98.2535.

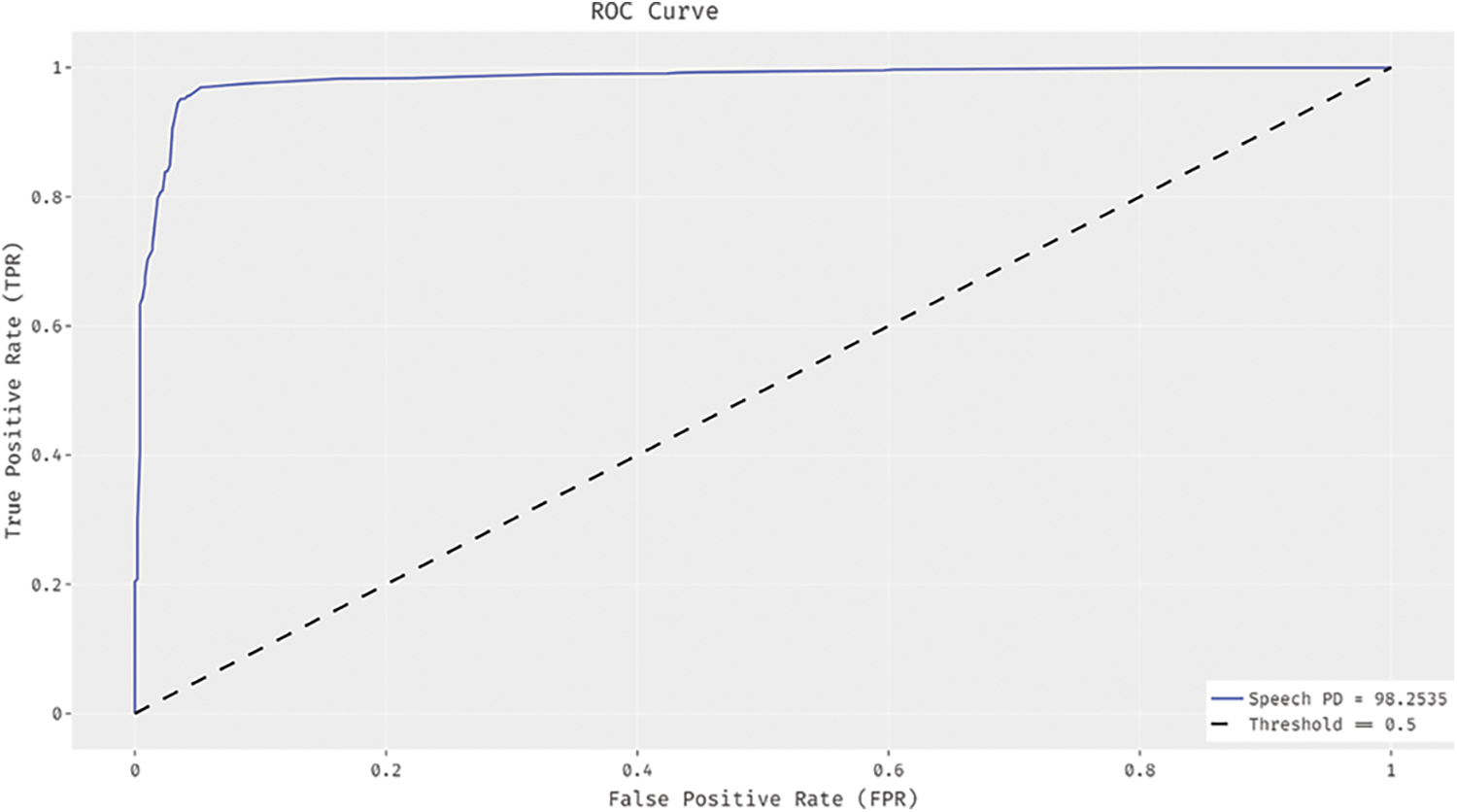
Figure 7: ROC analysis of CBO-OKELM technique

An execution time analysis as conducted between CBO-OKELM technique and other models and the results are shown in Tab. 3 and Fig. 8 [20]. The experimental values point out that the presented CBO-OKELM technique required the minimal execution time over other methods. For instance, on speech PD dataset, CBO-OKELM technique took the least execution time of 1.216 s, whereas TCFA and OCFA techniques consumed the highest execution times such as 1.812 and 1.564 s respectively. Likewise, on voice PD dataset, the proposed CBO-OKELM system required a low execution time of 1.852 s, whereas TCFA and OCFA techniques demanded more execution times such as 3.684 and 2.089 s correspondingly. Moreover, on hand PD meander dataset, CBO-OKELM technique demanded a desirable and minimal execution time of 0.687 s, whereas TCFA and OCFA methods required high execution times such as 1.261 and 0.893 s correspondingly. Furthermore, on hand PD spiral dataset, the proposed CBO-OKELM technique consumed the least possible execution time of 0.978 s, whereas TCFA and OCFA approaches obtained superior execution times such as 1.257 and 1.085 s correspondingly.

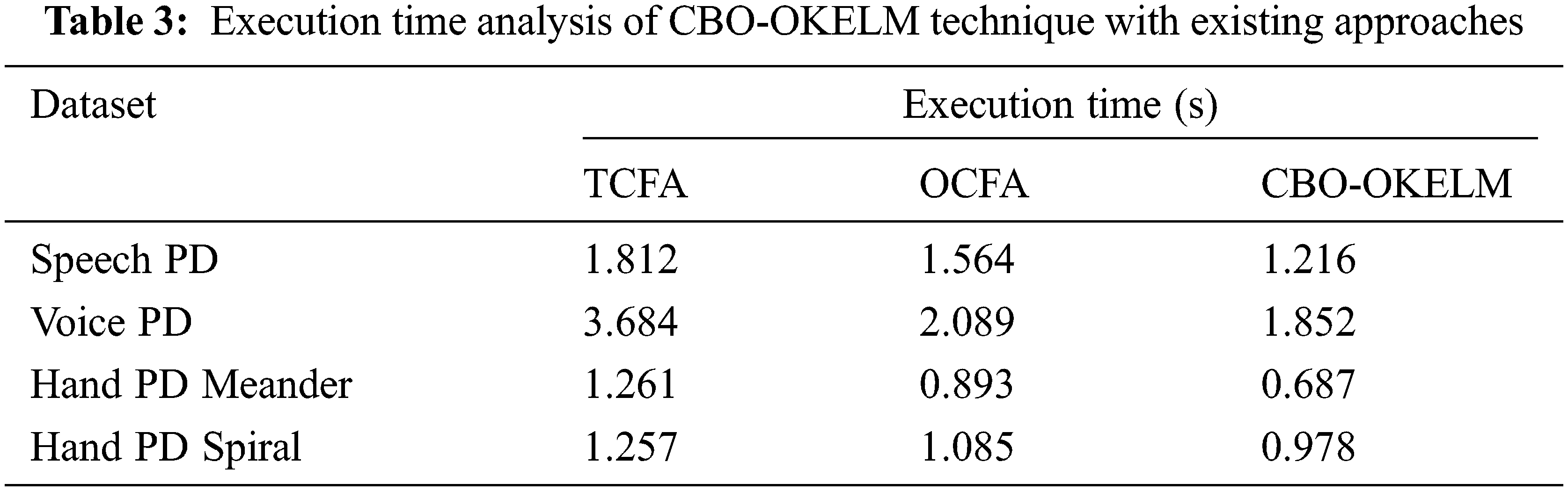
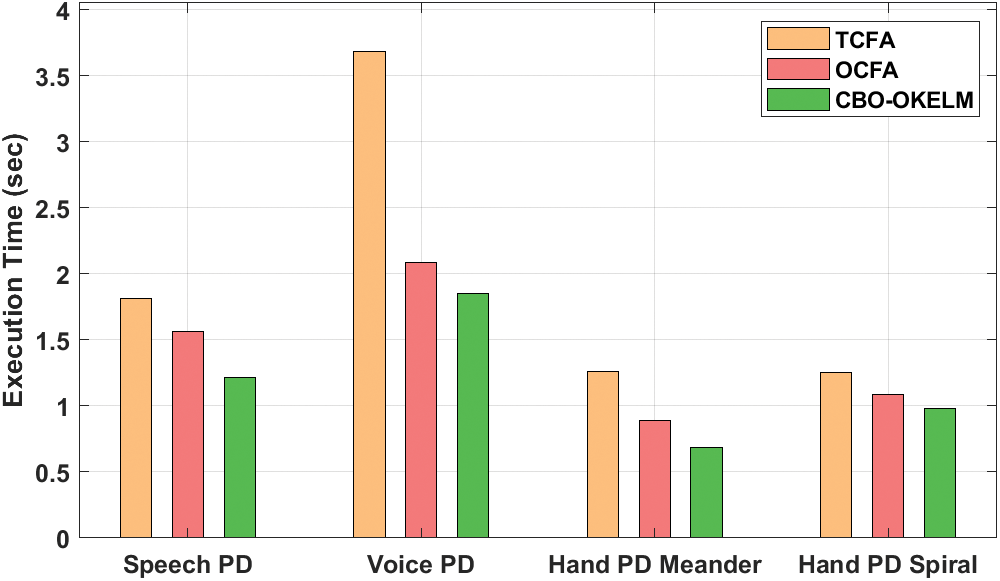
Figure 8: Execution time analysis of CBO-OKELM technique

Based on the results and discussion, it can be confirmed that the presented CBO-OKELM technique is superior to other methods on all the datasets considered for this study.

4  Conclusion

In this study, a new CBO-OKELM technique is presented for diagnosis and classification of PD. The aim of the presented CBO-OKELM is to determine whether PD exists or not. CBO-OKELM technique encompasses three major processes namely, CBO-FS based selection of features, KELM-based classification, and WSA-based parameter tuning. The utilization of CBO algorithm, to elect an optimal set of features, and WSA, for parameter tuning of KELM model, help in accomplishing the maximum PD diagnostic performance. The proposed CBO-OKELM technique was experimentally investigated against four benchmark datasets and the results were validated under different performance measures. The results established the supremacy of the proposed method over recent approaches. So, CBO-OKELM technique can be applied as an effective tool in the diagnosis and classification of PD. In future, improved PD classification performance of CBO-OKELM technique can be accomplished by using feature reduction and outlier removal approaches.

Acknowledgement: The authors would like to acknowledge the support provided by AlMaarefa University while conducting this research work.

Funding Statement: Taif University Researchers Supporting Project number (TURSP-2020/161), Taif University, Taif, Saudi Arabia.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  H. Gunduz, “Deep learning-based Parkinson’s disease classification using vocal feature sets,” IEEE Access, vol. 7, pp. 115540–115551, 2019. [Google Scholar]

 2.  S. Lahmiri and A. Shmuel, “Detection of Parkinson’s disease based on voice patterns ranking and optimized support vector machine,” Biomedical Signal Processing and Control, vol. 49, pp. 427–433, 2019. [Google Scholar]

 3.  M. Ugrumov, “Development of early diagnosis of Parkinson’s disease: Illusion or reality?,” CNS Neuroscience & Therapeutics, vol. 26, no. 10, pp. 997–1009, 2020. [Google Scholar]

 4.  S. Veeraragavan, A. A. Gopalai, D. Gouwanda and S. A. Ahmad, “Parkinson’s disease diagnosis and severity assessment using ground reaction forces and neural networks,” Frontiers in Physiology, vol. 11, pp. 587057, 2020. [Google Scholar]

 5.  I. Karabayir, S. M. Goldman, S. Pappu and O. Akbilgic, “Gradient boosting for Parkinson’s disease diagnosis from voice recordings,” BMC Medical Informatics and Decision Making, vol. 20, no. 1, pp. 228, 2020. [Google Scholar]

 6.  E. Rovini, C. Maremmani and F. Cavallo, “A wearable system to objectify assessment of motor tasks for supporting Parkinson’s disease diagnosis,” Sensors, vol. 20, no. 9, pp. 2630, 2020. [Google Scholar]

 7.  D. Braga, A. M. Madureira, L. Coelho and R. Ajith, “Automatic detection of Parkinson’s disease based on acoustic analysis of speech,” Engineering Applications of Artificial Intelligence, vol. 77, pp. 148–158, 2019. [Google Scholar]

 8.  R. Zhao, R. Yan, Z. Chen, K. Mao, P. Wang et al., “Deep learning and its applications to machine health monitoring,” Mechanical Systems and Signal Processing, vol. 115, pp. 213–237, 2019. [Google Scholar]

 9.  P. Drotar, J. Mekyska, I. Rektorova, L. Masarova, Z. Smekal et al., “Decision support framework for Parkinson’s disease based on novel handwriting markers,” IEEE Transactions on Neural Systems and Rehabilitation Engineering, vol. 23, no. 3, pp. 508–516, 2015. [Google Scholar]

10. Z. K. Senturk, “Early diagnosis of Parkinson’s disease using machine learning algorithms,” Medical Hypotheses, vol. 138, pp. 109603, 2020. [Google Scholar]

11. S. Kaur, H. Aggarwal and R. Rani, “Hyper-parameter optimization of deep learning model for prediction of Parkinson’s disease,” Machine Vision and Applications, vol. 31, no. 5, pp. 32, 2020. [Google Scholar]

12. M. A. Mohammed, M. Elhoseny, K. H. Abdulkareem, S. A. Mostafa and M. S. Maashi, “A Multi-agent feature selection and hybrid classification model for Parkinson’s disease diagnosis,” ACM Transactions on Multimedia Computing, Communications, and Applications, vol. 17, no. 2s, pp. 1–22, 2021. [Google Scholar]

13. C. Gao, H. Sun, T. Wang, M. Tang, N. I. Bohnen et al., “Model-based and model-free machine learning techniques for diagnostic prediction and classification of clinical outcomes in Parkinson’s disease,” Scientific Reports, vol. 8, no. 1, pp. 7129, 2018. [Google Scholar]

14. A. Rahman, S. S. Rizvi, A. Khan, A. A. Abbasi, S. U. Khan et al., “Parkinson’s disease diagnosis in cepstral domain using mfcc and dimensionality reduction with svm classifier,” Mobile Information Systems, vol. 2021, pp. 1–10, 2021. [Google Scholar]

15. R. Olivares, R. Munoz, R. Soto, B. Crawford, D. Cárdenas et al., “An optimized brain-based algorithm for classifying Parkinson’s disease,” Applied Sciences, vol. 10, no. 5, pp. 1827, 2020. [Google Scholar]

16. M. D. Monte, R. Meles and C. Circi, “Optimization of interplanetary trajectories using the colliding bodies optimization algorithm,” International Journal of Aerospace Engineering, vol. 2020, pp. 1–16, 2020. [Google Scholar]

17. A. Adamu, M. Abdullahi, S. B. Junaidu and I. H. Hassan, “An hybrid particle swarm optimization with crow search algorithm for feature selection,” Machine Learning with Applications, vol. 6, pp. 100108, 2021. [Google Scholar]

18. B. Shi, H. Ye, L. Zheng, J. Lyu, C. Chen et al., “Evolutionary warning system for COVID-19 severity: Colony predation algorithm enhanced extreme learning machine,” Computers in Biology and Medicine, vol. 136, pp. 104698, 2021. [Google Scholar]

19. A. Kaveh, N. G. Malek, A. D. Eslamlou and M. Azimi, “An open-source framework for the FE modeling and optimal design of fiber-steered variable-stiffness composite cylinders using water strider algorithm,” Mechanics Based Design of Structures and Machines, pp. 1–21, 2020. https://doi.org/10.1080/15397734.2020.1835489. [Google Scholar]

20. D. Gupta, A. Julka, S. Jain, T. Aggarwal, A. Khanna et al., “Optimized cuttlefish algorithm for diagnosis of Parkinson’s disease,” Cognitive Systems Research, vol. 52, pp. 36–48, 2018. [Google Scholar]

This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.