DOI:10.32604/csse.2023.026516

| Computer Systems Science & Engineering DOI:10.32604/csse.2023.026516 |  |
| Article |
A Secure Hardware Implementation for Elliptic Curve Digital Signature Algorithm
1Electronics and Micro-Electronics Laboratory (E. μ. E. L), Faculty of Sciences of Monastir, University of Monastir, Monastir, Tunisia
2College of Computer Science, King Khalid University, Abha, Saudi Arabia
3Université de Sousse, Institut Supérieur des Sciences Appliquées et de Technologie de Sousse, Sousse, Tunisie
*Corresponding Author: Mouna Bedoui. Email: mouna.bedoui1991@gmail.com
Received: 29 December 2021; Accepted: 23 March 2022
Abstract: Since the end of the 1990s, cryptosystems implemented on smart cards have had to deal with two main categories of attacks: side-channel attacks and fault injection attacks. Countermeasures have been developed and validated against these two types of attacks, taking into account a well-defined attacker model. This work focuses on small vulnerabilities and countermeasures related to the Elliptic Curve Digital Signature Algorithm (ECDSA) algorithm. The work done in this paper focuses on protecting the ECDSA algorithm against fault-injection attacks. More precisely, we are interested in the countermeasures of scalar multiplication in the body of the elliptic curves to protect against attacks concerning only a few bits of secret may be sufficient to recover the private key. ECDSA can be implemented in different ways, in software or via dedicated hardware or a mix of both. Many different architectures are therefore possible to implement an ECDSA-based system. For this reason, this work focuses mainly on the hardware implementation of the digital signature ECDSA. In addition, the proposed ECDSA architecture with and without fault detection for the scalar multiplication have been implemented on Xilinx field programmable gate arrays (FPGA) platform (Virtex-5). Our implementation results have been compared and discussed. Our area, frequency, area overhead and frequency degradation have been compared and it is shown that the proposed architecture of ECDSA with fault detection for the scalar multiplication allows a trade-off between the hardware overhead and the security of the ECDSA.
Keywords: Elliptic curve cryptography (ECC); Montgomery ladder; fault detection method; fault injection attack; digital signature; ECDSA; FPGA
In our daily life and with technological progress, the development of applications, especially those deployed in client-server mode over the Internet (such as e-mail, access to Web servers, access to databases, e-commerce, etc.) is rapidly growing. These applications require security by the use of symmetric or asymmetric cryptographic systems. Asymmetric cryptographic systems offer the best advantages in terms of security and easy implementation. On the other hand, used alone, encryption systems do not ensure authenticity, which is equal to Authentication + Integrity. In fact, the main security technique implemented so far is the digital signature. It makes it possible to ensure the authenticity and integrity properties of the exchange. It is based on asymmetric cryptography and hash functions. The digital signature is an encrypted fingerprint added to the message. It ensures integrity, authenticity and non-repudiation by the sender. It is based on asymmetric cryptography and hash functions.
ECDSA is a variant of digital signature algorithm (DSA) that uses cryptography on elliptic curves. It is the most standardized algorithm of signature schemes based on elliptic curves. It is important to remember that a cryptographic signature generated with an ECDSA algorithm having the size 64 bits has the same security level as an Rivest Shamir Adleman (RSA) cryptographic signature of size 2048 bits. In recent years, research on ECDSA hardware implementation has become very popular [1–6]. A lot of research is being done to improve ECDSA’s performance and this has led to a large number of implementations. In 2018, Asif et al. [6] developed a new architectural design of the ECDSA algorithm, for intelligent transport system (ITS) applications, which is able to validate the constraints in real time. The authors employed parallel processing techniques to minimize hardware delays which reduces real-time security and end-to-end delay of ITS messages. In a recent paper by Kamalakannan et al. [7], a modified ECDSA schema is proposed to be implemented in wireless sensor networks (WSNs) and radio frequency identification (RFIDs) devices. This schema offers more security and lower calculation costs by reducing the reverse operation applied in the key generation and signature phase.
Information security heavily relies on integrated circuits (ICs). Unfortunately, ICs face a lot of threats such as side channel or fault attacks. This work focuses on small vulnerabilities and countermeasures for the ECDSA. The motivation is that leakage sources may be used in different attack scenarios. By fixing the leakage, existing attacks are prevented but also undiscovered or non-disclosed attacks based on the leakage. Moreover, while the elliptic curve scalar algorithm is at the heart of the security of all elliptic curve related cryptographic schemes, all the ECDSA system needs security. A small leakage of few secret bits may conduct to fully disclose the private key and thus should be avoided. The ECDSA can be implemented in different flavors such as in a software that runs on a microcontroller or as a hardware self-contained block or also as a mix between software and hardware accelerator. Thus, a wide range of architectures is possible to implement an ECDSA system. In spite of their security, the hardware implementation of the ECDSA signature is subject to fault injection attacks aimed at recovering the secret key [8–11]. Fault injection attacks are known to be very effective and easy to implement. They are very effective against insecure implementations. The main objective of this works is to detect and prevent fault injection attacks. Therefore, one needs to protect the ECDSA implementation against fault-injection attacks by the implementation of countermeasure methods. The aim of our work was to obtain a Secure and robust ECDSA hardware implementation against faults injection attacks. First, we have presented a hardware implementation of the digital signature ECDSA. It is based on three steps: key generation, signature generation and signature verification. It requires the efficient implementation of three intellectual properties (IPs) for random key generation, asymmetric encryption and hash. We have chosen hash IP and random key generation IP, as well as asymmetric ECC encryption IP, which are the most efficient for all three IPs in terms of area, frequency and cost each time. For an implementation with a higher level of security and occupying less resource, we used the Keccak algorithm, as the Keccak algorithm is more secure than other hash algorithms. In addition to the above, another aspect is studied in this article, which is the resistance of the hardware implementation of the digital signature ECDSA to fault attacks. For this reason, we used a countermeasure at a higher hierarchical level of cryptography on elliptic curves, which is scalar multiplication, to protect against fault attacks. Scalar multiplication kP is the most expensive step. This operation is critical for the security of the secret key. In addition, the proposed ECDSA architecture with and without fault detection for the scalar multiplication have been implemented on Xilinx FPGA platform (Virtex-5). Both implementation results have been compared and discussed. Their area, frequency, area overhead and frequency degradation have been compared and it is shown that the proposed scheme allows a trade-off between the hardware overhead and the security of the ECDSA.
This paper is organized as follows. The second section gives a brief overview of some of the most relevant work in the literature. Section 3 is devoted to the proposed hardware architecture of ECDSA and discussion of the results of the proposed architecture synthesis. In the fourth section, a countermeasure at a higher hierarchical level of cryptography on elliptic curves, which is scalar multiplication, to protect ECDSA against fault attacks, is presented. Our conclusions are drawn in the final section.
This section focuses on the methods of countermeasures proposed for the ECDSA algorithm against fault injection attacks in the literature. Fault injection attacks are known to be very effective and easy to implement and consist of injecting one or more faults during the execution of the cryptographic process and using the wrong outputs to obtain information on the secret key. They are very effective against insecure implementations. Therefore, the need to protect implementations of the ECDSA against fault injection attacks. However, studies on the resistance of hardware implementation of ECDSA to faults injection attacks are lacking. One of the first examples of error analysis and detection procedures for signature is presented in [8]. The authors presented a countermeasure to protect systems based on ECC against fault attacks. It uses a check value together with the redundancy provided by the point representation to protect the data path and the program flow. Another method of countermeasure is described in [10]. The proposed countermeasures consist in adding a cyclic redundancy check (CRC) in the private key or using the public key to validate the signature before sending it. However, this method is expensive. In [12], the authors applied non-linear error detection codes to protect ECDSA operations from fault-based attacks. Their algorithms provide nearly perfect error detection capability at a reasonable overhead. Another countermeasure is described in [13]. The authors proposed a new algorithmic countermeasure capable of repelling all attacks by fault. The proposed countermeasure has a low computational cost and keeps its computational overhead around 30% w.r.t. the unprotected primitive.
3 Proposed Hardware Architecture for ECDSA Cryptosystem
The digital signature is one of the main advantages of asymmetric cryptography. It is a mechanism to authenticate a message, that is, to prove that a message is from a particular sender. The signature protocol ECDSA, proposed in 1992 by Serge Vaudenay, is a variant of the DSA standard which, unlike the original algorithm, uses cryptography on elliptic curves. It is now the most standardized signature scheme, appearing in the American national standards institute (ANSI) X9.62, federal information processing standards (FIPS) 186-3, institute of electrical and electronics engineers (IEEE) 1363-2000 and International organization for standardization (ISO)/international electrotechnical commission (IEC) 15946-2 [14] standards. The benefits of ECDSA over DSA and RSA are shorter key lengths and faster signing and encryption operations.
In this section, we introduce how to calculate the signature using ECC-based crypto-systems. For this, three Algorithms 1–3 are needed: private and public key pair generation, signature generation and signature verification. The ECDSA system is based like other algorithms processed on a public and a private key. To create its two keys, we follow algorithm 1.

The private and public key pair generation algorithm uses the random number generation (RNG) for random generation of the private key. Subsequently, the public key is computed by the scalar multiplication of the private key by the generating point of the elliptic curve E.

Having both keys (private and public), the algorithm 2 allows the generation of the signature of a message m by using a chosen hash function named H.
The verification step made by the algorithm 3 is needed to verify the signature (r, s).

An architectural description of the ECDSA signature authentication cryptosystem has been developed (see Fig. 1).
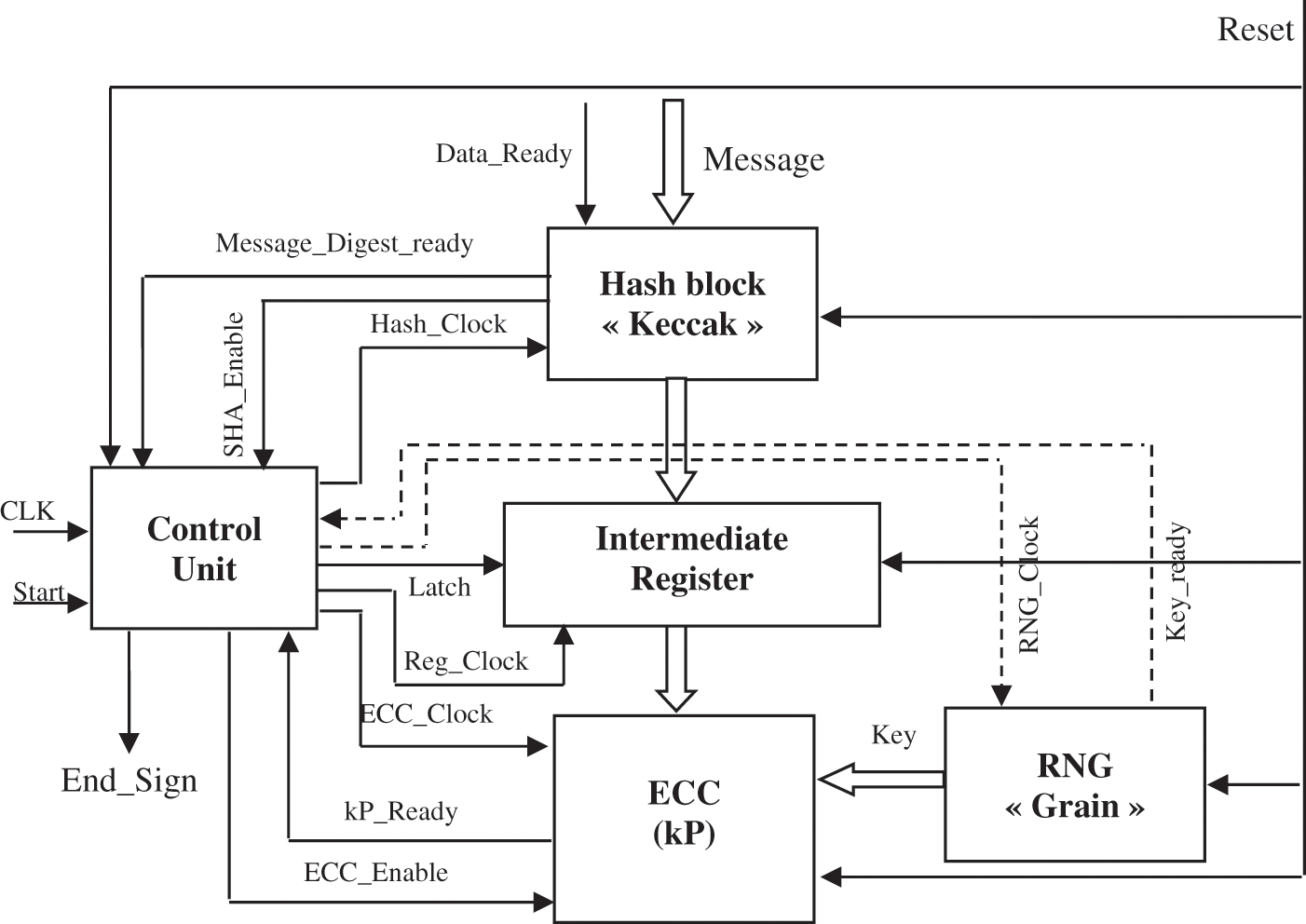
Figure 1: Proposed architecture of ECDSA
This architecture is composed of five modules:
■ A 163-bit ECC processor: based on the method of Montgomery, for the calculation on the scalar multiplication operation.
■ A hash block: Generates the hash used in both the electronic signature generation and verification operation of the message.
■ A Random Number Generator: generates a sequence of random numbers used as keys during the signature process.
■ An intermediate register to maintain the hash.
■ Control unit: Generates the control signals of the function blocks as well as the clock signals.
Since the signature is based on three IPs that are: the ECC IP, the RNG IP and the hash IP, we study the most efficient algorithms for these three IPs in terms of power, speed and cost each time. In this next section, we study these IPs and their architecture.The key represents the first parameter that must be well chosen to have a secure system. So having a key that is easy to implement on hardware platforms but at the same time difficult to attack is the first concern. It is therefore necessary to make the right choice of the algorithm to generate this key. There are several hardware methods for generating cryptographic keys, the best known are linear feedback back shift registers (LFSRs). These LFSRs can be used for other stream encryption generators such as those used for the Global system for mobile communications (GSM) standard (A5/1, A5/2 and W7). There are also generators based on non-linear feedback shift register (NLFSR), known as Grain [15]. In addition, cellular automata (CA) are an important family of stream ciphering generators [16]. The Tab. 1 compares the different stream cipher algorithms.

Being a synchronous stream encryption primitive, the Grain can be better implemented in hardware. It is bit-oriented while RC4 provides byte-by-byte encryption (used in secure sockets layer (SSL) and 802.11 wireless fidelity (WiFi)) but has weaknesses in initialization. On the other hand, we find the A5/1 (used in GSM) which is basically good but easily breakable. A characteristic that makes the Grain very powerful is the possibility of increasing the speed by means of hardware, which makes it very fast. It is well suited for real time applications. For this reason, we adopt this method in our implementation.
Grain 128 [17] supports 128-bit key and 96-bit initial vector (IV). It uses a linear feedback shift register (LFSR) to ensure good statistical properties. To exhibit non-linearity, a non-linear feedback shifts register (NFSR) is used with a non-linear filter. The nonlinear filter takes the contribution of both shift registers. The Fig. 2 illustrates the operation of this algorithm. Grain 128 provides high-performance security, small size, and simplicity when implemented [18]. It also offers the possibility to increase the speed thanks to the implementation of the polynomial functions (f (x) and g (x)) and the filter function (h (x)) several times. For this, we chose to ensure the generation of keys in the ECDSA protocol by the grain 128, given its hardware characteristics.
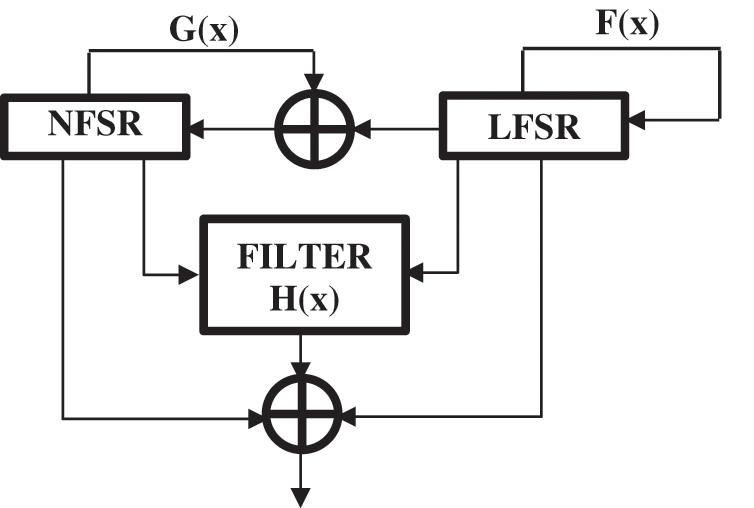
Figure 2: Grain diagram
The grain-128 synthesis results are presented in Tab. 2. They were created using the Virtex5 XC5VFX70T-FF665-(-3) platform and the integrated synthesis environment “ISE 14.7 tool” component’s packages.

According to the implementation results, the grain generator is the ideal trade between area and frequency. Moreover, the grain-128 preserves the benefits of the grain-80 by supporting a 128-bit key and a 96-bit initialization vector.
3.2 Keccak Architecture Design
One of the most important applications of hash functions is their use in electronic signatures. The electronic signature is a mechanism analogous to the handwritten signature to guarantee the integrity of an electronic document and proving to the reader of the document the identity of its author. Such mechanisms utilize the methods of asymmetric cryptography. There is a variant algorithm that performs the hashing, Tab. 3 gives the best known algorithms which are MD5 (Message Digest 5), SHA-0 (Secure Hash Algorithm 0), SHA-1, SHA-256, SHA-384, SHA-512 and Keccak.

These functions process a variable length input to output a fixed length message. Tab. 3 compares these different hashing algorithms according to different parameters: message size, Condensed size and number of rounds. From the Tab. 3, we note that MD5, SHA0 and SHA-1 have the same parameters except that the size of the MD5 digest is smaller (128 bits). In addition, we note that there are often collisions produced by these algorithms, so their security is no longer guaranteed. Cryptographic hash function standards since 1993 were the functions of the SHA family (SHA-0, SHA-1 and SHA-2), but some weaknesses were discovered for this set of functions. For this, national institute of standards and technology (NIST) launched a public competition in 2008, in order to choose a new function as standard. The Keccak family [24] won this competition in 2012, and subsequently became the new SHA-3 standard [25]. Therefore, the new algorithm is expected to be more secure. It is for this reason; we adopt the Keccak algorithm in our implementation. Keccak is a family of hash functions designed by Guido Bertoni, Joan Daemen, Michael Peeters and Gilles Van Assche [23]. Its instances are sponge functions, based on an internal permutation, called Keccak-f. Each instance of the family is characterized by the size of the permutation, b. There are 7 different Keccak-f permutations, denoted Keccak-f [b], with b ∈ {25, 50, 100, 200, 400, 800, 1600}. The Keccak-f [1600] function was submitted to the SHA-3 competition and was recently selected by NIST as the new standard.
Another construction called sponge construction has been proposed by Bertoni et al. in 2008 [26]. It is an iterated algorithm capable of producing arbitrary size outputs. Unlike the Merkle-Damgard construct which is based on a compression function, the sponge construction relies on an internal transformation of fixed size that is to say on a permutation f, operating on the words of b bits [20].
The footprint of a message m is calculated as follows: We start by adding a filling sequence (injective padding), then we divide the resulting string into blocks m1… mk of size t. Then, the b bits of the internal state are initialized with the value ‘0’. The procedure takes place in two successive steps (see Fig. 3):
■ The absorption step: During this phase, the blocks of the message are processed (“absorbed”) iteratively. The first block m1 is Xorated (exclusive OR) with the internal state. The result is then subjected to a transformation f. Then, the second block m2 is Xored with the state and the transformation f is applied again. The same operations are repeated until all message blocks are processed.
■ The pressing step: During this phase, values of the internal state are generated at different times by calls of the transformation f. The size of the prints extracted, can be chosen according to the needs.
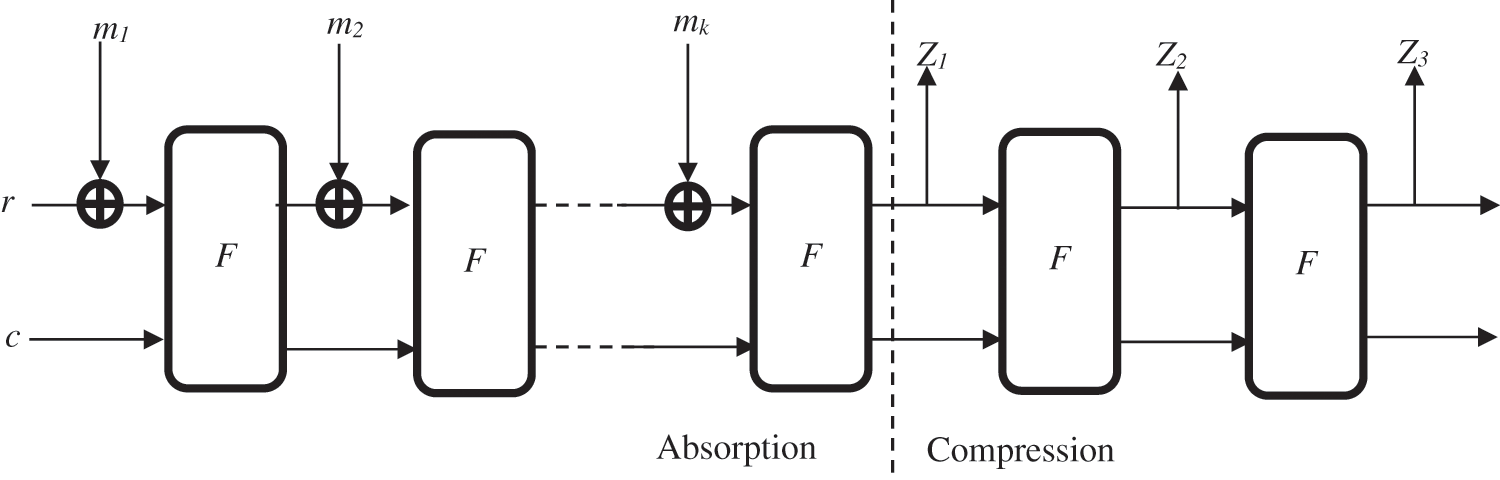
Figure 3: Principle of sponge functions
3.2.2 Description of the Keccak-f Permutation
The permutation Keccak-f applies to a state of 1600 bits, which is represented by a three-dimensional binary matrix, a [x] [y] [z], with 0 ≤ x, y < 5 and 0 ≤ z < 64. As a result, the state can be viewed as 64 slices, each of which contains 5 rows and 5 columns. The initial number of laps for the Keccak-f swap was set at 18 laps, but increased to 24 for the second round of the SHA-3 competition. This change is due to the publication of the zero-sum distinction by Aumasson and Meier [27]. These differences do not directly affect the security of the function, but violate the hermetic sponge strategy which guarantees the security of the hash function provided that the internal permutation has no exploitable structural properties. Each round R is composed of a sequence of 5 permutations, θ, ρ, π, χ, ι, which modify the state. Each transformation is charged with a different function, in order to ensure both confusion and a good diffusion in all directions of the state in three dimensions. The proposed architecture of Keccak is illustrated in Fig. 4.
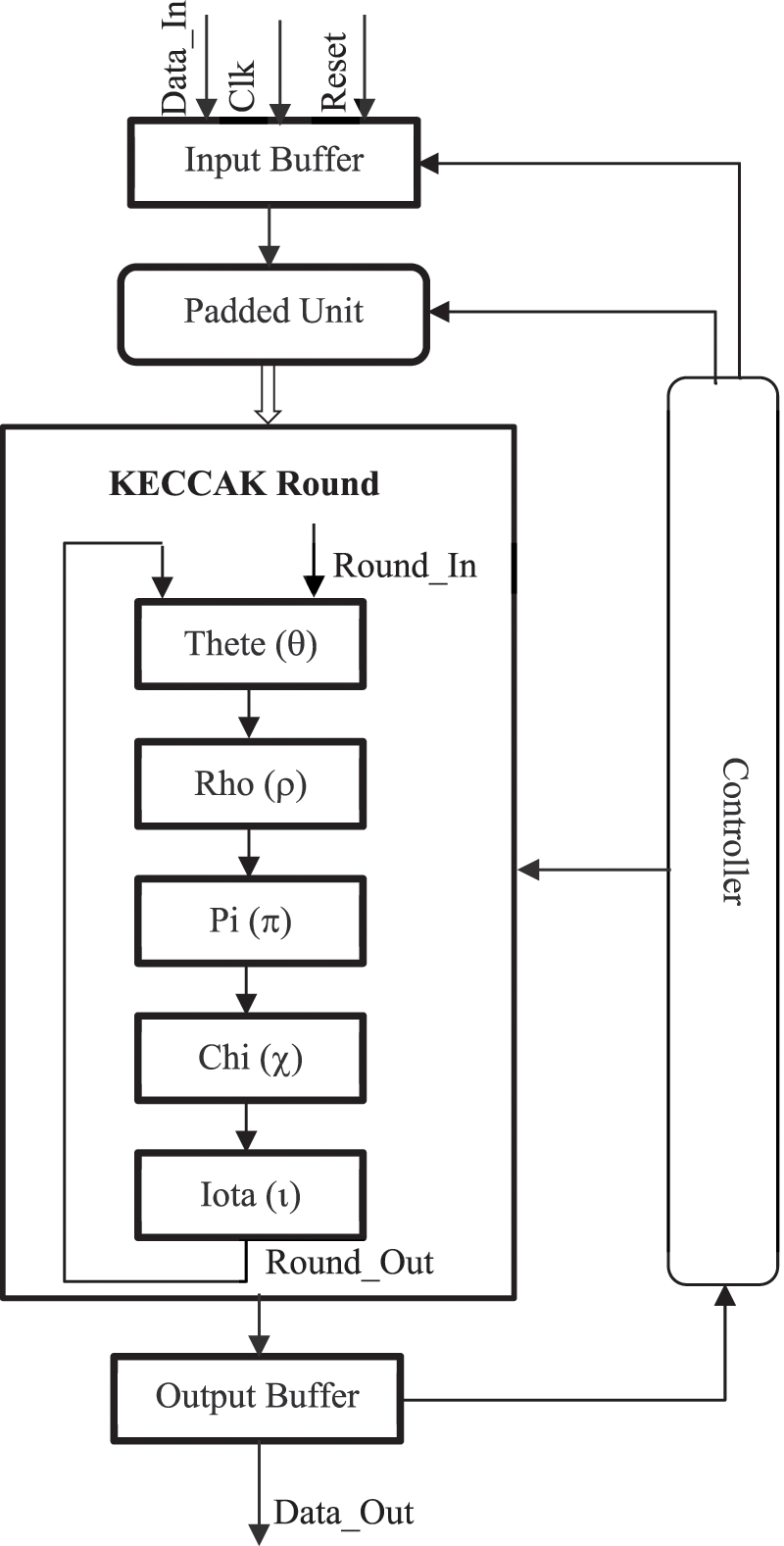
Figure 4: Proposed architecture of keccak
3.2.3 Simulation and Synthesis Results of Keccak IP
On the FPGA Virtex5 XC5VFX70T-FF665-(-3), the KECCAK IP was introduced. In terms of frequency, Area, Throughput (Gbps) and Efficiency (Mbps/slice), Tab. 4 shows its output.

With a performance of 256 bits each 25 clock cycles and a throughput of 14.054 Gbps, this design achieves a maximum operating frequency of 343.124 MHz.
3.3 Proposed Architecture of ECC Asymmetric Cryptosystem
The main operation in any protocol using elliptic curves is the multiplication of a point on the curve by a scalar; the calculation of kP = P + … + P, where k = (kiki-1…k1k0) is an integer and P a point on the curve. In order to carry out this operation effectively, many methods have been proposed. They are generally based on the so-called “double-and add” algorithm consisting in performing series of doubling interspersed with additions, according to the binary representation of the scalar K. To defend against simple power analysis (SPA) attacks, we will try to break the relation between current consumption and the branch side chosen in the algorithms and scalar multiplication. If the main bit ki is 1 or 0, there are many ways to standardize the calculations performed. The Montgomery scale allows scalar multiplication to be performed by performing an exact addition of points and doubling for each bit of k. Using this algorithm, one can expect the current consumption to vary only slightly depending on whether the bit ki is 1 or 0. The Montgomery algorithm is one of the effective parries against side channel attacks (SCA). Its original version was introduced by Montgomery, and applied only to a special category of elliptical curves (Montgomery curves). Recently, this method has also become applicable to elliptic curves defined on GF (2m) thanks to the addition and doubling formulas. The computation of kP is carried out by expressing the key k in the binary form: k = ki-1 ki-2 … k1 k0 and applying a chain of elementary doubling and addition operations. To obtain an efficient scalar multiplication, it is therefore necessary that the elementary operations be efficient and less expensive, such as the doubling and addition methods that have been used (addition and doubling of Montgomery). So the most efficient algorithm of scalar multiplication is the algorithm represented in projective coordinates which is given by the algorithm 4.

The architecture of an ECC cryptosystem is elucidated in Fig. 5. It consists of 7 modules: the first and second modules are successively addition and point doubling which constitute the basic calculation unit of the ECC, the third module is an affine-projective converter while the fourth serves to do the inverse conversion (from projective coordinates to affine coordinates), more than a controller that serves to synchronize the various modules via synchronization signals. The first step is to transform the affine coordinates into projective coordinates by the affine-projective converter, the latter receives the entries (x, y) and the transforms into X1, Z1, X2, Z2. The first converter outputs will be the inputs of the calculation unit, and they must undergo a succession of doubling and point addition operations according to the Ki test bit value. Finally, the outputs X1, Z1, X2, Z2 of the calculation unit must undergo a transformation at the second converter (projective-refinery) level to obtain the outputs (x, y) in affine coordinates. The three blocks of this architecture are synchronized by the synchronization signals from the controller.
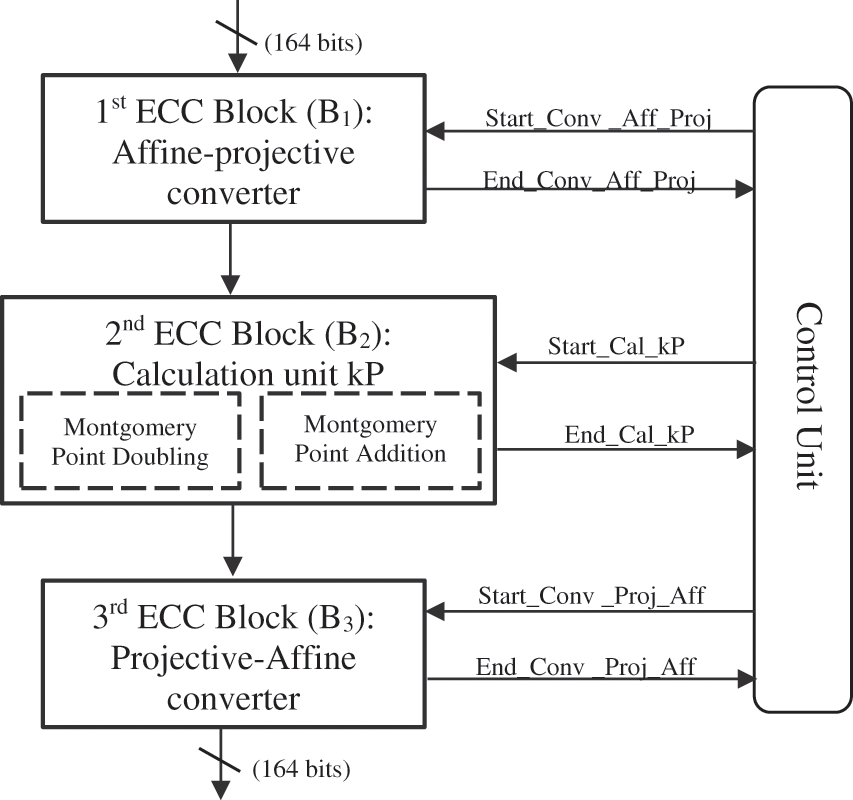
Figure 5: Proposed architecture of ECC asymmetric cryptosystem
In the proposed architecture, we have optimized the architecture of the ECC, it includes only two reusable Montgomery multipliers. This reuse of the multipliers increases the performance of the IP of the proposed architecture in this way from the point of view of slice occupancy and frequency. Tab. 5 shows the outcomes of the ECC implementation.

An FPGA Virtex 5 was used to test the proposed ECC-IP. The suggested FPGA implementation of ECC Point Multiplication is compared to numerous recent works in the literature in terms of area and frequency in Tab. 5. Our ECC Point Multiplication implementation takes considerably less area than other implementations. Our implementation has the highest frequency when compared to [30] and [31]. When compared to our work, the implementation proposed in [29] has the highest frequency. However, it require additional area. In comparison to the approach given in [28], our implementation utilizes 356.14% less occupied slices. The suggested version in [32] employs more Occupied Slices than ours, but has a higher total frequency. Our proposed implementation is more ideal for ECDSA implementation due to its efficiency.
4 Experimental Results and Comparisons
The synthesis was carried out using the integrated synthesis environment (ISE) 14.7 tool. The Xilinx Virtex5 XC5VFX70T-FF665-(-3) hardware target. The architecture synthesis results are presented in the Tab. 6. The Tab. 6 presents the results of ECDSA implementation in terms of area (look-up table (LUT) and Slices), frequency, number of cycles and execution time.

From the synthesis results, our proposed implementation of ECDSA can achieve an operating frequency of 110.521 MHZ and takes 7748 slices.
A comparative study was made between our results and the state of the art in the Tab. 7 in terms of frequency, occupation (signature + verification) and execution time.

The implementation proposed in [1] has the maximum frequency, but it requires more area than our work. However, our implementation has the highest frequency than [5], [7] and [34]. Compared to our work, the implementation proposed in [33] has the maximum frequency but uses more Occupied Slices then our implementation. In addition, by comparing our results to those found in [33], our results are the best in terms of area. Our architecture offers a 36% gain in terms of area.
5 Proposed Fault Detection Scheme for the ECDSA Implementations
When calculating an ECDSA signature, scalar multiplication kP is the most expensive step. The time required to calculate a signature, signature verification or shared secret exchange is mainly consumed by this operation. This operation is critical for the performance of the cryptographic system but also for the security of the secret key. The scalar used in an ECDSA signature is a number d chosen at random but if it is discovered by an attacker who also knows the signature (s,r) and the message m, as a result, the secret key K is compromised:
The ephemeral key has been the source of many publications to find the secret key. The most powerful attack in terms of complexity and the amount of signatures required is proposed by Schmit et al. [8]. Their attack is based on modification of the program flow to determine enough bits of the ephemeral key. The signature key d can be derived by a lattice attack. In addition, in the case of a particular implementation of the decomposition technique, Barthe et al. [9] described a hidden channel attack using leaked information when calculating a multiplication. This information makes it possible to find a certain number of low-order bits of the nonce k. Applied on a small amount of signatures, the secret key can be found through network reduction. This type of attack can be generalized to other implementations of the decomposition technique from the moment when the nonce k is manipulated with data known by the attacker. Scalar multiplication is therefore critical, because if the scalar used is discovered a secret can be compromised, except in the case of verification of an ECDSA signature because no secret elements are manipulated. From a performance point of view, this operation must also be implemented effectively.
To protect against these attacks, we used a countermeasure at a higher hierarchical level of cryptography on elliptic curves, which is scalar multiplication and can therefore be used on any elliptic curve that we proposed in our paper [35]. The proposed fault detection method is based on scrambling technique. The countermeasure is to duplicate the scalar multiplication scheme, so that the executions of the scalar multiplication algorithm are performed simultaneously. We used this approach to scramble the byte between the two executions of the scalar multiplication algorithm, so that each byte of the first data path is scrambled with the respective byte in the second data path. In this way, we have ensured that an error on one data path will produce an error on the second data path. The scrambling mechanism is used at the end of each block: Affine_procective converter, kP calculation unit and Projective_affine converter. This approach is simple and easy for hardware implementation. The proposed technique is presented in Fig. 6.
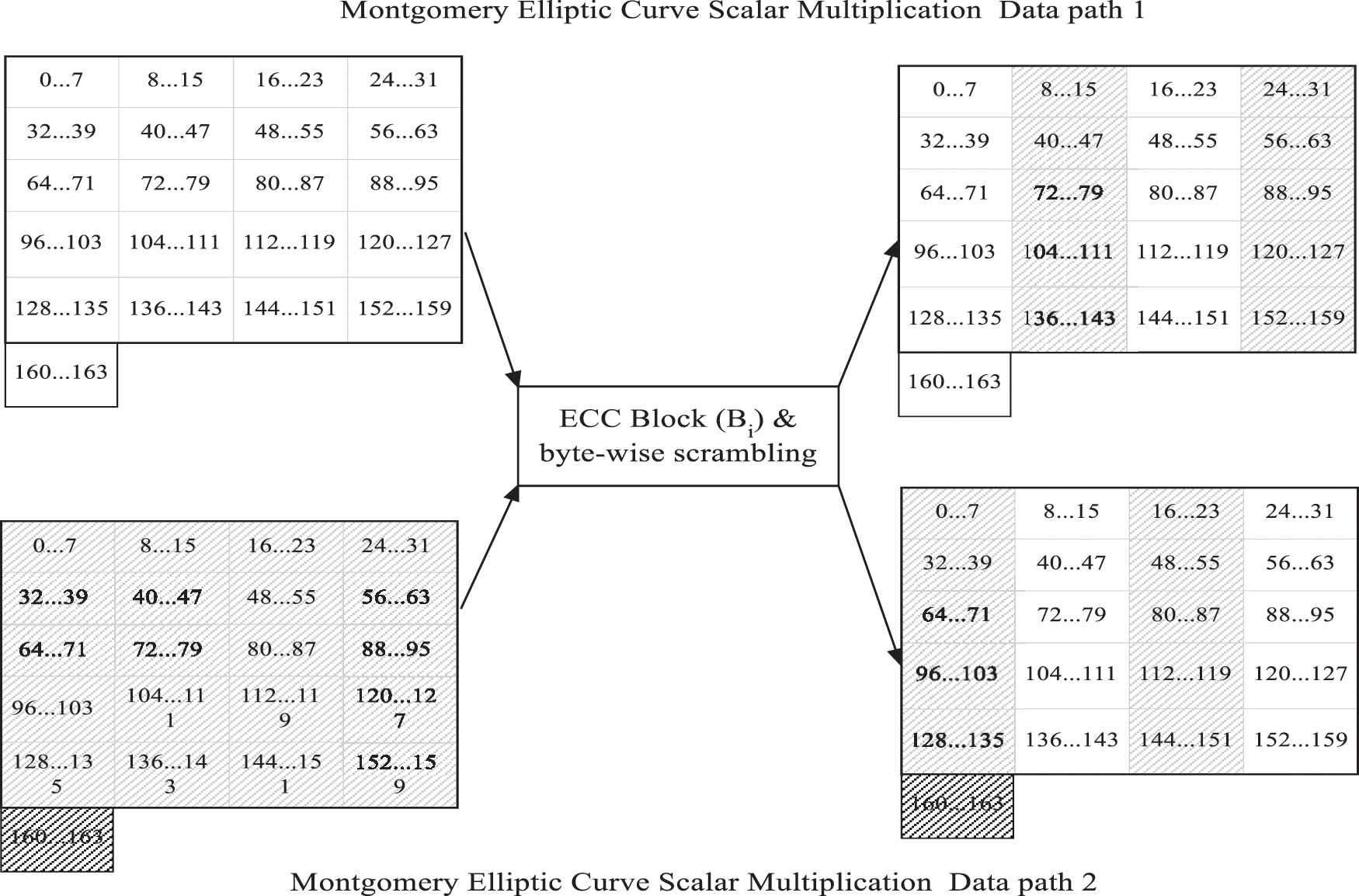
Figure 6: Technique of scrambling byte-wise in Montgomery Scalar Multiplication block [35]
Our design for hardware implementation of ECDSA digital signature with and without fault detection method for Montgomery scalar multiplication, was simulated, synthesized, and implemented using XC5VFX70T board from Xilinx Virtex-5 family. In addition, the developed method has been examined practically as shown in Fig. 7, the test results are fully functional. The FPGA implementation of the ECDSA digital signature algorithm with and without fault detection method for Montgomery scalar multiplication has been accomplished on a Xilinx Virtex-5 XC5VFX70T package FF1136 speed-3, using Xilinx ISE 13.1 as synthesis tool, ModelSim (PE Student Edition 6.4b); which provides a complete simulation and debugging environment for complex FPGA designs. It supports several description languages, including VHSIC hardware description language (VHDL) for simulation, and Xilinx ChipScope Pro 14.7 as a logic analyzer for debugging. The design was coded using VHDL.

Figure 7: Hardware implementation photo
The architecture of the ECDSA signature with and without fault detection method for the Montgomery scalar multiplication has been described using VHDL language, simulated by ModelSim simulator 6.4b and synthesized with XILINX ISE 14.7. The FPGA platform target was XC5VFX70T from Xilinx Virtex-5 family. Tab. 8 presents the results of the ECDSA synthesis on the Virtex 5 card.

The original ECDSA implementation necessitates 9921 occupied Slices for a frequency of 110.521 MHz. The ECDSA implementation with fault detection method need a 21.9% overhead of the Occupied Slices and 1.92% degradation of the frequency compared to ECDSA implementation against fault without fault detection method.
ECDSA’s suggested design is resistant to fault attack. The employment of a duplication scheme and scrambling approach for the Montgomery Scalar Multiplication algorithm as a countermeasure against fault attacks at a higher hierarchical level of cryptography on elliptic curves. Due to variances in FPGA technology employed and a lack of FPGA implementation results from other papers, a direct comparison of performance of hardware implementations with other reported results is not available. Therefore, it is difficult to give a fair comparison in this regard, but, in any case, our results clearly show that FPGA-based implementations of the ECDSA algorithm with and without fault detection methods are very attractive for many applications.
In this paper, we have presented a hardware implementation of the digital signature ECDSA. It is based on three steps: key generation, signature generation and signature verification. It requires the efficient implementation of three IPs for random key generation, asymmetric encryption and hash. we have chosen hash IP and random key generation IP, as well as asymmetric ECC encryption IP, which are the most efficient for all three IPs in terms of area, frequency and cost each time. However, other aspects can be studied: resistance to attacks, etc. For this reason, we used a countermeasure at a higher hierarchical level of cryptography on elliptic curves, which is scalar multiplication to protect against fault attacks. In addition, the proposed ECDSA architecture with and without fault detection for the scalar multiplication have been implemented on Xilinx FPGA platform (Virtex-5). Its frequency and area have been compared and discussed. The FPGA implementation results show that the proposed architecture achieves good performance in terms of frequency and area.
Acknowledgement: The authors extend their appreciation to the Deanship of Scientific Research at King Khalid University for funding this work through Research Group Project.
Funding Statement: The funding was provided by the Deanship of Scientific Research at King Khalid University through Research Group Project [grant number RGP.1/157/42].
Conflicts of Interest: No potential conflict of interest was reported by the authors.
1. E. Wajih, B. Noura, M. Mohsen and T. Rached, “Low power elliptic curve digital signature design for constrained devices,” International Journal of Security (IJS), vol. 6, no. 2, pp. 1–14, 2012. [Google Scholar]
2. P. Pessl and M. Hutter, “Curved tags–a low-resource ECDSA implementation tailored for RFID,” in Int. Workshop on Radio Frequency Identification: Security and Privacy Issues, Springer, Cham, pp. 156–172, 2015. [Google Scholar]
3. M. Knežević, V. Nikov and P. Rombouts, “Low-latency ECDSA signature verification-a road toward safer traffic,” IEEE Transactions on Very Large Scale Integration (VLSI) Systems, vol. 24, no. 11, pp. 3257–3267, 2016. [Google Scholar]
4. H. Zhong, R. Zhao, J. Cui, X. Jiang and J. Gao, “An improved ECDSA scheme for wireless sensor network,” International Journal of Future Generation Communication and Networking, vol. 9, no. 2, pp. 73–82, 2016. [Google Scholar]
5. A. Sghaier, M. Zeghid, C. Massoud and M. Mahchout, “Design and implementation of low area/power elliptic curve digital signature hardware core,” Electronics, vol. 6, no. 2, pp. 46, 2017. [Google Scholar]
6. A. Asif, U. Zahra, M. Ahmed, M. F. Siddiqui and M. A. Javed, “FPGA based implementation of ECDSA for secured ITS,” in 2018 10th Computer Science and Electronic Engineering (CEEC), IEEE, Colchester, UK, pp. 154–158, 2018. [Google Scholar]
7. K. Venkataraman and T. Sadasivam, “Fpqa implementation of modified elliptic curve digital signature algorithm,” Facta Universitatis-Series: Electronics and Energetics, vol. 32, no. 1, pp. 129–145, 2019. [Google Scholar]
8. J. M. Schmidt and M. Medwed, “A fault attack on ECDSA,” in 2009 Workshop on Fault Diagnosis and Tolerance in Cryptography (FDTC), IEEE, Lusanne, Switzerland, pp. 93–99, 2009. [Google Scholar]
9. G. Barthe, F. Dupressoir, P. A. Fouque, B. Grégoire and J. C. Zapalowicz, “Synthesis of fault attacks on cryptographic implementations,” in Proceedings of the 2014 ACM SIGSAC Conf. on Computer and Communications Security, Scottsdale, Arizona, USA, pp. 1016–1027, 2014. [Google Scholar]
10. C. Giraud and E. W. Knudsen, “Fault attacks on signature schemes,” in Australasian Conf. on Information Security and Privacy, Springer, Berlin, Heidelberg, vol. 3108, pp. 478–491, 2004. [Google Scholar]
11. C. Giraud and H. Thiebeauld, “A survey on fault attacks,” in Smart Card Research and Advanced Applications VI, Springer, Boston, MA, vol. 153, pp. 159–176, 2004. [Google Scholar]
12. N. F. Saudy, I. A. Ali and R. Al Barkouky, “Error analysis and detection procedures for signature and authentication schemes,” Journal of Advances in Mathematics and Computer Science, vol. 29, no. 1, pp. 1–12, 2018. [Google Scholar]
13. A. Barenghi, G. M. Bertoni, L. Breveglieri, G. Pelosi, S. Sanfilippo et al., “A fault-based secret key retrieval method for ECDSA: Analysis and countermeasure,” ACM Journal on Emerging Technologies in Computing Systems (JETC), vol. 13, no. 1, pp. 1–26, 2016. [Google Scholar]
14. A. B. Association, “Public key cryptography for the financial services industry: The elliptic curve digital signature algorithm (ECDSA),” ANSI X9, pp. 62–1998, 2005. [Google Scholar]
15. M. Hell, T. Johansson and W. Meier, “Grain: A stream cipher for constrained environments,” International Journal of Wireless and Mobile Computing, vol. 2, no. 1, pp. 86–93, 2007. [Google Scholar]
16. A. A. Kanso, “An efficient cryptosystem delta for stream cipher applications,” Computers & Electrical Engineering, vol. 35, no. 1, pp. 126–140, 2009. [Google Scholar]
17. J. M. Rodrigues, “Transfert sécurisé d’images par combinaison de techniques de compression, cryptage et de marquage,” in Thèse Soutenue, Université Montpellier II, Sciences et Techniques du Languedoc, Montpellier, France, 2006. [Google Scholar]
18. S. S. Mansouri and E. Dubrova, “An improved hardware implementation of the grain stream cipher,” in 2010 13th Euromicro Conf. on Digital System Design: Architectures, Methods and Tools, IEEE, Lille, France, pp. 433–440, 2010. [Google Scholar]
19. B. den Boer, A. Bosselaers, “Collisions for the compression function of MD5,” in Advances in Cryptology-Eurocrypt ‘93, Springer-Verlag (1994pp. 293–304. [Google Scholar]
20. N. Koblitz, “Cm-curves with good cryptographic properties,” in Annual Int. Cryptology Conf., Springer, Berlin, Heidelberg, pp. 279–287, 1991. [Google Scholar]
21. J. Neumann and A. W. Burks, “T heory of Self-Reproducing Automata,” University of Illinois press, Urbana, Vol. 1102024, 1966. [Google Scholar]
22. A. Canteaut, “Analyse et conception de chiffrements à clef secrète”, Ph.D. dissertation, Spécialité Informatique, Université Pierre et Marie Curie-Paris VI, Paris, France, 2006. [Google Scholar]
23. G. Bertoni, J. Daemen, M. Peeters and G. Van Assche, “Keccak sponge function family main document,” Submission to NIST (Round 2), vol. 3, no. 30, pp. 320–337, 2009. [Google Scholar]
24. G. Bertoni, J. Daemen, M. Peeters and G. Van Assche, “Keccak specifications,” Submission to NIST (Round 2), vol. 3, no. 30, pp. 320–337, 2009. [Google Scholar]
25. C. Boura, “Analyse de fonctions de hachage cryptographiques”, Ph.D. dissertation, Spécialité Informatique, Université Pierre et Marie Curie-Paris VI, Paris, France, 2012. [Google Scholar]
26. G. Bertoni, J. Daemen, M. Peeters and G. Van Assche, “On the indifferentiability of the sponge construction,” in Annual Int. Conf. on the Theory and Applications of Cryptographic Techniques, Springer, Berlin, Heidelberg, vol. 4965, pp. 181–197, 2008. [Google Scholar]
27. Jean-Philippe Aumasson et Willi Meier: Zero-sum distinguishers for reduced Keccak-f and for the core functions of Luffa and Hamsi, 2009. Comment on the NIST SHA-3 Hash Competition. [Google Scholar]
28. F. Rodrıguez-Henrıquez, N. A. Saqib and A. Dıaz-Pérez, “A fast parallel implementation of elliptic curve point multiplication over GF (2m),” Microprocessors and Microsystems, vol. 28, no. 5–6, pp. 329–339, 2004. [Google Scholar]
29. H. Mahdizadeh and M. Masoumi, “Novel architecture for efficient FPGA implementation of elliptic curve cryptographic processor over GF (2163),” IEEE Transactions on Very Large Scale Integration (VLSI) Systems, vol. 21, no. 12, pp. 2330–2333, 2013. [Google Scholar]
30. S. Liu, L. Ju, X. Cai, Z. Jia and Z. Zhang, “High performance FPGA implementation of elliptic curve cryptography over binary fields,” in 2014 IEEE 13th Int. Conf. on Trust, Security and Privacy in Computing and Communications, Beijing, China, pp. 148–155, 2014. [Google Scholar]
31. Z. U. Khan and M. Benaissa, “High speed ECC implementation on FPGA over GF (2m),” in 2015 25th Int. Conf. on Field Programmable Logic and Applications (FPL), IEEE, London, UK, pp. 1–6, 2015. [Google Scholar]
32. B. Rashidi, S. M. Sayedi and R. R. Farashahi, “High-speed hardware architecture of scalar multiplication for binary elliptic curve cryptosystems,” Microelectronics Journal, vol. 52, pp. 49–65, 2016. [Google Scholar]
33. N. B. H. Youssef, W. E. H. Youssef, M. Machhout, R. Tourki and K. Torki, “A low-resource 32-bit datapath eCDSA design for embedded applications,” in 2014 Int. Carnahan Conf. on Security Technology (ICCST), IEEE, Rome, Italy, pp. 1–6, 2014. [Google Scholar]
34. B. Panjwani and D. C. Mehta, “Hardware-software co-design of elliptic curve digital signature algorithm over binary fields,” in 2015 Int. Conf. on Advances in Computing, Communications and Informatics (ICACCI), IEEE, Kochi, India, pp. 1101–1106, 2015. [Google Scholar]
35. M. Bedoui, B. Bouallegue, B. Hamdi and M. Machhout, “An efficient fault detection method for elliptic curve scalar multiplication montgomery algorithm,” in 2019 IEEE Int. Conf. on Design & Test of Integrated Micro & Nano-Systems (DTS), IEEE, Gammarth, Tunisia, pp. 1–5, 2019. [Google Scholar]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |