Computer Systems Science & Engineering DOI:10.32604/csse.2023.026823
Article

Future Event Prediction Based on Temporal Knowledge Graph Embedding

Zhipeng Li1,2, Shanshan Feng3,*, Jun Shi2, Yang Zhou2, Yong Liao1,2, Yangzhao Yang2, Yangyang Li4, Nenghai Yu1 and Xun Shao5

1University of Science and Technology of China, Hefei, 230027, China
2 Shenzhen CyberAray Co., Ltd., Shenzhen, 518038, China
3Harbin Institute of Technology, Shenzhen, 518055, China
4National Engineering Research Center for Risk Perception and Prevention (RPP), Beijing, 100041, China
5School of Regional Innovation and Social Design Engineering, Kitami Institute of Technology, Kitami, 090-8507, Japan
*Corresponding Author: Shanshan Feng. Email: victor_fengss@foxmail.com
Received: 05 January 2022; Accepted: 25 March 2022

Abstract: Accurate prediction of future events brings great benefits and reduces losses for society in many domains, such as civil unrest, pandemics, and crimes. Knowledge graph is a general language for describing and modeling complex systems. Different types of events continually occur, which are often related to historical and concurrent events. In this paper, we formalize the future event prediction as a temporal knowledge graph reasoning problem. Most existing studies either conduct reasoning on static knowledge graphs or assume knowledges graphs of all timestamps are available during the training process. As a result, they cannot effectively reason over temporal knowledge graphs and predict events happening in the future. To address this problem, some recent works learn to infer future events based on historical event-based temporal knowledge graphs. However, these methods do not comprehensively consider the latent patterns and influences behind historical events and concurrent events simultaneously. This paper proposes a new graph representation learning model, namely Recurrent Event Graph ATtention Network (RE-GAT), based on a novel historical and concurrent events attention-aware mechanism by modeling the event knowledge graph sequence recurrently. More specifically, our RE-GAT uses an attention-based historical events embedding module to encode past events, and employs an attention-based concurrent events embedding module to model the associations of events at the same timestamp. A translation-based decoder module and a learning objective are developed to optimize the embeddings of entities and relations. We evaluate our proposed method on four benchmark datasets. Extensive experimental results demonstrate the superiority of our RE-GAT model comparing to various baselines, which proves that our method can more accurately predict what events are going to happen.

Keywords: Event prediction; temporal knowledge graph; graph representation learning; knowledge embedding

1  Introduction

From the 9/11 terrorist attacks to the COVID-19 pandemic, societal events often deeply affect people’s daily lives and cause huge economic burden. Predicting these events in advance is highly valuable to the risk perception and prevention of our society [1]. It is not surprising that computational social science has exploded in prominence as an active field for the need of analyzing societal events [2]. With the advent of the big data era, computational social science now focuses on social intelligence more than social information processing. This movement is achieved by capturing human social dynamics, and modelling social behavior through existing big data [3].

For the promising future of this field, considerable attention has been paid to get further development in the past decades. Relevant methods, systems, and event databases have been proposed in succession, e.g., the Integrated Crisis Early Warning System (ICEWS) [4], which helps US policy predict international crises. Another example is the Early Model Based Event Recognition using Surrogates (EMBERS) [5,6] for forecasting events include influenza-like illness, civil unrest, domestic political crises, and elections. Among existing researches, GDELT [7] has emerged as an interesting project because it is a free open platform which monitors societal events across nearly all countries of the world in over 100 languages.

Recently, Knowledge Graphs (KGs) [8–12] are widely used in many real-world applications. Since knowledge graphs can model/reflect real-world facts, event prediction problem can be transformed into a missing fact reasoning problem in the KGs. Most existing research studies on knowledge reasoning are based on static knowledge graphs. In particular, an event is normally defined in the form of a triplet including event subject, event object, and the relation between them, i.e., (subject, relation, object). However, as the facts are highly correlated with time, temporal knowledge graphs (TKGs) are proposed to associate events with their corresponding timestamps, i.e., (subject, relation, object, time). Fig. 1 shows an example for event predicting on a temporal knowledge graph. We can learn that events dynamically occur with the time, as the relations (suppress or negotiation) between the same entities (Taliban and Government) would be different at different dates (2021/07/09 and 2021/08/13).

Figure 1: Temporal knowledge subgraphs about the afghanistan battle situation between taliban and government over time

Reasoning tasks on temporal knowledge graph are mainly divided into two types: interpolation and extrapolation [13]. Given a temporal knowledge graph in which timestamps vary from t0 to tT, events are predicted for time t satisfied that (t0 ≤ t ≤ tT) in interpolation reasoning, while extrapolation reasoning focuses on predicting unseen events for t beyond tT (i.e., t > tT).

Existing researches attempt to solve KG reasoning problem by static knowledge graph embedding approaches, or simply extend the static KG embedding methods with timestamps. Besides, the latter mostly focuses on interpolation scenarios [14], or encoding patterns associated with the occurrence of events by using simple aggregation method [13]. Thus, it is desirable to develop a more efficient and comprehensive method that can extrapolate future events by representing historical event through modeling local graph within a time window.

In this work, we proposed a Recurrent Event Graph ATtention Network (RE-GAT) to predict events in the extrapolation setting. Unlike traditional temporal knowledge graph embedding methods that neglect the structure during the process of learning representations, RE-GAT employs an attention-based historical events embedding module to encode past events, and uses an attention-based concurrent events embedding module to model the associations of events at the same timestamp. A translation-based decoder module and a learning objective is used to optimize the embeddings of event entities and relations. The contributions of our work can be summarized as follows:

•   We formalize the future event prediction problem into a temporal knowledge graph extrapolation reasoning problem.

•   RE-GAT uses RNNs and GNNs to jointly encode temporal and structural event information from historical and concurrent events for predicting future events. In addition, we employ a novel attention mechanism to ensure better representations of sophisticated patterns associated with the events.

•   We conduct extensive experiments on four real-world datasets. The experimental results demonstrate that our proposed method outperforms various state-of-the-art baselines.

2  Related Works

2.1 Static Knowledge Graph Embeddings

Static knowledge graph embeddings without considering the temporal information have been extensively studied, which mostly target at embedding entities and relations into the latent vector spaces. A class of them focus on translation tasks [15–18], which models the relation of two entities into a translation vector. RotatE [19] defines relation as a rotation between entities in vector space to embed knowledge graph. Other models represent semantic information by using triangular norm to measure plausibility of facts [20,21]. There are also some works based on deep neural network [22–24]. However, these methods are not effective in predicting future events due to their incapability of capturing temporally dynamic facts.

2.2 Temporal Knowledge Graph Embedding

More recently, researchers attempt to model the varying facts over time in temporal knowledge graphs. TTransE [25] extends the traditional TransE [16] into temporal scenarios through embedding temporal information into score function. Similarly, HyTE [26] extends TransH [15]. DE-SimpIE [27] combines entity and timestamp to generate time-specific representations. Despite well performance in their tasks, these methods do not take into consideration the long-term temporal relationship of real-world events. These methods assume that all timestamps and corresponding knowledge graphs are available during the training process, hence they are not able to predict events in the future.

Another line of works tries to model graph sequences to capture long-term dependency of facts. DyREP [28] proposes a two-time scale deep process to jointly model global and local topological evolution. Historical Information Passing (HIP) [29] network models the evolution of event-based knowledge graph by passing information from three perspectives (temporal, structural, and repetitive). RE-GCN [30] based on GCN models knowledge graph sequence recurrently to learn representation at each timestamp. CyGNet [14] proposes a time-aware copy-generation representation learning method to model temporal knowledge graph. RE-NET [13] uses an autoregressive architecture based on RNN to inference over temporal knowledge graph of event sequences.

2.3 Event Prediction

Traditional event prediction tasks are mainly viewed as a classic machine learning classification problem, e.g., customer churn event prediction [31], civil unrest [32], adverse drug reaction [33], and etc. However, not all event prediction tasks can be modeled as classification problems. With the development of technology on graph, events can be represented as nodes or links in graph, and hence event prediction tasks are modeled as node/link prediction tasks. Abstract Causality Network [34] embeds real-world events into continuous vector space, and predicts causality event through minimizing a defined energy function. Dynamic Graph Convolution Network [35] is proposed to give context information of the result while predicting event, which is improved to be suitable in multi-event prediction tasks [36]. Overall, event prediction with reasoning over temporal knowledge graphs is relatively unexplored.

3  Problem Formulation

We start with describe notations for the temporal knowledge graph (TKG), and then we define the TKG reasoning problem.

An event-based TKG can be regarded as a sequence of static knowledge graphs (SKG) sorted by event timestamp, i.e., G = {G1, G2, …, Gt, …}. Each SKG in G can be represented as Gt=(E,R,T) , where E,R, and T denote the sets of event entities, event type, and timestamps, respectively. Gt consists of a set of events with the same timestamp t. An event in Gt can be represented as a time-stamped quadruple, i.e., (subject, relation, object, time) and is denoted by a quadruple (s, r, o, t) ∈ Gt. This means that an event is happened at timestamp t∈T between subject s∈E and object o∈E . The event type is denoted as relation r∈R .

The future event prediction problem is formalized as predict the event object or the event subject given all the set of historical events before timestamp t, namely (s, r, ?, t) or (?, r, o, t). We assume that the events at a time step t, i.e., Gt, depends on the events at the previous k time steps (i.e., {Gt−k, Gt−k+1, …, Gt−1}), denotes as Gt−k:t−1. We use Ht and Rt to describe embedding matrices of event entities, event types at t, respectively. To predict an event at time t, we use the information of the historical KGs is embedded in the matrices of event subjects and objects Ht−1∈R|E|×dE and the event types Rt−1∈R|R|×dR at timestamp t − 1, where dE and dR is the dimension of the event entity vector representations and event type vector representations, respectively.

Given all past events, i.e., the historical event sequences Gt−k:t−1, we can formulate the future event object prediction problem as a ranking problem. Given a future event prediction task (s, r, ?, t), our proposed RE-GAT model utilizes the event subject s, the event type r, and past events Gt−k:t−1 to calculate the conditional probability for all event objects:

p(o|Gt−k:t−1,s,r)=p(o|Ht−1,Rt−1,s,r). (1)

Similarly, we can define the problem of predicting future event subject entity (?, r, o, t) and event type (s, ?, o, t) as follows:

p(s|Gt−k:t−1,o,r)=p(s|Ht−1,Rt−1,o,r), (2)

p(r|Gt−k:t−1,s,o)=p(r|Ht−1,Rt−1,s,o). (3)

4  The RE-GAT Model

We introduce our proposed RE-GAT model in this section. RE-GAT uses an attention-based recurrent neural network to encode the informative sequential patterns across historical events. RE-GAT learns the local structural relations between concurrent events in a knowledge graph at each timestamp utilizing an attention-based graph neural network representation mechanism. Based on these learned temporal event subject embeddings, event object embeddings, and event type embeddings, future event at subsequent timestamp can be predicted with classical translation-based decoder. As shown in Fig. 2, RE-GAT consists of an entity and relation embedding encoder and a decoder. The former contains an attention-based concurrent events embedding module (Translational-based GAT) and an attention-based historical events embedding module (Time Gate, GRU, Attention, etc.) to encode the historical event KGs. The latter employs a translation-based score function for corresponding entity prediction task.

Figure 2: The overall architecture of RE-GAT

4.1 Attention-Based Concurrent Events Embedding Module

To capture the concurrent events information at the same timestamp, we use the attention-based historical events embedding module to encode the structural dependencies and associations among the entities and relations in these events. Since graph neural network (GNN) has strong expressive power for the unstructured graph data [23,37–40] and neighbors play different influences in reality [41–43], we utilize a ω layer graph attention network (GAT) to model the neighborhood concurrent events information. To represent the inverse event type (relation) of the event entities in our model, we add the inverse event quadruple (o, r−1, s, t) at the same timestamp to the event-based KG for each event (s, r, o, t). Without loss of generality, we take the object prediction problem (s, r, ?, t) for example. Specifically, for each knowledge graph at timestamp t, an event object o obtains its embeddings at layer l ∈ [0, ω − 1] from the corresponding event subjects and event types in the quadruples under a graph attention network framework at layer l and learns its vector representations at the l + 1 layer, i.e.,

zo(l)=W1(l)ho,t(l), (4)

eos(l)=LeakyReLU(a(l)T(zo(l)||zs(l))), (5)

αos(l)=exp(eos(l))∑(s,r),∃(s,r,o)∈Gt⁡exp(eos(l)), (6)

ho,t(l+1)=σ(∑(s,r),∃(s,r,o)∈Gt⁡αos(l)(hs,t(l)+rt)+W2(l)ho,t(l)), (7)

where ho,t(l) , hs,t(l) , and rt represent the lth layer vector embeddings of event object o, event subject s and event type r at timestamp t, respectively; αos(l) is the learnable attention weight, W1(l) and W2(l) are the learnable weight matrix parameters in the lth layer. We calculate a pairwise unnormalized attention score between event subject and event object in Eq. (5), where || denotes concatenation. We first concatenate the vector representations of event object and event subject, then take a dot product with a learnable weight vector a(l). Finally, we apply a LeakyReLU to the dot product result. In Eq. (6), a softmax function is applied to normalize the attention scores on all quadruples containing the event object entity. Similar to the aggregator of classic graph convolutional network (GCN), the embeddings from concurrent events are multiplied by the attention scores, summed together, and added by the self-loop embeddings in Eq. (7). Note that each KG Gt is composed of a set of events occur at the same timestamp. We use hs,t(l)+rt in Eq. (7) to capture the relationship between the event subject, event type, and event object. It also means that dE=dR . We use d in the following for short.

The attention-based concurrent events embedding module gets the event entity vector representations, namely embeddings, based on the concurrent events occurring with the target event and its own embeddings. These operations can be interpreted as the evolution and change of the events.

4.2 Attention-Based Historical Events Embedding Module

This module seeks to model the historical events patterns between entity pairs, encode the temporal information across time, and generate the temporal embeddings for entities and relations. For the event subject s and event object o in an event (s, r, o, t) or the inverse type event (o, r−1, s, t), the latent temporal event features and patterns contained in the historical events imply the historical trends and regularities. To cover as many temporal patterns of historical events as possible, the model needs to take time sequence of events into account. Since the output of the attention-based concurrent events embedding module (Translational-based GAT) in the final layer, i.e., ho,t−1ω , already encodes the vector representation of event objects at timestamp t − 1, we might think of using this entire output event entity embedding matrix Ht−1 directly as the input of the translational-based GAT module at time t, namely Ht0=Ht−1 . However, this is equivalent to stacking all the ɷ-layer translational-based GAT together, resulting in the over-smoothing problems [44]. The embeddings of event objects, event subjects, and event types will converge to the same vector values. The large number of stacked translational-based GAT modules may also introduce the vanishing gradient problem, preventing the weight from changing during the training iteration. Thus, we utilize a time gate component in our attention-based historical events embedding module to address these problems following [30]. The event entity matrix Ht is computed by the output at timestamp t of the attention-based concurrent events embedding module in the final layer ω, i.e., Htω and Ht−1 from the same module at timestamp t − 1. More specifically,

Ht=Ut⊗Htω+(1−Ut)⊗Ht−1, (8)

where ⊗ represents the element-wise product operation. The time gate matrix Ut∈R|E|×d applies non-linear sigmoid transformation as:

Ut=σ(W3Ht−1+b),  (9)

where σ(∙) denotes the sigmoid function and W3 is the parameter for weight matrix.

To better capture the event representation, we employ an historical event attention mechanism that allows the module to dynamically select and linearly combine different historical events of the relations [45]:

eτ=veTtanh⁡(Wert+Uerτ), (10)

ατ=exp(eτ)∑τ=1t⁡exp(eτ),  (11)

rt=∑τ=1t⁡ατrτ, (12)

where ve, We and Ue are parameters. The factors ατ determine which part of the historical event should be emphasized or ignored when making predictions. Relation embeddings rt form the embedding matrices of relations at t, i.e., Rt .

4.3 Translation-Based Decoder Module

Traditional knowledge graph entity prediction task [19,22,24,37] usually use a scoring function to measure the plausibility of quadruples given the embeddings. They utilize training data consists of positive and sampled negative quadruples to update the representation. Previous studies [22,24,37] have demonstrated that GNN with the convolutional score functions perform well on knowledge graph entity prediction task. For the purpose of cosidering the translational property of the vector representations in Eq. (7), ConvTransE [24] is chosen as the decoder model to compute the conditional probability in Eqs. (1), (2) and (3). Following [30], the probability of event object is:

p(o|Ht−1,Rt−1,s,r)=σ(Ht−1ConvTransE(st−1,rt−1)). (13)

In the same way, the probability score of the event type is:

p(r|Ht−1,Rt−1,s,o)=σ(Rt−1ConvTransE(st−1,ot−1)), (14)

where σ(⋅) denotes the widely used Sigmoid function and st−1, rt−1, ot−1 represent the vector representations of event subject s, event type r, and event object o in Ht−1 and Rt−1 at timestamp t − 1, respectively.

Note that the ConvTransE model can be replaced by any other translation-based score functions or decoders. We omit the details of ConvTransE for brevity.

4.4 Learning Objective

In this section, we discuss the training process of RE-GAT model. An event object entity prediction problem (s, r, ?, t) can be thought of as a multi-class classification problem in which each class corresponds to each event object entity. Similarly, we can also consider the subject entity prediction problem (?, r, o, t) as a multi-class classification task. Without loss of generality, we describe future event prediction problem as predicting the event object in a time-stamped quadruple (s, r, ?, t). We can easily extend the model to predict the event subject entity, i.e., (?, r, o, t).

Following [30], we use yte∈R|E| and ytr∈R|R| to represent the vector representations of labels for event entity prediction task and relation prediction task at the timestamp t. Then,

Le=∑t=1T⁡∑(s,r,o,t)∈Gt⁡∑i=0|E|−1⁡yt,ielog⁡pi(o|Ht−1,Rt−1,s,r), (15)

Lr=∑t=1T⁡∑(s,r,o,t)∈Gt⁡∑i=0|R|−1⁡yt,irlog⁡pi(r|Ht−1,Rt−1,s,o), (16)

where T denotes the total number of event-based KG timestamps in the training dataset, yt,ie and yt,ir represent the ith vector element in yte and ytr , respectively. Note that the elements of vector yte and ytr are 1 for events that do occur and 0 otherwise.

We use a multi-task learning framework [30,46] for the event entity prediction and event type prediction tasks. Therefore, the final loss score can be calculated as:

L=Le+λ1Lr, (17)

where λ1 is the importance parameter. We can choose the parameter value according to the task and control the importance of each component.

5  Experiments

We evaluate the performance of RE-GAT model with four public event datasets in this section. First, we explain experimental settings in detail, including the datasets and baselines. After that, we discuss the experimental results.

5.1 Experimental Setup

In this section, we compare the performance of our proposed model against various static knowledge graph embedding methods and some recent temporal knowledge graph models.

Datasets. We use four event-based temporal knowledge graphs datasets which record events with timestamps, namely ICEWS05-15 [47], ICEWS14 [47], ICEWS18 [13], and GDELT [13]. Integrated Crisis Early Warning System (ICEWS) dataset [48] and Global Database of Events, Language, and Tone (GDELT) dataset [7] are commonly used event-based datasets in previous studies.

Evaluation Settings and Metrics. We preprocess these datasets for extrapolation reasoning task following prior works [13,14,30]: we divide them into training, validation, and test sets by timestamps, i.e., train(80%)/valid(10%)/test(10%). Thus, (timestamps of training set) < (timestamps of valid set) < (timestamps of test set). More details about the four datasets can be found in Tab. 1.

Evaluation Metrics. The methods are evaluated on the link prediction and relation prediction task which evaluates whether the ground-truth event quadruple (fact) is ranked ahead of other event quadruple. We report the results of mean reciprocal rank (MRR), hits at 1/3/10 (H@1/3/10) in our experiments. Hits at k (H@k) measures the proportion of the correct quadruple appears in the top k ranked quadruples. Many previous works remove corrupted event quadruples during evaluation which is called filtered setting. As mentioned in [30,49,50], all event quadruples that occur in the training, validation, or test sets are removed from the ranking result, which is not suitable for temporal knowledge graph entity prediction tasks. To this end, we only report the experimental results under the raw settings.

Baselines. We mainly focus on comparing RE-GAT to the methods of static KGs and temporal KGs as previous works. Static KG reasoning models include TransE [16], DistMult [20], ComplEx [21], and RotatE [19]. And temporal KG learning methods include HyTE [26], TA-DistMult [47], RE-NET [13] and CyGNet [14] are selected.

5.2 Experimental Results

Tab. 2 presents the entity prediction performance of future event of RE-GAT and baseline models on four event-based datasets. The best scores are boldfaced and the second-best scores are underlined.

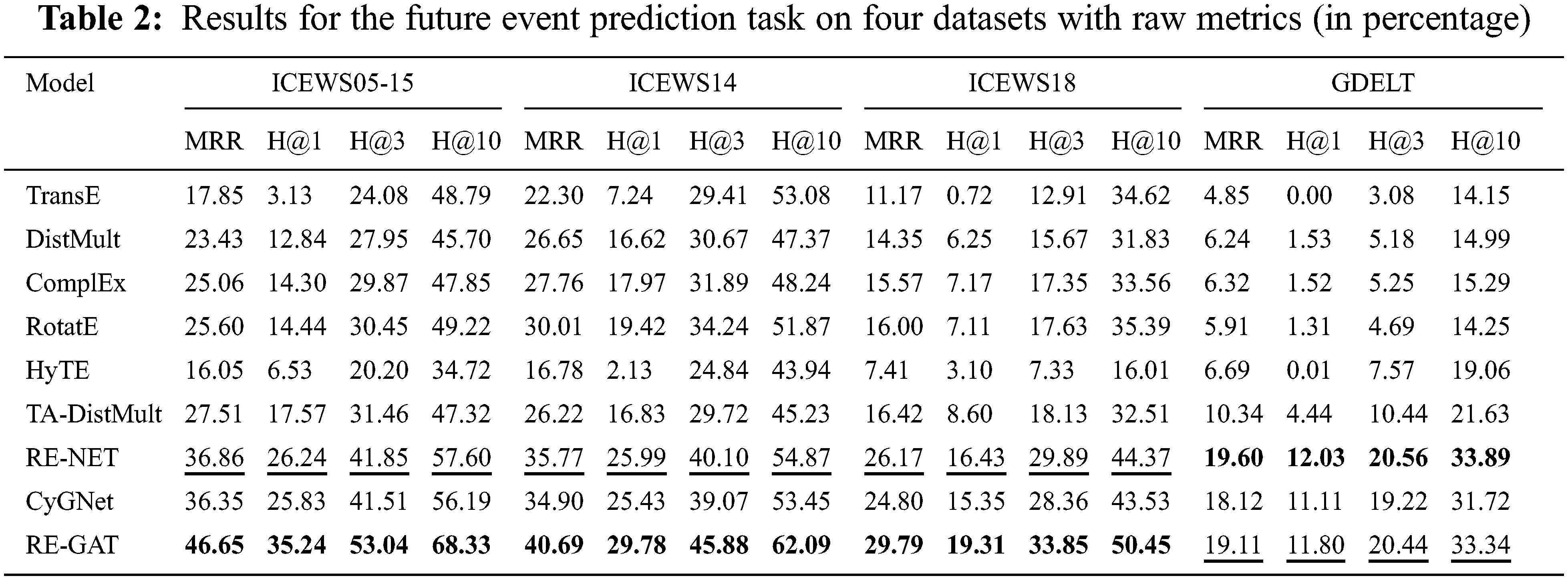
As we can see that Static KGE methods are much worse than RE-GAT since they cannot capture temporal events information. We can also observe that RE-GAT performs much better than HyTE and TA-DistMult with MRR and H@1/3/10 metrics. We believe this is because HyTE and TA-DistMult only learn events representations independently for each timestamp and lack the ability of capturing the long-term dependency.

It can also be observed from Tab. 2 that RE-GAT outperforms all the baselines on ICEWS05-15, ICEWS14 and ICEWS18 datasets. For instance, RE-GAT achieves the improvements of 11.19% over second-best results with H@3 metric on ICEWS05-15 dataset.

To further study the performance of our RE-GAT model and the visual advantage of knowledge graph, we present a case study of three subgraphs from the event-based temporal knowledge graph of ICEWS18 test dataset. As shown in Fig. 3, we are given historical events (quadruples) at timestamps 2018/09/26 and 2018/09/27, and attempt to predict which entity will Militant (Taliban) use unconventional violence to at the timestamp 2018/09/28. As we can see from the subgraph on 2018/09/28 in Fig. 3, RE-GAT successfully obtains the correct answer Military (Afghanistan), which shows that the temporal and structural event information can be learned by our RE-GAT model.

Figure 3: A case study of future event prediction using RE-GAT model

6  Conclusion

It is highly desirable to predict the occurrence of events (such as political events, pandemics, and crimes etc.) in advance to reduce the potential damage and social upheaval. In this paper, we formulate the event prediction problem as an extrapolation reasoning problem in temporal knowledge graphs. We propose a RE-GAT model to tackle the problem. RE-GAT learns event information from the historical and concurrent structural perspectives to make future predictions. The proposed RE-GAT model also considers the complex influence of historical events in the past and concurrent events at the same timestamp, which makes it can effectively capture the historical patterns and neighborhood event interactions. As shown by the experimental results on four real-world datasets, our proposed RE-GAT model significantly achieves improvements over baselines.

Acknowledgement: The authors would like to thank Yan Shi for helpful feedbacks. We appreciate the anonymous reviewers from ICAIS 2022 and CSSE for their insightful comments. Zhipeng Li would like to gratefully acknowledge the financial support from the China Scholarship Council (CSC).

Funding Statement: This work is supported by the National Natural Science Foundation of China under grants U19B2044 and National Key Research and Development Program of China (2021YFC3300500).

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  L. Zhao, “Event prediction in the big data era: A systematic survey,” ACM Computing Surveys, vol. 54, no. 5, pp. 1–37, 2021. [Google Scholar]

 2.  D. Lazer, A. Pentland, L. Adamic, S. Aral, A. L. Barabasi et al., “Computational social science,” Science, vol. 323, no. 5915, pp. 721–723, 2009. [Google Scholar]

 3.  D. Lazer, A. Pentland, D. J. Watts, S. Aral, S. Athey et al., “Computational social science: Obstacles and opportunities,” Science, vol. 369, no. 6507, pp. 1060–1062, 2020. [Google Scholar]

 4.  S. P. O’Brien, “Crisis early warning and decision support: Contemporary approaches and thoughts on future research,” International Studies Review, vol. 12, no. 1, pp. 87–104, 2010. [Google Scholar]

 5.  N. Ramakrishnan, P. Butler, S. Muthiah, N. Self, R. Khandpur et al., “Beating the news’ with EMBERS: Forecasting civil unrest using open source indicators,” in Proc. SIGKDD, New York, NY, USA, pp. 1799–1808, 2014. [Google Scholar]

 6.  S. Muthiah, P. Butler, R. P. Khandpur, P. Saraf, N. Self et al., “EMBERS at 4 years: Eperiences operating an open source indicators forecasting system,” in Proc. SIGKDD, New York, NY, USA, pp. 205–214, 2016. [Google Scholar]

 7.  K. Leetaru and P. A. Schrodt, “GDELT: Global data on events, location, and tone, 1979–2012.” in ISA Annual Convention, San Francisco, CA, USA, pp. 1–49, 2013. [Google Scholar]

 8.  Q. Yue, X. Li and D. Li, “Chinese relation extraction on forestry knowledge graph construction,” Computer Systems Science and Engineering, vol. 37, no. 3, pp. 423–442, 2021. [Google Scholar]

 9.  H. J. Zhou, T. T. Shen, X. L. Liu, Y. R. Zhang, P. Guo et al., “Survey of knowledge graph approaches and applications,” Journal on Artificial Intelligence, vol. 2, no. 2, pp. 89–101, 2020. [Google Scholar]

10. X. Zhang, X. Sun, X. Sun, W. Sun and S. K. Jha, “Robust reversible audio watermarking scheme for telemedicine and privacy protection,” Computers, Materials & Continua, vol. 71, no. 2, pp. 3035–3050, 2022. [Google Scholar]

11. D. Zhang, Q. Jia, S. Yang, X. Han, C. Xu et al., “Traditional Chinese medicine automated diagnosis based on knowledge graph reasoning,” Computers, Materials & Continua, vol. 71, no. 1, pp. 159–170, 2022. [Google Scholar]

12. C. R. Yang, R. J. Bu, Y. Kang, Y. C. Zhang, H. Li et al., “An importance assessment model of open-source community java projects based on domain knowledge graph,” Journal on Big Data, vol. 2, no. 4, pp. 135–144, 2020. [Google Scholar]

13. W. Jin, M. Qu, X. Jin and X. Ren, “Recurrent event network: Autoregressive structure inference over temporal knowledge graphs,” in Proc. EMNLP, Virtual Conference, Online, pp. 6669–6683, 2020. [Google Scholar]

14. C. Zhu, M. Chen, C. Fan, G. Cheng and Y. Zhang, “Learning from history: Modeling temporal knowledge graphs with sequential copy-generation networks,” in Proc. AAAI, Virtual Conference, Online, pp. 4732–4740, 2021. [Google Scholar]

15. Z. Wang, J. Zhang, J. Feng and Z. Chen, “Knowledge graph embedding by translating on hyperplanes,” in Proc. AAAI, Québec City, Québec, Canada, pp. 1112–1119, 2014. [Google Scholar]

16. A. Bordes, N. Usunier, A. Garcia-Duran, J. Weston and O. Yakhnenko, “Translating embeddings for modeling multi-relational data,” in Proc. NeurIPS, Lake Tahoe, Nevada, USA, pp. 1–9, 2013. [Google Scholar]

17. G. Ji, S. He, L. Xu, K. Liu and J. Zhao, “Knowledge graph embedding via dynamic mapping matrix,” in Proc. ACL, Beijing, China, pp. 687–696, 2015. [Google Scholar]

18. G. Ji, K. Liu, S. He and J. Zhao, “Knowledge graph completion with adaptive sparse transfer matrix,” in Proc. AAAI, Phoenix, Arizona, USA, pp. 985–991, 2016. [Google Scholar]

19. Z. Sun, Z. Deng, J. Nie and J. Tang, “RotatE: Knowledge graph embedding by relational rotation in complex space,” in Proc. ICLR, New Orleans, Louisiana, USA, pp. 1–18, 2019. [Google Scholar]

20. B. Yang, W. Yih, X. He, J. Gao and L. Deng, “Embedding entities and relations for learning and inference in knowledge bases,” in Proc. ICLR, San Diego, CA, USA, pp. 1–12, 2015. [Google Scholar]

21. T. Trouillon, J. Welbl, S. Riedel, E. Gaussier and G. Bouchard, “Complex embeddings for simple link prediction,” in Proc. ICML, New York City, NY, USA, pp. 2071–2080, 2016. [Google Scholar]

22. T. Dettmers, P. Minervini, P. Stenetorp and S. Riedel, “Convolutional 2d knowledge graph embeddings,” in Proc. AAAI, New Orleans, Louisiana, USA, pp. 1811–1818, 2018. [Google Scholar]

23. M. Schlichtkrull, T. N. Kipf, P. Bloem, R. van den Berg, I. Titov et al., “Modeling relational data with graph convolutional networks,” in Proc. ESWC, Heraklion, Crete, Greece, pp. 593–607, 2018. [Google Scholar]

24. C. Shang, Y. Tang, J. Huang, J. Bi, X. He et al., “End-to-end structure-aware convolutional networks for knowledge base completion,” in Proc. AAAI, Honolulu, Hawaii, USA, pp. 3060–3067, 2019. [Google Scholar]

25. T. Jiang, T. Liu, T. Ge, L. Sha, B. Chang et al., “Towards time-aware knowledge graph completion,” in Proc. COLING, Osaka, Japan, pp. 1715–1724, 2016. [Google Scholar]

26. S. S. Dasgupta, S. N. Ray and P. Talukdar, “HyTE: Hyperplane-based temporally aware knowledge graph embedding,” in Proc. EMNLP, Brussels, Belgium, pp. 2001–2011, 2018. [Google Scholar]

27. R. Goel, S. M. Kazemi, M. Brubaker and P. Poupart, “Diachronic embedding for temporal knowledge graph completion,” in Proc. AAAI, New York, New York, USA, pp. 3988–3995, 2020. [Google Scholar]

28. R. Trivedi, M. Farajtabar, P. Biswal and H. Zha, “DyREP: Learning representations over dynamic graphs,” in Proc. ICLR, New Orleans, Louisiana, USA, pp. 1–25, 2019. [Google Scholar]

29. Y. He, P. Zhang, L. Liu, Q. Liang, W. Zhang et al., “HIP network: Historical information passing network for extrapolation reasoning on temporal knowledge graph,” in Proc. IJCAI, Montreal, Canada, pp. 1915–1921, 2021. [Google Scholar]

30. Z. Li, X. Jin, W. Li, S. Guan, J. Guo et al., “Temporal knowledge graph reasoning based on evolutional representation learning,” in Proc. SIGIR, Virtual Conference, Online, pp. 408–417, 2021. [Google Scholar]

31. A. De Caigny, K. Coussement and K. W. De Bock, “A new hybrid classification algorithm for customer churn prediction based on logistic regression and decision trees,” European Journal of Operational Research, vol. 269, no. 2, pp. 760–772, 2018. [Google Scholar]

32. G. Korkmaz, J. Cadena, C. J. Kuhlman, A. Marathe, A. Vullikanti et al., “Combining heterogeneous data sources for civil unrest forecasting,” in Proc. ASONAM, New York, NY, USA, pp. 258–265, 2015. [Google Scholar]

33. S. Santiso, A. Casillas, A. Perez, M. Oronoz and K. Gojenola, “Adverse drug event prediction combining shallow analysis and machine learning,” in Proc. Louhi, Gothenburg, Sweden, pp. 85–89, 2014. [Google Scholar]

34. S. Zhao, Q. Wang, S. Massung, B. Qin, T. Liu et al., “Constructing and embedding abstract event causality networks from text snippets,” in Proc. WSDM, Cambridge, UK, pp. 335–344, 2017. [Google Scholar]

35. S. Deng, H. Rangwala and Y. Ning, “Learning dynamic context graphs for predicting social events,” in Proc. SIGKDD, Anchorage, Alaska, USA, pp. 1007–1016, 2019. [Google Scholar]

36. S. Deng, H. Rangwala and Y. Ning, “Dynamic knowledge graph based multi-event forecasting,” in Proc. SIGKDD, San Diego, California, USA, pp. 1585–1595, 2020. [Google Scholar]

37. S. Vashishth, S. Sanyal, V. Nitin and P. Talukdar, “Composition-based multi-relational graph convolutional networks,” in Proc. ICLR, Addis Ababa, Ethiopia, pp. 1–16, 2020. [Google Scholar]

38. K. Xu, W. Hu, J. Leskovec and S. Jegelka, “How powerful are graph neural networks?,” in Proc. ICLR, New Orleans, Louisiana, USA, pp. 1–17, 2019. [Google Scholar]

39. J. You, Z. Ying and J. Leskovec, “Design space for graph neural networks,” in Proc. NeuIPS, Virtual Conference, Online, pp. 17009–17021, 2020. [Google Scholar]

40. Z. Wu, S. Pan, F. Chen, G. Long, C. Zhang et al., “A comprehensive survey on graph neural networks,” IEEE Transactions on Neural Networks and Learning Systems, vol. 32, no. 1, pp. 4–24, 2021. [Google Scholar]

41. P. Veličković, G. Cucurull, A. Casanova, A. Romero, P. Liò et al., “Graph attention networks,” in Proc. ICLR, Vancouver, BC, Canada, pp. 1–12, 2018. [Google Scholar]

42. K. Wang, W. Shen, Y. Yang, X. Quan and R. Wang, “Relational graph attention network for aspect-based sentiment analysis,” in Proc. ACL, Seattle, Washington, USA, pp. 3229–3238, 2020. [Google Scholar]

43. Y. Xie, Y. Zhang, M. Gong, Z. Tang and C. Han, “MGAT: Multi-view graph attention networks,” Neural Networks, vol. 132, pp. 180–189, 2020. [Google Scholar]

44. T. N. Kipf and M. Welling, “Semi-supervised classification with graph convolutional networks,” in Proc. ICLR, Toulon, France, pp. 1–14, 2017. [Google Scholar]

45. P. Ren, Z. Chen, J. Li, Z. Ren, J. Ma et al., “RepeatNet: A repeat aware neural recommendation machine for session-based recommendation,” in Proc. AAAI, Honolulu, Hawaii, USA, pp. 4806–4813, 2019. [Google Scholar]

46. Y. Zhang and Q. Yang, “A survey on multi-task learning,” IEEE Transactions on Knowledge and Data Engineering, Early Access, 2021. https://dx.doi.org/10.1109/TKDE.2021.3070203. [Google Scholar]

47. A. García-Durán, S. Dumančić and M. Niepert, “Learning sequence encoders for temporal knowledge graph completion,” in Proc. EMNLP, Brussels, Belgium, pp. 4816–4821, 2018. [Google Scholar]

48. A. Shilliday and J. Lautenschlager, “Data for a worldwide ICEWS and ongoing research.” in Advances in Design for Cross-Cultural Activities, 1st ed, Part I. Boca Raton, FL, USA: CRC Press, pp. 455–465, 2012. [Google Scholar]

49. Z. Han, P. Chen, Y. Ma and V. Tresp, “Explainable subgraph reasoning for forecasting on temporal knowledge graphs,” in Proc. ICLR, Vienna, Austria, pp. 1–24, 2021. [Google Scholar]

50. P. Jain, S. Rathi, Mausam and S. Chakrabarti, “Temporal knowledge base completion: New algorithms and evaluation protocols,” in Proc. EMNLP, Virtual Conference, Online, pp. 3733–3747, 2020. [Google Scholar]

This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.