Computer Systems Science & Engineering DOI:10.32604/csse.2023.028614
Article

Cooperative Relay Networks Based on the OAM Technique for 5G Applications

Mohammad Alkhawatrah, Ahmad Alamayreh and Nidal Qasem*

Department of Electronics and Communications Engineering, Al-Ahliyya Amman University, Amman, Jordan
*Corresponding Author: Nidal Qasem. Email: Ne.qasem@ammanu.edu.jo
Received: 14 February 2022; Accepted: 17 March 2022

Abstract: Orbital Angular Momentum (OAM) is an intrinsic property of electromagnetic waves. Great research has been witnessed in the last decades aiming at exploiting the OAM wave property in different areas in radio and optics. One promising area of particular interest is to enhance the efficiency of the available communications spectrum. However, adopting OAM-based solutions is not priceless as these suffer from wave divergence especially when the OAM order is high. This shall limit the practical communications distance, especially in the radio regime. In this paper, we propose a cooperative OAM relaying system consisting of a source, relay, and destination. Relays help the source to transmit packets to the destination by providing an alternative connection between source and destination. This cooperative solution aims on the one hand, through best-path selection, on increasing the communications range. On the other hand, through the parallel transmission orders allowed by OAM carrying waves, the system could raise its total transmission throughput. Simulation results show that combining a cooperative relay with OAM improves the system throughput compared to using each element separately. In addition, the proposed cooperative relaying OAM outperforms the cooperative relaying non-orthogonal multiple access scheme, which is a key spectrally efficient technique used in 5G technology.

Keywords: 5G; cooperative network; OAM; relay; throughput

1  Introduction

In recent years, wireless connection has become the dominant form of communication, but also remains one of the most challenging. For example, the internet of things requires massive wireless connectivity, such as Fifth Generation (5G) technology, that cannot be realized with current network infrastructure, which cannot achieve sufficient throughput, where throughput measures the rate of successful transmission [1].

Cooperative communication is considered a key technology that can improve wireless network performance to meet future requirements [2]. In particular, cooperative communication technology exploits the broadcast nature of the wireless channel to increase the system’s throughput, thus extending the network coverage; this is performed by adding relay nodes to the network. Hence, cooperation via relay nodes has been used in modern wireless communications and forms part of LTE Release 10 [3].

There are two relay modes, named according to the method the relay node uses to process the received signal: Amplify-and-Forward (AF) and Decode-and-Forward (DF). In AF mode, the relay node amplifies the received signal and forwards it to users, this makes AF simple to implement, however, it also has the disadvantage of noise amplification [4].

In DF mode, the relay node decodes the received signal, re-encodes it, and then forwards it to users. The DF mode has no noise amplification drawback due to decoding operations at the relay node; however, to enable accurate decoding, a better channel is required compared to the one needed for AF mode [5–7].

Due to the relays’ capability in fighting path losses, combining cooperative relaying with other 5G techniques has become a trend in the current literature. For example, the authors in [8] utilized cooperative relaying to enhance millimeter-wave (mm-wave) network performance by extending its coverage. Furthermore, the authors in [9] combined cooperative relaying with Non-Orthogonal Multiple Access (NOMA), which led to higher overall system throughput.

In addition to mm-wave and NOMA performance, other advanced radio spectrum efficiency enhancement techniques are expected to play a role in the transition to 5G technology, which were investigated under cooperative relay channels. Among these are massive multiple-input multiple-output, co-frequency, co-time, and full-duplex techniques [10].

In addition, a new and promising resource for spectrum efficiency hinges on Allen et al.’s [11] discovery in the early 1990s of orthogonal Orbital Angular Momentum (OAM) orders possessed by electromagnetic waves. Since then, there has been significant interest in the application of OAM for optics [12] and, recently, for radio communications [13–20].

Waves carrying OAM exhibit helical phase-fronts owing to the azimuthal dependence of their spatial phase distribution (ejl∅) , where l is the OAM order (l=±1,±2,…) , and ∅ is the azimuthal angle in cylindrical coordinates (r,∅,z) . The field intensity varies in the form of annular rings in the transverse plane and vanishes along the axis of propagation due to destructive interference [21].

In this paper, we combine an OAM multi-access technique with a relay cooperative network. To the best of the authors’ knowledge, no previous studies have employed cooperative communication to enhance OAM performance. The combining of OAM and relay shows several mutual advantages to both of OAM and relay. The design overcomes many of the limitations usually encountered in the utilization of OAM-based solutions in radio, mainly the problem of wave divergence where the size of the null amplitude region at the beam axis expands during propagation.

Such beam divergence demands the use of large receivers and may severely reduce transmission distance, particularly for high-order OAM orders, where the null region is quite large. Raising the frequency of transmission helps to confine the wave over larger distances, making OAM-based solutions more practical for high-frequency mm-wave networks [15].

The relay-based solution adopted in this paper reduces the distance between the transmitter and receiver, as the best (i.e., shortest) path is inherently offered by the relay selection. The distance reduction via relays makes OAM viable for applications with lower frequencies than mm-wave networks. In addition, fading is a limiting factor of the OAM orders that can be used in transmission.

The use of relays adds a degree of freedom; rather than having only a direct source–destination link, there is another path through the relay. Hence, if one link has deep fading or low channel gain, the other link is available to avoid bad transmission. Furthermore, the OAM transmission approach accommodates the relay–receiver link with the orthogonal orders used to raise the throughput via parallel channel transmission. In summary, this paper suggests a novel system that employs OAM technique in a relay cooperative network to overcome the beam divergence limitation and deep fading. Hence, higher throughout is achieved.

This paper is organized as follows: Section 2 includes a general overview of the proposed cooperative relay network based on the OAM technique and describes the signal model. Numerical results and comparisons between derived formulas and those obtained via other studies are shown in Section 3. Finally, conclusions are drawn in Section 4.

2  System Model

2.1 Cooperative Relay Network

The system model of relay cooperative networks is shown in Fig. 1, where there is a source node, S, a half-duplex DF relay node denoted as R, and a destination, D. The channel coefficients for the S-R and R-D links are denoted as hsr and hrd , respectively. All channels have a flat Rayleigh fading coefficient that remains constant within each time slot and changes independently from one time slot to another.

Figure 1: System model for a cooperative relay network based on the OAM technique

We assume that the source always has sufficient information (i.e., it is saturated) to send to relays in all time slots. Due to path loss and shadowing, we assume that the source and destination are not directly connected. Without losing generality, we assume the transmission power to be Pt at all transmitting nodes; the noise variances at all receiving nodes are assumed to be σ2 .

The data rate is assumed to be fixed at a value of ϵ . If the link capacity is greater than or equal to ϵ , the link is up, and the transmission is successful. Retransmission occurs based on the acknowledgment (ACK) and negative ACK (NACK) mechanism; this mechanism happens between transmitters (source or relay) and receivers (relay or destination). Each receiver broadcasts the ACK/NACK signal to the transmitters: relay to source and destination to relay.

The channel state information at the receivers is assumed to be available. At time slot t , the corresponding link capacities for channels hsr and hrd are given by:

Csr=log⁡(1+γsr) (1)

Crd=log⁡(1+γrd) (2)

where γsr=Ptσ2|hsr|2 and γrd=Ptσ2|hrd|2 .

The channel gains |hsr|2 and |hrd|2 are exponentially distributed with the average θsr=E[|hsr|2] and θrd=E[|hrd|2] , where θsr and θrd denote average S-R channel gain and average R-D channel gain, respectively, and E[.] is the expectation operator. γsr and γrd are also exponentially distributed with average γsr¯=Ptσ2θsr and γrd¯=Ptσ2θrd . Thus, γsr and γrd are the instantaneous Signal to Noise Ratio (SNR) values, while γsr¯ and γrd¯ are the average SNR values for channels hsr and hrd , respectively.

Since the system throughput is a function of channel outage, we first describe the outage analysis of the relay network. An outage occurs if the link capacity is less than the target data rate:

P(log⁡(1+γsr)<ϵ)=1−e−2ϵ−1γsr¯ (3)

P(log⁡(1+γrd)<ϵ)=1−e−2ϵ−1γrd¯ (4)

2.2 OAM Wave Characteristics and Propagation

Assuming a wave is carrying an OAM order, l , its complex amplitude can be expressed in a so-called pseudo-nondiffracting, or Bessel–Gauss, form:

u(r,∅)=exp(−r2/d2)Jl(krr)ejl∅ (5)

The exponential term is a Gaussian envelope, where d denotes the envelope width. Jl is the l th-order Bessel function of the first kind, r is the radial coordinate, ∅ is the azimuth, and kr is a radial frequency [22].

The wave propagation in space is governed by the paraxial Helmholtz equation:

j∂u∂z+12ko(∂2u∂x2+∂2u∂y2)=0 (6)

where z is the propagation distance, and ko=2π/λ is the wavenumber in a vacuum, where λ represents the wavelength. An analytical solution to the Helmholtz wave equation can be found through well-known techniques, for example, the Fourier transform [23]. Finally, we arrive at the following general expression of the Bessel–Gauss wave in free propagation:

u(r,∅,z)=G(rz,zL,krd)Jl(krr1+jzL)ejl∅ (7)

where L=πd2/λ is the Rayleigh distance of the Gaussian envelope. Propagation of the Gaussian envelope is represented by the function G in (7), which notably does not depend on the OAM order l [24].

Fig. 2 depicts the transverse spatial distributions of Bessel–Gaussian waves for different OAM orders. All distances in the figure are normalized to the wavelength. In the figure, a change in the amplitude color from blue to yellow indicates an increase in the field value. The deep blue at the center indicates a null, the extent of which increases with an increase in OAM order. The field phase distribution for each of the illustrated cases exhibits a number of 360° changes about the origin equal to the OAM order.

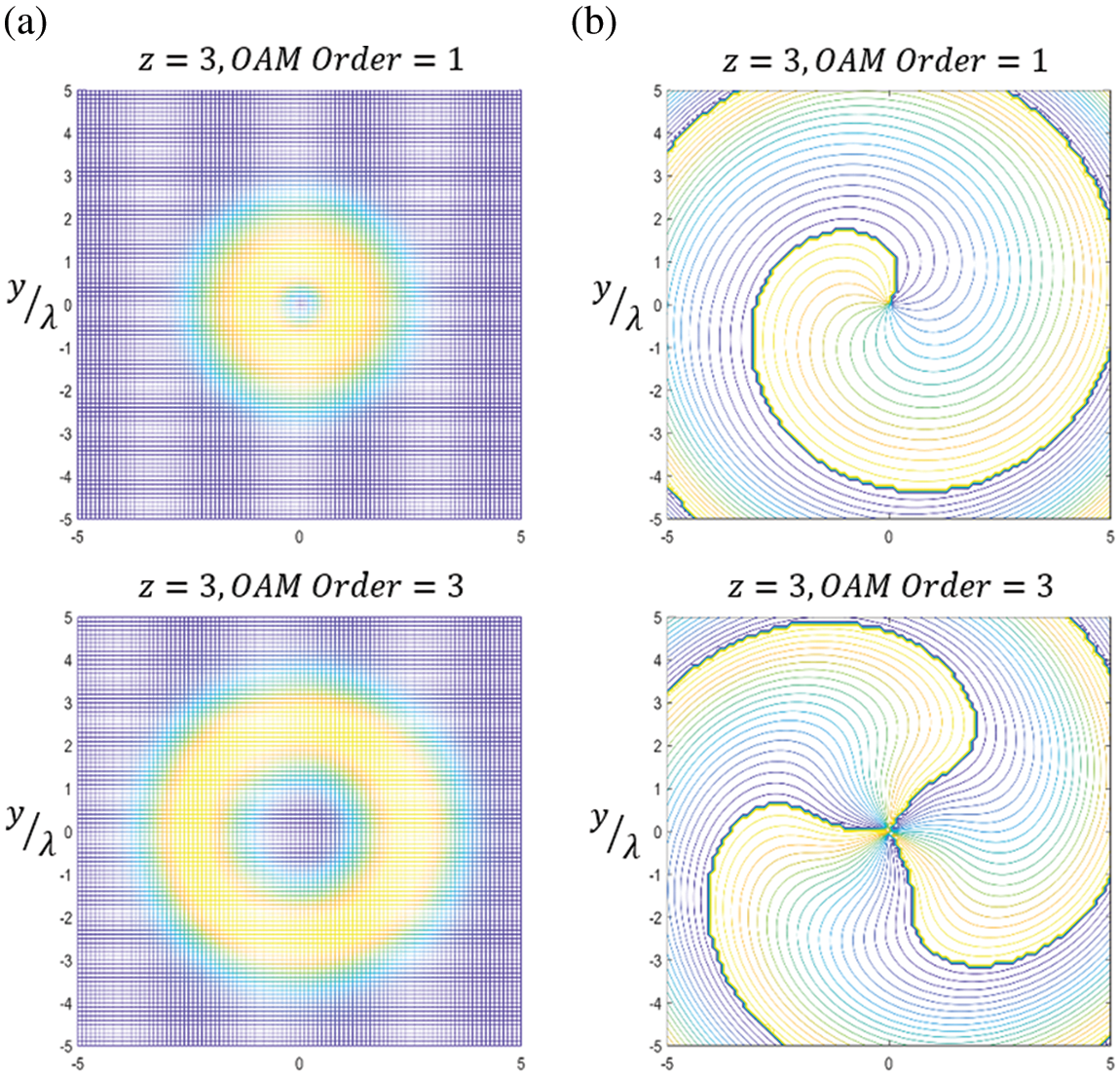
Figure 2: (a) Field spatial amplitude distribution and (b) phase distribution OAM order 1 (upper images) and OAM order 3 (lower images). Propagation distance z=3 and window size are wavelength-normalized

3  Simulations Results

In this section, we present simulation results to validate our analysis and design. We study the performance of our proposed relay cooperative OAM scheme. In the simulations, we assume that the noise variance ( σ2 ) is normalized to unity and we follow [9] in assuming that data rate ϵ= 2 bps/Hz. It is worth noting that the proposed system is for general applications hence normalized parameters are used in the simulation experiments. In some special applications, as discussed in [25,26], the level of noise and measured SNR are more restricted to meet some demanded qualifications.

In the first part of the simulation, we demonstrate the effect of receiving aperture size on received power. A receiver consisting of a sufficient number of sensors distributed around a circular circumference is considered. For the different cases demonstrated in Fig. 3, the size of the receiving aperture is chosen to match the maximum intensity radius of a certain OAM order.

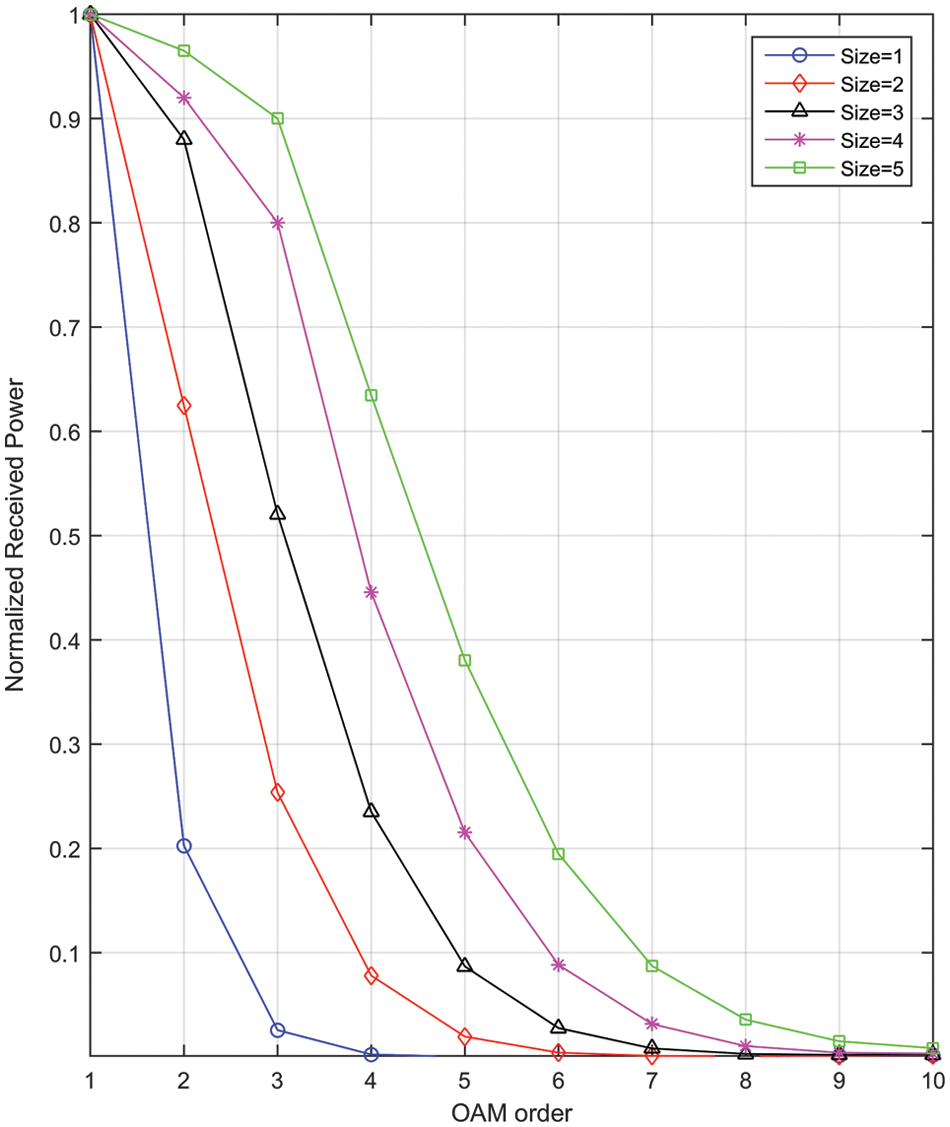
Figure 3: The graph illustrates the impact of receiver aperture size on system normalized received power for different OAM orders. An aperture of size n is matched to the maximum intensity radius of OAM order n

Recall from Fig. 2a that the maximum intensity is spatially distributed over an annual ring of certain radius. This is demonstrated in Fig. 3 by using apertures of different sizes, where, for instance, size 3 is meant to match the maximum intensity radius for OAM order 3, and so on.

As shown in Fig. 3, the normalized received power decreases generally as the wave OAM order increases. However, with an aperture of larger size, i.e., one that is matched to larger OAM order, an efficient amount of received power is sustained over a larger range of OAM orders. The normalized received power at size 5 (i.e., when the antenna aperture matches the 5th OAM order) shows an increment of almost 4 times in comparison to antenna size 1 that matches the 1st OAM order.

Different power-threshold values (as percentages of maximum power, see Fig. 4a) and their impact on the throughput are shown in Fig. 4b. In this figure, the throughput is the summation over all throughputs from every order that’s received power passed the threshold value. The received SNR is changed along the horizontal axis; raising the SNR helps passing the threshold step, thus enhancing the throughput.

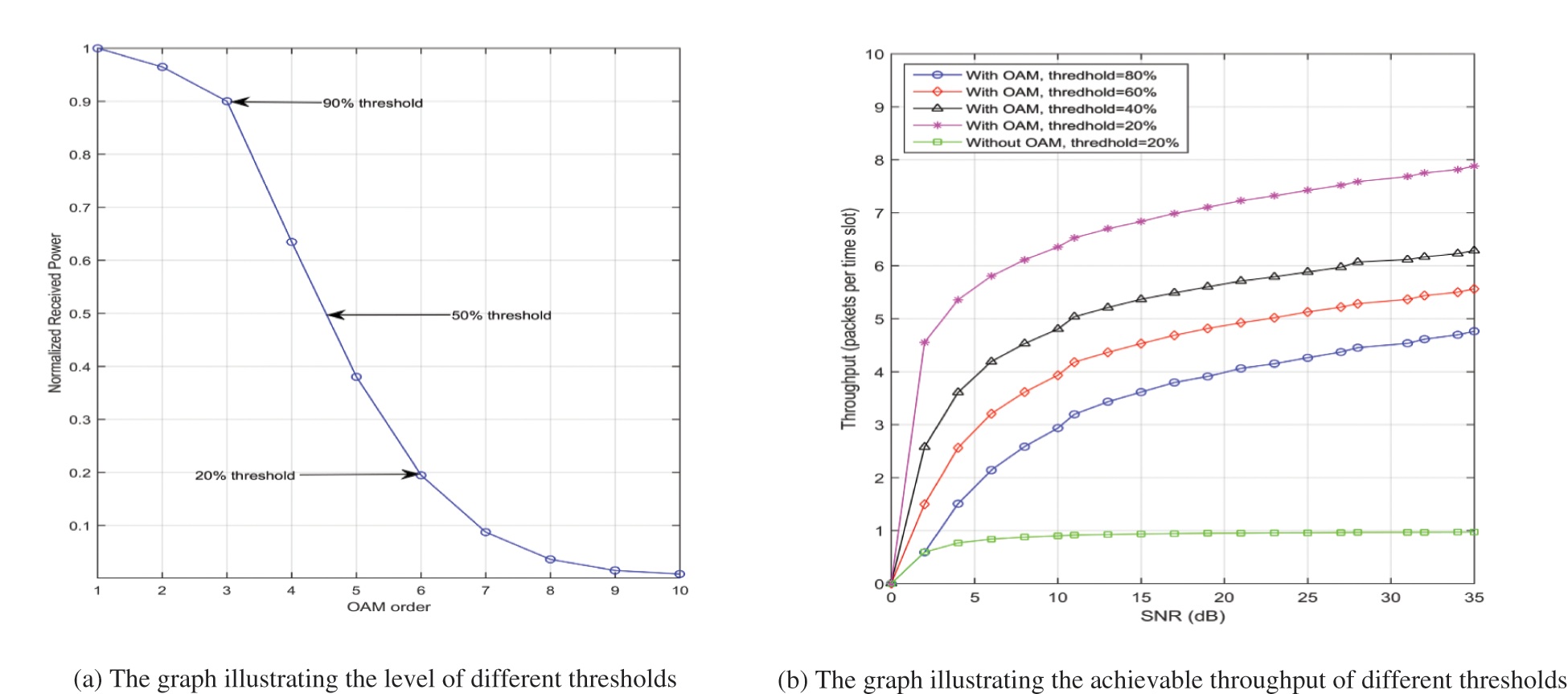
Figure 4: Impact of different thresholds on system throughput

It can be observed that lowering the threshold makes the reception less restrictive and allows higher OAM orders than raising the threshold; hence, higher throughput is achieved at low thresholds. For instance, from Fig. 4b, throughput of 7 packets per time-slot is achieved at 20% threshold in OAM-based case, and this is seven times as high as the non-OAM-based case in which only 1 packet per time-slot throughput is possible. It is worth noting that the restricted system employing OAM at threshold 80% outperforms the unrestricted system without OAM, as shown in Fig. 4b.

As mentioned previously, OAM suffers from divergence that accompanies the wave propagation. Fig. 5 shows the rise in the received power as the distance between the relay and the receiver decreases. Although the divergence effect is general for all orders, it is however more notable for larger orders. For OAM order 2 at 3 m relay-receiver separation distance the received normalized power is 80% higher than that of the same order at 25 m separation. This increment in normalized received power is only 10% for the same distances but at order 6.

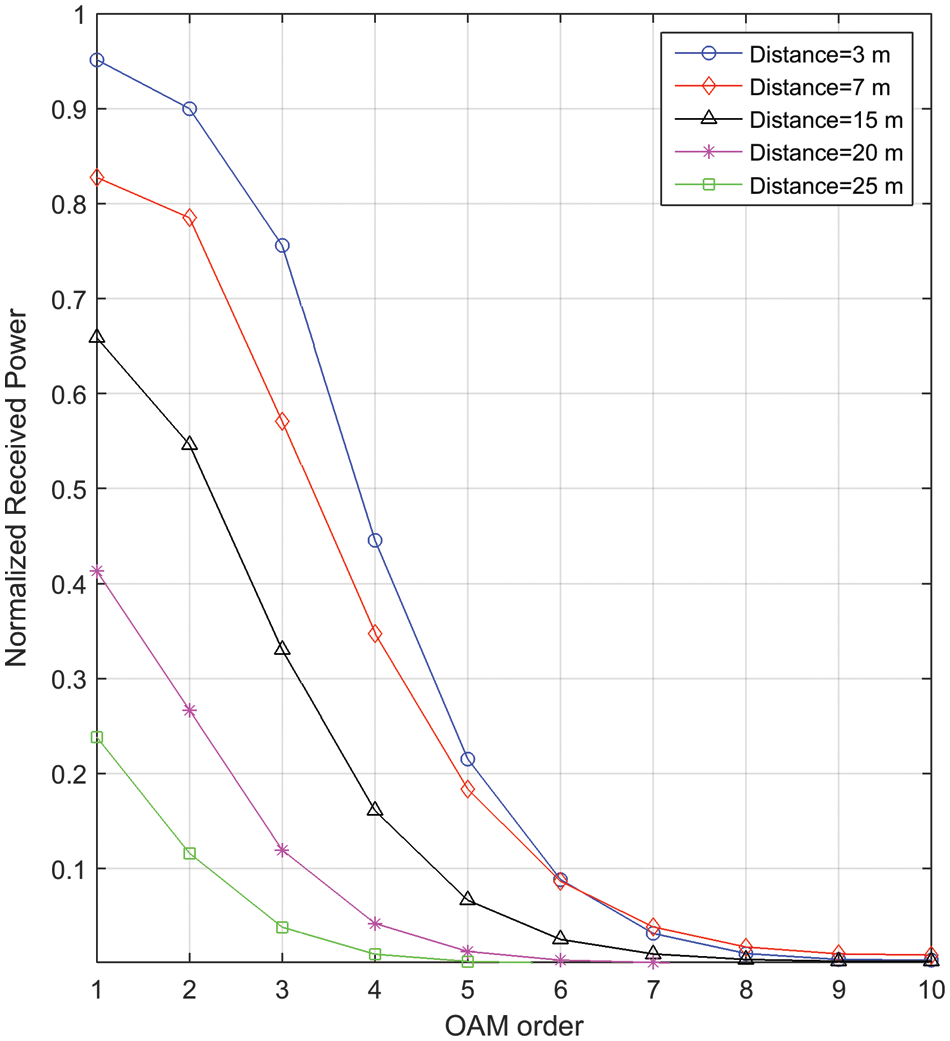
Figure 5: The graph illustrating the relationship between distance and OAM order. The impact of distance reduction by the relay is clearly illustrated. By reducing the distance between source and destination via the relay, higher orders of OAM can be achieved, which increases the system throughput

Finally, we present a comparison between our proposed system and other state-of-the-art research in Fig. 6. In [9], a milestone research article, relay technology was combined with NOMA 5G technology. The results show that the relay cooperative NOMA system can raise the throughput level to the number of served users at high SNR values.

We compared the relay cooperative NOMA system to our proposed cooperative OAM system. In [9], the number of users was 5; accordingly, we changed the number of orders for the OAM system to 5 to allow a fair comparison. Fig. 6 clearly illustrates that our proposed system achieves superior throughput to the relay cooperative NOMA system, especially at lower SNR values. For instance, at 6 dB level of SNR in Fig. 6, the currently available relay cooperative NOMA handles throughput of 2.25 packets per time-slot, while our proposed relay cooperative OAM system has higher throughput at 3.25 packets per time-slot. This is due to the orthogonality of OAM.

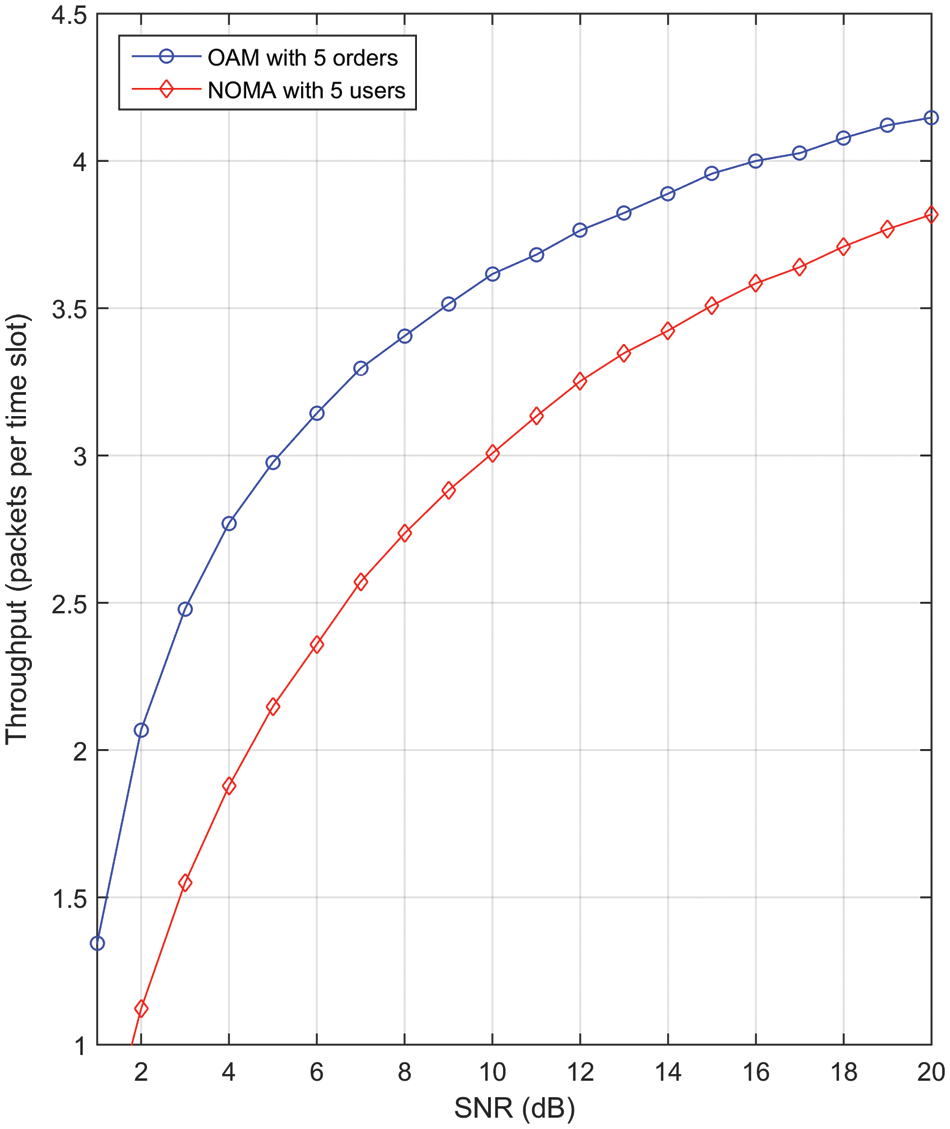
Figure 6: Comparison between our proposed cooperative OAM system and a NOMA cooperative system

4  Conclusions

This paper presented a cooperative relaying system based on the OAM technique. The results showed that the receiver could detect more orders as its size increased, which in turn enhanced the total system throughput. We enhanced the overall received power throughput of all orders by increasing the SNR. While the OAM system suffered from divergence as the wave propagated, we were able to reduce the received power as the distance between the relay and the receiver increased, an effect that was more notable for higher orders. In addition, the proposed model outperformed the cooperative relaying NOMA scheme, which is a key spectrally efficient technique in 5G technology.

Funding Statement: The authors received no specific funding for this study.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  Y. Su, X. Lu, Y. Zhao, L. Huang and X. Du, “Cooperative communications with relay selection based on deep reinforcement learning in wireless sensor networks,” IEEE Sensors Journal, vol. 19, no. 20, pp. 9561–9569, 2019. [Google Scholar]

 2.  A. Bletsas, H. Shin and M. Win, “Cooperative communications with outage-optimal opportunistic relaying,” IEEE Transactions on Wireless Communications, vol. 6, no. 9, pp. 3450–3460, 2007. [Google Scholar]

 3.  A. Nosratinia, T. Hunter and A. Hedayat, “Cooperative communication in wireless networks,” IEEE Communications Magazine, vol. 42, no. 10, pp. 74–80, 2004. [Google Scholar]

 4.  J. N. Laneman, G. W. Wornell and D. N. C. Tse, “An efficient protocol for realizing cooperative diversity in wireless networks,” in Proc. 2001 IEEE Int. Sym. on Information Theory (IEEE Cat. No. 01CH37252), Washington, DC, USA, 2001. [Google Scholar]

 5.  A. Sendonaris, E. Erkip and B. Aazhang, “User cooperation diversity. Part I. System description,” IEEE Transactions on Communications, vol. 51, no. 11, pp. 1927–1938, 2003. [Google Scholar]

 6.  M. Alkhawatrah, Y. Gong, O. Aldabbas and M. Hammoudeh, “Buffer-aided 5G cooperative networks: Considering the source delay,” in Proc. of the 3rd Int. Conf. on Future Networks and Distributed Systems (ICFNDS '19), New York, NY, USA, Association for Computing Machinery, Article 13, pp. 1–6, 2019. [Google Scholar]

 7.  M. Alkhawatrah, Y. Gong, G. Chen, S. Lambotharan and J. A. Chambers, “Buffer-aided relay selection for cooperative NOMA in the internet of things,” IEEE Internet of Things Journal, vol. 6, no. 3, pp. 5722–5731, 2019. [Google Scholar]

 8.  M. Alkhawatra and N. Qasem, “Improving and extending indoor connectivity using relay nodes for 60 GHz applications,” International Journal of Advanced Computer Science & Applications, vol. 51, no. 11, pp. 427–434, 2016. [Google Scholar]

 9.  Q. Zhang, Z. Liang, Q. Li and J. Qin, “Buffer-aided non-orthogonal multiple access relaying systems in Rayleigh fading channels,” IEEE Transactions on Communications, vol. 65, no. 1, pp. 95–106, 2017. [Google Scholar]

10. W. Cheng, W. Zhang, H. Jing, S. Gao and H. Zhang, “Orbital angular momentum for wireless communications,” IEEE Wireless Communications, vol. 26, no. 1, pp. 100–107, 2018. [Google Scholar]

11. L. Allen, M. W. Beijersbergen, R. J. Spreeuw and J. P. Woerdman, “Orbital angular-momentum of light and the transformation of Laguerre-Gaussian laser modes,” Physical Review A, vol. 45, no. 11, pp. 8185–8189, 1992. [Google Scholar]

12. C. Rui, Z. Hong, M. Marco, W. Xiaodong and L. Jiandong, “Orbital angular momentum waves: Generation, detection and emerging applications,” arXiv preprint arXiv:1903.07818, 2019. [Google Scholar]

13. B. Thidé, H. Then, J. Sjöholm, K. Palmer, J. Bergman et al., “Utilization of photon orbital angular momentum in the low-frequency radio domain,” Physical Review Letters, vol. 99, no. 8, pp. 087701, 2007. [Google Scholar]

14. B. Liu, Y. Cui and R. Li, “Delay in space: Orbital angular momentum beams transmitting and receiving in radio frequency,” Electromagnetics, vol. 36, no. 7, pp. 409–421, 2016. [Google Scholar]

15. W. Cheng, H. Zhang, L. Liang, H. Jing and Z. Li, “Orbital-angular-momentum embedded massive MIMO: Achieving multiplicative spectrum-efficiency for mmWave communications,” IEEE Access, vol. 6, pp. 2732–2745, 2017. [Google Scholar]

16. A. Alamayreh and N. Qasem, “Vortex beam generation in microwave band,” Progress in Electromagnetics Research C, vol. 107, pp. 49–63, 2021. [Google Scholar]

17. A. Alamayreh, N. Qasem and J. S. Rahhal, “General configuration MIMO system with arbitrary OAM,” Electromagnetics, vol. 40, no. 5, pp. 343–353, 2020. [Google Scholar]

18. A. Alamayreh and N. Qasem, “Lens antenna for 3D steering of an OAM-synthesized beam,” Wireless Networks, vol. 27, no. 8, pp. 5161–5171, 2021. [Google Scholar]

19. N. Qasem, A. Alamayreh and J. Rahhal, “Beam steering using OAM waves generated by a concentric circular loop antenna array,” Wireless Networks, vol. 27, no. 4, pp. 2431–2440, 2021. [Google Scholar]

20. N. Qasem and A. Alamayreh, “Wideband rectangular planar monopole antenna for OAM wave generation,” International Journal of Computer Science and Network Security, vol. 21, no. 3, pp. 55, 2021. [Google Scholar]

21. G. A. Turnbull, D. A. Robertson, G. M. Smith, L. Allen and M. J. Padgett, “The generation of free-space Laguerre-Gaussian modes at millimetre-wave frequencies by use of a spiral phase plate,” Optics Communications, vol. 127, no. 4–6, pp. 183–188, 1996. [Google Scholar]

22. J. Durnin, “Exact solutions for nondiffracting beams. I. The scalar theory,” Journal of the Optical Society of America A, vol. 4, no. 4, pp. 651–654, 1987. [Google Scholar]

23. D. Lahaye, J. Tang and K. Vuik, “Modern solvers for Helmholtz problems,” Birkhäuser, 2017. [Online]. Available: https://link.springer.com/book/10.1007/978-3-319-28832-1. [Google Scholar]

24. P. L. Greene and D. G. Hall, “Diffraction characteristics of the azimuthal Bessel-Gauss beam,” Journal of the Optical Society of America A, vol. 13, no. 5, pp. 962–966, 1996. [Google Scholar]

25. X. R. Zhang, W. F. Zhang, W. Sun, X. M. Sun and S. K. Jha, “A robust 3-D medical watermarking based on wavelet transform for data protection,” Computer Systems Science & Engineering, vol. 41, no. 3, pp. 1043–1056, 2022. [Google Scholar]

26. X. R. Zhang, X. Sun, X. M. Sun, W. Sun and S. K. Jha, “Robust reversible audio watermarking scheme for telemedicine and privacy protection,” Computers Materials & Continua, vol. 71, no. 2, pp. 3035–3050, 2022. [Google Scholar]

This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.