 Energy Engineering
Energy Engineering
 Energy Engineering Energy Engineering |  |
DOI: 10.32604/EE.2021.014513
ARTICLE
Adaptive Fractional-Order PID Control for VSC-HVDC Systems via Cooperative Beetle Antennae Search with Offshore Wind Integration
Faculty of Electric Power Engineering, Kunming University of Science and Technology, Kunming, 650500, China
*Corresponding Author: Zilong Cai. Email: caizilong2020@126.com
Received: 04 October 2020; Accepted: 21 October 2020
Abstract: Since the voltage source converter based high voltage direct current (VSC-HVDC) systems owns the features of nonlinearity, strong coupling and multivariable, the classical proportional integral (PI) control is hard to obtain content control effect. Hence, a new perturbation observer based fractional-order PID (PoFoPID) control strategy is designed in this paper for (VSC-HVDC) systems with offshore wind integration, which can efficiently boost the robustness and control performance of entire system. Particularly, it employs a fractional-order PID (FoPID) framework for the sake of compensating the perturbation estimate, which dramatically boost the dynamical responds of the closed-loop system, and the cooperative beetle antennae search (CBAS) algorithm is adopted to quickly and efficiently search its best control parameters. Besides, CBAS algorithm is able to efficiently escape a local optimum because of a suitable trade-off between global exploration and local exploitation can be realized. At last, comprehensive case studies are carried out, namely, active and reactive power tracking, 5-cycle line-line-line-ground (LLLG) fault, and offshore wind farm integration. Simulation results validate superiorities and effectiveness of PoFoPID control in comparison of that of PID control and feedback linearization sliding-mode control (FLSMC), respectively.
Keywords: Perturbation observer based fractional-order PID; VSC-HVDC system; cooperative beetle antennae search; offshore wind integration
Nomenclature
Variables
| R1 | equivalent resistance |
| L1 | equivalent inductance |
| C1 | DC bus capacitor |
| Vdc1 | DC voltages of rectifier |
| iL | DC cable current |
| R0 | equivalent DC cable resistance |
| urd, urq | d-q axis inputs voltage of rectifier |
| usd1, usq1 | d-q components of AC grid voltages |
| uid, uiq | d-q axis inputs voltage of inverter |
| usd2, usq2 | d-q components of AC grid voltages |
| Ddim | location dimensions |
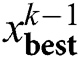 | current best solution until the (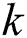 -1)th iteration -1)th iteration |
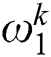 | dynamic weights of global exploration |
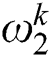 | dynamic weights of local exploitation |
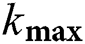 | maximum iteration number |
Abbreviations
| AC | alternating current |
| HCDC | high voltage direct current |
| VSC-HVDC | voltage source converter based high voltage direct current |
| FLC | fuzzy logic control |
| PI | proportional integral |
| FoPID | fractional-order PID |
| CSC-HVDC | conventional current source converter based HVDC |
| IGBT | insulated gate bipolar transistor |
| STATCOM | static synchronous compensator |
| ITLO | interactive teaching-learning optimizer |
| MMC-HVDC | modular multilevel converter based HVDC |
| PoFoPID | perturbation observer based fractional-order PID |
| CBAS | cooperative beetle antennae search |
| SMPO | sliding-mode perturbation observer |
| FLSMC | feedback linearization sliding-mode control |
Over the past few decades, excessive utilization of natural resources causes rapid fossil fuels depletion and serious environmental degradation [1], which inevitably accelerates ecological destruction and global energy crisis. Hence, energy revolution and transformation have become essential and imperative for social and economic development [2], which is also in line with global sustainable development strategy. With the rapid growth and wide application of renewable energy, the integration of renewable energy like wind and solar energy into grid has brought serious issues to the reliable and stable operation of grid [3]. Renewable energy is usually limited by environmental conditions, most of the renewable energy plants only own small installed capacity, low power quality and are far from the major network [4,5], like small and medium-sized hydropower stations [6], offshore wind power stations [7], and solar power stations [8]. Traditional alternating current (AC) power transmission and high voltage direct current (HVDC) cannot satisfy the access demands of renewable energy plants due to economic factors and technical level. To tackle this issue, voltage source converter based high voltage direct current (VSC-HVDC) can be adopted to reliably transmit long-distance power in the presence of renewable integration and installation [9,10].
Basically, VSC-HVDC is a novel type of HVDC based on voltage source converter (VSC) and controllable turn-off device with pulse width modulation technique. By contrast with conventional current source converter based HVDC (CSC-HVDC), its main technical advantages are as follows: (1) Insulated gate bipolar transistor (IGBT) based fully-controlled power electronic devices can self-shut off its current and can work in passive inverter mode without the need for an external system to provide commutation voltage, the receiving end system can be a weak AC system or passive network [11]; (2) During normal operation, VSC is able to quickly control active power and reactive power, so its DC system control method is flexible and convenient [12]; (3) When the flow of DC system is reversed, the orientation of DC current is reversed but the polarity of DC voltage remains unvaried, which is prone to construct a multi-terminal DC system [13]; (4) There is no need for AC side to provide reactive power, which can make full use of static synchronous compensator (STATCOM), dynamically compensating the reactive power of AC bus, and stabilizing the voltage of AC bus [14]; (5) The short circuit capacity of the system will not be increased. The addition of new VSC-HVDC lines eliminates the need to replace the protection setting values of AC systems and circuit breakers [15].
Proper control design for VSC-HVDC is of great importance for its operation. Traditional vector control (VC) combined with PI/PID mechanism is popularly adopted owing to its high dependability [16]. However, VSC-HVDC systems are highly nonlinear caused by converters and operate in power systems with modelling uncertainties, PI/PID control cannot maintain a global control consistency and might even lead to instability as its control parameters are tuned by one-point linearization technique [17]. Although work [18] optimally tune PID control gains via interactive teaching-learning optimizer (ITLO) for VSC-HVDC systems in order to remedy this issue to some extent, linear control is still inadequate to handle nonlinear systems. Thus, a large number of superior control techniques are presented to realize a uniform control performance under miscellaneous operating conditions. In literature [19], Lyapunov based controller is presented for rectifier side of VSC-HVDC systems, and the error equations of DC side voltage and reactive power are established, and the controller is designed on the inverter side to realize the stability of DC side voltage and standalone control of active and reactive power. Besides, an input-output feedback linearization method is presented for VSC-HVDC systems, which realizes a decoupling control of active and reactive power and can provide stable voltage to passive networks [20]. Guan et al. proposes a coordinated control strategy for ride-through under low voltage conditions, when low-voltage ride through, the converter stations at both ends are controlled to provide reactive power compensation, and a voltage-based power control strategy is adopted to rapidly reduce the output power of the wind farm to maintain DC voltage stability [21]. Nevertheless, the above techniques may not be competent to synchronously deal with modelling uncertainties and time-varying external disturbances [22].
With the view of enhancing the dynamic performance and robustness of VSC-HVDC systems, based on VSC-HVDC state space equation, constant power controller and constant voltage controller are developed by using 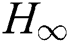 theory [23], whose simulation results indicate that the controller owns a good adaptiveness. Furthermore, Guibin et al designs the steady-state mathematical model of two-terminal VSC-HVDC systems and designed a steady-state inverse model controller with approximate linear decoupling according to the characteristics that VSC is a model containing two control quantities and two controlled quantities. But it belongs to indirect current control and has the disadvantage of being sensitive to system parameter change [24]. Besides, in reference [25], based on the transient nonlinear mathematical model of VSC-HVDC systems in
theory [23], whose simulation results indicate that the controller owns a good adaptiveness. Furthermore, Guibin et al designs the steady-state mathematical model of two-terminal VSC-HVDC systems and designed a steady-state inverse model controller with approximate linear decoupling according to the characteristics that VSC is a model containing two control quantities and two controlled quantities. But it belongs to indirect current control and has the disadvantage of being sensitive to system parameter change [24]. Besides, in reference [25], based on the transient nonlinear mathematical model of VSC-HVDC systems in  -
- coordinate system, VSC-HVDC systems is linearly decoupled through accurate linearization mode of state feedback, and the power controller and voltage controller are designed. The simulation results demonstrate that the transient control performance of the nonlinear controller is good and the robustness is strong. Numerous popular control methods have also been applied to VSC-HVDC systems in recent years, such as deadbeat control which owns simple algorithm, high control precision and fast response [26], and modified fuzzy logic control (FLC) which can effectively improve the dynamic characteristics and anti-interference of passive network access of modular multilevel converter based HVDC (MMC-HVDC) [27]. Also, a Type-2 fuzzy sliding mode control is designed which with the purpose of improving load disturbance of VSC-HVDC system and the damping behavior when parameters change [28].
coordinate system, VSC-HVDC systems is linearly decoupled through accurate linearization mode of state feedback, and the power controller and voltage controller are designed. The simulation results demonstrate that the transient control performance of the nonlinear controller is good and the robustness is strong. Numerous popular control methods have also been applied to VSC-HVDC systems in recent years, such as deadbeat control which owns simple algorithm, high control precision and fast response [26], and modified fuzzy logic control (FLC) which can effectively improve the dynamic characteristics and anti-interference of passive network access of modular multilevel converter based HVDC (MMC-HVDC) [27]. Also, a Type-2 fuzzy sliding mode control is designed which with the purpose of improving load disturbance of VSC-HVDC system and the damping behavior when parameters change [28].
However, the structures of nonlinear control schemes for VSC-HVDC systems are usually complex, which hinders its applications in practice. In order to realize a more realistic control design of VSC-HVDC systems, this paper is designed to adopt perturbation observer based fractional-order PID (PoFoPID) control [29] for VSC-HVDC systems under three case studies, which best control parameters are tuned by a new meta-heuristic algorithm named as cooperative beetle antennae search (CBAS) algorithm. Compared to the original beetle antennae search (BAS) [30] algorithm which mimicking searching mechanism of long-horn beetles, a cooperative group of multiple beetles instead of a single beetle is introduced by CBAS algorithm to realize a dynamic balance between local exploitation and global exploration, thus realizing the optimal control gains tunning of entire system.
Motivated by the above discussions, the finds/outcomes of this paper can be concluded as follows:
• Significant robustness: Compared to conventional PID control framework, it adopts fractional order to overall control framework, fully compensate the perturbation estimate and to significantly improve the dynamical responses of the closed-loop system, which also can simultaneously own the elegant merits of global control consistency and robustness of perturbation observer based control, high reliability and simple structure of FoPID control;
• Satisfactory control performance: Compared with PID control and feedback linearization sliding-mode control (FLSMC), PoFoPID owns the lowest entire control costs in all cases due to the integration of real-time perturbation estimation and FoPID structure. Besides, PoFoPID can provide strong robustness to handle system nonlinearities, parameter uncertainties, and unmodelled dynamics. And the overall control costs of PoFoPID are only 52.97% and 28.60% of that of PID and FLSMC in offshore wind farm integration;
• Efficient optimization: Compared to original BAS algorithm, CBAS algorithm can remarkably improve optimization efficiency via a cooperative group of multiple beetles instead of a single beetle. Besides, it can also acquire a high-quality optimum through a dynamic and suitable balance mechanism between local exploitation and global exploration.
The structure of this paper basically contains as following: Firstly, the modelling of VSC-HVDC systems can be shown in Section 2; Then, primary mechanism of CBAS algorithm is presented in Section 3; Section 4 offers detailed design of PoFoPID control strategies for VSC-HVDC systems; Section 5 undertakes three case studies to validate its effectiveness. At last, Section 6 concludes the whole paper.
A common VSC-HVDC system with two VSCs is given in Fig. 1 while offshore wind farm is connected at rectifier side in parallel. The aim of rectifier is to control DC voltage and reactive power, while active and reactive power are regulated by inverter. The dynamic equation of rectifier can be denoted at angular frequency 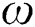 , yields [31].
, yields [31].

where 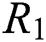 is equivalent resistance,
is equivalent resistance, 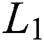 is equivalent inductance,
is equivalent inductance, 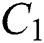 is the DC bus capacitor,
is the DC bus capacitor, 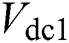 is DC voltages of rectifier,
is DC voltages of rectifier, 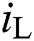 is the DC cable current,
is the DC cable current, 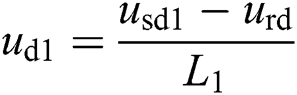 and
and 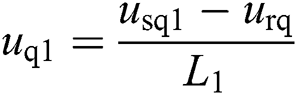 are d-q axis control inputs of rectifier,
are d-q axis control inputs of rectifier, 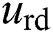 and
and 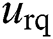 are d-q axis inputs voltage of rectifier;
are d-q axis inputs voltage of rectifier; 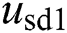 and
and 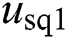 are d-q components of AC grid voltages;
are d-q components of AC grid voltages; 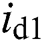 and
and 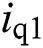 are corresponding line currents, respectively.
are corresponding line currents, respectively.
The dynamic equation of inverter can be represented as [32]

where 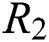 is equivalent resistance,
is equivalent resistance, 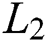 is equivalent inductance,
is equivalent inductance, 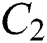 is DC bus capacitor,
is DC bus capacitor, 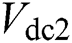 is DC voltage of inverter,
is DC voltage of inverter, 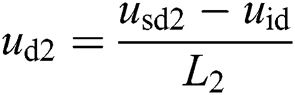 and
and 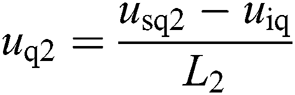 are d-q axis control inputs of inverter,
are d-q axis control inputs of inverter, 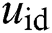 and
and 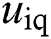 are d-q axis inputs voltage of inverter,
are d-q axis inputs voltage of inverter, 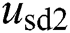 and
and 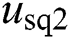 are d-q components of AC grid voltages,
are d-q components of AC grid voltages, 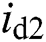 and
and 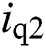 are corresponding line currents, respectively.
are corresponding line currents, respectively.
The rectifier and the inverter are connected by a DC cable, yields

where 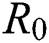 is the equivalent DC cable resistance.
is the equivalent DC cable resistance.
Not that AC grid voltage 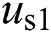 of rectifier side and
of rectifier side and 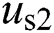 of inverter side are set to be in phase with q-axis in this paper. Therefore,
of inverter side are set to be in phase with q-axis in this paper. Therefore, 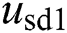 and
and 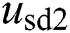 are set to be zero, and the magnitude of
are set to be zero, and the magnitude of 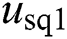 and
and 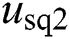 are equal to
are equal to 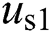 and
and 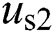 .
.
Lastly, power flows of AC grid can be described as [33]
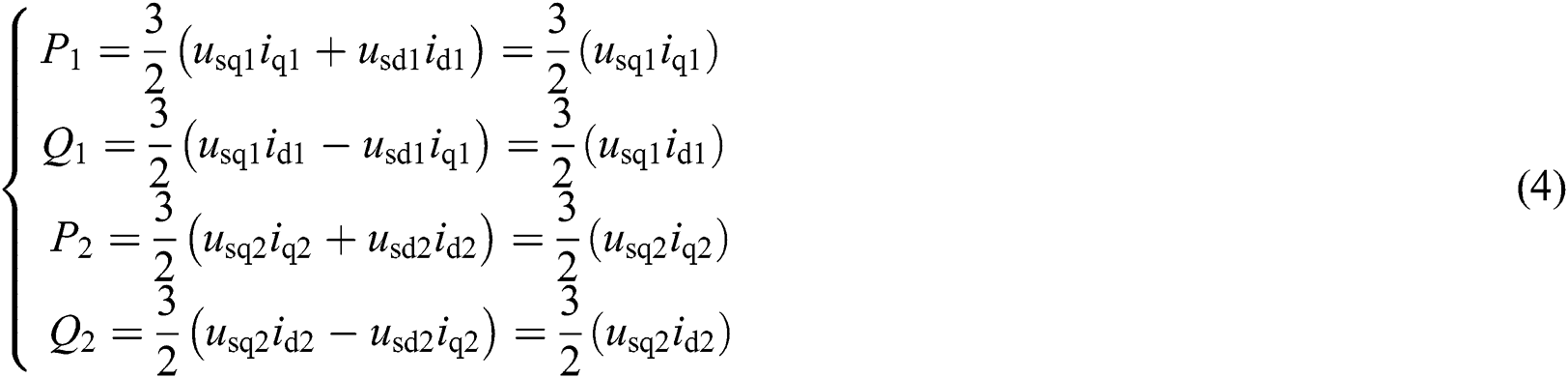
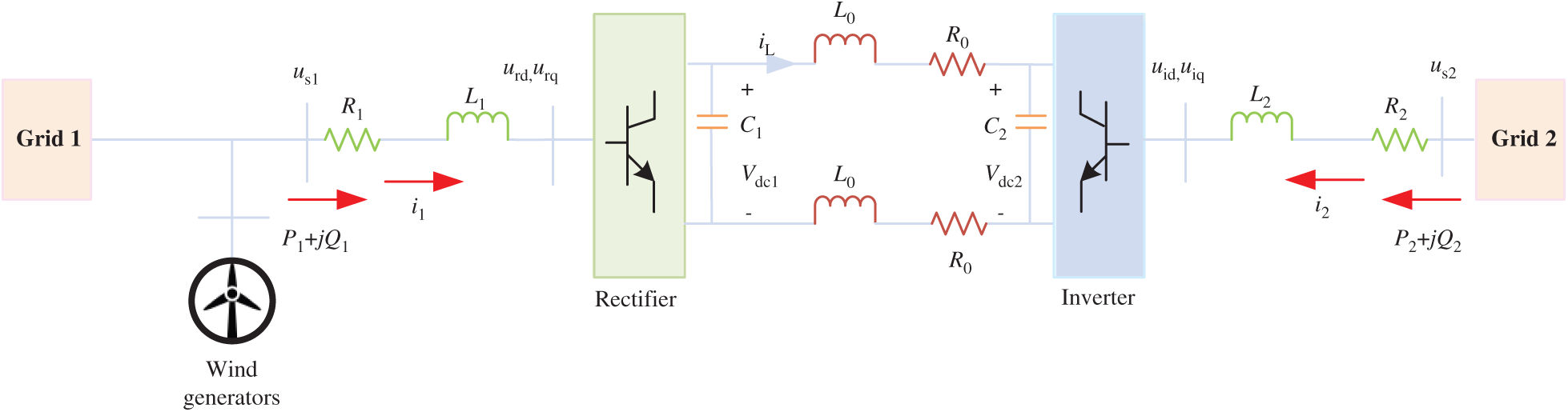
Figure 1: Configuration of VSC-HVDC system
BAS algorithm is a novel biology-based meta-heuristic algorithm, which is mainly based on special food detecting and searching behaviour of long-horn beetles characterized by extremely long antennae in nature [30]. Such long antennae are a very common symbol in most beetle species, and it is composed of various types of olfactory receptor cells. The main function of large antennae is to expand detection range, within this range, beetles can better capture the odour of prey and detect sex pheromones that may be suitable for mating. Basically, beetle uses two antennae to randomly detect nearby areas, and the detection direction depends on which side has a higher odour.
In BAS algorithm, at the 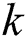 th time, the location of each beetle is considered as a vector
th time, the location of each beetle is considered as a vector 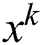 (
(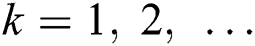 ). Meanwhile, the fitness function is represented by
). Meanwhile, the fitness function is represented by 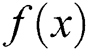 , which means odour concentration locates at x, while its maximum value directly relies on where odour begins to diffuse, called source point. Inspired by stochastic searching mechanism of beetles, two stages are mainly contained, namely, searching and detecting.
, which means odour concentration locates at x, while its maximum value directly relies on where odour begins to diffuse, called source point. Inspired by stochastic searching mechanism of beetles, two stages are mainly contained, namely, searching and detecting.
a) Searching: Stochastic searching direction of beetles is defined by

where 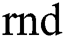 (.) means a stochastic function and
(.) means a stochastic function and 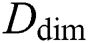 stands for location dimensions, respectively.
stands for location dimensions, respectively.
Besides, for more accurately replicating actual searching behaviour of beetle’s antennae, right-hand and left-hand searching behaviours are adopted, as follows:


where 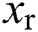 and
and 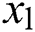 denote location in the right-hand and left-hand searching area, respectively; and
denote location in the right-hand and left-hand searching area, respectively; and 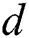 is sensing length of antennae, which initial value should be large enough to avoid premature convergence at the initial phase, and decreases over time.
is sensing length of antennae, which initial value should be large enough to avoid premature convergence at the initial phase, and decreases over time.
b) Detecting: An iterative model is presented which takes both odour detection and searching behaviour into consideration, as follows:

where 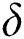 denotes step size that indicates convergence rate, while initialization of
denotes step size that indicates convergence rate, while initialization of 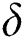 and searching area should be equal; and sign(.) means sign function, respectively.
and searching area should be equal; and sign(.) means sign function, respectively.
Particularly, the updating rule of parameters which directly influences searching behaviour, e.g., antennae length 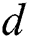 and step size
and step size 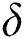 , can be expressed by:
, can be expressed by:


BAS algorithm only adopts a single beetle to seek a potentially better solution, which is prone to be sunk at a local optimum. To overcome such drawbacks, CBAS algorithm employs a cooperative group with multiple beetles to find potential better solutions, as demonstrated in Fig. 2. Hence, CBAS algorithm not only contains a detecting stage (i.e., global search) like BAS algorithm, but also a local searching behavior to approximate the current best solution, which can be described by
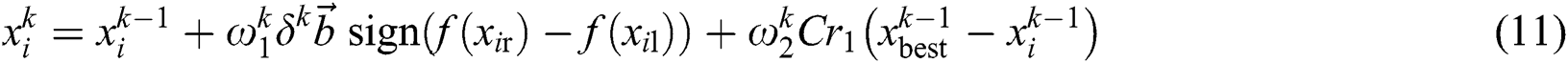
where subscript 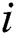 means the
means the 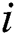 th beetle;
th beetle; 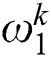 and
and 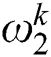 represent dynamic weights of global exploration and local exploitation, respectively;
represent dynamic weights of global exploration and local exploitation, respectively; 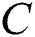 stands for a constant coefficient;
stands for a constant coefficient; 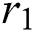 is a stochastic value from [0,1]; and
is a stochastic value from [0,1]; and 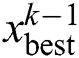 denotes current best solution until the (
denotes current best solution until the (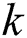 -1)th iteration.
-1)th iteration.
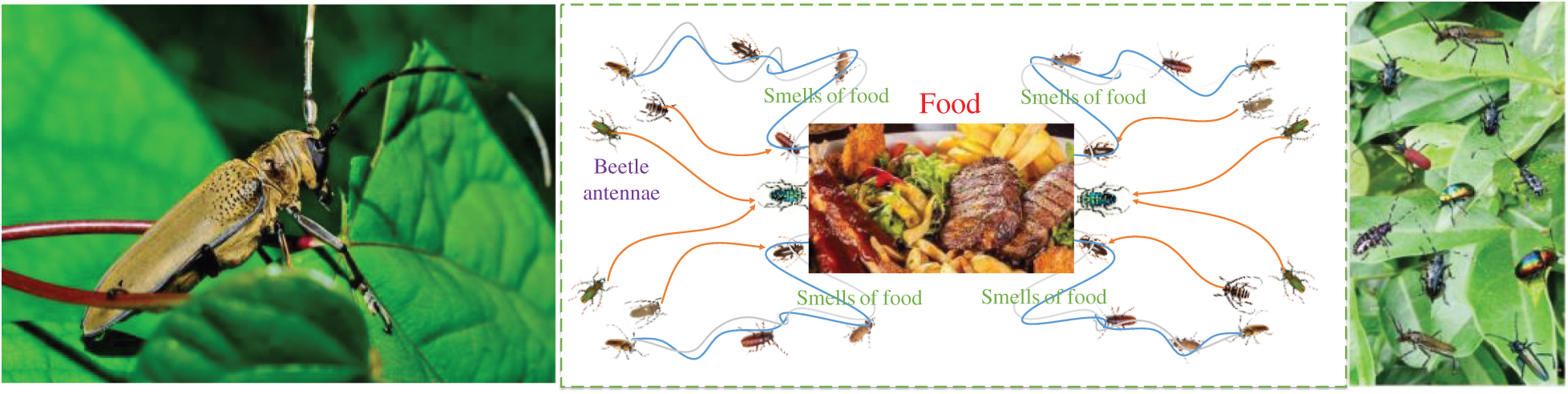
Figure 2: Optimization principle of CBAS algorithm
3.2.2 Dynamic Balance between Local Exploitation and Global Exploration
Like other meta-heuristic algorithms, it is significant to achieve a stable and desirable optimization of a suitable trade-off between local exploitation and global exploration. As an example, if CBAS algorithm attaches more attention to local exploitation, it will easily result in a low-quality local optimum; otherwise, it will result in a low optimization efficiency to seek a better solution. In order to realize optimal search, weights in Eq. (11) are designed to be time-varying as iteration increases, yields


where 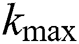 means maximum iteration number;
means maximum iteration number; 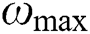 and
and 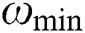 denote the maximum and minimum weights, respectively.
denote the maximum and minimum weights, respectively.
Note that global exploration weight 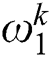 will gradually decrease as iteration number grows based on Eq. (12), while local exploitation weight
will gradually decrease as iteration number grows based on Eq. (12), while local exploitation weight 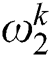 will gradually increase since their sum is equal to be 1 in Eq. (13). According to such improvement, global exploration ability of CBAS algorithm can be significantly improved in initial optimization stage, which can effectively boost searching efficiency and probability of high-quality solutions. As iteration number increases, CBAS algorithm tends to concentrate on local exploitation, which can further improve solution quality.
will gradually increase since their sum is equal to be 1 in Eq. (13). According to such improvement, global exploration ability of CBAS algorithm can be significantly improved in initial optimization stage, which can effectively boost searching efficiency and probability of high-quality solutions. As iteration number increases, CBAS algorithm tends to concentrate on local exploitation, which can further improve solution quality.
Furthermore, parameters of BAS method, e.g., 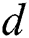 and
and 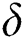 , are prone to considerably decrease with an exponential type in Eq. (14) and (15), upon which a broad global exploration cannot be achieved smoothly. To remedy such problem, an exponential reduction is displaced by a linear reduction in CBAS algorithm, as follows:
, are prone to considerably decrease with an exponential type in Eq. (14) and (15), upon which a broad global exploration cannot be achieved smoothly. To remedy such problem, an exponential reduction is displaced by a linear reduction in CBAS algorithm, as follows:


where 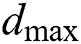 and
and 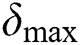 denote the maximum antennae length and maximum step size, respectively.
denote the maximum antennae length and maximum step size, respectively.
4 PoFoPID Control Design for VSC-HVDC System
Details for PoFoPID control can be referred to authors’ previous work [29] for interested readers. Note that this section directly uses this controller and optimally tune its control gains through CBAS.
4.1 Rectifier Controller Design
Let system output  ,
, 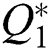 and
and 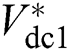 are the given references for reactive power and DC voltage, respectively. Make a definition of the tracking error
are the given references for reactive power and DC voltage, respectively. Make a definition of the tracking error 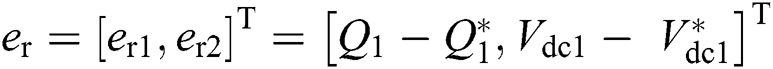 , differentiate
, differentiate 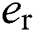 until control input appears explicitly, yields
until control input appears explicitly, yields

where
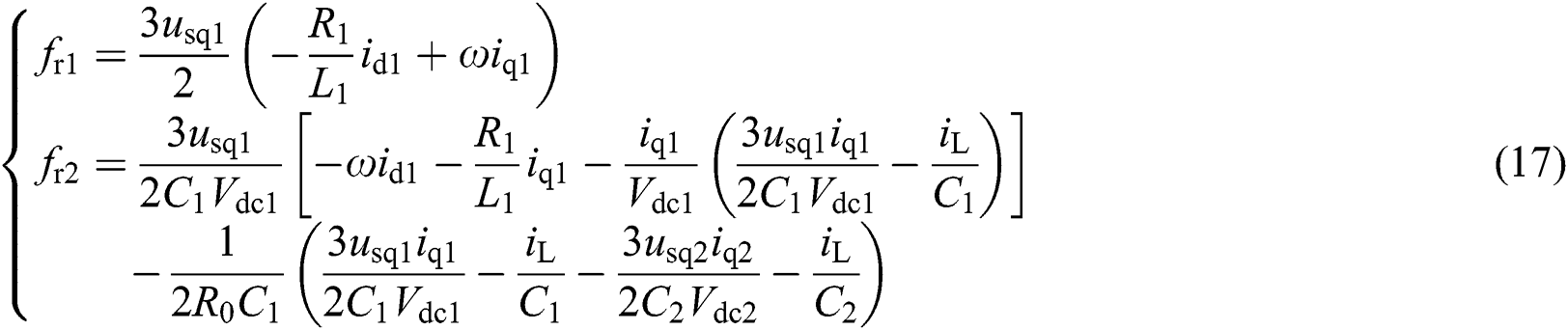
and

The determinant of matrix 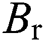 is generated as
is generated as 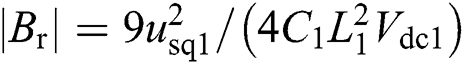 , which is nonzero within the operating extent of the rectifier, so system (16) is linearizable.
, which is nonzero within the operating extent of the rectifier, so system (16) is linearizable.
Suppose overall the nonlinearities are uncharted, make a definition of the perturbations 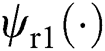 and
and 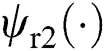 as
as

where constant control gain 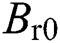 can be obtained by
can be obtained by

Then system (16) is able to rewritten as

Define 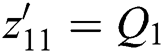 , it develops a second-order sliding-mode perturbation observer (SMPO) to evaluate
, it develops a second-order sliding-mode perturbation observer (SMPO) to evaluate 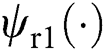 as
as
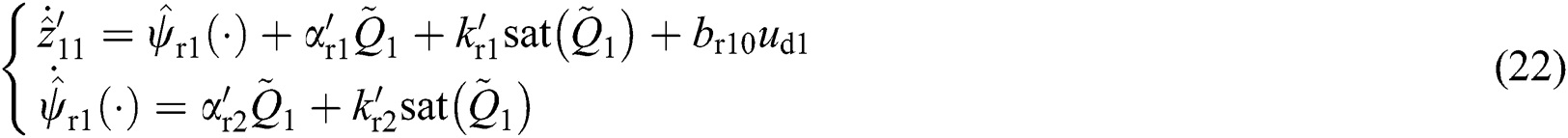
where observer gains 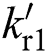 ,
, 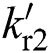 ,
, 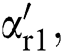 and
and 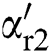 are positive constants.
are positive constants.
Define 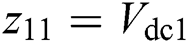 and
and 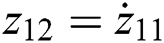 , it employs a third-order sliding-mode state and perturbation observer (SMSPO) to evaluate
, it employs a third-order sliding-mode state and perturbation observer (SMSPO) to evaluate 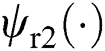 as
as
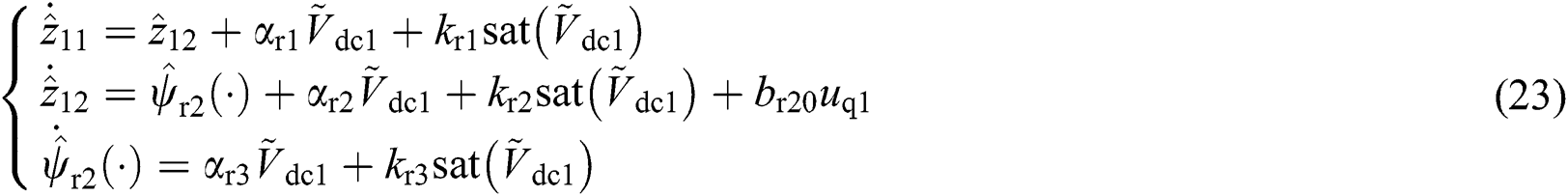
where observer gains 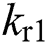 ,
, 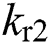 ,
, 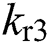 ,
, 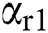 ,
, 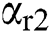 , and
, and 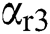 are positive constants.
are positive constants.
The PoFoPID control for VSC-HVDC systems (16) can then be described by [34]
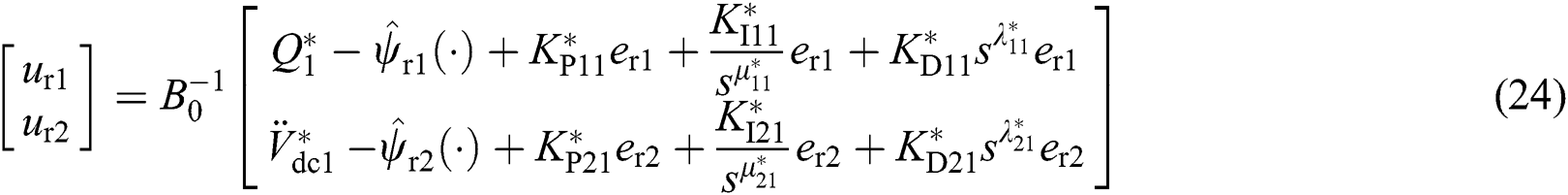
where optimal control parameters 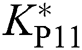 ,
, 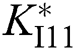 ,
,  ,
, 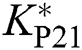 ,
, 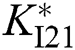 ,
, 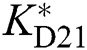 ,
, 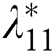 ,
, 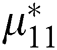 ,
, 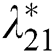 , and
, and 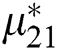 are tuned by CBAS.
are tuned by CBAS.
4.2 Inverter Controller Design
Choose system output 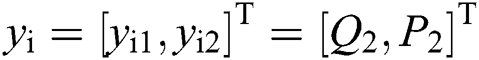 ,
, 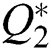 and
and  are the given references of reactive and active power, respectively. Make a definition of tracking error
are the given references of reactive and active power, respectively. Make a definition of tracking error 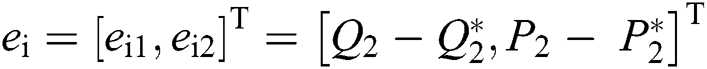 , differentiate
, differentiate 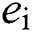 until control input appears explicitly, as follows:
until control input appears explicitly, as follows:

where

and

The determinant of matrix 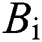 is generated as
is generated as 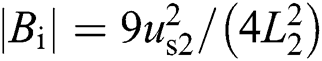 , which is nonzero within the operating extent of the rectifier, so system (25) is linearizable.
, which is nonzero within the operating extent of the rectifier, so system (25) is linearizable.
Suppose entire the nonlinearities are uncharted, make a definition of the perturbations 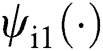 and
and 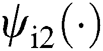 as
as

where the constant control gain 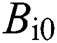 is obtained by
is obtained by

Then system (25) is able to overwritten as

Define 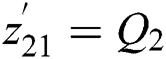 and
and 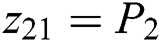 , it adopts two second-order SMPOs evaluate
, it adopts two second-order SMPOs evaluate 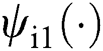 and
and 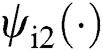 as
as
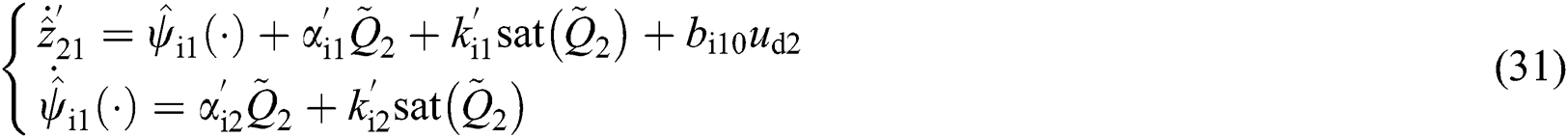
where observer gains 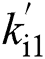 ,
, ,
,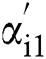 and
and 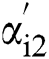 are positive constants.
are positive constants.
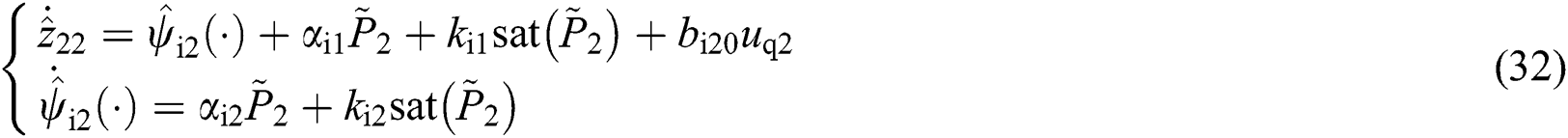
where observer gains 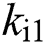 ,
,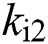 ,
,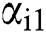 and
and 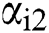 are positive constants.
are positive constants.
The PoFoPID control for VSC-HVDC systems (25) can then be described by
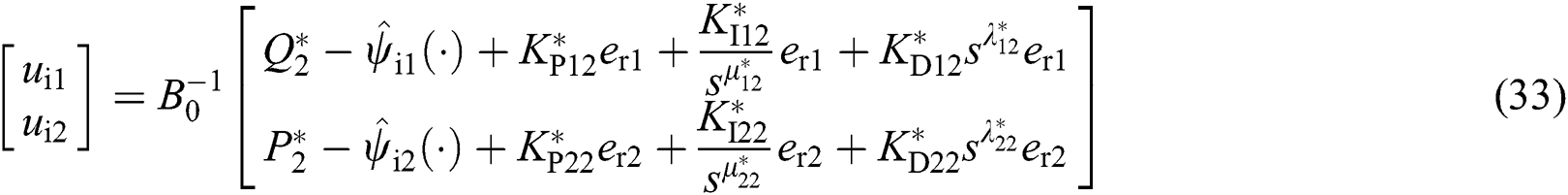
where optimal control parameters 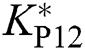 ,
, 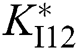 ,
, 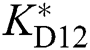 ,
, 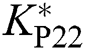 ,
, 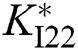 ,
, 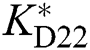 ,
, 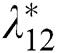 ,
, 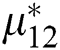 ,
, 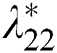 , and
, and  are tuned by CBAS. The optimization target is to minimize the tracking error of inverter and rectifier control and the entire control costs, as follows:
are tuned by CBAS. The optimization target is to minimize the tracking error of inverter and rectifier control and the entire control costs, as follows:
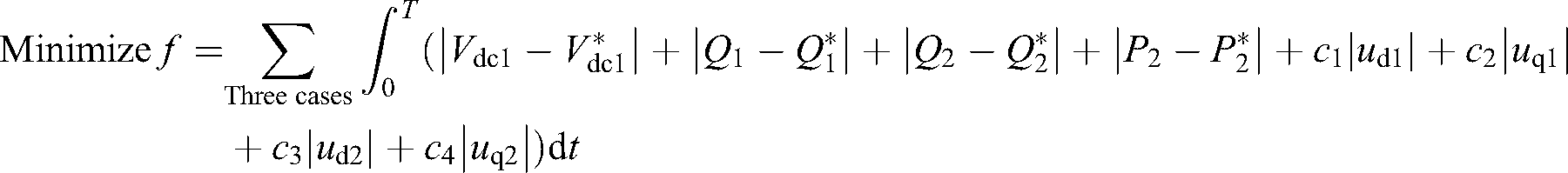
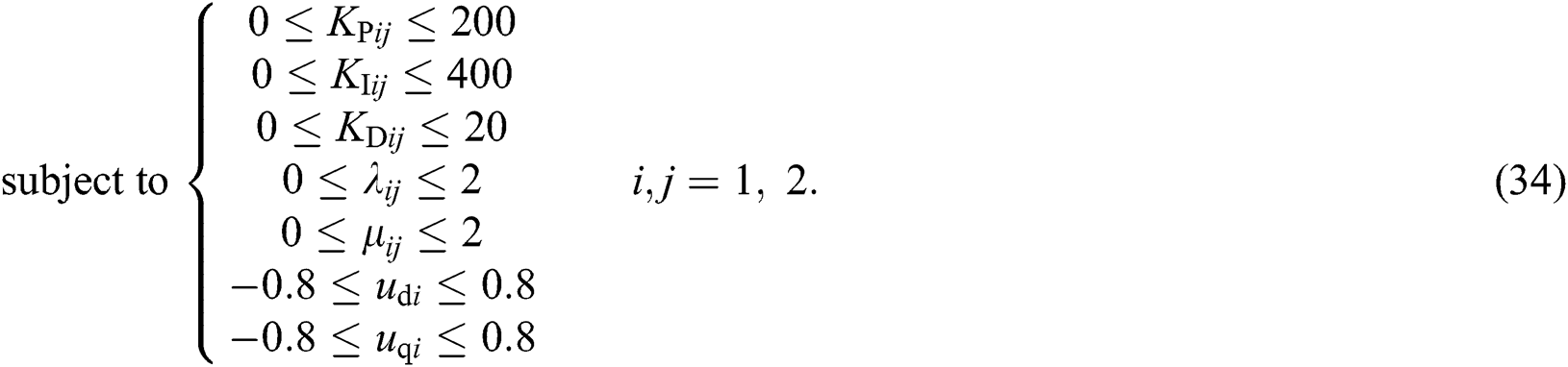
where the weights 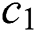 ,
, 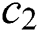 ,
, 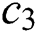 , and
, and 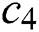 are adopted to scale the magnitude of control costs which are selected to be 1/4, simulation time
are adopted to scale the magnitude of control costs which are selected to be 1/4, simulation time 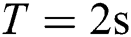 . Besides, the convergence criteria is maximum iteration number kmax=100.
. Besides, the convergence criteria is maximum iteration number kmax=100.
In addition, the Oustaloup approximation [35] is used for a recursive distribution of zeros and poles, which gives

where 2N+1 denotes the number of zeros and poles; K is the gain which causes both sides of Eq. (35) to have unit gain at 1 rad/s. 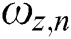 and
and 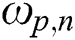 are given as
are given as


In Eqs. (36) and (37), lower limit 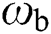 and upper limit
and upper limit 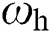 normally satisfy
normally satisfy 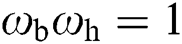 and
and 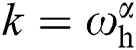 .
.
Lastly, the entire controller structure of PoFoPID can be depicted in Fig. 3.
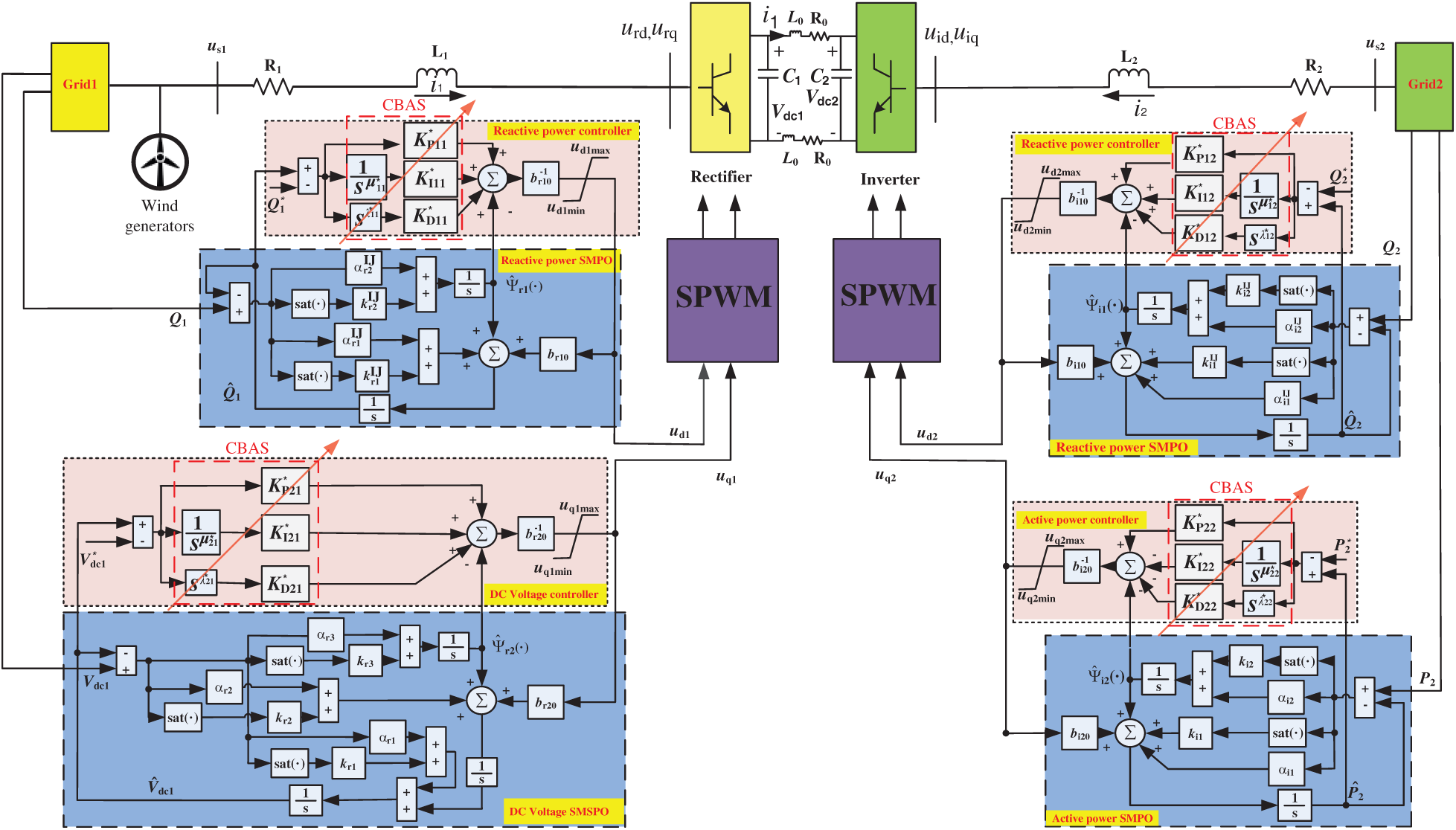
Figure 3: The entire controller structure of PoFoPID
For the sake of assessing the control performance of PoFoPID, two typical controllers, i.e., PID control [36] and feedback linearization sliding-mode control (FLSMC) [37] control are compared under three cases, namely, (a) active and reactive power tracking; (b) 5-Cycle line-line-line-ground (LLLG) fault at AC bus 1; and (c) offshore wind farm integration. In addition, AC grid frequency is 50 Hz, and the detailed parameters of VSC-HVDC systems can be referenced in literature [29]. Meanwhile, the control parameters of three controllers are both optimally tuned by CBAS in 30 repetitions, as shown in Tab. 1. And the maximum iteration number kmax is set to be 100. Tab. 2 gives the statistical outcomes of CBAS acquired by these three controllers. Comparison of the convergence performance and statistical results of fitness function of all controllers are depicted in Fig. 4, and Fig. 5, respectively. One can easily find that PoFoPID has the lowest fitness function and iteration number as well as the shortest convergence time among three controllers. Especially, the introduction of fractional-order mechanism in PoFoPID significantly improves the dynamic response performance such that the mean convergence time of PoFoPID is 16.22% and 8.11% lower than that of PID and FLSMC, respectively. In addition, the simulation is carried out on MATLAB/SIMULINK 2019a through a personal computer with an IntelR CoreTMi5 CPU at 3.4 GHz and 16 GB of RAM.
Table 1: The control parameters of three controllers optimally tuned by CBAS in 30 repetitions

Table 2: The statistical results of CBAS acquired by three controllers in 30 repetitions
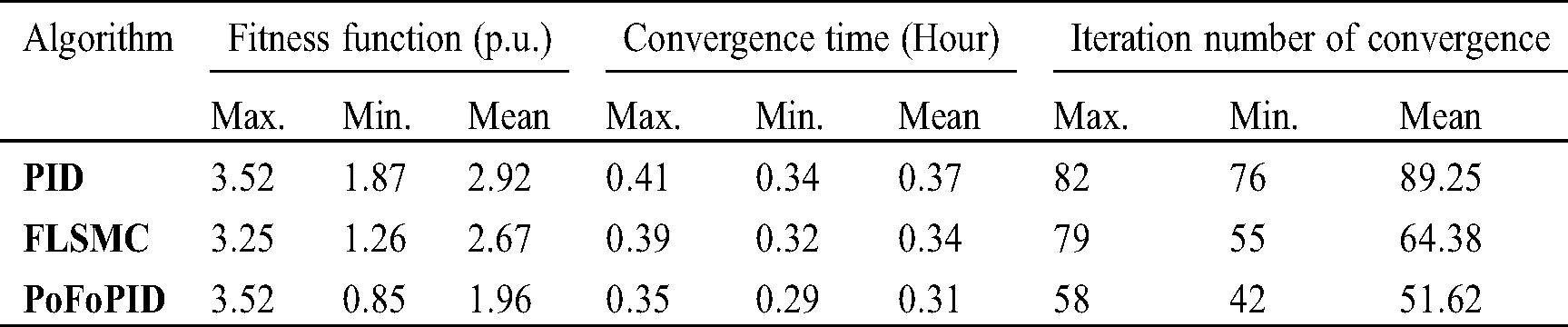
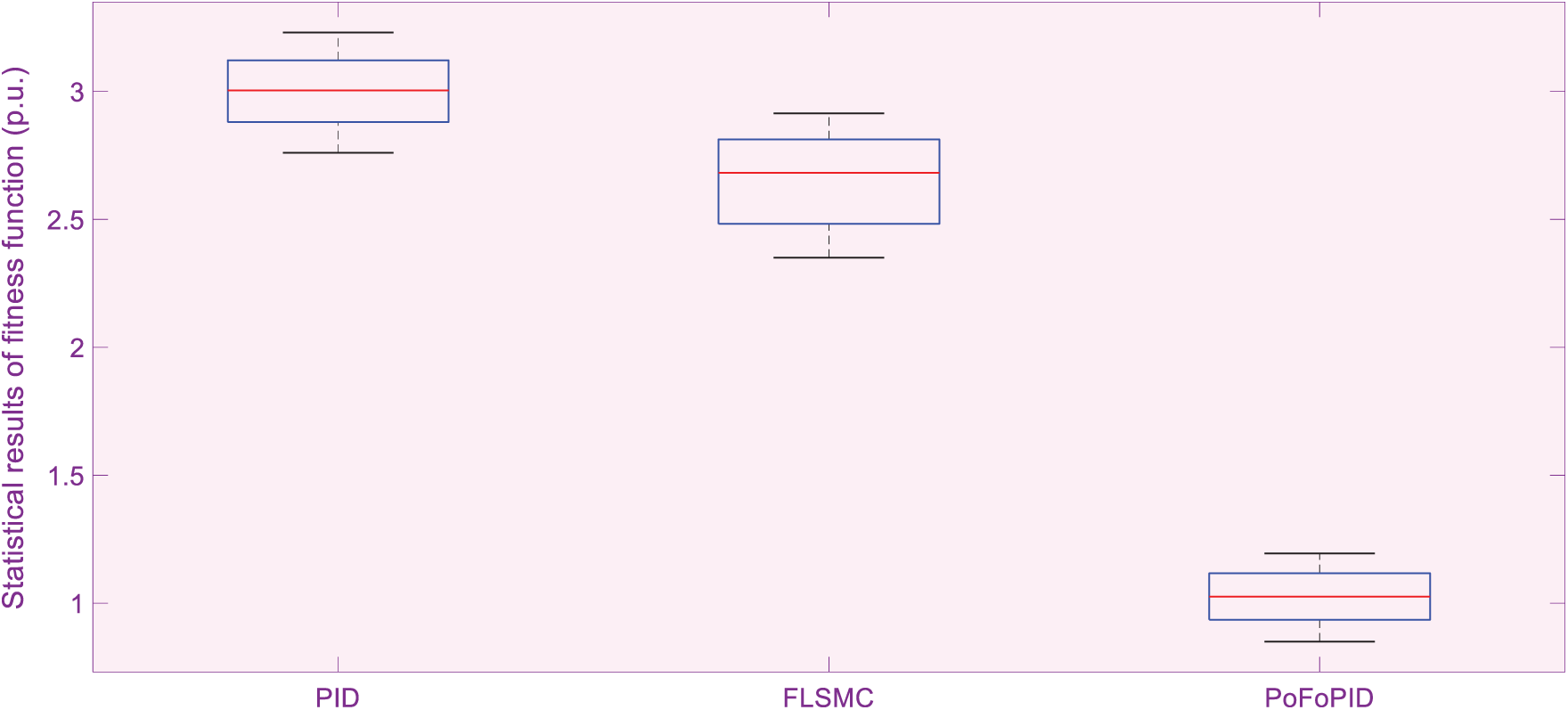
Figure 4: Statistical results of fitness function generated in 30 repetitions
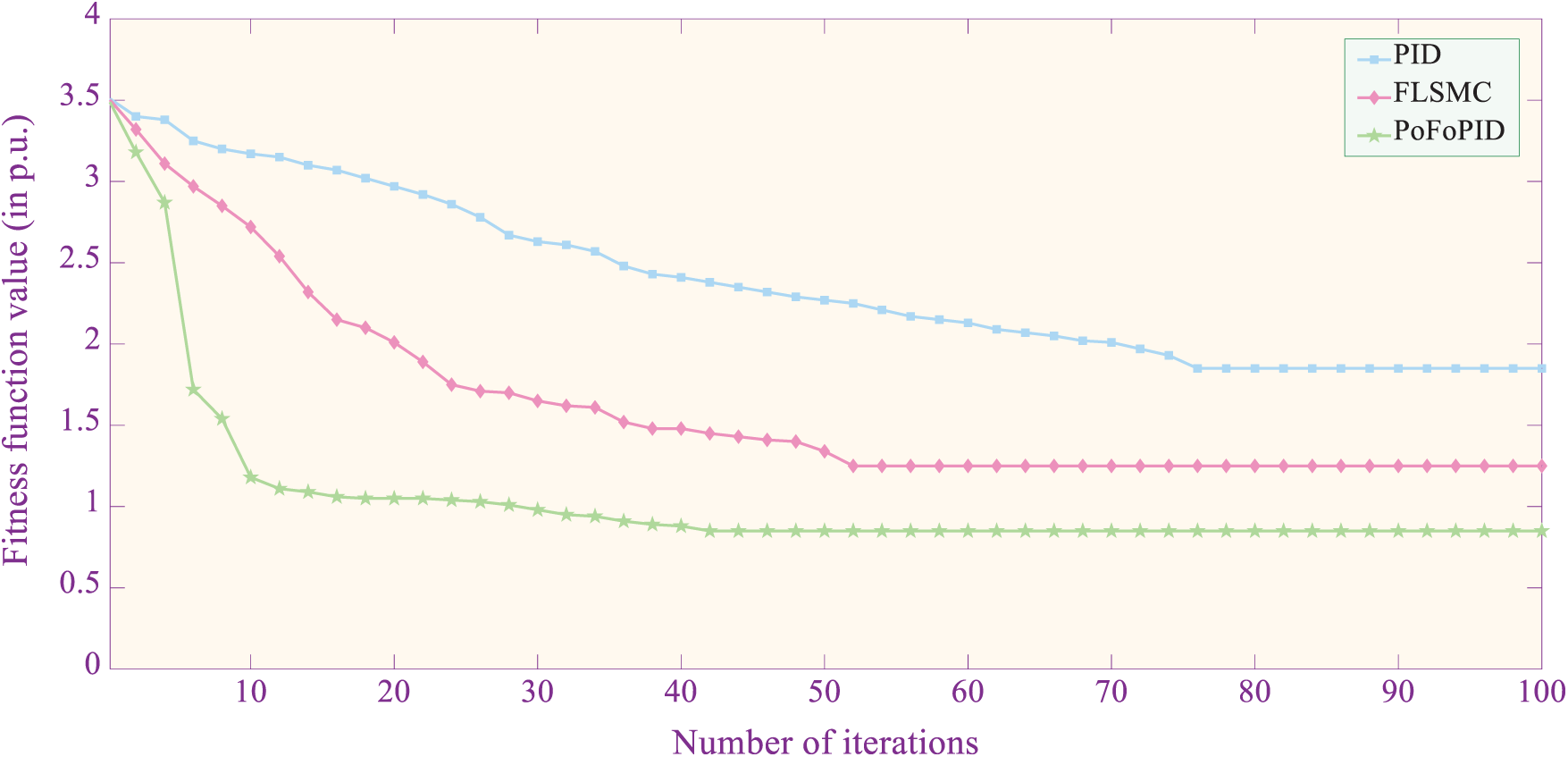
Figure 5: Comparison of the best convergence performance of three control schemes generated in 30 repetitions
5.1 Active and Reactive Power Tracking
A series of step changes of active and reactive power are implemented at 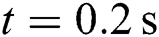 and
and 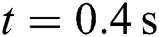 , which are restored to the primary value a
, which are restored to the primary value a 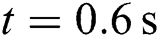 . Meanwhile, DC voltage is maintained at its rated value
. Meanwhile, DC voltage is maintained at its rated value 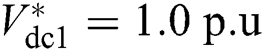 . Fig. 6 compares the system responses of three controllers. It can be seen that PoFoPID can obtain a consistent control performance with the fastest tracking speed and the smallest active and reactive power overshoot. Especially, the maximum overshoot of active power P1 of PID is 36.10% and 33.71% during the second and third step variation, while PoFoPID can realize smooth active and reactive power tracking. Meanwhile, the convergence time of P1 of PID, FLSMC, and PoFoPID are 0.16s, 0.10s, and 0.08s during the second step variation, respectively [38].
. Fig. 6 compares the system responses of three controllers. It can be seen that PoFoPID can obtain a consistent control performance with the fastest tracking speed and the smallest active and reactive power overshoot. Especially, the maximum overshoot of active power P1 of PID is 36.10% and 33.71% during the second and third step variation, while PoFoPID can realize smooth active and reactive power tracking. Meanwhile, the convergence time of P1 of PID, FLSMC, and PoFoPID are 0.16s, 0.10s, and 0.08s during the second step variation, respectively [38].
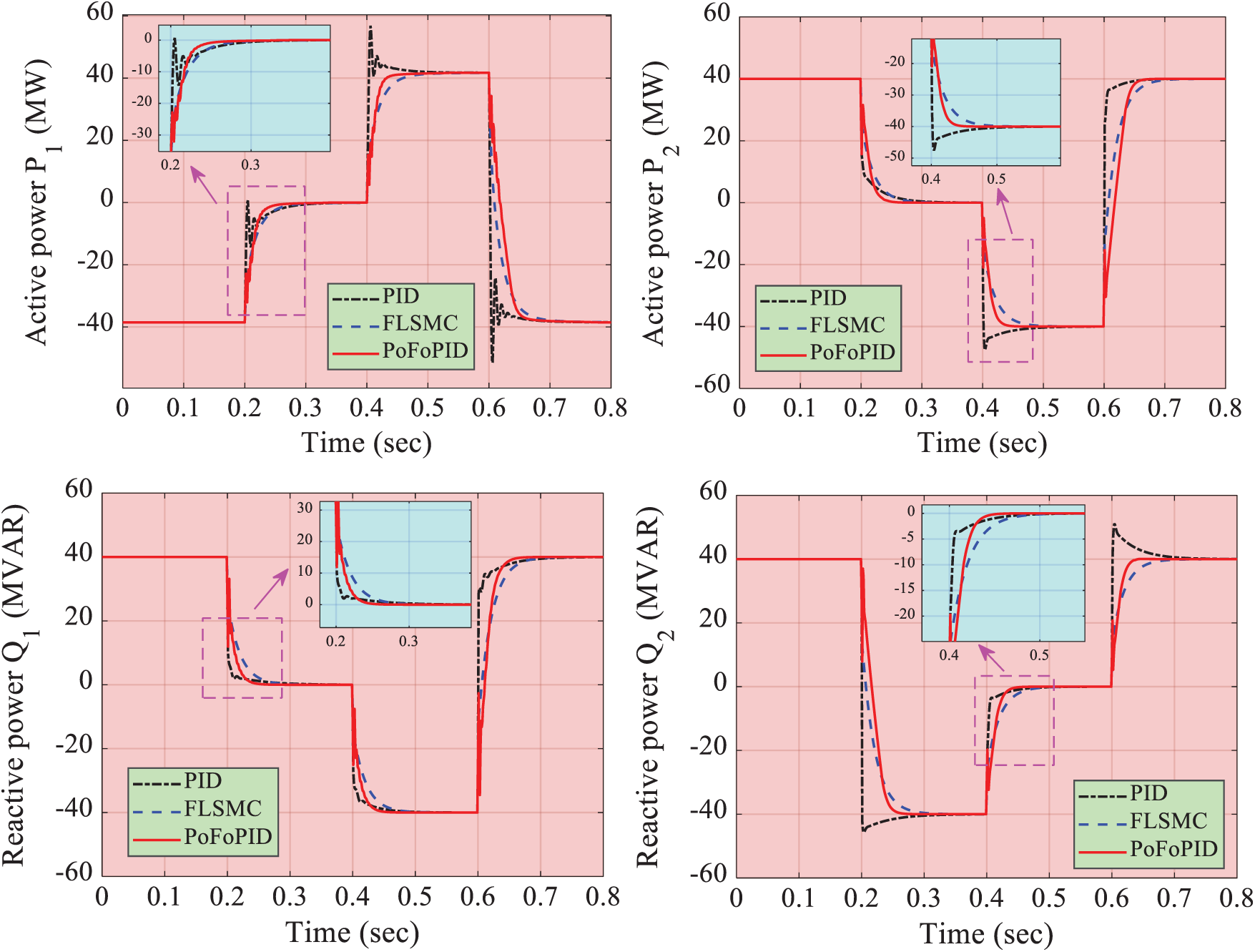
Figure 6: System responses generated under active and reactive power tracking
5.2 5-Cycle Line-Line-Line-Ground (LLLG) Fault
A 5-cycle LLLG fault occurs at AC bus 1 at when t = 0.1 s. As shown in Fig. 7, PID has the most drastic power and DC voltage oscillation due to its design based on local linearization of specific operation point. While PoFoPID can restrain the active power and reactive power oscillations effectively with the smallest recovery time because the introduction of fractional-order operators provides more degree of freedom for control system [39]. More specifically, the maximum overshoot of active power and reactive power of PoFoPID is 62.63% and 54.53% of that of PID, respectively. And the recovery time of DC voltage Vdc1 of PID, FLSMC, and PoFoPID are 0.46 s, 0.39 s, and 0.26 s, respectively. Moreover, Fig. 8 gives the perturbation estimation of observers, which demonstrates that the developed SMSPO and SMPO can realize satisfactory tracking performance.
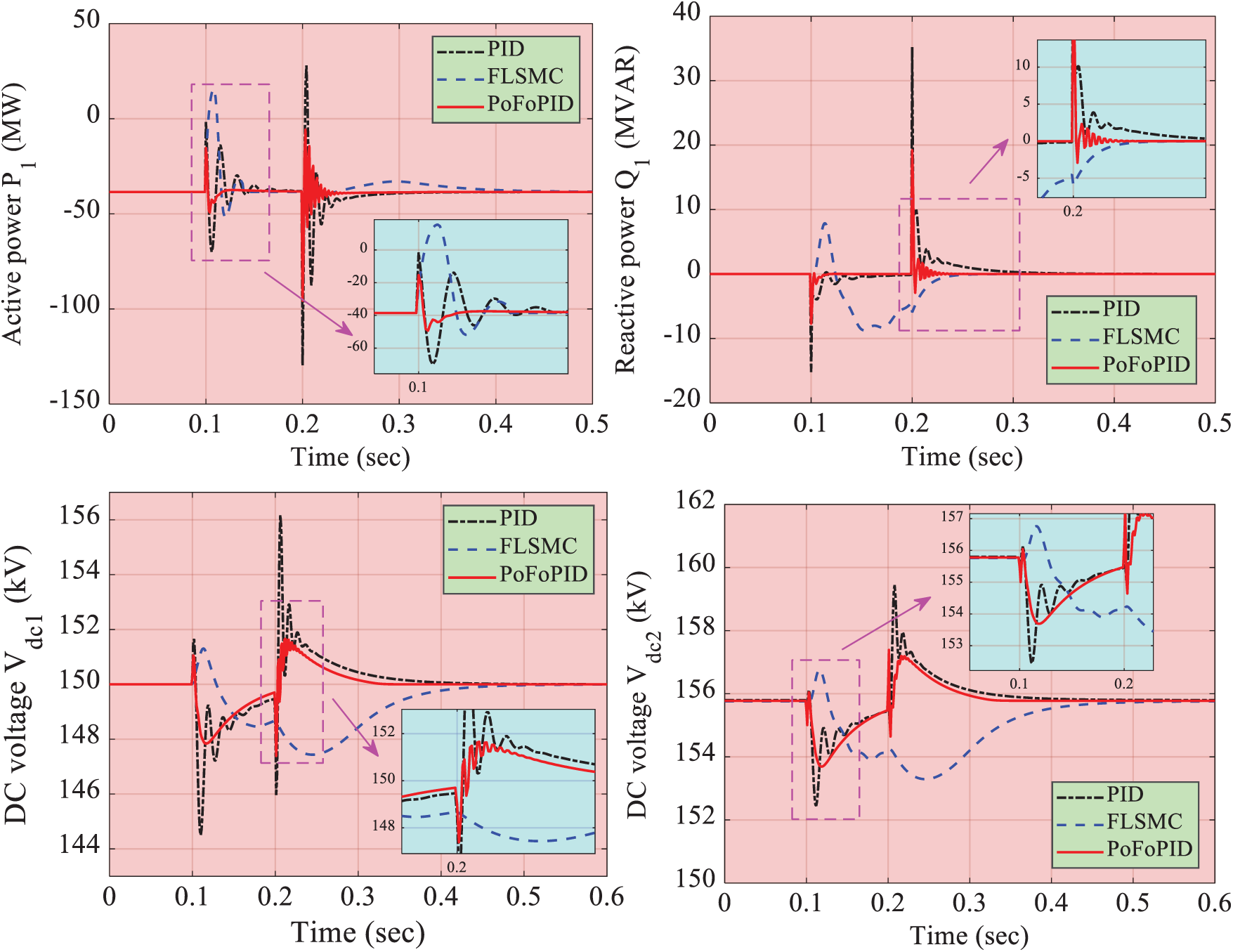
Figure 7: System responses generated under 5-cycle LLLG fault at AC bus 1
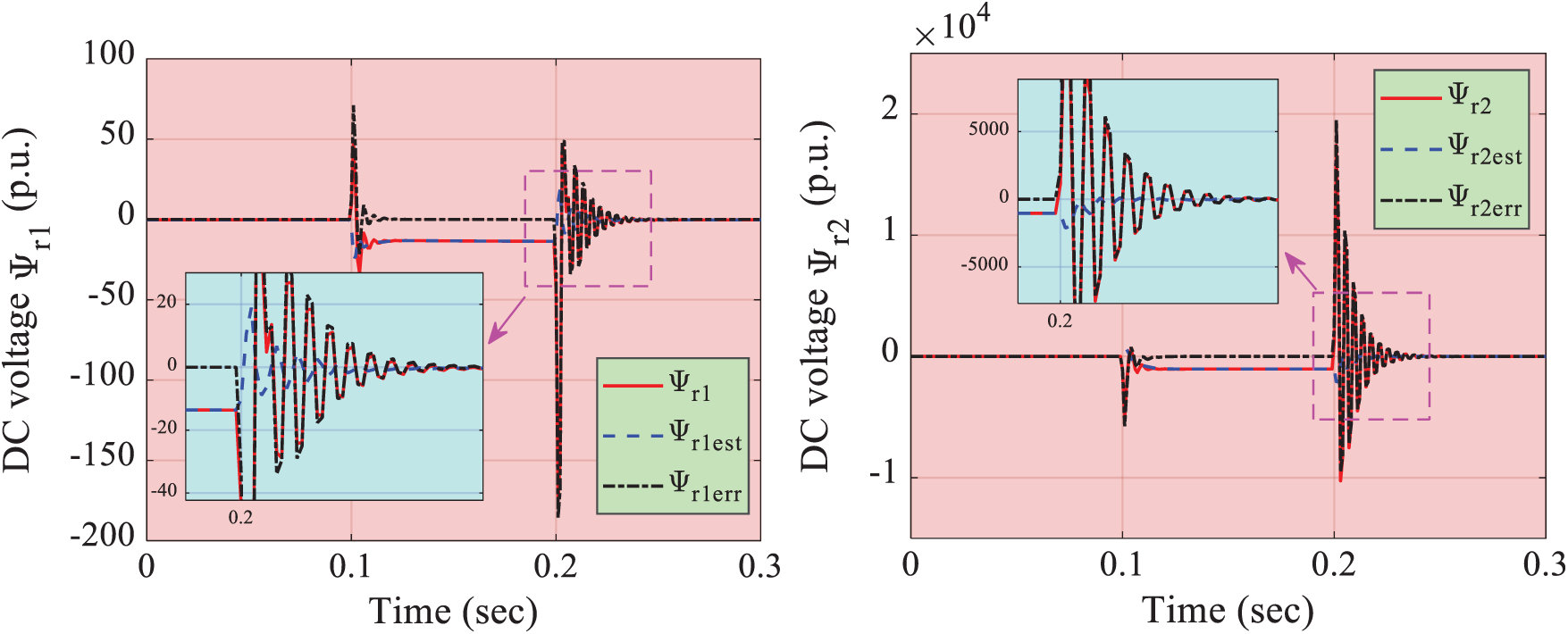
Figure 8: Estimation error of observers generated under 5-cycle LLLG fault at AC bus 1
5.3 Offshore Wind Farm Integration
Offshore wind farm has a more strong and constant wind speed than the onshore wind farm, which are the promising development trend in coming decades. In particular, AC side of offshore wind farm integration is as same as a weak power, which voltage us1 is a time-varying function. Hence, this case simulates a voltage fluctuation us1 = 1 + 0.15 sin (0.2 t) during t = 0.15 s to t = 1.05 s. Fig. 9 shows that PoFoPID has the strongest robustness with a smooth tracking performance. Moreover, the maximum overshoot of control input ud1 and uq1 of PoFoPID is 32.56% and 57.58% of that of PID, respectively.
t) during t = 0.15 s to t = 1.05 s. Fig. 9 shows that PoFoPID has the strongest robustness with a smooth tracking performance. Moreover, the maximum overshoot of control input ud1 and uq1 of PoFoPID is 32.56% and 57.58% of that of PID, respectively.
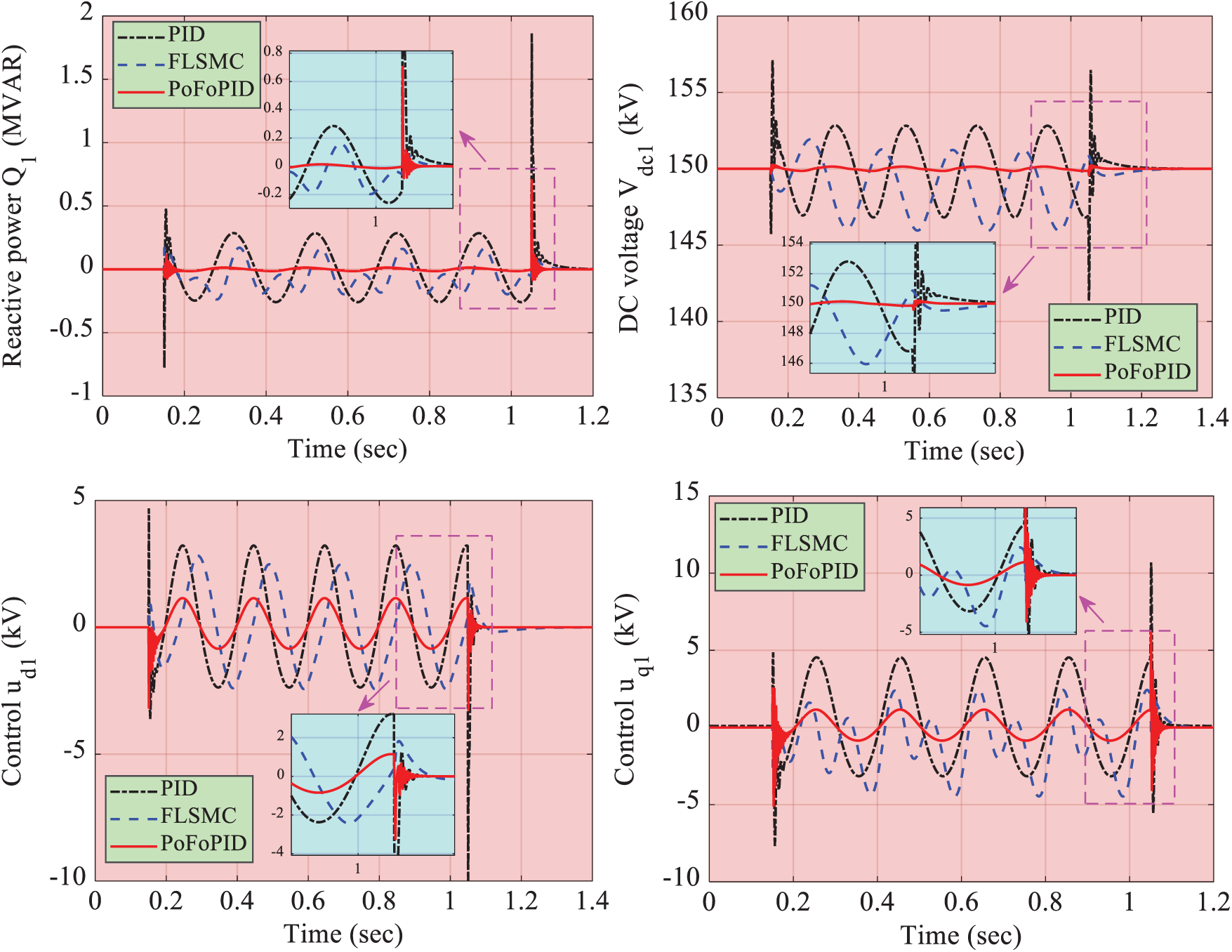
Figure 9: System responses generated under offshore wind farm integration
The integral absolute error (IAE) indices describe the error accumulation of the controlled variable relative to its reference value during time T. And Tab. 3 compares IAE indices of three controllers under above three cases, where 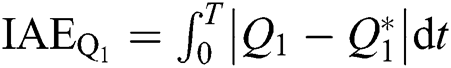 ,
, 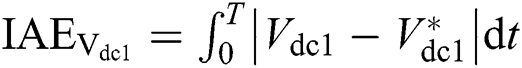 ,
,  , and
, and 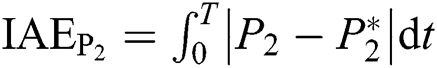 . Obviously, PoFoPID obtains the smallest IAE indices in all conditions, which proves that the proposed control strategy can realize the excellent control performance among all methods. Particularly, the
. Obviously, PoFoPID obtains the smallest IAE indices in all conditions, which proves that the proposed control strategy can realize the excellent control performance among all methods. Particularly, the 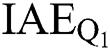 of PoFoPID is merely 55.10% and 89.72% of that of PID and FLSMC in active and reactive power tracking. And the
of PoFoPID is merely 55.10% and 89.72% of that of PID and FLSMC in active and reactive power tracking. And the 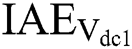 of PoFoPID are only 55.10% and 89.72% of that of PID and FLSMC in 5-cycle LLLG fault.
of PoFoPID are only 55.10% and 89.72% of that of PID and FLSMC in 5-cycle LLLG fault.
Furthermore, the overall control costs 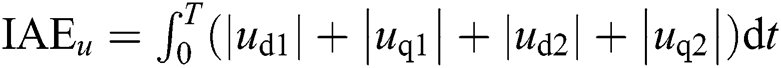 of three controllers under three cases are illustrated in Fig. 10. It indicates that PoFoPID has the lowest entire control costs in all cases because of the integration of real-time perturbation estimation and FoPID structure. Hence, PoFoPID can provide strong robustness to handle system nonlinearities, parameter uncertainties, and unmodelled dynamics. And the overall control costs of PoFoPID are only 52.97% and 28.60% of that of PID and FLSMC in offshore wind farm integration.
of three controllers under three cases are illustrated in Fig. 10. It indicates that PoFoPID has the lowest entire control costs in all cases because of the integration of real-time perturbation estimation and FoPID structure. Hence, PoFoPID can provide strong robustness to handle system nonlinearities, parameter uncertainties, and unmodelled dynamics. And the overall control costs of PoFoPID are only 52.97% and 28.60% of that of PID and FLSMC in offshore wind farm integration.
Table 3: IAE indices (in p.u.) of three controllers computed in different cases
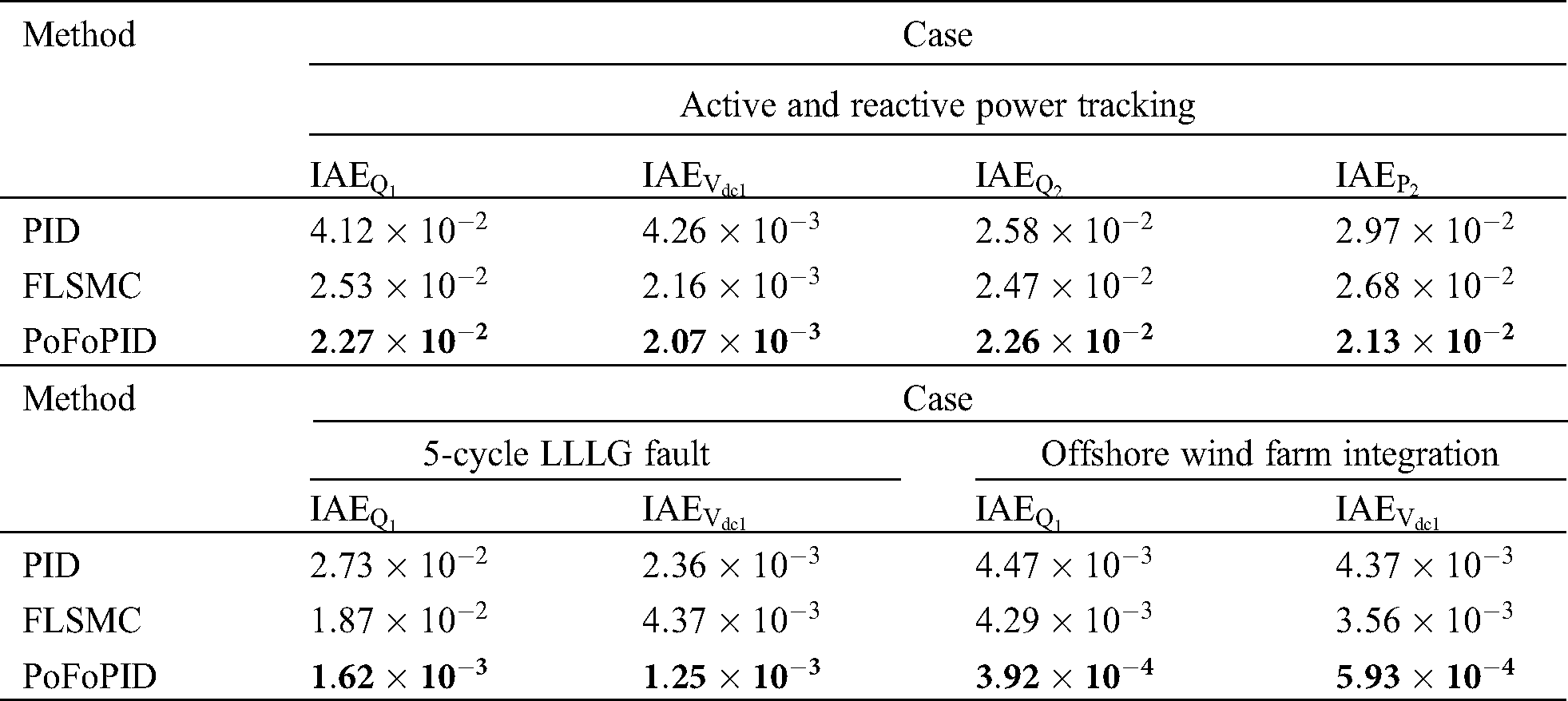
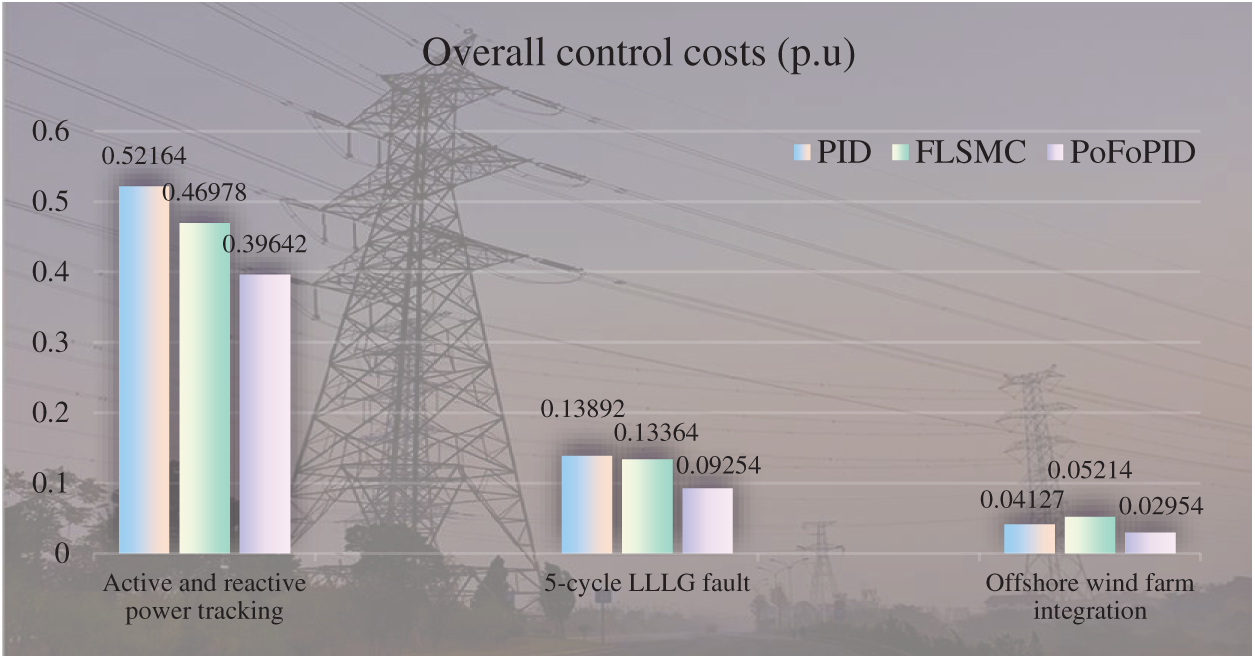
Figure 10: The entire control costs of three control schemes required in different cases
In this paper, a new PoFoPID controller is designed for VSC-HVDC systems, which with the purpose of enhancing the robustness and control performance of the system. The major novelties/contributions can be concluded as follows:
(1) PoFoPID control is able to dramatically boost dynamical responses of VSC-HVDC systems integrated with offshore wind farm, which owns great robustness against various uncertainties owing to real-time compensation of perturbation;
(2) Compared to original BAS algorithm, CBAS algorithm can remarkably improve optimization efficiency via a cooperative group of multiple beetles instead of a single beetle. Besides, it can also acquire a high-quality optimum through a dynamic and suitable balance mechanism between local exploitation and global exploration. CBAS algorithm is utilized to optimally tune PoFoPID controller parameters, such that the overall tracking error can be minimized under various operating conditions;
(3) Simulation results validate that PoFoPID controller can achieve the highest tracking speed and lowest tracking error, along with the lowest entire control costs compared with that of other two controllers. Especially, in active and reactive power tracking, the convergence time of P2 of PID, FLSMC, and PoFoPID are 0.048 s, 0.16 s, and 0.13 s during the second step variation, respectively; the maximum overshoot of active power and reactive power of PoFoPID is 62.63% and 54.53% of that of PID, respectively. In 5-cycle LLLG fault, the recovery time of DC voltage Vdc1 of PoFoPID is 56.52% and 84.78% of that of PID and FLSMC, respectively; the maximum overshoot of control input ud1 and uq1 of PoFoPID is 32.56% and 57.58% of that of PID, respectively. And in offshore wind farm integration, the convergence time of Q1 of PID, FLSMC, and PoFoPID are 0.03 s, 0.13 s, and 0.09 s, respectively; the maximum overshoot of control input ud1 and uq1 of PoFoPID is 32.56% and 57.58% of that of PID, respectively. Moreover, PoFoPID can obtain the smallest IAE indices and overall control costs in all cases, which has the highest efficiency and feasibility. Particularly, the 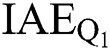 of PoFoPID is only 8.77% and 9.14% of that of PID and FLSMC in offshore wind farm integration, respectively; the overall control costs of PoFoPID are only 75.99% and 84.38% of that of PID and FLSMC in offshore wind farm integration, respectively.
of PoFoPID is only 8.77% and 9.14% of that of PID and FLSMC in offshore wind farm integration, respectively; the overall control costs of PoFoPID are only 75.99% and 84.38% of that of PID and FLSMC in offshore wind farm integration, respectively.
Future study will undertake a dSpace based hardware-in-loop (HIL) experiment for PoFoPID control of VSC-HVDC system, which aims to validate the implementation feasibility of the proposed approach. Besides, it can employ PoFoPID control for multiterminal VSC-HVDC systems via CBAS with offshore wind integration in future researches.
Funding Statement: The authors thankfully acknowledge the support of the National Natural Science Foundation of China (51807085).
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
1. Annamraju, A., Nandiraju, S. (2019). Robust frequency control in a renewable penetrated power system: An adaptive fractional order-fuzzy approach. Protection and Control of Modern Power Systems, 4(1), 1–15. DOI 10.1186/s41601-019-0115-7. [Google Scholar] [CrossRef]
2. Murty, V. V. S. N., Kumar, A. (2020). Multi-objective energy management in microgrids with hybrid energy sources and battery energy storage systems. Protection and Control of Modern Power Systems, 5(1), 304. DOI 10.1186/s41601-019-0147-z. [Google Scholar] [CrossRef]
3. Yang, B., Jiang, L., Wang, L., Yao, W., Wu, Q. H. (2016). Nonlinear maximum power point tracking control and modal analysis of DFIG based wind turbine. International Journal of Electrical Power & Energy Systems, 74, 429–436. DOI 10.1016/j.ijepes.2015.07.036. [Google Scholar] [CrossRef]
4. Yang, B., Yu, T., Shu, H. C., Dong, J., Jiang, L. (2018). Robust sliding-mode control of wind energy conversion systems for optimal power extraction via nonlinear perturbation observers. Applied Energy, 210, 711–723. DOI 10.1016/j.apenergy.2017.08.027. [Google Scholar] [CrossRef]
5. Yang, B., Yu, T., Shu, H. C., Zhang, Y. M., Chen, J. et al. (2018). Passivity-based sliding-mode control design for optimal power extraction of a PMSG based variable speed wind turbine. Renewable Energy, 119, 577–589. DOI 10.1016/j.renene.2017.12.047. [Google Scholar] [CrossRef]
6. Li, B., He, J., Li, Y., Li, B. (2019). A review of the protection for the multi-terminal VSC-HVDC grid. Protection and Control of Modern Power Systems, 4(3), 239–249. [Google Scholar]
7. Flourentzou, N., Agelidis, V. G., Demetriades, G. D. (2009). VSC-based HVDC power transmission systems: an overview. IEEE Transactions on Power Electronics, 24(3), 592–602. DOI 10.1109/TPEL.2008.2008441. [Google Scholar] [CrossRef]
8. Gomis-Bellmunt, O., Liang, J., Ekanayake, J., Jenkins, N. (2011). Voltage-current characteristics of multiterminal HVDC-VSC for offshore wind farms. Electric Power Systems Research, 81(2), 440–450. DOI 10.1016/j.epsr.2010.10.007. [Google Scholar] [CrossRef]
9. Liang, J., Gomis-Bellmunt, O., Ekanayake, J., Jenkins, N., An, W. (2012). A multi-terminal HVDC transmission system for offshore wind farms with induction generators. International Journal of Electrical Power & Energy Systems, 43(1), 54–62. DOI 10.1016/j.ijepes.2012.04.063. [Google Scholar] [CrossRef]
10. Fan, X., Guan, L., Xia, C., Ji, T. (2015). IDA-PB control design for VSC-HVDC transmission based on PCHD model. International Transactions on Electrical Energy Systems, 25(10), 2133–2143. DOI 10.1002/etep.1953. [Google Scholar] [CrossRef]
11. He, J. H., Chen, K. A., Li, M., Luo, Y. P., Liang, C. G. et al. (2020). Review of protection and fault handling for a flexible DC grid. Protection and Control of Modern Power Systems, 5(1), 3482. DOI 10.1186/s41601-020-00157-9. [Google Scholar] [CrossRef]
12. Yang, B., Jiang, L., Yu, T., Shu, H. C., Zhang, C. K. et al. (2018). Passive control design for multi-terminal VSC-HVDC systems via energy shaping. International Journal of Electrical Power & Energy Systems, 98, 496–508. DOI 10.1016/j.ijepes.2017.12.028. [Google Scholar] [CrossRef]
13. Zhang, L., Harnefors, L., Nee, H. (2011). Interconnection of two very weak AC systems by VSC-HVDC links using power-synchronization control. IEEE Transactions on Power Systems, 26(1), 344–355. DOI 10.1109/TPWRS.2010.2047875. [Google Scholar] [CrossRef]
14. Baran, M. E., Mahajan, N. R. (2007). Overcurrent protection on voltage-source-converter-based multiterminal DC distribution systems. IEEE Transactions on Power Delivery, 22(1), 406–412. DOI 10.1109/TPWRD.2006.877086. [Google Scholar] [CrossRef]
15. Prieto-Araujo, E., Bianchi, F. D., Junyent-Ferre, A., Gomis-Bellmunt, O. (2011). Methodology for droop control dynamic analysis of multiterminal VSC-HVDC grids for offshore wind farms. IEEE Transactions on Power Delivery, 26(4), 2476–2485. DOI 10.1109/TPWRD.2011.2144625. [Google Scholar] [CrossRef]
16. Li, S., Member, S., Haskew, T. A., Member, S. (2010). Control of HVDC light system using conventional and direct current vector control approaches. IEEE Transactions on Power Electronics, 25(12), 3106–3118. DOI 10.1109/TPEL.2010.2087363. [Google Scholar] [CrossRef]
17. Sun, L., Li, D., Lee, K. Y. (2015). Enhanced decentralized PI control for fluidized bed combustor via advanced disturbance observer. Control Engineering Practice, 42, 128–139. DOI 10.1016/j.conengprac.2015.05.014. [Google Scholar] [CrossRef]
18. Yang, B., Yu, T., Zhang, X. S., Huang, L. N., Shu, H. C. et al. (2018). Interactive teaching-learning optimiser for parameter tuning of VSC-HVDC systems with offshore wind farm integration. IET Generation, Transmission & Distribution, 12(3), 678–687. DOI 10.1049/iet-gtd.2016.1768. [Google Scholar] [CrossRef]
19. Shah, R., Sánchez, J. C., Preece, R., Barnes, M. (2018). Stability and control of mixed AC–DC systems with VSC-HVDC: A review. IET Generation, Transmission & Distribution, 12(10), 2207–2219. DOI 10.1049/iet-gtd.2017.1140. [Google Scholar] [CrossRef]
20. Moharana, A., Dash, P. K. (2010). Input-output linearization and robust sliding-mode controller for the VSC-HVDC transmission link. IEEE Transactions on Power Delivery, 25(3), 1952–1961. DOI 10.1109/TPWRD.2010.2042469. [Google Scholar] [CrossRef]
21. Guan, M., Pan, W., Zhang, J., Hao, Q., Cheng, J. et al. (2015). Synchronous generator emulation control strategy for voltage source converter (VSC) stations. IEEE Transactions on Power Systems, 30(6), 3093–3101. DOI 10.1109/TPWRS.2014.2384498. [Google Scholar] [CrossRef]
22. Yang, B., Jiang, L., Yu, T., Shu, H. C., Zhang, C. K. et al. (2018). Passive control design for multi-terminal VSC-HVDC systems via energy shaping. International Journal of Electrical Power & Energy Systems, 98, 496–508. DOI 10.1016/j.ijepes.2017.12.028. [Google Scholar] [CrossRef]
23. Nayak, N., Routray, S. K., Rout, P. K. (2012). State feedback robust Hinfinite controller for transient stability enhancement of Vsc-Hvdc transmission systems. Procedia Technology, 4, 652–660. [Google Scholar]
24. Guibin, Z., Zheng, X., Guangzhu, W. (2002). Steady-state model and its nonlinear control of VSC-HVDC system. Proceedings of the Csee, 22(1), 17–22. [Google Scholar]
25. Ye, F., Wei, Z. N., Sun, G. Q. (2011). Improved power flow algorithm incorporating multi-terminal VSC-HVDC. Advanced Materials Research, 383-390, 2188–2194. DOI 10.4028/www.scientific.net/AMR.383-390.2188. [Google Scholar] [CrossRef]
26. Zhang, M. G., Li, B. (2019). The sub-module voltage-balanced control strategy of MMC-HVDC based on model prediction control. Journal of Engineering, 2019(16), 2047–2052. DOI 10.1049/joe.2018.8627. [Google Scholar] [CrossRef]
27. Nayak, N., Routray, S. K., Rout, P. K. (2013). Non-linear control and stabilisation of VSC-HVDC transmission system based on Type-2 fuzzy sliding mode control. International Journal of Automation and Control, 7(1/2), 1–20. DOI 10.1504/IJAAC.2013.055087. [Google Scholar] [CrossRef]
28. Yang, B., Yu, T., Shu, H. C., Zhu, D. N., Zeng, F. et al. (2018). Perturbation observer based fractional-order PID control of photovoltaics inverters for solar energy harvesting via Yin-Yang-Pair optimization. Energy Conversion and Management, 171, 170–187. DOI 10.1016/j.enconman.2018.05.097. [Google Scholar] [CrossRef]
29. Jiang, X. Y., Li, S. (2018). BAS: Beetle antennae search algorithm for optimization problems. International Journal of Robotics and Control, 1(1), 1–5. DOI 10.5430/ijrc.v1n1p1. [Google Scholar] [CrossRef]
30. Ruan, S., Li, G., Jiao, X., Sun, Y., Lie, T. T. (2007). Adaptive control design for VSC-HVDC systems based on backstepping method. Electric Power Systems Research, 77(5-6), 559–565. DOI 10.1016/j.epsr.2006.05.006. [Google Scholar] [CrossRef]
31. Zhang, L., Harnefors, L., Nee, H. (2011). Modeling and control of VSC-HVDC links connected to island systems. IEEE Transactions on Power Systems, 26(2), 783–793. DOI 10.1109/TPWRS.2010.2070085. [Google Scholar] [CrossRef]
32. Du, C., Agneholm, E., Olsson, G. (2008). Comparison of different frequency controllers for a VSC-HVDC supplied system. IEEE Transactions on Power Delivery, 23(4), 2224–2232. DOI 10.1109/TPWRD.2008.921130. [Google Scholar] [CrossRef]
33. Beccuti, G., Papafotiou, G., Harnefors, L. (2014). Multivariable optimal control of HVDC transmission links with network parameter estimation for weak grids. IEEE Transactions on Control Systems Technology, 22(2), 676–689. DOI 10.1109/TCST.2013.2258021. [Google Scholar] [CrossRef]
34. Du, C., Bollen, M., Agneholm, E., Sannino, A. (2007). A new control strategy of a VSC–HVDC system for high-quality supply of industrial plants. IEEE Transactions on Power Delivery, 22(4), 2386–2394. DOI 10.1109/TPWRD.2007.899622. [Google Scholar] [CrossRef]
35. Yuan, Z., Li, S. E., Shao, B., Wang, B. (2016). State-space model with non-integer order derivatives for lithium-ion battery. Applied Energy, 161, 330–336. DOI 10.1016/j.apenergy.2015.10.025. [Google Scholar] [CrossRef]
36. Giddani, O. A., Abbas, A. Y., Adam, G. P., Anayalara, O., Lo, K. L. (2013). Multi-task control for VSC–HVDC power and frequency control. International Journal of Electrical Power and Energy Systems, 53, 684–690. DOI 10.1016/j.ijepes.2013.05.002. [Google Scholar] [CrossRef]
37. Jaen, A. D., Acha, E., Exposito, A. G. (2008). Voltage source converter modeling for power system state estimation: STATCOM and VSC-HVDC. IEEE Transactions on Power Systems, 23(4), 1552–1559. DOI 10.1109/TPWRS.2008.2004821. [Google Scholar] [CrossRef]
38. Beccuti, G., Papafotiou, G., Harnefors, L. (2014). Multivariable optimal control of HVDC transmission links with network parameter estimation for weak grids. IEEE Transactions on Control Systems Technology, 22(2), 676–689. DOI 10.1109/TCST.2013.2258021. [Google Scholar] [CrossRef]
39. Dash, P. K., Nayak, N. (2014). Nonlinear control of voltage source converters in AC–DC power system. ISA Transactions, 53(4), 1268–1285. DOI 10.1016/j.isatra.2014.03.011. [Google Scholar] [CrossRef]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |