

 | Energy Engineering |  |
DOI: 10.32604/EE.2021.014806
ARTICLE
Application of Superhydrophobic Surface on Boiling Heat Transfer Characteristics of Nanofluids
School of Electrical and Power Engineering, China University of Mining and Technology, Xuzhou, 221116, China
*Corresponding Author: Cong Qi. Email: qicong@cumt.edu.cn
Received: 30 October 2020; Accepted: 14 December 2020
Abstract: Boiling heat transfer is a mode using the phase change of working medium to strengthen the heat exchange due to its good heat exchange capability, and it is widely used in heat exchange engineering. Nanofluids have been used in the direction of enhanced heat transfer for their superior thermophysical property. The wetting, spreading and ripple phenomena of superhydrophobic surfaces widely exist in nature and daily life. It has great application value for engineering technology. In this article, the boiling heat exchange characteristics of nanofluids on superhydrophobic surface are numerically studied. It was found that with the increase of superheating degree, the steam volume ratio of unmodified heated surface increases to saturation, while the steam volume and evaporation ratio of modified superhydrophobic surface increase firstly and then decrease. At the same time, bubbles are generated and accumulated more fully on superhydrophobic surface. It was also found that nanofluids with low viscosity are more affected by superhydrophobic surface characteristics, and the increase is more significant with high superheating degree, and the superhydrophobic surface is beneficial to enhancing boiling heat exchange. Compared with the simulation results, it could be concluded that the boiling heat exchange performance of CuO-water nanofluids on the modified superhydrophobic surface is better than that of CuO-ethylene glycol nanofluids under high superheating degree.
Keywords: Nanofluids; superhydrophobic surface; pool boiling heat transfer; numerical simulation
Nomenclature
| cpnf: | specific heat of nanofluids, J·kg1·K–1 |
| cpf: | specific heat of base fluid, J·kg–1·K–1 |
| cpp: | specific heat of particles, J·kg–1·K–1 |
| cl: | relaxation factors, the reciprocal of relaxation time |
| cv: | relaxation factors |
| C | empirical coefficients |
| Ek: | energy of the k phase |
| F: | volume force |
| G: | turbulence kinetic energy increment |
| g: | gravity force |
| h: | heat transfer coefficient, W·m–2·K–1 |
| hk: | apparent enthalpy of the k phase |
| k: | thermal conductivity, W·m–1·K–1 |
| kf: | thermal conductivity of base fluid, W·m–1·K–1 |
| knf: | thermal conductivity of nanofluids, W·m–1·K–1 |
| kp: | thermal conductivity of nanoparticle, W·m–1·K–1 |
| | mass transfer of air pockets or user-defined mass sources |
| ml: | mass source terms of liquid phase |
| mv: | mass source terms of gas phase |
| Nu: | Nusselt number |
| P: | pressure drop of nanofluids, Pa |
| Q: | heating flux, W·m–2 |
| SE: | all volume heat sources |
| t: | heating time, s |
| Tl: | temperature of liquid, K |
| Tv: | temperature of gas, K |
| Tsat: | temperatures of saturation, K |
| V: | volume of vapor bubbles, m3 |
| | drift velocity of the second phase k, m/s |
| | average velocity of phase k, m/s |
| | average velocity of phase p, m/s |
| | average velocity of phase q, m/s |
| | mass average velocity, m/s |
| | gas phase velocity, m/s |
| X: | length of heating surface, m |
| Greek symbols | |
| | contact angle, ° |
| αk: | volume fraction of the phase k |
| αl: | volume fraction of the liquid phase |
| αv: | volume fraction of the gas phase |
| ρk: | density of the phase k, kg·m–3 |
| ρl: | density of liquid phase, kg·m–3 |
| ρm: | mixing density, kg·m–3 |
| ρnf: | density of nanofluids, kg·m–3 |
| ρf: | density of base fluid, kg·m–3 |
| ρp: | density of nanoparticle, kg·m–3 |
| ρv: | density of gas phase, kg·m–3 |
| φ: | dispersed phase component of nanoparticles |
| μi: | dynamic viscosity of fluid, Pa·s |
| μk: | dynamic viscosity of phase k, Pa·s |
| μm: | mixing dynamic viscosity, Pa·s |
| μnf: | dynamic viscosity of nanofluids, Pa·s |
| μf: | dynamic viscosity of base fluid, Pa·s |
| μt: | turbulent viscosity coefficient, Pa·s |
| σk: | turbulent prandtl number related to turbulence kinetic energy |
| σε: | turbulent prandtl number related to turbulent dissipation |
| ω: | evaporation ratio, % |
| ε: | phase of k-ε model |
| Subscripts | |
| F: | base fluid |
| k: | phase of k-ε model |
| l: | liquid |
| v: | gas |
| m: | mass |
| nf: | nanofluids |
| p: | nanoparticle |
With the vigorous progress of contemporary industry, the heat exchange process has penetrated into various fields; especially the electronic heat dissipation problem needs to be solved urgently to realize the efficient and stable operation of equipment. The traditional working media such as air and water commonly used in the heat dissipation process can no longer reach the work condition under overheating load, while nanofluids, as a new working medium, has superior and unique flow and heat exchange characteristics [1]. It has been widely studied and applied in industrial and scientific research fields, such as solar photothermal conversion [2–6], clear water preparation [7], phase change exchange transfer [8–10], natural convection [11–13], electronic component heat transfer [14], forced heat transfer [15–17], heat pipe [18,19], and magnetic nanofluid [20–24]. Compared with basic working fluids, nanofluids have superior heat transfer performance and thermal conductivity, and have great engineering application value in the fields of industrial heat dissipation and electronic cooling. Sheikholeslami et al. [25] studied the boiling heat transfer of nano-refrigerant in a flat channel, analyzed the effects of CuO mass fraction and steam mass on its heat transfer performance, and found that the heat transfer performance of fluid could be improved by increasing the mass fraction of nanoparticles. Shi et al. [26] proposed a new scheme to solve the thermal management problem of electronic equipment, and realized the external temperature control by remote control of the magnetic response of Fe3O4 magnetic nanofluids, to achieve the heat dissipation of electronic components.
Until now, many researchers have done a lot of researches on boiling and phase change heat transfer [27–29]. Li et al. [30] studied the key mechanism affecting the transient boiling heat exchange coefficient. The conclusions indicated that the increase of thermophysical property of nano-suspension and microscopic phenomena such as Brownian movement and thermophoresis effect improves the heat exchange coefficient, and at the same time, the heat exchange also be enhanced by the ascending concentration of nanoparticles. Masoud et al. [31,32] investigated the pool boiling of nanofluids on the copper surface with surfactant, and concluded that the boiling heat exchange can be increased by the deposition on the surface, and adding surfactant can also enhance heat transfer. Izadi et al. [33,34] researched the phase change heat exchange process under the action of magnetic field by using numerical method, and found the effect of magnetic field on melting process. Karimipour et al. [35–37] studied the flow characteristics of nanofluids in boiling process by molecular dynamics method, and found that the applied electric field is helpful to increase the temperature rate and velocity of nanofluids in boiling phase transition process. At the same time, the increasing container pressure is beneficial to boiling process, while excessive nanoparticle concentration will reduce the boiling heat exchange rate.
As important performance parameters of nucleate boiling heat transfer, critical heating flux (CHF) and heat transfer coefficient (HTC) have a great relationship with microstructure and wettability of the boiling surface. As a new bionic surface, superhydrophobic surface is widely used in the field of heat transfer and flow enhancement due to its wettability and roughness [38], and a lot of related researches have been done on heat dissipation and drag reduction. Može et al. [39] studied the functional interface to enhance the phase change process in thermal management, and showed a surface manufacturing method that can achieve extremely high boiling heat exchange performance. The superhydrophobic surface manufactured by laser fast and low-cost method can achieve enhanced boiling heat exchange. Allred et al. [40] found that the highly wetted textured surface increases the maximum critical heating flux that could be consumed during boiling, which enhances the heat exchange. Meanwhile, due to the superhydrophobic surface characteristics, the heated surface structure is wetted by liquid (Wenzel state), which significantly improves the heat exchange performance and maintaines the nucleate boiling behavior.
As mentioned above, many different studies on boiling heat transfer performance of superhydrophobic surfaces have been introduced in the references. However, there are few studies on boiling heat transfer of nanofluids on superhydrophobic modified surfaces, which needs further study. In this paper, the difference between the boiling research of superhydrophobic modified surface and some scholars’ are shown in Tab. 1. Aiming at boiling phase transition and superhydrophobic surface, the dynamic heat exchange and flow characteristics of boiling heat transfer process on specific surface are analyzed by simulation. Through numerical simulation, the bubble movement characteristics in boiling heat exchange process can be studied from a microscopic point of view, and the accurate changes in the whole model at different times can be obtained, which cannot be achieved by experiments. At the same time, the base fluid characteristics of nanofluids can be changed by setting numerical simulation conditions, to realize the comparison of different base fluid characteristics. So that, the aim of this work is to research the flow and heat exchange characteristics of nanofluids with different base fluids (CuO-water nanofluids and CuO-ethylene glycol nanofluids) on superhydrophobic surfaces at different superheating degrees. The innovation of this paper is that firstly, the bubble generation and aggregation mechanism of nanofluids at different superhydrophobic surfaces during heating are visually analyzed by using simulation method; Secondly, the boiling conditions of nanofluids with different base fluids on superhydrophobic surfaces are compared, and it is concluded that nanofluids with lower viscosity have better heat transfer performance during boiling; Finally, by comparing the Nusselt numbers of heated substrates under different working conditions, it is found that water-based nanofluids are greatly affected by the superhydrophobic surface characteristics, and have the best heat transfer performance on superhydrophobic surface under the condition that the superheating degree is 30 K.
Table 1: Comparison with some studies
The mixture model is selected in this paper to solve the equation of continuity, momentum equation, equation of energy, phase-to-phase slip velocity (relative velocity) equation and volume fraction formula of the second term. Because the mixture model is only aimed at a set of governing equations including energy and momentum, the mixture model belongs to the category of single-fluid model.
The continuity equation is as follows:
In Eq. (1),
Meanwhile, ρm in Eqs. (1) and (2) is the mixing density, which can be expressed by Eq. (3), and αk in Eqs. (2) and (3) is the volume fraction of the k phase:
The momentum equation of the mixed phase can be solved firstly for each single phase, and then the items are summed up, which is specifically expressed as Eq. (4):
In Eqs. (5) and (6), n represents the specific quantities of phases,
In Eq. (7) of energy equation, keff is the effective thermal conductivity, the first term on the right is the energy transfer caused by conduction, and SE represents all volume heat sources:
For the phase of compressible, Ek can be expressed as follows Eq. (8), for the phase of incompressible, Ek = hk, where hk is the apparent enthalpy of the k phase:
The relative speed (Eq. (9)) is described as the speed of the second phase p relative to the main phase q:
The relationship between drift velocity and relative velocity is described by Eq. (10) below:
The volume fraction equation of the second phase can be described by the the second phase’s equation of continuity, which is expressed as Eq. (11):
Traditional nanofluids are multiphase, and nanoparticles may deposit on the flowing surface. Because the simulation is a boiling model, nanofluids are constantly disturbed by bubbles, and the deposition of nanoparticles is not obvious. Therefore, nanofluids can be regarded as a single-phase fluid, and the physical parameter equations of nanofluids can be summarized as follows. The thermal conductivity of nanofluids is as Eq. (12), in which knf means the thermal conductivity of nanofluids, kf represents the thermal conductivity of base fluid, kp expresses the thermal conductivity of nanoparticles and φ means the dispersed phase component of nanoparticles:
Dynamic viscosity is shown in the following Eq. (13), in the formula, μnf means the dynamic viscosity of nanofluids, and μf represents the dynamic viscosity of base fluid:
The specific heat capacity is shown in Eq. (14), in which cpnf is the specific heat of nanofluids, cpf is the specific heat of base fluid and cpp is the specific heat of nanoparticles:
The density of nanofluids is shown in Eq. (15), ρnf means the specific heat of nanofluids, ρf represents the specific heat of base fluid, and ρp means the specific heat of nanoparticles:
2.3 Evaporation-Condensation Model
In the boiling process, the phase change process of heat and mass exchange occurs between liquid and gas, and the liquid phase is gasified to produce gas phase, and the gas phase condenses into liquid phase, which can be expressed by vapor phase transport equation (Eq. (16)):
In the equation, v is gas phase, αv is gas phase volume fraction, ρv is gas phase density and Vv is gas phase velocity. ml and mv are the mass source terms of liquid phase and gas phase in turn, which can be expressed by the following Eqs. (17) and (18), while cl and cv are relaxation factors, which represent the reciprocal of relaxation time [41]:
As an unsteady flow, turbulence is complex and irregular. At present, in the numerical method of heat exchange, the k-ε two-equation model has the best effect and is widely used, so the turbulence model used in this article is the standard k-ε two-equation model.
According to Navier-Stokes equation, the k equation is a turbulence kinetic energy conservation equation which can ensure the closure of Reynolds time-averaged equation by decomposing transient physical quantities. The ε equation represents the transport equation of energy transfer which is converted into heat energy of fluid due to the dissipation effect of fluid itself. And the k and ε equations are expressed by the following Eqs. (19) and (20):
In the above equations,
3.1 Superhydrophobic Surface Model
Wettability is an important property of solid surface and a common interface phenomenon in nature and daily life. Due to the great roughness and low surface energy of the surface, there are many small bubbles in the microstructure, which makes an air cushion layer between the fluid and the interface, and it makes the solid surface superhydrophobic. At the same time, superhydrophobic surfaces are widely used in engineering fields such as surface drag reduction and pipeline transportation. The surface wettability will be affected when the roughness and free energy of surface on solid surface change. Generally, when the contact between solid, liquid and gas is stable, the angle between solid and gas is called contact angle, which is usually expressed as

Figure 1: Contact angle diagram
According to Young’s equation, the solid surface can be called hydrophobic surface when
3.2 Geometric Model and Mesh Generation
In this work, a single-fluid model is adopted to simulate the boiling heat exchange of nanofluids. Firstly, the geometric dimensions are determined, the whole model is described in Fig. 2, then the geometric model is established and the grid is divided, and then the numerical simulation is carried out. The width and height of the calculated basin are 2 mm and 5 mm, and the quantity of grids is 80 × 200. In the industrial application field of boiling heat transfer, it is generally large in size. This simulation aims to study the mechanism at micro-scale and small scale, so the millimeter-scale model is chosen for discussion. Micro-boiling pool has been widely used in modern industry. As the integration of various electronic devices is getting higher and higher, the mechanism design is more complex, and the power requirement is also greater, so in order to solve the heat dissipation problem of micro-structure, the design of micro-boiling pool has been applied.

Figure 2: Geometric model of boiling simulation
3.3 Boundary Conditions and Initial Condition
There is a 1 mm heating wall in the middle of the container bottom, a pressure outlet at the top, and both sides of the container are set as walls. Boundary conditions of the simulation are set according to Tab. 2:
Table 2: Settings of boundary conditions

As boiling is a typical unstable transient process, physical quantities such as velocity, temperature and pressure will change with time, so the initial conditions must be given in transient conditions. At the beginning of calculation, the temperature of the fluid working medium in the container is set close to its boiling point, and it is assumed that only static liquid is contained in the calculation area, and the gas phase volume fraction is zero at the initial time. After comprehensive consideration, the time step finally selected in this paper is 0.001 s, and each time step is iterated 30 times to ensure convergence.
3.4 Grid Independence Validation
Because the simulation results will be affected by the number of grids in numerical simulation, for the purpose of ensuring the rationality of the calculation results and the irrelevance between the number of grids and the calculation results, grid independence validation is carried out. By setting different spacing sizes and node numbers, different numbers of grids are generated for irrelevant verification as Tab. 3. The verification process is to take the numerical value of the heat flux q of the heating wall calculated by three kinds of grids under the working condition of working fluid water at the heating temperature of 413 K. Based on the third grid, the deviation between the results of the first grid, the second grid and the third grid is calculated. The multiphase flow problem is sensitive to the grid, so when the error caused by the change of the grid number does not exceed 10%, it can be considered to be independent of the grid number.
Table 3: Grid independence validation
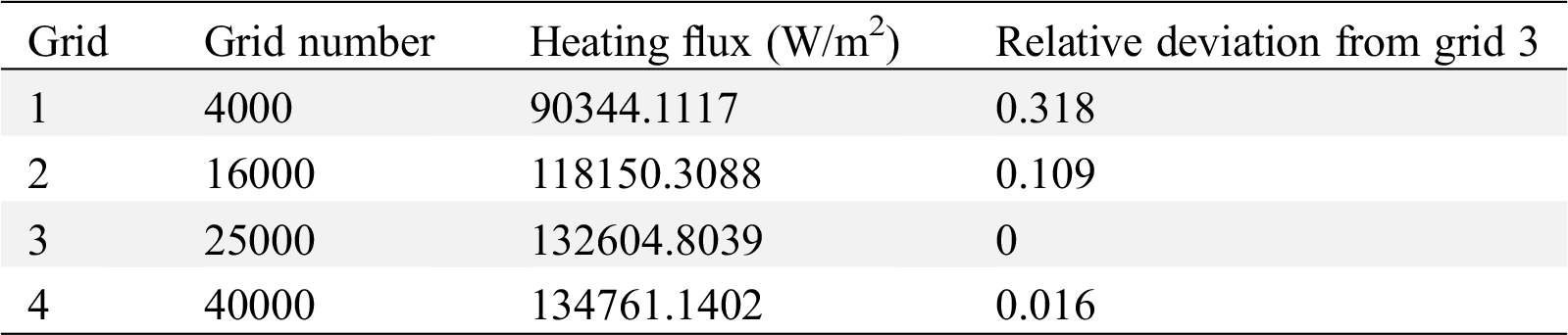
It can be seen that the error between the second grid and the third grid is about 10%. Under the condition of ensuring accuracy, considering the calculation time and speed, the third grid is finally selected.
Fig. 3 is a contrast between the heating flux results of numerical method and experimental results of Wang et al. [43]. It is exhibited in the figure that with the ascending trend of superheating, the heat flux increases, and the trend of numerical simulation conclusions is consistent with the experimental conclusions, and the deviation between the numerical analysis and experimental results is 8.53%, which proves that the model has a high accuracy.

Figure 3: Contrast between numerical simulation and experimental results
Due to the heat exchange of nanofluids boiling is complex. The following assumptions are made in this simulation: (1) Nanoparticles are uniformly dispersed in the base fluid, due to the fluid properties of nanoscale particles, therefore the nanofluids can be regarded as a single-phase fluid with the same properties. (2) The component concentration of nanofluids studied in this work is relatively low, so it is assumed that the component concentration of nanofluids will not change during boiling heat transfer. (3) Due to the limitation of high-precision correlation, this paper does not consider the effect of temperature on the physical properties of substrate fluid and nanofluids in the simulation process. (4) The influence of the fluid height in the container on the heat exchange influence is not considered, and the container is full of fluid. (5) The heating contact surface is an ideal superhydrophobic surface.
For the purpose of comparing the influences of components and superheating on the boiling exchange transfer of nanofluids, it is necessary to design multiple sets of operating conditions for parameter comparison. In this paper, a coupled solver based on pressure is used for unsteady calculation, considering the influence of gravity, and the value of gravity is –9.81 m/s2. Because there are positive and negative directions in the numerical simulation model, and there are direction requirements in gravity setting, it is necessary to add a negative sign before the value of 9.81 m/s2. Discrete governing equations are solved by the semi-implicit method (SIMPLE algorithm), and the SIMPLE algorithm’s core is the process of guessing and correcting. For gradient interpolation of diffusion term, it is set based on Green-Gaussian element. Momentum equation, turbulence kinetic energy equation, turbulent dissipation rate equation and energy equation are all solved by the QUICK scheme, which has higher accuracy in solving structured grids. VOF is a module in FLUENT software, which is a gas-liquid two-phase mixing module. In the simulation process, simulation calculation is carried out by setting the gas phase and liquid phase regions. For the relaxation factor, set the pressure to 0.5, and leave the rest settings at the default values. And the physical parameters of nanofluids used in this simulation are shown in Tabs. 4 and 5.
Table 4: Physical properties of CuO-water nanofluids

Table 5: Physical properties of EG-based nanofluids

According to the simulation conditions described above, the working parameters of the fluid are set. Figs. 4 and 5 are the vapor volume ratio change contour of CuO-water and CuO-ethanol glycol (CuO-EG) nanofluids with 5% mass fraction during boiling phase transition at 413 K and 510 K, respectively. Compared with the mass fraction of 1% and 3%, the nanofluids with 5% mass fraction have higher thermal conductivity and heat transfer performance. Consequently, in the process of numerical simulation, the nanofluids with higher thermal conductivity can better reflect the changes of flow and heat exchange performance in the micro-model, thus obtaining more accurate analysis results. In addition, the heated parts of these two working conditions are not superhydrophobic surfaces, and the two kinds of nanofluids have the same degree of superheating.

Figure 4: Vapor volume fraction contour of CuO-water (5%) nanofluids at different moments, (a) 0.1 s, (b) 0.2 s, (c) 0.3 s, (d) 0.4 s, (e) 0.5 s, (f) 0.6 s, (g) 0.7 s, (h) 0.8 s, (i) 0.9 s, (j) 1 s

Figure 5: Vapor volume fraction contour of CuO-EG (5%) nanofluids at different moments, (a) 0.1 s, (b) 0.2 s, (c) 0.3 s, (d) 0.4 s, (e) 0.5 s, (f) 0.6 s, (g) 0.7 s, (h) 0.8 s, (i) 0.9 s, (j) 1 s
It is exhibited in Fig. 4 that when the heating wall in the middle of the bottom of the container is heated at a constant temperature. The temperature of the nanofluids close to the heating area begins to rise. When the water temperature gradually reaches and exceeds the saturation temperature, boiling phase change will occur, and the fluid will generate water vapor from liquid phase gasification phase change. Under the action of buoyancy, the water vapor rises. Because the mixed multiphase flow model used in the simulation process refers to a distribution of the whole volume fraction of steam, two phases fill the whole area, and small bubbles cannot be observed. Meanwhile a cluster of steam bubbles is formed, and the steam bubbles rise freely through the free surface of the liquid to promote the water to flow in the container.
As Fig. 4(a) shown, the proportion of generated vapor is relatively small at 0.1 s, and the vapor volume fraction increases with the increase of time. Since the initial 0.1 s–0.2 s is not stable, the fluctuation increases from 0.665 to 0.761 in 0.7 s. Meanwhile, observing the contour at different times, it can be found that the vapor volume proportion is higher when it is closer to the bottom heating wall, while the heat exchange effect is better. And we can see from the Figs. 4(c)–4(e), because of the upward movement trend and the pull of the wall force, the shape of the bubble gradually lengthens from a flat elliptical sphere to a vertical elliptical sphere, and gradually breaks away. After that, the volume of the bubble increases continuously until it rises to the top of the container and breaks.
It can be observed from Fig. 5 that there are obvious differences between the changes of vapor volume contour of glycol-based and water-based nanofluids. Because the fluidity of water-based nanofluids is superior, the vapor change is chaotic compared to the glycol-based nanofluids. The viscosity of glycol-based nanofluids is an order of magnitude higher than the viscosity of water-based nanofluids, the fluidity is poor and the flow velocity is low. Therefore, the vapor generated in the boiling phase change process is relatively compact. At first, the vapor cluster is generated near the heating wall, and the size of the vapor cluster increases with time, and then the vapor cluster rises. When it reaches the top pressure outlet, the vapor enters the gas phase space.
It can be indicated that only the middle of the bottom is the heating area in the simulation, and the vapor is concentrated in the middle due to the high viscosity of ethylene glycol. At the same time, the proportion of gas increases with the ascending trend of mass fraction, which indicates that the thermal conductivity caused by the larger mass fraction increases the degree of phase change heat transfer, thus more liquid is converted into gas.
At the same time, by observing the change of gas volume in the simulation model, as shown in Fig. 6, it is found that with the increase of time, the bubble volume in the boiling process of water-based nanofluids and glycol-based nanofluids increases, but the growth rate of bubble volume in water-based nanofluids gradually slows down after 0.6 s. The maximum bubble volumes produced by two kinds of base fluid nanofluids during heating and boiling are 1.99315 × 10–6 m3 and 9.19809 × 10–7 m3, respectively. Comparing the vapor volume changes of nanofluids with the two substrates, it can be found that the vapor volume in water-based nanofluids is larger than that in glycol-based nanofluids, which is caused by the higher density of glycol-based nanofluids, the compression of bubbles and the difficulty in forming bubbles at the bottom.
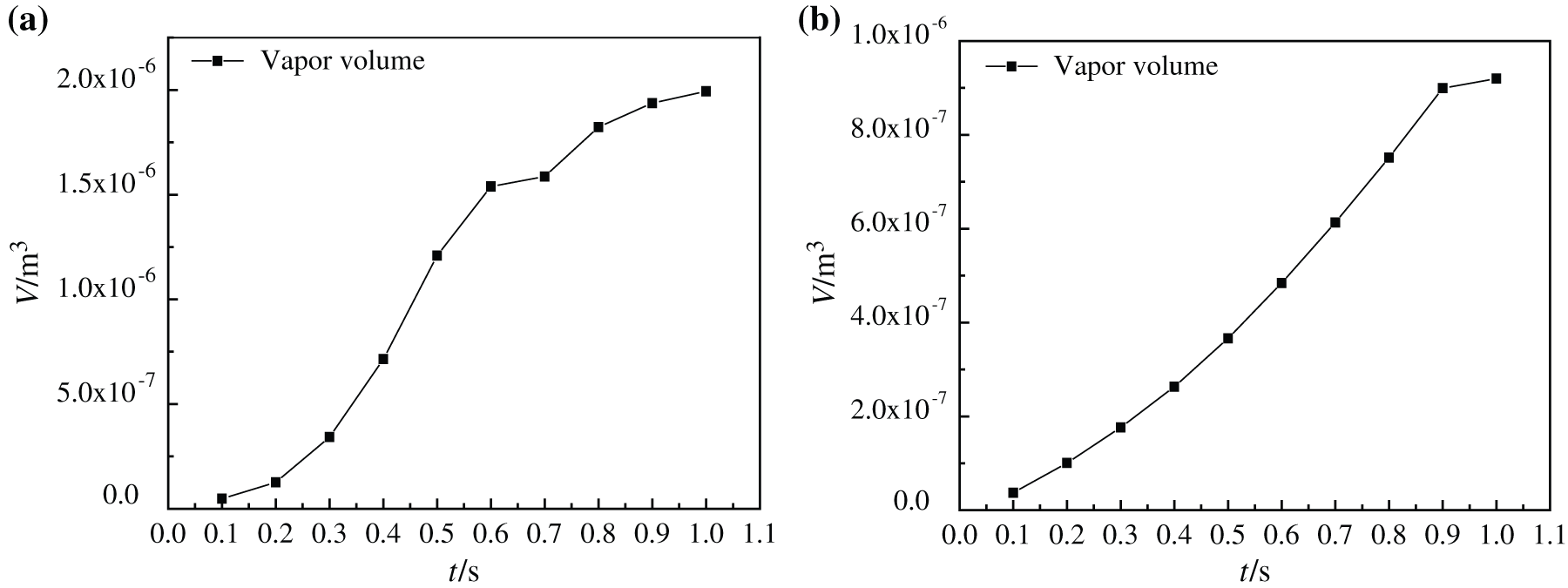
Figure 6: Vapor volume change of nanofluids boiling at different moments, (a) CuO-water (5%) nanofluids, (b) CuO-EG (5%) nanofluids
Figs. 7 and 8 are contours of velocity distribution of liquid phase of water-based nanofluids and that of glycol-based at different times, respectively. It can be seen that in the boiling process, the vapor generated in the container under two working conditions starts to rise, which drives the liquid near the bubble to flow, so that the fluid without macroscopic velocity has a certain velocity driven by the bubble. It also shows that the area with high water velocity is located near the vapor. The results demonstrate that the bubble generated in the boiling process interacts with the liquid phase through disturbance. Compared with water-based nanofluids, the glycol-based one has a slightly lower bubble rising speed due to their higher density and viscosity. Water-based nanofluids flow more rapidly and become more irregular in the later stage of boiling simulation due to the disturbance of bubble rising. The flow of glycol-based nanofluids is relatively orderly.

Figure 7: Velocity contour of CuO-water (5%) nanofluids at different moments, (a) 0.1 s, (b) 0.2 s, (c) 0.3 s, (d) 0.4 s, (e) 0.5 s, (f) 0.6 s, (g) 0.7 s, (h) 0.8 s, (i) 0.9 s, (j) 1 s
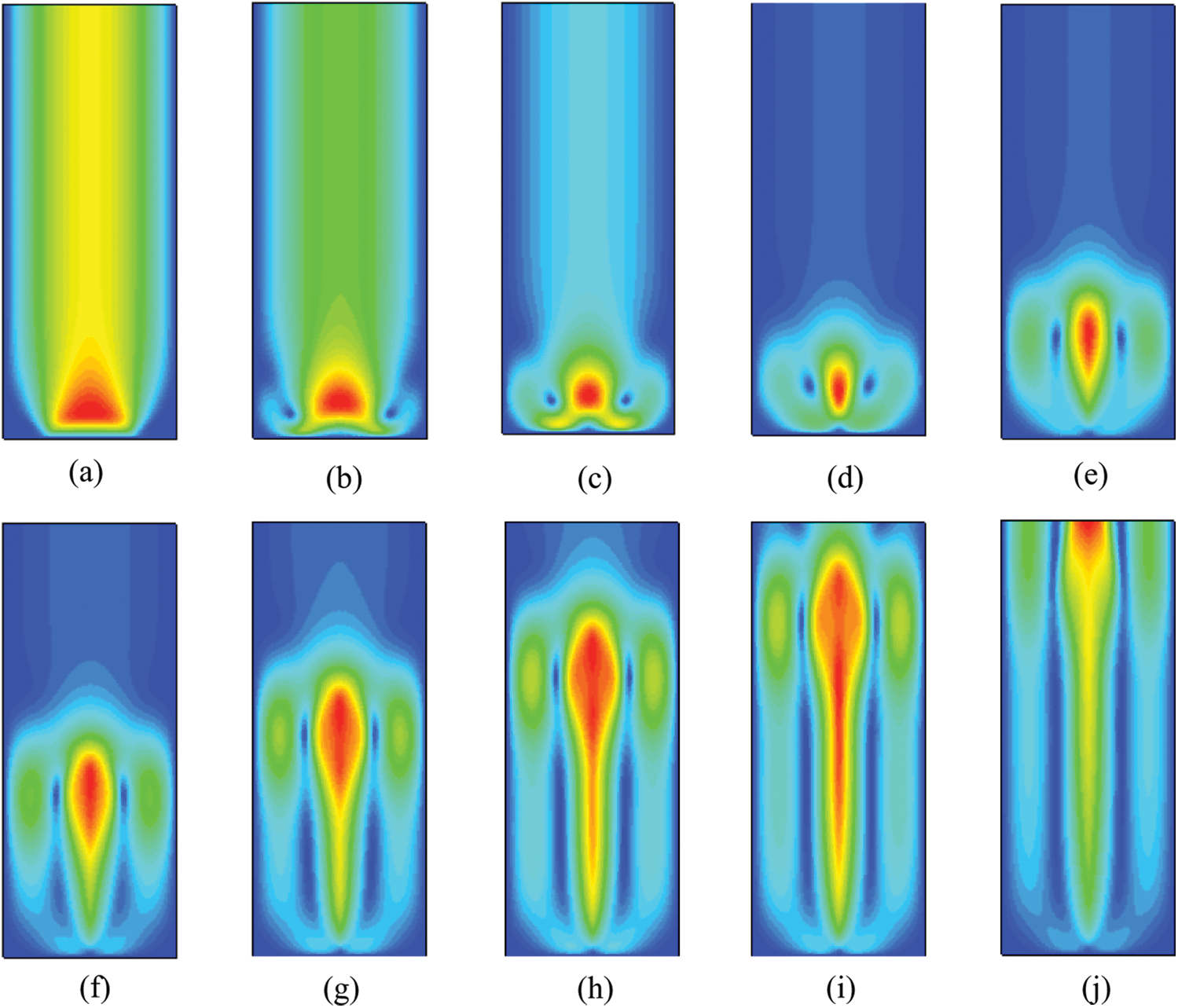
Figure 8: Velocity contour of CuO-EG (5%) nanofluids at different moments, (a) 0.1 s, (b) 0.2 s, (c) 0.3 s, (d) 0.4 s, (e) 0.5 s, (f) 0.6 s, (g) 0.7 s, (h) 0.8 s, (i) 0.9 s, (j) 1 s
The velocity vector indicates that the velocity has a direction. The vector diagram of velocity can be obtained by Tecplot software. It can be seen from the overall diagram of Fig. 9 and the partially enlarged diagram of the pressure outlet that two kinds of nanofluids have boiled, and the gas converted from liquid goes out from the top. When the bubbles are separated, the bursting of bubbles will cause the disturbance of the liquid surface and thus churn. At the same time, the velocity directions are different, which indicates that the interior is in an unstable state, and boiling occurs when the instability increases to a certain extent. It can be observed that the velocity vector diagram of water-based nanofluid is in an unstable state as a whole. Compared with water-based nanofluids, the velocity vector diagram of glycol-based nanofluids appears vortex, which is sparse on both sides and dense in the middle. The distribution density of velocity vector increases with the increase of temperature. This is because the thermal conductivity of glycol-based nanofluids is greater, which increases the heat transfer capacity. The increase of boiling phase transition promotes the increase of steam, and the rise of steam drives the liquid to flow. However, due to the higher viscosity, bubbles rise in a regular flow pattern.
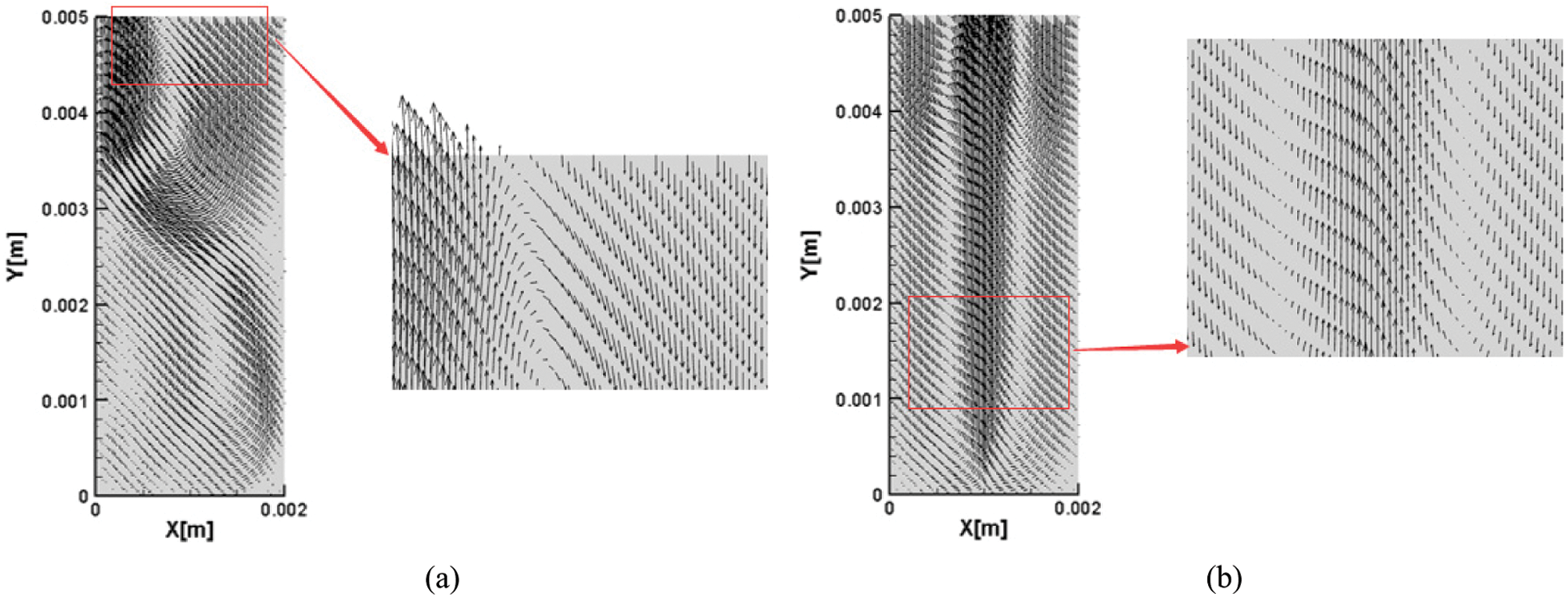
Figure 9: Velocity vector of nanofluids with different base fluid and the same degree of superheating, (a) CuO-water (5%) nanofluids, (b) CuO-EG (5%) nanofluids
Comparing the nanofluids of the two base fluids, it can be found that different viscosities of the base fluids will lead to different situations when bubbles leave the heating surface. When the viscosity of liquid is higher, bubbles are more difficult to get off the bottom surface, but when the viscosity is lower, bubbles are easier to get off the substrate and float upwards. The reason is that the bottom of the bubble is mainly affected by the adhesive force, which forms an obvious speed difference with other parts, providing a larger separation speed, and intensifying the fracture and rise of the bubble here. At the same time, under the action of gravity, the water-based nanofluids with lower density can be quickly replenished to the position before the bubble leaves the heating surface and rises with the gas phase, so the whole container is disturbed more violently. During the boiling process of water-based nanofluids, bubbles move more violently, and the degree of bubble rupture is greater. During the whole process, the energy of bubble movement is converted into kinetic energy, potential energy and surface energy, and its dynamic behavior is accompanied by greater energy dissipation, while the energy dissipation of bubbles is relatively small during the boiling process of glycol-based nanofluids. In the energy conversion process of bubble movement, the heat energy possessed by bubbles is gradually converted into potential energy with the increase of rising distance, while the energy required in the movement process is the consumed kinetic energy. At the same time, bubbles expand, and small bubbles gather into large bubbles to change the surface tension. However, with the increase in the number of small bubbles, the surface energy increases and the bubble energy is consumed. These energy transformations form a dynamic balance.
4.1.2 Effect of Superhydrophobic Surface
The boiling gas phase contour of water-based nanofluids and glycol-based nanofluids on the superhydrophobic surface can be seen from Figs. 10 and 11. By comparing Figs. 4 and 5, it can be found that modifying the contact angle of the heating surface by VOF method changes the boiling process of the two kinds of fluids. Firstly, it is the boiling process of water-based nanofluids. The two characteristics of superhydrophobic surface are low surface energy and roughness. Because of the limitation of simulation conditions, the surface energy cannot be modified. Therefore, before the boiling of water-based nanofluids, as shown in Figs. 10(a)–10(d), bubbles did not break away from the binding of heated substrate in advance due to the low surface energy of the contact surface, which is basically similar to the boiling process of unmodified surface. However, after 0.5 s of boiling process, the vapor bottom began to rise in disorder, which is due to the large contact angle of superhydrophobic surface. The large contact angle makes the solid surface difficult to be wetted, and the hard wetted surface is easier to form and separate bubbles, while the rough surface is easier to nucleate and grow bubbles, and bubbles grow to merge into a larger bubble at a certain time. After heating to a certain extent, bubbles with a larger number and volume than those on the unmodified surface leave the surface under the action of heat flow, which disturbs the boiling process, as shown in Figs. 10(f)–10(j). The action of superhydrophobic surface makes the whole boiling process flow more disordered.

Figure 10: Vapor volume fraction contour of CuO-water (5%) nanofluids on superhydrophobic surface at different moments, (a) 0.1 s, (b) 0.2 s, (c) 0.3 s, (d) 0.4 s, (e) 0.5 s, (f) 0.6 s, (g) 0.7 s, (h) 0.8 s, (i) 0.9 s, (j) 1 s

Figure 11: Vapor volume fraction contour of CuO-EG (5%) nanofluids on superhydrophobic surface at different moments, (a) 0.1 s, (b) 0.2 s, (c) 0.3 s, (d) 0.4 s, (e) 0.5 s, (f) 0.6 s, (g) 0.7 s, (h) 0.8 s, (i) 0.9 s, (j) 1 s
Secondly, by observing the gas phase changes in the boiling process of glycol-based nanofluids (as shown in Figs. 11(d),11(e)), it is found that compared with the boiling process of unmodified surfaces (as shown in Figs. 5(d),5(e)), bubbles can break away from the substrate in advance, but the shape of bubbles does not change obviously after 0.5 s. Because on the surface with large contact angle, the solid-liquid contact area is limited, the viscous force at the bottom of the vapor is small, the horizontal component of the pressure is also small, therefore the vapor is easy to separate. However, the viscosity of glycol-based nanofluids is relatively high, which is greatly influenced by the viscous force when bubbles rise in the boiling process, so the decrease of the viscous force reduces the binding of bubbles and enables them to be separated from the heated substrate faster. However, the viscosity and density of glycol-based nanofluids are larger, and the disturbance of the fluid by bubbles is greatly reduced, but the bubble volume and rising speed are increased. Therefore, the gas flow changes little during the boiling process of glycol-based nanofluids after 0.6 s.
By observing Fig. 12, it can be seen that in the boiling process, the steam volume in the two nanofluids firstly increases, but after the two kinds of nanofluids are heated for 0.6 s and 0.9 s respectively, the vapor volumes in both fluids show a decreasing trend. This is due to the existence of superhydrophobic surface, which makes the nanofluids of both substrates produce more bubbles at the bottom of the model. These bubbles rise continuously and finally break away from the whole model, resulting in the decrease of vapor volume. The maximum bubble volumes produced by the two kinds of base fluid nanofluids during heating boiling on superhydrophobic surface are 1.81944 × 10–6 m3 and 9.16291 × 10–7 m3. The difference is that the vapor volume in water-based nanofluids still has a process of decreasing at first and then increasing, which shows that at this temperature, the superhydrophobic surface makes the water-based nanofluids more affected, and the glycol-based nanofluids has a slower rate of bubble formation and rising due to its higher density and viscosity, so there is a lagging phenomenon compared with the water-based nanofluids.

Figure 12: Vapor volume change of nanofluids boiling on superhydrophobic surface at different moments, (a) CuO-water (5%) nanofluids, (b) CuO-EG (5%) nanofluids
4.2 Heat Exchange Characteristic
The boiling heat transfer characteristics of nanofluids with the two base fluids are obviously different, and the dispersion and agglomeration of nanoparticles in water and ethanol are also quite distinct. Because the density and viscosity of the two base fluids are different, the heat transfer characteristics of nanofluids are obviously affected, especially the critical heating flux (CHF) and heat transfer coefficient (HTC) of nanofluids. By observing the curves of bottom surface critical heating flux (CHF) with time in simulation of the two kinds of base liquid nanofluids in Fig. 13, it can be found that the CHF of water-based nanofluids heating substrate is much larger than that of glycol-based nanofluids. First of all, the CHF near the two side walls is very large, when the closer to the middle, the smaller the heat flux density is, because there are few bubbles generated at the two side walls, while bubbles are basically generated and agglomerated into larger bubbles in the middle. In Fig. 13, the CHF curve of water-based nanofluids heating surface basically accords with the bubble growth process in the simulation, while no bubble is generated at 0.1 s, so the heatiing flux at the bottom is larger and uniformly distributed. At 0.2 s, a local vapor film is generated on the heating surface, and the heating flux of gas is much smaller than that of liquid, so the heating flux decreases uniformly. After 0.3 s, the heating flux basically changes with the bubble growth process. When heated to 0.9 s, the bubbles in the nanofluids form large bubbles to break away from the heated substrate, and at the same time, their separation wake disturbs the heating surface, which enhances the heat exchange and makes the bottom heating flux increase uniformly. However, the change of critical heating flux of glycol-based nanofluids in Fig. 14 is not alike with that of water-based nanofluids in Fig. 13. When heated to 0.1 s, bubbles are not formed at the bottom, so the critical heating flux is larger. However, due to the higher viscosity and density of glycol-based nanofluids, it is more difficult to generate bubbles at the heating substrate, which makes the bubbles generated at the bottom always exist in the form of local vapor film. After heated to 0.3 s, the CHF at the bottom begins to change with the bubble generation process. In the bubble growth process of boiling glycol-based nanofluids, steam never completely escapes from the heated substrate, so the CHF is still small at 1.0 s. The whole heat transfer characteristics of this process are basically consistent with the relationship obtained by Feng et al. [44] by simulating bubble growth with the Lattice Boltzmann method.
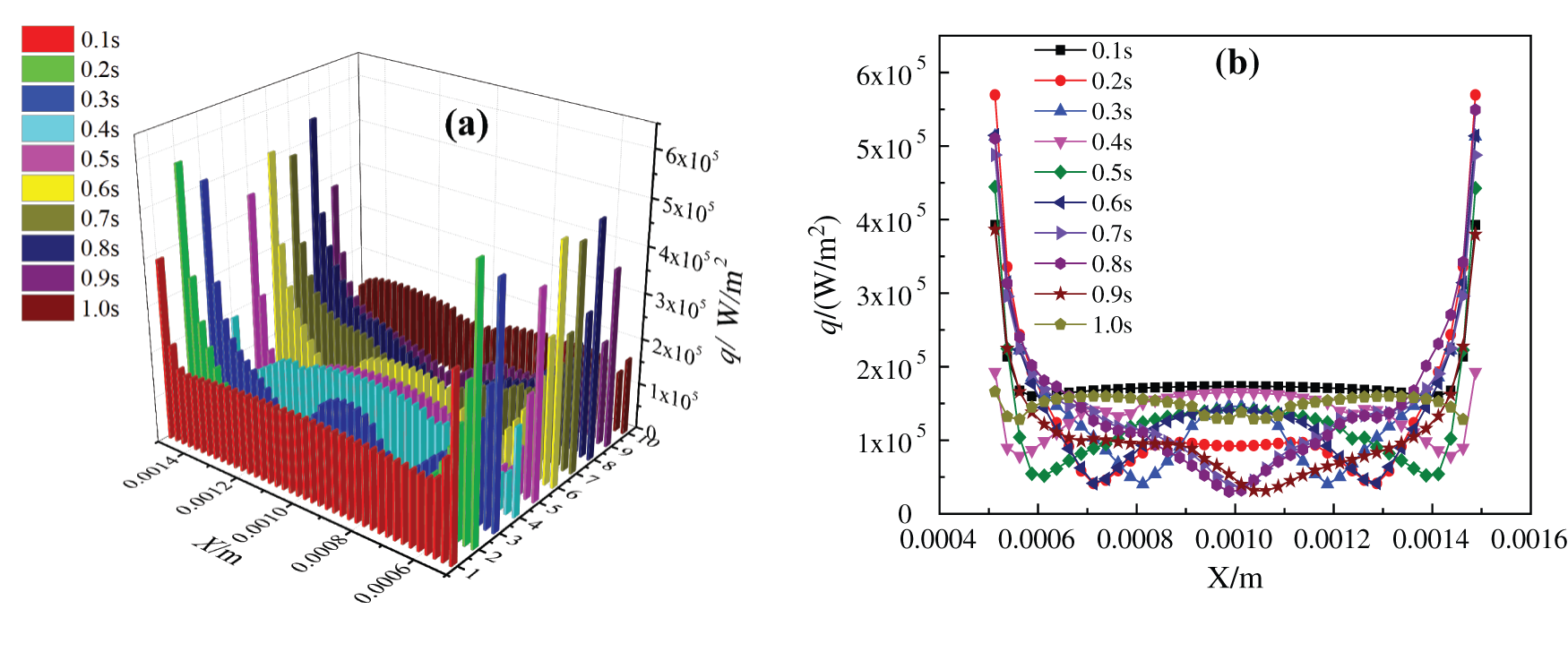
Figure 13: Critical heating flux of CuO-water (5%) nanofluids, (a) changes with time, (b) changes in x direction
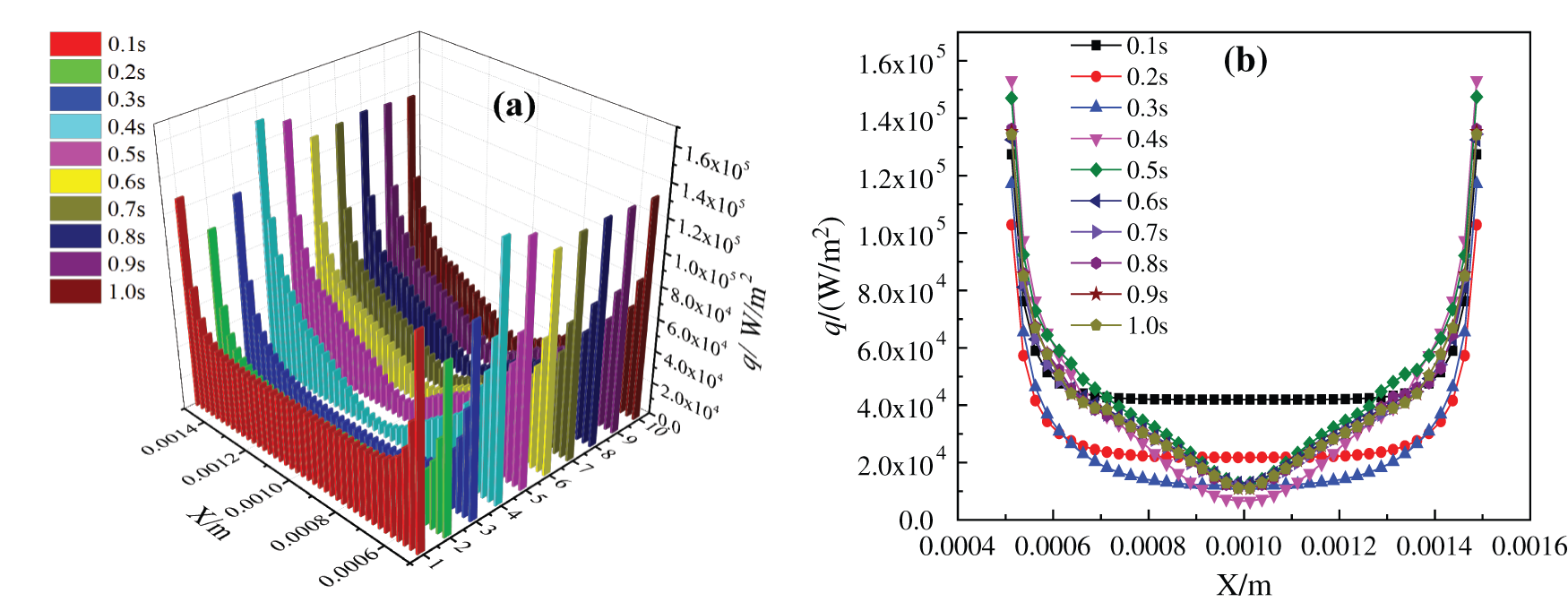
Figure 14: Critical Heating flux of CuO-EG (5%) nanofluids, (a) changes with time, (b) changes in x direction
Fig. 15 shows the heat exchange coefficient curves of two kinds of base fluid nanofluids heated to 1.0 s at different superheating degrees. It is exhibited in Fig. 15(a) that the curve of heat transfer coefficient is related to the shape of bubbles to a great extent. With the increase of superheating, tiny bubbles grow and gather into larger steam bubbles and rise faster, so the heat transfer coefficient of heated bottom also decreases, and the heat transfer coefficient curve is related to bubble shape. Compared with the superheating degree of 20 K, the heat transfer coefficient of 10 K superheating is larger, when the temperature is 20 K, more tiny bubbles gather to form large bubbles, which adhere to the heating bottom surface. At the same time, because the heat transfer coefficient of air in bubbles is lower than that of liquid, the heat transfer coefficient of CuO-water nanofluids is greater at 10 K. However, compared with the temperature of 20 K, the nanofluids at 30 K has a higher heat transfer coefficient, which is different from the previous superheat laws. Because when the superheat is greater, the speed of bubble generation and aggregation at the bottom is accelerated, and more large bubbles are formed. Meanwhile, the speed of bubbles rising in nanofluids increases, which increases the disturbance of the fluid in the container, and enhances the heat exchange to a certain extent, thus improving the heat transfer coefficient. But this phenomenon only exists when the viscosity of CuO-water nanofluids is low, because the flow of nanofluids with low viscosity is more affected by bubbles movement, and the disturbance caused by bubble rising is more obvious, so the disturbance of fluid will enhance heat transfer at higher superheat. Observing Fig. 15(b), it can be found that the heat exchange coefficient of glycol-based nanofluids decreases with the ascending trend of superheating degree. Due to the influence of viscosity of glycol-based nanofluids, it is difficult to form bubbles at the bottom, so the bubbles have not completely separated from the heated bottom, at the same time, because of the high viscosity of CuO-EG nanofluids, the bubble movement has little influence on the disturbance of fluid flow, which cannot enhance the heat exchange, the heat transfer coefficient decreases with the increase of superheat degree.
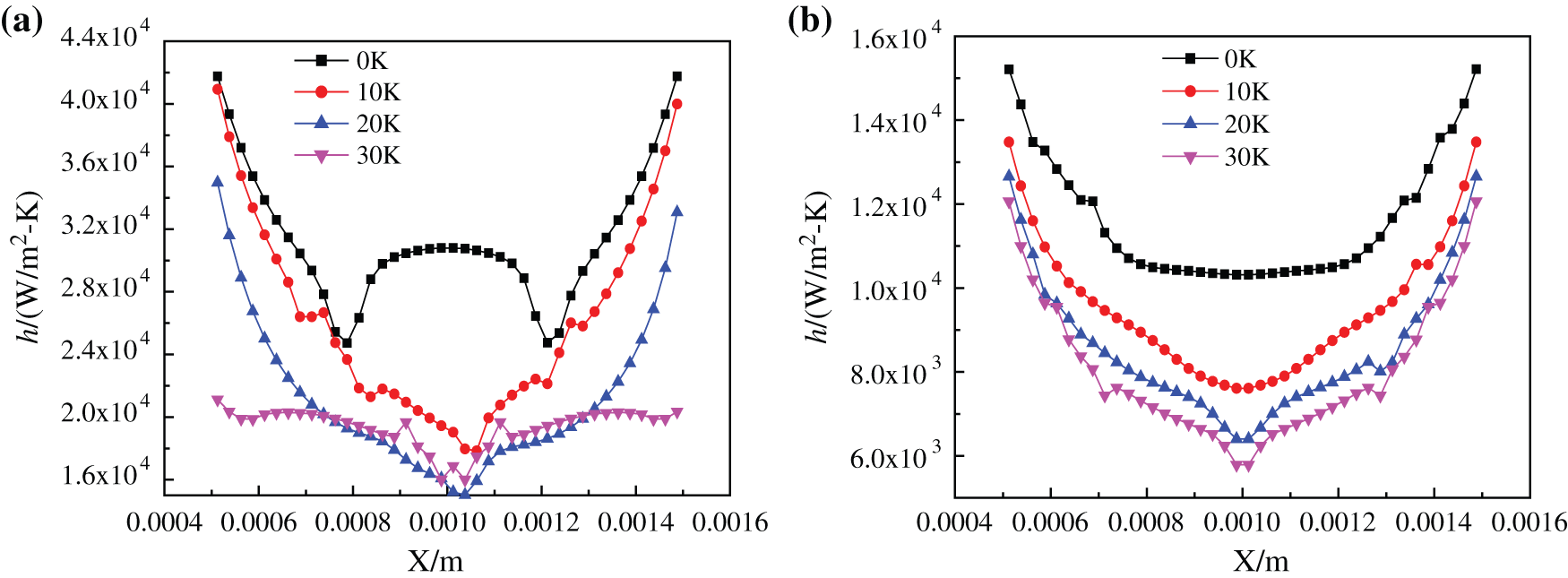
Figure 15: Heat transfer coefficient of nanofluids with different base fluids at different superheating degrees (a) CuO-water (5%) nanofluids, (b) CuO-EG (5%) nanofluids
It is shown in Fig. 16 that with the ascending trend of heating temperature, the heating surface Nusselt number of boiling process with the two kinds of base liquids firstly goes through a slow growth process and then increases sharply, which is caused by the change of vapor film state. When the heating temperature is low, the Nusselt number approaches a constant. The variation curve of the average Nusselt number is also consistent with the research results of Li et al. [45]: It is from approaching a constant to rising sharply. When the temperature rises, a large number of small bubbles gather on the heating bottom surface to form large bubbles that break away from the substrate and rise rapidly, which disturbs the heating surface. At the same time, the disturbance of vapor wake to the substrate enhances boiling heat transfer to a certain extent. Meanwhile, there are differences in heating surface Nusselt number changes during the boiling process of two kinds of base fluids. The average Nusselt numbers of water-based nanofluids are increased by about 32.78%, 46.49% and 47.88% respectively when the superheating degree is increased by every 10 K (0 K–30 K), however, the average Nusselt numbers of glycol-based nanofluids are increased by 53.89%, 37.35% and 25.72%, respectively. The Nusselt number of water-based nanofluids at low temperature increases slightly when the superheating degree is 30 K, which is due to the fact that water-based nanofluids are easier than glycol-based nanofluids to generate a large amount of steam, which makes the initial Nusselt number relatively large, so the Nusselt number changes less obviously. Compared with Nusselt numbers at other superheating degrees, the average Nusselt number of superheating degree 30 K is much larger. This shows that compared the nanofluids with two base fluids, the water-based nanofluids have the better boiling heat exchange characteristics when the superheating degree is 30 K.
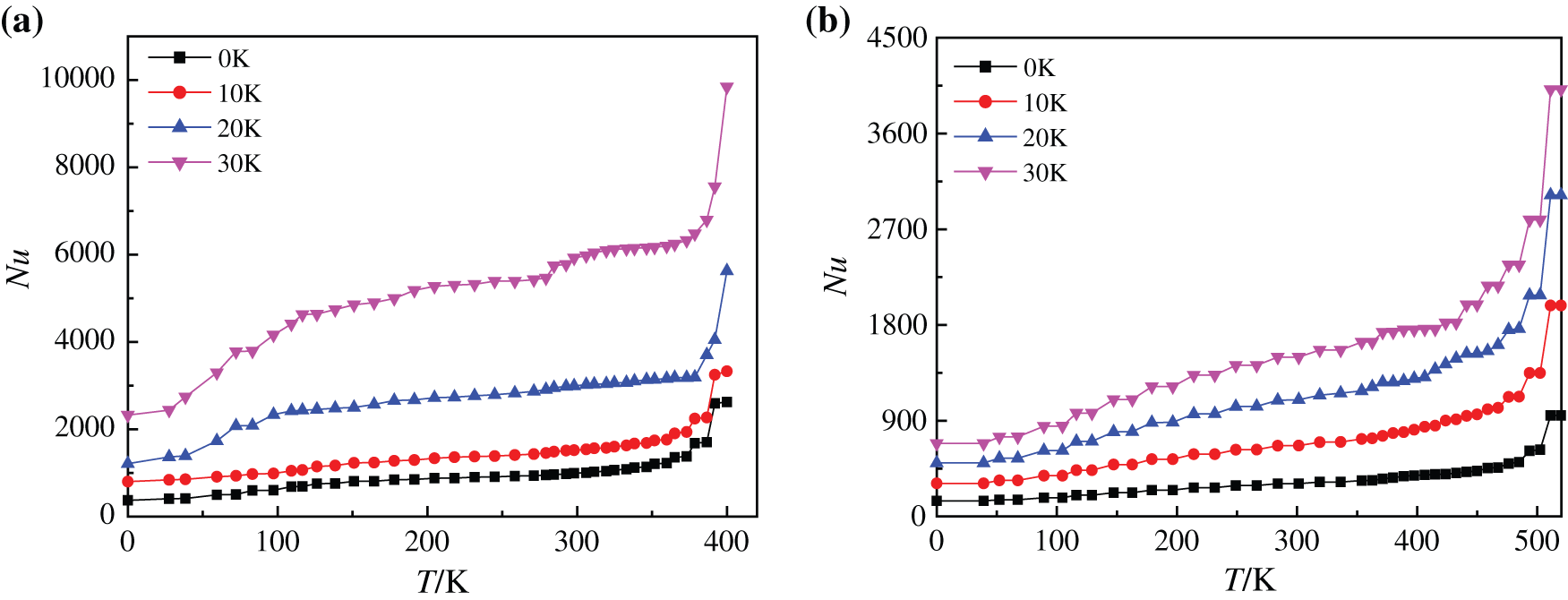
Figure 16: Nusselt number of nanofluids with different base fluids at different superheating degrees, (a) CuO-water (5%) nanofluids, (b) CuO-EG (5%) nanofluids
Fig. 17 indicates the change of evaporation ratio of two kinds of base liquid nanofluids at 413 K and 510 K, which shows that with the increase of heating time, the evaporation ratio of two kinds of nanofluids increases continuously, and their evaporation ratio are 20.08% and 9.20%, respectively. However, the evaporation rate of water-based nanofluids decreases gradually, and the evaporation rate of glycol-based nanofluids decreases only after 0.9 s. This is because the steam vapor flow in the boiling process of water-based nanofluids is more disordered, and its bubble formation, rise and flow need consume more energy, so the evaporation rate is affected and slowed down. However, the steam vapor flow in the boiling process of glycol-based nanofluids is more orderly and requires less energy consumption, so that the evaporation rate is less affected and keeps a larger rate increase. It also proves that water-based nanofluids need to consume more energy when they have better heat transfer characteristics than glycol-based nanofluids during boiling heating process.
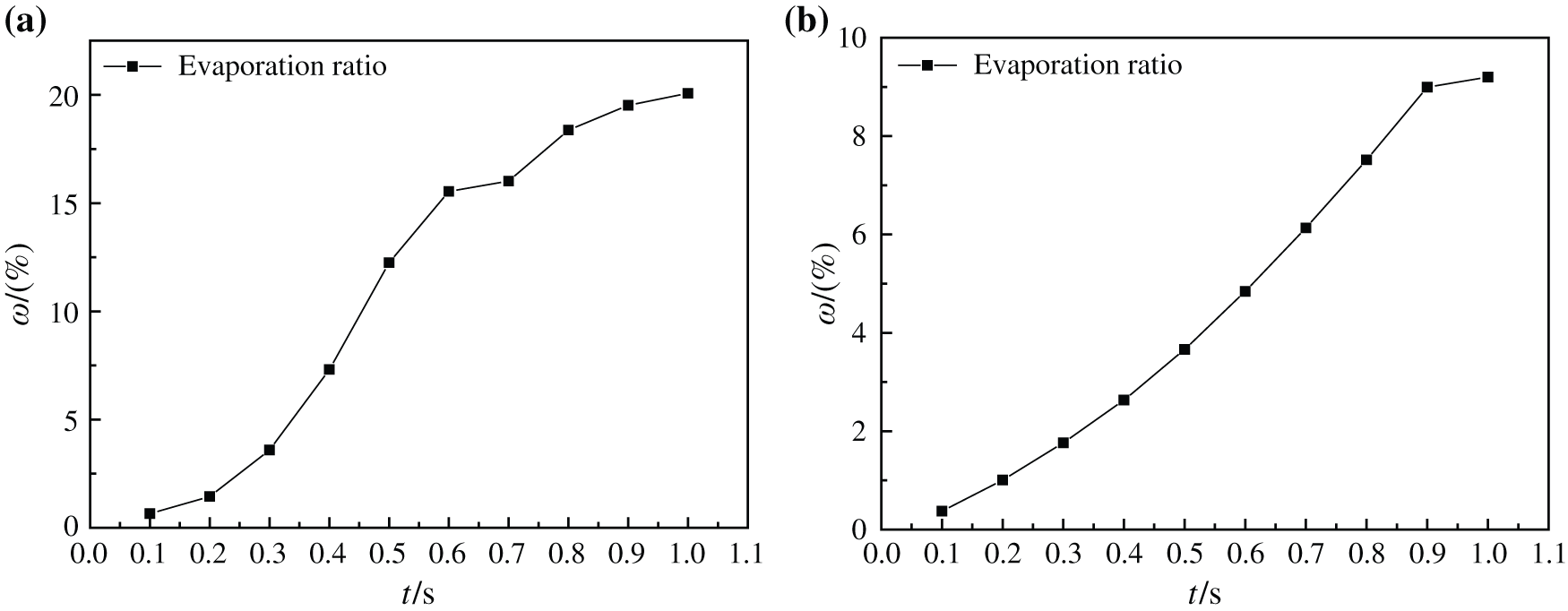
Figure 17: Evaporation ratio of nanofluids with different base fluids at different moments, (a) CuO-water (5%) nanofluids, (b) CuO-EG (5%) nanofluids
4.2.2 Effect of Superhydrophobic Surface
The boiling heat exchange performance of two kinds of base fluid nanofluids on the superhydrophobic surface has changed somewhat. By observing Figs. 18 and 19, it can be seen the change of bottom critical heating flux when the superhydrophobic surface boils and heats. Compared with the unmodified surface boiling heat exchange characteristics in Figs. 13 and 14, the change of CHF on the heating surface of glycol-based nanofluids is not obvious, which is because the viscosity and density of glycol-based nanofluids are relatively high, and the bottom microstructure is completely covered, which makes bubbles not easy to aggregate into large bubbles and rise to form disturbance. Comparing Fig. 18 with Fig. 13, it can be found that after the water-based nanofluids on the superhydrophobic surface is heated to 0.5 s, the critical heating flux on the bottom heating surface becomes more disordered, and the critical heating flux curve is similar to the bubble production shape on the superhydrophobic surface. This is because the bubbles on the modified superhydrophobic surface of the water-based nanofluids are easier to agglomerate into larger bubbles or local vapor films due to its superhydrophobicity. Moreover, the larger roughness makes it easier for the bottom heating surface to form vaporization cores, and the existence of superhydrophobicity enhances its role in strengthening the number of activated cores, and more small bubbles are generated, which disturbs the bottom heating surface, thus changing the critical heating flux. This is in line with the viewpoint verified by Ahn et al. [46] through pool boiling experiment: the wettability of surface caused by surface micro-nano structure and the change of liquid contact angle determine the level of CHF.
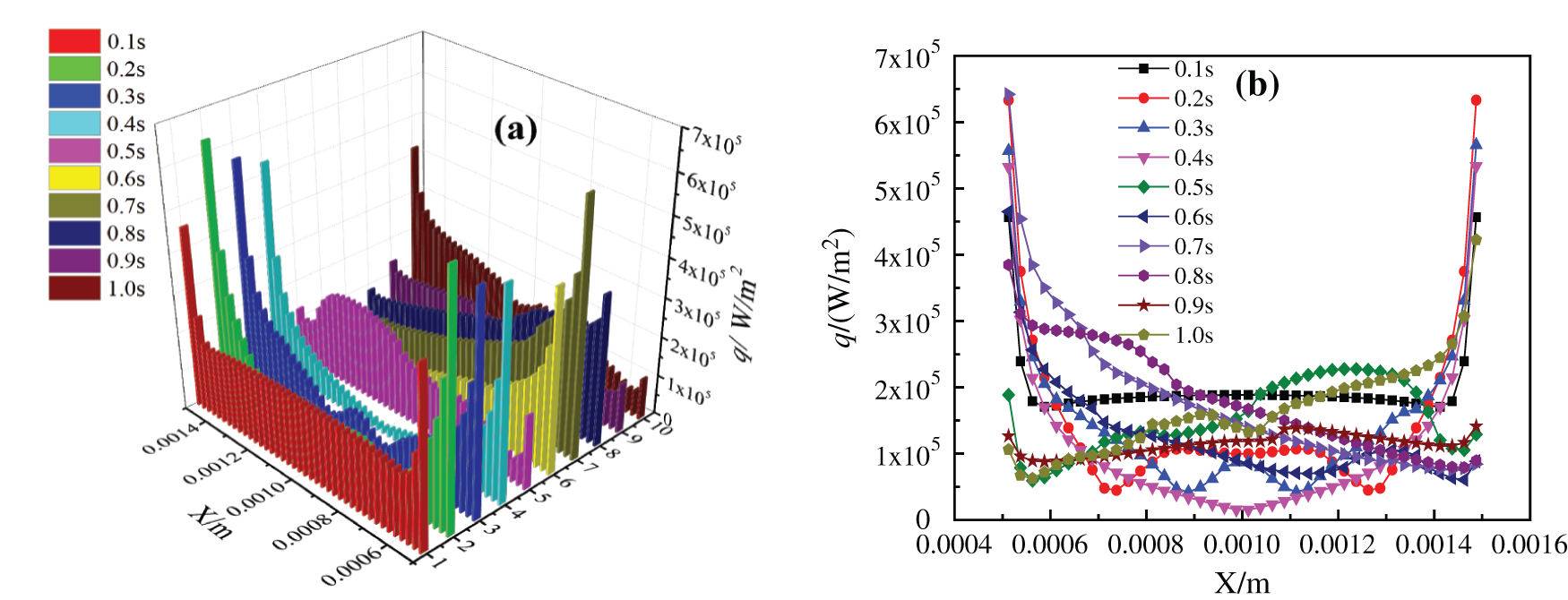
Figure 18: Critical heating flux of CuO-water (5%) nanofluids on superhydrophobic surface, (a) Changes with time, (b) Changes in x direction
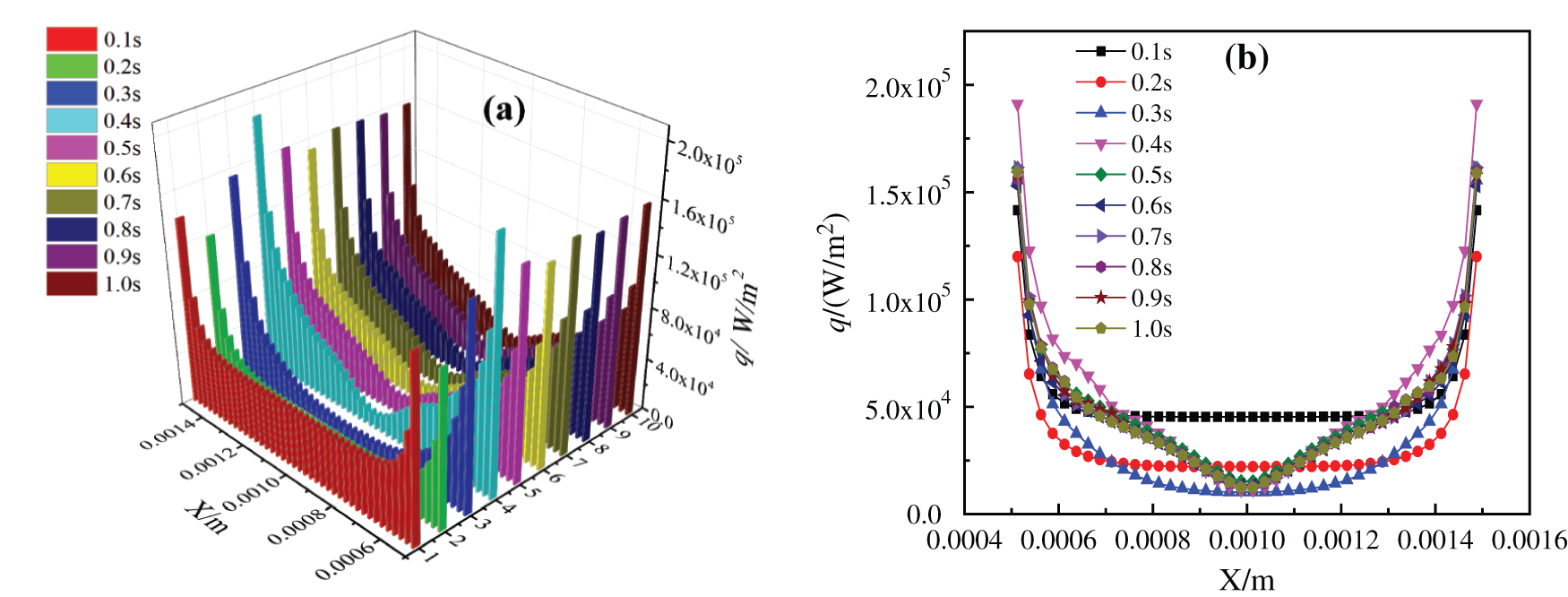
Figure 19: Critical heating flux of CuO-EG (5%) nanofluids on superhydrophobic surface, (a) Changes with time, (b) Changes in x direction
As shown in Fig. 20, the heat transfer coefficients of nanofluids with different base fluids on superhydrophobic surfaces heated to 1.0 s at different superheating degrees are basically consistent with bubble formation shapes. At the same time, the heat transfer coefficient curve of superhydrophobic surface is also consistent with the experimental conclusions of Wang et al. [43]. Compared with Fig. 14, the change of heat exchange coefficient of glycol-based nanofluids in Fig. 18 is not obvious on the superhydrophobic surface, because the superhydrophobic bottom surface is not easy to form vaporization core under the cover of glycol-based nanofluids with higher viscosity, and its heat exchange performance is not easy to be affected by generated bubbles. At the same time, it has higher density and lower bubble rising speed, so its bubble flow wake has little influence on heat exchange. However, water-based nanofluids will produce a large number of tiny bubbles on the superhydrophobic surface, and its vaporization core number is strengthened, so the surface flow is disturbed and the heat transfer is strengthened on the side. Meanwhile, the disturbance caused by the rapid rise of bubbles enhances the heat transfer of the whole model, which has a great positive influence on boiling heat exchange. The heat transfer coefficient curve in Fig. 20(a) is no longer symmetrical because it is disturbed by bubbles. However, when the superheating degree is 30 K, due to the superhydrophobic surface characteristics, the number of bubbles is large and the rising speed is fast, so that the bottom is quickly replenished by liquid and the heat exchange coefficient increases.
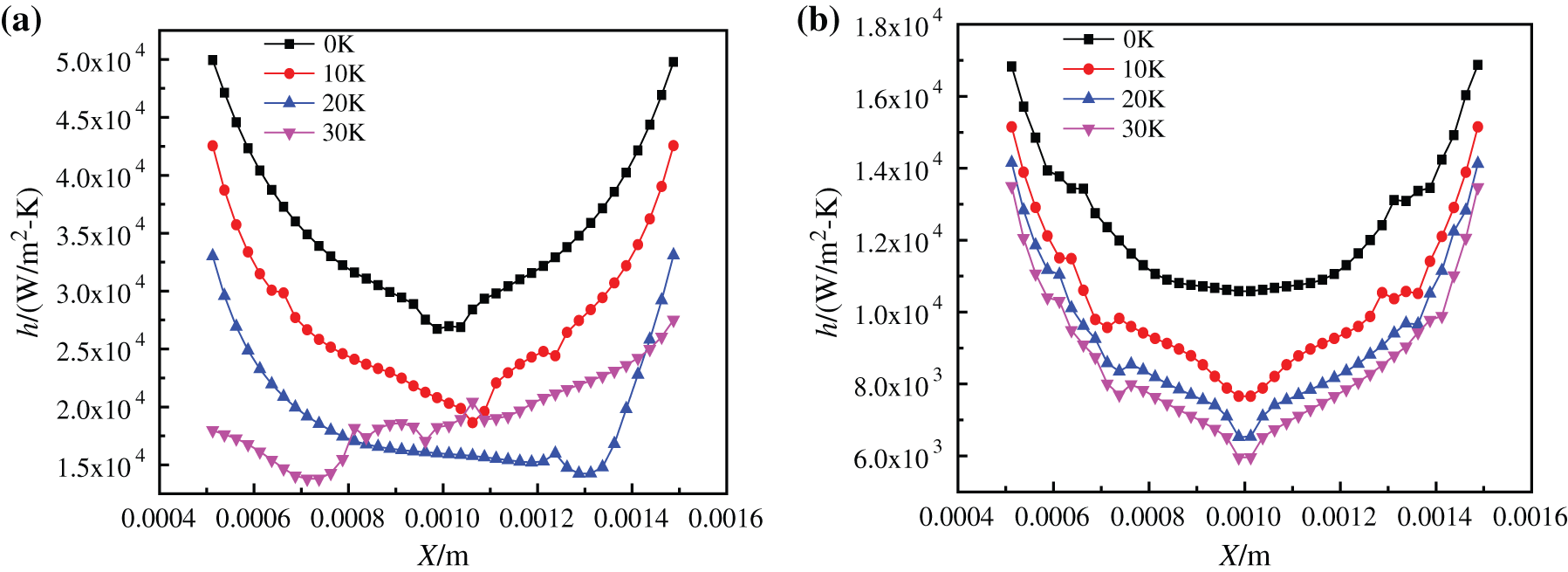
Figure 20: Heat transfer coefficient of nanofluids with different base fluids on superhydrophobic surface at different superheating degrees, (a) CuO-water (5%) nanofluids, (b) CuO-EG (5%) nanofluids
Fig. 21 indicates heating surface Nusselt numbers of different base fluid nanofluids on superhydrophobic surfaces at different superheating degrees. By comparing with Fig. 16, it can be found that superhydrophobic surfaces have little influence on glycol-based nanofluids with high viscosity, and the Nusselt numbers of heated substrates are only increased in number compared with those without modified substrate surfaces. The average Nusselt numbers of water-based nanofluids on superhydrophobic surface are increased by about 57.11%, 29.18% and 40.12% when the superheating degree is increased by every 10 K (0 K–30 K), while that of glycol-based nanofluids are increased by 56.46%, 35.65% and 34.56%, respectively. However, the Nusselt number of water-based nanofluids not only increases in number, but also increases greatly when the superheating degree is 30 K, and the reason is that a large amount of liquid in the water-based nanofluids evaporates while heating the bottom surface to form a large number of tiny bubbles, which rapidly rises under the driving of heat to disturb the heating surface, thus enhancing the heat exchange to a certain extent and increasing the Nusselt number.
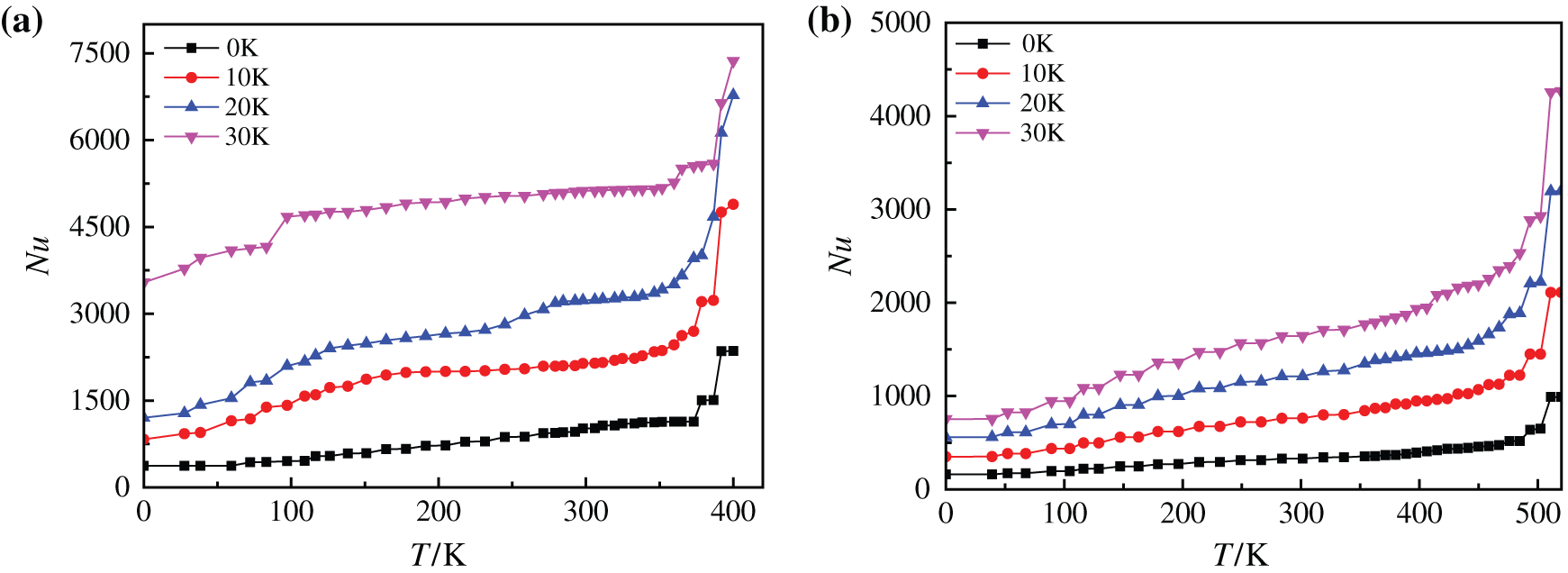
Figure 21: Nusselt number of nanofluids with different base fluids on superhydrophobic surface at different superheating degrees, (a) CuO-water (5%) nanofluids, (b) CuO-EG (5%) nanofluids
By observing Fig. 22, it can be found that the change of evaporation ratio of two kinds of base liquid nanofluids on superhydrophobic surface at 413 K and 510 K. With the increase of heating time, the evaporation ratio of water-based nanofluids in Fig. 22(a) firstly gradually increase to 18.19%, then decrease when heated to 0.6 s, and increase again until 0.9 s. The reason for this phenomenon is that with the increase of heating time and temperature, water-based nanofluids vaporize in large quantities, and tiny bubbles agglomerate and rise, which makes the evaporation rate increase gradually. The superhydrophobic property of superhydrophobic surface accelerates the bubble generation rate on heating surface, and more small bubbles are generated again when the agglomerated big bubbles are not completely evaporated and separated from the model, disturbing the previously generated bubbles, which makes the big bubbles burst and unable to be discharged. After the superhydrophobic surface generates a large number of small bubbles and drives the lower fluid to push new big bubbles to form, However, the heating process of glycol-based nanofluids is less affected by the characteristics of superhydrophobic bottom surface, and only small bubbles are generated to disturb large bubbles, but a large number of bubbles cannot be generated again to drive the fluid, so the evaporation ratio of glycol-based nanofluids gradually decreases when it rises to 9.16%.
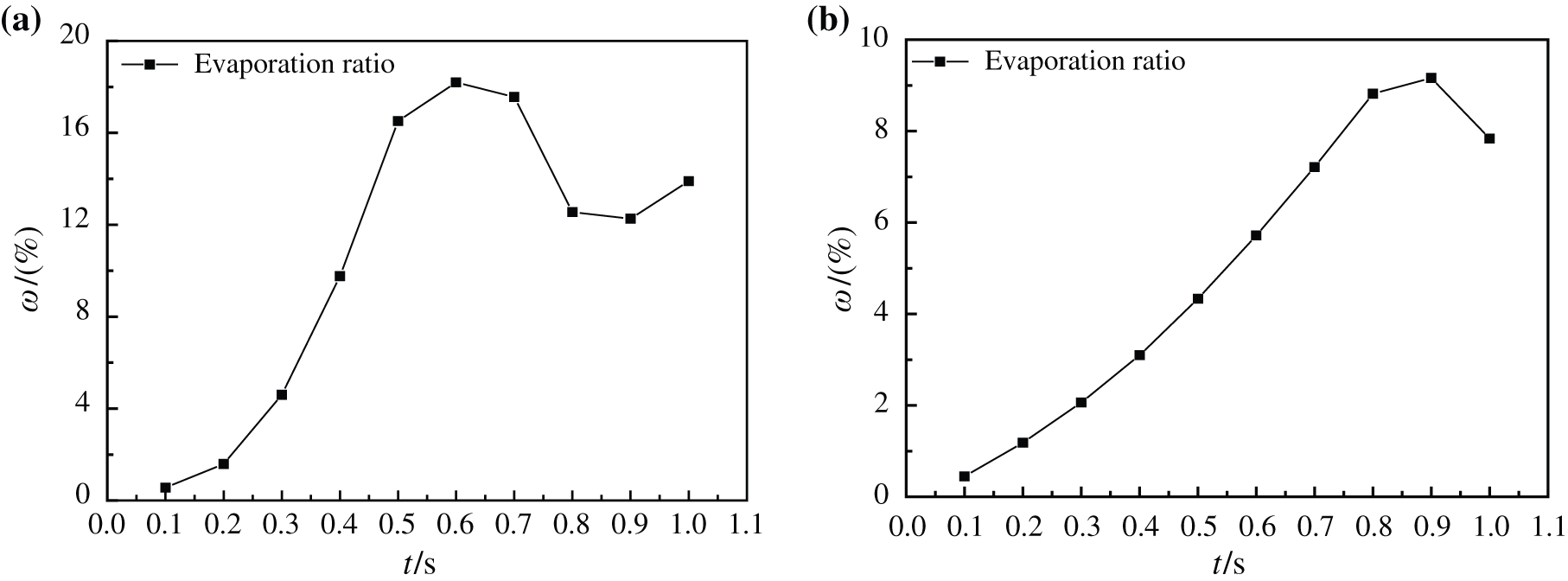
Figure 22: Evaporation ratio of nanofluids with different base fluids on superhydrophobic surface at different moments, (a) CuO-water (5%) nanofluids, (b) CuO-EG (5%) nanofluids
As indicated in the article, the flow and heat exchange characteristics of nanofluids with different base fluids on superhydrophobic surface are simulated in boiling state, and the effects of superhydrophobic surface, base fluids and superheating on boiling heat exchange performance under different working conditions are studied. Some conclusions can be summarized below:
1. The fluidity of water-based nanofluids is better than that of glycol-based nanofluids. In the process of heating and boiling, the flow of water-based nanofluids is more disordered, producing more bubbles with larger volume and consuming more energy, the maximum bubble volume produced by glycol-based nanofluids on unmodified surface is 50.36% of that of water-based nanofluids. However, the glycol-based nanofluids with higher viscosity have less energy dissipation and slower bubble generation during boiling.
2. The large contact angle of superhydrophobic surface makes it difficult for solid surface to wet, and it is easier for solid-liquid interface to form and separate bubbles, while rough surface is easier to form vaporization core, which makes a large number of bubbles generated in boiling process disturb the flow and enhance heat exchange.
3. Compared with glycol-based nanofluids, water-based nanofluids have smaller viscosity and density and are more affected by superhydrophobic surface characteristics. Therefore, the formation, bubble aggregation and evaporation of glycol-based nanofluids are about 0.3 s behind those of water-based nanofluids.
4. Superhydrophobic surface is beneficial to enhancing boiling heat exchange. By comparing various working conditions, it is found that water-based nanofluids with a superheating degree of 30 K on superhydrophobic surface has the best heat exchange performance, and its average Nusselt number is 5354.519, it is about 15 times higher than the average Nusselt number of glycol-based nanofluids with the unmodified surface at 10 K superheat degree.
Funding Statement: This work is financially supported by “National Natural Science Foundation of China” (Grant No. 51606214) and “Natural Science Foundation of Jiangsu Province, China” (Grant No. BK20181359).
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
1. Li, H., Wang, L., He, Y., Hu, Y., Zhu, J. et al. (2015). Experimental investigation of thermal conductivity and viscosity of ethylene glycol based ZnO nanofluids. Applied Thermal Engineering, 88, 363–368. DOI 10.1016/j.applthermaleng.2014.10.071. [Google Scholar] [CrossRef]
2. Chen, M., He, Y., Wang, X., Hu, Y. (2018). Complementary enhanced solar thermal conversion performance of core-shell nanoparticles. Applied Energy, 211, 735–742. DOI 10.1016/j.apenergy.2017.11.087. [Google Scholar] [CrossRef]
3. Hu, Y., He, Y., Zhang, Z., Wen, D. (2017). Effect of Al2O3 nanoparticle dispersion on the specific heat capacity of a eutectic binary nitrate salt for solar power applications. Energy Conversion and Management, 142, 366–373. DOI 10.1016/j.enconman.2017.03.062. [Google Scholar] [CrossRef]
4. Liu, X., Xuan, Y. (2017). Full-spectrum volumetric solar thermal conversion via photonic nanofluids. Nanoscale, 9(39), 14854–14860. DOI 10.1039/C7NR03912C. [Google Scholar] [CrossRef]
5. Sheikholeslami, M., Farshad, S. A., Shafee, A., Babazadeh, H. (2020). Performance of solar collector with turbulator involving nanomaterial turbulent regime. Renewable Energy, 163, 1222–1237. DOI 10.1016/j.renene.2020.08.144. [Google Scholar] [CrossRef]
6. Sheikholeslami, M., Farshad, S. A. (2020). Nanoparticle transportation inside a tube with quad-channel tapes involving solar radiation. Powder Technology, 378, 145–159. DOI 10.1016/j.powtec.2020.09.041. [Google Scholar] [CrossRef]
7. Nazari, S., Bahiraei, M., Moayedi, H., Safarzadeh, H. (2020). A proper model to predict energy efficiency, exergy efficiency, and water productivity of a solar still via optimized neural network. Journal of Cleaner Production, 277, 123232. DOI 10.1016/j.jclepro.2020.123232. [Google Scholar] [CrossRef]
8. Li, Z., Shahsavar, A., Al-Rashed, A. A., Talebizadehsardari, P. (2020). Effect of porous medium and nanoparticles presences in a counter-current triple-tube composite porous/nano-PCM system. Applied Thermal Engineering, 167, 114777. DOI 10.1016/j.applthermaleng.2019.114777. [Google Scholar] [CrossRef]
9. Sheikholeslami, M., Shehzad, S. A., Li, Z., Shafee, A., Abbasi, F. M. (2019). Time dependent conduction heat transfer during solidification in a storage system using nanoparticles. Microsystem Technologies, 25(6), 2153–2169. DOI 10.1007/s00542-018-4050-8. [Google Scholar] [CrossRef]
10. Sheikholeslami, M., Jafaryar, M., Shafee, A., Babazadeh, H. (2020). Acceleration of discharge process of clean energy storage unit with insertion of porous foam considering nanoparticle enhanced paraffin. Journal of Cleaner Production, 261, 121206. DOI 10.1016/j.jclepro.2020.121206. [Google Scholar] [CrossRef]
11. Qi, C., Tang, J., Wang, G. (2020). Natural convection of composite nanofluids based on a two-phase lattice Boltzmann model. Journal of Thermal Analysis and Calorimetry, 141(1), 277–287. DOI 10.1007/s10973-020-09519-9. [Google Scholar] [CrossRef]
12. Hu, Y., Zhang, B., Tan, K., He, Y., Zhu, J. (2020). Regulation of natural convection heat transfer for SiO2–solar salt nanofluids by optimizing rectangular vessels design. Asia-Pacific Journal of Chemical Engineering, 15(2), e2409. DOI 10.1002/apj.2409. [Google Scholar] [CrossRef]
13. Esfe, M. H., Bahiraei, M., Hajbarati, H., Valadkhani, M. (2020). A comprehensive review on convective heat transfer of nanofluids in porous media: Energy-related and thermohydraulic characteristics. Applied Thermal Engineering, 178, 115487. DOI 10.1016/j.applthermaleng.2020.115487. [Google Scholar] [CrossRef]
14. Zhao, N., Qi, C., Chen, T., Tang, J., Cui, X. (2019). Experimental study on influences of cylindrical grooves on thermal efficiency, exergy efficiency and entropy generation of CPU cooled by nanofluids. International Journal of Heat and Mass Transfer, 135, 16–32. DOI 10.1016/j.ijheatmasstransfer.2019.01.106. [Google Scholar] [CrossRef]
15. Qi, C., Li, K., Li, C., Shang, B., Yan, Y. (2020). Experimental study on thermal efficiency improvement using nanofluids in heat sink with heated circular cylinder. International Communications in Heat and Mass Transfer, 114, 104589. DOI 10.1016/j.icheatmasstransfer.2020.104589. [Google Scholar] [CrossRef]
16. Bahiraei, M., Monavari, A. (2020). Thermohydraulic characteristics of a micro plate heat exchanger operated with nanofluid considering different nanoparticle shapes. Applied Thermal Engineering, 179, 115621. DOI 10.1016/j.applthermaleng.2020.115621. [Google Scholar] [CrossRef]
17. Qi, C., Wang, C., Tang, J., Han, D. (2020). Experimental study on flow and heat transfer characteristics of nanofluids in a triangular tube at different rotation angles. Energy Engineering, 117(2), 63–78. DOI 10.32604/EE.2020.010433. [Google Scholar] [CrossRef]
18. Wang, X., Li, B., Yan, Y., Gao, N., Chen, G. (2019). Predicting of thermal resistances of closed vertical meandering pulsating heat pipe using artificial neural network model. Applied Thermal Engineering, 149, 1134–1141. DOI 10.1016/j.applthermaleng.2018.12.142. [Google Scholar] [CrossRef]
19. Wang, X., Yan, Y., Meng, X., Chen, G. (2019). A general method to predict the performance of closed pulsating heat pipe by artificial neural network. Applied Thermal Engineering, 157, 113761. DOI 10.1016/j.applthermaleng.2019.113761. [Google Scholar] [CrossRef]
20. Yan, S. R., Pordanjani, A. H., Aghakhani, S., Goldanlou, A. S., Afrand, M. (2020). Management of natural convection of nanofluids inside a square enclosure by different nano powder shapes in presence of Fins with different shapes and magnetic field effect. Advanced Powder Technology, 31(7), 2759–2777. DOI 10.1016/j.apt.2020.05.009. [Google Scholar] [CrossRef]
21. Sheikholeslami, M., Hayat, T., Alsaedi, A. (2017). On simulation of nanofluid radiation and natural convection in an enclosure with elliptical cylinders. International Journal of Heat and Mass Transfer, 115, 981–991. DOI 10.1016/j.ijheatmasstransfer.2017.07.119. [Google Scholar] [CrossRef]
22. Afrand, M., Abedini, E., Teimouri, H. (2017). How the dispersion of magnesium oxide nanoparticles effects on the viscosity of water-ethylene glycol mixture: Experimental evaluation and correlation development. Physica E: Low-Dimensional Systems and Nanostructures, 87, 273–280. DOI 10.1016/j.physe.2016.10.027. [Google Scholar] [CrossRef]
23. Fan, F., Qi, C., Tang, J., Liu, Q., Wang, X. et al. (2020). A novel thermal efficiency analysis on the thermo-hydraulic performance of nanofluids in an improved heat exchange system under adjustable magnetic field. Applied Thermal Engineering, 179, 115688. DOI 10.1016/j.applthermaleng.2020.115688. [Google Scholar] [CrossRef]
24. Qi, C., Wang, Y., Tang, J. (2020). Effect of squid fin bionic surface and magnetic nanofluids on CPU cooling performance under magnetic field. Asia-Pacific Journal of Chemical Engineering, 15(4), e2482. [Google Scholar]
25. Sheikholeslami, M., Rezaeianjouybari, B., Darzi, M., Shafee, A., Li, Z. et al. (2019). Application of nano-refrigerant for boiling heat transfer enhancement employing an experimental study. International Journal of Heat and Mass Transfer, 141, 974–980. DOI 10.1016/j.ijheatmasstransfer.2019.07.043. [Google Scholar] [CrossRef]
26. Shi, L., Hu, Y., He, Y. (2020). Magneto-responsive thermal switch for remote-controlled locomotion and heat transfer based on magnetic nanofluid. Nano Energy, 71, 104582. DOI 10.1016/j.nanoen.2020.104582. [Google Scholar] [CrossRef]
27. Salimpour, M. R., Abdollahi, A., Afrand, M. (2017). An experimental study on deposited surfaces due to nanofluid pool boiling: Comparison between rough and smooth surfaces. Experimental Thermal and Fluid Science, 88, 288–300. DOI 10.1016/j.expthermflusci.2017.06.007. [Google Scholar] [CrossRef]
28. Hu, Y., Li, H., He, Y., Liu, Z., Zhao, Y. (2017). Effect of nanoparticle size and concentration on boiling performance of SiO2 nanofluid. International Journal of Heat and Mass Transfer, 107, 820–828. DOI 10.1016/j.ijheatmasstransfer.2016.11.090. [Google Scholar] [CrossRef]
29. Li, Z., Sarafraz, M. M., Mazinani, A., Hayat, T., Alsulami, H. et al. (2020). Pool boiling heat transfer to CuO-H2O nanofluid on finned surfaces. International Journal of Heat and Mass Transfer, 156, 119780. DOI 10.1016/j.ijheatmasstransfer.2020.119780. [Google Scholar] [CrossRef]
30. Li, Z., Mazinani, A., Hayat, T., Al-Rashed, A. A., Alsulami, H. et al. (2020). Transient pool boiling and particulate deposition of copper oxide nano-suspensions. International Journal of Heat and Mass Transfer, 155, 119743. DOI 10.1016/j.ijheatmasstransfer.2020.119743. [Google Scholar] [CrossRef]
31. Etedali, S., Afrand, M., Abdollahi, A. (2019). Effect of different surfactants on the pool boiling heat transfer of SiO2/deionized water nanofluid on a copper surface. International Journal of Thermal Sciences, 145, 105977. DOI 10.1016/j.ijthermalsci.2019.105977. [Google Scholar] [CrossRef]
32. Tian, Z., Etedali, S., Afrand, M., Abdollahi, A., Goodarzi, M. (2019). Experimental study of the effect of various surfactants on surface sediment and pool boiling heat transfer coefficient of silica/DI water nano-fluid. Powder Technology, 356, 391–402. DOI 10.1016/j.powtec.2019.08.049. [Google Scholar] [CrossRef]
33. Mehryan, S. A. M., Tahmasebi, A., Izadi, M., Ghalambaz, M. (2020). Melting behavior of phase change materials in the presence of a non-uniform magnetic-field due to two variable magnetic sources. International Journal of Heat and Mass Transfer, 149, 119184. DOI 10.1016/j.ijheatmasstransfer.2019.119184. [Google Scholar] [CrossRef]
34. Izadi, M., Ghalambaz, M., Mehryan, S. A. M. (2020). Location impact of a pair of magnetic sources on melting of a Magneto-Ferro phase change substance. Chinese Journal of Physics, 65, 377–388. DOI 10.1016/j.cjph.2020.03.002. [Google Scholar] [CrossRef]
35. Dehkordi, K. G., Karimipour, A., Afrand, M., Toghraie, D., Isfahani, A. H. M. (2020). The electric field and microchannel type effects on H2O/Fe3O4 nanofluid boiling process: Molecular dynamics study. International Journal of Thermophysics, 41(9), 1–17. DOI 10.1007/s10765-019-2577-2. [Google Scholar] [CrossRef]
36. Salimpour, M. R., Darvanjooghi, M. H. K., Abdollahi, A., Karimipour, A., Goodarzi, M. (2019). Providing a model for Csf according to pool boiling convection heat transfer of water/ferrous oxide nanofluid using sensitivity analysis. International Journal of Numerical Methods for Heat & Fluid Flow, 30(6), 2867–2881. DOI 10.1108/HFF-01-2019-0009. [Google Scholar] [CrossRef]
37. Yan, S. R., Shirani, N., Zarringhalam, M., Toghraie, D., Nguyen, Q. et al. (2020). Prediction the boiling flow characteristics in rough and smooth microchannels using of molecular dynamics simulation: Investigation the effects of boundary wall temperatures. Journal of Molecular Liquids, 306, 112937. DOI 10.1016/j.molliq.2020.112937. [Google Scholar] [CrossRef]
38. Hosseini, S., Savaloni, H., Shahraki, M. G. (2019). Influence of surface morphology and nano-structure on hydrophobicity: A molecular dynamics approach. Applied Surface Science, 485, 536–546. DOI 10.1016/j.apsusc.2019.04.236. [Google Scholar] [CrossRef]
39. Može, M., Senegačnik, M., Gregorčič, P., Hočevar, M., Zupančič, M. et al. (2020). Laser-engineered microcavity surfaces with a nanoscale superhydrophobic coating for extreme boiling performance. ACS Applied Materials & Interfaces, 12(21), 24419–24431. DOI 10.1021/acsami.0c01594. [Google Scholar] [CrossRef]
40. Allred, T. P., Weibel, J. A., Garimella, S. V. (2018). Enabling highly effective boiling from superhydrophobic surfaces. Physical Review Letters, 120(17), 174501. DOI 10.1103/PhysRevLett.120.174501. [Google Scholar] [CrossRef]
41. Ding, S. T., Luo, B., Li, G. (2017). A volume of fluid based method for vapor-liquid phase change simulation with numerical oscillation suppression. International Journal of Heat and Mass Transfer, 110, 348–359. DOI 10.1016/j.ijheatmasstransfer.2017.03.015. [Google Scholar] [CrossRef]
42. Nguyen-Tri, P., Tran, H. N., Plamondon, C. O., Tuduri, L., Vo, D. V. N. et al. (2019). Recent progress in the preparation, properties and applications of superhydrophobic nano-based coatings and surfaces: A review. Progress in Organic Coatings, 132, 235–256. DOI 10.1016/j.porgcoat.2019.03.042. [Google Scholar] [CrossRef]
43. Wang, Y. Q., Luo, J. L., Heng, Y., Mo, D. C., Lyu, S. S. (2018). Wettability modification to further enhance the pool boiling performance of the micro nano bi-porous copper surface structure. International Journal of Heat and Mass Transfer, 119, 333–342. DOI 10.1016/j.ijheatmasstransfer.2017.11.080. [Google Scholar] [CrossRef]
44. Feng, Y., Li, H. X., Guo, K. K., Zhao, J. F., Wang, T. (2018). Numerical study of single bubble growth on and departure from a horizontal superheated wall by three-dimensional lattice Boltzmann method. Microgravity Science and Technology, 30(6), 761–773. DOI 10.1007/s12217-018-9618-5. [Google Scholar] [CrossRef]
45. Li, J. Q., Mou, L. W., Zhang, Y. H., Yang, Z. S., Hou, M. H. et al. (2018). An experimental study of the accelerated quenching rate and enhanced pool boiling heat transfer on rodlets with a superhydrophilic surface in subcooled water. Experimental Thermal and Fluid Science, 92, 103–112. DOI 10.1016/j.expthermflusci.2017.11.023. [Google Scholar] [CrossRef]
46. Ahn, H. S., Jo, H. J., Kang, S. H., Kim, M. H. (2011). Effect of liquid spreading due to nano/microstructures on the critical heat flux during pool boiling. Applied Physics Letters, 98(7), 071908. DOI 10.1063/1.3555430. [Google Scholar] [CrossRef]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |