

 | Energy Engineering |  |
DOI: 10.32604/EE.2022.015910
ARTICLE
Enhanced Atom Search Optimization Based Optimal Control Parameter Tunning of PMSG for MPPT
1Yunnan Power Grid Co., Ltd., Education and Training Evaluation Center, Kunming, 650041, China
2Yunnan Power Grid Co., Ltd., Kunming, 650041, China
3Yunan Dianzhong Huineng Intelligent Energy Co., Ltd., Kunming, 650041, China
4Zhengzhou Wante Electric Co., Ltd., Zhengzhou, 450500, China
5Chang’an University, Xi’an, 710064, China
*Corresponding Author: Jiawei Zhu. Email: jiawei.zhu@chd.edu.cn
Received: 22 January 2021; Accepted: 11 May 2021
Abstract: For the past few years, wind energy is the most popular non-traditional resource among renewable energy resources and it’s significant to make full use of wind energy to realize a high level of generating power. Moreover, diverse maximum power point tracking (MPPT) methods have been designed for varying speed operation of wind energy conversion system (WECS) applications to obtain optimal power extraction. Hence, a novel and meta-heuristic technique, named enhanced atom search optimization (EASO), is designed for a permanent magnet synchronous generator (PMSG) based WECS, which can be employed to track the maximum power point. One of the most promising benefits of this technique is powerful global search capability that leads to fast response and high-quality optimal solution. Besides, in contrast with other conventional meta-heuristic techniques, EASO is extremely not relying on the original solution, which can avoid sinking into a low-quality local maximum power point (LMPP) by realizing an appropriate trade-off between global exploration and local exploitation. At last, simulations employing two case studies through Matlab/Simulink validate the practicability and effectiveness of the proposed techniques for optimal proportional-integral-derivative (PID) control parameters tuning of PMSG based WECS under a variety of wind conditions.
Keywords: Enhanced atom search optimization; permanent magnetic synchronous generator; maximum power point tracking; wind energy conversion system
To meet the increasing demand for energy in this century and reduce the pollution caused by coal and oil power plants, there is an urgent need for a sustainable and environmentally friendly source of green energy. Under the background that coping with global climate change has become the international mainstream issue, energy transformation with the development of renewable energy as the main content has become the development strategy of many countries and regions [1]. In the last few decades, among numerous renewable energy resources, wind energy is known as one of the most dominant and significant resources [2]. Nowadays, distributed wind power is a natural mode of wind power development, which is an important way to achieve the harmony of wind power development with regional economic and social development and natural environment protection [3]. China’s distributed wind power development must be combined with the interests of rural areas, farmers, and agricultural poverty alleviation to become a new engine of county economic development and explore a new path for targeted poverty alleviation [4]. Besides, in a wind energy conversion system (WECS), the kinetic energy of wind is transformed into mechanical energy via a wind turbine, and then, this energy is converted into electrical energy via employing a generator [5].
Since the 1980 s, global wind power technology has been continuously developing at a high speed. Wind power generation technology has experienced the stages of constant speed constant frequency (CFCF) and variable speed constant frequency (VSCF) [6]. Compared with the former, the latter is relatively recent. Since the gradual development of VSCF technology, its advantages over CFCF lie in: under the condition of variable wind speed, it is easier to obtain the optimal tip speed ratio, the speed regulation range is relatively large, and the employment coefficient of wind energy is greatly improved. When the wind speed is high, in order to prevent wind damage to the unit, VSCF can store or release a certain amount of energy, so that the output power is more moderate, the overshoot is relatively small. At present, in many areas of wind power, both technologies can play their best role in the environment [7]. In the long development history of variable speed wind turbine, doubly fed induction generators (DFIG) and permanent magnet synchronous generator (PMSG) gradually have their own markets. However, PMSG generation system owns the following numerous remarkable advantages [8], (1) the system has less impact on the power grid and better compatibility of the power grid; (2) the gearbox and other components are removed from the system, so that the transmission structure is more simplified, so that the generator set can operate reliably; (3) the system directly drives the generator through the impeller of the wind turbine to generate electricity, which not only reduces the cost of power generation, but also reduces the power loss, thus increasing the power generation efficiency.
Although wind resources are abundant, the output power of wind turbine is unstable thanks to the change of wind speed. For the sake of solving this problem, the maximum power point tracking (MPPT) algorithm is usually used to enhance the efficiency of WECS [9], which major role of this algorithm is to keep the output power of the wind turbine at the maximum power point (MPP) without being affected by the change of wind speed. It is notable that wind power generation system is a strong time-varying nonlinear system. When the wind speed is below the rated wind speed, the essence of MPPT operation of wind turbine is to find the optimal speed. Traditional MPPT control methods contain tip speed ratio (TSR) method [10], hill climbing (HC) method [11], optimal characteristic curve method [12], etc. Heidari et al. [13] improved the traditional optimal torque control to compensate the given electromagnetic torque, so as to reduce the influence of large moment of inertia on the system, and greatly improve the efficiency of wind energy conversion. Moreover, Matayoshi et al. [14] used TSR method, which owns great advantages when the wind speed can be accurately known. This method uses a feedback control loop to maintain the fan running near the optimal TSR, which are fast response speed and high efficiency of maximum power tracking, but it owns drawbacks are that it must have the equipment to accurately measure the wind speed.
Besides, a MPPT control method with constant tracking bandwidth is designed, which aims at overcoming the disadvantage that the traditional power feedback method would reduce the tracking bandwidth [15]. Kazmi et al. [16] proposed a novel solution to the problems encountered in traditional mountain climbing search, which successfully solved the compromise between tracking speed and control effect. Meanwhile, the author designed a novel peak detection method, which utilized intelligent speed senseless sensors, and the experimental results verified the superiority of the method. Putri et al. [17] used the numerical change of DC bus voltage to indirectly observe the speed of generator, and realizes MPPT control of wind energy through direct control of grid side power. Kumar et al. [18] adopted the optimal characteristic curve algorithm to detect the initial position of the rotor, but there will inevitably be various losses in the system, which cannot capture the maximum power well. And Patnaik et al. [19] presented a novel MPPT control of wind energy based on the traditional power feedback method considering the influence of the changing loss of the power generation system.
On the other hand, the continuous flow of air in nature forms the wind, which can be seen that the wind will be affected by the circulation. In addition, temperature, pressure and so on are also indirect factors affecting the wind. The result of the above factors is that the wind power generation system has the characteristics of time-varying and nonlinear. In addition, the fan will also be affected by multiple factors, resulting in inaccurate system model parameters [20]. There is an urgent need for an effective power generation control method without precise mathematical model. Given the above problems, a large number of researchers have been pursuing diligently, and with the joint efforts of several generations, a series of modern control algorithms have been successfully developed, which have obvious optimization effect on the fan tracking output efficiency [21]. Kamal et al. [22] used robust control method to control the speed of wind turbine through adjusting the pitch angle and load, so as to shorten the mechanical stress and enhance the efficiency of wind power generation system. Sliding mode control (SMC) has fast dynamic characteristics and stable output range characteristics. The simulation results show that the sliding mode variable structure controller owns strong anti-interference ability and better dynamic performance [23]. Shotorbani et al. [24] designed the speed nonlinear proportional-integral-derivative (PID) controller for the PMSG, which enhances the accuracy of speed control, and has prominent effect on response time and overshoot. With the continuous optimization of automatic control technology and digital control technology, the continuous application of adaptive control [25], active disturbance rejection control [26] and other control methods in wind power generation can ensure the convergence of tracking error without accurate measurement of wind speed.
It’s worth noting that fuzzy control algorithm is a common algorithm in nonlinear intelligent control algorithm. Besides, fuzzy control algorithm does not need precise mathematical model, so it is very suitable for strongly nonlinear systems such as wind power generation. Wei et al. [27] designed a MPPT strategy with variable step size by using fuzzy logic controller, considering tracking speed and steady-state efficiency. Besides, a fuzzy radial basis function (RBF) neural network controller is designed and compared with the PI control by simulation. The results show that the former has more advantages in the variable speed pitch system [28]. Nevertheless, this type of MPPT method owns a complicated structure and heavy calculation burden. Recently, a novel meta-heuristic technique named enhanced atom search optimization (EASO), which with the purpose of not only can effectively escaping falling into a low-quality LMPP, but also to decrease the power fluctuation as far as possible. Moreover, compared with original atom search optimization (ASO), it owns higher convergence speed and optimal solution with a greater possibility.
The rest of the paper is arranged as follows. The Modelling of PMSG system is presented in Section 2. Section 3 gives a detailed description of EASO. And Section 4 provides the EASO design of optimal PID control parameters tuning of PMSG for MPPT. Besides, Case studies are carried out in Section 5. In the end, the conclusions of whole paper can be shown in Section 6.
As shown the framework of a PMSG system in Fig. 1, PMSG is connected to the infinite power grid through the back-to-back voltage source converter (VSC). And the dynamic characteristics of grid side VSC are neglected in this work since MPPT is mainly realized by generator side VSC [29].
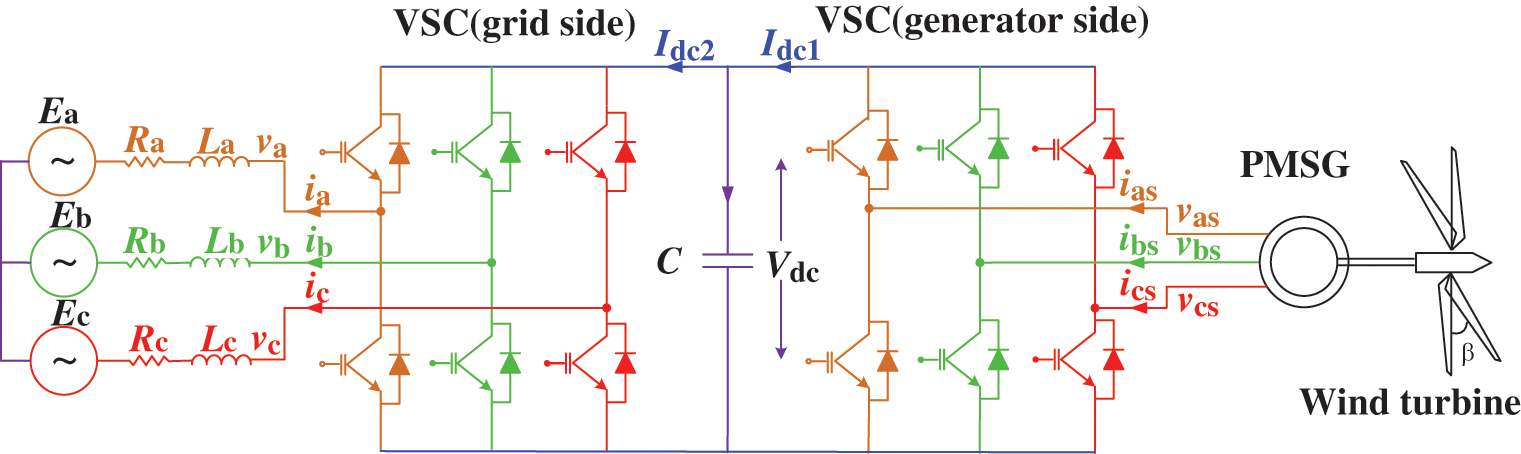
Figure 1: The framework of a PMSG system
The power coefficient CP(β, λ) is represented by TSR λ and pitch angle β, where λ can be defined as [30]
where R is the blade radius, ωm is the mechanical rotation speed, vwind is the wind speed.
Then power coefficient CP(β, λ) is calculated by
And the electrical power generated by WT can be denoted as
where ρ means the air density.
The dynamic equations of stator voltage in d-q axis are given as [31]
where Ld and Lq stand for d-q axis inductances, Rs means stator resistance, id and iq denote d-q axis stator currents, vd and vq represent d-q axis stator voltages, ψf denotes permanent flux. And ωe = pωm represents electrical speed where Ke is magnetic flux, p is pole pairs.
Under steady-state conditions, the system (5) can be rewritten as
where Vd and Vq represent d-q axis steady-state stator voltages, Id and Iq denote d-q axis steady-state stator currents.
Moreover, electromagnetic torque Te, stator active power Ps, and reactive power Qs can be described by
2.3 Mechanical Shafting System Model
The dynamics model of mechanical shafting system can be represented by
where Jtot denote the entire inertia of drive train, Tm means the mechanical torque, Te stands for the electromagnetic torque, D denotes the viscous damping coefficient.
Optimal tip speed ratio method is a commonly MPPT mechanism in current research. The optimal power coefficient
Hence, mechanical rotation speed needs to keep its optimum value
In this work, pitch angle β = 2°, optimum TSR λopt = 7.4, and optimal power coefficient
At this end, the description of optimal power curve can be obtained as
where
3 Enhanced Atom Search Optimization
EASO is improved by original ASO algorithm [32] which are both designed according to molecular dynamics. In other words, a molecule is made up of multiple atoms via covalent bonds, in which the whole atoms are keeping moving because of the microscopic interaction and the geometric constraint between atoms. In detail, microscopic interaction consists of the repulsive force (global search) and attractive force (local exploitation). And geometric constraint drives atoms to appropriate position for obtaining steady state.
3.1 Interaction Force among Atoms
The potential energy between two interactive atoms can be characterized by Lennard Jones (L-J) potential energy [33], as follows:
where U(rij) and Fij are the potential energy and the interaction force of jth atom to the ith atom, respectively. And ε means the depth of the potential well, σ stands for the length scale, rij denotes the Euclidian distance between the jth and the ith atoms, and xj and xi mean the locations of the jth and the ith atoms, respectively.
The potential energy of the atom is thoroughly determined by the proportional relation (σ/r) as demonstrated in Fig. 2. And the potential energy can be divided into the repulsive region and attractive region with equilibrium point of (σ/r = 1.12). In repulsive region, the potential energy would increase as the Euclidean distance decreases between two atoms. While in the other area, it decreases to zero as the gain of Euclidean distance. In order to expand local exploitation, more weights should distribute to attraction. Hence, Eq. (18) is updated as follows:
where η(k) is the depth function for guiding the repulsion or attraction intensity at the kth repeat, hij(k) means the distance ratio between the jth and the ith atoms, kmax is the maximum iterations number, α is the depth weight, hmax and hmin are the maximum and minimum distance ratios, and Xbest is the suit of the optimal L atoms with the optimal fitness values.
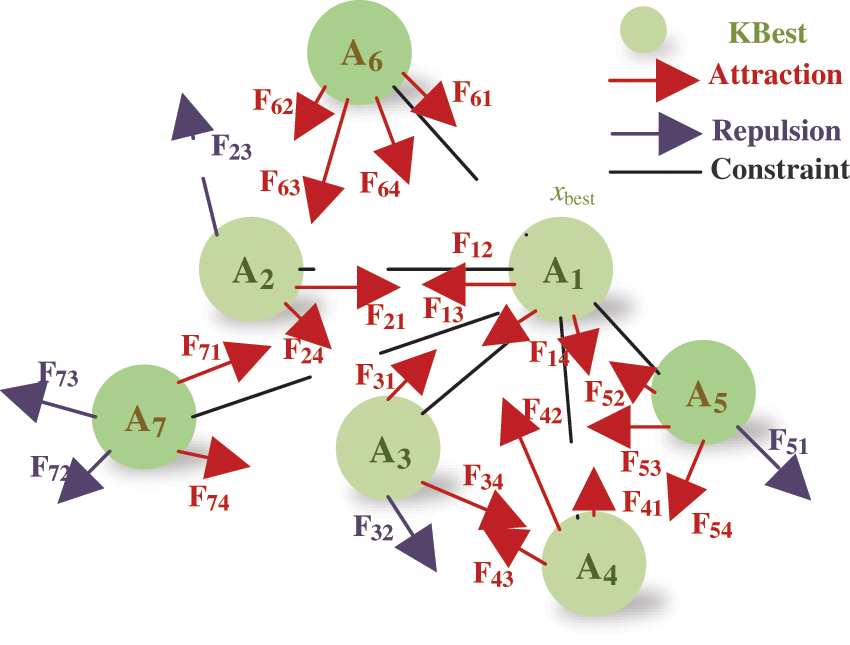
Figure 2: Schematic diagram of L-J potential
According to Eqs. (20)–(23), the variables η and h and parameter L have obvious influence to F′. For the sake of balancing interaction force (i.e., global search and local exploitation), EASO has carried out the following improvements compared with original ASO, yields
where Fit is the fitness function, xbest(k) is optimal solution produced at the kth repeat,
As shown in Fig. 3, the entire interaction force on the ith atom is able to be written as follows:
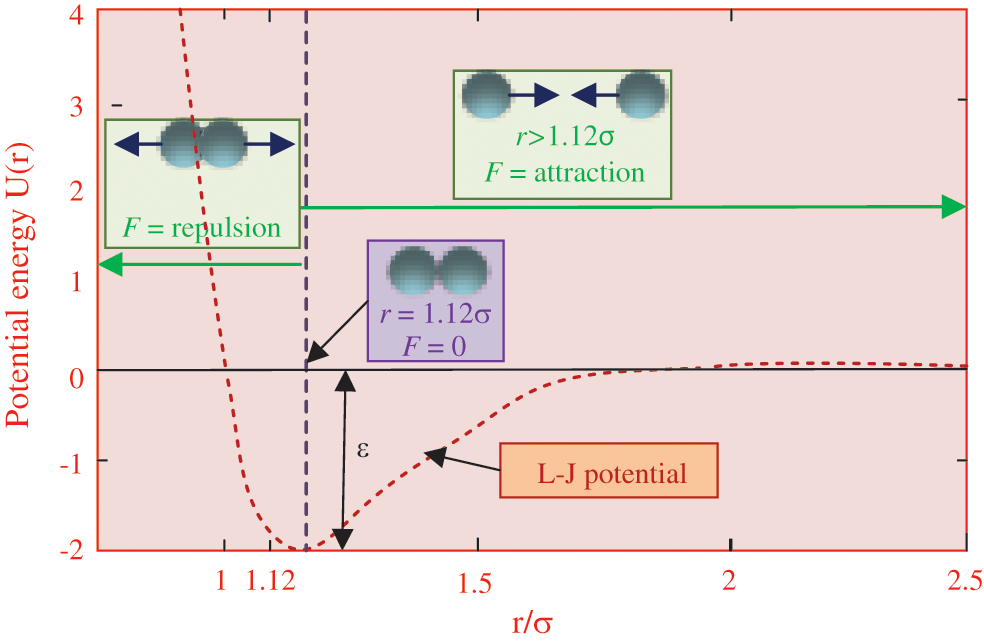
Figure 3: Interaction forces of bonded atoms
Geometric constraint is introduced to maintain the stability of molecular structure. Suppose each atom can bond to the optimal atom, then the geometric constraint for the ith atom is able to describe as
where θi is the geometric constraint for the ith atom, Gi is the constraint force for the ith atom, λ means the Lagrangian multiplier, and β stands for the multiplier weight.
3.3 Atomic Motion for Searching
Each atom will move to an updated location under the combined action of interaction forces and geometric constraints. The acceleration of each atom according to Newton’s second law can be given by
where mi(k) stands for the mass of the ith atom during the kth repeat, xworst(k) means the worst solution generated at the kth repeat.
The position of each atom can be denoted by
where vi(k) is the speed rate of the ith atom at the kth iteration, and c is a stochastic number uniformly distributed within the scope of [0,1].
4 EASO Based ID Controller Parameters Tuning
Fig. 4 gives the EASO based PID control structure of PMSG, where
EASO is used to optimize the parameters of three PID control loops in Fig. 4. And the optimization function considers minimum control error and control costs under three cases (step-variation of wind, low-frequency random-variation wind, and high-frequency random-variation wind), as follows:
where the value range of proportional gains KPi, integral gain KIi, and differential gains KDi are [0,1000], [0,1000], and [0,200], respectively. Moreover, simulation time T = 25 s, wind speed vwind varies between 8 m/s and 12 m/s, and weight coefficient ω1 = ω2 = 0.25.
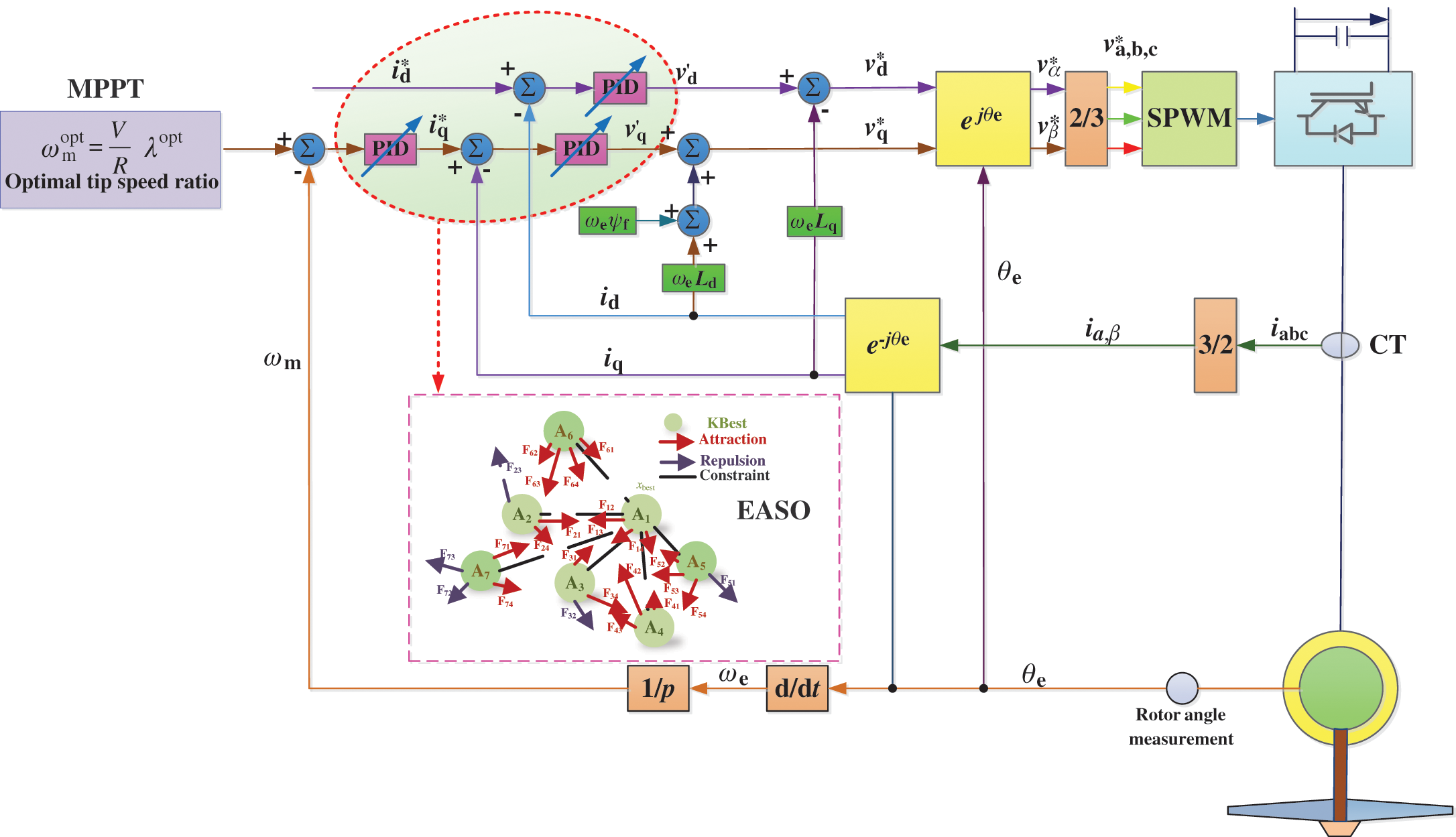
Figure 4: The optimization structure of EASO based PID control for PMSG
And the convergence criterion of EASO can be given as
where ε=10−6 is convergence error, Fk and Fk−1 are the fitness function value of the kth repeat and (k−1)th repeat, respectively.
At this end, the designed PID controllers for PMSG are expressed as follows:
The overall flowchart of EASO based PID control for PMSG is denoted in Fig. 5.
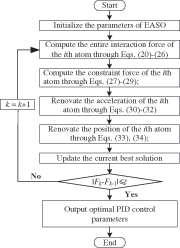
Figure 5: The entire flowchart of EASO based PID control for PMSG
The described EASO is compared with genetic optimization (GA) [34] and particle swarm optimization (PSO) [35] in three cases, namely, step-variation of wind speed, low-frequency random wind, and high-frequency random wind. Specially, step-variation of wind speed signals are obtained by step module of MATLAB/Simulink, and random wind signals are generated by designed random signal module which can be consulted in literature [36]. Meanwhile, the initial solutions are randomly selected from the feasible region to cover the larger search area, as follows:
where
The optimal PID controller parameters obtained by three algorithms after 30 runs are depicted in Table 1, and the PMSG system parameters can be founded in literature [37]. Note that the PID parameters are obtained by offline optimization due to the time-consuming process of MPPT for PMSG. Specially, the total fitness function of optimization algorithm under three cases are given in Eqs. (37) and (38). Then, optimization algorithm is adopted to tune PID parameters based on fitness function in each iteration until the convergence condition (39) is satisfied. The q-axis voltage Vq and d-axis voltage Vd are limited to [−0.65, 0.65] (p.u.). Lastly, the simulation is constructed on MATLAB/Simulink 2019a with IntelR CoreTMi5 at 2.5 GHz and 16 GB RAM of a personal computer.

Four successive step-variation wind speed signals from 8 m/s to 12 m/s are exected to WECS, and the simulation outcomes of three algorithms are given in Fig. 6. Obviously, EASO owns the fastest tracking rate and the smallest tracking error of mechanical rotation speed ωm, active power Pe and d-axis current id. Especially, the convergence time of Pe of GA, PSO, and EASO during the second step-variation are 3.04, 3.98, and 4.12 s, respectively. The maximum overshoot of ωm of GA, PSO, and EASO during the third step-variation are 5.93%, 3.93% and 1.20%, respectively. And the maximum overshoot of id of GA, PSO, and EASO from t = 10 s to t = 15 s are 12.23%, 10.21% and 4.56%, respectively. Moreover, the power coefficient CPof EASO is the largest which can capture the largest wind energy.
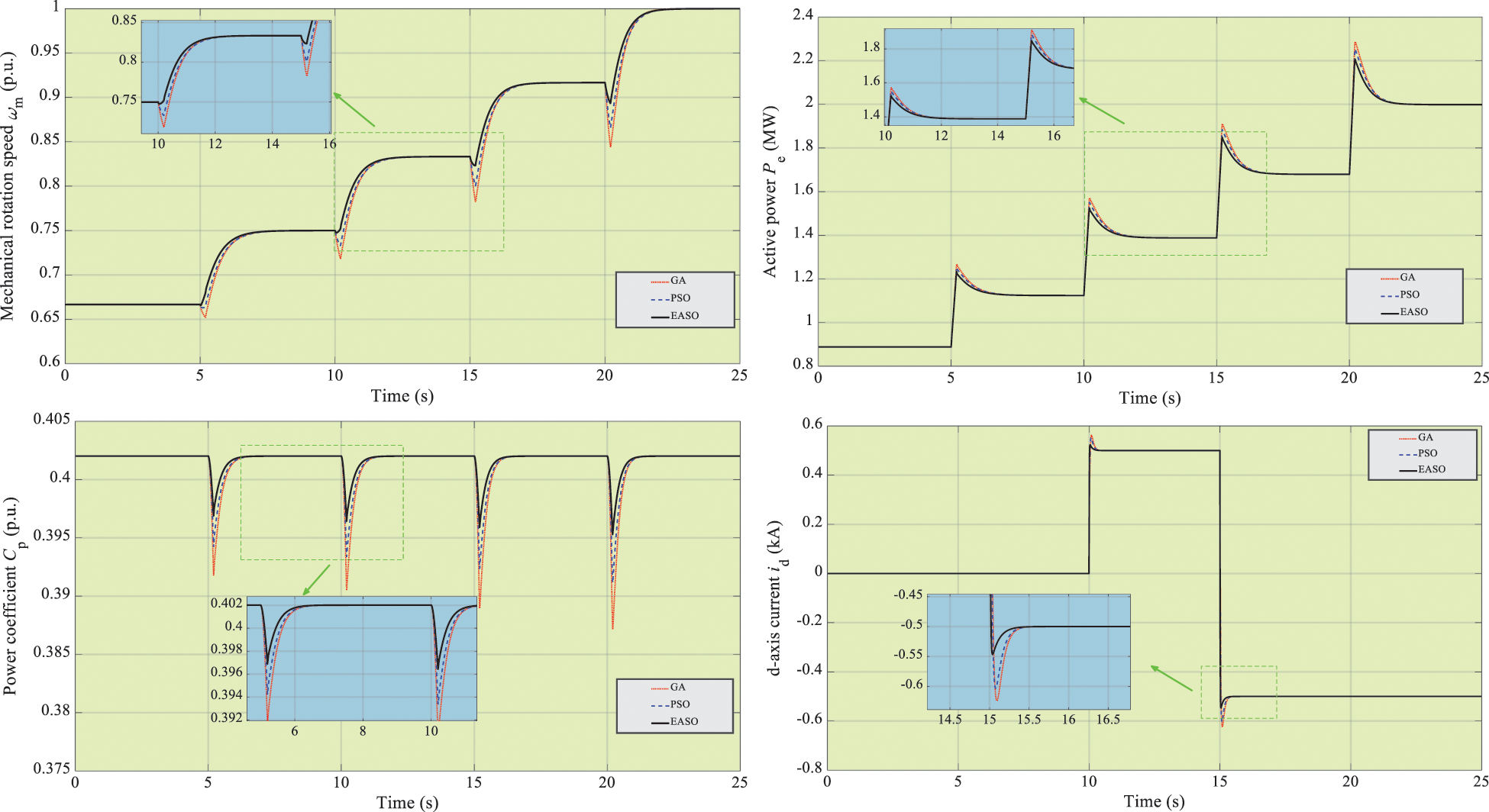
Figure 6: The simulation outcomes of three algorithms under step-variation of wind
5.2 Low-Frequency Random-Variation Wind
The low-frequency random-variation wind signals from 7 m/s to 11 m/s is exhibited in Fig. 7. And the simulation outcomes under such case are given in Fig. 8. One can easily find that EASO has the largest CP compared with other methods, which demonstrates the best MPPT performance. And EASO shows the smallest oscillation of all the controlled variables during the whole simulation time due to the adaptive update of dynamic optimization results based on Euclidian distance ratio.
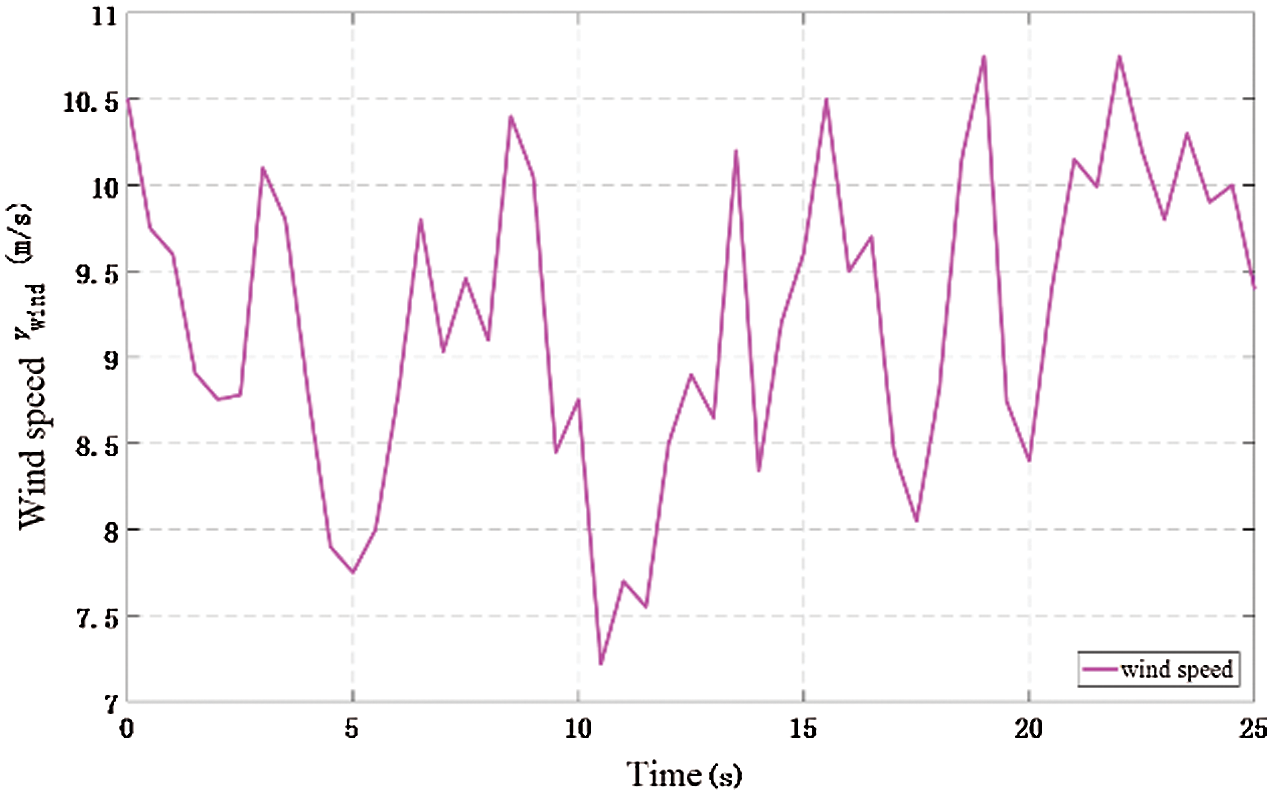
Figure 7: Low-frequency random-variation wind signals
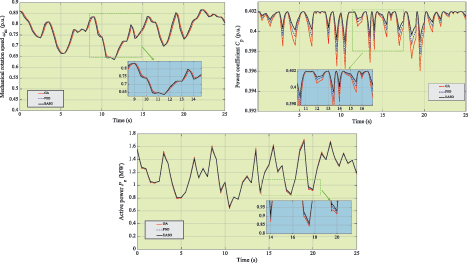
Figure 8: The simulation outcomes of three algorithms under low-frequency random-variation wind
5.3 High-Frequency Random Wind
In this case, the high-frequency random-variation wind signals from 6 m/s to 12 m/s (see in Fig. 9) is implemented to WECS to further evaluate MPPT performance of three methods. Fig. 10 denotes the simulation outcomes of this case. It is worth noting that EASO also can keep CP at its optimal value and get the smallest overshoot of ωm, Pe, and id during the whole simulation time thanks to its appropriate balance between global search and local exploration.
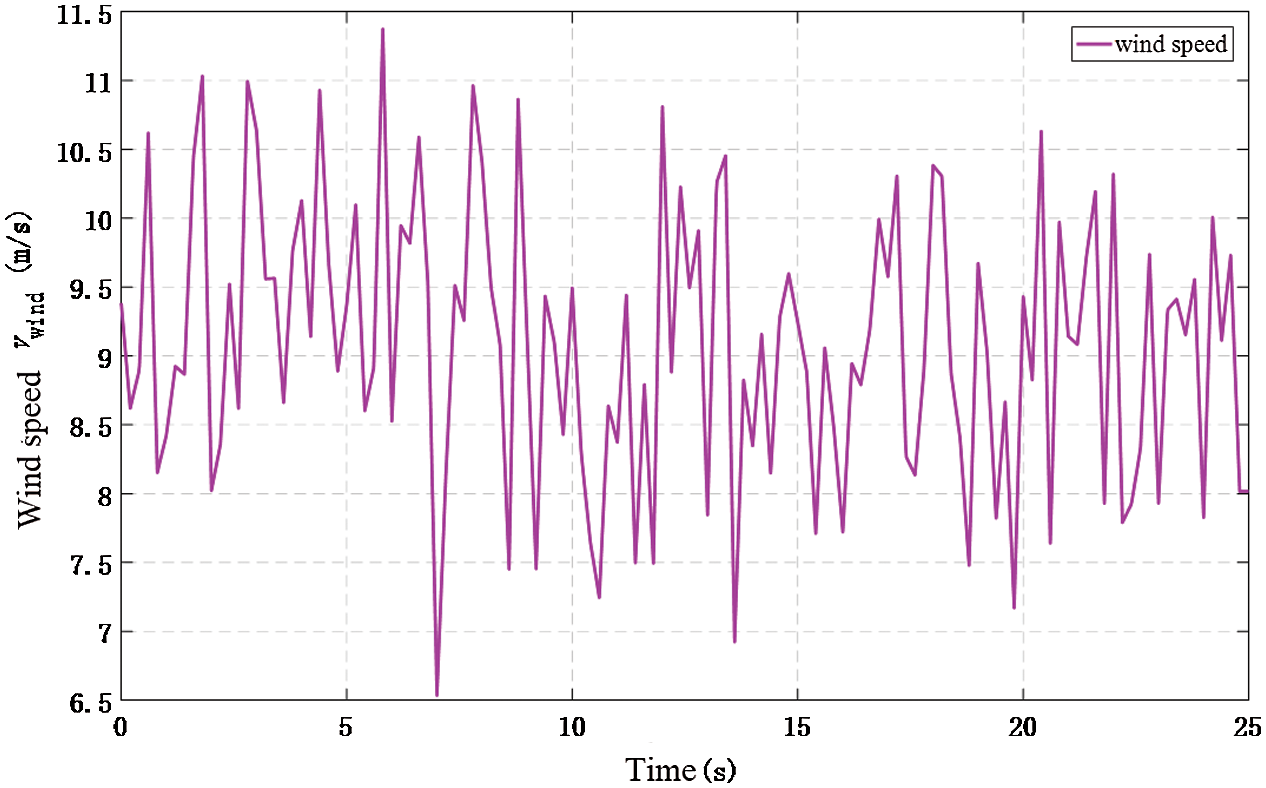
Figure 9: High-frequency random-variation wind signals
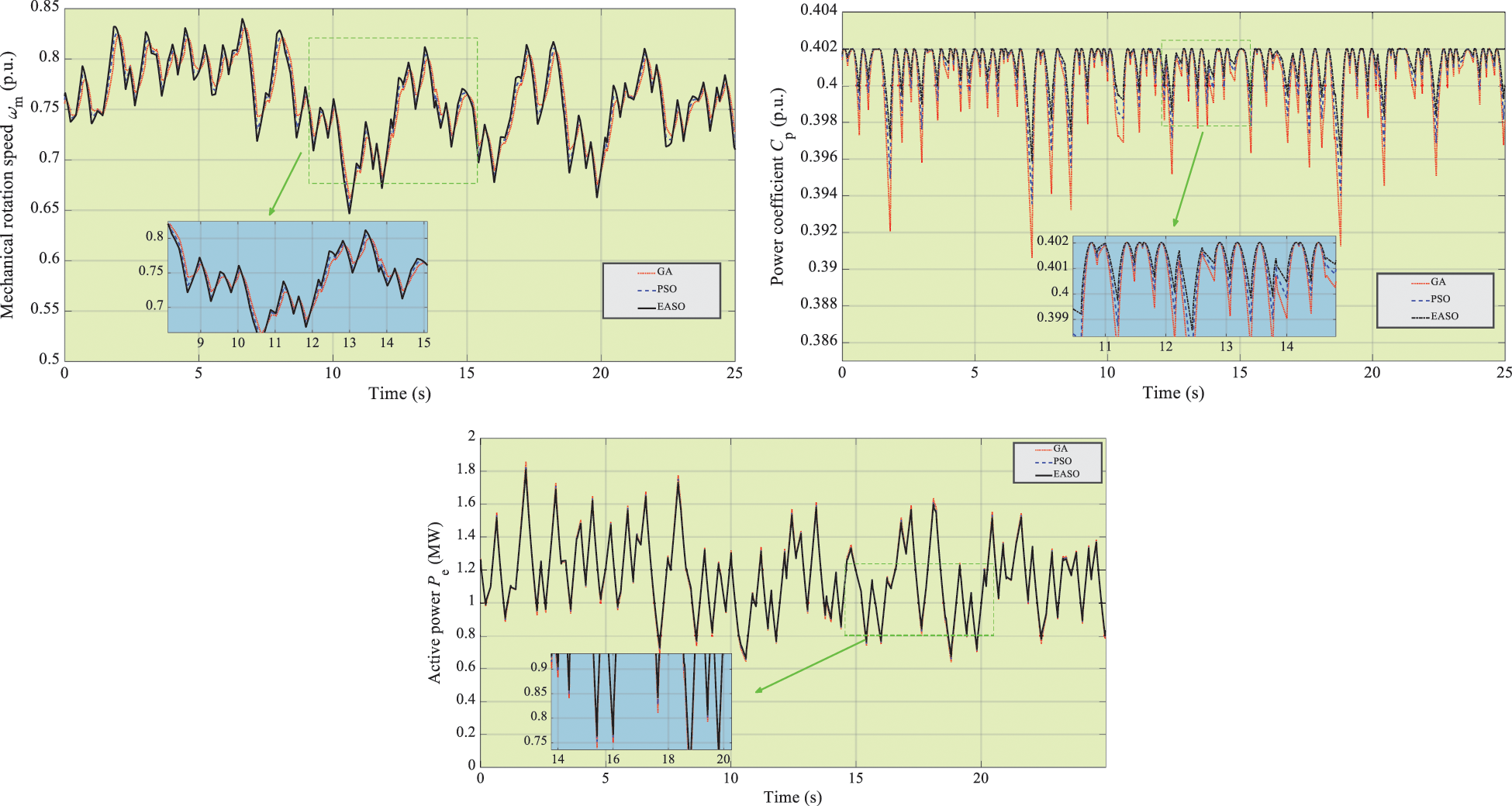
Figure 10: The simulation outcomes of three algorithms under high-frequency random-variation wind
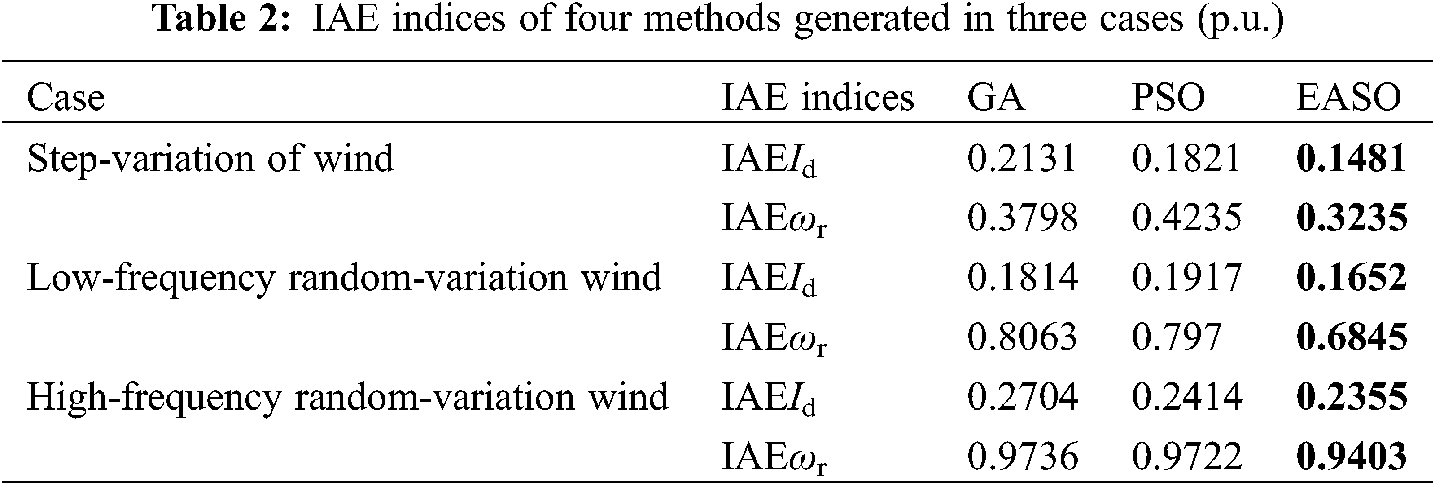
Integral absolute error (IAE) indices describe the error accumulation of controlled variable relative to its reference value over a period of time T which is widely used in the quantitative analysis of control error. And the smaller of IAE value means the smaller whole control error. Table 2 lists the IAE indices of the above three algorithms with 3% measurement errors in three cases. Besides,
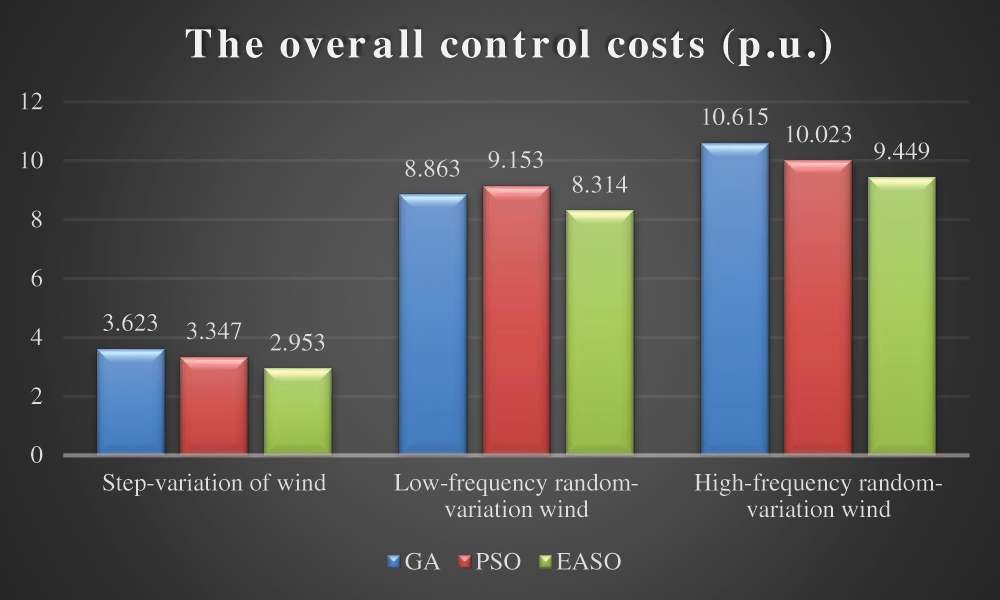
Figure 11: The entire control costs of four techniques generated in three cases (p.u.)
Wind energy, as a gift of nature, is a green and pollution-free energy that can be used, which also has played an increasingly significant role in power generation. However, wind power system is a very complex nonlinear time-varying system, how to realize the MPPT control of WECS is very meaningful. Although a large number of MPPT strategies have been developed for PMSG based WECS, these techniques are basically less efficient and difficult in searching the MPP. In this paper, a novel and prominent meta-heuristic algorithm named EASO is adopted for optimal power extraction of PMSG based WECS, which major novelties/outcomes can be summarized as follows:
(1) (1) In contrast to typical MPPT technique (namely, GA and PSO), EASO can efficiently escape being sinking into low-quality LMPP for PMSG based WECS since it owns a strong global search ability;
(2) (2) Compared with independent meta-heuristic algorithms, EASO can successfully obtain a dynamic balance between global exploration and local exploitation because it can adaptively adjust the weight between the exploration and exploitation based on the dynamic optimization results. Therefore, FASO is more prone to converge to a higher-quality optimal solution with a faster speed for MPPT under varieties of wind speed profiles;
(3) (3) EASO is adopted for optimal PID control parameters tuning of PMSG based WECS for MPPT under varying wind conditions. Three case studies through Matlab/Simulink verify that EASO possesses the lowest tracking error and control costs in all cases vs. that of GA and PSO;
(4) (4) Notable that EASO obtains the smallest IAE indices which indicates the best tracking performance. Specially, the IAE of EASO is only 69.50% and 81.33% of that of GA and PSO in step-variation of wind. Moreover, the IAEωr of EASO is only 96.58% and 96.72% of that of GA and PSO in high-frequency random-variation wind.
Future studies will focus on the following aspects:
(1) (1) This paper mainly carries on the theoretical analysis of WECS based on PMSG. Compared with the real wind power generation system, the established model still own some defects. The two wind conditions adopted are relatively single and have not yet accurately simulated the natural wind conditions. How to achieve maximum wind energy tracking under natural wind conditions still needs further research;
(2) (2) Comprehensive experiments like hardware-in-the-loop (HIL) experiment based on a dSpace will be carried out to confirm the practicality and meliority of EASO.
Funding Statement: The authors appreciatively acknowledge the support of rapid device state variation based system device invention of a training device for live-work electricity meter installation without electric shocks (YNZC202003110011) and National Natural Science Foundation of China (NSFC) under Grant (61902039).
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
1. Bani-Hani, E., Sedagha, T. A., Saleh, A., Ghulom, A., Al-Rahmani, H. et al. (2019). Evaluating performance of horizontal axis double rotor wind turbines. Energy Engineering, 116(1), 26–40. DOI 10.1080/01998595.2019.12043336. [Google Scholar] [CrossRef]
2. You, X., Zhou, B., Zuo, G. J., Guo, H. H. (2012). A novel algorithm for fast and adaptive maximum power point tracking of wind energy generation system. Advanced Materials Research, 383–390, 3633–3638. DOI 10.4028/www.scientific.net/amr.383-390.3633. [Google Scholar] [CrossRef]
3. Fathabadi, H. (2016). Novel high efficient speed sensorless controller for maximum power extraction from wind energy conversion systems. Energy Conversion and Management, 123, 392–401. DOI 10.1016/j.enconman.2016.06.046. [Google Scholar] [CrossRef]
4. Fathabadi, H. (2016). Maximum mechanical power extraction from wind turbines using novel proposed high accuracy single-sensor-based maximum power point tracking technique. Energy, 113, 1219–1230. DOI 10.1016/j.energy.2016.07.081. [Google Scholar] [CrossRef]
5. Alizadeh, O., Yazdani, A. (2013). A strategy for real power control in a direct-drive pmsg-based wind energy conversion system. IEEE Transactions on Power Delivery, 28(3), 1297–1305. DOI 10.1109/tpwrd.2013.2258177. [Google Scholar] [CrossRef]
6. Joyjit, C., Nina, D. (2021). Scientometric review of artificial intelligence for operations & maintenance of wind turbines: The past, present and future. Renewable and Sustainable Energy Reviews, 114, 111051. DOI 10.1016/j.rser.2021.111051. [Google Scholar] [CrossRef]
7. Nadhir, A., Naba, A., Hiyama, T. (2011). FIS/ANFIS based optimal control for maximum power extraction in variable-speed wind energy conversion system. IEEJ Transactions on Power and Energy, 131(8), 708–714. DOI 10.1541/ieejpes.131.708. [Google Scholar] [CrossRef]
8. Hu, J., He, Y., Xu, L. (2010). Improved rotor current control of wind turbine driven doubly-fed induction generators during network voltage unbalance. Electric Power Systems Research, 80(7), 847–856. DOI 10.1016/j.epsr.2009.12.010. [Google Scholar] [CrossRef]
9. Lin, W. M., Hong, C. M., Cheng, F. S. (2010). On-line designed hybrid controller with adaptive observer for variable-speed wind generation system. Energy, 35(7), 3022–3030. DOI 10.1016/j.energy.2010.03.040. [Google Scholar] [CrossRef]
10. Mousa, H. H. H., Youssef, A. R., Mohamed, E. E. M. (2019). Adaptive P&O MPPT algorithm based wind generation system using realistic wind fluctuations. International Journal of Electrical Power and Energy Systems, 112, 294–308. DOI 10.1016/j.ijepes.2019.04.038. [Google Scholar] [CrossRef]
11. Errami, Y., Ouassaid, M., Maaroufi, M. (2015). A performance comparison of a nonlinear and a linear control for grid connected pmsg wind energy conversion system. International Journal of Electrical Power and Energy Systems, 68, 180–194. DOI 10.1016/j.ijepes.2014.12.027. [Google Scholar] [CrossRef]
12. Mousa, H. H. H., Youssef, A. R., Mohamed, E. E. M. (2019). Variable step size P&O MPPT algorithm for optimal power extraction of multi-phase pmsg based wind generation system. International Journal of Electrical Power and Energy Systems, 108, 218–231. DOI 10.1016/j.ijepes.2018.12.044. [Google Scholar] [CrossRef]
13. Heidari, M. (2018). Maximum wind energy extraction by using neural network estimation and predictive control of boost converter. IAES International Journal of Robotics and Automation, 7(1), 59–68. DOI 10.11591/ijra.v7i1. [Google Scholar] [CrossRef]
14. Matayoshi, H., Howlader, A. M., Datta, M., Senjyu, T. (2018). Control strategy of PMSG based wind energy conversion system under strong wind conditions. Energy for Sustainable Development, 45, 211–218. DOI 10.1016/j.esd.2018.07.001. [Google Scholar] [CrossRef]
15. Kumar, D., Chatterjee, K. (2016). A review of conventional and advanced mppt algorithms for wind energy systems. Renewable and Sustainable Energy Reviews, 55, 957–970. DOI 10.1016/j.rser.2015.11.013. [Google Scholar] [CrossRef]
16. Kazmi, S. M. R., Goto, H., Guo, H. J., Ichinokura, O. (2011). A novel algorithm for fast and efficient speed-sensorless maximum power point tracking in wind energy conversion systems. IEEE Transactions on Industrial Electronics, 58(1), 29–36. DOI 10.1109/tie.2010.2044732. [Google Scholar] [CrossRef]
17. Putri, R. I., Mahmudi, I., Pujiantara, M., Priyadi, A., Purnomo, M. H. (2018). Modified firefly algorithm for improved maximum power extraction on wind energy conversion system. International Journal of Renewable Energy Research, 8(3), 1208–1216. DOI 10.1109/isitia.2016.7828719. [Google Scholar] [CrossRef]
18. Kumar, M. B. H., Saravanan, B., Sanjeevikumar, P., Blaabjerg, F. (2018). A review on control techniques and methodologies for maximum power extraction from wind energy systems. IET Renewable Power Generation, 12(14), 1609–1622. DOI 10.1049/iet-rpg.2018.5206. [Google Scholar] [CrossRef]
19. Patnaik, R. K., Dash, P. K., Mahapatra, K. (2016). Adaptive terminal sliding mode power control of DFIG based wind energy conversion system for stability enhancement. International Transactions on Electrical Energy Systems, 26(4), 750–782. DOI 10.1002/etep.2105. [Google Scholar] [CrossRef]
20. Barradi, Y., Zazi, K., Zazi, M., Khaldi, N. (2020). Control of PMSG based variable speed wind energy conversion system connected to the grid with PI and ADRC approach. International Journal of Power Electronics and Drive Systems, 11(2), 953–964. DOI 10.11591/ijpeds.v11.i2.pp953-968. [Google Scholar] [CrossRef]
21. Khan, S. A., Hossain, M. I. (2011). Intelligent control based maximum power extraction strategy for wind energy conversion systems. Revista Colombiana De Psiquiatría, 36(2), 1040–1043. DOI 10.1109/CCECE.2011.6030619. [Google Scholar] [CrossRef]
22. Kamal, E., Aitouche, A., Mohammed, W., Sobaih, A. A. (2016). Maximum energy extraction control for wind power generation systems based on the fuzzy controller. International Journal of Emerging Electric Power Systems, 17(5), 485–495. DOI 10.1515/ijeeps-2016-0075. [Google Scholar] [CrossRef]
23. Levron, Y., Shmilovitz, D. (2013). Maximum power point tracking employing sliding mode control. IEEE Transactions on Circuits and Systems I Regular Papers, 60(3), 724–732. DOI 10.1109/TCSI.2012.2215760. [Google Scholar] [CrossRef]
24. Shotorbani, A. M., Mohammadi-Ivatloo, B., Wang, L., Marzband, M., Sabahi, M. (2019). Application of finite-time control lyapunov function in low-power pmsg wind energy conversion systems for sensorless MPPT. International Journal of Electrical Power and Energy Systems, 106, 169–182. DOI 10.1016/j.ijepes.2018.09.039. [Google Scholar] [CrossRef]
25. Tiwari, R., Kumar, K., Babu, N. R., Prabhu, K. R. (2018). Coordinated MPPT and DPC strategies for PMSG based grid connected wind energy conversion system. Energy Procedia, 145, 339–344. DOI 10.1016/j.egypro.2018.04.061. [Google Scholar] [CrossRef]
26. Tiwari, R., Babu, N. R. (2019). Artificial neural network-based control strategies for pmsg-based grid connected wind energy conversion system. International Journal of Materials and Product Technology, 58(4), 323–341. DOI 10.1504/IJMPT.2019.100009. [Google Scholar] [CrossRef]
27. Wei, C., Zhang, Z., Qiao, W., Qu, L. (2016). An adaptive network-based reinforcement learning method for mppt control of pmsg wind energy conversion systems. IEEE Transactions on Power Electronics, 31(11), 7837–7848. DOI 10.1109/TPEL.63. [Google Scholar] [CrossRef]
28. Douanla, R. M., Kenne, G., Pelap, F. B., Fotso, A. S. (2018). A modified rbf neuro-sliding mode control technique for a grid connected pmsg based variable speed wind energy conversion system. Journal of Control Science and Engineering, 2018, 1–19. DOI 10.1155/2018/1780634. [Google Scholar] [CrossRef]
29. Hansen, A. D., Michalke, G. (2010). Modelling and control of variable-speed multi-pole permanent magnet synchronous generator wind turbine. Wind Energy, 11(5), 537–554. DOI 10.1002/we.278. [Google Scholar] [CrossRef]
30. Dey, L., Abulaish, M., Goyal, R., Shubham, K. (2011). Modeling and simulation of grid connected permanent magnet generator (pmg)-based small wind energy conversion systems. Open Renewable Energy Journal, 4(1), 1–6. DOI 10.1109/EPEC.2010.5697174. [Google Scholar] [CrossRef]
31. Zhu, Y., Cheng, M., Hua, W., Wang, W. (2012). A novel maximum power point tracking control for permanent magnet direct drive wind energy conversion systems. Energies, 5(5), 1398–1412. DOI 10.3390/en5051398. [Google Scholar] [CrossRef]
32. Zhao, W. G., Wang, L. Y., Zhang, Z. X. (2019). Atom search optimization and its application to solve a hydrogeologic parameter estimation problem. Knowledge-Based Systems, 163, 283–304. DOI 10.1016/j.knosys.2018.08.030. [Google Scholar] [CrossRef]
33. Yang, B., Zhang, M. T., Zhang, X. S., Wang, J. B., Shu, H. C. et al. (2020). Fast atom search optimization based MPPT design of centralized thermoelectric generation system under heterogeneous temperature difference. Journal of Cleaner Production, 248, 119301. DOI 10.1016/j.jclepro.2019.119301. [Google Scholar] [CrossRef]
34. Hasanien, H. M., Muyeen, S. M. (2012). Design optimization of controller parameters used in variable speed wind energy conversion system by genetic algorithms. IEEE Transactions on Sustainable Energy, 3(2), 200–208. DOI 10.1109/TSTE.2012.2182784. [Google Scholar] [CrossRef]
35. Narayana, M., Putrus, G. A., Jovanovic, M., Leung, P. S., Mcdonald, S. (2012). Generic maximum power point tracking controller for small-scale wind turbines. Renewable Energy, 44(4), 72–79. DOI 10.1016/j.renene.2011.12.015. [Google Scholar] [CrossRef]
36. Yang, B., Yu, T., Shu, H. C., Chen, J., Sang, Y. Y. et al. (2018). Passivity-based sliding-mode control design for optimal power extraction of a PMSG based variable speed wind turbine. Renewable Energy, 119, 577–589. DOI 10.1016/j.renene.2017.12.047. [Google Scholar] [CrossRef]
37. Yang, B., Yu, T., Shu, H. C., Zhang, X. S., Qu, K. P. et al. (2018). Democratic joint operations algorithm for optimal power extraction of PMSG based wind energy conversion system. Energy Conversion and Management, 159, 312–326. DOI 10.1016/j.enconman.2017.12.090. [Google Scholar] [CrossRef]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |