

 | Energy Engineering |  |
DOI: 10.32604/EE.2022.017396
ARTICLE
Sustainability Evaluation of Modern Photovoltaic Agriculture Based on Interval Type-2 Fuzzy AHP-TOPSIS and Least Squares Support Vector Machine Optimized by Fireworks Algorithm
1School of Management, Hebei GEO University, Shijiazhuang, 050031, China
2Strategy and Management Base of Mineral Resources in Hebei Province, Hebei GEO University, Shijiazhuang, 050031, China
3Long Yuan (Beijing) Wind Power Engineering & Consulting Co., Ltd., Beijing, 100034, China
4Department of Information Management, Oriental Institute of Technology, New Taipei, Taiwan
*Corresponding Author: Haichao Wang. Email: ncepuwhc@163.com
Received: 07 May 2021; Accepted: 05 August 2021
Abstract: Photovoltaics (PV) has been combined with many other industries, such as agriculture. But there are many problems for the sustainability of PV agriculture. Timely and accurate sustainability evaluation of modern photovoltaic agriculture is of great significance for accelerating the sustainable development of modern photovoltaic agriculture. In order to improve the timeliness and accuracy of evaluation, this paper proposes an evaluation model based on interval type-2 Fuzzy AHP-TOPSIS and least squares support vector machine optimized by fireworks algorithm. Firstly, the criteria system of modern photovoltaic agriculture sustainability is constructed from three dimensions including technology sustainability, economic sustainability and social sustainability. Then, analytic hierarchy process (AHP) and technique for order preference by similarity to an ideal solution (TOPSIS) methods are improved by using interval type-2 fuzzy theory, and the traditional evaluation model based on interval type-2 Fuzzy AHP-TOPSIS is obtained, and the improved model is used for comprehensive evaluation. After that, the optimal parameters of least squares support vector machine (LSSVM) model are obtained by Fireworks algorithm (FWA) training, and the intelligent evaluation model for the sustainability of modern photovoltaic agriculture is constructed to realize fast and intelligent calculation. Finally, an empirical analysis is conducted to demonstrate the scientificity and accuracy of the proposed model. This study is conducive to the comprehensive evaluation of the sustainability of modern photovoltaic agriculture, and can provide decision-making support for more reasonable development model in the future of modern photovoltaic agriculture.
Keywords: Modern photovoltaic agriculture; sustainability evaluation; interval type-2 fuzzy numbers; AHP; TOPSIS; FWA; LSSVM
In recent years, the application field of photovoltaic renewable energy is expanding and the application depth is deepening [1]. Photovoltaic power generation technology has expanded from the simple use of solar power to the field of agriculture. It has been popularized in many fields of agriculture, such as power generation, planting, breeding, fishery, tourism, biological protection and so on. The concept of photovoltaic agriculture is gradually accepted by the professionals in the photovoltaic field and agricultural field [2]. The healthy and sustainable development of photovoltaic agriculture can not only accelerate the pace of agricultural transitory development, provide green and sustainable energy for agricultural production, but also solve the development dilemma of photovoltaic industry, alleviate the overcapacity problem of photovoltaic industry, and increase the proportion of renewable energy utilization [3]. However, the sustainable development of photovoltaic agriculture still faces some problems, which has badly affected the construction and operation of modern photovoltaic agriculture. How to solve the difficulties and problems encountered in the development of photovoltaic agriculture, promote the better and deeper combination of photovoltaic power generation and agriculture development, so as to truly realize the sustainable development of photovoltaic agriculture, is well worthy of study. Therefore, in order to solve the problem of sustainable development of modern photovoltaic agriculture, this paper will evaluate the sustainability of modern photovoltaic agriculture, find out the problems in its development timely and accurately, and take more targeted measures.
According to existing literature, it can be found that no scholars have carried out the sustainability evaluation of modern photovoltaic agriculture. The researches about modern photovoltaic agriculture mainly focus on the influencing factors of the development of photovoltaic agriculture [4], the operating mode of photovoltaic agriculture [5] and the technical design of photovoltaic agriculture [6,7]. Li et al. [4] showed that technical training had a significant positive impact on farmers’ construction and operation of photovoltaic agricultural projects, while photovoltaic investment cost had a significant negative impact. Yeoh et al. [5] introduced the application modes of photovoltaic agriculture, such as photovoltaic agricultural greenhouse, photovoltaic breeding, photovoltaic wastewater purification, photovoltaic pumping and new rural solar power station. At the same time, they believed that more theoretical research and practical exploration were needed to achieve the optimal combination of photovoltaic power generation and agricultural planting. For photovoltaic agriculture, Chen [6] designed KNT-SPV02 photovoltaic power generation inverter system, and studied the application of unipolar control mode SPWM in photovoltaic power generation inverter system. Yang et al. [7] proposed using modular design method to design and develop a multi-functional power supply system of agricultural internet of things based on solar power generation. The functions of power generation, storage, display, protection and remote control were designed in the system, which can provide reliable power for users, and can also increase the extension functions such as automatic day-to-day tracking and anti-theft alarming based on the actual demand. From the above researches, we can find that photovoltaic agriculture is getting more and more attention, and some existing research results can provide references for us to build a sustainable evaluation index system of photovoltaic agriculture, but there is a lack of systematic and multi-dimensional quantitative evaluation of the sustainability of photovoltaic agriculture. Therefore, this paper intends to make a qualitative and quantitative analysis on the sustainability evaluation of photovoltaic agriculture, build a scientific and reasonable evaluation index system of photovoltaic agriculture sustainability, and select appropriate methods to carry out the quantitative analysis of photovoltaic agriculture sustainability.
Considering that no scholars have carried out evaluation research on the sustainability of photovoltaic agriculture, this paper combs other research methods of sustainability evaluation [8–12]. At present, the main methods used in sustainable evaluation research include data envelopment analysis (DEA), network analysis process (ANP), matter-element extension method, analytic hierarchy process (AHP) and technique for order preference by similarity to an ideal solution (TOPSIS). Among them, AHP is a multi-criteria analysis method, which can deal with qualitative problems quantitatively. AHP has been one of the most commonly used multi criteria decision-making methods because of its scientific hierarchy construction and clear logical structure [13]. TOPSIS is another traditional multi criteria decision-making model. It is a method of ranking according to the gap between the evaluation objects and the ideal solutions, so as to determine the quality of the evaluation objects [14]. Because AHP and TOPSIS methods cannot deal with semantic variables with strong fuzziness and uncertainty effectively, interval type-2 fuzzy numbers are introduced in this paper to improve AHP and TOPSIS, respectively [15], and the traditional evaluation model of modern photovoltaic agriculture sustainability based on interval type-2 fuzzy AHP-TOPSIS is constructed. By combining fuzzy set theory with AHP-TOPSIS analysis method, we can better deal with the uncertainty involved in the problem and form pairwise comparison, and ensure the consistency of the ranking made by decision makers [16].
The above evaluation methods belong to the traditional evaluation methods, which are mature and accurate, but the calculation process is very complex. Intelligent evaluation methods can process data quickly and accurately [17], so this paper intends to use artificial intelligence methods to complete the sustainability evaluation of modern photovoltaic agriculture. Modern intelligent evaluation methods mainly include back propagation neural network (BPNN), support vector machine (SVM) and least squares support vector machine (LSSVM) evaluation methods [18–20]. LSSVM chooses the least square linear system as the loss function, which avoids the process of quadratic programming. At the same time, the kernel function is used to transform the prediction problem into the solution of equations, and the inequality constraint is transformed into the equality constraint, which increases the accuracy and the speed of prediction. Considering that LSSVM theory is relatively mature, and it is widely used [21], this paper uses LSSVM model for intelligent evaluation. However, in view of the blind selection of key parameters of LSSVM, it is necessary to select appropriate intelligent algorithm to optimize it [22]. Inspired by the phenomenon of fireworks exploding in the air, fireworks algorithm (FWA) is a new swarm intelligence algorithm with explosive search mechanism for global optimization. It shows excellent performance and high efficiency in solving complex optimization problems [23]. Therefore, this paper applies FWA to optimize the parameters of LSSVM.
The main contributions of this paper are as follows:
(1) The criteria system of modern photovoltaic agriculture sustainability is constructed from three dimensions including technology sustainability, economic sustainability and social sustainability.
(2) AHP and TOPSIS are improved by using interval type-2 fuzzy theory, and the traditional evaluation model based on interval type-2 Fuzzy AHP-TOPSIS is obtained.
(3) The optimal parameters of LSSVM model are obtained by Fireworks algorithm training, and the intelligent evaluation model for the sustainability of modern photovoltaic agriculture is constructed to realize fast and intelligent calculation.
Above all, this paper constructs the sustainability evaluation index system of modern photovoltaic agriculture, and establishes sustainability evaluation models of modern photovoltaic agriculture based on interval type-2 fuzzy AHP-TOPSIS and FWA-LSSVM. The rest of this paper is arranged as follows: Section 2 designs the evaluation index system of modern photovoltaic agriculture sustainability from three aspects including technological sustainability, economic sustainability and social sustainability; Section 3 introduces the main theories of the evaluation methods used in this paper, including interval type-2 fuzzy AHP, interval type-2 fuzzy TOPSIS, LSSVM model and fireworks algorithm, and constructs modern photovoltaic agriculture sustainability evaluation models based on these theories; Section 4 outlines the case study to verify the accuracy and effectiveness of the proposed model; and Section 5 summarizes the research results of this article.
2 Constructing an Evaluation Criteria System of Modern Photovoltaic Agriculture
In order to construct the sustainability evaluation criteria system of modern photovoltaic agriculture, we need to understand the connotation of modern photovoltaic agriculture. Modern photovoltaic agriculture is a new type of agriculture which widely applies solar power generation to many fields, such as modern agricultural research, planting, breeding, irrigation, pest control and agricultural machinery power supply [24]. In fact, photovoltaic agriculture means that photovoltaic power generation and agricultural production are carried out at the same time and in the same place. On the same land, it cannot only be used to build photovoltaic power station, but also to carry out agricultural production activities, such as planting, breeding, tourism and so on. Specifically, photovoltaic agriculture is the application of photovoltaic technology in the field of agriculture, which integrates photovoltaic power generation and agricultural production. By erecting solar panels, the current generated by the photovoltaic power generation system is connected to the nearest substation for grid-connected generation, the power generated by solar panels can also solve the problems of irrigation, lighting, heat preservation and temperature rise in agriculture, and play the role of biological insecticidal lamp, nutrient solution circulation system and plant protection facilities. It accomplishes the perfect combination of agriculture and photovoltaic new energy power generation, so as to achieve the effect of clean photovoltaic power generation and efficient agricultural development [25].
Modern photovoltaic agriculture includes many aspects, which are high systematic and hierarchical. Following the principles of comprehensiveness, independence, measurability and guidance is conducive to the sustainable evaluation of modern photovoltaic agriculture. According to the above construction principles, combined with the actual development of modern photovoltaic agriculture, this paper constructs the sustainable evaluation criteria system of modern photovoltaic agriculture.
As the future direction of agricultural development, modern photovoltaic agriculture plays a positive role in cost saving, environmental protection, social development and technological innovation. With the increasing concern for sustainable development, modern photovoltaic agriculture has already started to seek the coordinated development of economy, society and technology instead of the simple pursuit of economic growth in the past. Therefore, the sustainability evaluation of modern photovoltaic agricultural technology is conducive to a profound and comprehensive understanding of the impact from various aspects. On the basis of the index selection criteria, the objective environment of projects and the difficulty of data acquisition are fully considered, and the criteria system of modern photovoltaic agriculture sustainability is constructed. The criteria system mainly includes technology sustainability, economic sustainability and social sustainability. And the criteria system for sustainability evaluation of modern photovoltaic agriculture consists of 15 s level indexes, as shown in Table 1. According to the connotation of modern PV agriculture and the principles of comprehensiveness, independence, measurability and orientation, these indicators are selected in this paper.

3.1 Interval Type-2 Fuzzy AHP Model
The sustainability evaluation of modern photovoltaic agriculture is complicated, the evaluation process is affected by a variety of complex factors, with a certain degree of uncertainty. And the method of interval type-2 fuzzy numbers is effective to deal with many uncertain factors and obtain robust results. Interval type-2 fuzzy numbers have been widely used in many fields [26].
AHP is a multi-criteria analysis method which can deal with qualitative problems quantitatively. AHP is one of the most commonly used multi criteria decision-making methods because of its scientific hierarchy construction and clear logical structure [27]. By combining the fuzzy set theory with AHP analysis method, we can better deal with the uncertainty involved in the problem and form pairwise comparison, and ensure the consistency of the ranking made by decision makers. Therefore, this section applies the interval type-2 fuzzy AHP model to evaluate the sustainability of modern photovoltaic agriculture to calculate the weight of the indexes.
The calculation process of interval type-2 fuzzy AHP model is as follows:
(1) Combined with interval type-2 fuzzy numbers theory, pairwise comparison matrix is established for indexes of different levels and types.
Decision makers usually use semantic form to evaluate the objects in the measurement analysis of research projects. But it is difficult for decision-makers to define interval type-2 fuzzy numbers directly. Therefore, according to the semantic expression given by the decision-maker, it needs to be transformed into interval type-2 fuzzy numbers.
(2) Test the consistency of comparison matrix
The interval type-2 fuzzy numbers are calculated with Eq. (1), and then the consistency of the matrix can be tested.
The consistency index (CI) of the weight matrix of the object to be measured is tested, and the calculation process is shown in Eqs. (2) and (3).
(3) Integrate the interval type-2 fuzzy number comparison matrix by geometric average method
The interval type-2 fuzzy number comparison matrix of the object to be measured can be integrated according to Eq. (5).
The fuzzy weight of each index of the object to be measured can be calculated by Eq. (6).
3.2 Interval Type-2 Fuzzy TOPSIS Model
TOPSIS is one of the traditional multi criteria decision-making models. It is a method to rank based on the distance between the evaluation objects and the ideal solutions, so as to determine the quality of the evaluation objects [28]. For interval type-2 fuzzy TOPSIS model, the elements in the decision matrix will be calculated with interval type-2 fuzzy method.
Assuming that there are m items to be evaluated, N indexes and T experts in related fields to score, the main steps of interval type-2 fuzzy ideal point method are as follows:
(1) Transform semantic variables into interval type-2 fuzzy numbers
There are both quantitative and qualitative indicators in the index system. It is difficult to realize the horizontal comparison of semantic expression of different types of indexes, so it is necessary to standardize them and transform semantic variables into interval type-2 fuzzy numbers. Then the interval type 2 fuzzy decision matrix of expert k can be expressed by Eq. (7).
(2) Integrate interval type-2 fuzzy matrix
Collect the measurement score data of all objects to be measured for input, and then the integrated interval type-2 fuzzy decision matrix can be determined as Eqs. (8) and (9).
(3) Construct weighted normalized fuzzy decision matrix
The weighted normalized fuzzy decision matrix of the object to be measured can be calculated by Eqs. (10) and (11).
(4) Determine fuzzy positive and negative ideal solutions
The positive ideal solution and the negative ideal solution are expressed as
(5) Calculate the distance between each alternative and the fuzzy positive and negative ideal solutions
The calculation formulas of the distance between the measurement score of each index of the object to be measured and the positive and negative ideal solutions are shown in Eqs. (14) and (15), respectively.
(6) Calculate and sort the similarity coefficients of each alternative
The similarity coefficients of each alternative can be calculated with Eq. (16).
3.3 Least Squares Support Vector Machine
Least squares support vector machine (LSSVM) is an improvement of standard support vector machine (SVM). LSSVM uses equality constraints instead of inequality constraints of SVM, and uses kernel function to transform the prediction problem into solving equations, which can greatly improve the accuracy and speed of evaluation [29].
It is supposed that the given sample set is
For LSSVM, the optimization problem changes into the following:
In order to solve the above problems, Lagrange function is established as below:
Take a derivation of each variable of the function and make them have a value of 0, as shown in Eq. (21).
Eliminate
By solving the above linear equations, the following results are obtained:
Considering that the RBF kernel function has a wide range of convergence and application, this paper chooses it as the kernel of LSSVM. The expression is as follows:
By analyzing the relevant theories of LSSVM, we can see that the difficulty of establishing LSSVM model is determining kernel function parameter
FWA is a simulation of the whole process of fireworks explosion. When fireworks explode, a large number of sparks will be generated, which can continue to explode and produce new sparks, thus it will make beautiful and colorful patterns. In the FWA, each firework can be regarded as a feasible solution in the solution space of the optimization problem, so the process of fireworks explosion can be regarded as the process of searching for the optimal solution. In the specific optimization problem, FWA involves the number of sparks produced by fireworks explosion, the radius of explosion, and how to select a group of optimal fireworks and sparks to carry out the next explosion [32].
In the FWA, the number of sparks and explosion radius of fireworks are different. The fireworks with poor fitness have larger explosion radius, which makes them have greater exploration ability, while the fireworks with good fitness have smaller explosion radius, which makes them have greater excavation ability. In addition, the introduction of Gauss mutation sparks can further increase the diversity of the population [33].
Therefore, we can know that the three most important parts of FWA are explosion parameters, mutation parameters and selection strategy [34].
(1) Explosion parameters
In the explosion parameters, the number of sparks and explosion radius of fireworks are calculated according to the fitness value of fireworks. For firework
(2) Mutation parameters
The setting of mutation parameters is to increase the diversity of explosion spark population. The mutation sparks in FWA generate Gaussian mutation sparks by Gaussian mutation. Suppose that firework
In FWA, the explosion sparks and mutation sparks generated by explosion parameters and mutation parameters may exceed the boundary range of feasible region, so they must be mapped to a new location by mapping rules by Eq. (31).
(3) Selection strategy
In order to transmit the information of excellent individuals to the next generation, it is necessary to select a certain number of individuals as the fireworks of the next generation from the explosion sparks and variation sparks.
Suppose that there are K candidates and the population number is N. The individuals with the best fitness value in the candidate set will be identified as the next generation fireworks. And the remaining
Based on the previous description, the specific steps of FWA are as follows [35,36]:
Step 1. Randomly select N fireworks in the solution space and initialize their coordinates.
Step 2. Calculate the fitness value
Step 3. Generate M Gauss mutation sparks, randomly select spark
Step 4. From the fireworks, explosion sparks and Gauss mutation spark population, N individuals are selected as the fireworks for next generation iterative calculation by using probability selection Eqs. (32) and (33).
Step 5. Judge the stop condition. If the stop condition is satisfied, jump out of the program and output the optimal result; if not, return to Step 2 to continue the loop.
3.5 Sustainability Evaluation Model of Modern Photovoltaic Agriculture Based on Interval Type-2 Fuzzy AHP-TOPSIS and FWA-LSSVM
In this section, on the basis of the evaluation model of modern photovoltaic agriculture sustainability based on interval type-2 Fuzzy AHP-TOPSIS, the intelligent evaluation model of modern photovoltaic agriculture sustainability based on FWA-LSSVM is proposed, that is, the index value of modern photovoltaic agriculture sustainability evaluation index system is taken as the input, and the LSSVM is optimized by FWA, so as to obtain the optimal value of LSSVM, finally, the sustainability evaluation results of modern photovoltaic agriculture can be obtained and analyzed. The flow chart of the proposed model is shown in Fig. 1.
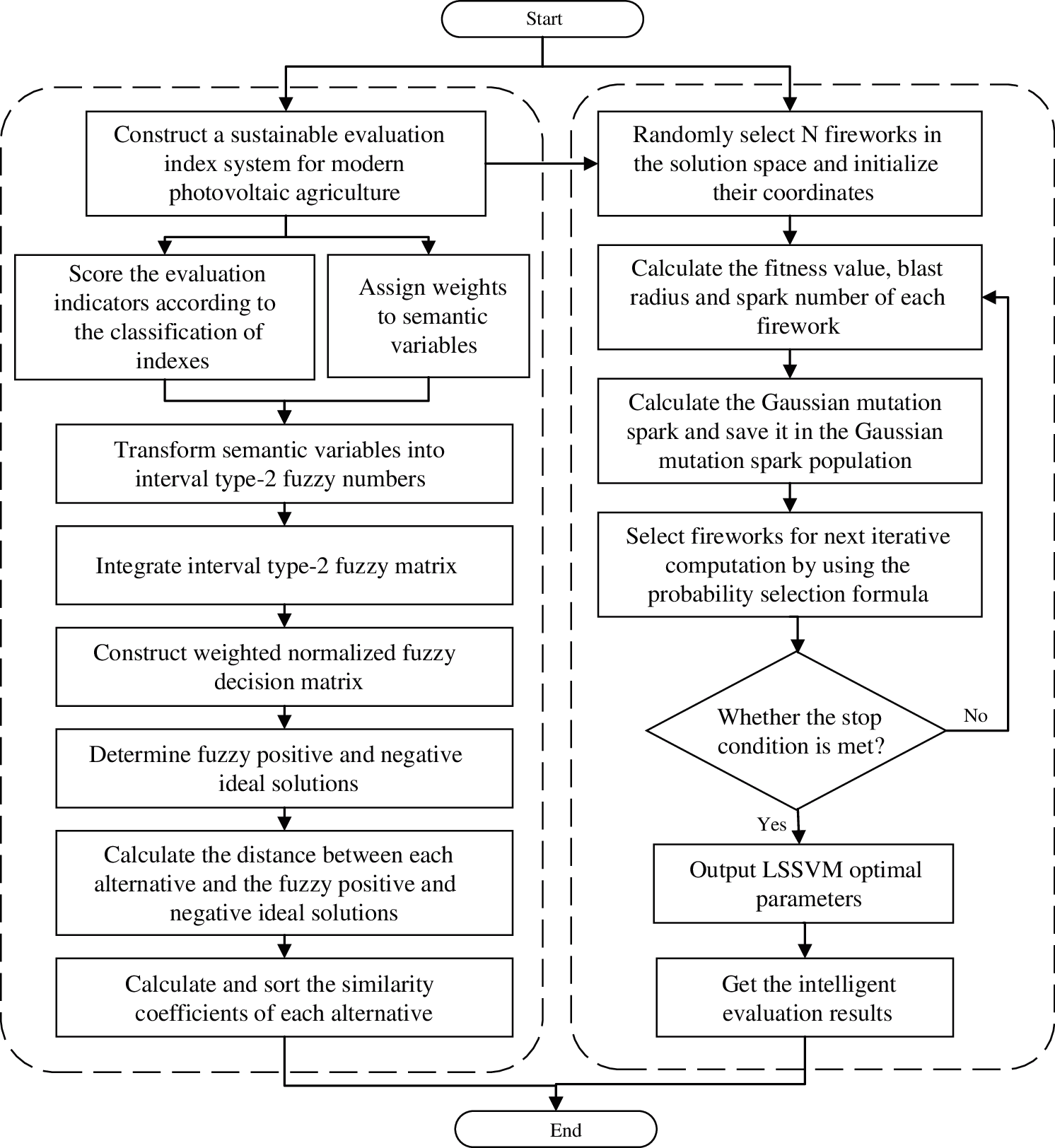
Figure 1: The flow chart of the evaluation
The specific steps are as follows:
Step 1. Construct a sustainable evaluation index system for modern photovoltaic agriculture.
Step 2. Score the evaluation indexes according to the classification of indexes and assign weights to semantic variables.
Step 3. Transform semantic variables into interval type-2 fuzzy numbers, integrate interval type-2 fuzzy matrix and construct weighted normalized fuzzy decision matrix.
Step 4. Determine fuzzy positive and negative ideal solutions, calculate the distance between each alternative and the fuzzy positive and negative ideal solutions, then calculate and sort the similarity coefficients of each alternative.
Step 5. Initialize the parameters of LSSVM and FWA, optimize the parameters of LSSVM model with FWA, then output and analysis the intelligent evaluation results.
4.1 Determination of the Index Set
In order to achieve the hierarchical measurement of different levels of indexes, it is necessary to classify different indexes on the basis of the level differences, that is, to define the index set. Here, according to the evaluation index system, we divide the indexes into different levels, including the first level indexes and the second level indexes.
(1) Set of the first level indexes
The set of the first level indexes can be expressed as Eq. (35).
(2) Set of the second level indexes
The set of the first level indexes can be expressed as follows:
a. Technical characteristic index
b. Economic characteristic index
c. Social characteristic index
4.2 Determination of the Evaluative Language
Due to the differences in various aspects of the projects to be measured, the measurement results also have the characteristics of diversity. Through the integration of semantic variables, the corresponding set of comments V is established, as shown in Eq. (39).
All possible states of the objects to be measured should be fully included in the set of comments. The reasonable construction of the comments set will have an important impact on the accuracy and scientificity of the measurement results. Therefore, we should define the comments set on the basis of full investigation and expert advice.
(1) Comments set of the interval type-2 fuzzy AHP model
There are five semantic variables in the comments set of the interval type-2 fuzzy AHP model. They are absolutely strong (AS), very strong (VS), fairly strong (FS), slightly strong (SS) and equal (E). The expression is shown in Eq. (40).
The correspondence between semantic variables of interval type-2 fuzzy AHP model and interval type-2 fuzzy numbers can be shown in Table 2.

(2) Comments set of the interval type-2 fuzzy TOPSIS model
There are seven semantic variables in the comments set of the interval type-2 fuzzy TOPSIS model. They are very low (VL), low (L), medium low (ML), medium (M), medium high (MH), high (H), very high (VH). The expression is shown in Eq. (41).
The correspondence between semantic variables of interval type-2 fuzzy TOPSIS model and trapezoidal interval type-2 fuzzy numbers can be shown in Table 3.

4.3 Calculation and Analysis Based on Interval Type-2 Fuzzy AHP-TOPSIS Model
4.3.1 Weight Calculation Based on Interval Type-2 Fuzzy AHP Model
In order to comprehensively evaluate the sustainability of modern photovoltaic agriculture, this paper selects five modern photovoltaic agricultural projects for research. The basic information of the five projects is shown below:
(1) A1: The installed photovoltaic capacity is 75 MW, with an estimated annual average power generation capacity of 98.86 million kWh. 50 new vegetable greenhouses, 25 flower greenhouses and 20 Chinese herbal medicine greenhouses are arranged in the field with steel structure.
(2) A2: This project is a fishery-photovoltaic complementary photovoltaic power plant project. The installed PV capacity is 200 MW, and the average annual power generation is expected to be 257.86 million kWh. The project covers an area of 3,333,300 square meters. In addition, 22 vegetable greenhouses are arranged in the field with steel structure.
(3) A3: This project is a distributed photovoltaic power plant for cowshed. The installed PV capacity is 20 MW, with an estimated annual average power generation capacity of 27.12 million kWh. The cowshed covers an area of 666,700 square meters.
(4) A4: The installed photovoltaic capacity is 50 MW, with an estimated annual average power generation capacity of 63.92 million kWh. 60 new vegetable greenhouses are arranged in the field with steel structure.
(5) A5: This project is a water conservancy PV model. The installed capacity of photovoltaic is 35 MW, and the average annual power generation is expected to be 45.02 million kWh. The PV is used to supply power to farmland drainage and irrigation, water-saving irrigation and its control system. 16 flower greenhouses are arranged in the field with steel structure.
30 experts are invited from photovoltaic industry, agricultural development and energy economy to form a decision-making group to score the alternatives, so as to judge the advantages and disadvantages of the sustainability of modern photovoltaic agricultural projects.
Based on the established sustainability evaluation index system of modern photovoltaic agriculture, experts evaluated this five modern photovoltaic agricultural projects. The scoring results evaluated by experts are shown in Table 4.

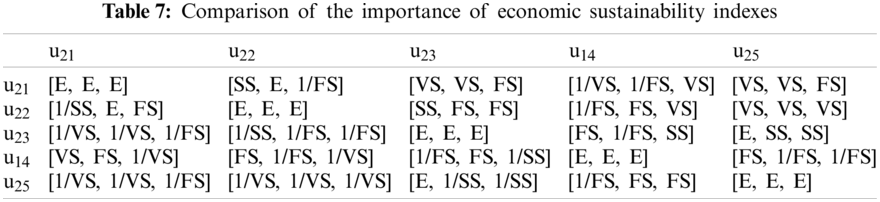
According to the corresponding relationship between semantic variables and interval type-2 fuzzy numbers in Table 3, the semantic variables are transformed into corresponding interval type-2 fuzzy numbers. After that, each expert compares the importance of each modern photovoltaic agricultural sustainability index and establishes a pairwise comparison matrix of semantic variables. The comparison results are shown in Tables 5–8.



Similarly, based on the corresponding relationship between semantic variables and interval type-2 fuzzy numbers in Table 2, the semantic variables in Tables 6–8 are transformed into corresponding interval type-2 fuzzy numbers. The consistency of the transformed results is checked and calculated by using Eqs. (1)–(4). The calculation results of consistency ratio of indexes at all levels are shown in Table 9.

From the data in Table 9, it can be seen that the CR values of all levels of index comparison matrix of modern photovoltaic agriculture sustainability are less than 0.1, and the judgment matrix meets the calculation requirements, with good consistency.
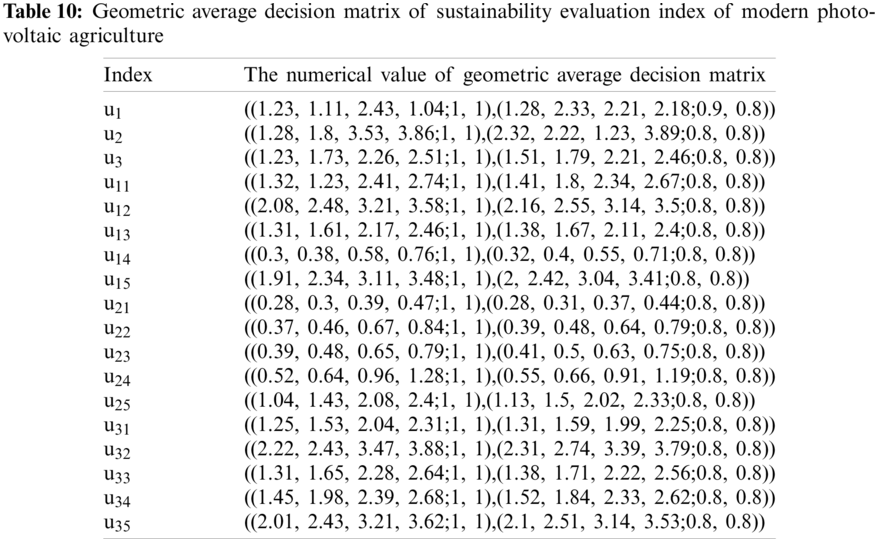
The geometric average decision matrix of sustainability evaluation indexes of modern photovoltaic agriculture is obtained by Eq. (5), and the calculation results are shown in Table 10.
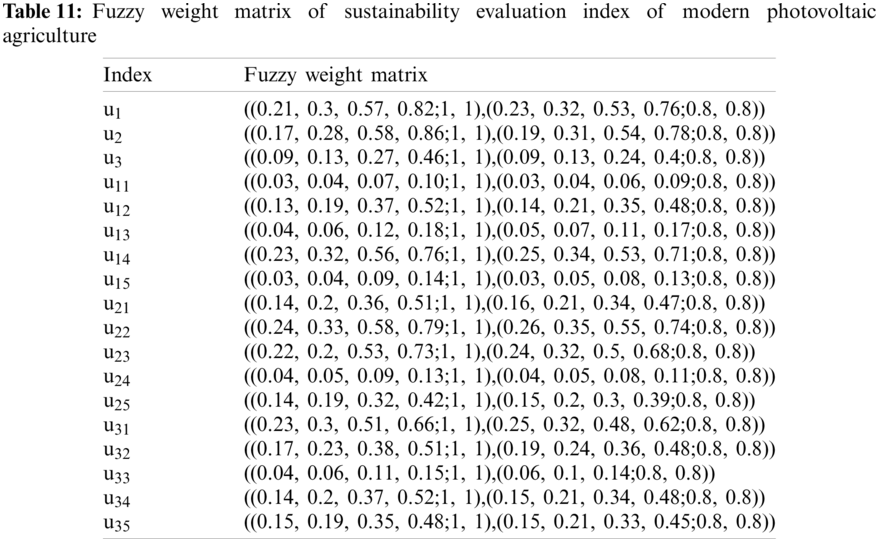
According to the data in Table 10, the fuzzy weight of each index is calculated with Eq. (6), and the calculation results of fuzzy weight matrix of each index are shown in Table 11.
4.3.2 Sustainability Evaluation of Modern Photovoltaic Agriculture Based on Interval Two Type Fuzzy TOPSIS Model
According to the interval type-2 fuzzy TOPSIS model, the positive and negative ideal solutions of interval type-2 fuzzy numbers are calculated, as shown in Table 12.

Combined with the positive and negative ideal solutions, the distance between modern photovoltaic agricultural projects and the positive and negative ideal solutions can be obtained, as shown in Table 13.

Finally, the similarity coefficient of sustainability of each modern photovoltaic agricultural project is calculated. The calculation results are shown in Table 14 and Fig. 2.

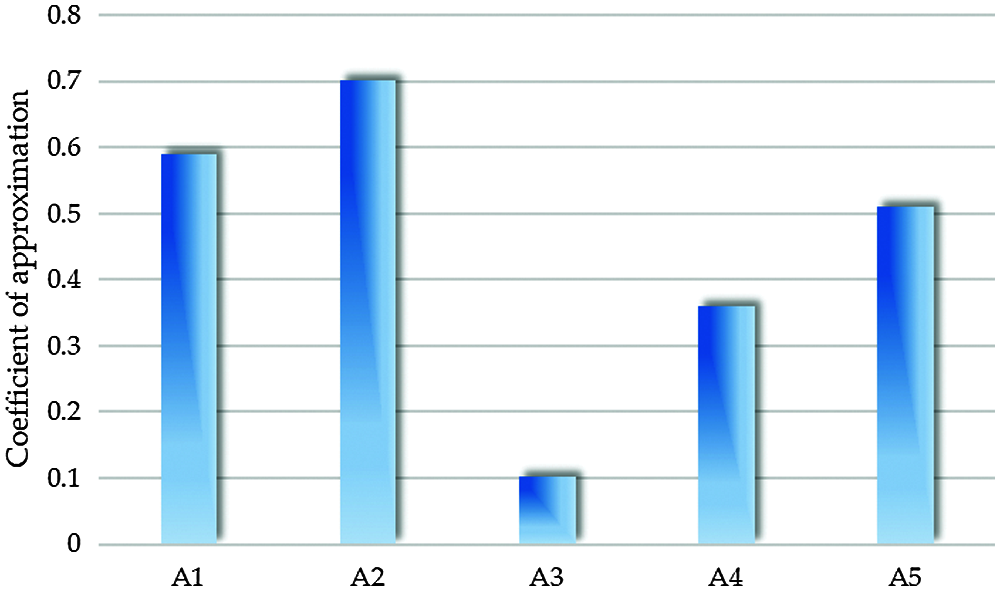
Figure 2: Calculation results
From the sustainability evaluation results, we can see that the order of sustainability of the five modern photovoltaic agricultural projects is as follows: C(A2)>C(A1)>C(A5)>C(A4)>C(A3). It can be concluded that the sustainability evaluation result of modern photovoltaic agricultural project A2 is the best.
4.4 Calculation and Analysis Based on FWA-LSSVM Model
In this paper, the sustainability evaluation model of modern photovoltaic agriculture based on interval type-2 Fuzzy AHP-TOPSIS method is used to get the objective and accurate results of 5 samples of modern photovoltaic agriculture sustainability evaluation. However, according to the above calculation, it can be found that the calculation of the model is more complex, the efficiency is low, and the workload is large. When facing the massive data of modern photovoltaic agriculture projects, this method is bound to be difficult to quickly and effectively calculate the sustainability evaluation results of modern photovoltaic agriculture. Therefore, this paper will further use the FWA-LSSVM model constructed above for research. The other 15 samples are selected as the training set, and the existing 5 samples are used to complete the sustainability evaluation of the modern photovoltaic agriculture. After that, the intelligent evaluation results are compared with the evaluation results in the previous section to verify the effectiveness of the FWA-LSSVM model.
The parameters of FWA are set as follows: the maximum number of iterations
In order to verify the effectiveness of the intelligent evaluation model proposed in this paper, this part continues to use the above 5 photovoltaic agricultural projects for empirical analysis, taking these five photovoltaic agricultural projects as test samples, and selecting another 15 photovoltaic agricultural projects as training samples. FWA-LSSVM, PSO-LSSVM, LSSVM and SVM models are applied to the sustainability evaluation of modern photovoltaic agriculture projects for comparative experiments. The calculation results are shown in Table 15 and Fig. 3.
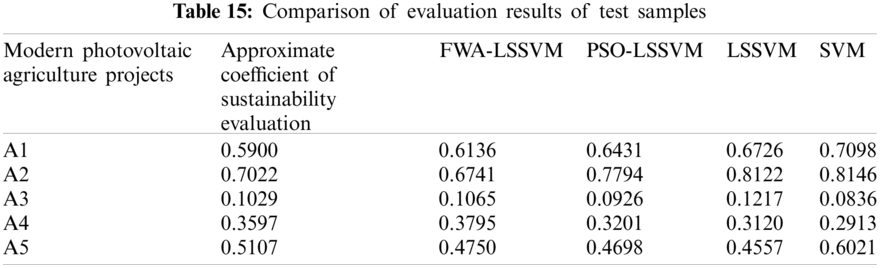
Fig. 3 shows the maximum and minimum relative distances of the intelligent evaluation results. In SVM model, the maximum and minimum relative distances are 0.1198 and 0.0193, respectively; while in LSSVM model, the maximum and minimum relative distances are 0.1100 and 0.0188 respectively. The two distance values of LSSVM are less than that of SVM, which indicates that the evaluation accuracy of LSSVM is higher than that of SVM. In the PSO-LSSVM model, the maximum and minimum relative distances are 0.0772 and 0.0103, respectively. The deviation between the maximum and minimum relative distance is 0.0669, which is smaller than that of LSSVM and SVM, showing that the stability of PSO-LSSVM model is higher than that of LSSVM and SVM. In FWA-LSSVM model, the maximum relative distance is only 0.0357, the minimum relative distance is 0.0036, and the deviation between the maximum and minimum relative distance is only 0.0321. Compared with the other three models, the three values of FWA-LSSVM model are smaller, which shows that the proposed FWA-LSSVM model has higher accuracy and higher stability.
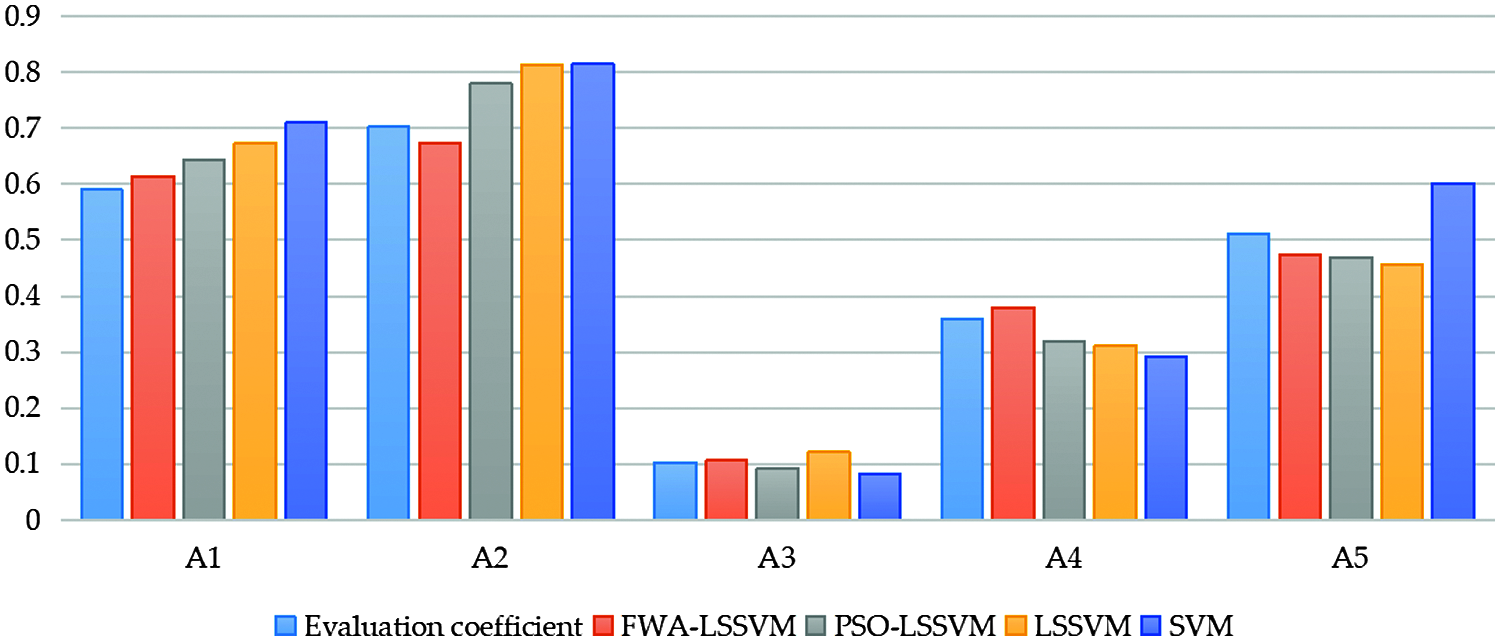
Figure 3: Comparison of evaluation results
Mean absolute percentage error (MAPE), root mean square error (RMSE) and average absolute error (AAE) are used to compare the evaluation errors of each intelligent evaluation model. Fig. 4 shows the MAPE, RMSE, and AAE for each model.
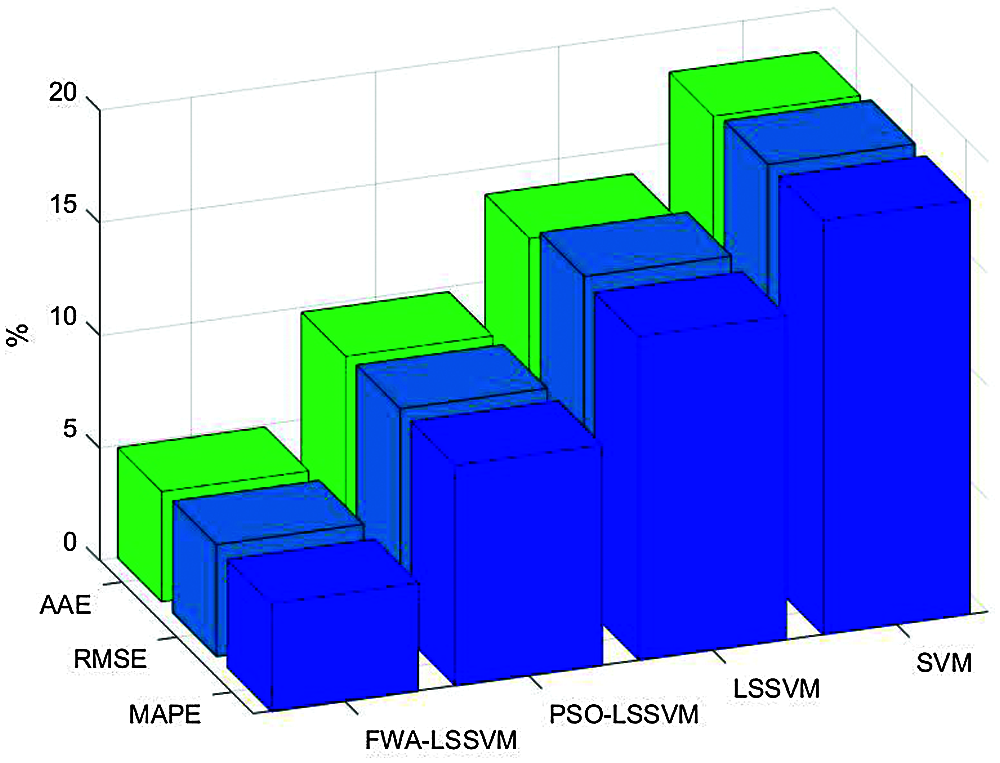
Figure 4: Comparison of the model errors
It can be seen from Fig. 4 that the sustainability evaluation results of modern photovoltaic agriculture calculated by FWA-LSSVM have the highest accuracy, and the MAPE, RMSE and AAE are 4.80%, 4.97% and 4.89%, which are the optimal values. The MAPE, RMSE and AAE of PSO-LSSVM are 9.80%, 9.87% and 9.76%, respectively. The MAPE, RMSE and AAE of standard LSSVM are 14.39%, 14.61% and 13.86%, respectively. The MAPE, RMSE and AAE of standard SVM model are 18.40%, 18.45% and 18.15%, respectively. It shows that the error of the evaluation results of the proposed FWA-LSSVM model is the smallest, and the overall accuracy of the evaluation is the highest. Compared with PSO-LSSVM model, FWA has better optimization performance for LSSVM model. Compared with the original LSSVM model, the generalization ability and classification accuracy can be improved by optimizing the parameters of LSSVM. Compared with SVM model, LSSVM model can use kernel function to transform the prediction problem into the solution of equations and greatly improving the accuracy of evaluation. Overall, the evaluation performance of FWA-LSSVM model is the best.
Therefore, the results of the example analysis show that the proposed FWA-LSSVM model can evaluate the sustainability of modern photovoltaic agriculture scientifically and effectively. On the basis of interval type-2 fuzzy AHP-TOPSIS evaluation method, the intelligent algorithm is introduced, and expert knowledge is obtained by intelligence learning to generalize the expert scoring process in comprehensive evaluation. Then, the sustainable evaluation results of modern photovoltaic agriculture are obtained through FWA-LSSVM model, finally achieve the purpose of fast calculation and supporting relevant decision-making.
The healthy and sustainable development of modern photovoltaic agriculture can reduce the consumption of non-renewable energy in agriculture, improve the utilization rate of renewable energy, and significantly promote the efficiency of agricultural development. In order to realize the healthy and sustainable development of photovoltaic agriculture, this paper designs a set of modern photovoltaic agriculture sustainability evaluation system, mainly including an evaluation index system and a new hybrid evaluation method. Firstly, the evaluation index system of the sustainability of modern photovoltaic agriculture is constructed from three aspects, including technology sustainability, economic sustainability and social sustainability, and it solves the problems in which aspects the sustainability of modern photovoltaic agriculture is mainly reflected. Then, based on the interval type-2 fuzzy AHP-TOPSIS method, the comprehensive evaluation is carried out after the evaluation indexes are scientifically weighted, and the evaluation results are obtained from the perspective of traditional evaluation methods. After that, FWA is chosen to optimize the parameters of LSSVM, and finally the FWA-LSSVM model of modern photovoltaic agriculture sustainability is constructed, and the evaluation results are obtained from the perspective of modern intelligent evaluation method. Through the analysis of an example, the scientificity and accuracy of the evaluation model proposed in this paper are verified. The traditional evaluation model can get accurate results, while the intelligent evaluation model can achieve the purpose of fast calculation and supporting relevant decisions. To sum up, the research conclusions of this paper can provide decision-making support for putting forward a more reasonable development mode for modern photovoltaic agriculture. The application of the model proposed in this paper to other fields is an important direction for future research.
Funding Statement: This work is supported by Humanities and Social Science Research Project of Hebei Education Department, China (No. SD2021044) and Graduate Demonstration Course Construction Project of Hebei Province, China (No. KCJSX2021091).
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
1. Abdel-Basset, M., Mohamed, R., Mirjalili, S., Chakrabortty, R. K., Ryan, M. J. (2020). Solar photovoltaic parameter estimation using an improved equilibrium optimizer. Solar Energy, 209, 694–708. DOI 10.1016/j.solener.2020.09.032. [Google Scholar] [CrossRef]
2. Ke, A., Hf, B., Aw, C., Ab, A., Aa, A. et al. (2020). Performance of photovoltaic canarian greenhouse: A comparison study between summer and winter seasons. Solar Energy, 198, 275–282. DOI 10.1016/j.solener.2020.01.057. [Google Scholar] [CrossRef]
3. Moustafa, K. (2016). Toward future photovoltaic-based agriculture in sea. Trends in Biotechnology, 34(4), 257–259. DOI 10.1016/j.tibtech.2015.12.012. [Google Scholar] [CrossRef]
4. Li, B., Ding, J. D., Wang, J. Q., Zhang, B., Zhang, L. X. (2021). Key factors affecting the adoption willingness, behavior, and willingness-behavior consistency of farmers regarding photovoltaic agriculture in China. Energy Policy, 149, 112101–112112. DOI 10.1016/j.enpol.2020.112101. [Google Scholar] [CrossRef]
5. Yeoh, M. E., Chan, K. Y. (2021). A review on semitransparent solar cells for real-life applications based on dye-sensitized technology. IEEE Journal of Photovoltaics, 11(2), 354–361. DOI 10.1109/JPHOTOV.2020.3047199. [Google Scholar] [CrossRef]
6. Chen, X. R. (2014). Research on photovoltaic inverter system for photovoltaic agriculture. Journal of Chinese Agricultural Mechanization, 35(3), 245–247 + 251. DOI 10.13733/j.jcam.issn.2095-5553.2014.03.060. [Google Scholar] [CrossRef]
7. Yang, C. D., Zhang, H., Li, S., Ren, S. H., Yi, S. J. (2020). Design of small agricultural internet of things power supply system based on solar power generation. Journal of Chinese Agricultural Mechanization, 41(2), 183–189. DOI 10.13733/j.jcam.issn.2095-5553.2020.02.28. [Google Scholar] [CrossRef]
8. Serrano-Baena, M. M., Trivio-Tarradas, P., Ruiz-Díaz, C., Fernández, R. E. H. (2020). Implications of BREEAM sustainability assessment on the design of hotels. Sustainability, 12(16), 6550. DOI 10.3390/su12166550. [Google Scholar] [CrossRef]
9. Borges, L. A., Hammami, F., Wangel, J. (2020). Reviewing neighborhood sustainability assessment tools through critical heritage studies. Sustainability, 12(4), 1605. DOI 10.3390/su12041605. [Google Scholar] [CrossRef]
10. Stylianou, A., Sdrali, D., Apostolopoulos, C. D. (2020). Capturing the diversity of mediterranean farming systems prior to their sustainability assessment: The case of cyprus. Land Use Policy, 96, 104722. DOI 10.1016/j.landusepol.2020.104722. [Google Scholar] [CrossRef]
11. Opon, J., Henry, M. (2020). A multicriteria analytical framework for sustainability evaluation under methodological uncertainties. Environmental Impact Assessment Review, 83, 106403. DOI 10.1016/j.eiar.2020.106403. [Google Scholar] [CrossRef]
12. Li, S. Q., Li, R. R. (2017). Energy sustainability evaluation model based on the matter-element extension method: A case study of Shandong Province, China. Sustainability, 9(11), 2128. DOI 10.3390/su9112128. [Google Scholar] [CrossRef]
13. Mondragon, A., Mastrocinque, E., Tsai, J. F., Hogg, P. J. (2019). An AHP and fuzzy AHP multifactor decision making approach for technology and supplier selection in the high-functionality textile industry. IEEE Transactions on Engineering Management, 1–14. DOI 10.1109/TEM.17. [Google Scholar] [CrossRef]
14. Si, C., Dong, C., Gan, M. (2016). The regional logistics hubs location problem based on the technique for order preference by similarity to an ideal solution and genetic algorithm: A case of Sichuan. Journal of Computational and Theoretical Nanoscience, 13(9), 6065–6075. DOI 10.1166/jctn.2016.5529. [Google Scholar] [CrossRef]
15. Bi, J. W., Liu, Y., Fan, Z. P. (2019). Representing sentiment analysis results of online reviews using interval type-2 fuzzy numbers and its application to product ranking. Information Sciences, 504, 293–307. DOI 10.1016/j.ins.2019.07.025. [Google Scholar] [CrossRef]
16. Hosseini-Pozveh, M. S., Safayani, M., Mirzaei, A. (2020). Interval type-2 fuzzy restricted boltzmann machine. IEEE Transactions on Fuzzy Systems, 99, DOI 10.1109/TFUZZ.91. [Google Scholar] [CrossRef]
17. Yang, Y., Yong, Q., Jia, L., Dong, H. (2017). Traffic safety region estimation based on SFS–PCA–LSSVM: An application to highway crash risk evaluation. International Journal of Software Engineering and Knowledge Engineering, 26(9–10), 1555–1570. DOI 10.1142/S0218194016400179. [Google Scholar] [CrossRef]
18. Zhang, Y., Hu, Z., Ji, L., Sun, N., Lin, Y. (2020). Evaluation model of enterprise operation based on BP neural network optimization algorithm. Journal of Physics: Conference Series, 1570(1), 12084–12091. DOI 10.13766/j.bhsk.1008-2204.2007.03.016. [Google Scholar] [CrossRef]
19. Arong, Murakami, S., Ichikawa, H., Yiliguoqi. (2020). Utilizzation of SVM in the soundness evaluation of reinforced concrete slab bridge. Journal of JSCE, 8(1), 59–70. DOI 10.2208/journalofjsce.8.1_59. [Google Scholar] [CrossRef]
20. Ye, M., Sun, J., Huang, S. (2019). Comprehensive evaluation of cleaner production in thermal power plants based on an improved least squares support vector machine model. Environmental Engineering Research, 24(4), 559–565. DOI 10.4491/eer.2018.344. [Google Scholar] [CrossRef]
21. Song, X., Zhao, J., Song, J., Dong, F., Xu, L. et al. (2020). Local demagnetization fault recognition of permanent magnet synchronous linear motor based on S-transform and PSO–LSSVM. IEEE Transactions on Power Electronics, 35(8), 7816–7825. DOI 10.1109/TPEL.63. [Google Scholar] [CrossRef]
22. Ge, Q., Guo, C., Jiang, H., Lu, Z., Hua, Q. (2020). Industrial power load forecasting method based on reinforcement learning and PSO-lSSVM. IEEE Transactions on Cybernetics, 99, 1–13. DOI 10.1109/TCYB.6221036. [Google Scholar] [CrossRef]
23. Li, J., Zheng, S., Tan, Y. (2017). The effect of information utilization: Introducing a novel guiding spark in the fireworks algorithm. IEEE Transactions on Evolutionary Computation, 21(1), 153–166. DOI 10.1109/TEVC.2016.2589821. [Google Scholar] [CrossRef]
24. Bey, M., Hamidat, A., Benyoucef, B., Nacer, T. (2016). Viability study of the use of grid connected photovoltaic system in agriculture: Case of algerian dairy farms. Renewable & Sustainable Energy Reviews, 63, 333–345. DOI 10.1016/j.rser.2016.05.066. [Google Scholar] [CrossRef]
25. Mostefaoui, Z., Amara, S. (2018). Renewable energy analysis in the agriculture–greenhouse farms: A case study in the mediterranean region (sidi bel abbes, Algeria). Environmental Progress & Sustainable Energy, 38(3), 13029–13037. DOI 10.1002/ep.13029. [Google Scholar] [CrossRef]
26. Kchaou, H., Kechaou, Z., Alimi, A. M. (2021). Interval type-2 fuzzy C-means data placement optimization in scientific cloud workflow applications. Simulation Modelling Practice and Theory, 107, 102217. DOI 10.1016/j.simpat.2020.102217. [Google Scholar] [CrossRef]
27. Alif, A., Arlingga, I. R., Suciati, I. N., Priambodo, B. (2021). Perbandingan penggunaan SAW dan AHP untuk penentuan prioritas maintenance rusunawa depok. Jurnal Sisfokom (Sistem Informasi dan Komputer), 10(1), 10–17. DOI 10.32736/sisfokom.v10i1.942. [Google Scholar] [CrossRef]
28. Bahrami, S., Rastegar, M., Dehghanian, P. (2020). An FBWM-TOPSIS approach to identify critical feeders for reliability centered maintenance in power distribution systems. IEEE Systems Journal, 99, 1–9. DOI 10.1109/JSYST.4267003. [Google Scholar] [CrossRef]
29. Wang, H., Liang, Y., Ding, W., Niu, D., Li, S. et al. (2020). The improved least square support vector machine based on wolf pack algorithm and data inconsistency rate for cost prediction of substation projects. Mathematical Problems in Engineering, 2020(6), 1–14. DOI 10.1155/2020/6663006. [Google Scholar] [CrossRef]
30. Liang, Y., Wang, H., Hong, W. C. (2021). Sustainable development evaluation of innovation and entrepreneurship education of clean energy major in colleges and universities based on SPA-VFS and GRNN optimized by chaos bat algorithm. Sustainability, 13(11), 1–26. DOI 10.3390/su13115960. [Google Scholar] [CrossRef]
31. Li, J., Tan, Y. (2019). A comprehensive review of the fireworks algorithm. ACM Computing Surveys, 52(6), 1–28. DOI 10.1145/3362788. [Google Scholar] [CrossRef]
32. Cheng, R., Bai, Y., Zhao, Y., Tan, X., Xu, T. (2019). Improved fireworks algorithm with information exchange for function optimization. Knowledge-Based Systems, 163(1), 82–90. DOI 10.1016/j.knosys.2018.08.016. [Google Scholar] [CrossRef]
33. Chen, Y., Li, L., Zhao, X., Xiao, J., Wu, Q. et al. (2019). Simplified hybrid fireworks algorithm. Knowledge-Based Systems, 173, 128–139. DOI 10.1016/j.knosys.2019.02.029. [Google Scholar] [CrossRef]
34. Guendouz, M., Amine, A., Hamou, R. M. (2017). A discrete modified fireworks algorithm for community detection in complex networks. Applied Intelligence, 46(2), 373–385. DOI 10.1007/s10489-016-0840-9. [Google Scholar] [CrossRef]
35. Babu, T. S., Ram, J. P., Sangeetha, K., Laudani, A., Rajasekar, N. (2016). Parameter extraction of two diode solar PV model using fireworks algorithm. Solar Energy, 140(15), 265–276. DOI 10.1016/j.solener.2016.10.044. [Google Scholar] [CrossRef]
36. Han, X., Yue, L., Dong, Y., Xu, Q., Xie, G. et al. (2020). Efficient hybrid algorithm based on moth search and fireworks algorithm for solving numerical and constrained engineering optimization problems. The Journal of Supercomputing, 76(12), 9404–9429. DOI 10.1007/s11227-020-03212-2. [Google Scholar] [CrossRef]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |