Energy Engineering

DOI: 10.32604/ee.2022.018160

ARTICLE

Impacts of Rotation on Unsteady Fluid Flow and Energy Distribution through a Bending Duct with Rectangular Cross Section

Mohammad Zohurul Islam1, Rabindra Nath Mondal2 and Suvash C. Saha1,*

1School of Mechanical and Mechatronic Engineering, University of Technology Sydney, Ultimo, NSW 2007, Australia
2Department of Mathematics, Jagannath University, Dhaka, 1100, Bangladesh
*Corresponding Author: Suvash C. Saha. Email: Suvash.Saha@uts.edu.au
Received: 04 July 2021; Accepted: 17 September 2021

Nomenclature

1  Introduction

Rotating flow and consequent heat conduction through the curved duct have been drawn considerable interest to the researchers for their vast applications not only in the field of fluids engineering (cooling and heating systems) and aviation engineering [1] but also in biomedical engineering, for instance, inertial based cell separation [2,3]. In practice, rotating thermal flux frequently occurs in a variety of rotational setups. A wide range of studies [4–8] has been conducted to analyze the flow and heat transfer for the rotational/non-rotating domain.

In a curved duct, centrifugal force is produced due to the duct’s curvature, resulting in a lateral rotating vortex acting in the axial direction. In the bending domain, these vortices have the properties of spiraling motion known as secondary flow [9–12]. These vortices are a pair of additional counter-rotating vortices that form on the duct’s external hollow surface [13–16]. A wide range of theoretical/numerical studies [17–20] and limited experimental [21–23] studies were conducted to analyze the flow characteristics and formation of the Dean vortices for curved ducts. The mismatch of the primary and secondary flows due to the centrifugal and Coriolis forces in the rotational bent duct influences the fluid flow and generates Dean vortices. These outcomes of rolling either increase or decrease in nonlinear mathematical features of flow that rely upon the instability of heat flux and the streaming region. Yanase et al. [24] performed spectral analyhsis of laminar flow through a stationary curved duct over a wide of aspect ratio (1 ≤ l ≤ 12). The investigation was performed to analyse the steady solution with the help of Newton-Rapson method employing symmetry flow condition. They obtained five branches of steady solutions and examined linear stability of the solutions. Chen et al. [25] performed a bifurcation study of the flow passing through a bent tube with increasing Dn and aspect ratio (Ar), where two types of bifurcations depending on the range of Ar were observed. Recently, Hasan et al. [26] applied a spectral-based numerical technique to investigate the critical points considering stationary and non-stationary bent square duct flow. In continuation of this study, very recently, Chanda et al. [27,28] investigated the effects of heat-flux and curvature ratio on fluid flow and thermal distribution in a bent rectangular duct maintaining a temperature difference between the horizontal walls using the method that was used by Islam et al. [29]. The study investigated the flow scenario over a wide range of the curvature (0.001 ≤ δ ≤ 0.5) for both co-rotating and counter-rotation of the system and noticed 2- to 11-pair of vortices. Effects of curvature on secondary vortices were also obtained and displayed in the bar diagrams. Wang et al. [30] demonstrated a bisectional inspection on the flow past in a circular tube, and the study applied a finite volume scheme for flow characterization. Most of the studies, available in literature, have been conducted for small Dean numbers that investigated the flow characteristics and temperature distribution through a bent square or rectangular-shaped duct for small pressure gradient force. However, bifurcation structure as well as flow transition and energy distribution through a bent rectangular duct considering a significant temperature difference between the vertical walls with combined effects of Coriolis and centrifugal forces is less performed, which attracts the authors to fill up this gap.

Time-dependent solution structures of the fully developed flow were investigated first by Yanase et al. [31] for the curved rectangular duct. The study reported the time-dependent results, where both steady and unsteady solutions subsisted together. Very recently, Dolon et al. [32] developed a computational model on curved rectangular duct flow and investigated the combined effects of centrifugal and heating-induced buoyancy instability of the flow where this investigation built up a relationship between the flow velocity and isotherms. Impacts of Dean vortex on overall heat transfer were also shown. Nobari et al. [33] investigated the three-dimensional computational analysis of incompressible real fluid and heat transference through a U-type square channel. The author found that the centrifugal force due to curvature is dominating over coriolis force in bending region, while the opposite results were observed in straight part of the duct. Most of the previous studies focused on rotating geometries with small pressure gradient, and researchers did not give much attention to investigate effect of high Dean number in the steady or transient solution along with the number of secondary near-wall vortices for increasing or decreasing the rotation. The effect of high pressure gradient on fluid flow through a rotating curve rectangular-shaped duct is not considered though it has huge applications in engineering approach. Hence, motivated from these unresolved issues, the present paper investigates fluid characteristics for high pressure gradient with simultaneous change in system rotation and aspect ratio because flow instability and heat transfer enhancement is certainly affected by the high gyration with strong pressure gradient force applied along the centre-line of the duct.

One of the most features of fluid flow over a curved channel is heat conduction between two walls. Dean flow can help to transport energy and consequently increase heat transfer between two side walls. Chandratilleke et al. [34] showed the effect of aspect ratios (starting from 1 to 8) on convective heat transfer through the curved rectangular duct without considering the rotational effects. The authors compared their findings with the experimental study and found good agreement. Mondal et al. [35] performed a non-isothermal analysis for square channels and observed Dean flow to enhance heat conduction. Norouzi et al. [36] investigated the inertial and creeping motion for 2nd-grade fluid to analyze the stress and heat transfer in a curved channel by employing the finite difference scheme. They observed that heat transfer was dominated by the normal stress difference for the viscoelastic fluid. Centrifugal force and curvature of the outlet were yielding the first two regular stress varieties in the flow region.

The hydro-thermal efficiency of coupled rotating cylinders with partially porous system in the bifurcation duct was investigated by Kolsi et al. [37] using the finite element method and hybride nanofluid as the working fluid. They found that the distribution of heat energy of distinct hot wall portions varied depending on the cylinders’ Reynolds number and rotational speed, which intensify the heat transfer nearly 25% compard to non-rotation cylinder. Another study was conducted by Selimefendigil et al. [38] on rotating adiabatic circualr cylinder with the help of Galerkin weighted residual finite element method to understand convective heat trnsfer by CNT-water nanofluid. The numerical findings showed that the rate of heat enhancement of the cylinder was dependent on the rotational speed and nondimentional tarbulance parameter (Richardson number). They also found that the mean heat transfer coefficient was calculated to be low computational cost with higher accuracy compared to high fidelity of 3D intensive CFD calculation.

Alsabery et al. [39] applied FEM and Arbitrary Lagrangian-Eulerian numerical procedure to investigate transient entropy and mixed convection in a cavity with flexible wall. They validated their computational code using the previous data. The results revealed an essential impact of the elastic modulus on the flow and heat transfer in the fluid. Recently, Hasan et al. [40] performed numerical simulation with convective heat transfer through a rotating bent square duct for various curvatures. The authors discussed the steady and unsteady solutions with linear stability and found that secondary flow enhances heat transfer significantly, and the chaotic flow, which occurs at large Dn’s, enhances heat transfer more efficiently than the other unsteady solution. Very recently, Chanda et al. [41] investigated the convective heat transfer and fluid flow, and they clearly showed that the convective heat transfer is significantly enhanced by the secondary flow and the chaotic solutions enhance heat transfer more effectively than the steady-state or even periodic or multi-periodic solutions. As par authors’ knowledge, very little research has been conducted on the time-dependent flow characteristics through a curved channel caused by the development of buoyancy-induced centrifugal-Coriolis instability with rotational effects, and the impact of rotation on convective heat transfer is not much studied. On the other hand, the temperature difference between the walls affects in changing fluid density, which eventually creates buoyancy instability the curved channel. Considering this issue importantly, the present study shows how Dean vortices are produced at the outer concave wall and how it contributes to developing and transferring heat in the bending duct as the system is rotated in the positive direction. The present investigation, therefore, demonstrates to fulfil this research gap on curved channel flows. From the engineering standpoint, it is essential to analyse such type of flows as it is often faced in engineering applications. The present study also reports the transient behaviour of real fluid past a bent rectangular channel having aspect ratios 2 and 3 by employing a numerical algorithm and elucidate an increase of heat flow by the secondary and axial flow distribution.

2  Model Development and Numerical Calculation

In a fixed orthogonal coordinate system, the unsteady flow of an incompressible Newtonian fluid in a curved pipe with fixed curvature is studied. A rectangular shape cross-section is considered, where the height and width are 2h and 2d, respectively, and maintaining the various aspect ratios (l = h/d). The geometry with the corresponding notations has been illustrated in Fig. 1. The coordinates of x′ and y′ axes have been considered the base components and z′ axial flow direction. The whole arrangement revolves at a constant spinning velocity ΩT about the y′ axis. The outer bending wall of the channel is in high temperature (T0+ΔT), while the inner part has kept significantly low temperature (T0−ΔT), where, ΔT > 0. The upper and lower surface of the duct are set adiabatically isolated from other parts of the domain. The fluid flow is invariant along the central line, which is controlled with fixed pressure, as explained in Fig. 1.

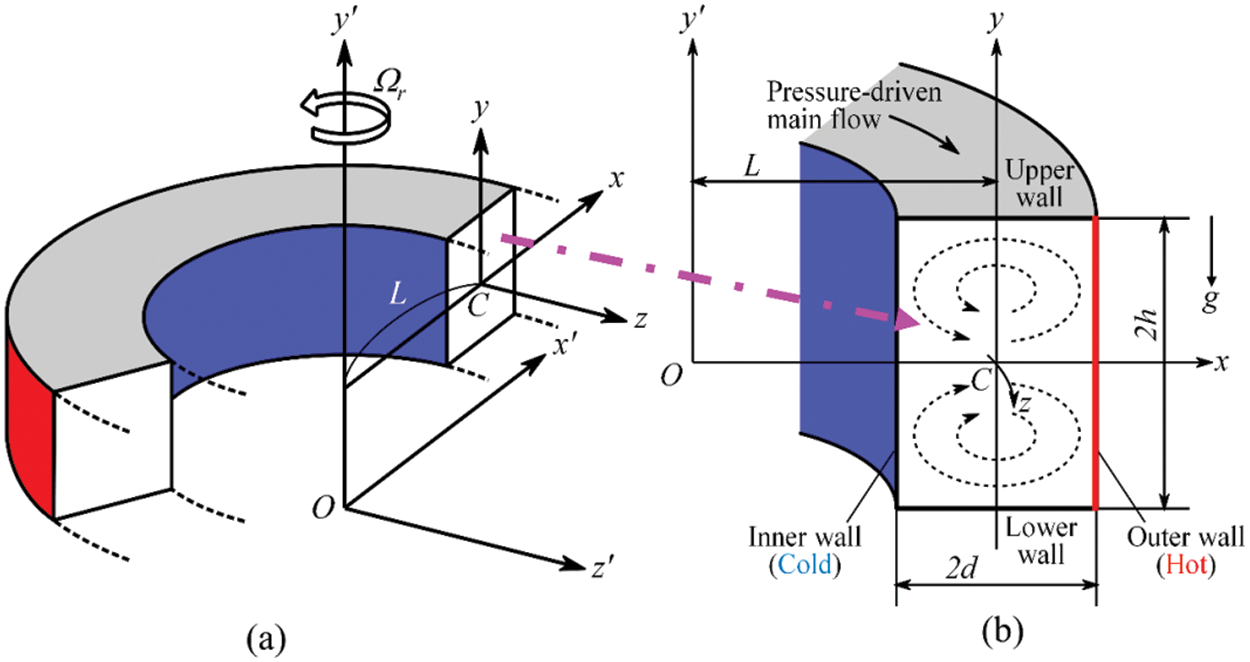
Figure 1: (a) Schematic coordinate system of the model and (b) Cross-sectional view of the duct

All the dimensional quantities are converted into the non-dimensional component by employing the representative length (d), the representative free stream velocity (U0 = υ/d), and representative time (t = d/U0 = d2/υ), where υ is the kinematic viscosity. The velocity vectors (u, v) along horizontal (x), vertical (y) are being dimensionless by U0, and w for axial (z) directions by √(2δ)/U0, where δ = d/L is known as curvature of the curved pipe. The non-dimensional temperature and pressure are obtained from the transformation by T = T/∆T and ρU02 = P/P, respectively. Hereafter, all the variables are dimensionless, if it is not specified. The flow field is taken to be homogeneous along the axial path; the single-stream function ψ is set up along the x and y lines as:

u=11+δx∂ψ∂y,v=−11+δx∂ψ∂x (1)

A unique variable y is then incorporate on the y′ axis as y = ly′, where l = h/d is the aspect ratio of pipe cross section. For the sake of simplicity, from now, y denotes y′. Then, the rudimental mathematical dimensionless expressions for axial velocity (w) and stream function/secondary flow (ψ) are derived from the Navier-Stokes equations and the energy equation take the following form:

(1+δx)∂w∂t=Dn−1l∂(w,ψ)∂(x,y)−δ2w1+δx+(1+δx)Δ2w−1lδ(1+δx)∂ψ∂yw+δ∂w∂x−δTr∂ψ∂y (2)

(Δ2−δ1+δx∂∂x)∂ψ∂t=−1l1(1+δx)∂(Δ2ψ,ψ)∂(x,y)+1lδ(1+δx)2          ×[∂ψ∂y(2Δ2ψ−3δ1+δx∂ψ∂x+∂2ψ∂x2)−∂ψ∂x∂2ψ∂x∂y]+δ(1+δx)2          ×[3δδ2ψ∂x2−3δ21+δx∂ψ∂x]−2δ1+δx∂∂xΔ2ψ+Δ22ψ+1lw∂w∂y          −Gr(1+δx)∂T∂x−12Tr∂ψ∂y, (3)

∂T∂t=1Pr(Δ2T+δ1+δx∂T∂x)−1l(1+δx)∂(T,ψ)∂(x,y) (4)

where,

Δ2≡∂2∂x2+1l2∂2∂y2,∂(p,q)∂(x,y)≡∂p∂x∂q∂y−∂p∂y∂q∂x. (5)

The dimensionless parameters Dn, the Dean number; Tr, the Taylor number; Gr, the Grashof number, and Pr, the Prandtl number, which are contained in Eqs. (2) to (4) are expressed as:

Dn=Gd3μυ2dL,Tr=22δΩTd3υδ,Gr=βgΔTd3υ2,Pr=υκ,d1∗−d2∗/Δz∗=G, (6)

d1∗−d2∗dz∗=λdh∗12ρ⟨w∗⟩2 and λ=8l2δDn(1+l)⟨w⟩2,

where, G be the pressure gradient, μ be the dynamic viscosity, α be the coefficient of thermal diffusivity, β be the coefficient of thermal expansion, g be the acceleration due to gravity, and λ be the resistance coefficient. The flow patterns are monitored with varying the rotational parameter (Tr) for two different aspect ratios (l = 2, 3), and the other flow controlling parameters (Dn = 1500, Gr = 500, δ = 0.1, Pr = 7.0) are kept constant. The given boundary conditions employed in this study for w, ψ and T are illustrated in the following diagram (Fig. 2), where T is considered invariant near the walls.

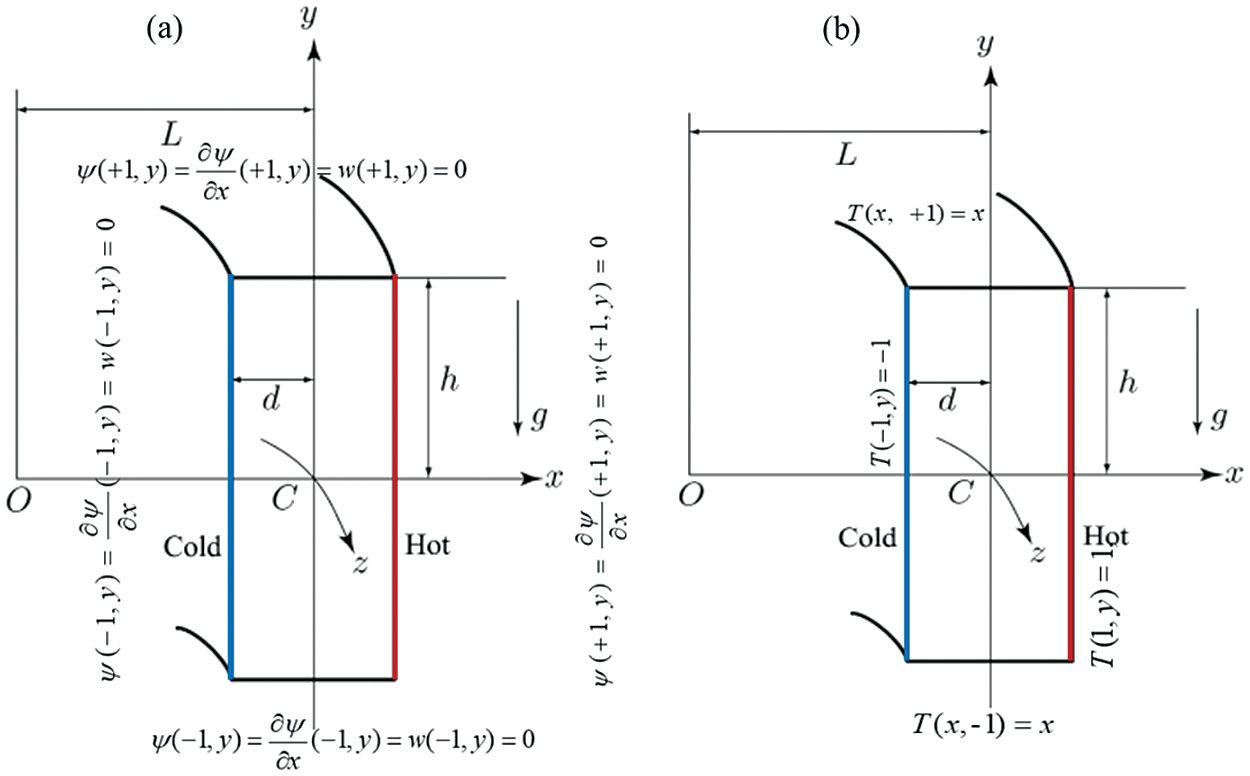
Figure 2: (a) Boundary conditions for axial flow (w) and secondary flow (ψ), and (b) Boundary conditions for temperature (T)

The governing Eqs. (2) to (4) have been solved by using the spectral method with boundary conditions (stated in Fig. 2) numerically. It may consider as a better approach to solve the Navier-Stokes equation together with heat conduction equations (Gottlieb et al. [42] because the variables have presented in a class of functions (Known as Chebyshev polynomials). The functions φn(x) and ψn(x) are expressed as:

ϕn(x)=(1−x2)Tn(x),ψn(x)=(1−x2)2Tn(x)} (7)

where, Tn(x)=cos⁡(ncos−1⁡(x)) is the first kind Chebyshev polynomial of n-th order. Also, w(x,y,t),ψ(x,y,t) and T(x,y,t) are set by using the function ϕn(x) and ψn(x) as:

w(x,y,t)=∑m=0M∑n=0Nwmn(t)ϕm(x)ϕn(y),ψ(x,y,t)=∑m=0M∑n=0Nψmn(t)ψm(x)ψn(y),T(x,y,t)=∑m=0M∑n=0NTmnϕm(x)ϕn(y)+x,} (8)

where M and N are called grid size. The coefficients of wmn,ψmn and Tmn are discarded into Eqs. (2)–(4), and finally, the collocation procedure is employed with the coordinates as given

xi=cos⁡[π(1−iM+2)],yi=cos⁡[π(1−iN+2)] (9)

where i=1,…,M+1 and j=1,…,N+1. The convergence test is confirmed by accepting ∈p<10−10, where p refers to the repetition of the loop and ∈p is defined as:

∈p=∑m=0M∑n=0N[(wmn(p+1)−wmn(p))2+(ψmn(p+1)−ψmn(p))2+(Tmn(p+1)−Tmn(p))2] (10)

For evaluating the time-dependent results, both Crank-Nicolson and Adams-Bashforth schemes with Eq. (4) are then driven.

2.1 Model Validation and Grid Dependency Test

Before starting the investigation, the proposed model was validated comprehensively with published numerical modeling conducted by Mondal et al. [19]. Our model with numerical results are verified as shown in Fig. 3. The code was carefully developed for our model to optimize the flow conditions with geometrical configuration by adjusting the flow controlling parameters. Fig. 3 compares the averased Nu as the function of Dean numner at heated and cooled sidewalls of the channel. The general trend of Nusselt number concerning the corresponding Dean number consistently up surging with minimal fluctuation and agrees with numerical (Mondal et al. [19]) results. At the lower temperature wall, the calculated Nu from both studies show excellent agreement, whereas at high temperature wall, the present model produces lower Nu than Mondal et al. [19] findings but maintain the increasing trend of Nu. This discrepancy maybe for unknown cause of the model as the code was optimize as close as possible with Mondal et al. [19] study, which does not interfare the solution substabtially. For more validation, the present result is compared with Yamamoto et al. [43] and Chandratilleke’s [34] findings, as presented in Fig. 4. The author conducted an assay using the visualization method of flow with a curved rectangular duct for the non-rotation case by keeping l = 2 and considered air as a working fluid to generate the primary flow and smoke as a flow indicator captured as a flow indicator cross-sectional view of Dean vortex patterns. The number of vortices of the numerical finding is the same containing some distorted streamlines. Fig. 4c also displays the non-isothermal laboratory finding (for l = 4) by Chandratilleke et al. [44]. The results of the present simulations are more in line with the laboratory inspection in both quantitative and qualitative manner.

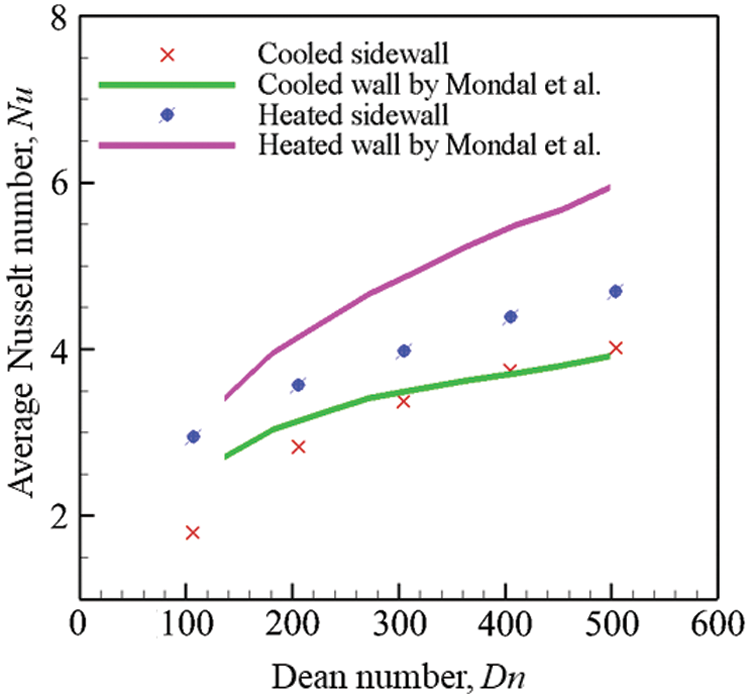
Figure 3: Comparison of averaged Nusselt number as the function Dean number from present study with numerical findings conducted by Mondal et al. [19]

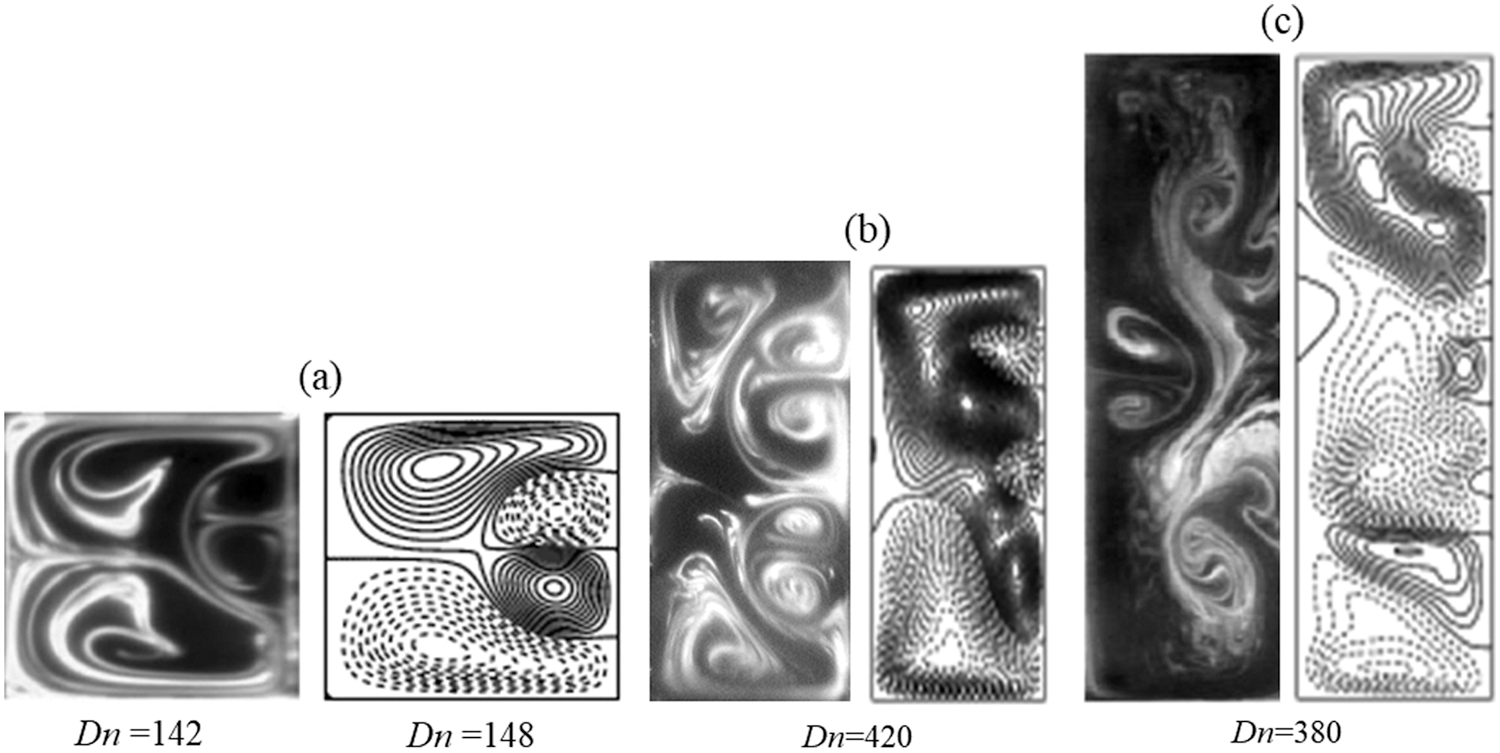
Figure 4: Comparison of secondary flows between experimental (left) and numerical (right) results. (a) Experimental result for rotating bend square duct flow (Tr = 150) by Yamamoto et al. [43] (left), (b) Chandratilleke [34] (left) for aspect ratio, l = 2 and (c) Chandratilleke et al. [44] (left) for aspect ratio, l = 4

The speed of rotation of the duct affects heat transfer through the Nusselt number. In order to measure the effect of rotation on heat generation, the Nusselt number was calculated and compared with the experimental results conducted by Becker et al. [45] and computational findings by Dallil et al. [46], as shown in Fig. 5. As the speed of the rotation of the system increases, the calculated Nusselt number is increasing. The Nusselt number from the present model lies between the experimental and computational results with some discrepancies. The maximum fluctuations were determined 14.63% and 7.32% for experimental and computational results, respectively, that lie in an acceptable range. Based on this comparison, the present model could be considered a well-validated model and could reproduce the best outcomes. After the model validation, the exactness of the numerical solution is tested by employing the grid dependency analysis. To establish the verification of the numerical results, taking N is equal to 2M and 3M for both aspect ratios (l = 2 and 3), respectively. The grid sizes are considered for sufficient accuracy, illustrated in Table 1. As it is observed from Table 1, M = 16 and N = 32 prove adequate validity of the numerical solutions for l = 2, while M = 16 and N = 48 for l = 3.

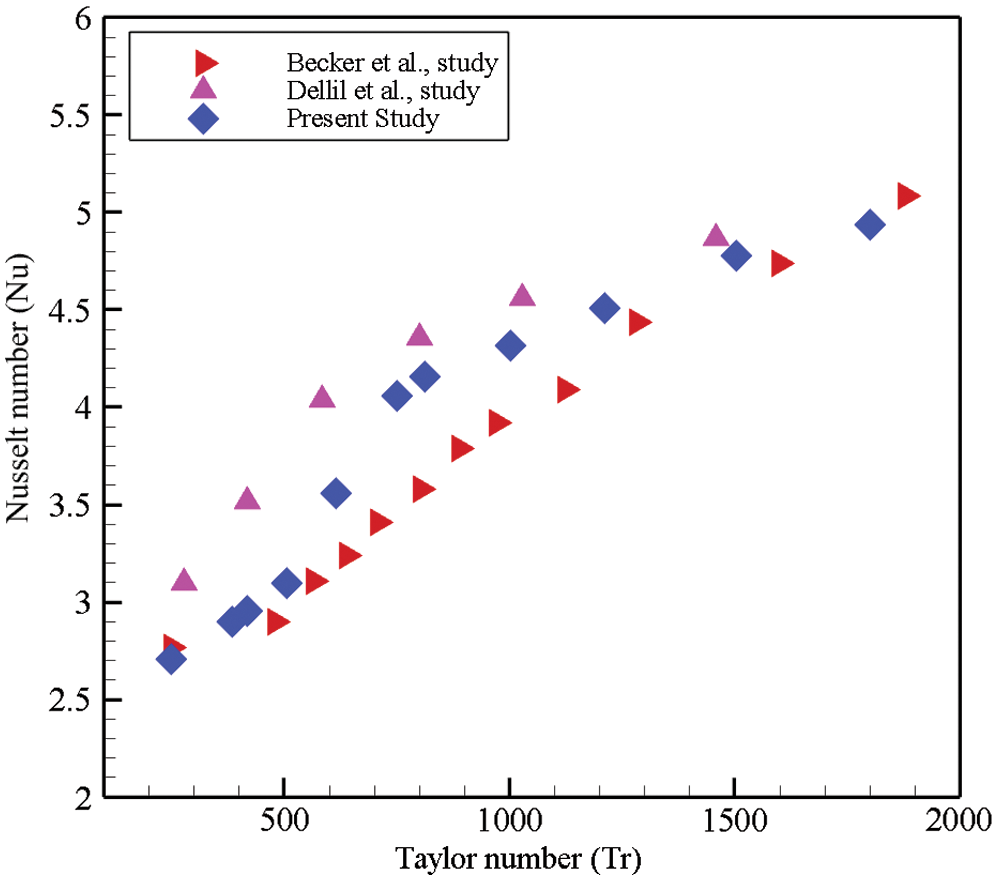
Figure 5: Comparison of Nusselt number as a function of Taylor number from experimental finding by Becker et al. [45] and numerical result by Dallil et al. [46] with the data from the current study

3  Results and Discussion

3.1 Time Evolution Calculation of the Solution

To explore the effect of Tr on the nonlinear behavior of the time-dependent solution, the time evaluation results have been investigated for Dn=1500, and Gr = 500 over a wide range of Tr. Fig. 6 shows the time-dependent solutions for Tr = 100–2000. Time evolution curves (Figs. 6a–6c report an oscillating flow pattern for different rotational values. The calculated value of λ shows a significant difference between Tr = 100 and 1000 (0.15 < λ < 0.30), while λ for other Tr is found almost the same (0.288 < λ < 0.289). Initially, at low rotation (Tr = 100), the time evolution λ shows strongly unstable oscillation, ensuring the high degree of chaotic flow patterns. The chaotic nature of the flow patterns is declining up to Tr < 2000. Once the rotation exceeds a specific value (Tr = 2000), then it turns into multi-periodic/periodic patterns if the Taylor number lies between (2000 < Tr < 2205). The transitional behavior of the flow is investigated to observe flow characteristics more explicitly. Figs. 6d–6e report a strong asymmetrical oscillating mode, which means the flow is strongly turbulent in nature. The flow is analyzed by the phase plot of the calculated data for Tr = 100–2205, as illustrated in Figs. 6d–6h. The phase diagram analyzes the flow on the γ−λ surface where γ=∬ψdxdy. This value is null at the center of the duct. Fig. 7 shows the number of vortices formation and the contour of the axial flow distribution, secondary flows patterns, and isotherms profiles at some of representative Tr for two specific aspect ratios (l = 2, 3). The secondary flows form two opposing re-circulating locations: one is outer flow (clockwise), as indicated by the thick lines, and the other is inner flow (clockwise), as indicated by the scattered lines. These line curves are affected owing to the united operation of the centrifugal, Coriolis, and buoyancy forces. Centrifugal force has formed because of flow over the duct, while Coriolis force is caused for rotation of the channel around the y-direction. The buoyant force is incorporated for the thermal gradient of the curved duct. Imprinting the configuration of secondary flow, isotherms, axial flow distribution, grid size, Δψ = 0.9, ∆T = 0.3, and Δw = 10.0 are considered for this study. The corresponding value of Δψ, ΔT, and Δw are taken the same for all the contours in this analysis or else stated, where solid lines (ψ≥0) exhibit the counter-clockwise direction while dotted lines (ψ<0) indicate the opposite. Fig. 7 also reveals the flow domain that forms a number of vortex flow consisting of large primary vortices. The vortex generation also controls the rate of fluid flow along the radial axis, as seen from the streamline of axial flow distribution (Fig. 8). The number of generated vortices contributes to heat transmission from the hot wall to the cold fluid, which is illustrated by depicting the temperature contours. As seen in the secondary flow patterns, the secondary flow consists of two- or more-vortex solutions which are asymmetric with respect to the horizontal plane y = 0. The reason is that heating the outer wall causes deformation of the secondary flow and yields asymmetry of the flow. With the heating and cooling the sidewalls changes of fluid density that induce thermal convection in the fluid; the resulting flow behavior in the cross section is, therefore, determined by the combined action of the radial flow caused by the centrifugal body force and the convection caused by the buoyancy force due to temperature difference between the walls. This asymmetry of the flow is well discussed in the papers by Yanase et al. [47] and Mondal et al. [35].

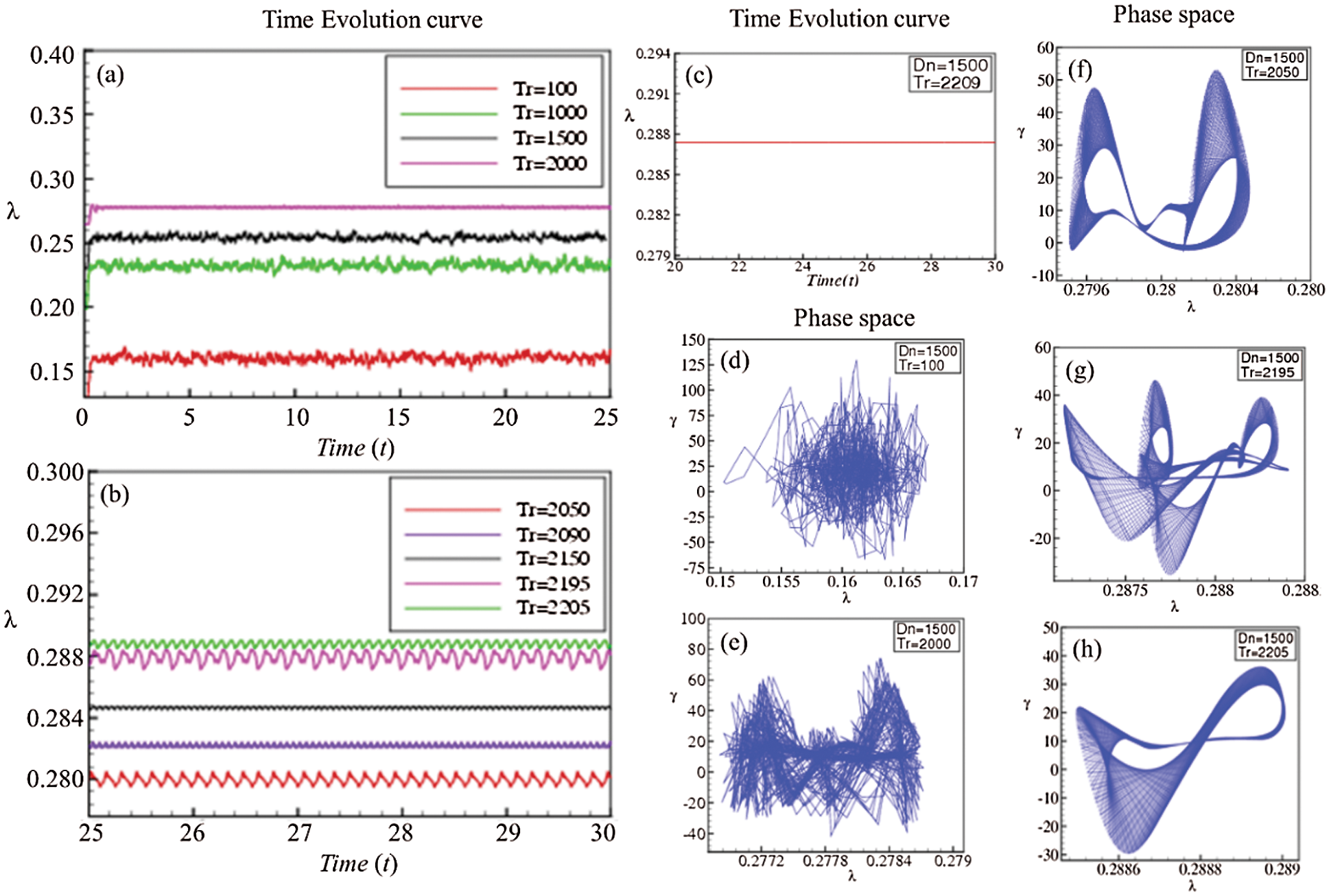
Figure 6: Time-dependent solution at Dn = 1500 for various Taylor number (Tr); time evolution data (a–c) and phase space diagram (d–h) for l = 2

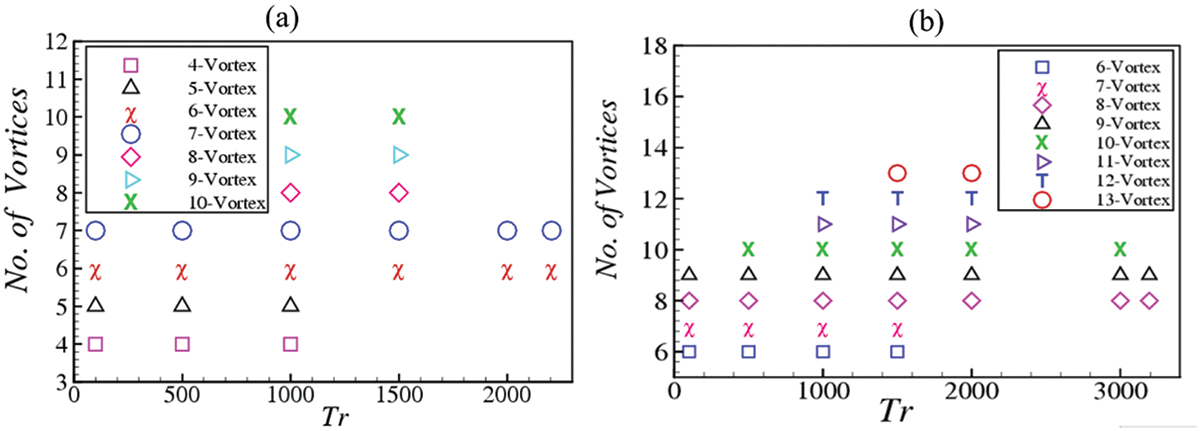
Figure 7: The vortices generation as a function of Taylor number (Tr) at Dn = 1500 and Gr = 500 for (a) aspect ratio l = 2 and (b) aspect ratio l = 3

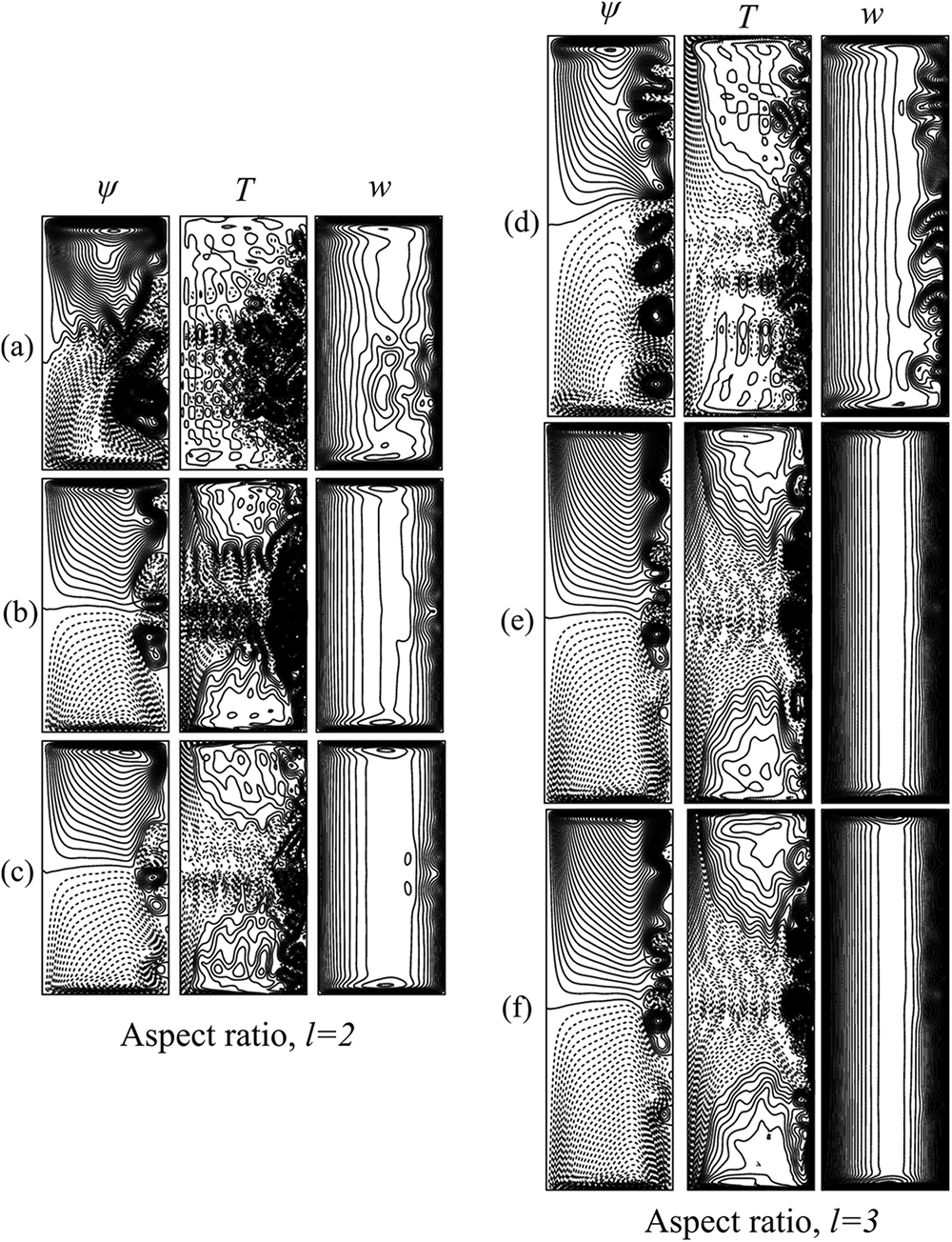
Figure 8: Secondary vortex structure for various Tr at Dn = 1500 and Gr = 500. The contours are displayed for (a, d) chaotic solution (Tr = 1000 for aspect ratios 2 and 3), (b, e) Periodic or multi-periodic solution (Tr = 2050 for l = 2 and Tr = 3150 for l = 3) and (c, f) steady solution (Tr = 2209 for l = 2 and Tr = 3195 for l = 3)

After a certain rotational speed, the time evolution curve will shift into the periodic or multi-periodic oscillating flow. The flow patterns are irregular in shape, while the oscillation and amplitude of the oscillation are lower than low rotational speed (Tr = 100). So before shifting into a periodic or multi-periodic flow, the time evolution curve does not follow any patterns, which reveals that the flow is transient chaos. The phase space diagram indicates the flow beats are still distorted, and it confirms that the flow is indeed the prediction for Tr = 2000. The orbit of the oscillation is going to become a shape like multi-periodic or periodic oscillation as Tr becomes larger. The time-dependent solution forms a patchy five-vortex configuration, where isotherms are consistent with the vortex structure. The formation of an extra pair of vortices is primarily separated from the flow in a duct having slight curvature; at low Dn, the flow patterns make two large counter-rotating primary structures. This configuration constructs on account of the composition of all the forces introduced by the curvature of the duct and thermal gradient. The isotherm lines are denser at a low Taylor number, and gradually these patterns are declining with the increase of rotation. The stratification of the isotherm is affected by other forces, but the rotation effects are partially acted on the isotherm line. As a result, the core region of vortices is seen unstably stratified. For the dominance of Coriolis force, the isotherm lines are denser curved, implying more heat flux is produced in that region. Additionally, flow is also dominated by centrifugal force, and a pressure gradient is constructed along the radial direction of the flow passage. These centrifugal body forces also induce outer directional fluid velocity that acts against radial pressure gradient towards the heated wall of the curved duct. The interaction between the centrifugal force and the pressure gradient that makes fluid mixing with the axial flow triggers the spiral fluid motion as a basis of Dean vortices. These vortices can be observed as a giant pair counter-rotating regime with some smaller extra pairs of vortices. Most of these secondary vortices are formed at the heated wall for increasing flow rate with some critical values of flow condition. The present study shows that as Tr is increased, the Coriolis force becomes strong which dominates the centrifugal force and consequently the steady-state flow turns into chaos via periodic and multi-periodic flows with large windows of quasi-periodic oscillations. In this study, it is observed that if Tr is increased, an alternating occurrence of the oscillating and chaotic nature is perceived. This chaotic nature is well determined by obtaining phase space of the transient solution in Figs. 6d and 6e. The occurrence of the chaotic state, as justified by the phase spaces in the present study, may suggest that the Ruelle-Takens [48] mechanism plausibly works for the existence of chaos in the present system. The transition to chaos of the periodic oscillation may correspond to destabilization of the traveling waves in the bending duct like that of Tollmien-Schlichting waves in a boundary layer. It is, therefore, suggested that occurrence of the chaotic nature in the present study is related with destabilization of the periodic or quasi-periodic solutions, which reminds us the case of Lorenz attractor [49].

3.2 Heat Transfer Through Vortex Generation

Nusselt number (Nu) is considered as the ratio of convective to conductive heat transfer across the boundary of the channel wall. It mainly describes the heat transfer in the boundary surface within the domain. Mathematically it can be written as Nu=hLk where h is the heat transfer coefficient, L is the characteristic length, and k is the thermal conductivity of the fluid. In the present study, the average Nusselt number is utilizing as an index of heat transfer along the horizontal direction of the domain. The average Nusselt number can be estimated by the expression Nu¯=−d′ΔT′(∂T′∂x′)x=0, here the prime sign indicates the dimensional quantity and x is the distance from the wall of the duct. In this regard, the Nusselt number is altered in the cooling and heating sidewalls of the channel. In this study, for the unsteady solutions, we define the Nusselt number for the cooled (Nuc) and heated (Nuh) walls as follows:

Nuτc=12∫−11⟨⟨∂T∂x|x=−1⟩⟩dy,Nuτh=12∫−11⟨⟨∂T∂x|x=1⟩⟩dy (11)

where ⟨⟨⟩⟩ denotes an average over a time interval τ. If the flow field is periodic, τ is usually taken as one period, and if it is aperiodic i.e., chaotic, τ is chosen as an appropriate time interval. If the flow field is not steady, time-average of Nu is calculated to understand the enhancement of heat transfer from the heated wall to the fluid. For the precise understanding of the transfer, the mean Nusselt number for both heating (Nu¯h) as well as cooling (Nu¯c) sidewalls are calculated instead of the local Nusselt number. Time-average of the Nusselt number for unsteady flow field can be evaluated from the following equations for both sidewalls as:

Nu¯h=12∫−11∂T∂x|x=+1dy (12)

Nu¯c=12∫−11∂T∂x|x=−1dy (13)

Note that, if the fluid free-stream temperature and the wall-surface temperature vary, a thermal boundary layer develops near the vicinity of the wall and due to the energy exchange resulting from the temperature variation between the walls, a temperature profile is formed. As a temperature difference between the outer and inner walls is applied, a thermal boundary layer is developed for both heated and cooled walls, which contributes to the characterise the flow nature. To measure such nature of the unsteady fluid flow for the steaming motion in the bending channel Eqs. (12) and (13) are employed.

The calculated values of the time-averaged Nusselt number (Nu) are plotted in Fig. 9 for aspect ratios 2 and 3 (l = 2, 3) and time evolution calculation of inner and outer bend of the duct at several magnitudes of the rotational parameter (Tr) has been considered to find the time-averaged of Nu. The Nusselt number at different rotational parameters (Tr) has been illustrated. The symbol indicated by a circle (red color) demonstrates the index of heat conduction along the heated sidewall, whereas the symbol with the circle (blue color) reveals the rate of heat transfer in the cooled bending wall at aspect ratio 2. The calculated Nu for both heated and cooled surfaces shows almost the same trend that describes the increasing hot wall energy shifting rate increases gradually. For the outer bending wall, Nu has been found ranging 2.92 ≤ Nu ≤ 3.28 within the flow domain, whereas for the inner wall, the value is observed for 1.63 ≤ Nu ≤ 1.98 at l = 2. On the other hand, for aspect ratio 3 (l = 3), the heated wall Nu has been noticed ranging 2.58 ≤ Nu ≤ 3.76 but for the cooled wall 1.54 ≤ Nu ≤ 1.95. The overall scenario is that the low aspect ratio dominates heat generation over large aspect ratio for all Tr at the cooled sidewall and for Tr ≤ 1000 at the heated wall. In contrast, the opposite effect is observed if rotational speed exceeds (Tr ≥ 1000) for the heated sidewall. It is found that the unsteady flow is periodic/multi-periodic for 2000 ≤ Tr ≤ 2205 when l = 2 and in 3100 ≤ Tr ≤ 3195 when l = 3; chaotic for 0 ≤ Tr < 2200 for l = 2 and in 0 ≤ Tr < 3100 for l = 3. Yanase et al. [47] and Mondal et al. [35] showed that periodic/multi-periodic and chaotic solution enhances heat transfer most effectively where Nu is higher, and this happens for l = 2 in the present case for Tr ≤ 1000. Actually, Nu is higher as Tr becomes large (Tr > 1000) for aspect ratio 3 than aspect ratio 2. The most significant findings are the gradual increase of Nu at the low and the high-temperature walls. The upsurge of this temperature is occurred because of the effect of the rotational parameter to maintain the constant heat flux (for cooling wall Qc = 671.23 Wm-2 and for heating wall Qh = 819.74 Wm-2). It is also mentioned that the variation of viscosity at the cooling bending wall is dampening the secondary flow and the vortex construction due to the energy gradient between these two side walls. Along the vertical centerline, the temperature management of fluid contributes to altering the density of the fluid due to the heated wall, and the fluid gets accelerated to travel. Consequently, heat is transferred to the low-temperature region. The rate of temperature distribution on the flow domain is analyzed to get a clear insight about the advection of the curved channel, as presented in Fig. 8. The inner bend's heat flux is lower than the outer bending wall, which validates our computational results. In order to isolate this effect, the temperature gradients at both the colled and heated sidewalls have been analyzed that has been discussed explicitly in the next section.

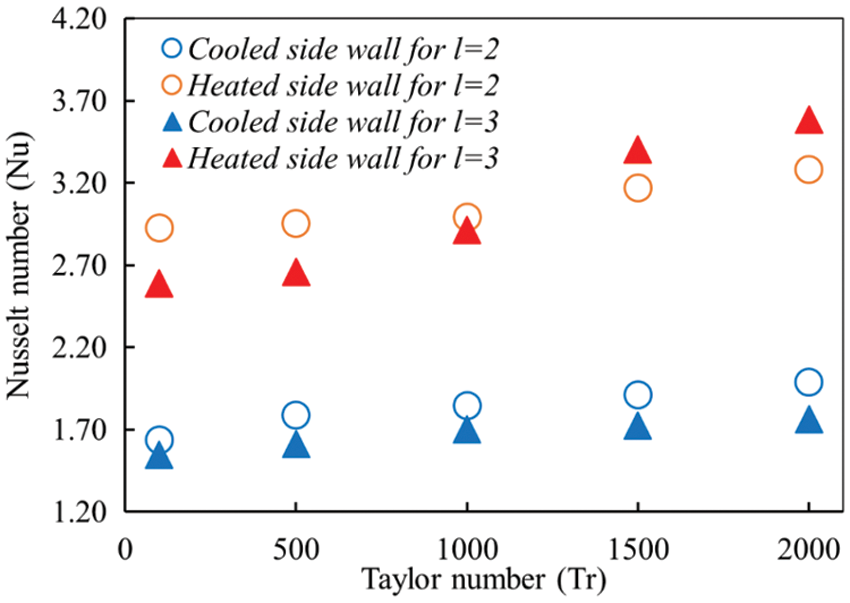
Figure 9: Variation of time average Nusselt at the inner and the outer bending walls of the channel concerning the Taylor number at aspect ratio l = 2, 3

3.3 Temperature Gradient Analysis

The temperature distribution of the outer and inner walls has been analyzed by calculating the temperature gradient of the flow domain (see Fig. 10) along the vertical axis. Convective heat flux at heating and the cooling walls illustrate various rotating speeds at the channel aspect ratio l = 2 and 3. The general trend of the temperature gradient (dTdx) is in a decreasing manner, and it reaches lowest at the central region around the line y = 0 of the duct. But the other areas are observed in the opposite scenario. The main reason for such characteristics of the fluid is the effects of centrifugal force as well as the advection of the Dean vortices on the wall. The variation of the revolving speed of the channel, the heating wall shows higher temperature distribution compared with the cooling side. The maximum value of the dTdx reaches at Tr =0, which is nearly 4 units for a low-temperature wall, but for a higher temperature wall, it crosses 5 units at Tr = 1300. It is concluded that the outer bending wall dominates the distribution of vertical temperature gradient. The Dean flow can promote to uplift the heat transfer in curved rectangular ducts due to the Dean drag force. The addition of temperature at two bending sides of the channel and the rotational effect on the fluid enhance fluid mixing. As a result, a maximum number of secondary vortices produce and improve heat transfer to a great extent. As seen in Fig. 10, the temperature gradient shows more heat generation rate for the large aspect ratio l = 3 compared with l = 2, keeping the same decreasing trend of temperature gradient curves for both the walls. It is observed that increasing the number of vortices play an important role in fluid mixing as well as the enhancement of heat transfer in the fluid.

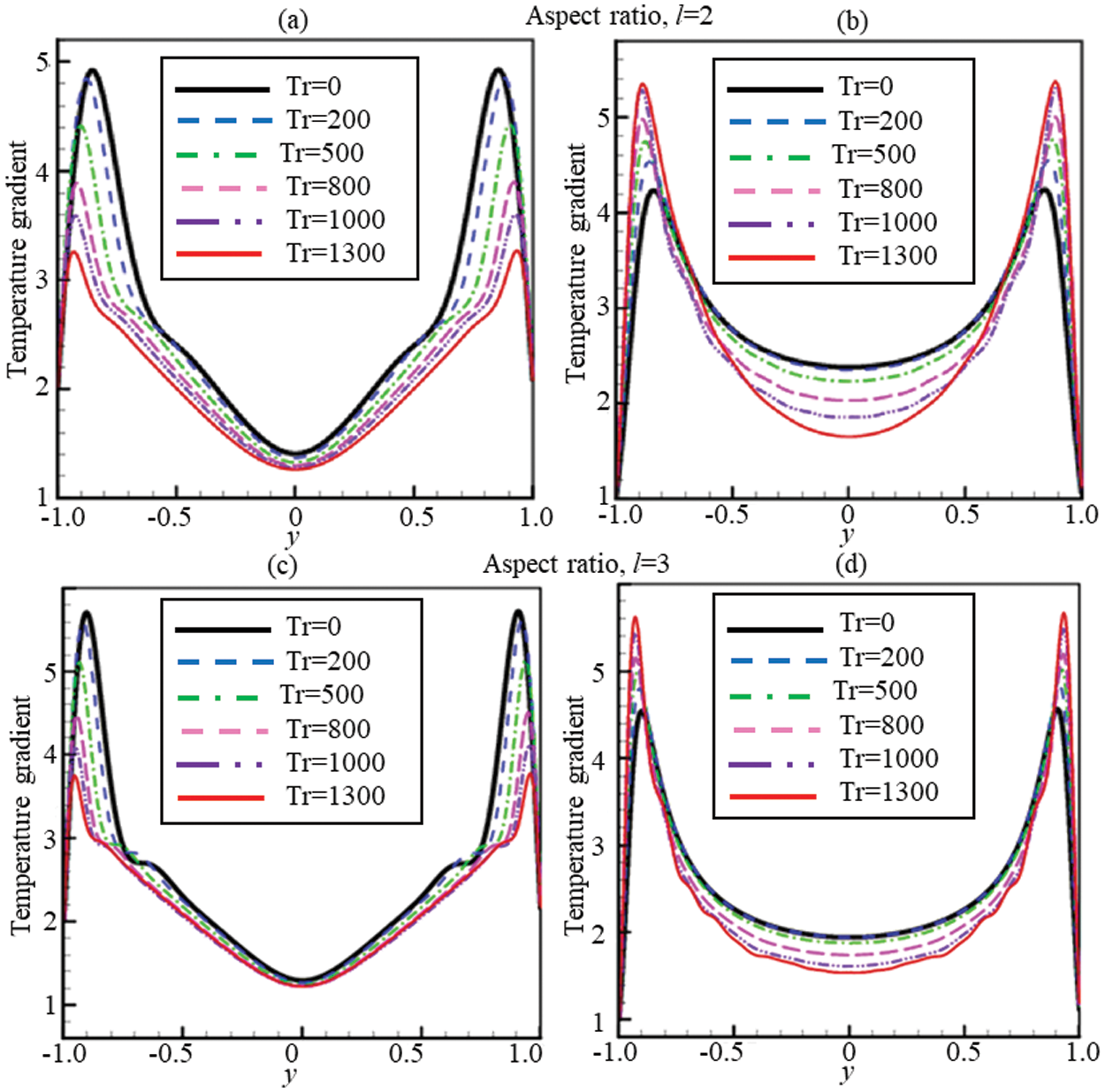
Figure 10: Temperature gradients (TG) for 0 ≤ Tr ≤ 1300 at Dn = 1500 and Gr = 500. (a) TG for l = 2 at the cooled wall (b) TG for l = 2 at the heated wall. (c) TG for l = 3 at the cooled wall (d) TG for l = 3 at the heated wall

4  Conclusion

The present computational study has been performed to characterize fluid flow and energy distribution through a rotating bent rectangular channel of aspect ratio 2 and 3. The effect of rotational parameters on fluid flow for a constant pressure gradient is investigated by analysing Dean-vortex formation, temperature contour, and axial flow distribution for low to high-speed of rotation. The numerical code has been developed to optimize the present model by validating existing experimental and computational studies, and found excellent agreement. The overall calculation is performed for a variable wall temperature, and an adiabatic condition is employed at the upper and the lower walls of the bending channel. The following conclusions have been drawn from the present study:

•   Time-dependent solutions followed by phase-space analysis of the solutions exhibit that the transitient flow endures in the scenario ‘chaotic→ multi-periodic→ periodic→ steady-state’ if the rotational speed is increased in the positive direction.

•   The numerical results report that maximum 10-vortex solution is attained for aspect ratio 2, while 13-vortex for aspect ratio 3. The study shows that 6- to 10-vortex solutions are available for the periodic solution, while 5- to 13-vortex for the chaotic solution. The chaotic regime of the flow exhibits maximum number of Dean vortices.

•   The study illustrates that higher temperature difference occurs for lower Tr, while lower temperature difference for higher Tr.

•   Gradual increase of the Nusselt number at the high and low temperatured walls happens because of the effect of Coriolis force to maintain the constant heat flux into the computational domain.

•   The current study shows that there arises a strong interaction between the heating-induced buoyancy force and the centrifugal-Coriolis instability in the rotating bending channel that stimulates fluid mixing and thus increases heat transfer in the fluid.

The present study investigates effects of various forces, e.g., heating-indiced buoyancy force, curvature-induced centrifugal force, and rotation-induced Coriolis force, on fluid flow and energy distribution in the rotating bent duct, which will improve the understanding of the transitional behavior and temperature distribution for real-life problems. The study may be helpful in solving various industry problems including microchannel and microfluidics flow in a serpentine or spiral model and in heat exchangers. Due to increasing applications in engineering and energy-related fields, the authors plan to study MHD and nanofluid flow in a bent channel in future by CFD.

Acknowledgement: The authors would like to thank Dr. Saidul Islam, Scholarly Teaching Fellow, University of Technology Sydney, for his contribution to formatting the manuscript.

Funding Statement: The authors received no specific funding for this study.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  Fu, Y., Xu, G., Wen, J., Huang, H. (2018). Thermal oxidation coking of aviation kerosene RP-3 at supercritical pressure in helical tubes. Applied Thermal Engineering, 128(2), 1186–1195. DOI 10.1016/j.applthermaleng.2017.09.101. [Google Scholar] [CrossRef]

 2.  di Carlo, D. (2009). Inertial microfluidics. Lab on a Chip, 9(21), 3038–3046. DOI 10.1039/b912547g. [Google Scholar] [CrossRef]

 3.  Martel, J. M., Toner, M. (2013). Particle focusing in curved microfluidic channels. Scientific Reports, 3(1), 1–8. DOI 10.1038/srep03340. [Google Scholar] [CrossRef]

 4.  Chatterjee, S., Sugilal, G., Prabhu, S. (2018). Heat transfer in a partially filled rotating pipe with single phase flow. International Journal of Thermal Sciences, 125(1), 132–141. DOI 10.1016/j.ijthermalsci.2017.11.024. [Google Scholar] [CrossRef]

 5.  Du, W., Luo, L., Wang, S., Liu, J., Sunden, B. (2019). Heat transfer and flow structure in a rotating duct with detached pin fins. Numerical Heat Transfer, Part A: Applications, 75(4), 217–241. DOI 10.1080/10407782.2019.1580957. [Google Scholar] [CrossRef]

 6.  Gong, K., Cao, Y., Feng, Y., Zhang, Y., Qin, J. (2021). Flow and mass transfer of pyrolytic aviation kerosene in curved channel. Journal of Thermophysics and Heat Transfer, 35(1), 53–62. DOI 10.2514/1.T5941. [Google Scholar] [CrossRef]

 7.  Hasan, M. S., Rashid, S., Dolon, S. N., Chanda, R. K., Islam, M. M. et al. (2021). Investigation on energy distribution in steady and unsteady flow instabilities through a bend square pipe. Reports in Mechanical Engineering, 2(1), 86–104. DOI 10.31181/rme200102086h. [Google Scholar] [CrossRef]

 8.  Rigo, L., Biau, D., Gloerfelt, X. (2021). Flow in a weakly curved square duct: Assessment and extension of Dean's model. Physical Review Fluids, 6(2), 024101. DOI 10.1103/PhysRevFluids.6.024101. [Google Scholar] [CrossRef]

 9.  Cheng, K., Lin, R. C., Ou, J. W. (1976). Fully developed laminar flow in curved rectangular channels. Journal of Fluids Engineering, 75, 41–48. DOI 10.1115/1.3448205. [Google Scholar] [CrossRef]

10. Lupi, V., Canton, J., Schlatter, P. (2020). Global stability analysis of a 90°-bend pipe flow. International Journal of Heat and Fluid Flow, 86, 108742. DOI 10.1016/j.ijheatfluidflow.2020.108742. [Google Scholar] [CrossRef]

11. Sun, X., Wang, S., Zhao, M. (2021). Viscoelastic flow in a curved duct with rectangular cross section over a wide range of Dean number. Physics of Fluids, 33(3), 033101. DOI 10.1063/5.0035002. [Google Scholar] [CrossRef]

12. Vinuesa, R., Schlatter, P., Nagib, H. (2018). Secondary flow in turbulent ducts with increasing aspect ratio. Physical Review Fluids, 3(5), 054606. DOI 10.1103/PhysRevFluids.3.054606. [Google Scholar] [CrossRef]

13. Ajgoun, S., Naciri, J. K., Khatyr, R. (2020). Dean vortex for laminar flows in curved pipes with various cross-sections. Journal of Advanced Research in Fluid Mechanics and Thermal Sciences, 79(1), 111–127. DOI 10.37934/arfmts.79.1.111127. [Google Scholar] [CrossRef]

14. Dean, W. R. (1927). XVI. Note on the motion of fluid in a curved pipe. London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science, 4(20), 208–223. DOI 10.1080/14786440708564324. [Google Scholar] [CrossRef]

15. Ligrani, P., Niver, R. (1988). Flow visualization of Dean vortices in a curved channel with 40 to 1 aspect ratio. Physics of Fluids, 31(12), 3605–3617. DOI 10.1063/1.866877. [Google Scholar] [CrossRef]

16. Moyers-Gonzalez, M., Frigaard, I. A. (2020). Dean flow of a Bingham fluid in a curved rectangular duct. Journal of Non-Newtonian Fluid Mechanics, 286, 104440. DOI 10.1016/j.jnnfm.2020.104440. [Google Scholar] [CrossRef]

17. Bhuyan, D., Giri, A. (2021). Heat transfer and second law analysis of turbulent flow mixed convection condensation inside a vertical channel. International Journal of Heat and Mass Transfer, 165(19), 120658. DOI 10.1016/j.ijheatmasstransfer.2020.120658. [Google Scholar] [CrossRef]

18. Mondal, R. N., Islam, S., Uddin, K., Hossain, A. (2013). Effects of aspect ratio on unsteady solutions through curved duct flow. Applied Mathematics and Mechanics, 34(9), 1107–1122. DOI 10.1007/s10483-013-1731-8. [Google Scholar] [CrossRef]

19. Mondal, R. N., Watanabe, T., Hossain, M. A., Yanase, S. (2017). Vortex-structure and unsteady solutions with convective heat transfer through a curved duct. Journal of Thermophysics and Heat Transfer, 31(1), 243–254. DOI 10.2514/1.T4913. [Google Scholar] [CrossRef]

20. Zhang, J., Zhang, B., Jü, J. (2001). Fluid flow in a rotating curved rectangular duct. International Journal of Heat and Fluid Flow, 22(6), 583–592. DOI 10.1016/S0142-727X(01)00126-6. [Google Scholar] [CrossRef]

21. Chandratilleke, T. (1998). Performance enhancement of a heat exchanger using secondary flow effects. Proceedings of 2nd Pacific-Asia Conference on Mechanical Engineering, Manila, Philippines. [Google Scholar]

22. Chandratilleke, T. (2001). Secondary flow characteristics and convective heat transfer in a curved rectangular duct with external heating. 5th World Conference on Experimental Heat Transfer, Fluid Mechanics and Thermodynamics, Thessaloniki, Greece. [Google Scholar]

23. Huang, C. N., Kharangate, C. R. (2020). Consolidated model for predicting flow boiling critical heat flux in single-sided and double-sided heated rectangular channels. International Journal of Heat and Mass Transfer, 160, 120132. DOI 10.1016/j.ijheatmasstransfer.2020.120132. [Google Scholar] [CrossRef]

24. Yanase, S., Kaga, Y., Daikai, R. (2002). Laminar flows through a curved rectangular duct over a wide range of the aspect ratio. Fluid Dynamics Research, 31(3), 151–183. DOI 10.1016/S0169-5983(02)00103-X. [Google Scholar] [CrossRef]

25. Chen, K., Yarn, K., Chen, H., Tsai, C., Luo, W. et al. (2017). Aspect ratio effect on laminar flow bifurcations in a curved rectangular tube driven by pressure gradients. Journal of Mechanics, 33(6), 831–840. DOI 10.1017/jmech.2017.93. [Google Scholar] [CrossRef]

26. Hasan, M. S., Mondal, R. N., Lorenzini, G. (2020). Physics of bifurcation of the flow and heat transfer through a curved duct with natural and forced convection. Chinese Journal of Physics, 67(3), 428–457. DOI 10.1016/j.cjph.2020.07.004. [Google Scholar] [CrossRef]

27. Chanda, R., Hasan, M., Lorenzini, G., Mondal, R. (2021). Effects of rotation and curvature ratio on fluid flow and energy distribution through a rotating curved rectangular channel. Journal of Engineering Thermophysics, 30(2), 243–269. DOI 10.1134/S1810232821020089. [Google Scholar] [CrossRef]

28. Chanda, R. K., Hasan, M. S., Alam, M. M., Mondal, R. N. (2021). Taylor-heat flux effect on fluid flow and heat transfer in a curved rectangular duct with rotation. International Journal of Applied and Computational Mathematics, 7(4), 1–31. DOI 10.1007/s40819-021-00986-8. [Google Scholar] [CrossRef]

29. Islam, M. Z., Mondal, R. N., Rashidi, M. (2017). Dean-Taylor flow with convective heat transfer through a coiled duct. Computers & Fluids, 149(6), 41–55. DOI 10.1016/j.compfluid.2017.03.001. [Google Scholar] [CrossRef]

30. Wang, L., Cheng, K. (1996). Flow transitions and combined free and forced convective heat transfer in rotating curved channels: The case of positive rotation. Physics of Fluids, 8(6), 1553–1573. DOI 10.1063/1.868930. [Google Scholar] [CrossRef]

31. Yanase, S., Nishiyama, K. (1988). On the bifurcation of laminar flows through a curved rectangular tube. Journal of the Physical Society of Japan, 57(11), 3790–3795. DOI 10.1143/JPSJ.57.3790. [Google Scholar] [CrossRef]

32. Dolon, S. N., Hasan, M. S., Lorenzini, G., Mondal, R. N. (2021). A computational modeling on transient heat and fluid flow through a curved duct of large aspect ratio with centrifugal instability. European Physical Journal Plus, 136(4), 1–27. DOI 10.1140/epjp/s13360-021-01331-0. [Google Scholar] [CrossRef]

33. Nobari, M., Nousha, A., Damangir, E. (2009). A numerical investigation of flow and heat transfer in rotating U-shaped square ducts. International Journal of Thermal Sciences, 48(3), 590–601. DOI 10.1016/j.ijthermalsci.2008.04.001. [Google Scholar] [CrossRef]

34. Chandratilleke, T. T. (2003). Numerical prediction of secondary flow and convective heat transfer in externally heated curved rectangular ducts. International Journal of Thermal Sciences, 42(2), 187–198. DOI 10.1016/S1290-0729(02)00018-2. [Google Scholar] [CrossRef]

35. Mondal, R. N., Kaga, Y., Hyakutake, T., Yanase, S. (2006). Effects of curvature and convective heat transfer in curved square duct flows. Journal of Fluids Engineering, 128(5), 1013–1022. DOI 10.1115/1.2236131. [Google Scholar] [CrossRef]

36. Norouzi, M., Kayhani, M., Shu, C., Nobari, M. (2010). Flow of second-order fluid in a curved duct with square cross-section. Journal of Non-Newtonian Fluid Mechanics, 165(7–8), 323–339. DOI 10.1016/j.jnnfm.2010.01.007. [Google Scholar] [CrossRef]

37. Kolsi, L., Selimefendigil, F., Öztop, H. F., Hassen, W., Aich, W. (2021). Impacts of double rotating cylinders on the forced convection of hybrid nanofluid in a bifurcating channel with partly porous layers. Case Studies in Thermal Engineering, 26, 101020. DOI 10.1016/j.csite.2021.101020. [Google Scholar] [CrossRef]

38. Selimefendigil, F., Öztop, H. F. (2019). Conjugate mixed convection of nanofluid in a cubic enclosure separated with a conductive plate and having an inner rotating cylinder. International Journal of Heat and Mass Transfer, 139, 1000–1017. DOI 10.1016/j.ijheatmasstransfer.2019.05.053. [Google Scholar] [CrossRef]

39. Alsabery, A., Selimefendigil, F., Hashim, I., Chamkha, A., Ghalambaz, M. (2019). Fluid-structure interaction analysis of entropy generation and mixed convection inside a cavity with flexible right wall and heated rotating cylinder. International Journal of Heat and Mass Transfer, 140, 331–345. DOI 10.1016/j.ijheatmasstransfer.2019.06.003. [Google Scholar] [CrossRef]

40. Hasan, M., Mondal, R., Lorenzini, G. (2019). Centrifugal instability with convective heat transfer through a tightly coiled square duct. Mathematical Modelling of Engineering Problems, 6(3), 397–408. DOI 10.18280/mmep.060311. [Google Scholar] [CrossRef]

41. Chanda, R. K., Hasan, M. S., Alam, M. M., Mondal, R. N. (2020). Hydrothermal behavior of transient fluid flow and heat transfer through a rotating curved rectangular duct with natural and forced convection. Mathematical Modelling of Engineering Problems, 7(4), 501–514. DOI 10.18280/mmep.070401. [Google Scholar] [CrossRef]

42. Gottlieb, D., Orszag, S. A. (1977). Numerical analysis of spectral methods: Theory and applications. In: Society for industrial and applied mathematics. USA. DOI 10.1137/1.9781611970425. [Google Scholar] [CrossRef]

43. Yamamoto, K., Wu, X., Nozaki, K., Hayamizu, Y. (2006). Visualization of Taylor-Dean flow in a curved duct of square cross-section. Fluid Dynamics Research, 38(1), 1–18. DOI 10.1016/j.fluiddyn.2005.09.002. [Google Scholar] [CrossRef]

44. Chandratilleke, T. T., Nadim, N., Narayanaswamy, R. (2012). Vortex structure-based analysis of laminar flow behaviour and thermal characteristics in curved ducts. International Journal of Thermal Sciences, 59(1), 75–86. DOI 10.1016/j.ijthermalsci.2012.04.014. [Google Scholar] [CrossRef]

45. Becker, K. M., Kaye, J. (1962). Measurements of diabatic flow in an annulus with an inner rotating cylinder. ASME Journal of Heat Transfer, 84(2), 97–104. DOI 10.1115/1.3684335. [Google Scholar] [CrossRef]

46. Dellil, A., Azzi, A. (2013). Numerical investigation of the transfer heat in a annulus cylindrical space. Mechanics, 19(1), 25–32. DOI 10.5755/j01.mech.19.1.3613. [Google Scholar] [CrossRef]

47. Yanase, S., Mondal, R., Kaga, Y. (2005). Numerical study of non-isothermal flow with convective heat transfer in a curved rectangular duct. International Journal of Thermal Sciences, 44(11), 1047–1060. DOI 10.1016/j.ijthermalsci.2005.03.013. [Google Scholar] [CrossRef]

48. Ruelle, D., Takens, F. (1971). On the nature of turbulence. Communications in Mathematical Physics, 23(4), 343–344. DOI 10.1007/BF01893621. [Google Scholar] [CrossRef]

49. Lorenz, E. N. (1963). Deterministic nonperiodic flow. Journal of Atmospheric Sciences, 20(2), 130–141. DOI 10.1175/1520-0469(1963)020<0130:DNF>2.0.CO;2. [Google Scholar] [CrossRef]

This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.