

 | Energy Engineering |  |
DOI: 10.32604/ee.2022.019646
ARTICLE
Kalman-Filtering-Based Frequency Control Strategy Considering Electrolytic Aluminum Load
Marketing Service Center, State Grid Jiangsu Electric Power Co., Ltd., Nanjing, 210004, China
*Corresponding Author: Shihai Yang. Email: ysh.young@163.com
Received: 05 October 2021; Accepted: 27 October 2021
Abstract: Traditional thermal power units are continuously replaced by renewable energies, of which fluctuations and intermittence impose pressure on the frequency stability of the power system. Electrolytic aluminum load (EAL) accounts for large amount of the local electric loads in some areas. The participation of EAL in local frequency control has huge application prospects. However, the controller design of EAL is difficult due to the measurement noise of the system frequency and the nonlinear dynamics of the EAL’s electric power consumption. Focusing on this problem, this paper proposes a control strategy for EAL to participate in the frequency control. For the controller design of the EAL system, the system frequency response model is established and the EAL transfer function model is developed based on the equivalent circuit of EAL. For the problem of load-side frequency measurement error, the frequency estimation method based on Kalman-filtering is designed. To improve the performance of EAL in the frequency control, a fuzzy EAL controller is designed. The testing examples show that the designed Kalman-filter has good performance in de-noising the measured frequency, and the designed fuzzy controller has better performance in stabilizing system frequency than traditional methods.
Keywords: Electrolytic aluminum load; kalman-filtering; frequency control
With the increased renewable energy sources such as wind power and photovoltaic connected to the power grid, the active power balance of the power system is facing huge challenges. On the one hand, as renewable energy replaces traditional thermal power units, the proportion of traditional power generation in the total power generation capacity continuously declines, resulting in a decline in the system's active power regulation capability. On the other hand, due to the strong fluctuations of renewable energy sources, it causes disturbances to the system. The problem of active power imbalance caused by the penetration of renewable energy is reflected in the anti-peaking characteristics of power in a longer time scale, and reflected in the frequency stability problem in a short time scale. Since frequency reflects the active power balance, when the power balance is affected, the frequency will increase or decrease.
As a method to stabilize the power fluctuation of renewable energy, demand response (DR) has received more and more attention. DR supports active power balance by adjusting the power consumption on the demand side [1,2]. DR cannot only reduce the peak-to-valley difference by peak load shifting [3], but also participate in system frequency control by rapidly adjusting the power consumption [4]. It is reported that smart home appliances can flexibly respond to the needs of the power grid through the Internet of Things technology [5], and many research works are published. In [6], a demand response control strategy of the aggregated inverter ACs for load reduction is proposed. The inverter AC is modeled based on virtual energy storage system (VESS), based on which the temperature holding strategy is designed to reduce the electric power of an AC. In [7], an electric water heater control strategy is proposed based on the dynamic programming and load profile classification, which allows recognizing the the highest power consumption contributors during the peak periods. In [8], scalable demand response strategy for domestic hot water heaters is proposed. The strategy is based on reinforcement learning and is tested by hardware-in-loop experiments.
Beside smart home appliances, electrolytic aluminum load (EAL) plays an important role in DR. On the one hand, as a typical high energy-consuming industrial load, electrolytic aluminum occupies a large proportion of the regional electricity loads and has a large regulating capacity [9,10]. On the other hand, the EAL can be controlled by saturable reactor or terminal voltage to realize flexible power adjustment, and the response of EAL is very fast [11,12]. The EAL participating in frequency control can greatly improve the frequency stability of the power system.
Focusing on the EAL participating in frequency control, scholars have carried out a lot of researches. To improve frequency stability in an isolated system, the authors in [13] proposed a demand-side frequency control scheme. In [14], to improve load frequency control performance of EAL, an integrated control strategy is proposed. The authors in [15,16] focus on isolated power systems with high penetration of wind power, and a frequency control method is proposed in [15] in order to eliminate the power imbalance. The authors in [17] proposed a hierarchical control architecture and consider the anode effect in EAL. In [18], the dynamic characteristics of the EAL based on a field experiment data are modeled. To improve the frequency stability, a load-damping characteristic control scheme which based on the characteristic of EAL is proposed in [19].
Although a large number of theoretical results have been obtained, the above-mentioned literatures do not consider the process of frequency estimation. As a frequency control method on the demand side, the power system frequency is difficult to obtain like the generator side by measuring the speed of the generator rotor. However, measuring the frequency by DR faces the measurement noise problems caused by the electromagnetic transient process. In addition, the above control strategies are mostly PID-based control strategies [13,14,16,17]. Due to the non-linear characteristics of EAL, the PID control strategy is difficult to obtain satisfactory results in some cases.
To fill this gap, this paper proposes the Kalman-filtering-based frequency control strategy for the EAL. The system and measurement noise are greatly reduced through Kalman-filtering. By designing the fuzzy control strategy, the performance of frequency control by EAL is improved.
The remainder of this paper is organized as follows. In Section 2, system modeling is described. In Section 3, Kalman-Filtering-based EAL control method is presented. In Section 4, simulation results are carried out to verify the proposed method. Conclusions are drawn in Section 5.
In this subsection, the controllable EAL model is developed and the system frequency response model considering EAL is established.
2.1 Modeling of the Controllable EAL
The equivalent circuit of EAL is shown in Fig. 1 [14]. The DC-side components of EAL are the combination of back electromotive force E and resistance REAL.
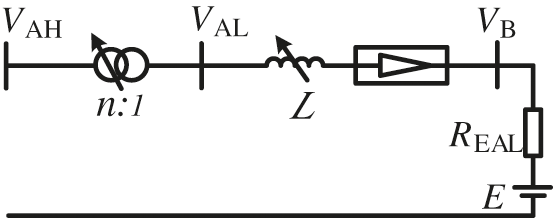
Figure 1: The equivalent circuit diagram of EAL
where VAH and VAL are the high-voltage and low-voltage side of the load bus, n represents the ratio of the aluminum plant transformer and L is the saturated reactor inductance value.
The EAL power consumption PEAL can be expressed by Eq. (1):
It can be seen that the power consumption PEAL can be controlled by the DC-side voltage VB. REAL and E represent the internal resistant and the heat effect during the process of EAL smelting. During transients, they are assumed as constants. At the same time, the main rectifier circuit is diode-based full bridges, which is uncontrollable. Therefore, saturable reactor L is the only controllable component for DC-side voltage VB. In Fig. 1, the saturable reactor is represented as a controllable inductance, and its value can be controlled by adjusting the control winding current.
Based on the EAL steady flow control system, the EAL can be modelled as a transfer function, which reflects the relationship between the reference control signal and the actual power output, and can be formulated by:
where a and b are coefficients of the transfer function. Eq. (2) can be transformed into the equivalent form:
Eq. (3) describes the dynamic characteristics of the EAL.
2.2 The Frequency Response Model
Based on the EAL model represented by (3), the system frequency response model considering EAL can be derived. Fig. 2 shows the diagram of power system frequency response model considering EAL. The parameters are defined as following:
Δf System frequency deviation
Ki Integral gain of the secondary frequency control
s The Laplace operator
R Speed droop parameter
Tg Speed governor time constant
ΔY Valve/gate position deviation
PSP Power set-point of secondary frequency control
ΔPr Deviation of the reheated turbines’ thermal power
ΔPm Deviation of the generators’ mechanical power
ΔPd Disturbance power. Negative indicating load decreasing, while positive indicating load increasing.
ΔPEAL Deviation of EAL power
FHP Fraction of the high pressure turbine section
Tr Reheat time constant
Tt Turbine time constant
H Inertia of the Generators
D Load-damping factor
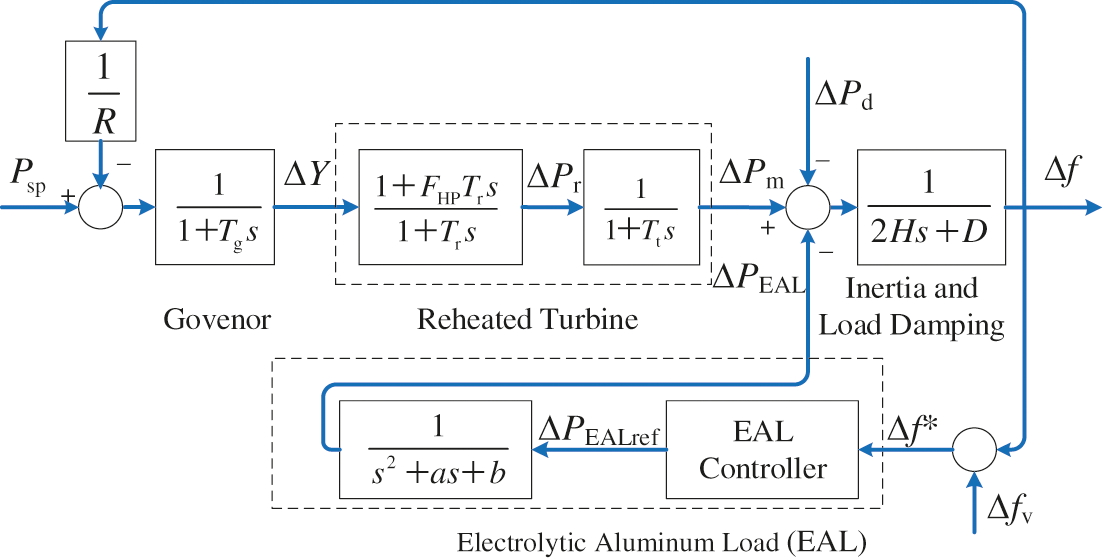
Figure 2: System Frequency response model considering EAL
The system dynamics can be described by a set of differential equations, which are listed as following:
By some calculation, the above frequency response model can be transformed into the following state-space form:
where X is the state vector, Y is the observation vector, U is the control vector, D is the disturbance vector, W and V are system noise and measurement noise, respectively. Matrix A, B, C and R are coefficient matrixes. The vectors and matrixes are derived as following:
To utilize Kalman-filtering method to (10), the continuous state-space function needs to be transformed into discrete form. The discrete form of matrix A, B, C and R can be derived by the following calculation:
And the discrete state-space function can be finally obtained:
where Xk, Yk, Uk, Wk and Vk are discrete form of X, Y, U, W and V.
3 Kalman-Filtering-Based EAL Control Method
In this subsection, the EAL control method is designed. Firstly, the framework of the proposed method is given, and then the components of the method is introduced in detail.
3.1 The Framework of the Control Method
The framework of the control method is shown in Fig. 3. The EAL controller consists of Kalman-filter and EAL fuzzy controller. The measured system frequency Δf* contains measurement noises, which is filtered by the Kalman-filter. The output of the Kalman-filter is the estimated system frequency fest. which is input to the EAL fuzzy controller. After calculating by the EAL fuzzy controller, the control output ΔPEALref is obtained, and delivered to the EAL.
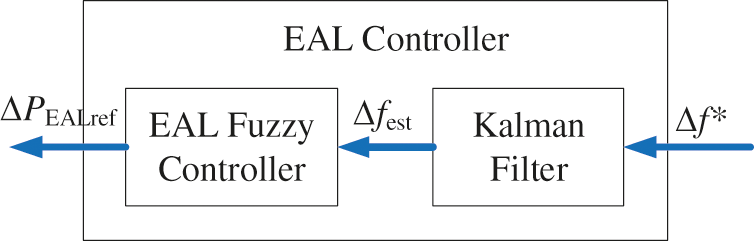
Figure 3: The diagram of the fuzzy controller
The details Kalman-filter and the EAL fuzzy controller are presented as following.
Kalman-filtering can be used to cope with control problem such as the measurement errors, when the discrete form of the system state space equation is known [20].
Kalman-filtering method can be divided into two process including prediction process and correction process. The prediction is to estimate the current state based on the state at the previous moment, while correction is to integrate the estimated state and the observed state at the current moment to estimate the optimal state. The whole process can be summarized as following:
where
The EAL Fuzzy controller is adopted herein to control the power consumption of the EAL. The estimated frequency deviation Δfest and the integral of the estimated frequency deviation Iinteg are selected as the input of the fuzzy controller, and ΔPEALref is defined as the output of the fuzzy controller. The diagram of the fuzzy controller is shown in Fig. 4.
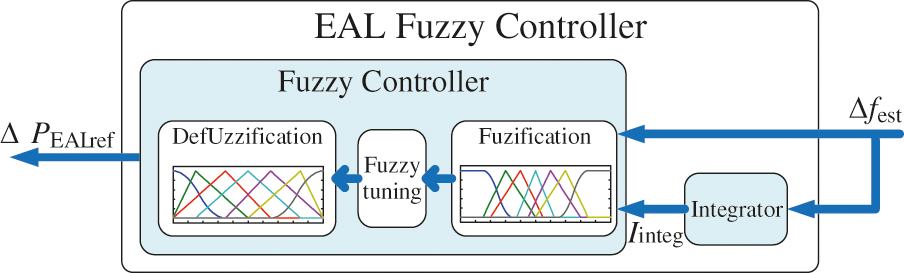
Figure 4: The diagram of the fuzzy controller
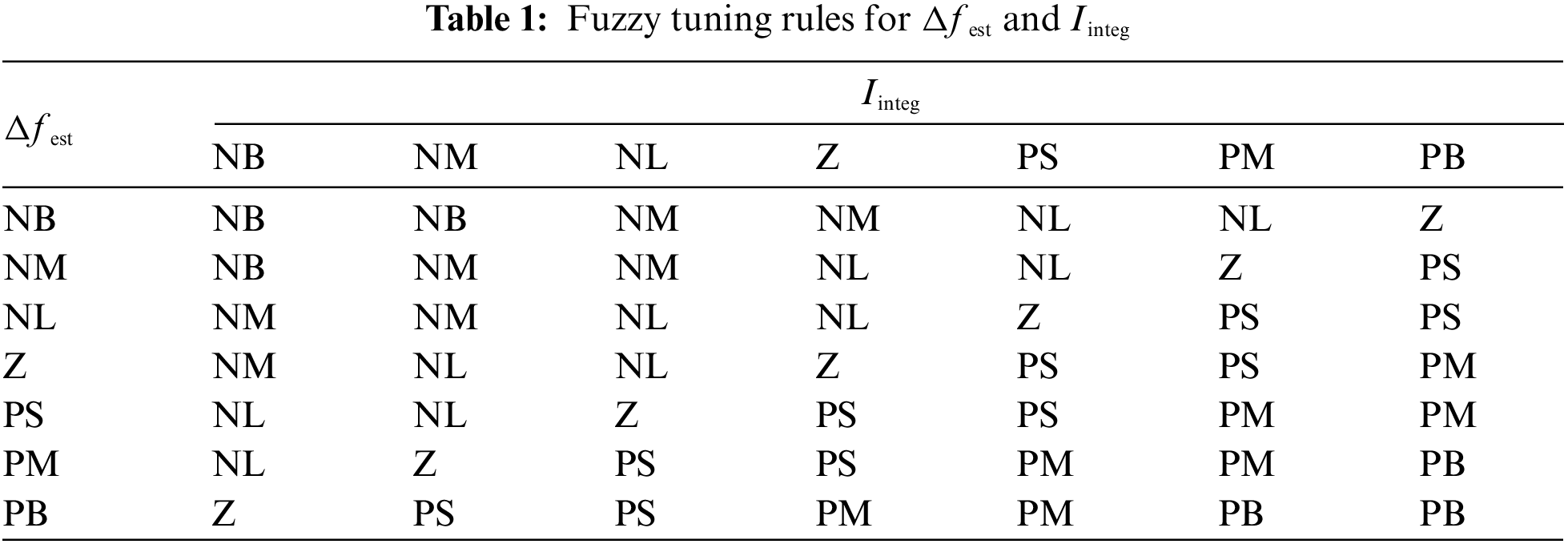
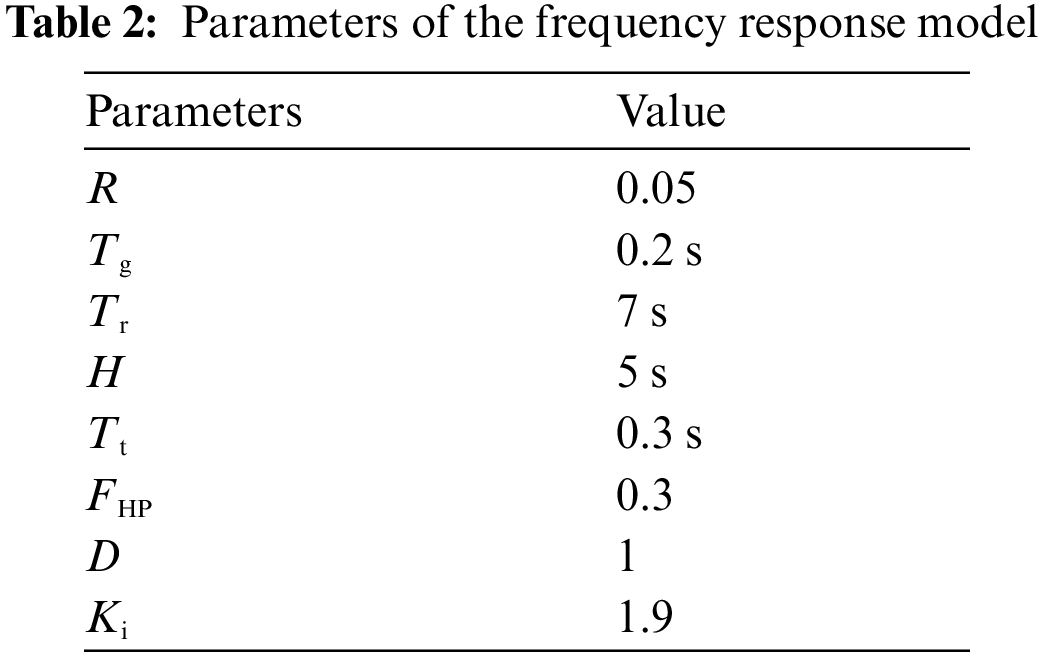
The input variables Δfest, Iinteg and the output variable ΔPEALref are divided into 7 fuzzy subsets, including Negative Big (NB), Negative Middle (NM), Negative Small (NS), Zero (Z), Positive Small (PS), Positive Middle (PM), Positive Big (PB). The membership functions for Δfest, Iinteg and ΔPEALref are shown in Fig. 5, by which fuzzification and defuzzification can be implemented. The fuzzy tuning rules between Δfest and Iinteg are listed in Table 1, by which the fuzzification form of ΔPEALref can be calculated.
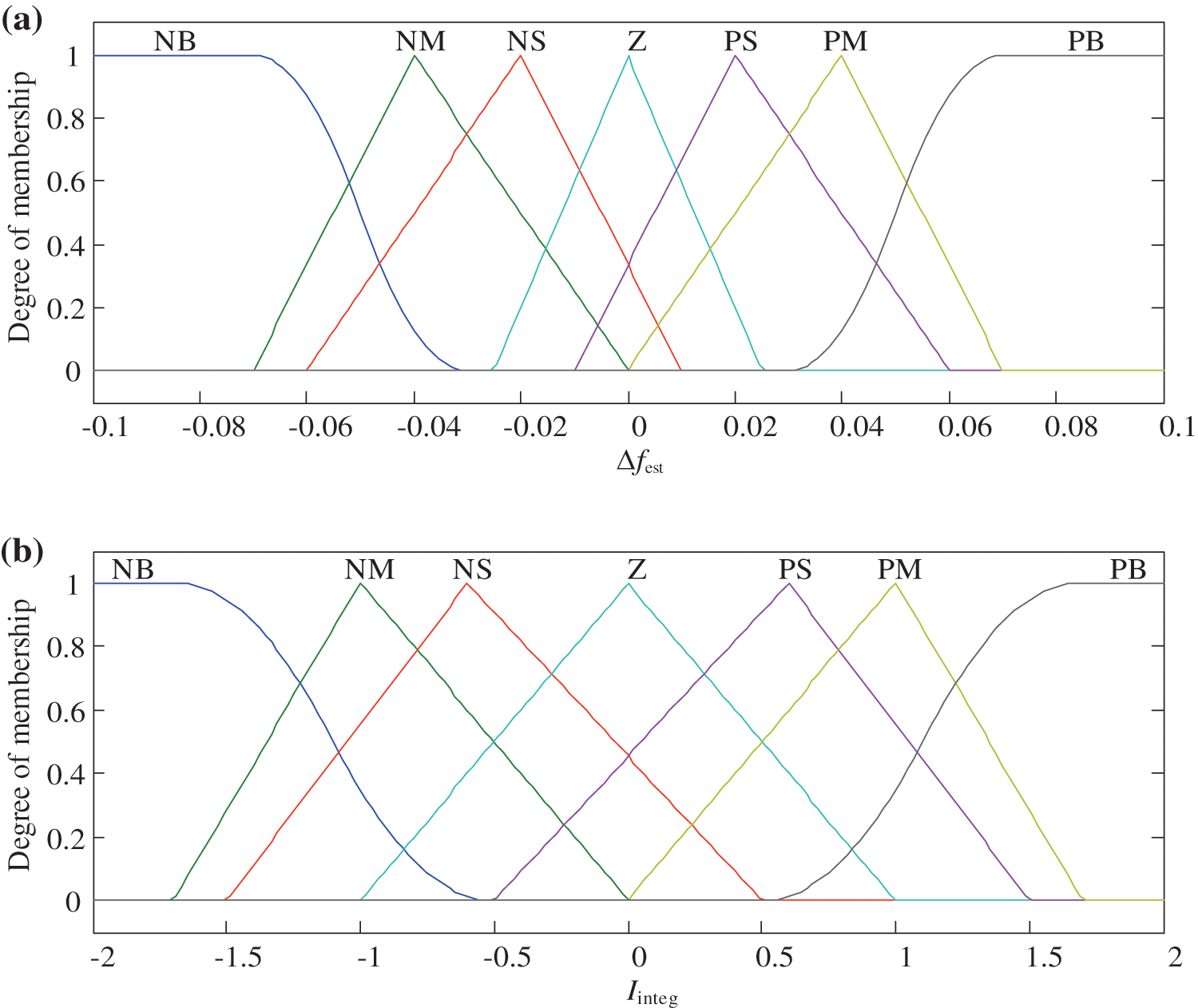
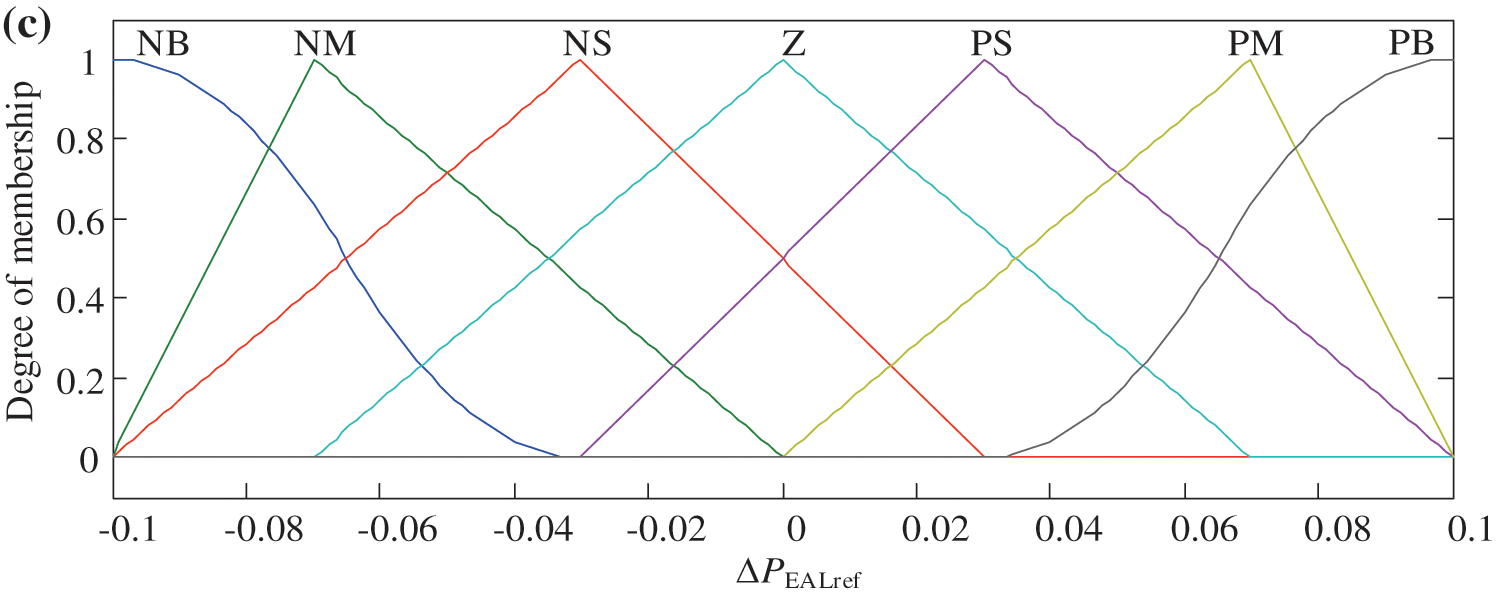
Figure 5: The membership functions of the fuzzy controller. (a) Δfest. (b)Iinteg. (c) ΔPEALref
The system frequency response model is developed based on Fig. 2 to verify the effectiveness of the proposed method. The parameters of the frequency response model are listed in Table 2.
4.2 The Performance of EAL in the Frequency Control
In this subsection, the performance of EAL in the frequency control is examined. The system is supposed to be imposed by step disturbances, of which magnitude denoted by Pdmax. The frequency control performance with EAL is compared with that without EAL. The simulation results with Pdmax varying from 0.02 p.u. to 0.08 p.u. are shown in Fig. 6. It can be seen Fig. 6 that EAL participating in the frequency control can significantly reduce the maximum frequency deviation under different disturbance magnitudes.
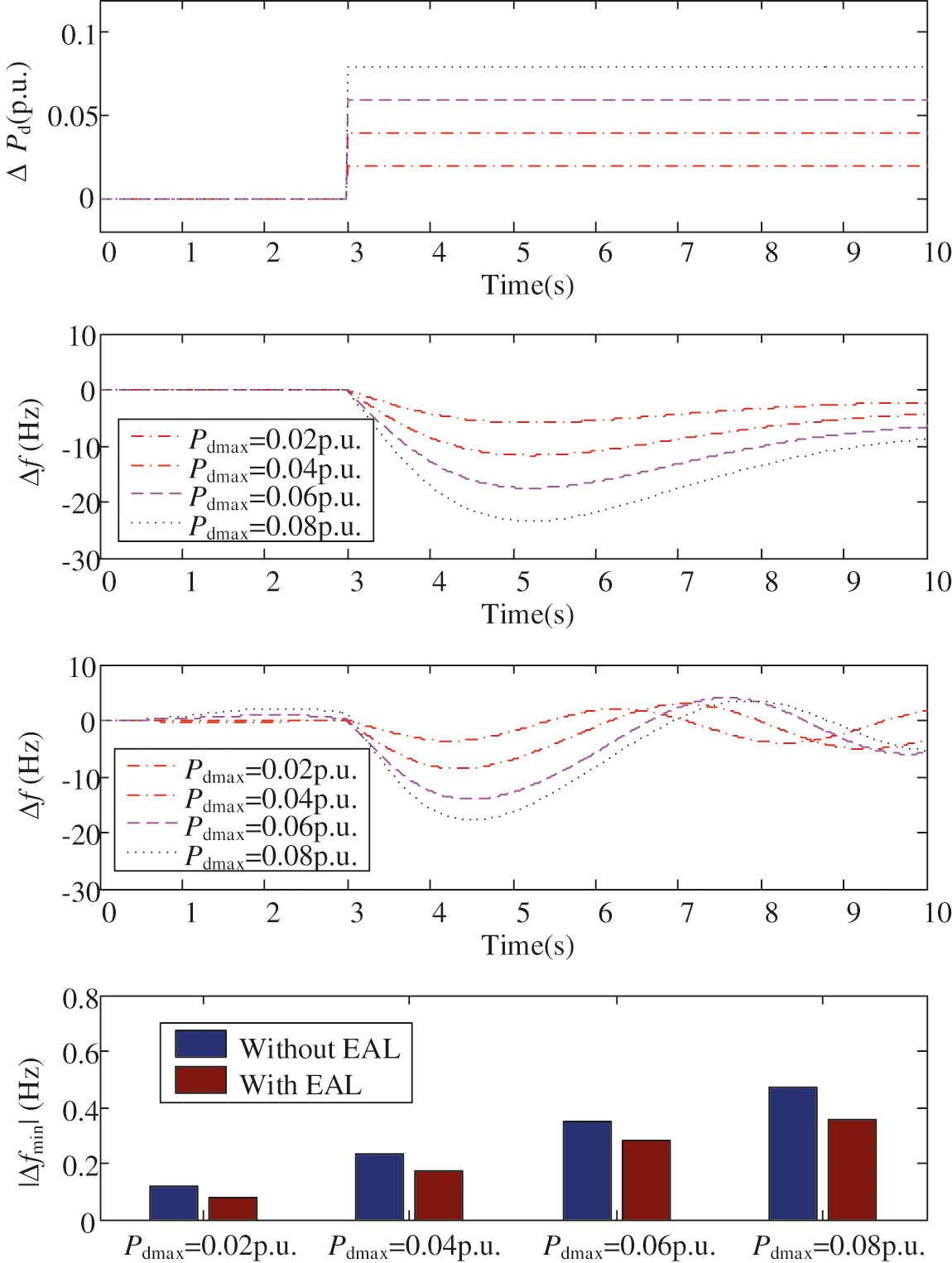
Figure 6: Simulation results under different magnitudes of frequency step-disturbances. (a) ΔPd. (b) Δf without EAL in the frequency conrol. (c) Δf with EAL in the frequency conrol. (d) Maximum frequency drop |Δfmin| under different values of Pdmax
4.3 Comparison of Different Frequency Estimation Methods
In this subsection, the performance of the Kalman-filtering is examined. To verify the effectiveness of the Kalman-filtering method, the following 3 cases are compared:
Case 1: the frequency deviation Δf is estimated without any de-noising method.
Case 2: the frequency deviation Δf is estimated with traditional low-pass-filtering (LPF) method.
Case 3: the frequency deviation Δf is estimated by the proposed Kalman-filtering method.
The EAL with fuzzy controller is considered in each case. The system responses of the above three cases under the continuously varying load disturbances are shown in Fig. 7. It can be seen from Fig. 7c that the LPF method (Case 2) and the proposed method (Case 3) can significantly reduce the measurement noise. LPF method (Case 2) leads to delay of the measured frequency, and the measured frequency is about 0.2 s lagging behind the frequency measured by Kalman filter (Case 3). And the frequency control performance therefore deteriorates. From Fig. 7b it can be seen that the proposed Kalman filtering method (Case 3) has better performance in lower the frequency deviation than the traditional methods (Case 1 and Case 2).
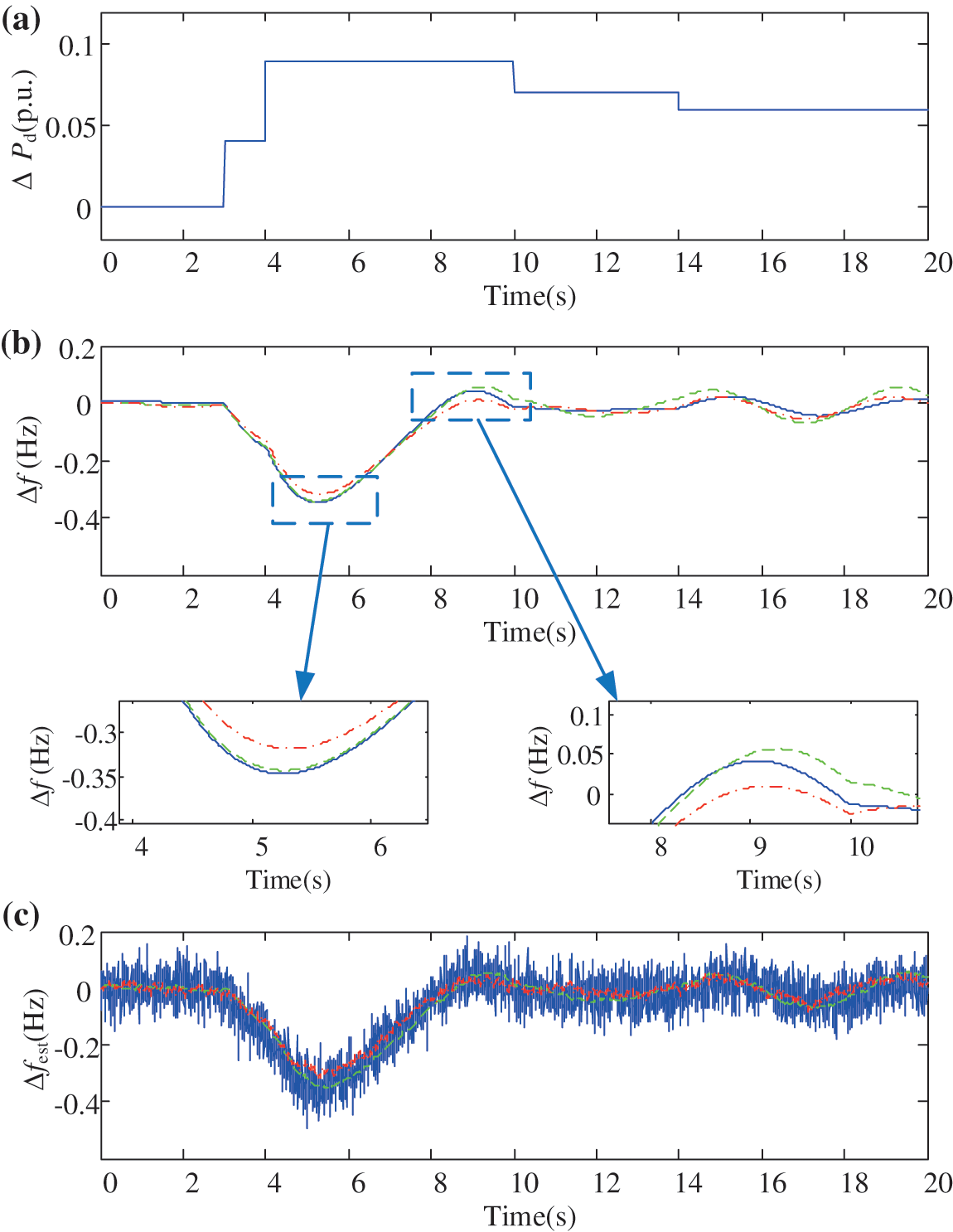
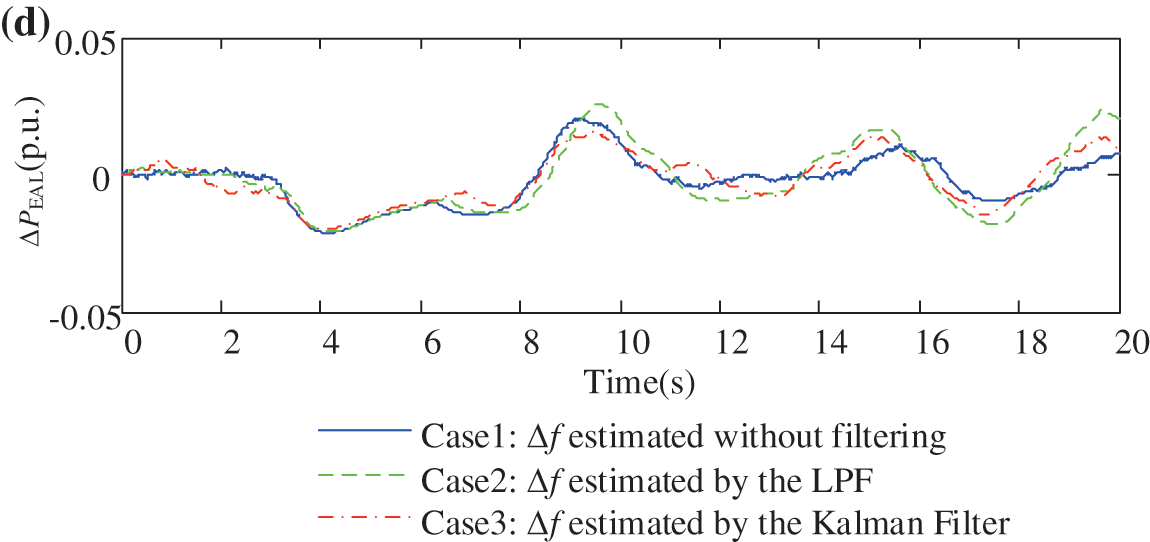
Figure 7: The frequency control performances under different Δf estimation methods. (a) Power disturbance ΔPd. (b) Actual frequency deviation Δf. (c) Estimated frequency deviation Δfest. (d) The power response of the EAL
The reason for the proposed Kalman-filtering (Case 3) better than LPF method (Case 2) lies in that the proposed method can utilize the system frequency response model, and predict the system states. Compared with traditional LPF method, the frequency measured by the Kalman filter does not introduce response delay. It is of significant importance for the controller to quickly receive the signal, and make response in time. The control performance is therefore improved.
4.4 Comparison of Different Control Methods of EAL
This subsection is to compare the frequency control performances under different EAL control methods, in order to verify the effectiveness of the fuzzy EAL controller. The following methods are compared.
Method 1: Only thermal generation units is considered in the frequency control. The EAL does not participate in the frequency control.
Method 2: EAL participates in the frequency control with traditional PID control method.
Method 3: EAL participates in the frequency control with the proposed fuzzy controller.
The simulation results of the above 3 methods are shown in Fig. 8. It can be seen from Fig. 8b that without EAL in the frequency control (Method 1), the maximum drop of the system frequency is as large as 0.51 Hz. With the traditional PID controller for the EAL (Method 2), the maximum frequency drop is reduced to about 0.45 Hz. With the proposed fuzzy controller (Method 3), the frequency deviation can be reduced to as small as 0.34 Hz, which is significantly superior to the other two methods.
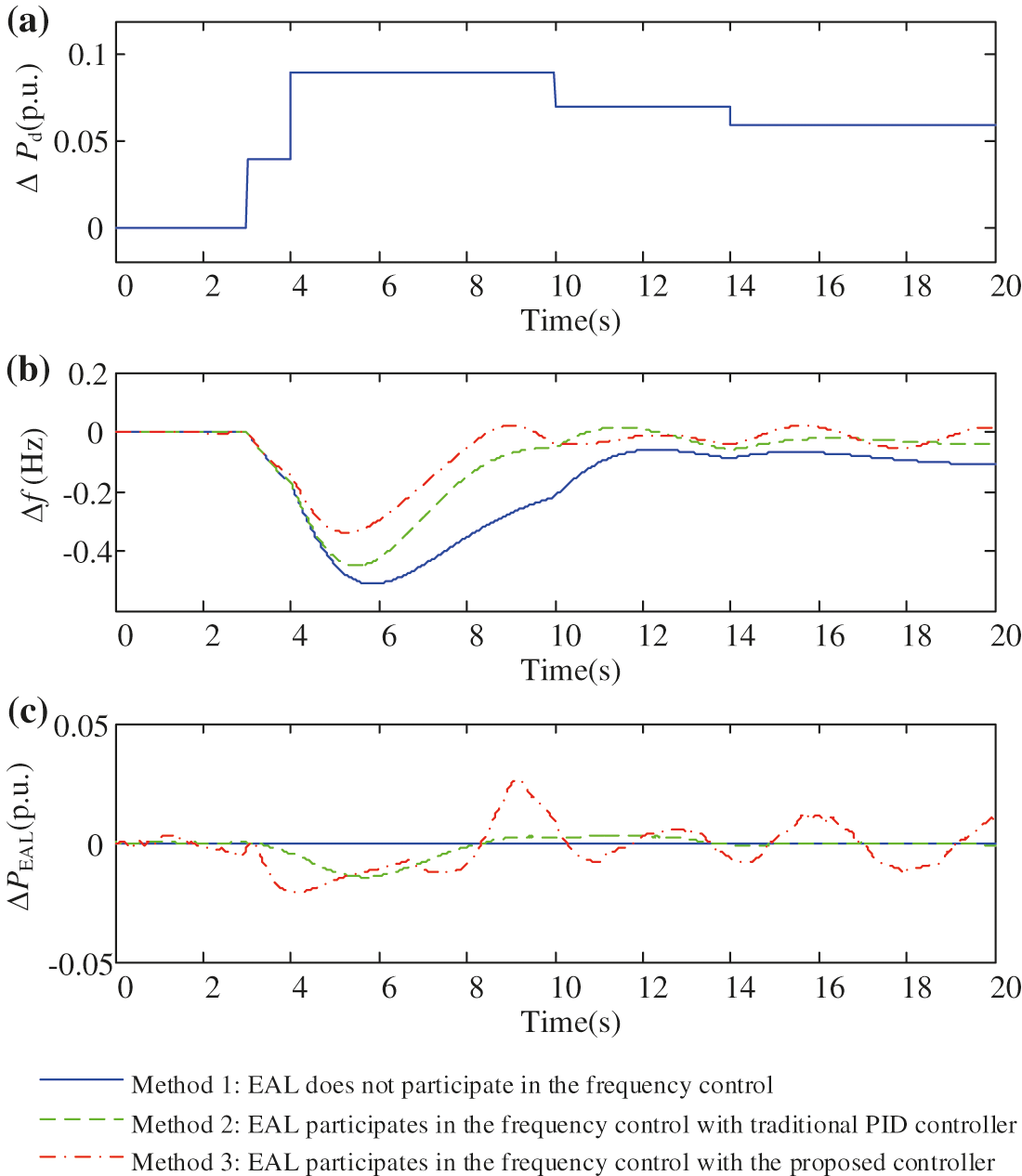
Figure 8: The frequency control performances under different control methods. (a) Power disturbance ΔPd. (b) Actual frequency deviation Δf. (c) The power response of the EAL
The reason for the proposed method (Method 3) better than the traditional PID control method (Method 2) lies in that the proposed method (Method 3) can better adapt to the nonlinear dynamic characteristics of EAL through fuzzy rules. The controller established by fuzzy rules can imitate the process and method of manual control, enhancing the adaptability and intelligence of the control system.
In this paper, Kalman-filtering based fuzzy control method is proposed for the EAL participating in the system frequency control. The main contributions of this paper can be summarized as following:
1. Kalman-filtering based method is designed for EAL participating in the frequency control of the power system. Kalman-filtering can precisely estimate system frequency suffered from measurement noise.
2. Fuzzy control method is adopted for EAL in the system frequency control. Fuzzy controller can better adapt to the nonlinear dynamic characteristics of EAL through fuzzy rules.
The simulation results show that Kalman-filtering performs well in lowering the measurement noise, and exhibits more effectiveness than traditional LPF method. The method with Kalman-filtering can reduce the frequency drop by 0.02 Hz than that without Kalman-filtering. The Fuzzy controller takes into account the nonlinear dynamic characteristics of EAL, and therefore performs better than traditional PID methods by lowing the frequency drop by 0.09 Hz. Future work may be investigating the feasibility proposed method on the other industrial loads, and developing corresponding controllers.
Funding Statement: This research was funded by Science and Technology Project of State Grid Corporation of China: Research on the Construction and Evaluation Technology of the Data-Driven-based Adjustable Resource Pool of Typical Industrial Enterprises, Grant No. 1400-202016386A-0-0-00.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
1. Ellman, D., Xiao, Y. (2021). Incentives to manipulate demand response baselines with uncertain event schedules. IEEE Transactions on Smart Grid, 12(2), 1358–1369. DOI 10.1109/TSG.2020.3024208. [Google Scholar] [CrossRef]
2. Martínez-Godoy, J. L., Martell-Chávez, F., Sánchez-Chávez, I. Y., Castillo-Velásquez, F. A., Torres-Falcón, M. D. C. P. (2021). A peak demand control algorithm for multiple controllable loads in industrial processes. IEEE Access, 9, 116315–116325. DOI 10.1109/ACCESS.2021.3105654. [Google Scholar] [CrossRef]
3. Mohsenian-Rad, H. (2015). Optimal demand bidding for time-shiftable loads. 2015 IEEE Power & Energy Society General Meeting, pp. 1. Denver, CO, USA. [Google Scholar]
4. Clarke, T., Slay, T., Eustis, C., Bass, R. B. (2020). Aggregation of residential water heaters for peak shifting and frequency response services. IEEE Open Access Journal of Power and Energy, 7, 22–30. DOI 10.1109/OAJPE.2019.2952804. [Google Scholar] [CrossRef]
5. Jindal, A., Singh, M., Kumar, N. (2018). Consumption-aware data analytical demand response scheme for peak load reduction in smart grid. IEEE Transactions on Industrial Electronics, 65(11), 8993–9004. DOI 10.1109/TIE.2018.2813990. [Google Scholar] [CrossRef]
6. Che, Y., Yang, J., Zhou, Y., Zhao, Y., Wu, J. (2019). Demand response from the control of aggregated inverter air conditioners. IEEE Access, 7, 88163–88173. DOI 10.1109/ACCESS.2019.2925659. [Google Scholar] [CrossRef]
7. Alvarez, M. Z., Agbossou, K., Cardenas, A., Kelouwani, S., Boulon, L. (2019). Demand response strategy applied to residential electric water heaters using dynamic programming and k-means clustering. IEEE Transactions on Sustainable Energy, 11(1), 524–533. DOI 10.1109/TSTE.2019.2897288. [Google Scholar] [CrossRef]
8. Liu, M., Peeters, S., Callaway, D. S., Claessens, B. J. (2019). Trajectory tracking with an aggregation of domestic hot water heaters: Combining model-based and model-free control in a commercial deployment. IEEE Transactions on Smart Grid, 10(5), 5686–5695. DOI 10.1109/TSG.2018.2890275. [Google Scholar] [CrossRef]
9. Zeng, K., Wang, H., Liu, J., Dong, C., Ai, X. (2020). A bi-level programming guiding electrolytic aluminum load for demand response. 2020 IEEE/IAS Industrial and Commercial Power System Asia (I&CPS Asia), pp. 426–430. Weihai, China, [Google Scholar]
10. Yao, M., Hu, Z., Zhang, N., Duan, W., Zhang, J. (2015). Low-carbon benefits analysis of energy-intensive industrial demand response resources for ancillary services. Journal of Modern Power Systems & Clean Energy, 3(1), 131–138. DOI 10.1007/s40565-015-0102-6. [Google Scholar] [CrossRef]
11. Chen, S., Gong, F., Sun, T., Yuan, J., Liu, Z. (2021). Research on the method of electrolytic aluminum load participating in the frequency control of power grid. 2021 IEEE 2nd International Conference on Big Data, Artificial Intelligence and Internet of Things Engineering (ICBAIE), pp. 798–801. Nanchang, China. [Google Scholar]
12. Jiang, H., Lin, J., Song, Y., Gao, W., Xu, Y. et al. (2014). Demand side frequency control scheme in an isolated wind power system for industrial aluminum smelting production. IEEE Transactions on Power Systems, 29(2), 844–853. DOI 10.1109/TPWRS.2013.2284032. [Google Scholar] [CrossRef]
13. Jiang, H., Lin, J., Song, Y., Gao, W., Xu, Y. et al. (2013). Frequency control by aluminum smelter load response in an isolated wind power system: A study for an industrial case. 2013 IEEE Power & Energy Society General Meeting, pp. 1–5. Vancouver, BC. [Google Scholar]
14. Shen, X., Shu, H., Fan, Z., Mo, X. (2021). Integrated control strategy for electrolytic aluminum load participation in frequency modulation. IEEE Access, 9, 56955–56964. DOI 10.1109/ACCESS.2021.3070864. [Google Scholar] [CrossRef]
15. Xu, J., Liao, S., Sun, Y., Ma, X., Gao, W. et al. (2015). An isolated industrial power system driven by wind-coal power for aluminum productions: A case study of frequency control. IEEE Transactions on Power Systems, 30(1), 471–483. DOI 10.1109/TPWRS.2014.2322080. [Google Scholar] [CrossRef]
16. Bao, Y., Xu, J., Liao, S., Sun, Y., Li, X. et al. (2018). Field verification of frequency control by energy-intensive loads for isolated power systems with high penetration of wind power. IEEE Transactions on Power Systems, 33(6), 6098–6108. DOI 10.1109/TPWRS.2018.2834520. [Google Scholar] [CrossRef]
17. Bao, P., Zhang, W., Cheng, D., Liu, M. (2020). Hierarchical control of aluminum smelter loads for primary frequency support considering control cost. International Journal of Electrical Power & Energy Systems, 122(3), 106202. DOI 10.1016/j.ijepes.2020.106202. [Google Scholar] [CrossRef]
18. Jiang, H., Lin, J., Song, Y., Hill, D. J. (2015). MPC-based frequency control with demand-side participation: A case study in an isolated wind-aluminum power system. IEEE Transactions on Power Systems, 30(6), 3327–3337. DOI 10.1109/TPWRS.2014.2375918. [Google Scholar] [CrossRef]
19. Liao, S., Xu, J., Sun, Y., Gao, W., Ma, X. Y. et al. (2016). Load-damping characteristic control method in an isolated power system with industrial voltage-sensitive load. IEEE Transactions on Power Systems, 31(2), 1118–1128. DOI 10.1109/TPWRS.2015.2424240. [Google Scholar] [CrossRef]
20. Mathieu, J. L., Koch, S., Callaway, D. S. (2013). State estimation and control of electric loads to manage real-time energy imbalance. IEEE Transactions on Power Systems, 28(1), 430–440. DOI 10.1109/TPWRS.2012.2204074. [Google Scholar] [CrossRef]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |