Energy Engineering

---

DOI: 10.32604/ee.2022.020787

ARTICLE

Implementing an Optimal Energy Management System for a Set of Microgrids Using the Harmony Search Algorithm

Xiangjian Shi1,*, Teng Liu2, Wei Mu2 and Jianfeng Zhao1

1School of Electrical Engineering, Southeast University, Nanjing, 210096, China
2NR Electric Co., Ltd., Nanjing, 211106, China
*Corresponding Author: Xiangjian Shi. Email: nrec_reg@126.com
Received: 12 December 2021; Accepted: 25 February 2022

Nomenclature Quantity

PtWT,n	Wind turbine (WT) generated power
PtPV,n	Photovoltaic (PV) generated power
PtMT,n	Micro-turbine (MT) generated power
PtVG,n	Virtual generation source generated power
PtES−,n	Energy storage (ES) generated power
PtES+,n	ES consumed power
PtRLD,n	Responsive load demand (RLD) load consumed power
PtVL,n	Virtual load consumed power
Ptload,n	Non-responsive load demand (NRLD) load consumed power
PtLL,n	Lumped load (LL) load consumed power
PtGRID+,n	Power sold to the main grid from the nth MG
PtGRID−,n	Power purchased from the main grid by the nth MG
PtMG+,kn	Power sold to the kth MG by the nth MG
PtMG−,kn	Power purchased from the kth MG from the nth MG
PBUY	Maximum purchased power by the nth MG
PSELL	Maximum sold power by the nth MG

1  Introduction

The human population is concerned with the reliable and extensive use of renewable energy sources (RESs) to reduce greenhouse gas emissions and supply distributed loads remotely. RESs are clean and infinite; they can therefore be appropriate alternatives for fossil fuels [1]. The emergence of dispersed generation RES and need for supplying the consumed load at the point of use have led to the emergence of microgrids (MGs). When global electricity cannot be distributed, the use of MGs is suggested. Based on International Energy Agency’s report, more than 1 billion people worldwide do not have access to the electricity network. Plans are being made to supply the electricity needed by these people via developing the global electricity network and using MGs [2]. Based on the high fluctuation of accessible power at the distribution voltage level, the MG systems may fail to supply major consumers. Therefore, by dividing the consumers into smaller units, several MGs are used and each unit of load is fed by one MG. Using several MGs in a low-voltage grid, integrated multi-owner MGs emerge [3]. To monitor the performance of MGs and optimize their operation, it is essential to provide an energy management system (EMS) in different conditions. The energy management system (EMS) is used to control the performance of all generation units (GUs), controllable loads and ESS in all the MGS, demand-side management, all the interactions of MGs with the grid and the power exchange between MGs. In [4], the economic issues and confidence of distributed MGs are discussed. In [5], the location of DG sources is examined in distribution systems and the research projects are proposed on this topic. The advantages of MGs, including promotion of local confidence factor, reduction of supply line losses, support and improvement of local voltage, correction of voltage drop or working as an uninterruptible power supply were noted in [6]. The gravity search algorithm was used to determine optimal energy management [7]. Moreover, a stochastic framework was provided for the optimal scheduling of MGs by considering the islanded mode [8]. In this approach, different uncertainties are taken into account and the daily scheduling of resources is determined by considering emergency conditions. An independent hybrid MG as a combination of RES such as wind and solar energy, fuel cell and ESS was proposed in [9]. This MG used fuzzy logic controllers and employed a management strategy based on the battery’s state of charge (SOC) in order to keep the energy balance. In [10], the performance of the hybrid system was optimized in the presence of a pumped hydro storage (PHS) by a modified search algorithm to reduce fuel consumption.

In [11], a smart EMS was proposed by using the genetic algorithm (GA) to optimize the MG performance. In this study and in the optimization process, a prediction module, an ESS management module and an optimization module were used. In [12], a control algorithm based on distributed model predictive control (DMPC) was presented for the economic programming of a network of integrated MGs with a hybrid ES. This algorithm tried to provide the maximum economic profit of network MGs, reduce the ESS destruction and meet different system constraints. In [13], a company-based EMS was proposed to facilitate power exchange between MGs by using demand-response and energy storage. The penetration of wind and solar energy in power systems was noted in [14], while also considering the uncertainties in ESS and HPS and examining the units’ participation problem. To improve the optimization performance, it introduced a binary artificial sheep algorithm (BASA). In [15], an EMS was introduced for industrial MGs. In this model, optimization was performed in a bi-level structure to optimize the operations of industrial MGs by scalability and uncertainties. In [16], a two-stage energy management strategy was introduced for the participation of charging stations in load management and use of electricity price uncertainty in the optimal operation of MGs. In [17], a new forecast-based optimization method was proposed to provide real-time planning that takes into account future environmental trends. The recently proposed duel-based deep reinforcement learning approach has been adopted to optimally deploy home energy management systems. In [18], a new method based on the Gaussian process (GP) was proposed to improve the probabilistic prediction of groups or regions of WF. The covariance function (CF), called the kernel, is an important factor when using GP. One of the most common of these functions is the squared index (SE). This, along with other functions, applies to the model of the proposed method. In [19], Centralized EMS (CEMS) was presented as a unique tool. Two dispatch options are the improved Prey-Prey Optimization (IPPO) algorithm and the improved Mixed Integer Linear Programming (IMILP). These methods are provided for planning UC and economical dispatch in microgrid units. In the suggested approach, system constraints such as voltage and charging facilities and unit limitations had been discussed. In [20], Planakis et al. proposed a framework for the design and experimental evaluation of power split control systems for ship propulsion. Machine learning is used to process data from vessel operations and recognize 20 loading patterns. A typical template that can be used as a ship load cycle is extracted in the development and testing of energy management systems. A ship propulsion model with wave disturbance is used to simulate a realistic load scenario in a test facility. In [21], Ahmadpour et al. evaluated the results of the well-known EP as a Renewable Energy Certificate (REC) and its impact on the welfare surplus based on the Power Generation Expansion Plan (GEP). To achieve the paper goals, we mix the desired EP and GEP and present a comprehensive model from the perspective of the RES maker. The model is solved in the form of a mixed integer nonlinear problem (MINLP) using GAMS optimization software with the BARON optimizer.

In this paper, a multi-company system is proposed for energy management in the systems consisting of several MGs with multiple owners. This structure aims to optimally manage the current GUs in the MG, demand-side management and MGs’ exchange with the main grid and the interactions between MGs. In this method, each part of the MG is regarded as a company and the coordinated behavior of the companies in the MG minimizes the generation cost. Therefore, in integrated MGs, there is no need for supervisory control by an independent operator that monitors the MGs’ performance and each of the MG self-controls with the supervision of an independent operator. As the model intended for the MG is non-linear and discrete, the harmony search algorithm is used to implement this system in order to find the best solution possible. In this problem, the technical constraints including full load supply, technical characteristics of each resource in the MG, constraints on connection to the main grid and constraints on power exchange among MGs are included.

2  Structure of the Studied Gird

The schematic representation of the studied system is given in Fig. 1. The system has several MGs, each involving their own local loads, DG resources and ESS systems. Each MG can operate in both grid-connected and islanded modes. Each MG has a unique EMS and a central EMS (CEMS) at a high level to control all these EMSs. A set of condensive loads is also considered for this grid. A condensive load is a group of consumers who do not belong to any MG or the main grid and independently receive demand from the introduced grid.

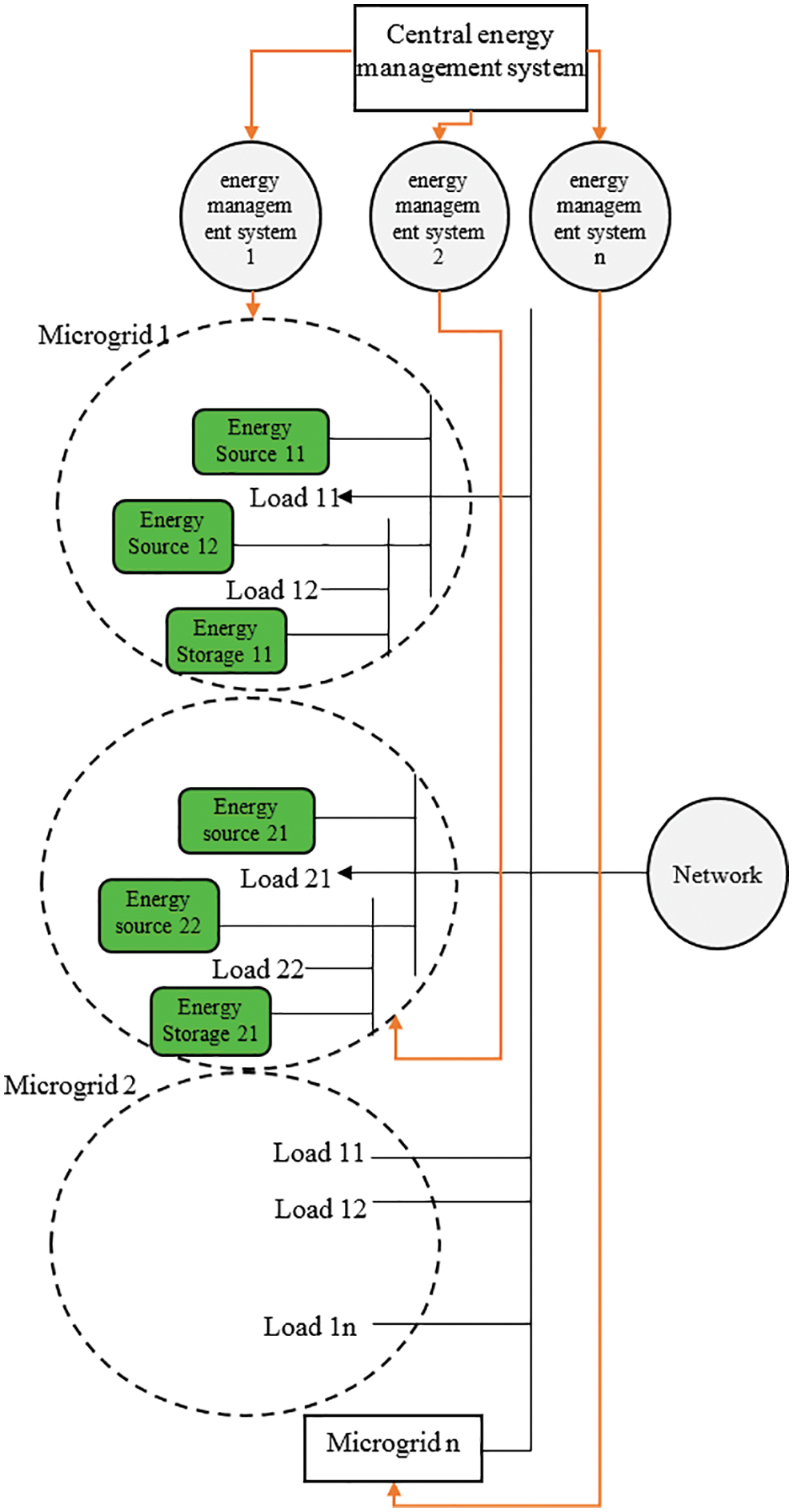
Figure 1: The studied system

The prices suggested by each resource in the MGs and their power exchange with the grid are summarized in Table 1. Some bids in some intervals interfere with the prices suggested by the GUs or other consumptions. Therefore, the proposed EMS and CEMS should be able to choose the best power generation source and lateral consumer by considering the minimum generated power cost. The data of the RES and the local load profile of the MGs are taken from [22,23]. These data are derived from the actual values of the meteorological area of Belladona, Barcelona (Spain) online. To demonstrate the algorithm’s rapid responsiveness to the occurrence of any event, different scenarios are considered in the system.

Scenario 1: In this case, the whole system is operating normally and no unwanted error has been created.

Scenario 2: Sudden load increase (from 17:00 to 17:30 and from 18:00 to 18:30).

Scenario 3: In this case, in addition to system performance, the presence of electric vehicles and their role in microgrid performance and how energy is exchanged are examined.

3  Optimization Problem Formulation

The studied system has n MGs, each consisting of several wind and solar RES and non-renewable energy sources as spinning reserve microturbine, ESS and several types of uninterruptible and controllable loads connected to the grid as well as several condensive loads. The mathematical relations formulated for EMSs and CEMS implementation are given below.

3.1 Mathematical Implementation of EMS-MICA Objective Function

For all EMSs separately, a cost function is defined aiming to minimize the objective function and manage the generation and consumption resources of each MG. The cost function defined for the EMS in the nth MG is modeled as follows:

zEMS,n=min{∑t=124{∑s∈SμsWTPs,tWT,n×πtWT,n+∑s∈SμsPVPtPV,n×πtPV,n+PtMT,n×πtMT,n+PtVG,n      ×πtVG,n+PtES−,n×πtES−,n−PtES+,n×πtES+,n−PtRLD,n×πtRLD,n−PtVL,n×πtVL,n     +PtUP,n×πtUP,n}×Δt}(1)

In this model, Ps,tWT,n, Ps,tPT,n , PtMT,n, PtVG,n and PtES−,n denote the power generated by wind sources under scenario s (s is the total number of scenarios), solar power under scenario s, microturbine, virtual generation source and ESS for the nth MG at time interval t, respectively.

Coefficients μsWT and μsPV respectively denote the probability of occurrence of scenario s for wind and solar resources. PtES+,n, PtRLD,n and PtVL,n respectively indicate the consumed power by ESS, RLD load and virtual load for the nth MG at time interval t. πtWT,n, πtPV,n, πtMT,n, πtVG,n, πtES−,n, πtES+,n, πtRLD,n and πtVL,n respectively are bid made by wind source, solar source, microturbine, virtual generation source, ESS as the generator, ESS as the consumer, RLD load and virtual load in the nth MG in interval t. Moreover, PtUP n is the un-supplied power and πtUP,n is the penalty for this power in the nth MG in interval t. In each interval, the EMSs first receive the bids of all generation and consumption sources in each MG. Then, depending on the prices, the proposed algorithm decides to use the generation and supply sources of the consumers to maximize social welfare. In the daily operation of the system, based on the bid made by the GU and virtual load, MGs can have surplus or deficit generation. The surplus power or deficit power in the MGs are notified to the CEMS by the suggested EMSs using variables PtVG,n and PtVL,n:

Ptn=(PtWT,n+PtPV,n+PtMT,n+PtES−,n)−(Ptload,n+PtES+,n+PtRLD,n)(2)

If Ptn is positive, it means surplus generation. In this situation, the MG can sell power to other MGs and the grid; the surplus power is to be paid to the virtual load. However, when Ptn is negative, it means a deficit in generation. In this situation, the MG cannot supply its internal demand and must seek the help of other MGs and the grid. Therefore, this power deficit is regarded as a virtual generation source.

3.2 Implementation of the Objective Function in CEMS-MICA

This function aims to supply the decision and surplus generation of the MGs, such that the total system social welfare is maximized. The objective function defined for the CEMS can be formulated as:

zCEMS=min{∑n=1N∑t=124{PtVL,n×πtVL,n−PtLL,n×πtLL,n−PtGRID+,n×πtGRID+,n      −∑k=1k≠nkPtMG+,kn×πtMG+,kn−PtVG,n×πtVG,n+PtGRID−,n×πtGRID−,n       +∑k=1k≠nkPtMG−,kn×πtMG−,kn}×Δt}(3)

In this figure, PtLL,n, PtGRID+,n and PtMG+,kn respectively denote the power sold to load LL, grid and kth MG by the nth MG in time interval t; n is the power purchased from the grid and kth MG by the nth MG in interval t. Moreover, πtLL,n,πtGRID+,n and πtMG+,knrespectively stand for the bids on power sales to LL load, gird and kth MG, while πtGRID−,nand πtMG−,knrespectively show the bid on power purchase from the grid and kth MG.

4  Problem Constraints

The constraints for the optimization problem include the following.

4.1 Balance Constraint

In each MG, the total power generated by the generators in each interval should be equal to the total consumer demand.

In every MG, the total generated power should be equal with the demand:

PTot,tMG+,n+∑k=1k≠nk⁡PtMG+,kn+PtGRID+,n+PtLL,n=PTot,tMG−,n+∑k=1k≠nk⁡PtMG−,kn+PtGRID−,n(4)

4.2 ES Constraints

Energy storage constraint

The maximum and minimum power in the charge and discharge period [23,24].

4.3 Energy Balance

Constraints of spinning reserve devices

The constraints on these devices include the maximum and minimum power generated by the non-renewable energy sources [24].

4.4 Constraints of RLD Loads

The total power consumed by RLD must be less than or equal to the maximum load considered for the RLD [23,24].

4.5 Constraints on Power Exchange between MGs and the Main Gird

In fact, the nth MG cannot purchase power more than P−BUY from the grid and other MGs or sell power to the grid, other MGs and the LL load more than P−SELL. In fact, this constraint results from the limitation of transfer lines connecting the grid and the MG, and aims to constrain the exchanges with the grid and promote the use of the existing resources within the MG.

4.6 RES Uncertainty Constraint

Based on the predicted data, a proper probability density function will be selected for each specified parameter. The random change in Weibull and its distribution has extensive applications in power and control systems, as well as the weather forecast. Wind speed is modeled by the Weibull distribution in the following equation [25]:

PDF(v)=kc(v−v0c)k−1×exp−(v−v0c)k(5)

k=(δμ)−1.086,c=μΓ(1+1k)(6)

In these formulas, k and c are constants for determining the power produced by wind units based on wind speed. The Γ gamma distribution function, μ is the mean associated with wind speed data. v and v0 are the base wind speed and current wind speed, respectively.

Solar irradiation is modeled by using the Weibull distribution beta model. The beta Weibull model is depicted in the following equations:

PDF(si)={Γ(α+β)Γ(α)+Γ(β)×sia−1(1−si)(β−1)0≤si≤1,α≥0,β≥00otherwise(7)

α and β are the parameters based on the average amount of radiation (μ) and standard deviation (σ) for power generation. The si is the intensity of sunlight.

β=(1−μ)×(μ×(1+μ)σ2−1),α=μ×β1−μ(8)

A conventional Weibull function is used to model electricity price and electricity load as follows:

PDF(χ)=1σ2πexp(−(χ−μ)22σ2)(9)

χ is the sunlight per unit time.

4.7 Scenario Generation

Latin Hypercube Sampling (LHS) is a group sampling method. Since the Weibull distribution function of each stochastic variable is known, the sampling stratification is done with the sampling delay mean to ensure the integrity of sampling data and increase the data volume. For each uncertain parameter, the Weibull distribution should be classified into several parts. The LHS method is adopted to generate the scenarios. These methods are presented below:

Step 1: Determining the number of scenarios and dividing the probability distribution of each uncertain parameter by N levels;

Step 2: Selecting the mean value from the probabilistic distance [(i−1)/N,i/N] where 1≤i≤N;

Step 3: Calculating the values of the sample of wind speed, solar irradiation, electricity price and electric charge based on the inverse cumulative distribution function.

4.8 Scenario Reduction

Calculating a large number of scenarios can disrupt the computation efficiency. Therefore, a scenario reduction method must be applied. The k-means algorithm is used in the current study to reduce the number of states owing to its flexibility and applicability for large-scale reduction.

The processes of this algorithm are presented below:

Step 1: Randomly select k scenarios from the central cluster ci, where i=1,2,3,…k from the generated scenarios.

Step 2: Calculate the distance D between any scenario Sjand the cluster centers. Then, determine each scenario from the closest cluster center.

Dj=||Sj−Ci||,j=1,2,..N(10)

Step 3: Update the cluster center.

Ci=1Ni∑h=1Ni⁡Sh,i(11)

Step 4: Calculate the objective function J.

Jh,i=∑i=1k⁡∑h=1Ni⁡||Sh,i−Ci||(12)

Step 5: If J converges, stop the updating and keep the results; otherwise, return to Step 2.

5  Implementation of the Proposed EMS Structure with Two Control Layers

The proposed EMS for MGs with multiple owners has two control layers, i.e., primary and secondary.

5.1 Primary Control

After choosing the MGs’ mode of operation in the first level control, the EMS is independently applied to each MG. Based on the constraints for the problem, the optimal power of the GUs and consumers in that MG is determined. If the MG is islanded, it will have no exchanges with the main grid. However, if it is grid-connected, it can exchange power with the grid and other MGs. Power exchange means purchasing power from the grid and other MGs when there is a power deficit and selling power to them when there is a power surplus. The grid-connected MG can also supply external condensive loads. In other words, the primary control of grid-connected MGs determines the optimal power for the units in the MG in addition to two other variables known as the virtual GU (PtVG,n) and virtual load (PtVI,n). These two variables are, in fact, the sum of powers allocated for sales to the grid, other MGs and supply the external condensive loads as a virtual load, as well as the sum of powers allocated for purchasing from the grid and other MGs as a virtual generation source. In other words, the virtual load is the probable generation surplus and the virtual generation source is the probable generation deficit in the MG. Based on the objective function, the bid made by the units in the MGs and the bid made by external elements, i.e., the main grid and other MGs, the EMS of each MG in primary controls decides whether power exchange with the outside world would benefit the MG operator or not. Thus, the amount of power allocated to the load and virtual generation source by the EMS of each MG is determined based on the technical and economic constraints. Deciding how much of this load and virtual generation is to be allocated to which element is beyond the scope of responsibility of the MG EMS at the primary control level. Thus, in each interval, the MG’s generation deficit or surplus is inputted to the CEMS at the secondary control level in the form of a dataset.

Data such as the technical constraints of the devices in the MG, the load prediction and RES data, the prices suggested by each source in the MG are dispatched to the EMSs at the primary control level.

5.2 Secondary Control

The CEMS is presented in the secondary control. After receiving the data from the EMSs of all the MGs, the energy management process commences in the secondary control. This system specifies the status of loads and virtual generations determined at the primary control level. In this situation, various scenarios may occur depending on the number of MGs in the power system. If n MGs are present in the system, n2 scenarios will occur in the system. If all the MGs have a generation deficit, this means that the independent EMS of the GMs has allocated some power to the virtual generation source. As noted earlier, virtual generation means purchasing from the grid and other MGs. As all the MGs have a generation deficit, they cannot allocate any power for sales and will supply their generation deficit only from the main grid. In this scenario, no MG can supply the external condensive load and this load will be fully supplied by the main grid. When all the MGs have a generation surplus, this surplus will be consumed to supply the external condensive load and sold to the main grid. In this scenario, the MGs first compete to supply the external condensive load and the MG with the lowest bid will win this competition. The winning MG may not supply the external condensive load fully; in this situation, other MGs will act in the same way to supply this load. If the external condensive load is still not fully supplied, the main gird will help. Finally, if the MGs still have a generation surplus, this surplus will be sold to the main grid. It is also possible that some MGs might have a surplus and others have a deficit. In this case, among the MGs with a surplus, the one with the lowest bid will first be selected and its surplus can be used to compensate for the deficit of other MGs, supplying the external condensive load, or sold to the main grid. In this situation, first, the generation deficit of the MG with the lowest bid is compensated for. The CEMS decides how much of the surplus is to be allocated to these three components.

This trend will continue until the surplus of all the MGs is used. Finally, if the MGs with a deficit and the external condensive load are not fully supplied, the main grid will help and establish power balance. Thus, we will have three general states in the CEMS. First, all the MGs may have a generation deficit; in this case, there is no need for optimization because clearly all the deficits and external condensive load must be supplied by the main grid.

6  Harmony Search Algorithm

At first, musicians randomly play on their musical instruments. This harmony is stored in their memory. In the next parts, based on the stored harmony, musicians play new music which differs from the previous part. Playing impromptu follows one of the following rules: Playing a sound stored in the memory playing a close sound to that in the memory and playing a random sound from the probable sounds. Assume a jazz trio (a saxophone, a violin and a guitar). A certain degree of justifiable sound exists in each musician’s (saxophonist, violinist and guitarist) memory. If the saxophonist randomly plays sol, the guitarists do, and the violinist si, the existing harmony (sol, si, do) creates a new harmony. If the new harmony is better than the one in memory, the old one will be replaced by the new one and the old one will be deleted. This process will continue until a unique harmony is achieved. The problem is formulated based on the harmony search algorithm and the structure of the solution is assumed as a harmony. Then, the algorithm randomly generates a harmony based on the feasibility conditions and stores it in the memory. The operation of a harmony search algorithm is fully explained below [26]. First, the optimization problem is formulated as follows:

Minimizef(x),x(i)∈Xi,i=1,2,…N(13)

The value of the following parameters is specified:

The harmony memory consideration rate (HMCR), the pitch adjustment rate (PAR) and the total scale.

The second part of the algorithm creates and forms the harmony memory based on the following matrix:

HM=[x11x21xn1f(x1)x12x22xn2f(x2)⋮⋮⋮⋮x1HMSx2HMSxnHMSf(xHMS)](14)

Here, the memory matrix is randomly constructed by solution generating vectors and the real objective function f(x) and will play the role of a memory.

The is the most important part of this algorithm because changes in the current harmonies in the memory are applied in this stage. Based on the previous equation, the HMCR specifies the extent, to which the harmony memory is used for constructing a new harmony, and HMCR-1 indicates the probability of randomly generating the new harmony.

xt′←{xt′∈{x12,xt2,…,xtHMS}xt′∈xi(1−HMCR)(15)

For instance, an HMCR of 95% means the 95% probability, by which the algorithm should select the values of the new harmony from the values stored in the memory, and the 5% probability of random generation. When a value is selected from the memory, it may change depending on the PAR probability and the probability of this change is obtained by adding an integer to the value. In the following equations, bw is the optional distance for the examination width and rand()is a random number between 0 and 1.

Rtnew←Rtnew±rand()×bw(16)

f(x)={YESPARNO(1−PAR)(17)

If the new harmony is better than the worst member of the harmony memory, the new harmony will be stored in the memory and the worst harmony will be deleted from the memory. In the end, the stop condition, which in this algorithm is examining the number of iterations, is examined.

7  Results and Discussion

It should be mentioned that the simulation has been done in MATLAB version 2016 software on a personal computer with 8 GB of RAM and a 3 GB 7-core processor with 1 terabyte of internal memory and 6 MB of cache.

The energy source programming for MGs obtained by the proposed algorithm is presented in Figs. 2a and 2b, respectively.

Figs. 3a and 3b show the power sold to the grid, power sold to LL load by each MG, power sold to other MGs, RLD supply power and ES charge power.

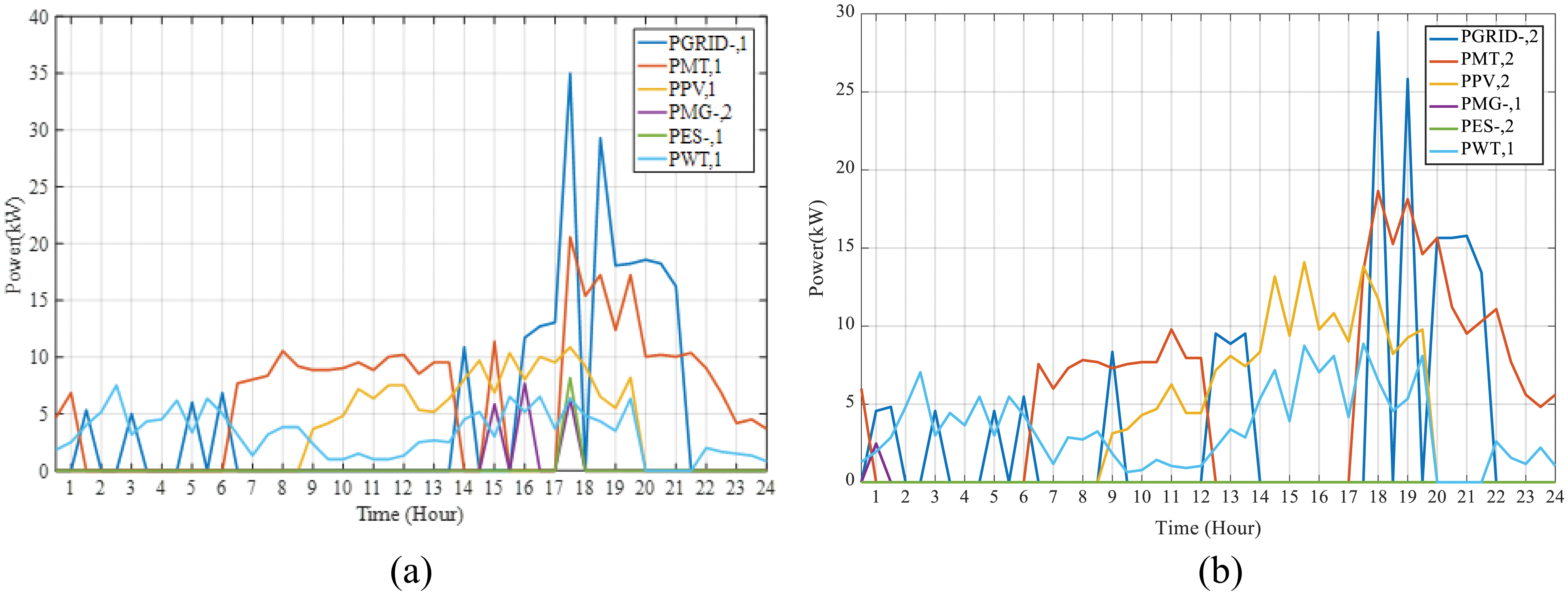
Figure 2: The energy source programming for MGs

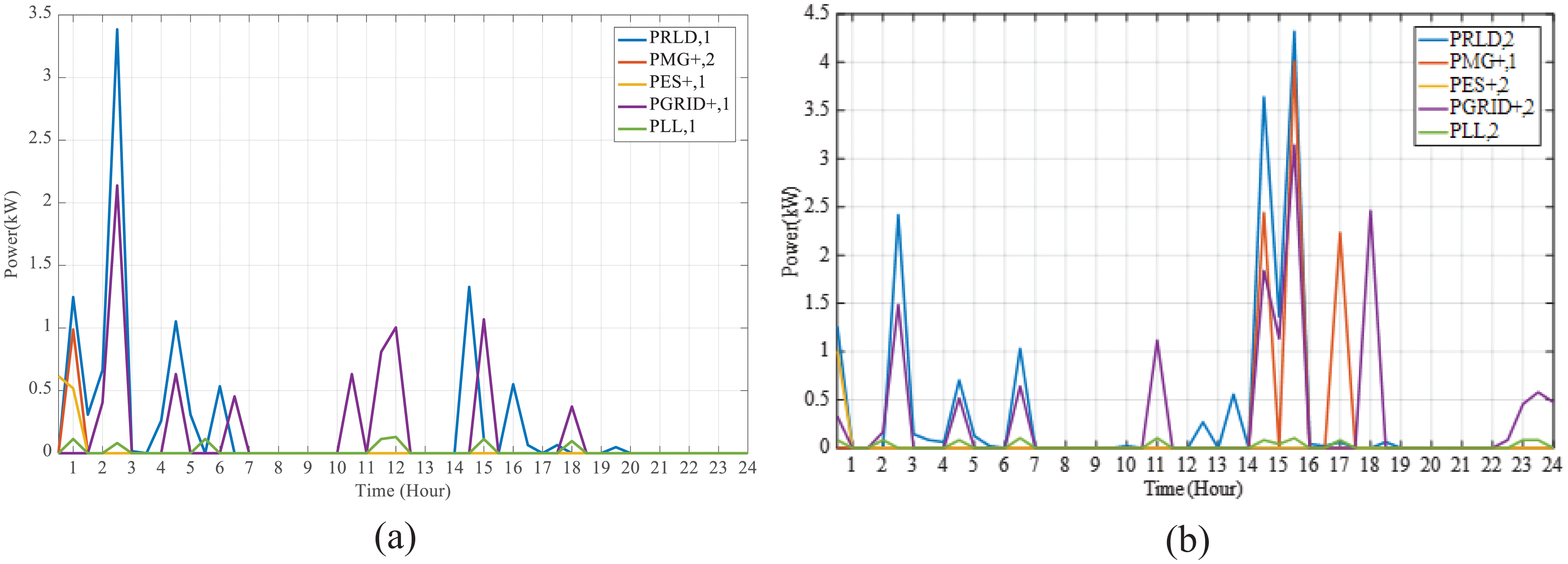
Figure 3: The sold power to the grid

The power generation by PV and WT is affected by climatic conditions (wind speed and solar irradiation). These sources participate in supplying the power demanded by the consumers more intensively than the other sources because their bids are lower, which is more competitive than the rest of the sources. As a result, the algorithm tries to purchase the maximum accessible power from these sources. Based on the figures, from 00:30 to 01:00, based on the lower bids of MT and the greater profit compared to other bids, MG1 supplies RLD and ES, as well as a part of the power needed by MG2 and LL. The optimization algorithm allocates this source for supplying the power of other sources to reduce the total generation cost. In later hours, despite higher πtGRID−,n than all the other bids, EMS of MG1 decides to supply a part of the RLD by purchasing from the grid.

At 20:00, due to the drop in the local load demand, more PtMG,1 power is generated; this power is mostly used for supplying the grid due to the higher bid of πtGRID+,n. Furthermore, between RLD and LL loads, despite higher πtLL−,1 than πtRLD,1, RLD is the next candidate for supplying the surplus power generated by MG1 in this interval. EMS-MICA reduces the consumed load of both MGs to avoid paying the penalty during the peak period when the diagram reaches maximum consumption, or the occurrence of scenarios 2 and 3 when the combination of all generation sources does not suffice load supply. ES charge occurs only in three hours in both MGs and does not greatly affect the total consumed power. After this interval, the SOC of both MGs reaches its maximum value and ES is kept on stand-by to support the MGs when they are islanded. The related prices of generated power can be quoted from [3,4].

The daily power generation percentages by the generation sources of the percentage share of each consumer for consuming the surplus are given in Figs. 4 and 5 for MG1, respectively. During the first hours of the day when the consumed load is low, RESs supply most of them and some power is also purchased from the grid. In these hours, as load demand increases, due to the reduced WT output, the higher load demand is supplied by the MT first; gradually, as PV is commissioned, MT’s participation gradually decreases. The EMS of MG1 uses MT to supply its needs partly by the power purchased from the grid.

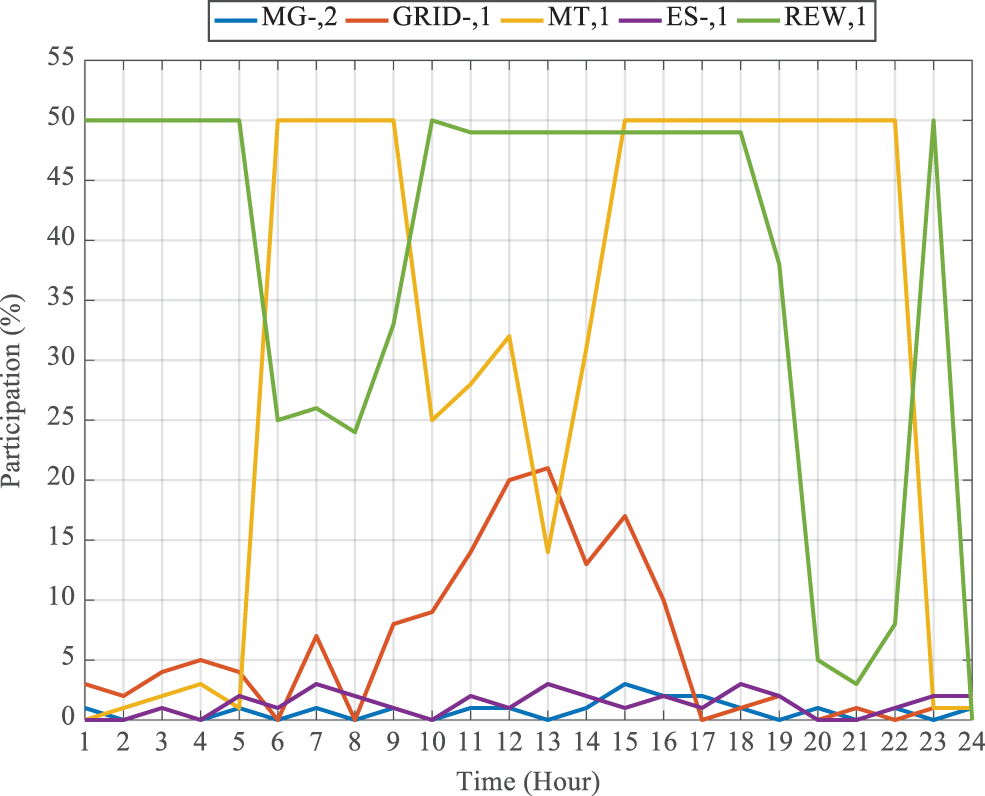
Figure 4: Daily participation percentage of generation sources of MG1

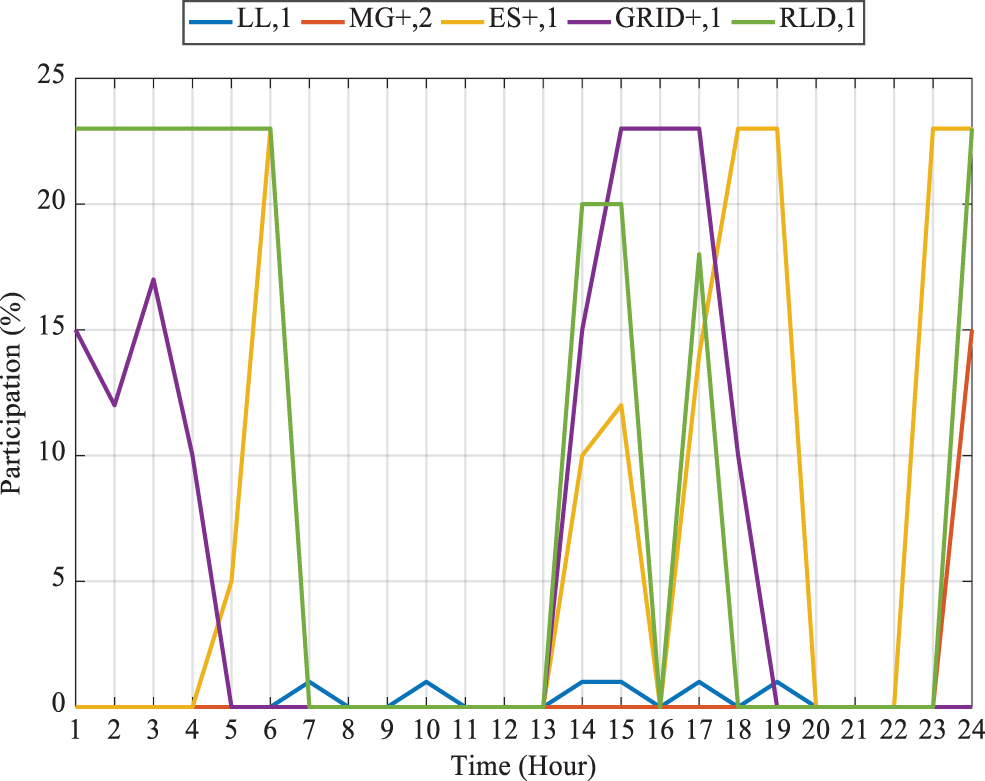
Figure 5: Daily participation percentage of consumption sources of MG1

Based on Fig. 5, in the first hour of the day when the load demand is low, EMS allocates some of the generated power for charging the ES in this period; based on the ES constraint, the maximum ES charge is P; thus, the rest of the surplus is used to supply the RLD. In this period, a part of the surplus power is sold to MG1 which is used for charging the ES. Due to the lower bid of purchasing from MG2 than ES charge, the MG1 operator makes a good profit.

The daily power generation percentages by the generation sources of the percentage share of each consumer for consuming the surplus are given in Figs. 6a and 6b for MG2, respectively. Like MG1, MG2 uses MT sources and the gird in hours when the local load begins to increase (06:00–09:00) before the commissioning of PV, during peak hours, or when scenarios 2 and 3 occur (00:18–00:24). The EMS of MG2 does not purchase power from MG1, except at 00:30 (00:10). At this hour, based on the bids, the ES loads, RLD and MG2 are respectively supplied; from 00:18 to 00:24, due to the higher bid of MT than purchasing from the grid, the MT is commissioned with the power of P and the rest of the power is purchased from the grid. Due to the priority of consumers’ bids, the surplus generation supplies internal RLD and ES, and no surplus power is generated for being sold to MG2.

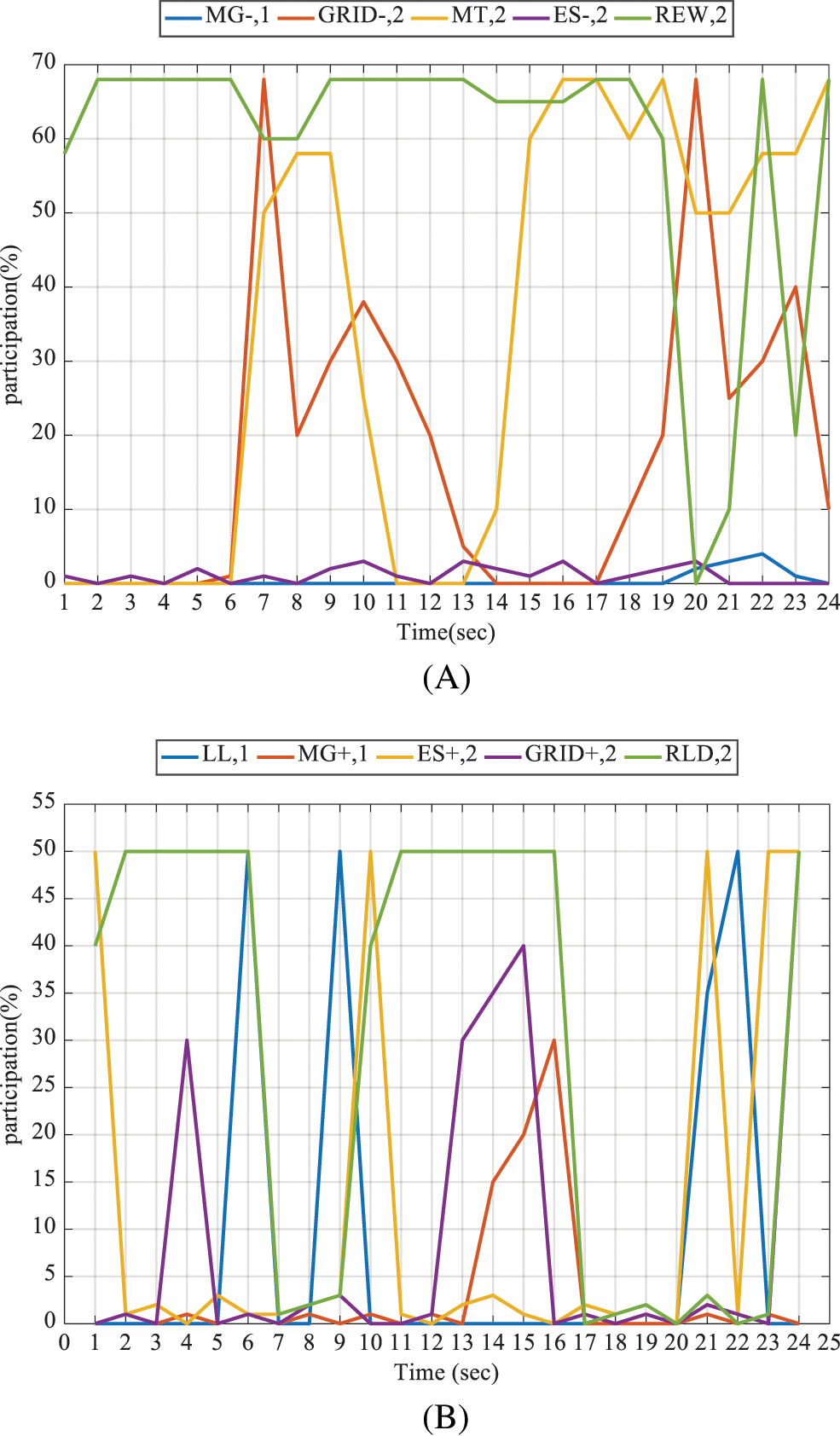
Figure 6: (A) Daily participation percentage of the generation sources of MG2; (B) Daily participation percentage of consumption sources of MG2

Finally, a comparison of the proposed method with other methods is presented. In order to better evaluate the efficiency of the proposed method compared to other methods, we have chosen a larger range. This function is defined as follows:

f(x)=−∑i=1nsin(xi)(sin(i×xi2π))2mM=10,  i=1,…,n,  −50≤xi≤50(18)

Fig. 7 shows a three-dimensional image with greater resolution in the smaller range (−5.5).

Figure 7: Three-dimensional representation of the standard test function

For better comparison, the best coefficients have been extracted from other papers and we have considered only the same initial population number for them. Fig. 8 shows the convergence of the proposed algorithms after 10 different implementations. The method proposed in this paper is compared with particle aggregation and genetics methods. As shown in the figure, the proposed method has high speed and accuracy in finding the final answer.

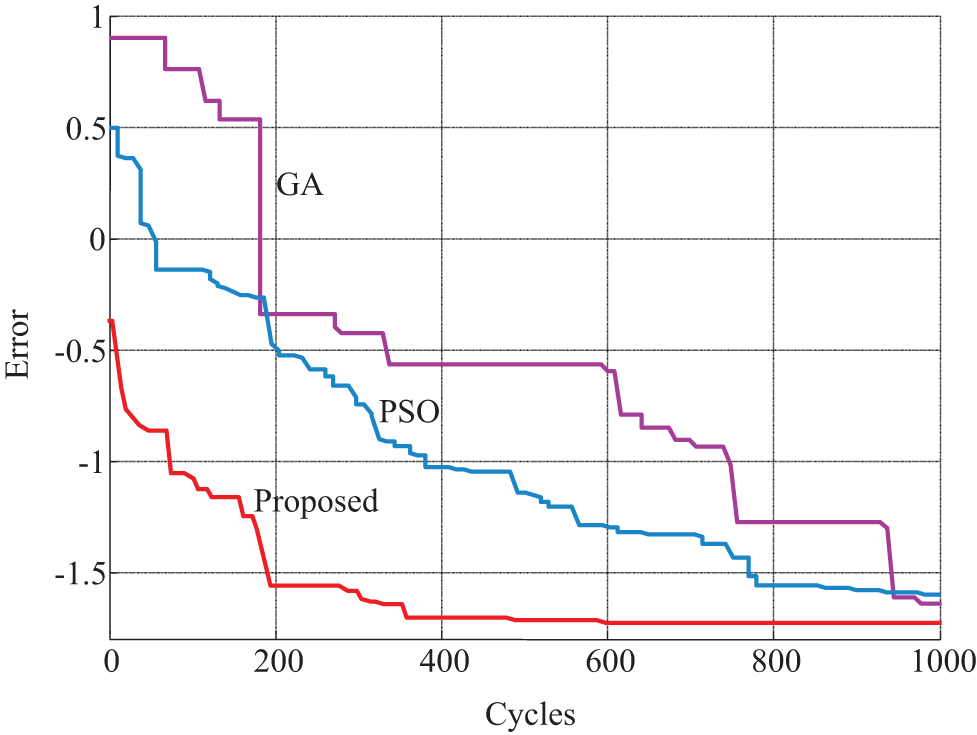
Figure 8: Convergence of the proposed algorithms to solve the proposed test function

In studies, the effect of these modifications has been evaluated as quite useful so that the modified method will be able to achieve better results in less time than the conventional method. Evaluation of the final model of the algorithm shows that the proposed method is a very effective method in solving large system problems that are often impossible to solve with conventional methods. In other words, the value and efficiency of the proposed operators start from the point where the common operators of the algorithm stop and are unable to move forward.

8  Conclusion

The present study proposed a structure with two control layers for energy management of multi-owner MGs, determining the optimal power of generation and consumption sources in the Mga as well as controlling their exchanges with one another and the main grid by using multi-company systems. The developed multi-company system was implemented via a multi-dimensional harmony search algorithm and presented for controlling the operation of islanded and grid-connected MGs. In the proposed algorithm, a set of optimal solutions was taken into account, such that they fully satisfied the technical constraints. The results of two MGs and a condensive load confirmed the performance of the introduced structure in energy management of several MGs. The findings demonstrated that the proposed multi-company system was economically effective as it effectively managed DG sources with the minimum cost of operation. The proposed structure could precisely monitor, control and operate the power system; it was also scalable, robust and easily re-adjusted. Thus, this system can be developed for various needs and conditions to manage and control any structural of power systems by extending the functions of companies and creating additional companies in the system. A developed algorithm is proposed to solve the problem. The purpose of this algorithm is to optimally generate the units of production in the microgrid, demand side management and power exchange with the global network. The proposed algorithm is adapted to control the microgrid connected to the network by creating a primary population with respect to independent and dependent variables and taking into account the technical constraints proposed in this problem. The results show that the proposed optimization algorithm can provide reliable and high-certainty solutions in an acceptable simulation time for energy management system problems. The resulting results clearly demonstrate the effective usability of the proposed structure in systems based on independent and network-connected microgrids.

Funding Statement: The authors received no specific funding for this study.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  Kumar, R. S., Raghav, L. P., Raju, D. K., Singh, A. R. (2021). Impact of multiple demand side management programs on the optimal operation of grid-connected microgrids. Applied Energy, 301, 117466. DOI 10.1016/j.apenergy.2021.117466. [Google Scholar] [CrossRef]

 2.  Ouammi, A., Achour, Y., Dagdougui, H., Zejli, D. (2020). Optimal operation scheduling for a smart greenhouse integrated microgrid. Energy for Sustainable Development, 58, 129–137. DOI 10.1016/j.esd.2020.08.001. [Google Scholar] [CrossRef]

 3.  Raghav, L. P., Rangu, S. K., Dhenuvakonda, K. R., Singh, A. R. (2021). Optimal energy management of microgrids integrated nonconvex distributed generating units with load dynamics. International Journal of Energy Research, 45(13), 18919–18934. DOI 10.1002/er.6995. [Google Scholar] [CrossRef]

 4.  Wang, S., Li, Z., Wu, L., Shahidehpour, M., Li, Z. (2013). New metrics for assessing the reliability and economics of microgrids in distribution system. IEEE Transactions on Power Systems, 28(3), 2852–2861. DOI 10.1109/TPWRS.2013.2249539. [Google Scholar] [CrossRef]

 5.  Georgilakis, P. S., Hatziargyriou, N. D. (2013). Optimal distributed generation placement in power distribution networks: Models, methods, and future research. IEEE Transactions on Power Systems, 28(3), 3420–3428. DOI 10.1109/TPWRS.2012.2237043. [Google Scholar] [CrossRef]

 6.  Lopes, J. P., Moreira, C. L., Madureira, A. G. (2006). Defining control strategies for microgrids islanded operation. IEEE Transactions on Power Systems, 21(2), 916–924. DOI 10.1109/TPWRS.2006.873018. [Google Scholar] [CrossRef]

 7.  Niknam, T., Golestaneh, F., Malekpour, A. (2012). Probabilistic energy and operation management of a microgrid containing wind/photovoltaic/fuel cell generation and energy storage devices based on point estimate method and self-adaptive gravitational search algorithm. Energy, 43(1), 427–437. DOI 10.1016/j.energy.2012.03.064. [Google Scholar] [CrossRef]

 8.  Vahedipour-Dahraie, M., Rashidizadeh-Kermani, H., Anvari-Moghaddam, A., Siano, P. (2020). Flexible stochastic scheduling of microgrids with islanding operations complemented by optimal offering strategies. CSEE Journal of Power and Energy Systems, 6(4), 867–887. DOI 10.17775/CSEEJPES.2019.02560. [Google Scholar] [CrossRef]

 9.  Benlahbib, B., Bouarroudj, N., Mekhilef, S., Abdeldjalil, D., Abdelkrim, T. et al. (2020). Experimental investigation of power management and control of a PV/wind/fuel cell/battery hybrid energy system microgrid. International Journal of Hydrogen Energy, 45(53), 29110–29122. DOI 10.1016/j.ijhydene.2020.07.251. [Google Scholar] [CrossRef]

10. Makhdoomi, S., Askarzadeh, A. (2020). Optimizing operation of a photovoltaic/diesel generator hybrid energy system with pumped hydro storage by a modified crow search algorithm. Journal of Energy Storage, 27, 101040. DOI 10.1016/j.est.2019.101040. [Google Scholar] [CrossRef]

11. Chen, C., Duan, S., Cai, T., Liu, B., Hu, G. (2011). Smart energy management system for optimal microgrid economic operation. IET Renewable Power Generation, 5(3), 258–267. DOI 10.1049/iet-rpg.2010.0052. [Google Scholar] [CrossRef]

12. Garcia-Torres, F., Bordons, C., Ridao, M. A. (2018). Optimal economic schedule for a network of microgrids with hybrid energy storage system using distributed model predictive control. IEEE Transactions on Industrial Electronics, 66(3), 1919–1929. DOI 10.1109/TIE.2018.2826476. [Google Scholar] [CrossRef]

13. Nunna, H. K., Doolla, S. (2013). Energy management in microgrids using demand response and distributed storage—A multiagent approach. IEEE Transactions on Power Delivery, 28(2), 939–947. DOI 10.1109/TPWRD.2013.2239665. [Google Scholar] [CrossRef]

14. Wang, W., Li, C., Liao, X., Qin, H. (2017). Study on unit commitment problem considering pumped storage and renewable energy via a novel binary artificial sheep algorithm. Applied Energy, 187, 612–626. DOI 10.1016/j.apenergy.2016.11.085. [Google Scholar] [CrossRef]

15. Vu, D. H., Muttaqi, K. M., Sutanto, D. (2020). An integrated energy management approach for the economic operation of industrial microgrids under uncertainty of renewable energy. IEEE Transactions on Industry Applications, 56(2), 1062–1073. DOI 10.1109/TIA.28. [Google Scholar] [CrossRef]

16. Tavakoli, M., Shokridehaki, F., Marzband, M., Godina, R., Pouresmaeil, E. (2018). A two stage hierarchical control approach for the optimal energy management in commercial building microgrids based on local wind power and PEVs. Sustainable Cities and Society, 41, 332–340. DOI 10.1016/j.scs.2018.05.035. [Google Scholar] [CrossRef]

17. Ren, M., Liu, X., Yang, Z., Zhang, J., Guo, Y. et al. (2022). A novel forecasting based scheduling method for household energy management system based on deep reinforcement learning. Sustainable Cities and Society, 76, 103207. DOI 10.1016/j.scs.2021.103207. [Google Scholar] [CrossRef]

18. Ahmadpour, A., Farkoush, S. G. (2020). Gaussian models for probabilistic and deterministic wind power prediction: Wind farm and regional. International Journal of Hydrogen Energy, 45(51), 27779–27791. DOI 10.1016/j.ijhydene.2020.07.081. [Google Scholar] [CrossRef]

19. Dejamkhooy, A., Ahmadpour, A. (2021). Optimal UC and economic dispatching with various small energy resources in the micro-grid using IPPOA and IMILP. Energy Reports, 7, 7572–7590. DOI 10.1016/j.egyr.2021.10.124. [Google Scholar] [CrossRef]

20. Planakis, N., Papalambrou, G., Kyrtatos, N. (2022). Ship energy management system development and experimental evaluation utilizing marine loading cycles based on machine learning techniques. Applied Energy, 307, 118085. DOI 10.1016/j.apenergy.2021.118085. [Google Scholar] [CrossRef]

21. Ahmadpour, A., Mokaramian, E., Anderson, S. (2021). The effects of the renewable energies penetration on the surplus welfare under energy policy. Renewable Energy, 164, 1171–1182. DOI 10.1016/j.renene.2020.10.140. [Google Scholar] [CrossRef]

22. Marzband, M., Sumper, A., Ruiz-Álvarez, A., Domínguez-García, J. L., Tomoiagă, B. (2013). Experimental evaluation of a real time energy management system for stand-alone microgrids in day-ahead markets. Applied Energy, 106, 365–376. DOI 10.1016/j.apenergy.2013.02.018. [Google Scholar] [CrossRef]

23. Marzband, M., Sumper, A., Domínguez-García, J. L., Gumara-Ferret, R. (2013). Experimental validation of a real time energy management system for microgrids in islanded mode using a local day-ahead electricity market and MINLP. Energy Conversion and Management, 76, 314–322. DOI 10.1016/j.enconman.2013.07.053. [Google Scholar] [CrossRef]

24. Marzband, M., Ghadimi, M., Sumper, A., Domínguez-García, J. L. (2014). Experimental validation of a real-time energy management system using multi-period gravitational search algorithm for microgrids in islanded mode. Applied Energy, 128, 164–174. DOI 10.1016/j.apenergy.2014.04.056. [Google Scholar] [CrossRef]

25. Ma, Y., Li, C., Zhou, J., Zhang, Y. (2020). Comprehensive stochastic optimal scheduling in residential micro energy grid considering pumped-storage unit and demand response. Journal of Energy Storage, 32, 101968. DOI 10.1016/j.est.2020.101968. [Google Scholar] [CrossRef]

26. Yang, X. S. (2009). Harmony search as a metaheuristic algorithm. In: Music-inspired harmony search algorithm, pp. 1–14. Berlin, Heidelberg: Springer. [Google Scholar]

This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.