Fluid Dynamics & Materials Processing

DOI: 10.32604/fdmp.2021.014429

ARTICLE

MHD and Viscous Dissipation Effects in Marangoni Mixed Flow of a Nanofluid over an Inclined Plate in the Presence of Ohmic Heating

D. R. V. S. R. K. Sastry1, Peri K. Kameswaran2 and Mohammad Hatami3,*

1Department of Mathematics, SASTRA University, Tamilnadu, India
2Department of Mathematics, School of Advanced Sciences, VIT University, Tamilnadu, India
3Mechanical Engineering Department, Esfarayen University of Technology, Esfarayen, Iran
*Corresponding Author: Mohammad Hatami. Email: M.Hatami@xjtu.edu.cn
Received: 26 September 2020; Accepted: 08 January 2021

1  Introduction

Mathematical modeling of natural phenomena generally involves partial differential equations and nonlinear ordinary differential equations. Boundary-layer problems are the best examples in this case. Fluid flow, heat transfer, and mass transfer are relevant problems in many industrial processes like metal and polymer extrusion processes, crystal growing, glass-fiber, paper production, and so on. Since magneto-hydro-dynamics (MHD) is an electrically conducting fluid flow in presence of a magnetic field, it is significantly important in many areas of engineering and technology. The effect of the magnetic field over a stretching surface in various states is investigated by Andersson [1], and Parsa et al. [2]. Further, Hamad et al. [3] observed the hydrodynamic slip impact on Nusselt and Sherwood numbers over a plate that is moving with constant velocity. Over an inclined surface, Noor et al. [4] examined the effect of heat source over the flow behavior. The porosity effect is studied by Bhuvanseswari et al. [5] over an inclined plate. Effect of mixed convection on Heat and mass transfer over a non-linear stretching sheet is noticed by Pal et al. [6] along with Soret and Dufour effects. A non-Newtonian mixed convection flow characteristics along an inclined plate are studied by Sui et al. [7]. The angle of inclination suppresses the skin friction and the heat transfer rate is observed by Orhan Aydin et al. [8]. A further effect of the magnetic parameter in unsteady natural convection over an inclined plate is studied by Ganesan et al. [9]. Scaling transformation for a free convective heat and mass transfer in an inclined plate is analyzed by Gnaneswar Reddy [10]. The surface tension gradients produce Marangoni convection. Wang et al. [11], found experimentally that the Marangoni effect is the most dominant force in shaping the weld pool. In semiconductors, Nishino et al. [12] found silicon crystals are influenced by Marangoni convection. Effect of temperature for melting parameter and Rayleigh number in a Marangoni convection is elevated by Sheikholeslami et al. [13]. Al-Mudhaf et al. [14] obtained a similarity solution for magneto hydro-dynamic thermosolutal Marangoni convection. Flow equations are developed for the Marangoni forced convective boundary layers by Pop et al. [15]. Nanofluid flow over an inclined porous plate in presence of radiation and heat generation is studied by Sudarsana Reddy et al. [16]. Numerical study of turbulent flow of regular and nanofluid inside heat exchangers using perforated louvered strip inserts is investigated by Nakhchi et al. [17–19]. They noticed that an additional vortex flow near the holes is the main reason for Nu number enhancement. Hayat et al. [20] observed the impact of Cattaneo–Christov heat flux fluid model over a variable thicked surface. It is noticed that higher thermal relaxation decreases temperature profiles. Khan et al. [21] noticed the velocity profiles decrement with Hartmann number in their comparative study of Casson fluid with chemical reaction. Recently, Nayak et al. [22] observed a significant heat transfer rate for even small estimation of radiation parameter in rotating disk problem. Abbas et al. [23] have considered the entropy optimized Darcy–Forchheimer nanofluid and noticed a rise in temperature of the fluid particles in presence of Biot number. Later, Abbas et al. [24] solved the governing equations of motion using the shooting method and obtained numerical results. Further, they identified a significant impact of the magnetic field on the flow field and as well as entropy rate. Very recently, Muhammad et al. [25] considered a viscous material flow by a curved surface with the second order slip and entropy generation. It is found a numerical solution using MATHEMATICA. They noticed that both Bezan number and entropy generation is upsurged versus heterogeneous reaction parameter. Ijaz Khan et al. [26,27] analyzed the problem of the binary reaction effect in Walter–B nanofluid. The mixed convection parameter enhances the velocity field. Ibrahim et al. [28] studied the problem of carbon nanotubes flow over a stretchable sheet. They have used the finite element method to solve flow equations and found that single-walled carbon nanotubes move with faster velocity than that of multi-walled carbon nanotubes water-based nanofluid. Very recently, Ijaz Khan et al. [29] considered a micropolar ferrofluid with Darcy porous medium. khan et al. [30] in their problem of unsteady heat and mass transfer in MHD Carreau nanofluid flow observed both Nusselt and Sherwood numbers are decreasing functions of thermophoresis parameter. Further, Azam et al. [31–33] have considered a notable amount of work over the flow of Cross nanofluid. The local heat transfer rate is reduced with an increase in the thermophoresis parameter. The magnitude of surface drag force is diminished for significant values of the Weissenberg number. Houda et al. [34] observed the viscous and thermal conductivity effects on heat transfer in Alumina–water based nanofluid. Heat transfer is enhanced only when the temperature exceeds 40°C . Steady convective slip flow with uniform heat and mass flux in the presence of Ohmic heating is numerically studied by Machireddy [35]. It is found that the Grashof numbers for heat transfer Gr and mass transfer Gm accelerate the flow velocity. Slama et al. [36] considered a mixed convective nanofluid flow over a vertical anisotropic porous channel. A stronger reverse flow is noticed by increasing the buoyancy force strength, the porous medium permeability, the heat flux ratio and by decreasing the anisotropic thermal conductivity ratio.

As mentioned above of the literature reveals that the majority of the researchers have explored the attributes of the Marangoni mixed convective heat transfer in MHD nanofluid flow over an inclined flat plate. However, to the best of our knowledge, such a phenomenon, along with viscous dissipation, is not examined over the water-based nanofluid containing Copper, Alumina nanoparticles. The fourth-order RK scheme combined with the shooting method is implemented for solving the governing equations of flow and energy. The influence of numerous pertinent parameters on flow velocity, temperature, and heat transfer has been illustrated through graphs.

2  Problem Formulation

Consider a nanofluid flow containing two different nano-sized metallic particles namely Copper and Alumina through an inclined plate (Tab. 1). Assume the state of thermal equilibrium between nanoparticles and base fluid with no-slip condition. Further, assume that fluid is viscous dissipative, incompressible, and laminar. The geometry of the problem is shown in the Fig. 1. It is also assumed that flow takes place at y ≥ 0. Further, the induced magnetic field is nullified when compared to the applied magnetic field by taking the magnetic Reynolds number less than unity. The nanofluid equations of motion are obtained as follows.

∂u∂x+∂v∂y=0 (1)

ρnf(u∂u∂x+v∂u∂y)=μnf∂2u∂y2−δ∗H02usin2ζ+ρnfg~β(T−Tr)sinξ (2)

(ρcp)nf(u∂T∂x+v∂T∂y)=knf∂2T∂y2+μnf(∂u∂y)2+δ∗H02u2sin2ζ (3)

u∂C∂x+v∂C∂y=DS∂2C∂y2−K0(C−Cr) (4)

where u and v are the fluid velocity components along x and y axes respectively, g~ is the acceleration due to gravity, T is the fluid temperature, C is the solutal concentration, Tr is the reference temperature, Cr is reference concentration of the fluid, β is thermal expansion coefficient, DS is the species diffusivity, δ∗ is the electrical conductivity of the fluid, H0 is the applied magnetic field and K0 is chemical reaction parameter of the first order. Further, the effective dynamic viscosity ( μnf ), effective density ( ρnf ), effective thermal diffusivity ( αnf ), effective heat capacitance (ρcp)nf , and effective thermal conductivity knf of the nanofluid are defined by

μnf=μf(1−ϕ)2.5,ρnf=(1−ϕ)ρf+ϕρs,αnf=knf(ρcp)nf,(ρcp)nf=(1−ϕ)(ρcp)f+ϕ(ρcp)sandknf=kf(ks+2kf−2ϕ(kf−ks)ks+2kf+ϕ(kf−ks)) (5)

where volume fraction is denoted by ϕ . The subscripts nf, f, and s represent properties defined for nano, base fluids, and nano species, respectively. The convective boundary conditions for Eqs. (1)–(4) may be taken in the form:

aty=0:v=0,T=Tr+ax2,C=Cr+bx2,μnf∂u∂y=γ∂T∂x+γ∗∂C∂xandu→0,T→Tr,C→Crasy→∞ (6)

where a, b are constants. Further, the values of γ and γ∗ are obtained from the interfacial surface tension relation, σ=σ0[1−γ(T−Tr)−γ∗(C−Cr)] , σ0 is interface surface tension and γ=−∂σ∂T , γ∗=−∂σ∂C . The following similarity variables are taken into consideration to convert the governing equations of motion to a set of coupled nonlinear ordinary differential equations.

ψ=C1xf(η),η=C2y,T=Tr+θ(η)ax2,C=Cr+h(η)bx2 (7)

where η is the similarity variable, f(η) , θ(η) and h(η) are the dimensionless stream function, temperature, and concentration respectively. Further C1 and C2 are taken as

C1=(dσdT|Caμfρf2)1/133,C2=(dσdT|Caρfμf2)1/133 (8)

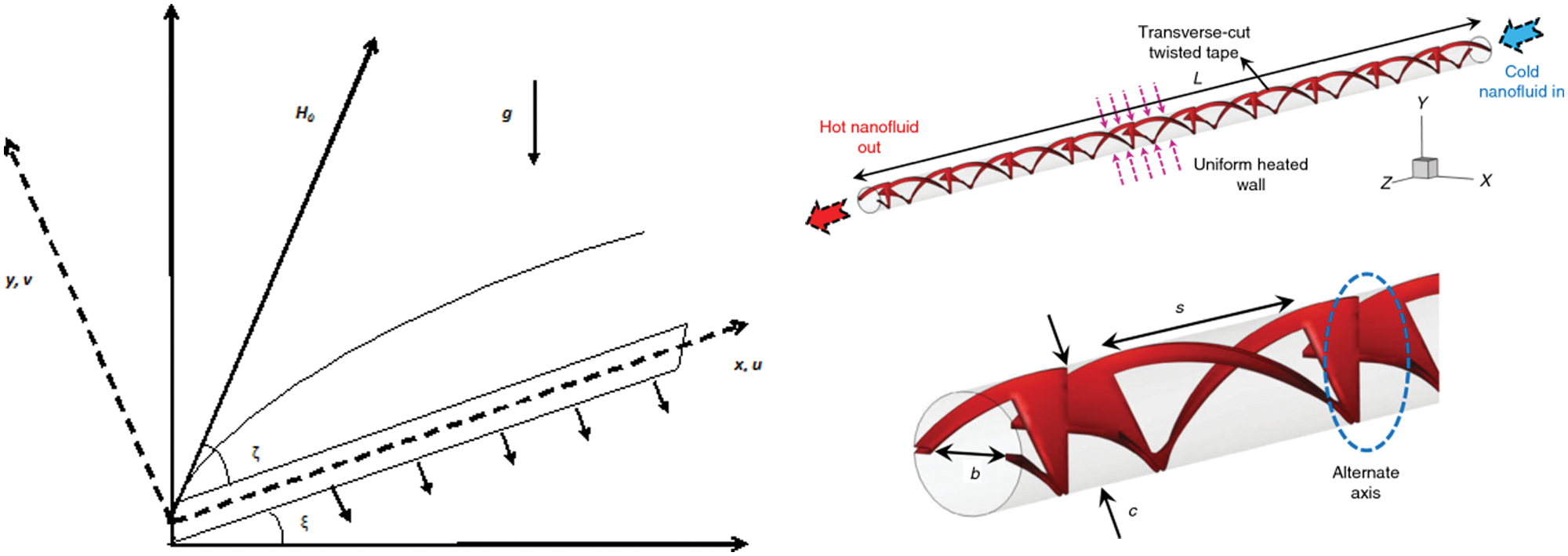
Figure 1: Schematic diagram of the physical problem and its application (Right)-Nakhchi et al. [19]

Table 1: Thermo physical properties of nanoparticles (Oztop et al. [37])

The incompressibility condition is identically satisfied and the governing Eqs. (2)–(4) are transformed to the following set of non-dimensional coupled ordinary differential equations.

f′′′=λ1λ2(f′2−ff″)+λ1M2f′sin2ζ−λ1λ2λθsinξ (9)

λ3θ′′=Prλ4(2f′θ−fθ′)−PrEc(M2f′2sin2ζ−f′′2) (10)

h′′=Sc(2hf′−fh′+K∗h) (11)

along with the boundary conditions in non-dimensional form

atη=0:f(0)=0,θ(0)=1,h(0)=1,f′′(0)=−2λ1(1+ϵ)and

asη→∞:f′(∞)=0,θ(∞)=0,h(∞)=0 (12)

λ1=(1−ϕ)2.5,λ2=1−ϕ+ϕ(ρsρp),λ3=ks+2kf−2ϕ(kf−ks)ks+2kf+ϕ(kf−ks),λ4=1−ϕ+ϕ((ρCp)s(ρCp)f)

where Hartmann magneto hydrodynamic parameter (M), scaled chemical reaction parameter (K*), Schmidt number (Sc), mixed convection parameter ( λ ), Eckert number (Ec), marangoni parameter (ϵ) , and Prandtl number (Pr) may be taken as follows:

M=δ∗12H0μ16ρ13dσdT|C13a13,K∗=k0μfρfdσdT|C2a23,Sc=υfDs,λ=ag~βxC12C22,Ec=C12C22a(Cp)f,ϵ=ΔCdσdC|TΔTdσdT|C,Pr=ϵf(ρCp)fkf

The quantities of practical interest, in this study, are local Nusselt number Nux and local Sherwood number Shx . These parameters respectively characterize the heat and mass transfer rates near the wall. Heat transfer rate of the wall surface,

q(x)=−knf(∂T∂y)y=0=−knfC2ax2θ′(0) (13)

The Nusselt number, a measure of heat transfer,

Nux=xq(x)kf_[T−Tr] (14)

Using the Eqs. (8), (13) and (14), one can get the dimensionless wall heat transfer rate as

NuxC2x(kfknf)=−θ′(0) (15)

The mass flux at the wall,

m=−Ds(∂C∂y)y=0=−DsC2bx2h′(0) (16)

Sherwood number, measure of mass transfer,

Shx=xmDs(C−Cr) (17)

From the Eqs. (8), (16) and (17), one can get the dimensionless mass transfer rate as

ShxC2x=−h′(0) (18)

where C2x is a dimensionless quantity.

3  Problem Solution

From Eqs. (9)–(12), we obtain the following system:

y1′=y2

y2′=y3

y3′=λ1λ2(y22−y1y3)+λ1M2y2sin2ζ−λ1λ2λy4sinξ

y4′=y5

y5′=Prλ3λ4(2y2y4−y1y5)−PrEc(M2y22sin2ζ−y32)

y6′=y7

y7′=Sc(2y6y2−y1y7+K∗y6) (19)

Initial conditions in terms of yi are as follows:

y1(0)=0,y4(0)=1,y3(0)=−2λ1(1+ϵ),y6(0)=1,y2(∞)=y4(∞)=y6(∞)=0 (20)

We obtained a numerical solution for (19) along with (20) through a fourth-order Runge–Kutta scheme of integration associated with shooting technique subject to an order of convergence 10−6 .

4  Results and Discussion

The analysis result is carried out by taking Prandtl number 6.785 (water) and various values for defined parameters. The influence of the magnetic parameter M on the velocity profile is displayed in Fig. 2. It is found that velocity decreases with an increase in M. This is due to the impact of the Lorentz force, induced by the transverse magnetic field. In both forced convection ( λ=0 ) and mixed convection, Copper nano species experience higher momentum boundary layer thickness than Alumina species. Figs. 3 and 4 depict the effect of magnetic number M on temperature and concentration respectively. The temperature and concentration increase by an increase in the value of M.

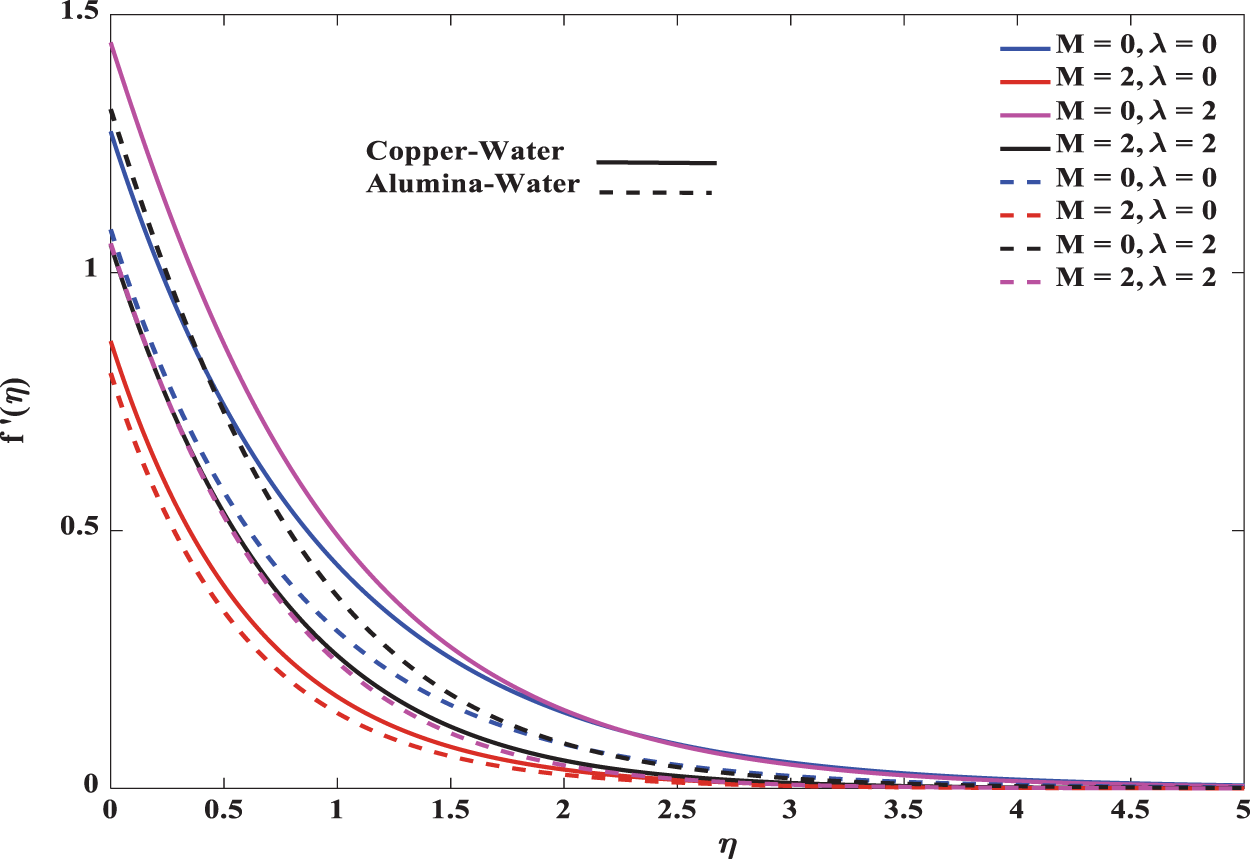
Figure 2: Influence of M on velocity in both forced and mixed convection flows for ζ=π3,ξ=π4,Ec=Sc=K∗=ϵ=ϕ=0.2

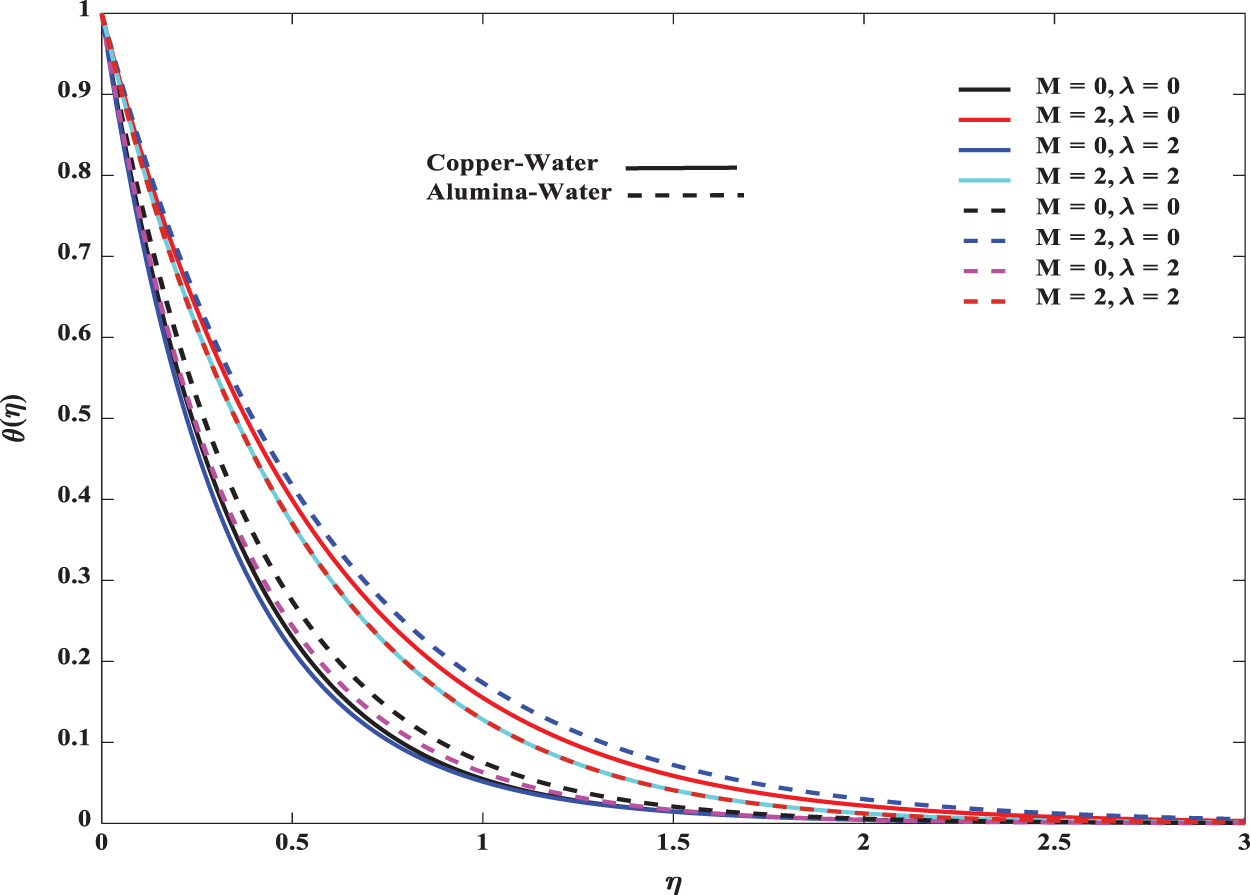
Figure 3: Influence of M on temperature in both forced and mixed convection flows for ζ=π3,ξ=π4,Ec=Sc=K∗=ϵ=ϕ=0.2

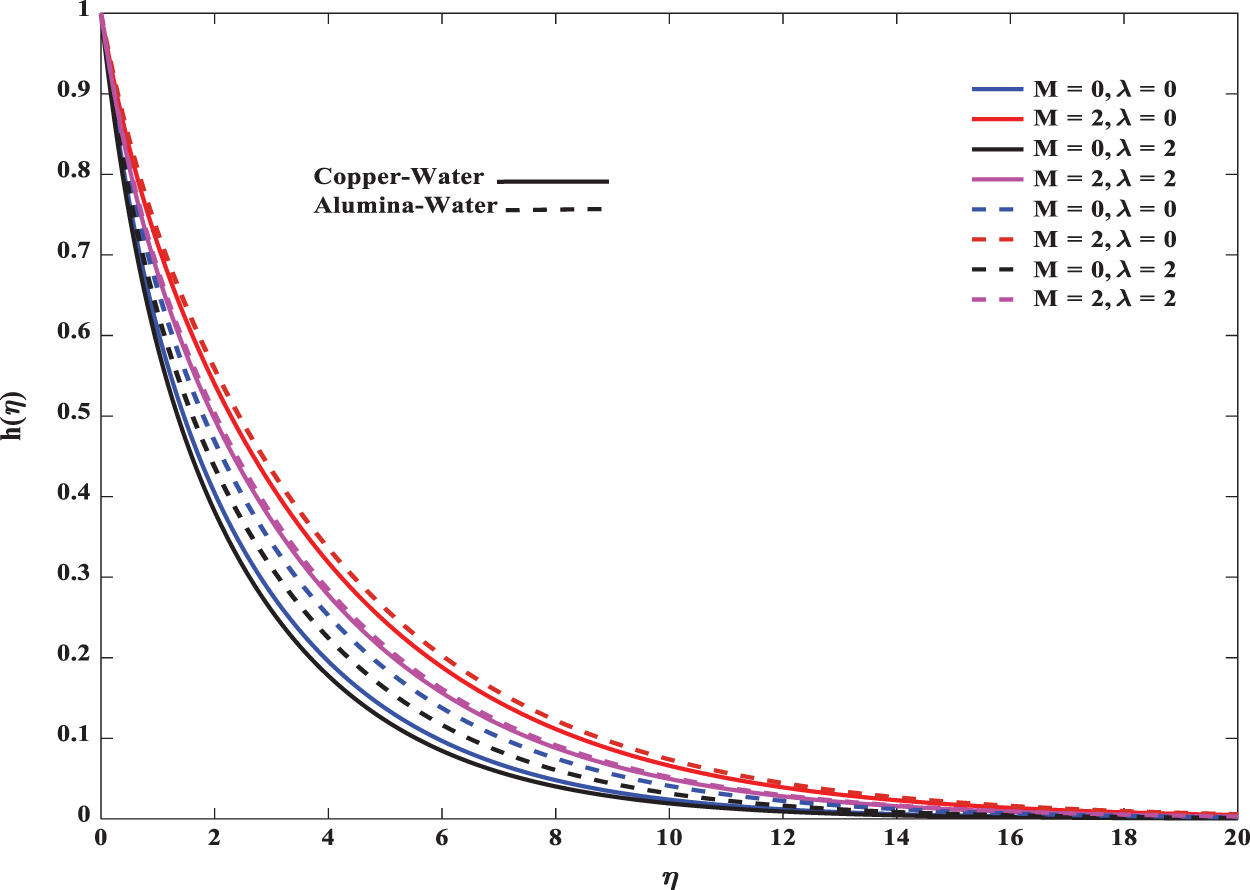
Figure 4: Influence of M on concentration in both forced and mixed convection flows for ζ=π3,ξ=π4,Ec=Sc=K∗=ϵ=ϕ=0.2

The resistive force produces more heat which leads a hike in temperature. Both thermal and concentration boundary layers are predominant in Alumina nanofluid particles. The mixed convection parameter plays a vital role in reducing this dominance. Both momentum and thermal boundary layers are affected by mixed convection. Fluid gets momentum with increasing convection parameter and hence the thickness of the thermal boundary layer decreases. This change is impressive in nanofluids compared to regular fluids. Further, increase in volume fraction, reduces velocity profile. The combined effect of mixed convection parameter and volume fraction over temperature and velocity profiles can be investigated through Figs. 5 and 6, respectively. The velocity of the regular fluid is low compared to nanofluid. It is clear from the figure that the momentum boundary layer thickness is lower for nanofluid particles. Mixed convection parameter regulates both temperature and velocity profiles. Temperature decreases and velocity increases with increasing mixed convection parameter. This change is significant in nanofluid particles.

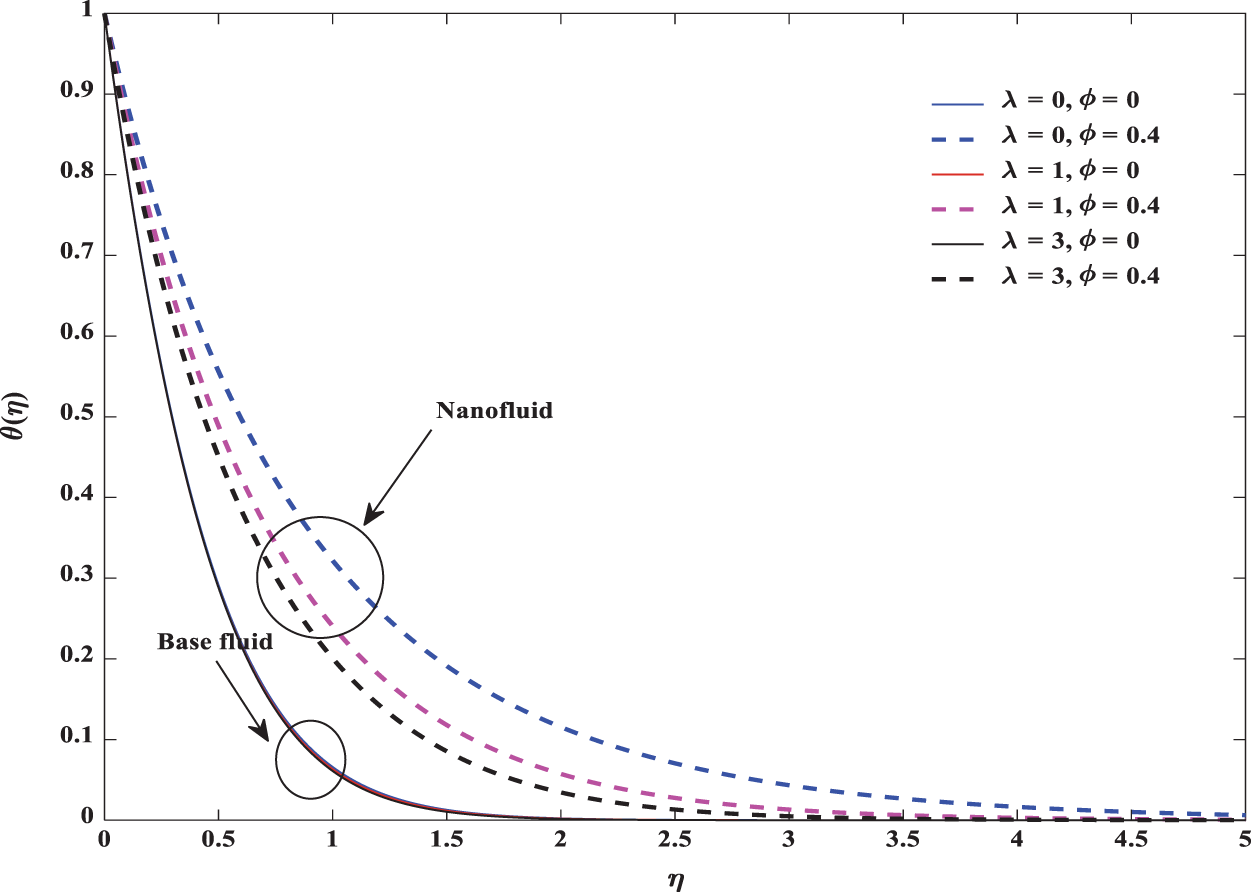
Figure 5: Influence of λ on temperature in both regular and nanofluid flows for ζ=π3,ξ=π4,Ec=Sc=K∗=ϵ=0.2,M=2

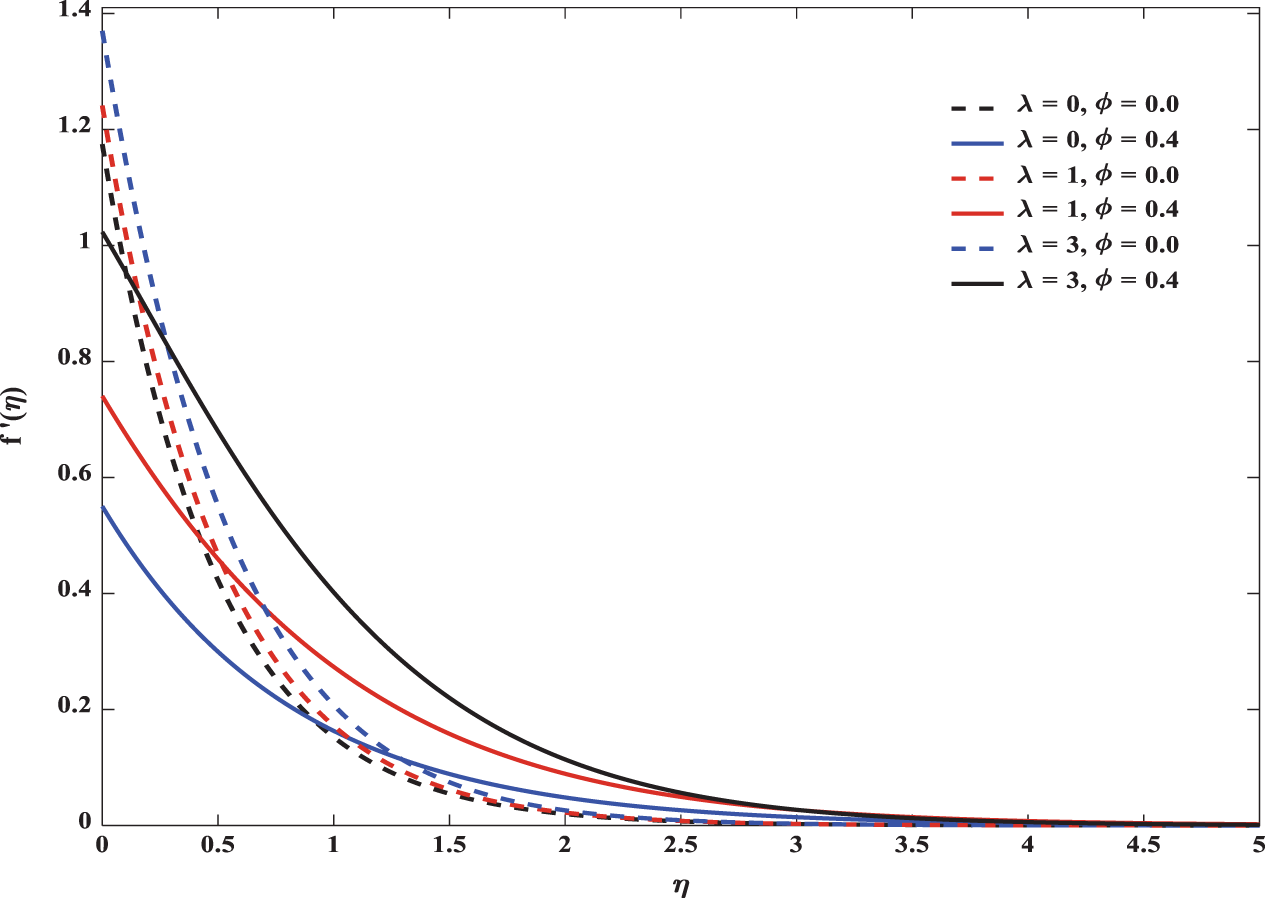
Figure 6: Influence of λ on velocity in both regular and nanofluid flows for ζ=π3,ξ=π4,Ec=Sc=K∗=ϵ=0.2,M=2

Fig. 7 shows how velocity is affected by the angle of inclination ζ. Velocity decreases with an increase in that angle. The reason is that more angle of inclination provides a greater magnetic field which enhances the resistive force. Further Figs. 8 and 9 ensure, both temperature and concentration profiles whose boundary layer thickness increase with an increase in the angle of inclination.

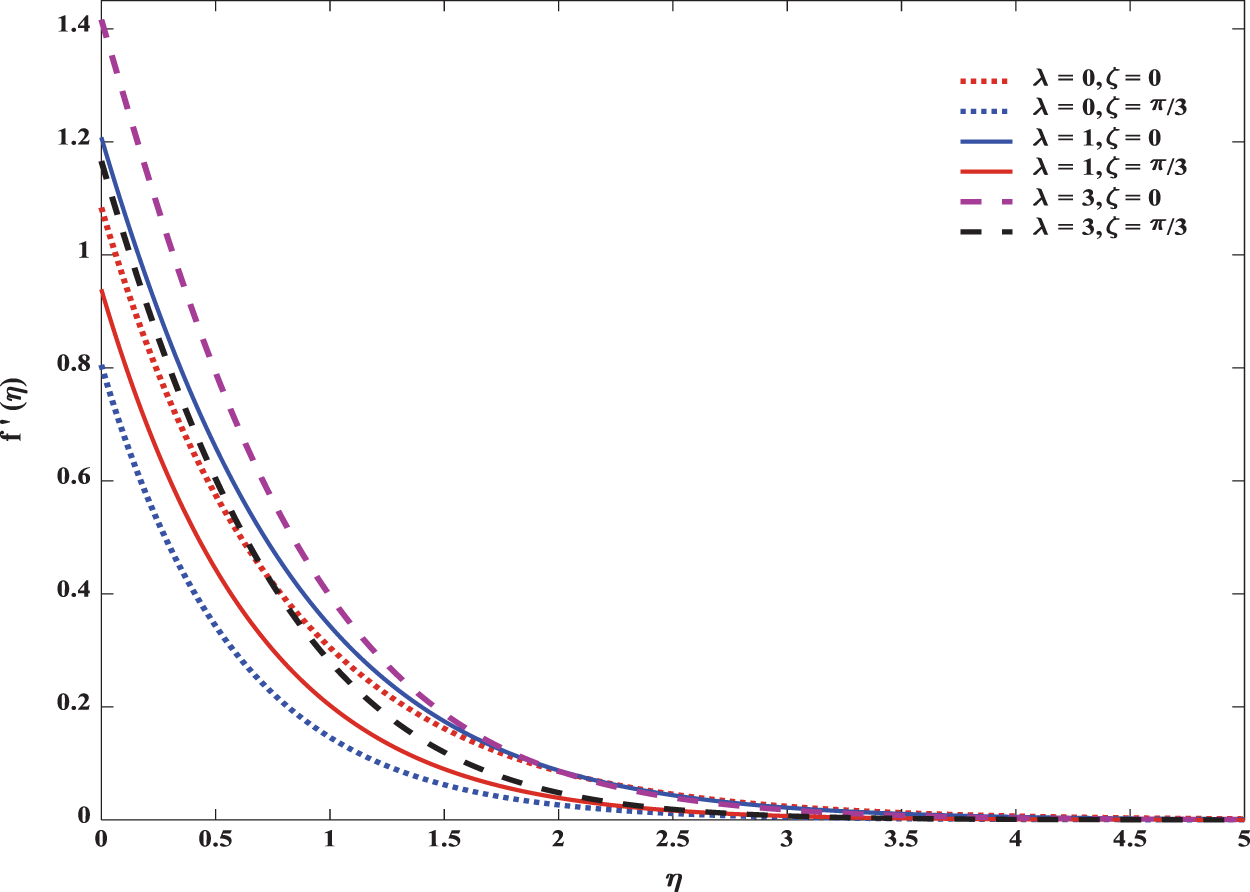
Figure 7: Influence of ζ on velocity in both forced and mixed convection flows for ξ=π4,Ec=Sc=K∗=ϵ=ϕ=0.2,M=2

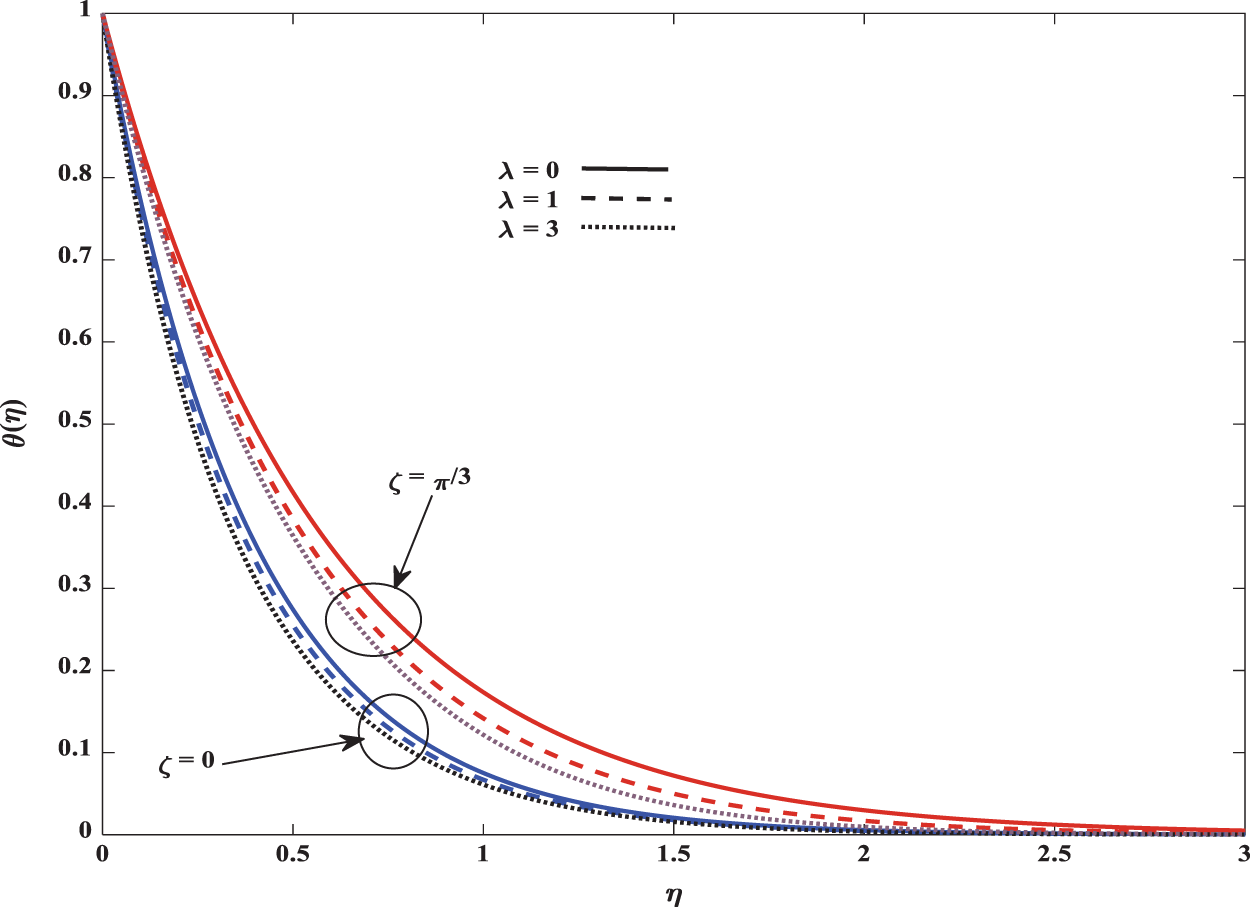
Figure 8: Influence of ζ on temperature in both forced and mixed convection flows for ξ=π4,Ec=Sc=K∗=ϵ=ϕ=0.2,M=2

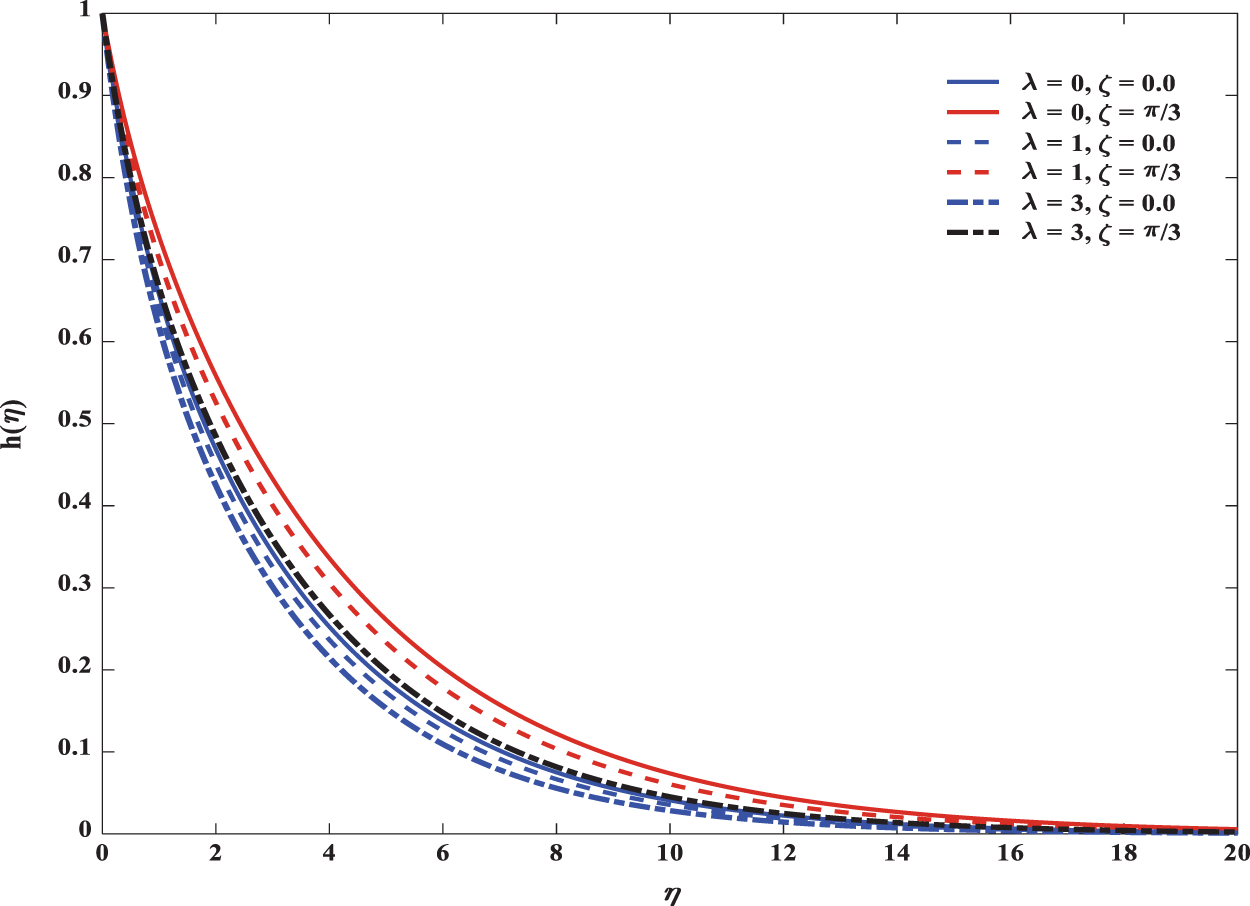
Figure 9: Influence of ζ on concentration in both forced and mixed convection flows for ξ=π4,Ec=Sc=K∗=ϵ=ϕ=0.2,M=2

The variations in the temperature profiles along with Eckert number, mixed convection parameter and Marangoni parameter are exhibited in Fig. 10. Temperature and thermal boundary layer increase for an increase in the Eckert number. An increase in Eckert number takes place because of generation of more heat due to friction.

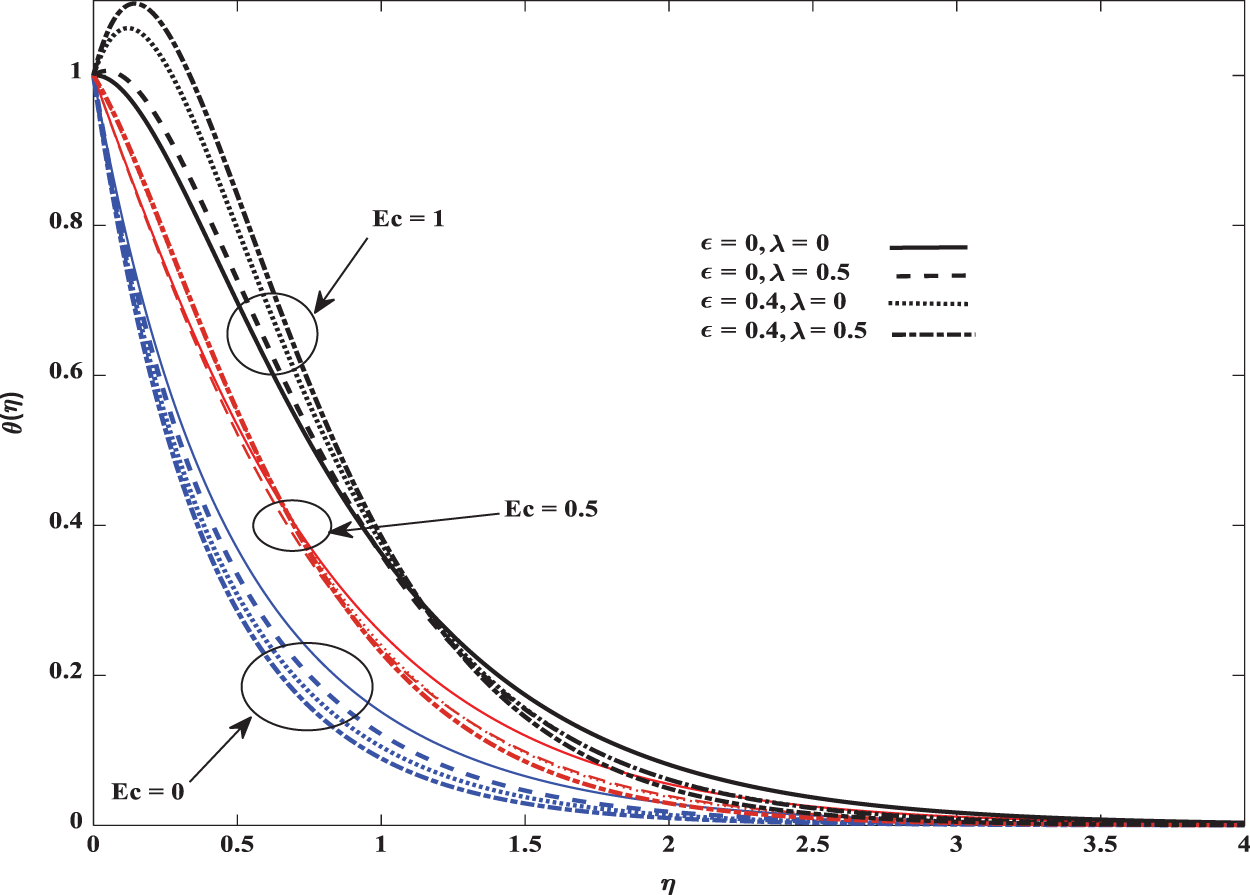
Figure 10: Influence of Ec on temperature in both forced and mixed convection flows for ζ=π3,ξ=π4,Sc=K∗=ϕ=0.2,M=2

It is clear evidence from Fig. 11 that an increase in the angle ξ, reduces the temperature of the fluid. The temperature distribution is significantly high for the flat plate compared to the inclined plate. Also the thermal boundary layer thickness for Copper –water nanofluid is less than that of Alumina–water nanofluid. This is due to the fact that buoyancy effects dominate for larger values ξ. It is worth noting from Figs. 12 and 13 that the heat and mass transfer rates are enhanced by increasing mixed convection numbers. These rates are high in regular fluids ( ϕ = 0). In nanofluids, Alumina particles possess a high rate of heat transfer compared to Copper particles. Further, Nusselt and Sherwood numbers are decreased with respect to an increase in volume fraction. The minimum peak for both them is noticed for the Copper–water nanofluid at ϕ = 0.4. This may be due to the high density of the Copper particles at a higher volume fraction produces more momentum among the particles and hence posses less heat and mass transfer rates. From Fig. 14, it is observed that at low values of Marangoni parameter ϵ , rate of heat transfer is more in Copper particles, but it is worthy to note that at high Marangoni number, Alumina species possess greater heat transfer rate.

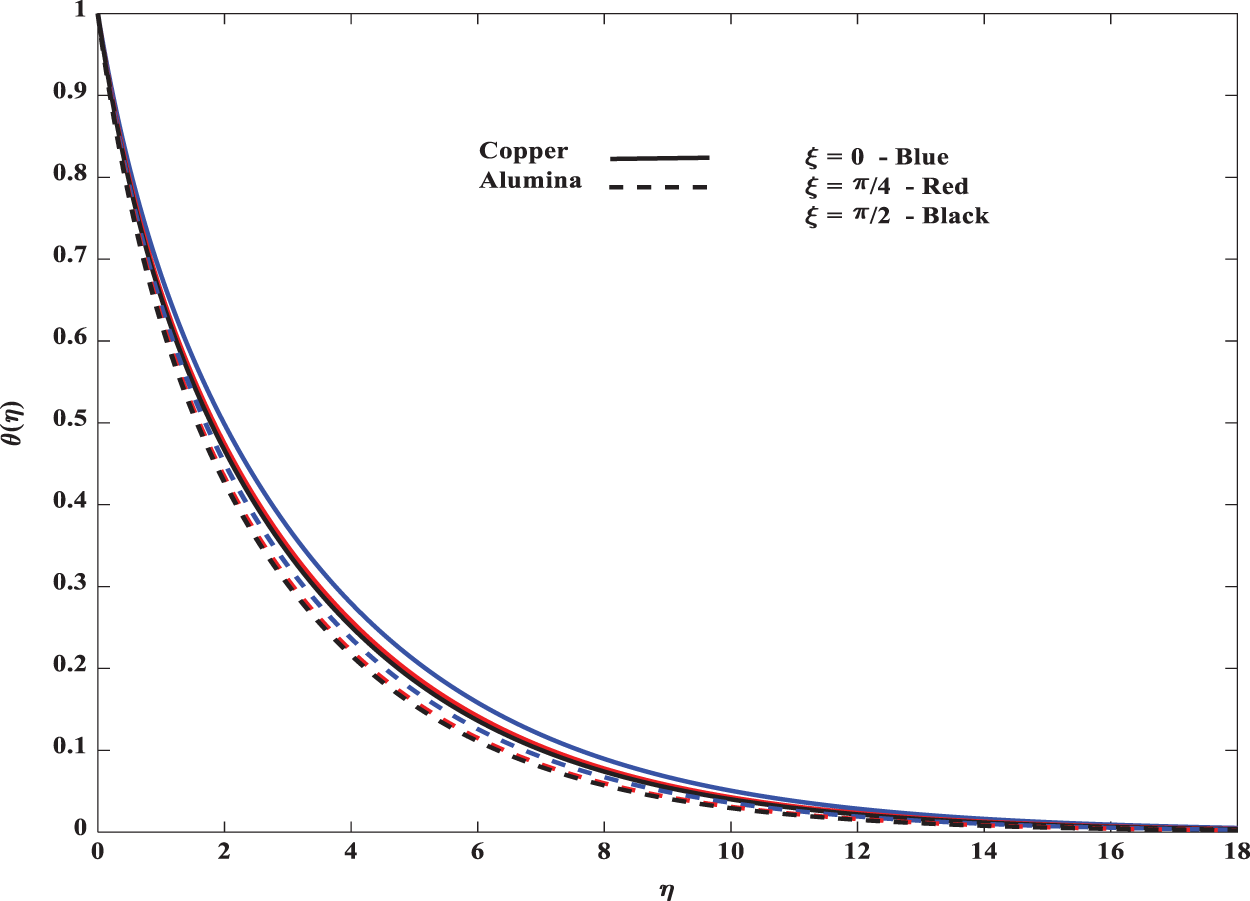
Figure 11: Influence of ξ on temperature profile for ξ=π4,Ec=Sc=K∗=ϵ=ϕ=0.2,M=2,λ=1

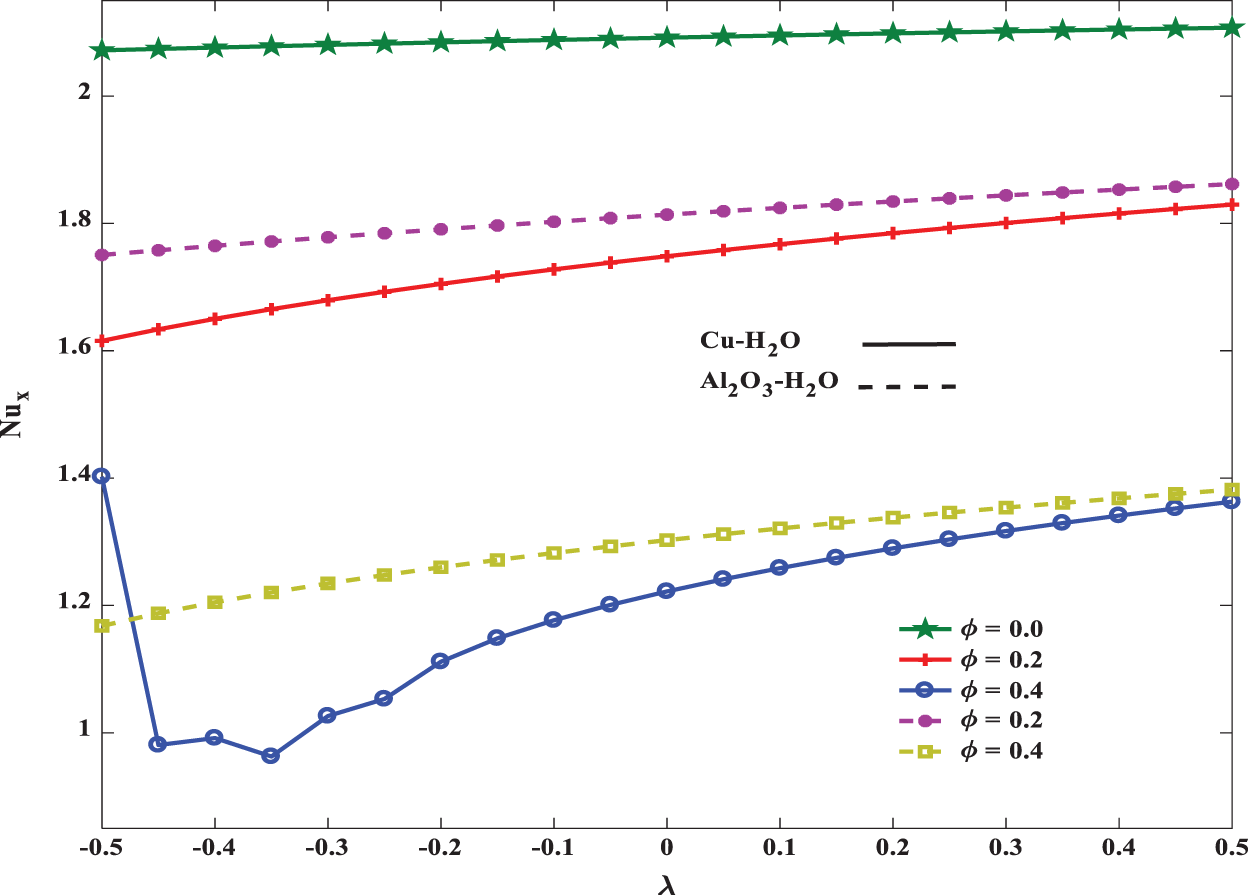
Figure 12: Influence of λ on Nusselt number for ζ=π3,ξ=π4,Ec=Sc=K∗=ϵ=0.2,M=2

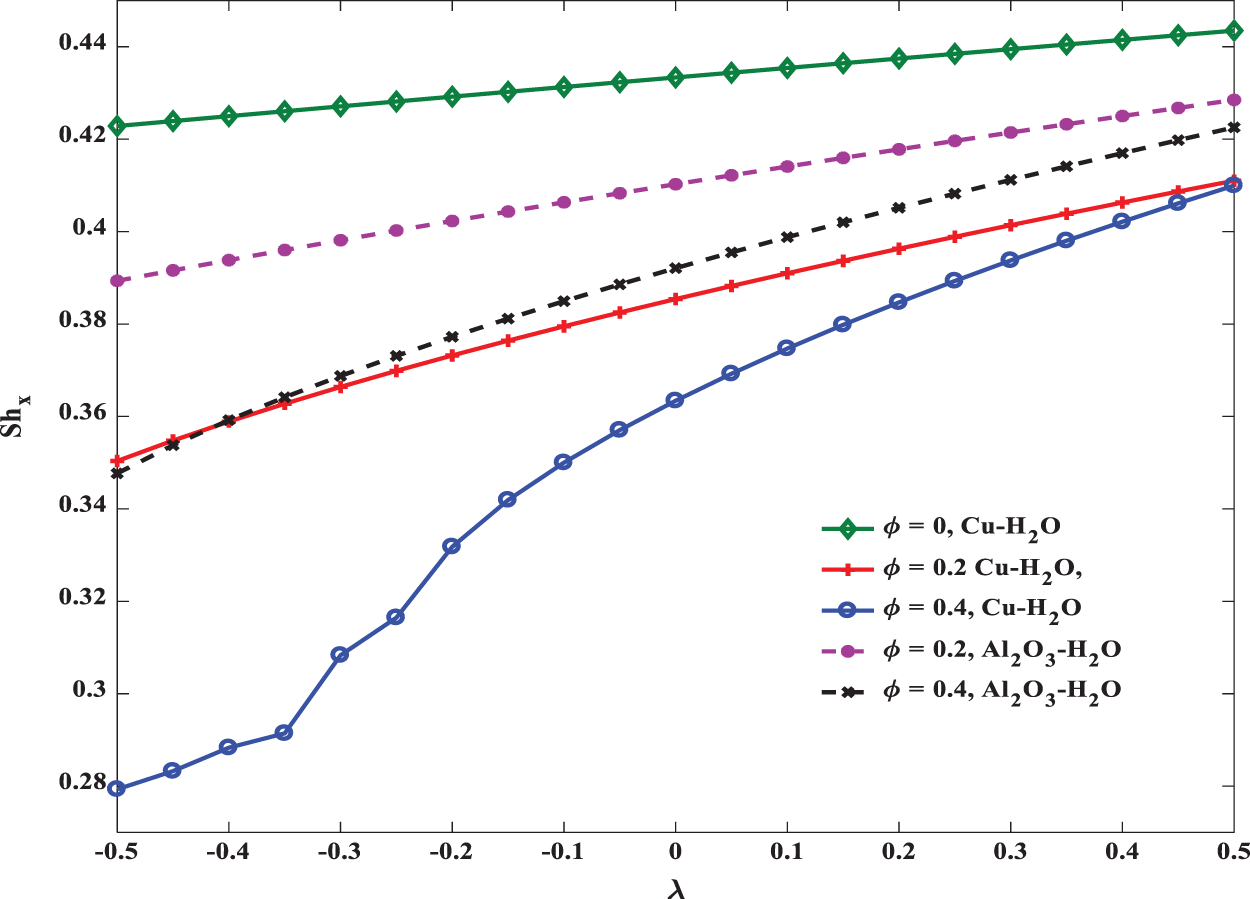
Figure 13: Influence of λ on Sherwood number for ζ=π3,ξ=π4,Ec=Sc=K∗=ϵ=0.2,M=2

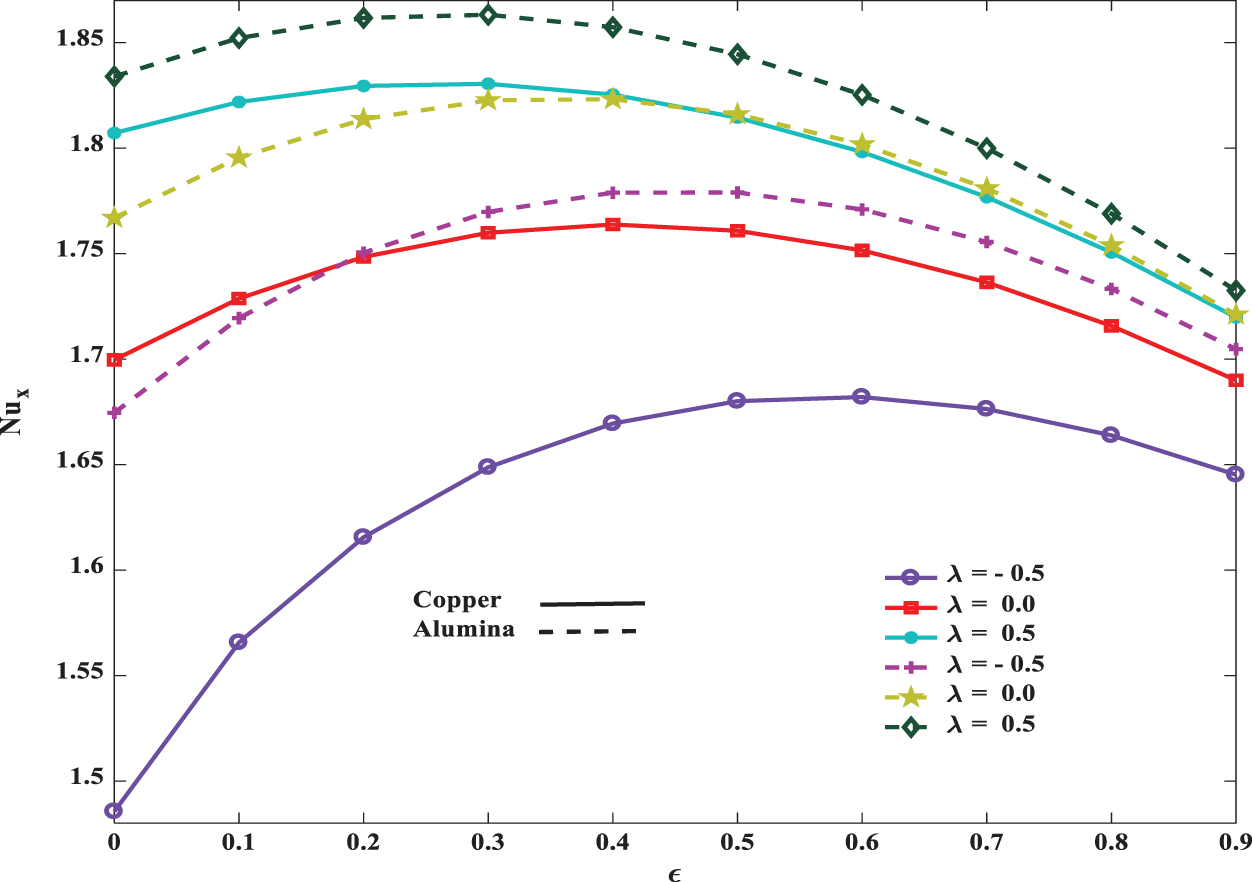
Figure 14: Influence of ε on Nusselt number for ζ=π3,ξ=π4,Ec=Sc=K∗=ϕ=0.2,M=2

The quantities that measure rate of heat and mass transfer, Nusselt number and Sherwood number respectively, are noted in the Tab. 2. It is worth to note that both Nusselt and Sherwood numbers decrease with increasing the magnetic parameter M, and inclination angle ζ. Further, an increase in the inclination angle ξ enhances the heat and mass transfer rates. Tab. 3 also confirms the accuracy of obtained results by comparing to Al-Mudhaf et al. [14] results.

Table 2: Numerical values of Nusselt and Sherwood numbers (λ=0.5,Pr=7,Ec=0.5,ϕ=ϵ=Sc=K∗=0.2)

Table 3: Comparison values of velocity and temperature gradients (λ=0,Pr=0.72,Ec=0.1,ϕ=0,ϵ=1,Sc=0.6,K∗=0,ξ=0,ζ=π/2)

5  Conclusions

The problem of Marangoni MHD mixed convective nanofluid flow subject to viscosity, chemical reaction effects past an inclined plate is considered. Results are carried over two different nanoparticles, Copper and Alumina. Heat and mass transfer effects along with velocity, temperature, and concentration profiles are discussed graphically. The following key points are observed:

•   Mixed convection enhances both Nusselt and Sherwood numbers.

•   Increase in the angle of inclination ζ, velocity is reduced whereas thermal and concentration boundary layer thicknesses are enhanced.

•   Solid volume fraction reduces the heat and mass transfer rates of the nanofluid.

Thermo-solutal surface tension ratio ϵ accelerates the rate of heat transfer in Alumina-water nanofluid.

Funding Statement: There is no financial support for current study.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  Andersson, H. I. (1992). MHD flow of a viscoelastic fluid past a stretching surface. Acta Mechanica, 95(1–4), 227–230. DOI 10.1007/BF01170814. [Google Scholar] [CrossRef]

 2.  Parsa, A. B., Rashidi, M. M., Hayat, T. (2013). MHD boundary layer flow over a stretching surface with internal heat generation or absorption. Heat Transfer—Asian Research, 42(6), 500–514. DOI 10.1002/htj.21054. [Google Scholar] [CrossRef]

 3.  Hamad, M. A., Uddin, M. J., Ismail, A. I. M. (2012). Investigation of combined heat and mass transfer by Lie group analysis with variable diffusivity taking into account hydrodynamic slip and thermal convective boundary conditions. International Journal of Heat and Mass Transfer, 55(4), 1355–1362. DOI 10.1016/j.ijheatmasstransfer.2011.08.043. [Google Scholar] [CrossRef]

 4.  Noor, N. F. M., Abbasbandy, S., Hashim, I. (2012). Heat and mass transfer of thermophoretic MHD flow over an inclined radiate isothermal permeable surface in the presence of heat source/sink. International Journal of Heat and Mass Transfer, 55(7–8), 2122–2128. DOI 10.1016/j.ijheatmasstransfer.2011.12.015. [Google Scholar] [CrossRef]

 5.  Bhuvaneswari, M., Sivasankaran, S., Kim, Y. J. (2010). Exact analysis of radiation convective flow heat and mass transfer over an inclined plate in a porous medium. World Applied Sciences Journal, 36(7), 114–120. [Google Scholar]

 6.  Pal, D., Mondal, H. (2011). Mhd non-darcian mixed convection heat and mass transfer over a non-linear stretching sheet with soret-dufour effects and chemical reaction. International Communications in Heat and Mass Transfer, 38(4), 463–467. DOI 10.1016/j.icheatmasstransfer.2010.12.039. [Google Scholar] [CrossRef]

 7.  Sui, J., Zheng, L., Zhang, X., Chen, G. (2015). Mixed convection heat transfer in power law fluids over a moving conveyor along an inclined plate. International Journal of Heat and Mass Transfer, 85(7), 1023–1033. DOI 10.1016/j.ijheatmasstransfer.2015.02.014. [Google Scholar] [CrossRef]

 8.  Aydın, O., Kaya, A. (2009). MHD mixed convective heat transfer flow about an inclined plate. Heat and Mass Transfer, 46(1), 129–136. DOI 10.1007/s00231-009-0551-4. [Google Scholar] [CrossRef]

 9.  Ganesan, P., Palani, G. (2004). Finite difference analysis of unsteady natural convection MHD flow past an inclined plate with variable surface heat and mass flux. International Journal of Heat and Mass Transfer, 47(19–20), 4449–4457. DOI 10.1016/j.ijheatmasstransfer.2004.04.034. [Google Scholar] [CrossRef]

10. Gnaneswara Reddy, M. (2013). Scaling transformation for heat and mass transfer effects on steady MHD free convection dissipative flow past an inclined porous surface. International Journal of Applied Mathematics and Mechanics, 9(10), 1–18. [Google Scholar]

11. Wang, S., Roy, N., Pasang, T., Ramezani, M. (2015). Modeling of gas tungsten arc welding pool under marangoni convection. Universal Journal of Mechanical Engineering, 3(5), 185–201. DOI 10.13189/ujme.2015.030504. [Google Scholar] [CrossRef]

12. Nishino, K., Kawamura, H. (2007). Chaos, turbulence and its transition process in marangoni convection. KIBO Japanese Experiment Module, Japan Aerospace Exporation Agency, 19, 84–86. [Google Scholar]

13. Sheikholeslami, M., Ellahi, R., Fetecau, C. (2017). Cuo-water nanofluid magnetohydrodynamic natural convection inside a sinusoidal annulus in presence of melting heat transfer. Mathematical Problems in Engineering, 2017, 1–9. DOI 10.1155/2017/5830279. [Google Scholar] [CrossRef]

14. Al-Mudhaf, A., Chamkha, A. J. (2005). Similarity solutions for MHD thermosolutal Marangoni convection over a flat surface in the presence of heat generation or absorption effects. Heat and Mass Transfer/Waerme- und Stoffuebertragung, 42(2), 112–121. DOI 10.1007/s00231-004-0611-8. [Google Scholar] [CrossRef]

15. Pop, I., Postelnicu, A., Grosan, T. (2001). Thermosolutal marangoni forced convection boundary layers. Meccanica, 36(5), 555–571. DOI 10.1023/A:1017431224943. [Google Scholar] [CrossRef]

16. Sudarsana Reddy, P., Al-Mudhaf, A. (2017). MHD heat and mass transfer flow of a nanofluid over an inclined vertical porous plate with radiation and heat generation/absorption. Advanced Powder Technology, 28(3), 1008–1017. DOI 10.1016/j.apt.2017.01.005. [Google Scholar] [CrossRef]

17. Nakhchi, M. E., Esfahani, J. A., Kim, K. C. (2020). Numerical study of turbulent flow inside heat exchangers using perforated louvered strip inserts. International Journal of Heat and Mass Transfer, 148(7–8), 119143. DOI 10.1016/j.ijheatmasstransfer.2019.119143. [Google Scholar] [CrossRef]

18. Nakhchi, M. E., Esfahani, J. A. (2020). CFD approach for two-phase CuO nanofluid flow through heat exchangers enhanced by double perforated louvered strip insert. Powder Technology, 367(5), 877–888. DOI 10.1016/j.powtec.2020.04.043. [Google Scholar] [CrossRef]

19. Nakhchi, M. E., Rahmati, M. T. (2020). Entropy generation of turbulent cu-water nanofluid flows inside thermal systems equipped with transverse-cut twisted turbulators. Journal of Thermal Analysis and Calorimetry, 135(3), 1863. DOI 10.1007/s10973-020-09960-w. [Google Scholar] [CrossRef]

20. Hayat, T., Ijaz Khan, M., Farooq, M., Alsaedi, A., Waqas, M. et al. (2016). Impact of Cattaneo-Christov heat flux model in flow of variable thermal conductivity fluid over a variable thicked surface. International Journal of Heat and Mass Transfer, 99, 702–710. DOI 10.1016/j.ijheatmasstransfer.2016.04.016. [Google Scholar] [CrossRef]

21. Khan, M. I., Waqas, M., Hayat, T., Alsaedi, A. (2017). A comparative study of casson fluid with homogeneous-heterogeneous reactions. Journal of Colloid and Interface Science, 498, 85–90. DOI 10.1016/j.jcis.2017.03.024. [Google Scholar] [CrossRef]

22. Nayak, M. K., Shaw, S., Ijaz Khan, M., Pandey, V. S., Nazeer, M. (2020). Flow and thermal analysis on Darcy-Forchheimer flow of copper-water nanofluid due to a rotating disk: A static and dynamic approach. Journal of Materials Research and Technology, 9(4), 7387–7408. DOI 10.1016/j.jmrt.2020.04.074. [Google Scholar] [CrossRef]

23. Abbas, S. Z., Khan, W. A., Kadry, S., Khan, M. I., Khan, M. I. (2020). Entropy optimized Darcy-Forchheimer nanofluid (Silicon dioxide, Molybdenum disulfide) subject to temperature dependent viscosity. Computer Methods and Programs in Biomedicine, 190, 105363. DOI 10.1016/j.cmpb.2020.105363. [Google Scholar] [CrossRef]

24. Abbas, S. Z., Khan, M. I., Kadry, S., Khan, W. A., Waqas, M. (2020). Fully developed entropy optimized second order velocity slip MHD nanofluid flow with activation energy. Computer Methods and Programs in Biomedicine, 190, 105362. DOI 10.1016/j.cmpb.2020.105362. [Google Scholar] [CrossRef]

25. Muhammad, R., Khan, M. I. (2020). Magnetohydrodynamics (MHD) radiated nanomaterial viscous material flow by a curved surface with second order slip and entropy generation. Computer Methods and Programs in Biomedicine, 189, 105294. DOI 10.1016/j.cmpb.2019.105294. [Google Scholar] [CrossRef]

26. Ijaz Khan, M., Alzahrani, F. (2020). Activation energy and binary chemical reaction effect in nonlinear thermal radiative stagnation point flow of Walter-B nanofluid. Numerical computations, 34(13), 2050132. [Google Scholar]

27. Ijaz Khan, M., Alzahrani, F., Hobiny, A. (2020). Heat transport and nonlinear mixed convective nanomaterial slip flow of Walter-B fluid containing gyrotactic microorganisms. Alexandria Engineering Journal, 59(3), 1761–1769. DOI 10.1016/j.aej.2020.04.042. [Google Scholar] [CrossRef]

28. Ibrahim, M., Khan, M. I. (2020). Mathematical modeling and analysis of SWCNT-Water and MWCNT-Water flow over a stretchable sheet. Computer Methods and Programs in Biomedicine, 187, 105222. DOI 10.1016/j.cmpb.2019.105222. [Google Scholar] [CrossRef]

29. Ijaz Khan, M., Faris, A., Aatef, H. (2020). Simulation and modeling of second order velocity slip flow of micropolar ferro fluid with Darcy-Forchheimer porous medium. Journal of Materials Research and Technology, 9(4), 7335–7340. DOI 10.1016/j.jmrt.2020.04.079. [Google Scholar] [CrossRef]

30. Khan, M., Azam, M. (2017). Unsteady heat and mass transfer mechanisms in MHD Carreau nanofluid flow. Journal of Molecular Liquids, 225(4), 554–562. DOI 10.1016/j.molliq.2016.11.107. [Google Scholar] [CrossRef]

31. Azarn, M., Xu, T., Shakoor, A., Khan, M. (2020). Effects of arrhenius activation energy in development of covalent bonding in axisymmetric flow of radiative-cross nanofluid. International Communications in Heat and Mass Transfer, 113(4), 104547.1–104547.9. [Google Scholar]

32. Azam, M., Shakoor, A., Rasool, H. F., Khan, M. (2019). Numerical simulation for solar energy aspects on unsteady convective flow of MHD cross nanofluid: A revised approach. International Journal of Heat and Mass Transfer, 131(3), 495–505. DOI 10.1016/j.ijheatmasstransfer.2018.11.022. [Google Scholar] [CrossRef]

33. Azam, M., Xu, T., Khan, M. (2020). Numerical simulation for variable thermal properties and heat source/sink in flow of cross nanofluid over a moving cylinder. International Communications in Heat and Mass Transfer, 118, 104832. [Google Scholar]

34. Houda, J., Hassan, A. (2019). Analysis of the influence of viscosity and thermal conductivity on heat transfer by Alumina-water nanofluid. Fluid Dynamics & Materials Processing, 15(3), 253–270. DOI 10.32604/fdmp.2019.03896. [Google Scholar] [CrossRef]

35. Machireddy, G. R. (2014). Thermal radiation and chemical reaction effects on steady convective slip flow with uniform heat and mass flux in the presence of ohmic heating and a heat source. Fluid Dynamics & Materials Processing, 10(4), 417–442. [Google Scholar]

36. Slama, S., Kahalerras, H., Fersadou, B. (2017). Mixed convection of a nanofluid in a vertical anisotropic porous channel with heated/cooled walls. Fluid Dynamics & Materials Processing, 13(3), 155–172. [Google Scholar]

37. Oztop, H. F., Abu-Nada, E. (2008). Numerical study of natural convection in partially heated rectangular enclosures filled with nanofluids. International Journal of Heat and Fluid Flow, 29(5), 1326–1336. DOI 10.1016/j.ijheatfluidflow.2008.04.009. [Google Scholar] [CrossRef]

This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.