Fluid Dynamics & Materials Processing

DOI: 10.32604/fdmp.2021.016507

ARTICLE

Investigation on the Changing Characteristics of Flow-Induced Noise in a Centrifugal Pump

Guanpeng Li1, Lihui Sun2, Zhaoyang Wang1, Chunguo An1, Chang Guo3,*, Shen Cheng3 and Ming Gao2,*

1Shandong Electric Power Engineering Consulting Institute Corp., Ltd., Jinan, 250013, China
2Shandong Engineering Laboratory for High-Efficiency Energy Conservation and Energy Storage Technology & Equipment, School of Energy and Power Engineering, Shandong University, Jinan, 250061, China
3School of Energy and Power Engineering, Qilu University of Technology (Shandong Academy of Sciences), Jinan, 250353, China
*Corresponding Authors: Chang Guo. Email: changg@qlu.edu.cn; Ming Gao. Email: gm@sdu.edu.cn
Received: 13 March 2021; Accepted: 10 May 2021

1  Introduction

The centrifugal pumps are the main fluid transporting devices, which have played an indispensable role in many fields [1–3]. With the increasingly stringent environmental requirements, on the basis of high hydraulic performance of centrifugal pumps, the noise performance has received wide attention. Actually, the noise induced by unsteady flow in pumps has a decisive effect on whole noise level evaluation. Therefore, how to control the flow-induced noise has become an important topic for centrifugal pumps.

Currently, a number of researches have been conducted through experimental measurements and numerical simulations, to explore the generation mechanisms, distribution and propagation characteristics of flow-induced noise in centrifugal pumps. The generation of flow-induced noise was associated with various complex phenomena in pumps, including rotor-stator interaction and cavitation, etc. [3]. The rotor-stator interaction was the main cause of flow-induced noise. Generally, under the effect of rotor-stator interaction, the physical quantities (pressure, velocity, etc) in pumps showed the periodic fluctuation characteristics [4], so the flow-induced noise reached to maximum at blade-passing frequency (fb), and also decreased with the increase of frequency [5]. The cavitation, which could affect the hydraulic performance and pump structure, was another cause of flow-induced noise [6]. With the development of cavitation, the rotor-stator interaction intensity weakened, and the noise in high frequency range increased gradually [7]. At present, the improvement of computational fluid dynamics (CFD) technology has facilitated the related researches, and the numerical model combining the CFD and Lighthill acoustic analogy theory [8,9] has been widely adopted for noise simulations. Based on the numerical model, Yang et al. [10], Si et al. [11] and Mao et al. [12] analyzed the noise directivity distribution characteristics in circumferential direction. It was revealed that the noise showed dipole symmetric distribution characteristics. Besides, the noise distribution characteristics in other directions were also revealed by Dong et al. [13] and Guo et al. [14], and the spatial directivity distribution characteristics were obtained. In addition, Guo et al. [15] conducted experiments and simulations to explore the noise propagation mechanisms from view of flow and sound fields synergy concept. The results manifested that the noise tended to propagate outside the pump with increasing the synergy degree.

The purpose of the researches on the flow-induced noise is to realize the noise control, and the passive control method [16] is the most frequently used method. Based on the passive control principle, the effect of different pump structures on the pressure fluctuation and noise has been extensively explored. Cheng et al. and Dai et al. [17,18], discussed the different structures on pressure fluctuation at various locations in pumps. Wang et al. [19] analyzed the influence of blade number on flow-induced noise at pump outlet. It was showed that the noise decreased first, then increased with the increase of blade number. Cheng et al. [20] investigated the impact of blade outlet cutting on the noise at pump inlet and outlet. The results showed that the V-shaped cutting improved the noise performance. Currently, the noise reduction researches based on bionics principle have drawn more attention. Dai et al. [21] extracted the surface features of shark and designed the V-groove surface blades for noise reduction. Zhang et al. [22] designed the orthogonal test and revealed the optimization effect of bionic blade on the noise at pump inlet and outlet. The flow-induced noise in centrifugal pumps was impacted by various structures, so the optimization of various structures was considered to reduce the noise at pump outlet. Guo et al. [23] employed the response surface method to analyze the influence of blade profile on noise at pump outlet. What’s more, Si et al. [24,25], also compared the different structure combinations on the noise at pump outlet. The relevant conclusions promoted the noise optimization design of centrifugal pumps significantly.

According to the references above, the majority of researches focused on the noise distribution characteristics, while the corresponding mechanisms were rarely involved. The numerical model combining the Lighthill acoustic analogy and CFD has developed much in exploring the distribution characteristics and changing trends of noise, but the flow and sound fields are simulated separately, which is not applicable to explore the generation and changing mechanisms of flow-induced noise. Additionally, the noise optimization design was mainly realized by comparing the noise at pump outlet with different geometry parameters of pump structures, then revealing the optimal geometry parameter. However, the flow instability degree at various locations is different in pumps [17,18], the flow-induced noise at pump outlet may not be sufficient to evaluate the overall noise level in the noise optimization design process. Besides, the centrifugal pumps need to operate under various operating conditions to meet different demands, and the flow-induced noise changes accordingly. The flow-induced noise at various locations in pumps may have different changing trends with the change of operating condition, and the changing trends of noise at pump outlet with operating condition cannot be enough to reflect the overall noise accurately, which also limits the development of noise prediction research. Therefore, it is necessary to develop new numerical model to compare the flow-induced noise at various locations and explore the changing mechanisms under various operating conditions, then propose a more suitable noise evaluation criterion.

Compared with Lighthill acoustic analogy theory, Powell vortex sound theory takes great advantages in exploring the generation and changing mechanisms of flow-induced noise [15,26]. Therefore, the numerical model combining the Powell vortex sound theory and CFD is established, and the corresponding experimental measurements are conducted to verify the accuracy of the model. Based on the numerical model and experiments, the flow-induced noise at different locations in the pump is compared under various operating conditions, and the corresponding changing mechanisms are also revealed. Then, a more suitable noise evaluation criterion is presented. The research can be used to guide the researches on the establishment of noise prediction model and the noise optimization design of centrifugal pumps.

2  Research Methodology

2.1 Physical Model

The design parameters of the model pump are listed in Tab. 1. Fig. 1 presents the 3D geometric model, which includes inlet, impeller, volute and outlet. A mesh system with tetrahedral element is generated. Tab. 2 shows the sensitivity analysis results of mesh system. It can be found that the pump head grows with the increase of mesh number. When the mesh number increases from 1.5 to 2.1 million, the growth rate of pump head is relatively large, while the pump head has little growth with the mesh number increasing from 2.1 to 2.4 million. To improve the accuracy while reducing the computational costs, Mesh-C is chosen, as shown in Fig. 2.

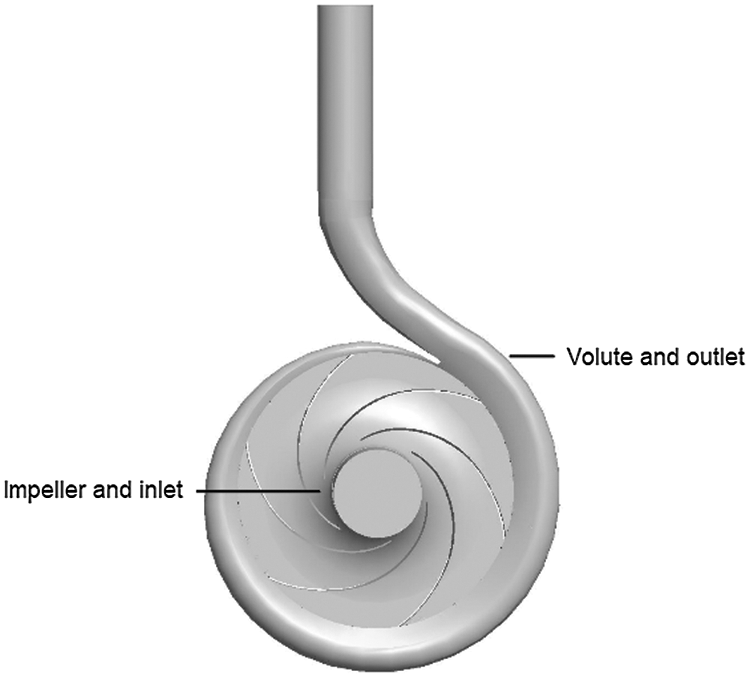
Figure 1: Geometric model

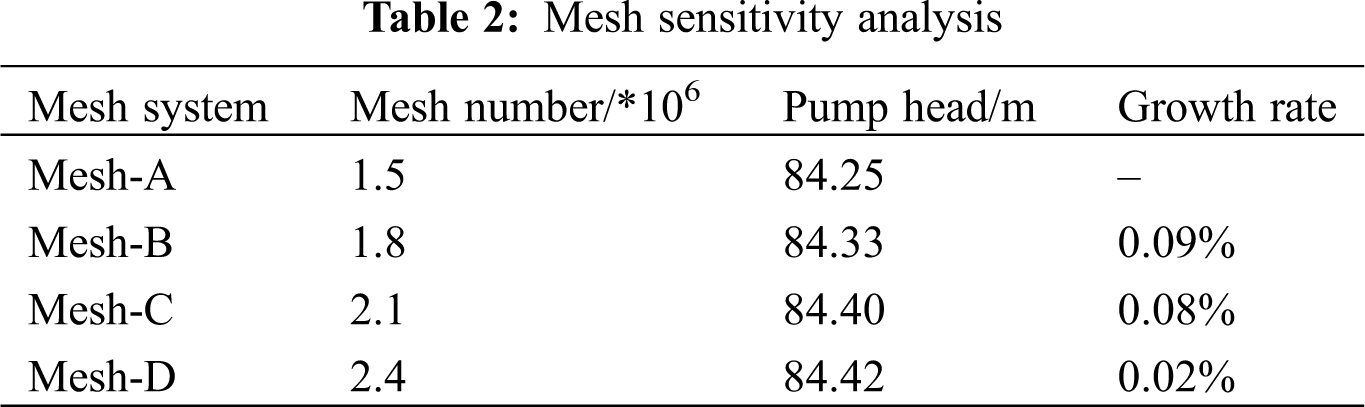
Figure 2: Mesh system

2.2 Mathematical Model

Water is used as the medium, which means that the flow field can be regarded as incompressible. The continuity and momentum equations of flow flied are expressed as,

∇·u→=0 (1)

∂u→∂t+(u→·∇)u→=f→−1ρ∇p+ν∇2v→ (2)

where u→ and f→ are the velocity and volume force vectors, ρ, p and υ are the density, pressure and kinematic viscosity. The Eqs. (1) and (2) are solved by using the Reynolds-averaged method. Reynolds-averaged governing equations are defined as,

∂u¯i∂xi=0 (3)

∂u¯i∂t+u¯j∂u¯i∂xj=f¯i−1ρ∂p¯∂xi+1ρ∂∂xj(μ∂u¯i∂xj−ρuj′ui′¯) (4)

where the superscript “-” represents the averaged value. To solve the Eqs. (3) and (4), the standard k-ε model is adopted. The k and ε can be obtained by the following equations:

∂∂t(ρk)+∂∂xi(ρkui)=∂∂xi((μ+μtσk)∂k∂xi)+Gk+Gb−ρε (5)

∂∂t(ρε)+∂∂xi(ρεui)=∂∂xi((μ+μtσε)∂ε∂xi)+C1εεk(Gk+C3εGb)−C2ερε2k (6)

Here, Gk and Gb represent the generation of turbulent kinetic energy. C1ε, C2ε, and C3ε are 1.44, 1.92 and 0.09, respectively, while σk and σε are 1.0 and 1.3, respectively.

The contribution of viscosity to noise is small, without considering the effect of fluid viscosity, the Powell vortex sound equation is adopted for the sound field simulation, which is defined as,

∇2p′−1c02∂2p′∂t′2=−∇·(ρ(ω→×u→)+∇(ρu22)) (7)

where t’ is the time of sound field. The equation includes spatial, time and sound source items. p’ is the sound pressure, c0 is the sound speed, ω→ represents the vorticity vector.

2.3 Numerical Method

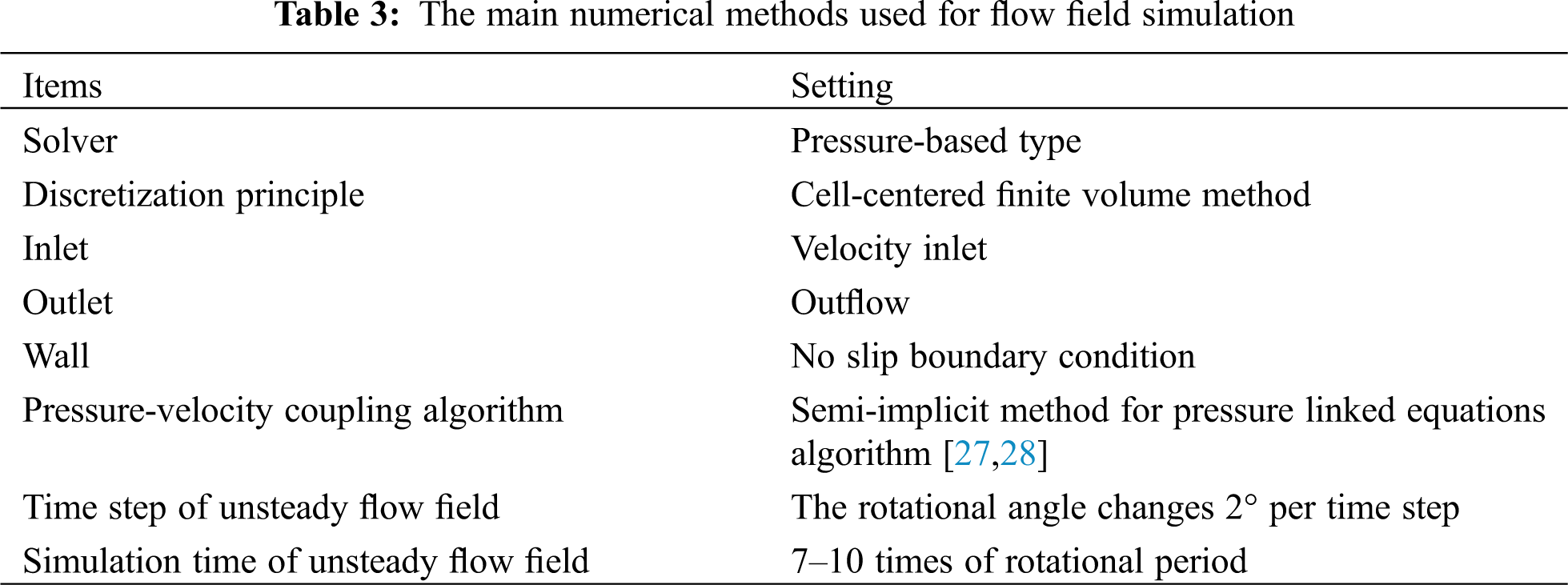
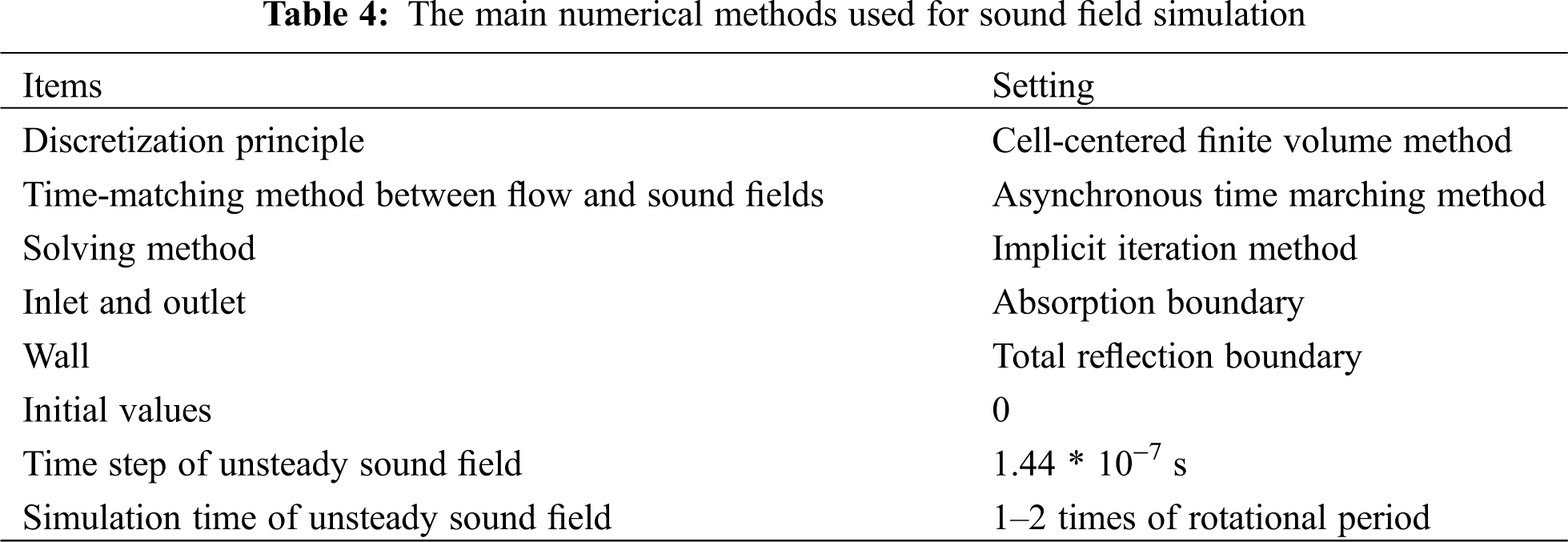
The steady and unsteady flow field simulations, as well as the unsteady sound field simulation are conducted by using Fluent. The main numerical methods used for simulation are listed in Tabs. 3 and 4.

The absorption boundary and total reflection boundary conditions are defined as,

1c0∂p′∂t′+∇p′·n→=0 (8)

p′=0 (9)

where n’ is the unit normal vector of boundary surface. In order to compare the flow-induced noise at various locations in impeller and volute, 10 monitoring points are arranged. As shown in Fig. 3, I1–I5 are set from inlet to outlet in the impeller, and V1–V5 are arranged along the circumferential extension of the volute. The operating conditions include various rotational speeds with design flow rate (Condition 1) and various rotational speeds with the opening of the valve kept unchanged (Condition 2). The detailed operating parameters are listed in Tabs. 5 and 6.

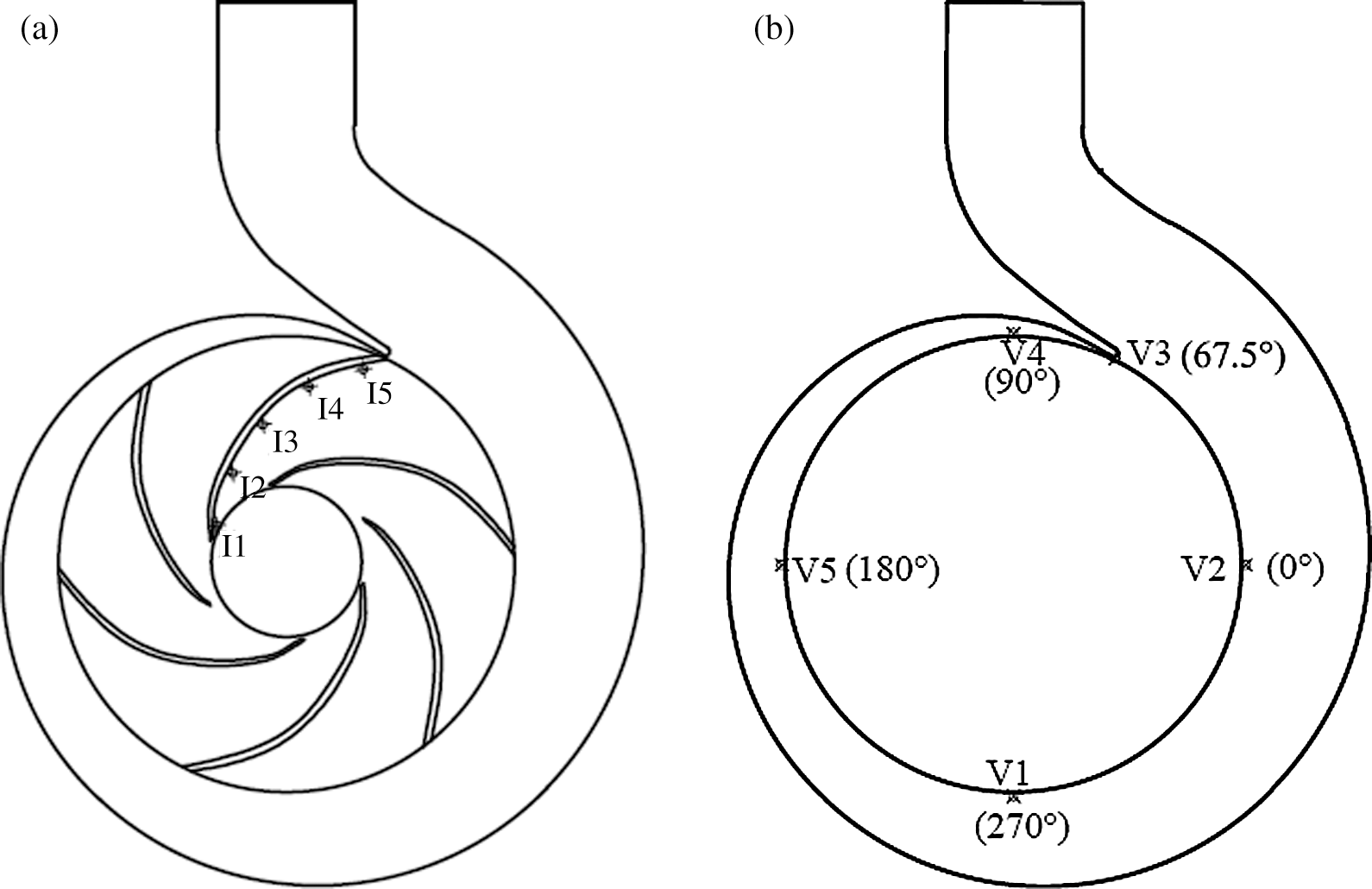
Figure 3: Monitoring arrangement (a) Monitoring points in the impeller (b) Monitoring points in the volute

The total sound pressure level (TSPL) and total sound source intensity (TSSI) are calculated to present the noise level and noise source level at different monitoring points. Here, TSPL and TSSI are defined as,

TSPL=10lg∑l=1nm10SPLl/10 (10)

TSSI=10lg∑l=1nm10SSIl/10 (11)

where nm represents the number of frequencies, while the SPL and SSI are the sound pressure level and sound source intensity at different frequencies. Besides, the averaged-total sound pressure level (Lp) and averaged-total sound source intensity (Ls) are calculated to characterize the overall noise level and noise source level of various monitoring points or different operating conditions. The Lp and Ls are defined as,

Lp=10lg⁡(1m∑l=1m10TSPLl/TSPLl1010) (12)

Ls=10lg⁡(1m∑l=1m10TSSIl/TSSIl1010) (13)

where m is the number of monitoring points or operating conditions (m = 10 or 5).

3  Experimental Validation

3.1 Experimental Setup

Owing to the difficulty of flow-induced noise measurement in impeller and volute, the noise at pump inlet and outlet is measured. The experimental setup is shown in Fig. 4. To reduce the influence of environmental noise, the measurement is conducted in a semi-anechoic chamber. The DHP8501 type hydrophone is used to measure the noise, which has the advantages of high sensitivity and wide measuring range. The rotational speed of the pump is regulated by a YVF2180L-2 type motor mounted outside the chamber, and the flow rate is controlled by a SLDG-800 type flow valve installed near the water tank.

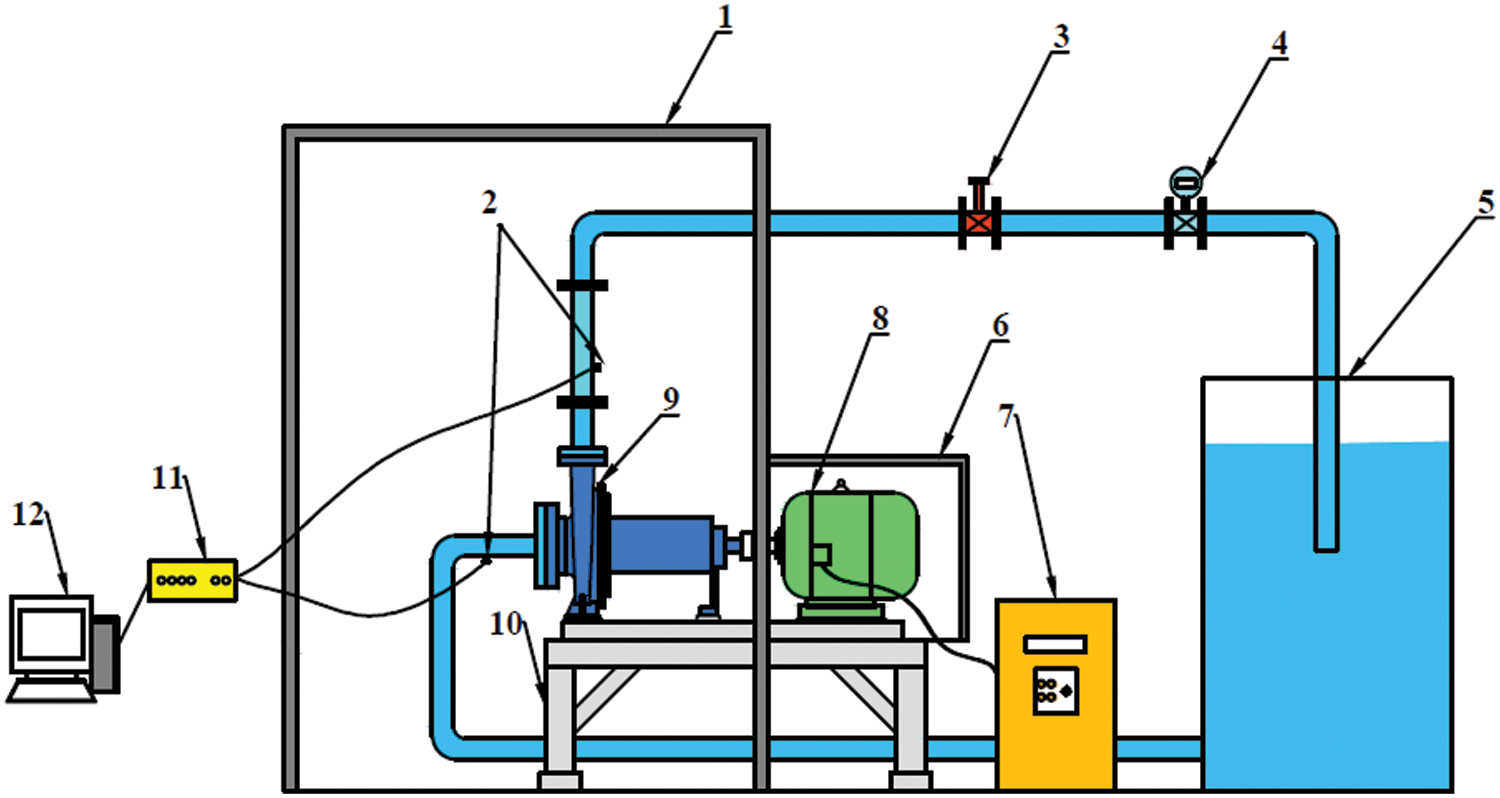
Figure 4: Experimental setup 1: Semi-anechoic chamber; 2: Monitoring points at inlet and outlet; 3: Valve; 4: Flow meter; 5: Water tank; 6: Acoustic enclosure; 7: Frequency converter; 8: Motor; 9: Pump; 10: Bracket; 11: USB switch; 12: Computer

3.2 Model Validation

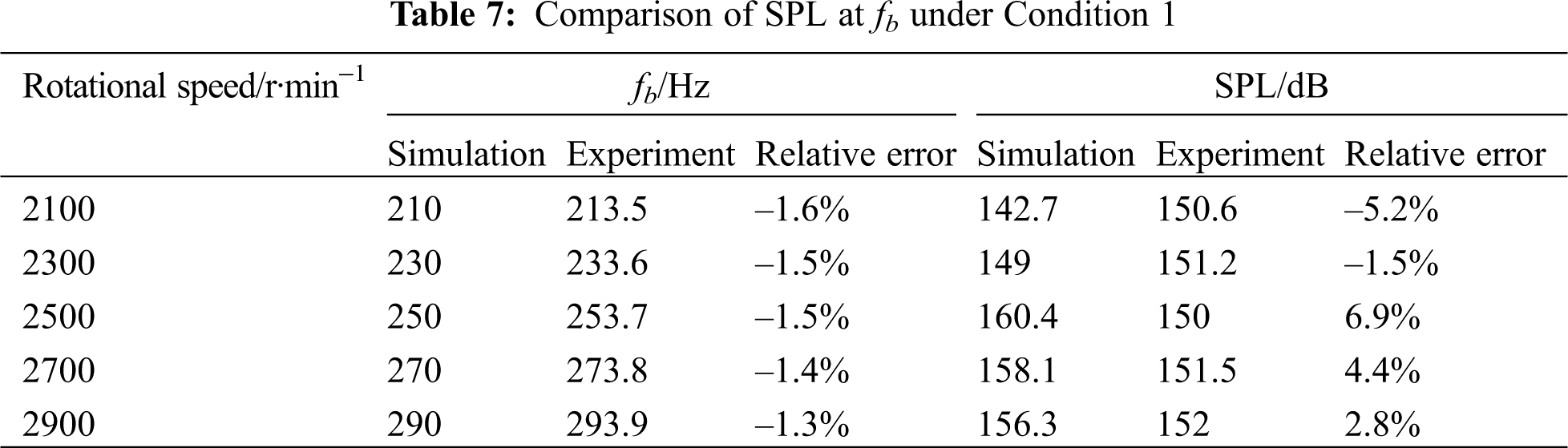
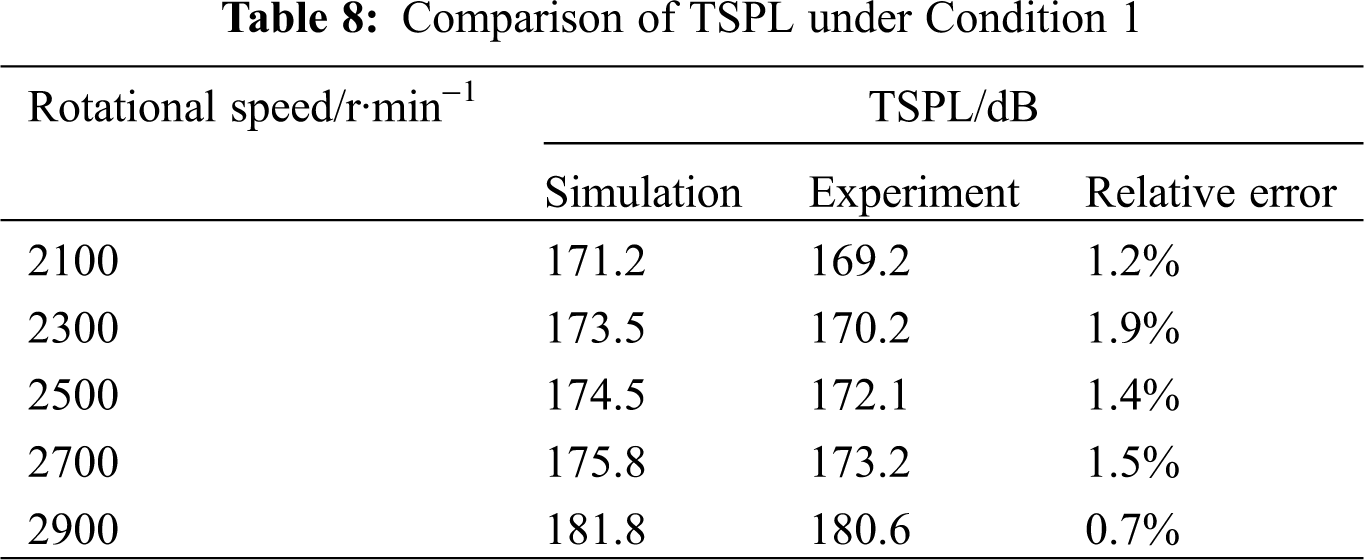
The flow-induced noise at pump outlet is analyzed to validate the feasibility of the numerical model. Tab. 7 shows the comparison of fb and corresponding SPL obtained by simulation and experiment under Condition 1. Due to the complexity and instability of the real flow in the pump, as well as the effects of environmental noise and simulation assumptions, the simulation results of flow-induced noise cannot be completely same as the experimental results, and the deviation widely exists. It can be found that the relative errors of fb and SPL obtained by simulation and experiment are small, and the maximum errors are −1.6% and 6.9%, respectively. In addition, the noise is the superposition result of SPL at different frequencies, thus the TSPL is also compared. As shown in Tab. 8, the TSPL at pump outlet obtained by simulation and experiment shows the similar increasing trends with the growth of rotational speed, and the maximum relative error is 1.9%. The comparison results in Tabs. 7 and 8 can validate the accuracy of the numerical model.

4  Results

4.1 Noise Comparison at Pump Inlet and Outlet

Fig. 5 shows the changing trends of TSPL at pump inlet and outlet obtained by experiment under various operating conditions. It can be found that the TSPL increases with the growth of rotational speed, and the TSPL at outlet is higher than that at inlet. When the rotational speed grows from 2100 to 2900 r/min, the TSPL at inlet and outlet increases by 1.8% and 6.5% under Condition 1, while it at inlet and outlet under Condition 2 increases by 2% and 6.9%, respectively. Besides, the TSPL at inlet and outlet under Condition 1 is 0.4% and 0.1% higher than that at inlet and outlet under Condition 2, respectively.

Figure 5: Changing trends of TSPL at inlet and outlet under various operating conditions

To explore the changing mechanisms of TSPL, the changing trends of TSSI with operation condition are analyzed. As shown in Fig. 6, the TSSI at outlet is higher than that at inlet, and the changing trends of TSSI with operation condition are similar to those of TSPL. When the rotational speed grows from 2100 to 2900 r/min, the TSSI at inlet and outlet increases by 2.2% and 2.9% under Condition 1, while it at inlet and outlet under Condition 2 increases by 2.6% and 4.3%, respectively. Besides, the TSSI at inlet and outlet under Condition 1 is 0.3% and 0.6% higher than that at inlet and outlet under Condition 2, respectively.

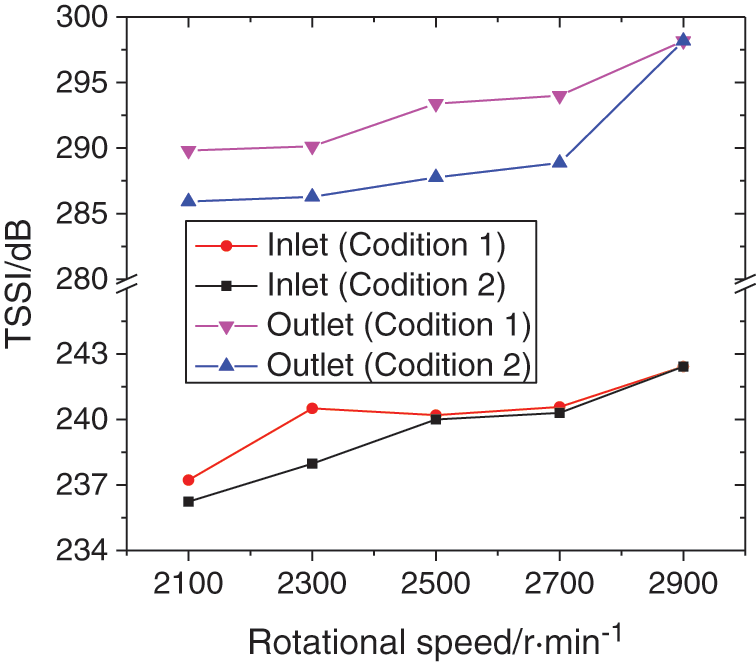
Figure 6: Changing trends of TSSI at inlet and outlet under various operating conditions

By comparing Figs. 5 and 6, it can be concluded that with the growth of rotational speed, the flow instability degree at pump inlet and outlet intensifies, which is reflected by the increase of TSSI, and the TSPL increases accordingly. Furthermore, the TSSI under Condition 1 is higher than that under Condition 2, resulting in the same changing characteristics of TSPL.

4.2 Noise Comparison at Various Locations in Impeller and Volute

Take the 2100 and 2700 r/min conditions as example, Fig. 7 shows the comparison of TSSI and TSPL at various locations in the impeller. It can be found that the TSSI increases from inlet to outlet in the impeller, which causes the similar increasing trends of TSPL, and the two parameters at different monitoring points are higher than those at inlet and outlet of the pump. Additionally, different with the changing trends of TSSI and TSPL at pump inlet and outlet, the two parameters under Condition 2 are higher than those under Condition 1 in the impeller. Specifically, the TSSI and TSPL of the monitoring points under Condition 2 are 0.2% and 0.8% higher than those under Condition 1 at 2700 r/min, while at 2100 r/min, the growing rate are 0.3% and 1.7%, respectively.

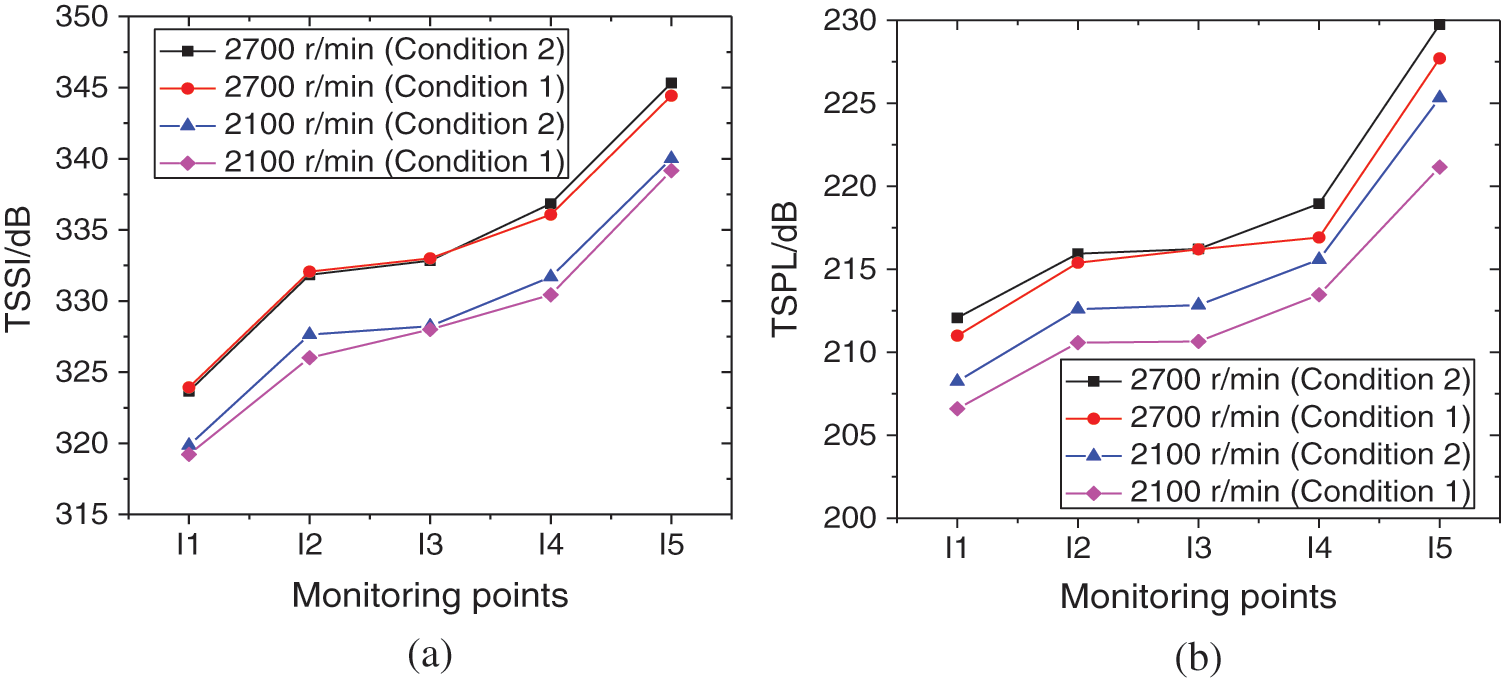
Figure 7: Changing trends of TSSI and TSPL at various locations in the impeller (a) TSSI (b) TSPL

Fig. 8 depicts the TSSI and TSPL distribution characteristics in the volute at 2100 and 2700 r/min conditions. It is revealed that the TSSI and TSPL in the volute are close to those in the impeller, and also higher than those at inlet and outlet. Similar to the changing trends of TSSI and TSPL in the impeller, the two parameters in the volute under Condition 2 are higher than those under Condition 1. More concretely, when the rotational speed is 2700 r/min, the TSSI and TSPL of the monitoring points under Condition 2 are 0.4% and 0.2% higher than those under Condition 1, while at 2100 r/min, the growing rate are 0.9% and 2.3%, respectively.

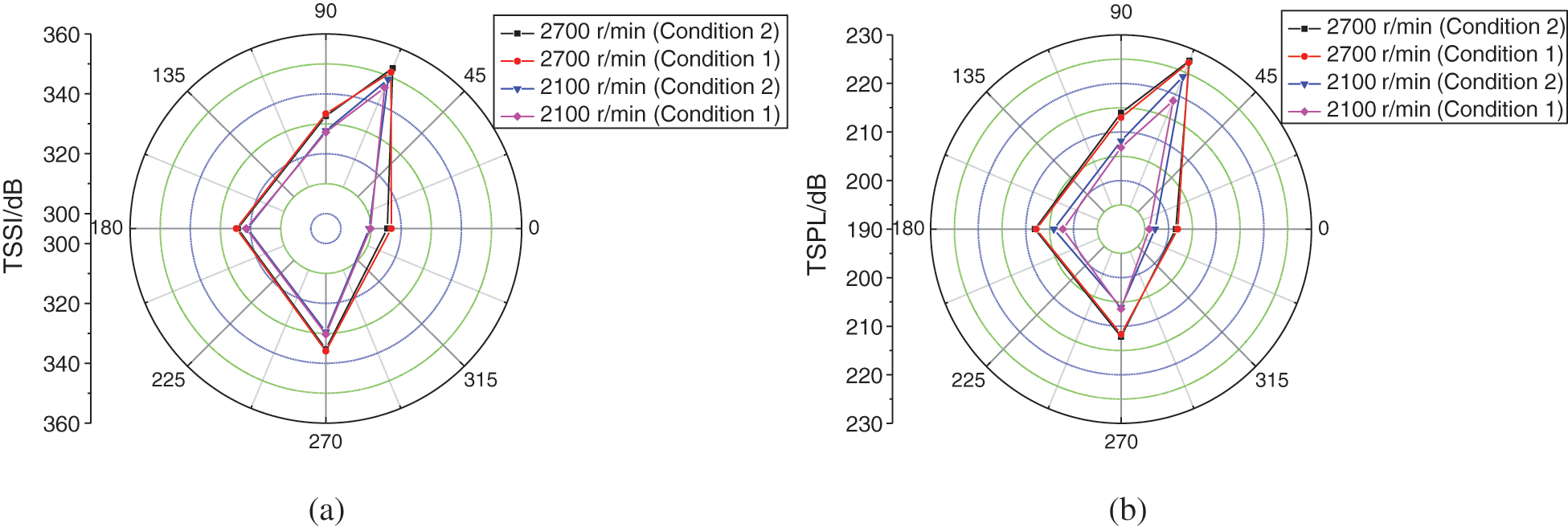
Figure 8: Distribution characteristics of TSSI and TSPL in the volute (a) TSSI (b) TSPL

Fig. 9 illustrates the changing trends of Ls and Lp of the monitoring points in impeller and volute under various operating conditions. It can be observed that the Ls and Lp increase with the growth of rotational speed, and the two parameters under Condition 2 are 0.3% and 0.6% higher than those under Condition 1. Besides, under the same rotational speed, the lower the flow rate is, the higher the Ls representing flow instability degree in impeller and volute is, thus the Lp increases.

Figure 9: Changing trends of Lp and Ls under various operating conditions

By comparing the Figs. 5–9, it can be revealed that the changing trends of the sound source intensity at pump inlet and outlet are different with those in impeller and volute, further causing the different changing trends of noise. Therefore, it is not suitable for the noise at pump inlet and outlet to evaluate the overall noise level in the pump. The flow-induced noise in centrifugal pumps should be evaluated by the superposition result of noise at various locations in impeller from inlet to outlet and along the circumferential extension of volute.

5  Discussion

The accurate noise evaluation is an important basis for noise optimization of centrifugal pumps. During the noise optimization process, the previous researches mainly aimed at reducing the flow-induced noise at pump outlet. By comparing the changing trends of flow-induced noise at various locations with the change of operating condition, this research proposes that the noise evaluation should consider the comprehensive result of noise at various locations in impeller from inlet to outlet and along the circumferential extension of volute.

According to the Powell vortex sound theory, the generation of flow-induced noise is associated with the unsteady fluid flow, and the flow instability degree reflected by sound source intensity is the decisive factor on noise level. The research results imply that the flow in impeller and volute is the most unstable under the effect of impeller rotation, following by outlet pipe, and the flow in inlet pipe is relative stable, consequently, the noise at outlet is higher than that at inlet, but lower than that in impeller and volute. Furthermore, under the same rotational speed, with the decrease of flow rate, the flow at pump inlet and outlet becomes stable, while that in impeller and volute tends to be unstable, which is demonstrated by the changing trends of sound source intensity, so the noise at pump inlet and outlet, as well as that in impeller and volute show opposite changing trends. In summary, the flow-induced noise in impeller and volute should be used for noise evaluation of centrifugal pumps, which is beneficial to the noise optimization and noise prediction accurately.

Although there are important discoveries revealed by this research, the limitation also exists. The detailed monitoring points used for noise evaluation are not discussed. In the following research, we will further compare the changing trends of noise at various locations with the change of operating condition and pump structure, then propose the representative monitoring points and corresponding noise evaluation formula.

6  Conclusions

To reveal the deficiency of current noise evaluation method, and figure out a more suitable noise evaluation criterion for noise optimization of centrifugal pumps, based on the Powell vortex sound theory, numerical simulations and experimental measurements, the flow-induced noise at various locations in a centrifugal pump is compared under various operating conditions. The conclusions are as follows:

(1) The flow instability degree at pump outlet is more intense than that at inlet, which is characterized by the TSSI at outlet being higher than that at inlet, consequently, the TSPL at outlet is higher than that at inlet under different operating conditions. In addition, under the same rotational speed, the TSSI under large flow rate condition is higher than that under small flow rate condition, which further causes the similar distribution characteristics of TSPL. Specifically, the TSSI and TSPL at pump inlet and outlet under Condition 1 are 0.3% and 0.6%, 0.4% and 0.1% higher than those under Condition 2, respectively.

(2) Compared with the TSSI at pump inlet and outlet, the TSSI at various locations in impeller from inlet to outlet and along the circumferential extension of volute is much higher, which means that the flow in impeller and volute is more unstable, and further induces high-level noise. Besides, under the same rotational speed, the TSSI and TSPL at various locations under small flow rate condition is higher than that under large flow rate condition. The Ls and Lp of various monitoring points in impeller and volute under Condition 2 are 0.3% and 0.6% higher than those under Condition 1, which are opposite with the changing trends of those at pump inlet and outlet of the pump.

Briefly, the changing trends of flow-induced noise at pump inlet and outlet are different with those in impeller and volute, and the noise in impeller and volute is much higher than that at pump inlet and outlet. Therefore, the superposition result of noise at various locations in impeller from inlet to outlet and along the circumferential extension of volute should be considered to evaluate the flow-induced noise in centrifugal pumps.

Funding Statement: This research was funded by the Key Research and Development Project of Shandong Province (2019GSF109084), and Qilu University of Technology (Shandong Academy of Sciences) Young Doctors Cooperative Fund (2019BSHZ022).

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  Tian, P., Huang, J., Shi, W. D., Zhou, L. (2019). Optimization of a centrifugal pump used as a turbine impeller by means of an orthogonal test approach. Fluid Dynamics & Materials Processing, 15(2), 139–151. [Google Scholar]

 2.  Miao, S. C., Zhao, H. B., Shi, F. X., Wang, X. H., Ma, X. J. (2021). Study on energy conversion characteristics in volute of pump as turbine. Fluid Dynamics & Materials Processing, 17(1), 201–214. [Google Scholar]

 3.  Guo, C., Gao, M., He, S. Y. (2020). A review of the flow-induced noise study for centrifugal pumps. Applied Science–Basel, 10(3), 1022. [Google Scholar]

 4.  Guo, R., Li, R. N., Zhang, R. H. (2019). Reconstruction and prediction of flow field fluctuation intensity and flow-induced noise in impeller domain of jet centrifugal pump using gappy POD method. Energies, 12(1), 111. [Google Scholar]

 5.  Rui, X. P., Zhao, Y. (2016). Numerical simulation and experimental research of flow-induced noise for centrifugal pumps. Journal of Vibroengineering, 18(1), 622–636. [Google Scholar]

 6.  Li, Y., Liu, H. L., Wang, K., Chen, K. (2017). Research on cavitation induced noise feature of marine centrifugal pump under various cavitation numbers. Water Resources and Power, 35, 162–165. [Google Scholar]

 7.  Lu, J. X., Liu, X. B., Zeng, Y. Z., Zhu, B. S., Hu, B. et al. (2020). Investigation of the noise induced by unstable flow in a centrifugal pump. Energies, 13(3), 589. [Google Scholar]

 8.  Zhang, Y. D., Zhang, J. Y. (2020). Numerical simulation of the aeroacoustic performance of the DSA380 high-speed pantograph under the influence of a crosswind. Fluid Dynamics & Materials Processing, 16(1), 105–120. [Google Scholar]

 9.  Wang, L., An, C. G., Wang, N. N., Ping, Y. M., Wang, K. et al. (2020). Numerical simulation of axial inflow characteristics and aerodynamic noise in a large-scale adjustable-blade fan. Fluid Dynamics & Materials Processing, 16(3), 585–600. [Google Scholar]

10. Yang, J., Yuan, S. Q., Yuan, J. P., Si, Q. R., Pei, J. (2014). Numerical and experimental study on flow-induced noise at blade-passing frequency in centrifugal pumps. Chinese Journal of Mechanical Engineering, 27(3), 606–614. [Google Scholar]

11. Si, Q. R., Sheng, G. C., Heng, Y. G., Cui, Q. L., Huang, K. L. (2018). Numerical simulation for flow-induced noise in a centrifugal pump based on Lighthill acoustic analogy theory. Journal of Vibration and Shock, 37(23), 84–90. [Google Scholar]

12. Mao, X. L., Pavesi, G., Chen, D. Y., Xu, H. S., Mao, G. J. (2019). Flow induced noise characterization of pump turbine in continuous and intermittent load rejection processes. Renewable Energy, 139, 1029–1039. [Google Scholar]

13. Dong, L., Dai, C., Kong, F. Y., Fu, L., Xia, B. (2016). Flow-induced exterior noise characteristics of a centrifugal pump as a turbine and different noise contribution analysis. Journal of Vibration and Shock, 35(5), 168–174. [Google Scholar]

14. Guo, R., Li, R. N., Zhang, R. H., Song, Q. C. (2018). Characteristic analysis of exterior hydrodynamic noise of jetting centrifugal self-priming pump. Journal of Huazhong University of Science & Technology (Natural Science Edition), 46(6), 43–48. [Google Scholar]

15. Guo, C., Gao, M. (2020). Investigation on the flow-induced noise propagation mechanism of centrifugal pump based on flow and sound fields synergy concept. Physics of Fluids, 32, 035115. [Google Scholar]

16. Anureka, R., Srinivasan, K. (2020). Passive control of pipe-jet noise using trailing-edge castellations. Applied Acoustics, 170, 107516. [Google Scholar]

17. Cheng, X. R., Jiang, Y. M., Li, M., Zhang, S. Y. (2020). Influence of the axial position of the guide vane on the fluctuations of pressure in a nuclear pump. Fluid Dynamics & Materials Processing, 16(5), 1047–1061. [Google Scholar]

18. Dai, J. C., Mou, J. G., Liu, T. (2020). Influence of tip clearance on unsteady flow in automobile engine pump. Fluid Dynamics & Materials Processing, 16(2), 161–179. [Google Scholar]

19. Wang, Y. Q., Ding, Z. W. (2020). Influence of blade number on flow-induced noise of centrifugal pump based on CFD/CA. Vacuum, 172, 109058. [Google Scholar]

20. Cheng, X. R., Li, T. P., Wang, P. (2020). Study on the influence of blade outlet cutting on hydraulic noise of centrifugal pump with low specific speed. Advances in Mechanical Engineering, 12(9), 1–12. [Google Scholar]

21. Dai, C., Ge, Z. P., Dong, L., Liu, H. L. (2020). Research on characteristics of drag reduction and noise reduction on V-groove surface of bionic blade of centrifugal pump. Journal of Huazhong University of Science & Technology (Natural Science Edition), 48(9), 113–118. [Google Scholar]

22. Zhang, J. F., Jia, J., Hu, R. X., Wang, Y., Cao, P. Y. (2018). Flow noise of pipeline pump and bionic sound optimization. Transactions of the Chinese Society of Agricultural Engineering, 49(9), 138–145. [Google Scholar]

23. Guo, R., Li, R. N., Zhang, R. H., Li, J., Shen, Z. J. (2019). Influence of blade profile on the hydraulic and rotating noise characteristics of a jet centrifugal pump. Journal of Vibration and Shock, 38(18), 223–230. [Google Scholar]

24. Si, Q. R. (2014). Investigation on hydraulic design of centrifugal pumps with low noise and mechanism of rotor-stator interaction (Ph.D. Thesis). China: Jiangsu University. [Google Scholar]

25. Dai, C. (2014). Flow-induced noise characteristics for centrifugal pump as turbine theoretical, numerical and experimental investigations (Ph.D. Thesis). China: Jiangsu University. [Google Scholar]

26. Guo, C., Gao, M., Wang, J. Y., Shi, Y. T., He, S. Y. (2019). The effect of blade outlet angle on the acoustic field distribution characteristics of a centrifugal pump based on Powell vortex sound theory. Applied Acoustics, 155, 297–308. [Google Scholar]

27. Cheng, H., Du, G. S., Zhang, M., Wang, K., Bai, W. B. (2020). Determination of the circulation for a large-scale wind turbine blade using computational fluid dynamics. Fluid Dynamics & Materials Processing, 16(4), 685–698. [Google Scholar]

28. Cheng, X. R., Wang, P., Zhang, A. M., Tu, Y. X. (2020). Study on the influence of blade slot of centrifugal pump on its sound field characteristics. Technical Acoustics, 39(5), 611–617. [Google Scholar]

This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.