

 | Fluid Dynamics & Materials Processing |  |
DOI: 10.32604/fdmp.2021.017256
ARTICLE
On the Stability of Carbon Shale Slope under Rainfall Infiltration
1Guangxi Beitou Transportation Maintenance Technology Group Co., Ltd., Nanning, 530029, China
2School of Civil and Architecture, China Three Gorges University, Yichang, 443000, China
*Corresponding Author: Zhao Li. Email: cl26f8@163.com
Received: 26 April 2021; Accepted: 30 June 2021
Abstract: Carbonaceous shale is a sedimentary rock containing a large amount of dispersed carbonaceous organic material. It is easy to crack and soften when exposed to water. In the present work, the stability of such a rock and its sensitivity to the formation of infiltrations due to rainfall are analyzed numerically using the GeoStudio software. The slope stability coefficient is calculated and verified using the landslide thrust calculation method. The results show that under the action of heavy rainfall, water infiltrates into the slope layer by layer, and, accordingly, the soil volume water content is different with respect to that typical of a homogeneous soil. It is also shown that, although in an initial stage, rainfall infiltration leads to the decline of the slope stability coefficient, with the progress of rainfall, this coefficient can temporarily increase, that is, these phenomena can display a lag phase.
Keywords: Carbonaceous shale slope; stability; volume moisture content; pore water pressure; numerical simulation
Carbonaceous shale is a sedimentary rock containing a large amount of dispersed carbonaceous organic matter. It is easy to crack, disintegrate and soften when exposed to water. Slope composed of carbonaceous shale is prone to landslide and collapse under the action of long-term rainfall and dry-wet cycle. During the construction of many infrastructures, this kind of rock and soil mass is often regarded as bad geology.
In recent years, the research on the stability of carbonaceous shale slope has yielded fruiul results. Htet et al. [1] According to the shear strength theory of unsaturated soil, calculated the stability of riverbank slope during the rapid decline of riverbank water level by using the sliding arc stability analysis method based on finite element calculation and combining with a specific riverbank. Balendra et al. [2] used multiple regression (MR) analysis method to calculate the critical safety factor of the slope, which reduced the time and complexity involved in slope stability evaluation. Paolo et al. [3] proposed a comprehensive method for slope stability analysis based on the remote geomechanical analysis of the high-resolution 3D point cloud collected by the ground laser scanner (TLS), and the results showed that the 3D model implemented by the method was more accurate. Liu et al. [4,5] studied the creep characteristics of carbon shale and the particle size distribution of disintegration residues of carbon shale under simulated dry-wet cycle conditions. Zhang et al. [6–8] used GeoStudio software to simulate the change law of seepage characteristics and stability of slope under the combined action of rainfall and reservoir water level. The research results provided an intuitive understanding of the law of seepage stability of slope under the condition of sudden drop of reservoir water level under different types of rainfall. At present, many scholars generally recognize that there is a great correlation between rainfall and slope stability, and think that rainfall infiltration is the main reason that leads to the transition of slope from unsaturated state to saturated state. Liu et al. [9,10] studied the influence of rainfall on the instability characteristics of the bank slope of unsaturated soil road by combining runoff-underground seepage and fluid-solid coupling. The analysis showed that rainfall intensity, rainfall duration and long-term intensity had the greatest influence on slope stability, and the cohesion force and internal shear Angle decreased with the increase of soil water content. Bao et al. [11,12] studied the properties of unsaturated soil and the influence of rain infiltration on slope stability in unsaturated state, and concluded that the existence of cracks has great influence on pore water pressure and volume water content distribution in slope. Zhu et al. [13,14] conducted experimental analysis on the engineering characteristics of carbon shale, such as swelling, disintegration and creep, and studied the reinforcement methods of high slopes of carbon shale, which provided some new reinforcement methods for practical projects.
Many scholars have done a lot of research on the influence of rainfall infiltration on slope stability, especially on the saturated unsaturated seepage problem through numerical model, hydraulic parameters and laboratory tests, and achieved certain results. However, there is still a big gap between the research on the infiltration of carbonaceous shale and the solution of practical engineering problems. In this paper, based on previous studies, taking the third junior middle school landslide in Jinchengjiang District, Hechi City, Guangxi Province as an example, the stability of carbon shale slope is studied by using landslide thrust calculation method, and the seepage law of carbonaceous shale slope is studied with numerical simulation method, and the numerical analysis of seepage field of slope rock mass under rainfall condition is carried out. The stability coefficient of the slope is calculated and verified, which can provide reference for slope stability evaluation and drainage reinforcement design.
A The third junior middle school in Jinchengjiang District of Hechi City is located in the east longitude 108°03′52″, 24°N. The junction of Nanxin East Road and Xinhua Road in Jinchengjiang District, 41′40″. The landslides are mainly distributed in the teaching area of the third junior middle school in Jinchengjiang district. It has been found that there are strong deformation areas and potential deformation areas. Among them, the landslide is located in the strong deformation area, and its plane shape is semicircular. According to the investigation, the potential landslide is 52 m long, 84 m wide and 30°, the thickness is 8 m, and the location and shape of the landslide are shown in Fig. 1. According to the regional geological data, drilling and other methods, the landslide sliding bed is carbonaceous shale and mudstone, completely weathered to strongly weathered, and the exposed thickness of drilling is 5.0 m. The water content of carbonaceous shale and mudstone at the sliding zone is high, and the rock mass is broken, and most of them are in clay shape. Among them, the carbonaceous rock disintegrates and softens with water under the action of dry wet cycle, and then disintegrates and argillates, which is the important reason for the appearance of landslide mass.
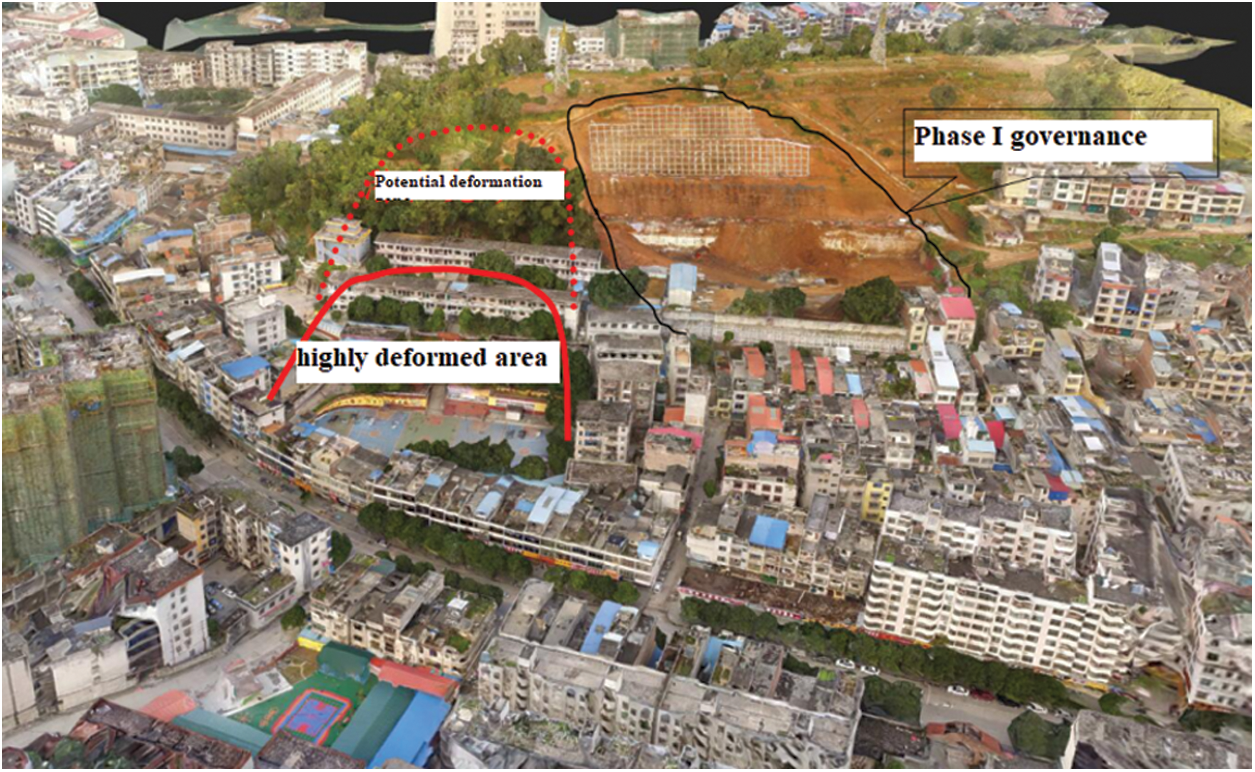
Figure 1: Distribution range of sliding mass in the third junior middle school
3 Stability Analysis of Carbonaceous Shale Slope
3.1 Calculation Principle and Parameter Selection
According to the investigation and analysis, the sliding surface of the landslide mass (the sliding surface is located at the contact surface between the overburden and carbonaceous shale) can be determined as the approximate broken line type. Therefore, the calculation formula of the broken line type transfer coefficient method can be used for calculation.
where:
Calculation formula of residual sliding force:
Among them:
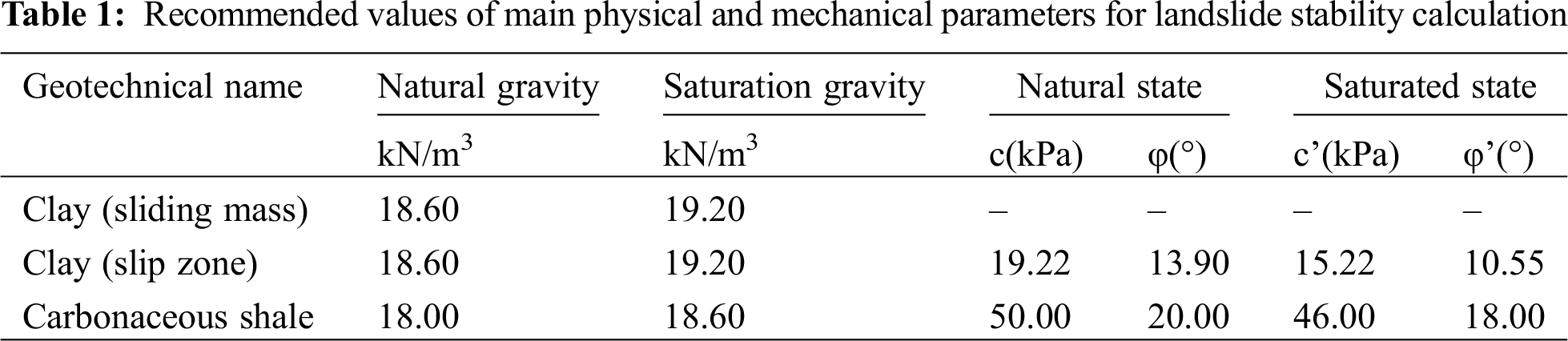
Whether the shear strength parameters of landslide soil are reasonable or not plays a key role in the calculation of landslide stability. The shear strength parameters of landslide soil are determined by indoor test value, field large shear test and inversion value, combined with regional experience. The physical and mechanical parameters of landslide stability calculation are shown in Tab. 1.
3.2 Calculation Condition and Result Analysis
At present, three working conditions are proposed to analyze the stability and calculate the thrust of landslides at different sections: Condition I: dead weight, Ks = 1.40; Condition II: dead weight + rainstorm + groundwater, Ks = 1.15; Condition III: dead weight + earthquake + groundwater, Ks = 1.15; As shown in Fig. 2, the landslide sections are mainly calculated as follows: A-A′, B-B′, C-C′, D-D′, E-E′;the representative section is shown in Fig. 3. According to the above design safety factor of landslide prevention and control engineering, the results of residual sliding force are shown in Tab. 2.
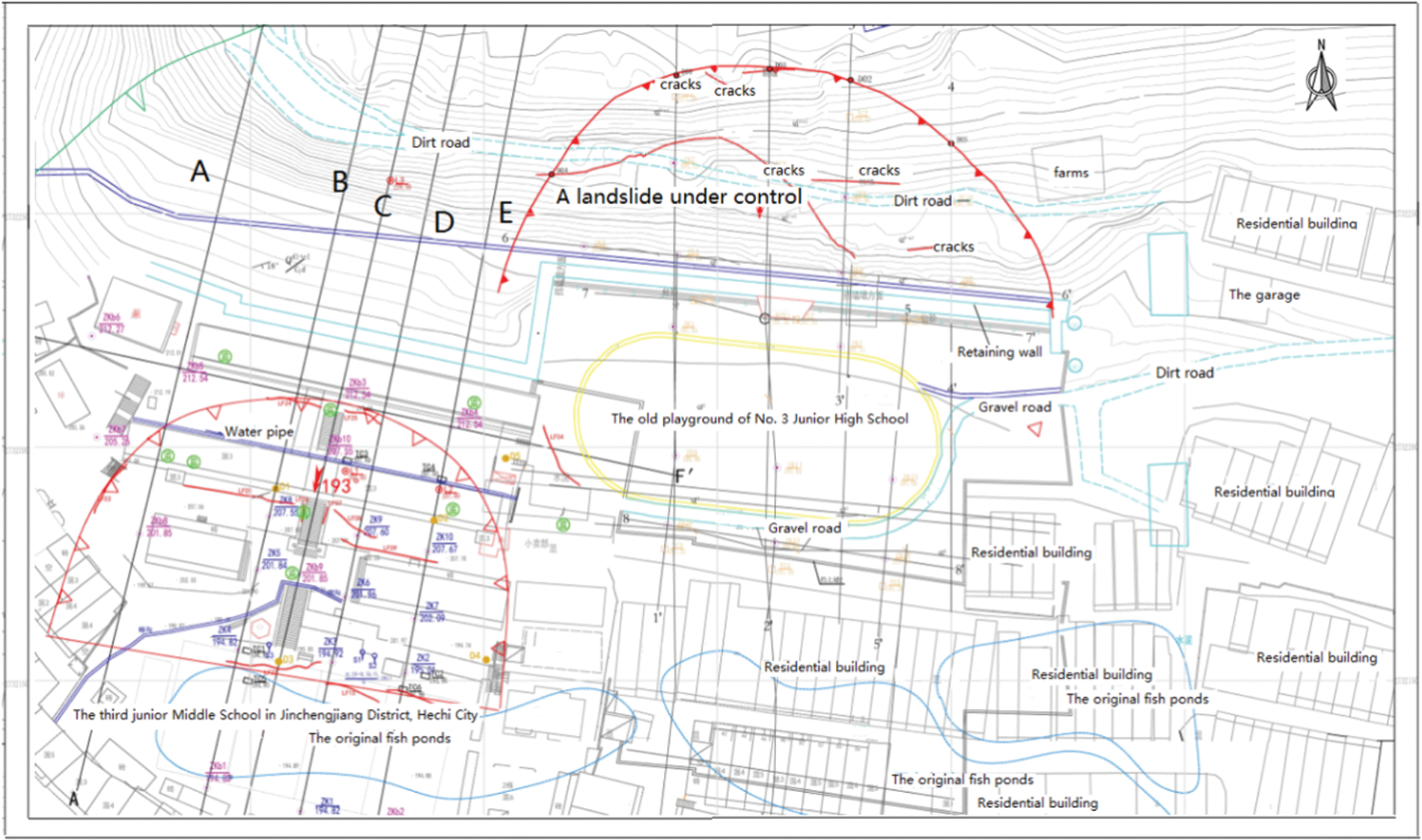
Figure 2: Landslide plan of the third junior middle school in Jinchengjiang District, Hechi City
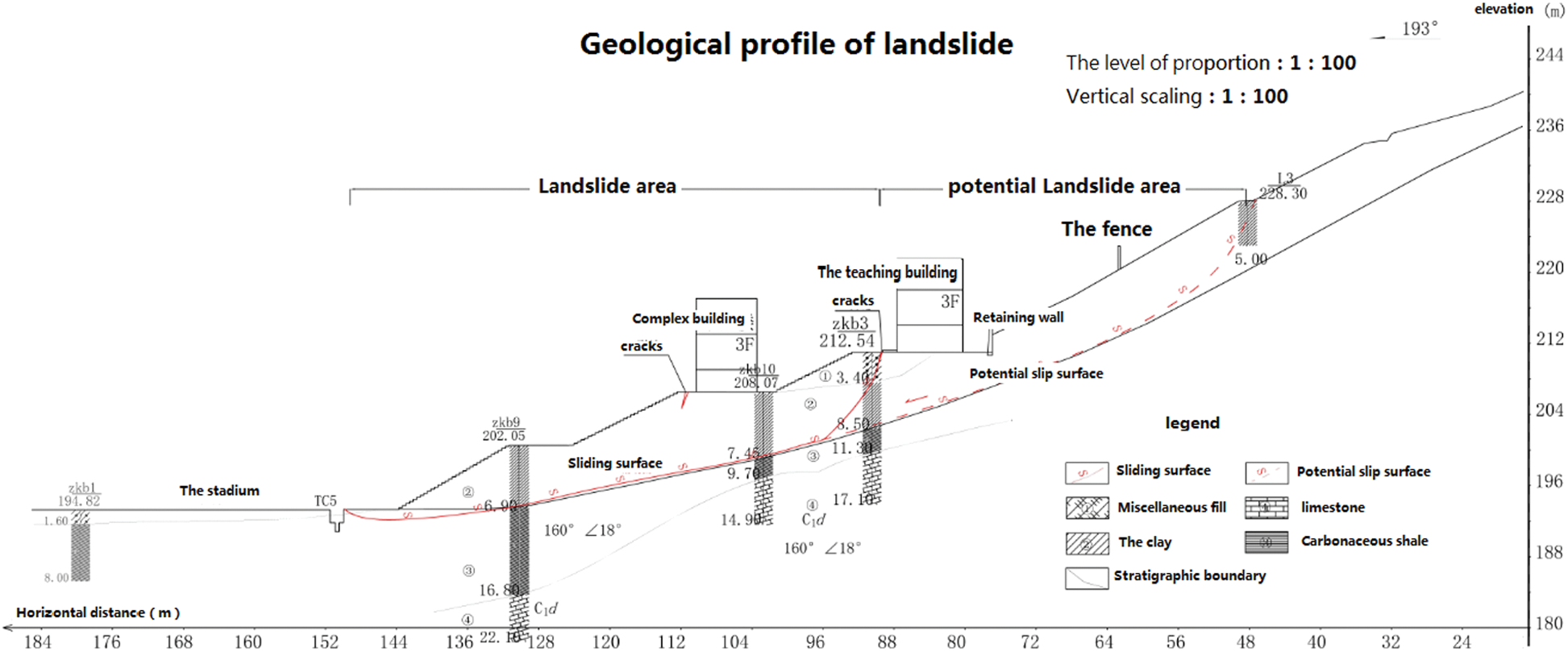
Figure 3: Engineering geological section of landslide in the third junior middle school in Jinchengjiang District, Hechi City
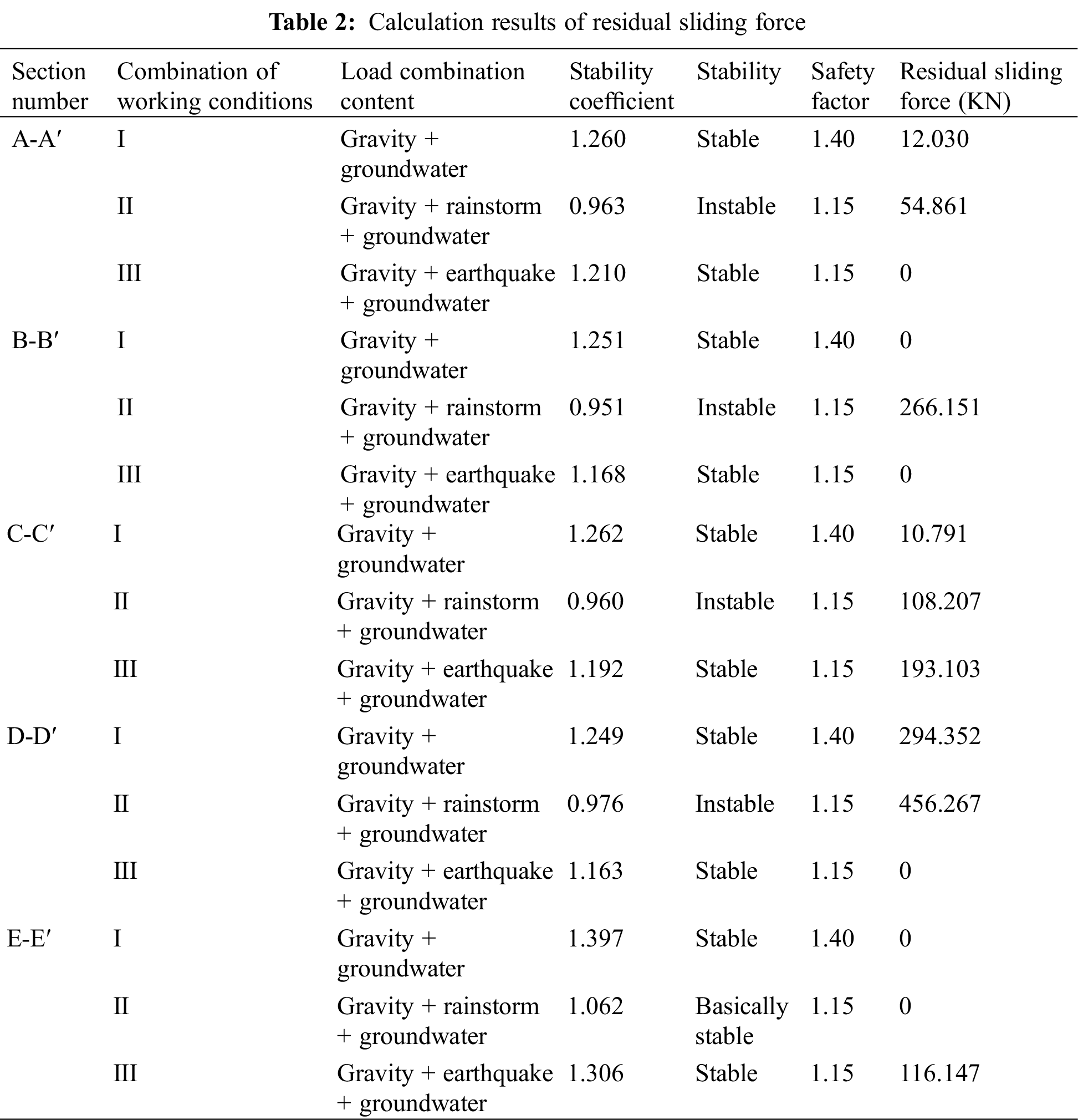
According to the classification standard of landslide stability evaluation in code for investigation of landslide prevention and Control Engineering (GB/T 32864-2016), the stability coefficient calculation results of different sections in Tab. 2 are analyzed.
(1) Under Condition I, i.e., Gravity + groundwater state, the stability coefficients of A-A′, B-B′, C-C′, D-D′, E-E′ sections of the landslide are all greater than 1.15, which is in a stable state.
(2) Under Condition II, i.e., dead weight + rainstorm + groundwater, the stability coefficient K values of A-A′, B-B′, C-C′, D-D′ are 0.963, 0.951, 0.960 and 0.976 respectively, which are all less than 1.0, and are in unstable state; The stability coefficient K value of profile E-E′ is 1.062, ranging from 1.05 to 1.15, which is basically stable.
(3) Under Condition III, i.e., gravity + earthquake + groundwater, the stability coefficient K values of A-A′, B-B′, C-C′, D-D′ and E-E′ sections are 1.210, 1.168, 1.192, 1.163 and 1.306, respectively, which are all greater than 1.15, and are in stable state.
At present, the landslide has not yet slipped as a whole, but various factors still exist, which is not conducive to the stability of the landslide. Recently, tension and shear cracks have been formed in the front, middle and upper part of the sliding mass, which indicates that the landslide is creeping and deforming. Under the influence of comprehensive factors such as rain infiltration, rising of underground water level and continuous decrease of mechanical strength of rock and soil mass, the landslide is undergoing creep deformation. It is likely that large-scale sliding will occur, and the overall southward sliding will cause the buildings above the landslide mass to slide along with the sliding mass, and the hazard level is Grade I.
According to the analysis of landslide lithology and current situation, residual thrust value and construction conditions, it is suggested that the landslide should be divided into two areas for treatment and design, and the maximum sliding force of each block should be selected as the design landslide thrust: the first area is the area where A-A′ section is located, and the remaining sliding force is 54.861 kN/m; the second area is the area where B-B′, C-C′, D-D′, E-E′ sections are located, and the maximum residual sliding force is 456.267 kN/m.
According to the stability of the landslide at different positions, the slope behind the teaching building is reinforced with anchor cable lattice beam (the length of anchor cable is 18 m), and the anti slide pile is reinforced in front of the teaching building (Level 4 Platform) and the comprehensive building (Level 3 platform) (pile length is 17 m, pile diameter is 1.2 m, a total of 109 piles). A reinforced concrete retaining wall with a height of 6.0 m, top width of 1.5 m and bottom width of 2.0 m is set in front of the retaining wall between the playground and dormitory building (secondary platform). The site needs to build a perfect drainage system to prevent rainwater infiltration and further reduce the stability of the slope. At the same time, according to the characteristics of the slope, long-term monitoring of slope deformation is carried out, including surface displacement and deformation, support structure displacement, stress change monitoring, deep displacement monitoring, etc. the location of each platform and building distribution are shown in Fig. 4.
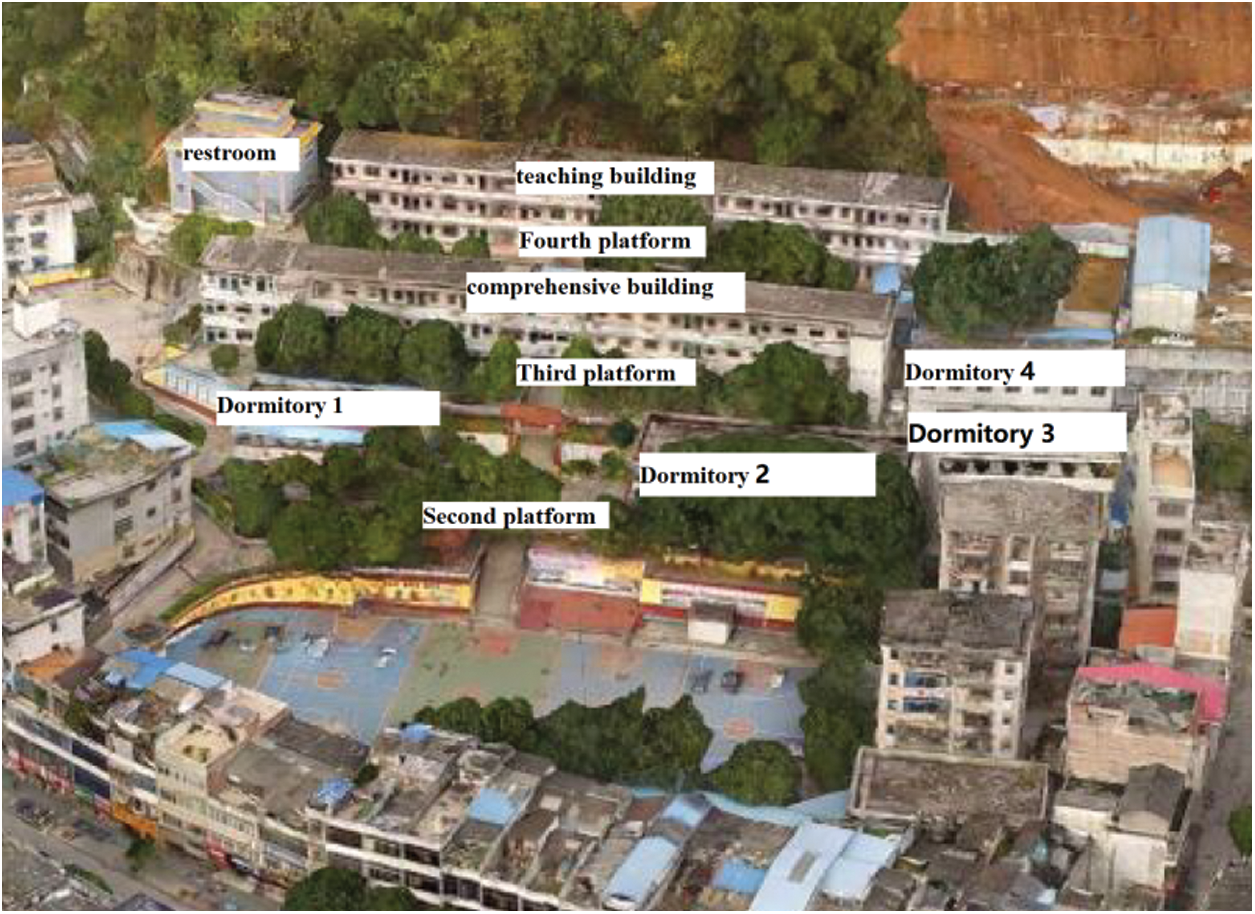
Figure 4: Building distribution of teaching area
4 Numerical Simulation Analysis of Carbonaceous Shale Slope under Heavy Rainfall and Groundwater
The seep/w (groundwater seepage analysis software) and slope/w (slope stability analysis software) modules of GeoStudio software were used to simulate the slope stability under heavy rainfall and groundwater conditions. According to the continuity equation, the basic differential equation of steady seepage can be expressed as follows:
When the direction of the coordinate axis is consistent with the direction of the seepage principal axis, according to the variational principle, the three-dimensional seepage problem is equivalent to the extremum problem of the energy functional.
According to the hydrogeological structure of the study area, the seepage field is discretized.
The water head interpolation function of a unit can be expressed as follows:
where:
4.2 Implementation of Numerical Model
(1) Numerical model implementation
According to the field exploration results, the soil layer is divided into four layers: miscellaneous fill, clay, calcareous shale and limestone. The values of soil layer and parameters under various working conditions are shown in Tab. 1. According to the geological profile, a numerical model for slope stability analysis under heavy rainfall and groundwater conditions is implemented. As shown in Fig. 5, it is A-A′ profile slope numerical model and soil layer distribution. The calculation range of slope model is 189.5 m in X direction, 195 m in Y direction and 233.5 m in long side.
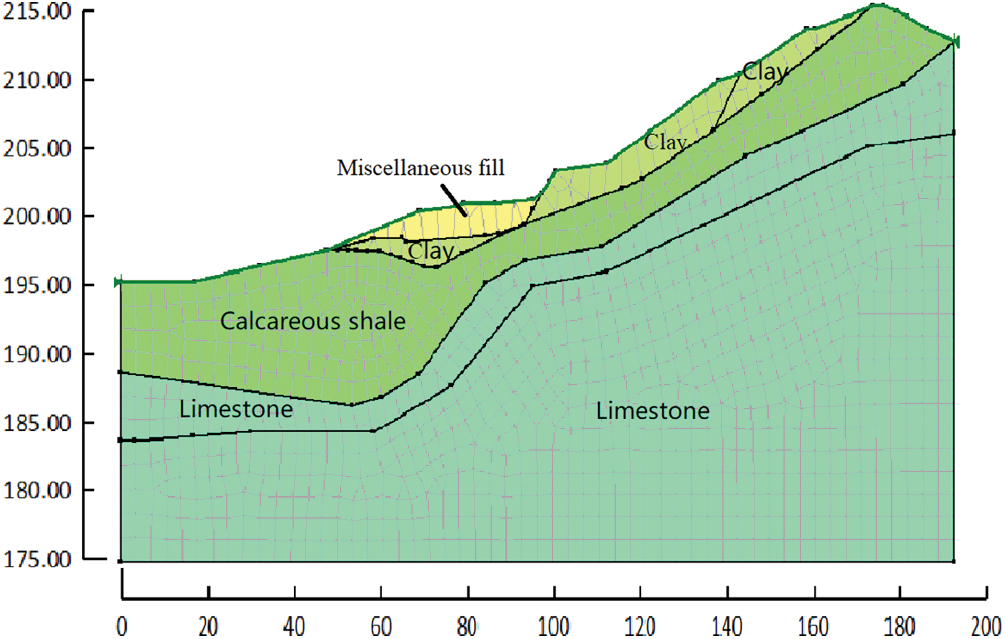
Figure 5: Numerical model and soil layer distribution of A-A′ section slope
In order to analyze the change of volume moisture content in different sections of the slope, 13 monitoring points were set up horizontally and 17 monitoring points were set up longitudinally. The vertical monitoring points are mainly used to analyze the relationship between the volume water content and the height, and the horizontal monitoring points are mainly used to analyze the relationship between the pore water content and the distance. The positions of each point are shown in Fig. 6. Fig. 7 is the schematic diagram of the initial position of the infiltration line and the monitoring point of pore water pressure in profile A-A before rainfall.
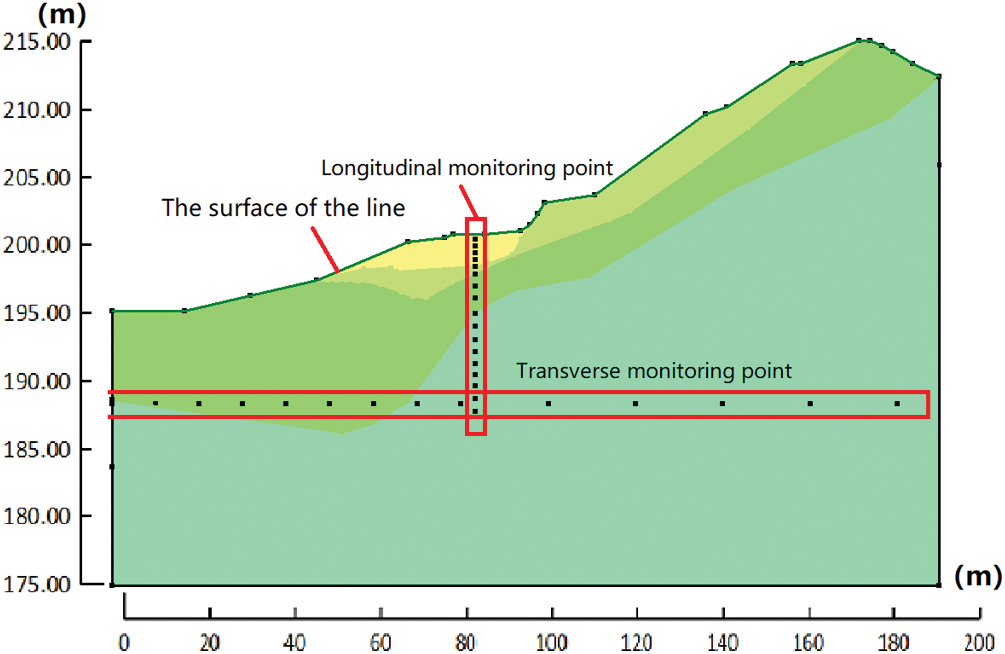
Figure 6: Location of monitoring points
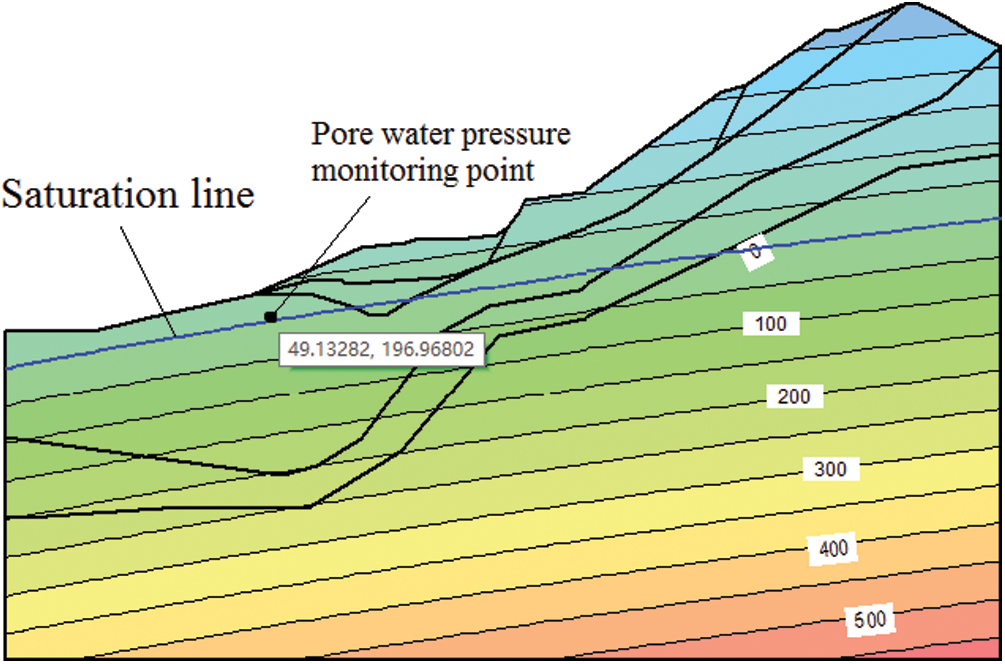
Figure 7: Schematic diagram of wetting line and pore water pressure monitoring points
Continuous heavy rainfall is the most important condition affecting the deformation and failure of slope, and has a significant impact on slope stability. According to the results of slope stability calculation by the broken line transfer coefficient method, the slope is the most dangerous under Condition II, i.e., dead weight + rainstorm + groundwater. Therefore, in the numerical simulation analysis of carbon shale slope, the saturated state of landslide mass and groundwater on sliding surface are mainly considered, i.e., Condition II (Gravity + rainstorm + groundwater state).
In steady-state analysis, the upper surface of the model is free boundary, and the two sides and bottom are impermeable boundary. The transient analysis includes two sections: rainfall and no rainfall. During rainfall, the slope surface is set as the unit flow boundary, the flow is equal to the rainfall, and the free boundary is set after the rain stops.
(2) Research on mesh refinement
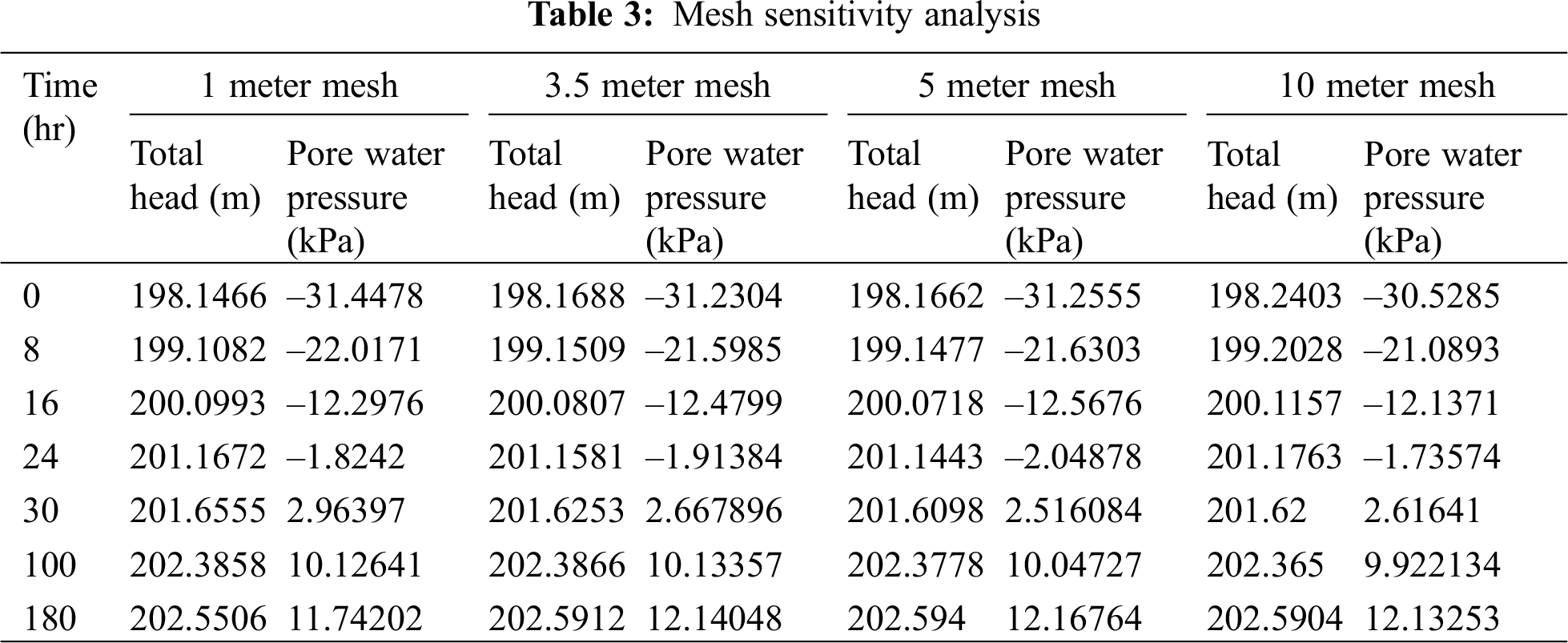
The type, size distribution and quality of model mesh division will affect the analysis results, so the size of mesh division should not be too large. Theoretically speaking, the smaller the size of the model mesh is, the higher the calculation accuracy will be, but it will often bring a large amount of calculation workload and waste a lot of time. Therefore, sensitivity analysis of model mesh is required: Tab. 3 shows that the size of model mesh has little influence on the total water head, and the maximum difference between the total water head of 1-meter grid and 10-meter grid is only 0.0946 m. The influence of pore water pressure is relatively great, and decreases with the increase of mesh size. When the rainfall lasts for 30 h, the maximum difference of pore water pressure between 1 m and 10 m mesh is 0.3475 m. Since the calculation amount of 1 m grid is too large, and the calculation accuracy of 10 m grid is not enough, the model with 3.5 m grid is chosen for calculation.
4.3 Analysis of Calculation Results
4.3.1 Analysis of Slope Seepage Characteristics
(1) Change of volume water content
By analyzing the water content change law of different parts of the landslide, combined with the calculation results of sliding force and safety factor, the potential dangerous sliding surface is further analyzed. Relationship between volume water content and height is shown in Fig. 8. Compared with A-A′, B-B′, C-C′, D-D′, and E-E′, the volume water content of B-B′ section and C-C′ section is the largest, with the value of 0.32 m (m212)/M (m212). At this time, the elevation is 203 m, which is in the cohesive soil layer with large porosity, and the volume water content of E-E′ section at the same elevation is increased by 10.34% compared with that of E-E′ section at the same elevation. At the same time, it can be seen from the curve that the volume moisture content reaches the maximum at the height of 204 m. With the decrease of height, the volume water content gradually decreases and finally tends to be stable. This is due to the existence of soil interface, which makes the volume moisture content of soil different from that of homogeneous soil.
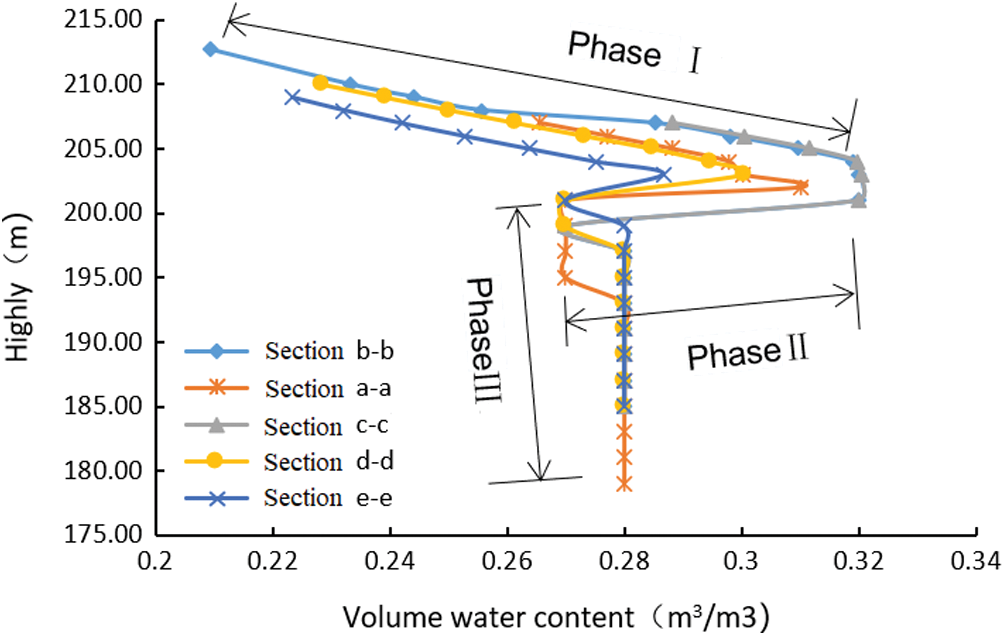
Figure 8: Curve of volume moisture content with height
Due to the influence of rainfall process and soil properties, the change of pore volume water content in slope can be divided into three stages: ① Stage I is the initial stage of rainfall infiltration, in which rainwater gradually infiltrates from the slope surface, and the volume water content increases with the decrease of height, and the maximum volume water content appears at this stage due to the loose soil layer on the slope surface; ② The second stage is the transitional stage of rainfall infiltration. With the continuous infiltration of rainfall, rainwater begins to enter the relatively dense soil layer, and because of the existence of groundwater, the volume water content decreases sharply; ③ Stage III is the saturation stage of rainfall infiltration. After rainfall infiltration for a period of time, the groundwater level will also rise, so that the groundwater pressure will correspondingly increase until it reaches the final saturation state.
(2) Variation of pore water pressure
Fig. 9 shows the relationship curve of pore water pressure with distance. According to the analysis in Fig. 9, except for e-e′ section, the pore water pressure value and its change trend of the other four sections are relatively close, and the pore water pressure at the same part of the E-E′ section is obviously smaller than that of the other four sections. The maximum difference of pore water pressure between the two is 33.48 kPa. Therefore, indirectly reflected from the side, E-E′ profile is more stable than the other four profiles under rainstorm conditions, and the analysis results are consistent with the calculation results of sliding force and safety factor. At the same time, it can be found that the pore water pressure increases linearly with the increase of distance.
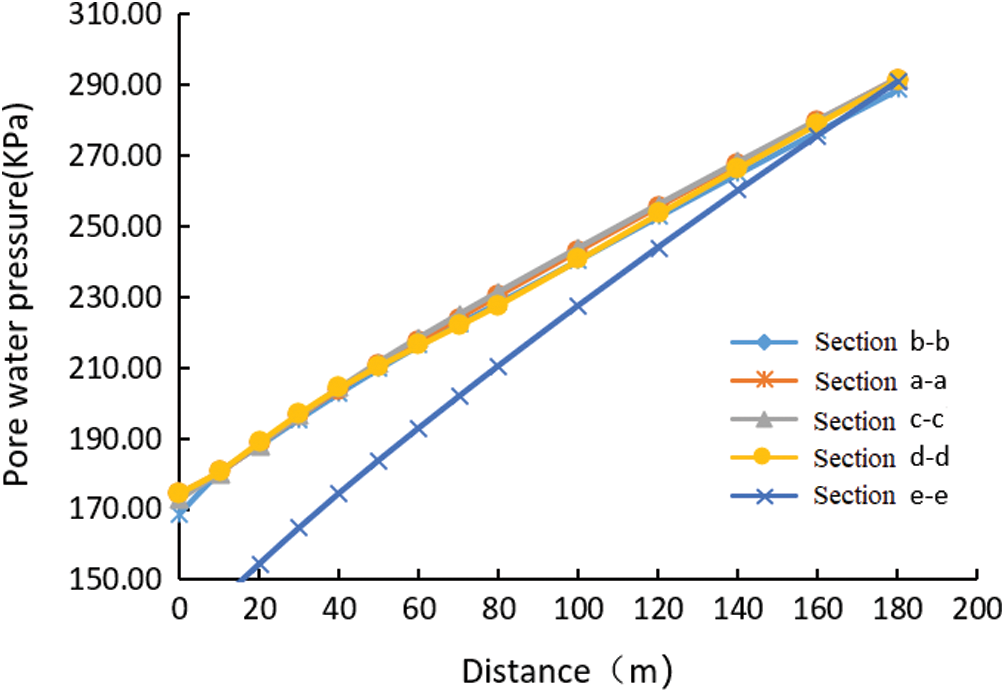
Figure 9: Variation curve of pore water pressure with distance
Fig. 10 shows the variation curve of pore water pressure with time at a certain point of each profile after rainfall infiltration. This point is the point within the variation range of the infiltration line. As can be seen from Fig. 9 and Tab. 4, with the continuous rainfall, the variation of pore water pressure over time presents a logarithmic function rule, with a high degree of fitting. From 0 h to 24 h, the pore water pressure in the soil layer of each profile increased rapidly, increasing by 1.58 kPa per hour, and the growth rate gradually leveled off after 24 h. By comparing the pore water pressure of the five sections, it can be seen that the maximum pore water pressure of C-C section reaches 47.98 kPa, and the minimum pore water pressure of E-E section reaches 17.7 kPa.
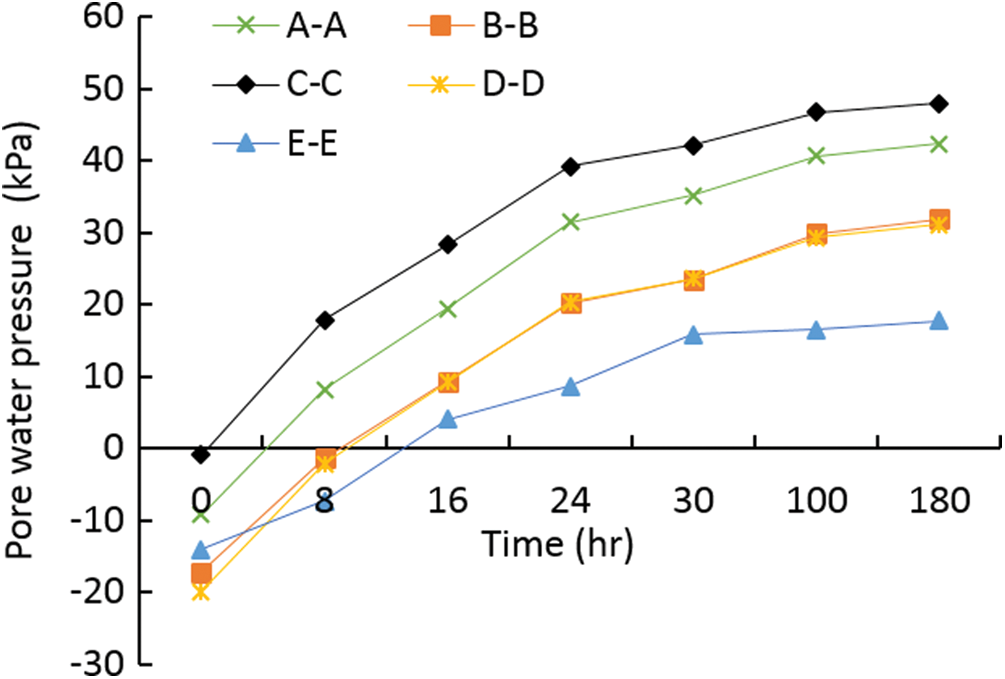
Figure 10: Curve of pore water pressure over time
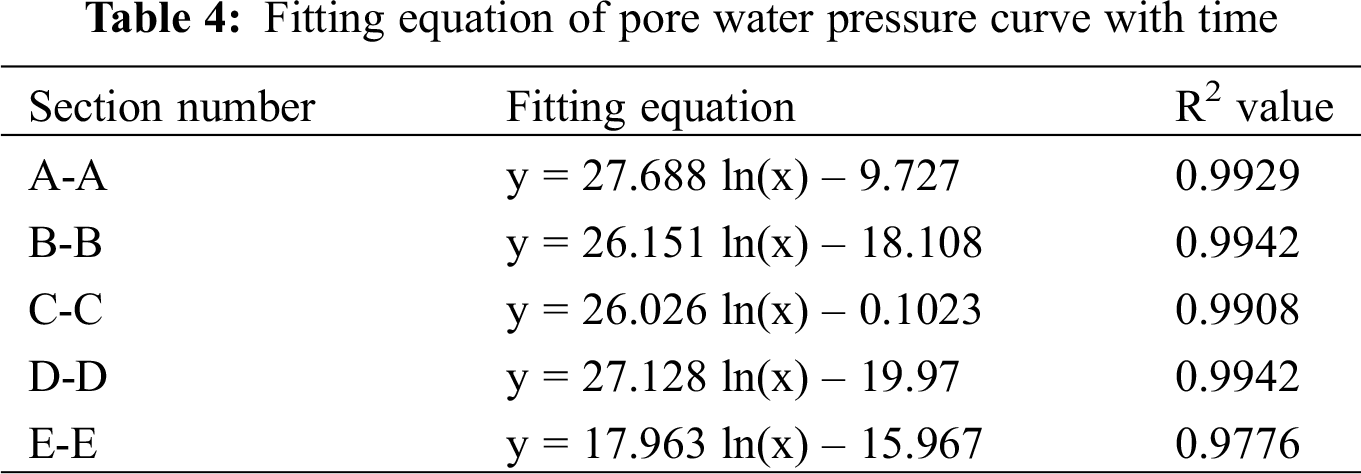
4.3.2 Slope Stability Analysis
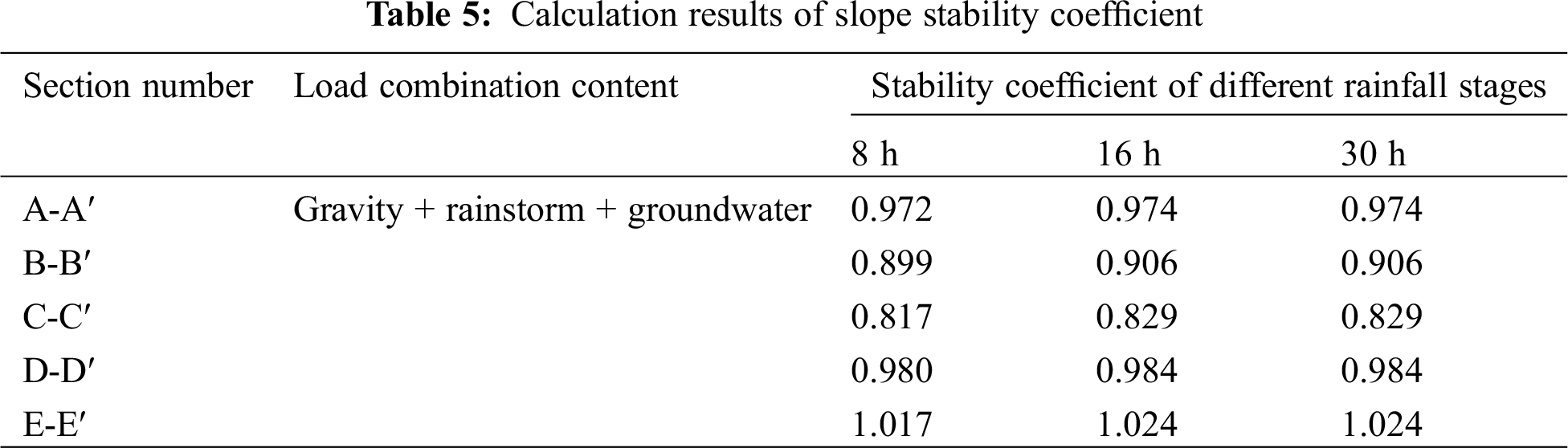
According to the slope numerical model, the slope stability coefficient of gravity + rainstorm + groundwater under different rainfall stages is calculated, and the results are shown in Tab. 4.
It can be seen from Tab. 5 that the section E-E′ has the highest stability coefficient, and the section C-C′ has the lowest stability coefficient. As shown in Fig. 11, there is a dangerous slip zone on the back edge of the slope on the C-C′ section. The conclusion obtained is basically consistent with the stability calculation result. Generally, rainfall infiltration will cause the slope stability coefficient to decrease, but with the rainfall, the slope stability coefficient will rise temporarily during the rainfall, and the slope stability coefficient will start to decrease after the rainfall stops, that is, the rainfall infiltration effect has a certain lag.
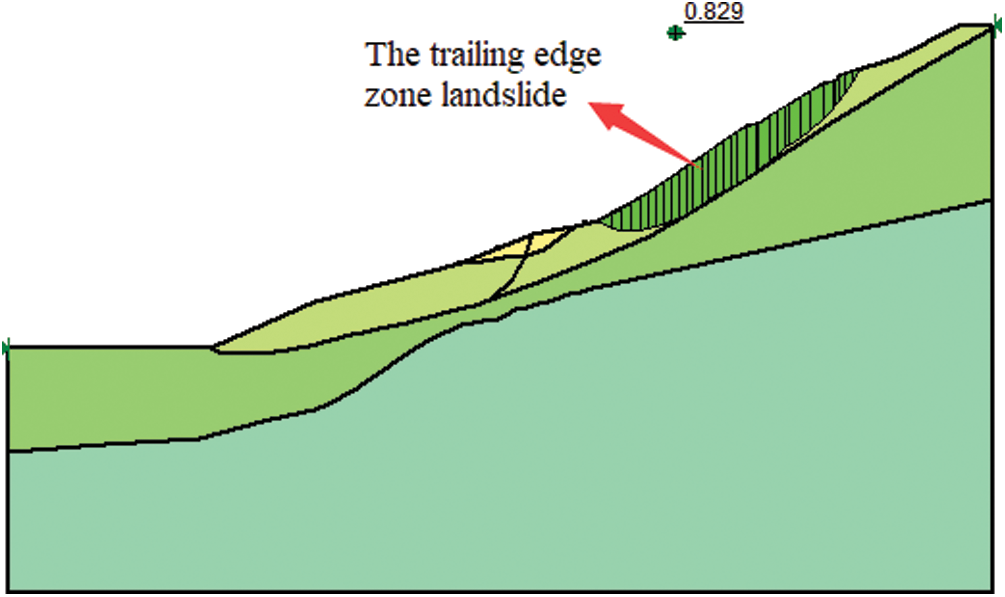
Figure 11: Landslide mass in C-C′ section
Taking the landslide of the third junior middle school in Jinchengjiang District, Hechi City, Guangxi Province as an example, the stability of the carbon shale slope is calculated and analyzed. According to the field survey data, the numerical model of slope stability analysis under the condition of heavy rainfall and groundwater is implemented. The variation law of volume moisture content and pore water pressure on different sections of the slope is analyzed, and the stability coefficient of the slope is verified.
(1) The stability coefficients of A-A′, B-B′, C-C′ and D-D′ are 0.963, 0.951, 0.960 and 0.976, respectively, under Condition II, i.e., gravity + rainstorm + groundwater, which are in unstable state, and E-E′ is basically stable; The slope is in stable state under the condition of Gravity of Condition I and Condition III of Gravity + earthquake + groundwater.
(2) Under the action of heavy rainfall, rainwater seeps into the slope layer by layer; Among them, the volumetric water content of C-C section and B-B section is the largest, reaching 0.32 m3/m3, which is 10.34% higher than that of E-E′ section at the same elevation.
(3) Rainfall infiltration will lead to the decrease of slope stability coefficient, but in the initial stage of rainfall, the slope stability coefficient will rise temporarily, and the slope stability coefficient will start to decrease after the rainfall stops, that is, the rainfall infiltration has a certain lag, The results show that the landslide sections a-a′, b-b′, c-c′ and d-d′ are in an unstable state, and the landslide section e-e′ is in A basically stable state.
Funding Statement: This study was supported by the “Reinforcement Theory and Technology of Multi-point Restraint Anchor Cable and Monitoring Warning for Highway High Slope” (Grant: 2020-MS3-082) and the “Research and Application of Ecological Slope Protection Technology in Carbonaceous Rock Slopes” (Grant: AD19110124).
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
1. Htet, Z. O., Huy, T. P., Cheng, J. (2013). Stability of slope and seepage analysis in earth dam using numerical finite element model. Study of Civil Engineering and Architecture, 2(4), 104–108. [Google Scholar]
2. Balendra, M. M., Ravi, S. J. (2017). Assessment of slope stability using multiple regression analysis. Geomechanics and Engineering, 13(2), 237–254. [Google Scholar]
3. Paolo, M., Luca, S, Salvatore, M., Benedetta, A., Elisa, B. et al. (2018). The contribution of terrestrial laser scanning to the analysis of cliff slope stability in Sugano (Central Italy). Remote Sensing, 10(9), 237–254. [Google Scholar]
4. Liu, X. M., Li, S. N., Xu, Z. P., Li, Y., Zhou, Y. M. (2018). Research on creep model of carbonaceous shale under freeze-thaw cycle. China Journal of Highway and Transport, 32(11), 137–145. [Google Scholar]
5. Luo, G. C., Fu, H. Y., He, W. (2012). Experimental study on disintegration characteristics of carbonaceous shale. Journal of China & Foreign Highway, 32(3), 309–311. [Google Scholar]
6. Zhang, K. F. (2018). Joint effect of rainfall and reservoir water level-based analysis on landslide seepage stability. Water Resources and Hydropower Engineering, 49(9), 170–177. [Google Scholar]
7. Marković, M., Živanović, N., Gajić, G. (2019). Stability analysis of slopes along roads in bio-reinforced soil conditions. Glasnik Šumarskog Fakulteta: Univerzitet u Beogradu, 2019(119), 91–104. [Google Scholar]
8. Xu, X., Wang, Y. X., Fang, Z. (2019). Analysis on stability of a slope under rainfall and reservoir water level variation. The Chinese Journal of Geological Hazard and Control, 30(2), 51–58. [Google Scholar]
9. Liu, J. X., Yang, C. H., Gan, J. J., Liu, Y. T., Wei, L. et al. (2017). Stability analysis of road embankment slope subjected to rainfall considering runoff-unsaturated seepage and unsaturated fluid-solid coupling. International Journal of Civil Engineering, 15(6), 865–876. [Google Scholar]
10. Gusman, M., Nazki, A., Putra, R. R. (2018). The modelling influence of water content to mechanical parameter of soil in analysis of slope stability. Journal of Physics: Conference Series, 1008(1), 012022. [Google Scholar]
11. Bao, C. G., Gong, B., Zhan, L. T. (1998). Properties of unsaturated soils and slope stability of expansive soils. Proceedings of the Second International Conference on Unsaturated Soils, 2, 81–108. [Google Scholar]
12. Yao, H. L., Zheng, S. H., Li, W. B., Chen, S. Y. (2002). Parametric study on the effect of rain infiltration on stability of unsaturated expansive soil slope. Chinese Journal of Rock Mechanics and Engineering, 21(7), 1034–1039. [Google Scholar]
13. Zhu, S. N., Yin, Y. P., Li, B., Wei, Y. J. (2020). Shear creep characteristics of weak carbonaceous shale in thick layered Permian limestone, southwestern China. Journal of Earth System Science, 128(2), 28. [Google Scholar]
14. Yang, Y. H., Lu, D. W. (2006). Study on treatment of high-cut carbonaceous shale slope in expressway. Chinese Journal of Rock Mechanics and Engineering, 25(2), 392–398. [Google Scholar]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |