Fluid Dynamics & Materials Processing

DOI: 10.32604/fdmp.2022.017593

ARTICLE

Analysis of the Microstructure and Macroscopic Fluid-Dynamics Behavior of Soft Soil after Seepage Consolidation

Fang Jin*, Dong Zhou and Liying Zhu

Institute of Civil Engineering, Huanghe S&T University, Zhengzhou, 450063, China
*Corresponding Author: Fang Jin. Email: d1ixav@163.com
Received: 22 May 2021; Accepted: 29 July 2021

1  Introduction

The characteristics of the microstructure of soil have important practical significance in engineering. A large number of studies show that the state and change of the microstructure of soil affect mechanical properties [1]. Many facts prove that the mechanical properties of soil depend essentially on its microstructure [2,3]. The purpose of the previous research on the microstructure of soil is to explore the influence of internal factors on external physical and mechanical properties, and find out the internal relationship between microstructure and macroscopic mechanical parameters. The macroscopic mechanical properties of soil are extremely complex, and they cannot be properly analyzed by traditional methods [4]. Generally speaking, soil structure refers to the form of arrangement, void properties, soil particles, or the interaction between particles and fabric [5]. Soil has a certain structure, which is reflected in the evolution law and the natural structure of soil. The fuzziness and uncertainty of physical and mechanical behavior are embodied at the macro level.

The calculation models and constitutive relations in the soil mechanics theory are established based on traditional methods. These calculation models are widely used in engineering and have made some achievements. However, these models cannot show the characteristics of the microstructure of soil only at the macro level, or significant differences between theoretical calculation and actual monitoring are caused in the engineering field [6]. it is necessary to explore the internal relationship between the microstructure and the macroscopic physical and mechanical properties of soil, which enriches the traditional calculation theory and helps to construct the mechanical theory suitable for analyzing the mechanical behavior of soil. Although the concept of microstructure is proposed several decades ago and there is a lot of research on the microscopic mechanism of soil, the research on the internal relationship between soil microstructure and macroscopic mechanical properties is still in its infant.

The soft clay in and around the area is taken as the research object. Based on the SEM test, the quantitative analysis of the microstructure of soft clay is made according to the statistics. Combined with the macro properties and micro parameters of soft clay, the relationship between the macro physical parameters and micro parameters of the clay is constructed, and the research is conducted by bringing microstructure into the macro mechanical calculation. The innovation of the study is to find new analysis ideas and methods to predict the change trend and range of some properties by the relationship between macro properties and microstructure of soil, which is helpful to explaining the mechanical behavior of soil.

2  Research Progress of Soft Soil

Among 137 papers in the field of soil mechanics and engineering in the early 20th century, there are 53 on the deformation of the soft soil base (including embankments, dams and airports), accounting for the largest proportion of 39% of the total. The studies on the deformation of the sand case take up 20%. Those on the deformation of the pile foundation account for 15%. The number of the studies on the deformation of the construction base is 12, accounting for 9%. From the academic conference and the studies on the deformation of the soil base in recent years, the characteristics of the research on the deformation of soil are summarized as follows: (1) Although the problem of base deformation and differential settlement is from the 1990s, more and more attention has been paid, and a lot of manpower and material resources have been invested in research. (2) Settlement calculation is conducted by various methods, which not only process and utilize the observed data, but also the research on advanced prediction methods; (3) With the development of science and technology, new methods of treating the deformation of the soil base are emerging. In addition, some old methods are updated, like the vacuum preloading method.

Li et al. [7] comprehensively and systematically studied the rheological deformation mechanism of soil. On the basis of studying the physical nature of deformation, various forms of creep are analyzed in detail, and a comprehensive equation describing deformation is proposed. The processing method and equation application method are illustrated by examples, and the rheological properties of soil are simply revealed. Gao et al. [8] systematically summarized the experience of treating the problem of soft soil, including the deformation, strength and permeability characteristics of soft clay. Zhai et al. [9] discussed the characteristics of soft clay in coastal areas and the engineering problems caused by it, the shear strength and deformation characteristics of soft clay, and the calculation method that has a significant impact on the study of the engineering properties of soft clay. Zhang et al. [10] studied the basic theory and analysis method of rheological mechanics in geotechnical engineering, and promoted the development and popularization of soil rheology. Cała et al. [11] summarized the characteristics and laws of deformation displacement and stress of rock and soil under external forces, such as the construction and excavation according to the system of soft clay, and described the rheological test of rock and soil, the rheological theory and method of rock and soil, the numerical method of rheological analysis of rock and soil, and the application of rheological analysis in various geotechnical engineering field. Hu et al. [12] obtained several numerical solutions of soil consolidation and rheology by studying the consolidation rheological theory of soft soil, and the influence of consolidation and rheology on the stability of soil. In recent years, with the rapid development of urban construction, the research on rheological properties of soft soil is more extensive and profound.

3  Methods of Microstructure Analysis and Macro-Mechanics

3.1 Characteristics of the Microstructure of Soft Soil

3.1.1 Micro-Porosity of Soft Soil

The soft clay is cut into small pieces and dried in the oven, and the dried soil samples are crushed and sieved, and then placed in a sealed bucket [13]. The microstructure of the low-temperature treated soil sample remains unchanged, and it is dried by a high-speed pump. The groove in the middle of the small sample keeps its original structure. The soil sample is separated at the groove and the flat section is selected for gold spraying. Finally, the SEM electron microscope is used to do scanning. The density is measured by sealing and the porosity of the sample is calculated.

The volume of holes is calculated by calculus, that is, the volume is obtained by multiplying the area of each section by the corresponding height [14]. The image pixel represents the plane direction, and the threshold represents the height. In the SEM image, different threshold values correspond to the area of holes in different sections. The gray values corresponding to the threshold values Y1,Y2 are considered to be the areas surrounded by small and large circles A1,A2 , and the volume of holes under these two thresholds is calculated by:

V1=(A1+A22)×(Y2−Y1) (1)

The volume of the irregular body is obtained by infinitely reducing △Yi . According to the principle of calculus, when the value of △Yi is small enough, Ai+1 and Ai will be very close. The calculated pore volume is close to the real volume, and the solution is pushed to the whole pore to obtain the pore volume:

V3D=∑i=1255(Ai+Ai−12)×(Yi−Yi−1) (2)

The equation of the three-dimensional porosity of soil at any threshold gray level is as follows:

n3D=∑i=11n(Ai+Ai+12)×(Yi+1−Yi)(Ym−Y0)×SA (3)

In Eq. (3), Ai is the area surrounded by small and medium circles, and the threshold value m corresponds to the gray level under the threshold Yi . SA is the regional pixel selected in the analysis of IPP (Image-Pro Plus), and its value is fixed. When the initial threshold is 0, the equation can be rewritten as:

n3D=∑i=1m(Ai+Ai+12)×(Yi+1−Yi)Ym×SA (4)

3.1.2 Average Contact Area Ratio of Soft Soil

The macro-porosity obtained by the indoor geotechnical test is compared with the statistical method combined with the three-dimensional porosity of microscopic images. When the three-dimensional porosity calculated by statistics is equal to the macro-porosity in numerical value, the contact area is defined as the corresponding pixel in the threshold gray analysis of IPP images. The average contact area rate is the ratio of the pixel area to the total pixel area, and it is expressed by RCA . Here, SEM images obtained when the magnification is 1600 times are selected for analysis [15]. The SEM image of the hole magnified 1600 times is shown in Fig. 1.

Figure 1: The SEM image of a soft soil hole magnified 1600 times

According to the statistical method of the average contact area ratio, 200 SEM images obtained by the scanning electron microscope are analyzed and counted. The average contact area ratio is used to express the samples with different porosity by the statistical mean of five SEM images. The contact area on the soil section is AC , AP is the pore area, and A is the total area. If ACA=RCA , RCA is the average contact area ratio. APA=RPA is the average pore area ratio, and it is also the average concept of the area ratio of pores in the cross-section. After the above are put into the above equation, the following equation can be obtained:

RCA+RPA=1 (5)

Since porosity n and average pore area ratio RPA of soil can represent the pore features of soil, the relationship between the average pore area ratio and porosity can be obtained. If RPA=f(n) , the relationship between macro-porosity and the average contact area ratio is:

RCA=1−f(n) (6)

f(n) is the average pore area ratio expressed by macro-porosity.

The statistical results of porosity and average contact area ratio of soft soil in the three regions are fitted by OriginPro 9.1 software. Annular area AC of the bound water film is calculated by an approximate method. The thickness of the contact area of soft soil is obtained by the thickness of bound water film multiplied by the circumference of the article:

AC=A+S×H×10−40.3448 (7)

According to the above equation, the relationship between porosity and the average pore area rate of soft soil is calculated by the statistical method. Since the thickness of water film changes with the change of the quality of soil, the relationship between porosity n and average pore area rate RPA of soft soil is calculated when the thickness of the bound water film is 200~450 Å. The fitting of the power function is:

RPA=βnα (8)

The values of β and α are different for soft soil in different regions. Since the soil properties are different, the thickness of the bound water film is set to be 300 Å, and the value range of β and α of soft soil can be deduced. The value of the coefficient β obtained from the fitting curve equation is very close to l, so the value of β is determined to be l, and the value of α is close to 0.6. Therefore, if α=23α , the above equation is changed to:

RPA=n23α (9)

According to the above equation, average contact area ratio RPA can be calculated when the thickness of the bound water film is 300 Å. The porosity is obtained by the geotechnical test and α is calculated.

3.2 Macroscopic Permeable Fluid Dynamics

The viscoelastic deformation of soil under the action of external force generally occurs. When the stress exceeds a certain finite value, the plastic flow deformation of soil will arise with time instead of the flow deformation under the action of any small shear force. The finite value is the yield stress of soft clay, and this kind of flow is a plastic fluid. The rheology of soft clay can be expressed by the plastic fluid. When the shear stress is less than the yield stress, the soil will not flow and it is solid. When the shear stress exceeds the yield stress, the plastic flow appears like the Newtonian fluid, which is called the Bingham fluid. The plastic rheological model of soft clay can be divided into the Newtonian fluid model and the non-Newtonian fluid model. The non-Newtonian fluid model includes the Bingham fluid model and the generalized Bingham fluid model. The soil has both viscous and plastic properties, and it is called viscoelasticity. When the stress of the viscoelastic body reaches a critical value under load, yield and flow occur and its deformation rate is related to the viscosity of the body. The important engineering properties of soil include its permeability. The parameters needed to analyze the stability of geotechnical structures under rainfall, water level changes, and the dynamic water pressure in soil are permeability coefficients. Soil particle skeleton and fluid properties are two factors affecting the permeability coefficients of soil [16].

3.2.1 Permeability Coefficient Equations

It is generally concluded that there is a proportional relationship between the square and size of the characteristic particle and the permeability coefficient of non-viscous soil. For example, when d10=0.10∼3 mm , the empirical equation is as follows:

k=cd102 (10)

c is the empirical parameters related to soil properties, and the size of the characteristic particle is generally taken d10 [17].

There are many empirical equations about the permeability coefficient of coarse-grained soil in the field of geotechnical science, which can reflect the main factors affecting the permeability coefficient. First, the Terzaghi permeability coefficient equation is expressed as:

k=2e2d102 (11)

The effective particle size d102 of soil particles is the soil particle size (cm) corresponding to the ordinate of 10% in the particle size distribution curve. k is the permeability coefficient of coarse-grained soil (cm/s).

Second, the permeability coefficient equation of China’s Academy of Water Resources and Hydropower Research is expressed as:

k10=234n3d202 (12)

The effective particle size d20 of soil particles is the corresponding particle size (cm) when the ordinate of particle size distribution curve is 20%. k10 is the permeability coefficient of coarse granular soil when the water temperature is 10∘C .

Third, the Coson-Carmen permeability coefficient equation is expressed as:

k=c2ρWZe3S2η(1+e) (13)

ρWZ is the density (g/cm3) of free water. c2 is the coefficient related to the particle shape and the actual flow direction of water, and it is about 0.124. s is the specific surface area of soil particles (cm−1) . η is the dynamic viscosity coefficient for free water (g⋅s⋅cm) .

Fourth, the consolidation degree equation is expressed as:

k=CVmVγWZ=CVγWZαγ1+e (14)

CV is the consolidation coefficient of soil (cm2/a) , mV is the volumetric compression coefficient of soil (MPa−1) , γwz is the gravity of free water (KN/m3) , and aV is the compression coefficient of soil (MPa−1) .

Fifth, the Darcy permeability coefficient equation is expressed as:

k=βγWZληe21+ed2 (15)

d is particle size (cm) . β is the spherical coefficient of particles, and the ball is taken π/6 . λ is the influence coefficient of adjacent particles, and the sphere in infinite water is taken 3π .

Sixth, Stokes established a more classical capillary model by using capillary instead of pore channel to derive the Darcy flow theory, which is expressed as:

k=γWZR28ηn=γWZR2e8η(1+e) (16)

R is the capillary radius and η is the dynamic viscosity coefficient.

3.2.2 Equations of Modified Permeability Coefficients

Total void ratio e is modified according to the average contact area ratio, which is defined as the effective void ratio, expressed by eP . The relationship between the average contact area ratio of clay and macro-porosity is expressed as:

eP=n1−n=RPA32α1−RPA32α (17)

The empirical equation applicable to the permeability coefficient of cohesive soil is obtained by using the effective void ratio to modify the equation of the permeability coefficient of a large sand base:

k′=2ep2d102=2(RPA32α1−RPA32α)2d102 (18)

The effective particle size d10 of soil particles is the diameter of soil particles (cm) corresponding to the ordinate of 10% in the particle size distribution curve. k is the permeability coefficient of coarse-grained soil (cm/cmss) [18].

The modified equation expressed by the permeability coefficient of the China’s Academy of Water Resources and Hydropower Research is:

k10′=234(RPA32α)3d202=234RPA92αd102 (19)

The effective particle size d20 of soil is the corresponding particle size (cm) when the ordinate of particle size distribution curve is 20%. k10 is the permeability coefficient of coarse granular soil when the water temperature is 10∘C .

The above equation is modified when it is expressed by the Cusson Carmen permeability coefficient equation, and the empirical equation of the permeability coefficient of cohesive soil is as follows:

k′=c2ρWZeP3S2η(1+eP) (20)

After it is simplified, the equation is expressed as:

k′=c2ρWZRPA92αS2η(1−RPA92α)2 (21)

ρWZ is the density of free water (g/cm3) . c2 is the coefficient related to the particle shape and the actual flow direction of water, and it is about 0.124. s is the specific surface area of soil particles (cm−1) . η is the dynamic viscosity coefficient for free water (g⋅s⋅cm−2) .

The empirical equation for the permeability coefficient of cohesive soil expressed by consolidation degree equation is modified as:

k′=CVγWZαγ1+eP=CVγWZαγ(1−RPA32α) (22)

CV is the consolidation coefficient of soil (cm2/a) , mV is the volumetric compression coefficient of soil (MPa−1) , γwz is the gravity of free water (KN/m3) , and aV is the compression coefficient of soil (MPa−1) .

The empirical equation of the permeability coefficient of clay expressed by the Darcy permeability coefficient equation is modified as:

k′=βγWZληe21+ed2=βγWZληRPA3α1−RPA32αd2 (23)

d is particle size (cm) . β is the spherical coefficient of particles, and the ball is taken π/6 . λ is the influence coefficient of adjacent particles, and the sphere in infinite water is 3π .

Average pore area ratio RPA of the three kinds of soft soil in each region is 60.91%, 64.55%, and 71.01%, respectively. The parameters α of the three kinds of soft soil are taken as 0.8 by comprehensive comparison to unify the equation and facilitate the calculation. The parameters are put into the equation of the Hydropower Sciences, the Coson-Kamen permeability coefficient, and the empirical equation of the Terzaghi, and the permeability coefficient of each soil sample is calculated [19,20].

4  Analysis of the Results of Microstructure and Macro-Mechanics

4.1 Relationship between the Average Contact Area Ratio and Macro-Porosity

The relationship between the porosity and the threshold is shown in Fig. 2.

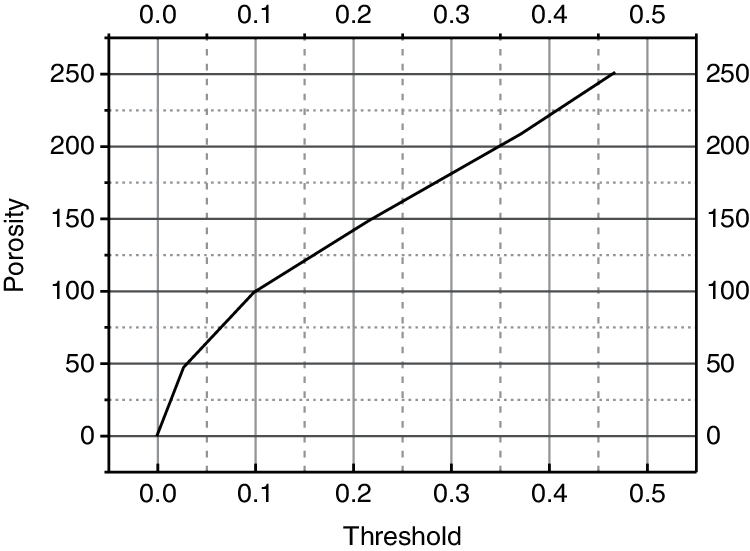
Figure 2: Relationship between the porosity and the threshold

The above figure shows the relationship between the three-dimensional porosity of the SEM image and the threshold when the magnification of the soil sample is 1600. The macro-porosity of the soil sample is 0.369, and the binary gray pixel is 100300. The average contact area of the soil sample is RCA=100300/100300903309903309=11.10% . The statistical results of the contact area ratio of enlarged SEM images are shown in Figs. 3–5.

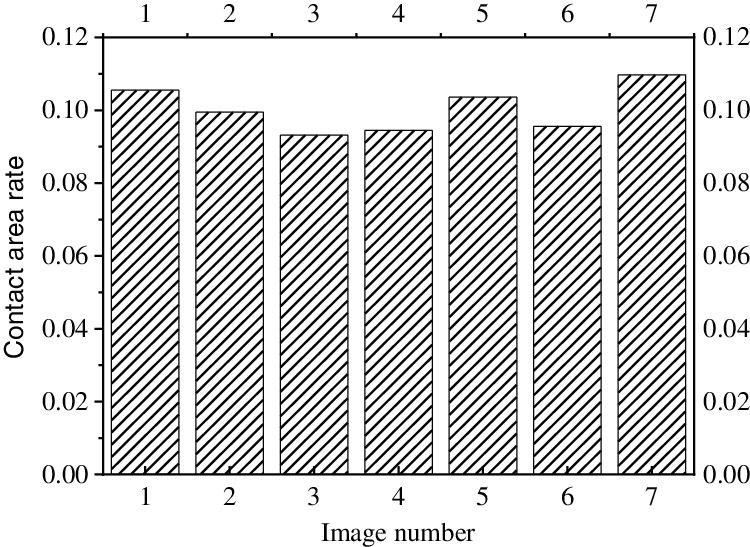
Figure 3: Analysis of contact area ratio at 800 magnification

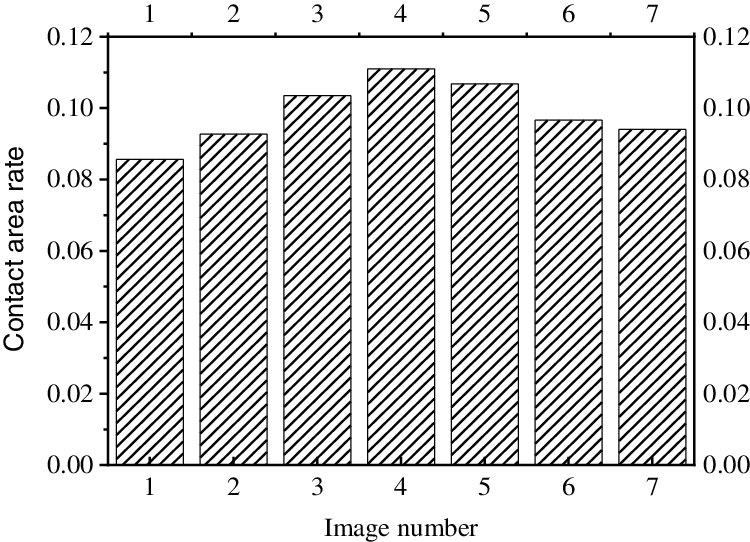
Figure 4: Analysis of contact area ratio at 1600 magnification

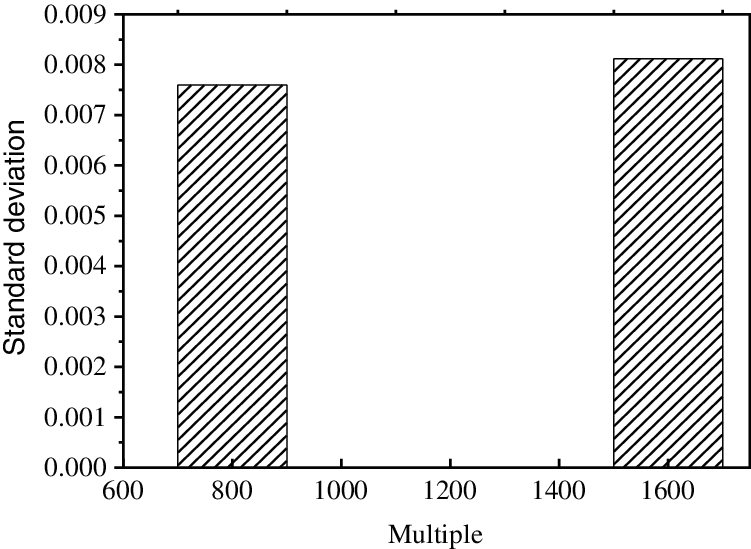
Figure 5: Analysis of contact area ratio of standard deviation

The data in the figure show that the standard deviation is very small, and the contact area rate is about 10%, which is obtained based on the equality of the three-dimensional porosity and macro-porosity. The relationship between the average contact area ratio and the porosity of soil under different porosity is shown in Fig. 6.

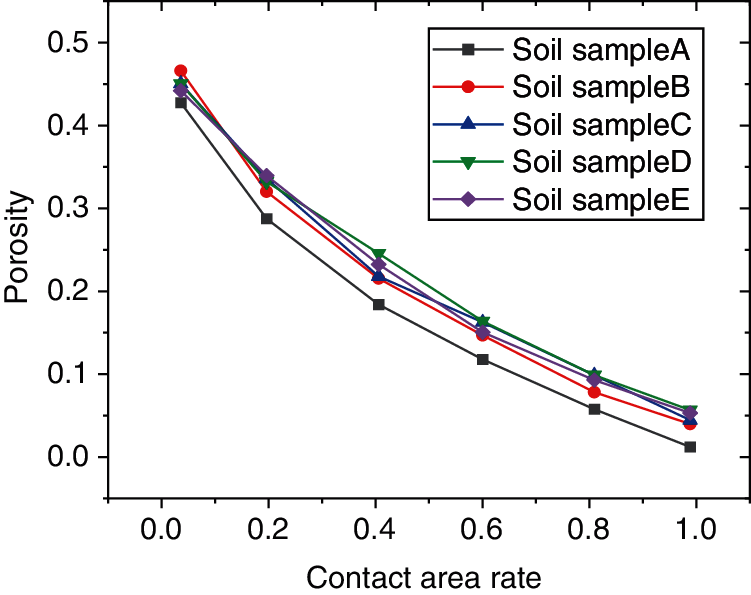
Figure 6: Relationship between porosity and the average contact area ratio

The above figure shows that the average contact area ratio increases with the decrease of porosity. The porosity obtained in this experiment is between 0.372 and 0.541, because the structure of the soil sample with macro-pores is relatively loose, and it is impossible to carry out the electron microscope test. The small porosity is hindered by adhesive water and limited by compressive work, so it is difficult to compact. When the porosity increases to a certain value, the contact area ratio decreases. The final result should be that the porosity tends to 1 when the average contact area ratio tends to zero, and the average contact area ratio tends to 1 when the statistical porosity approaches zero. This phenomenon conforms to the objective law between porosity and the contact area ratio.

The physical indexes of soft soil obtained from indoor geotechnical tests are shown in Figs. 7–9.

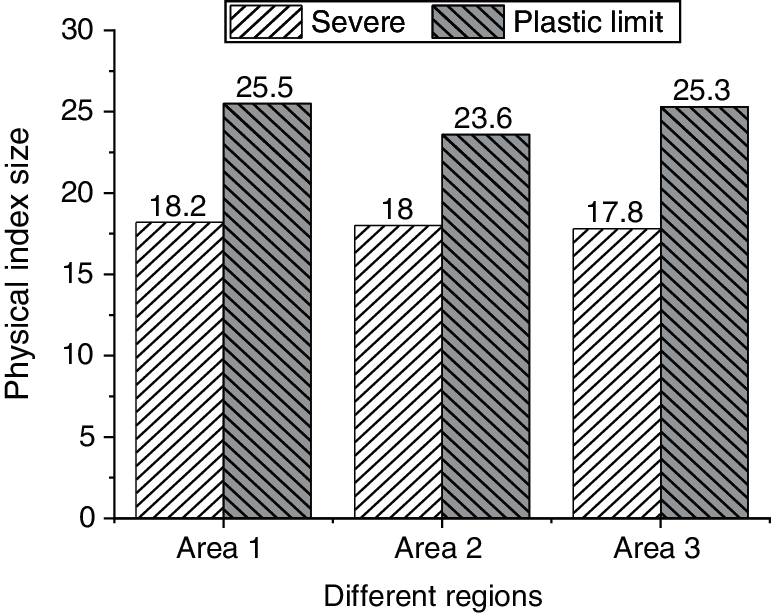
Figure 7: Severe and plastic limit of soft soil

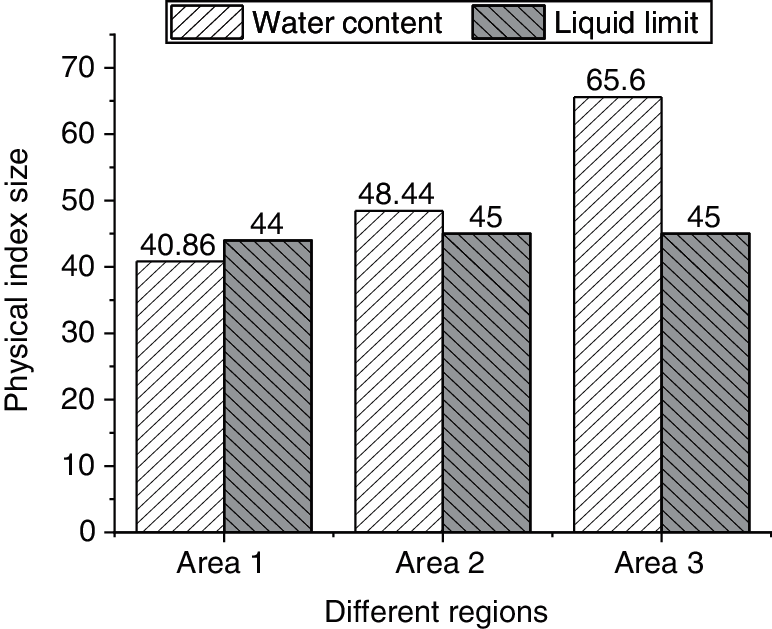
Figure 8: Water content and liquid limit of soft soil

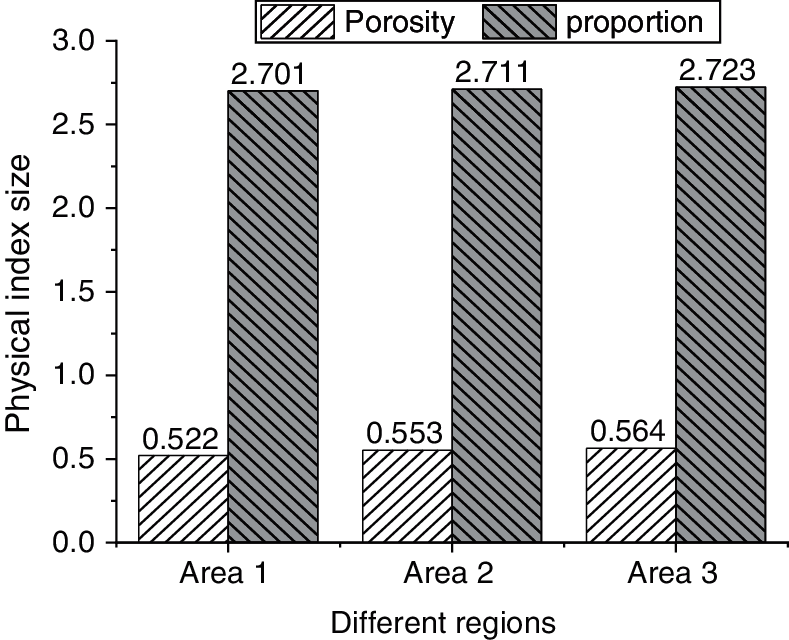
Figure 9: Porosity and proportion of soft soil

The layers of soft soil are extended in the coastal areas. The soil used here is the soft soil in the selected study areas and is not limited to a certain area. Three different kinds of soft soil are collected to be tested and have made some achievements. These kinds of soil belong to the typical soft soil in coastal areas and have the general engineering characteristics, such as high content of natural water, large void ratios, high compressibility, low strength, and poor permeability. The minerals of the soil are mainly illite. And then, the fitting curve is obtained. It is known from the law of mathematical statistics that the fitting effect of the curve is good. The fitting of soft soil in different regions shows that the relationship between RPA and n is a power function, and the maximum and minimum of the correlation coefficient of the fitting curve are 0.81 and 0.70, respectively. When the thickness of the bound water film is 200~500 Ω, the relationship between porosity n and average pore area ratio RPA of soft soil is shown in Figs. 10–15.

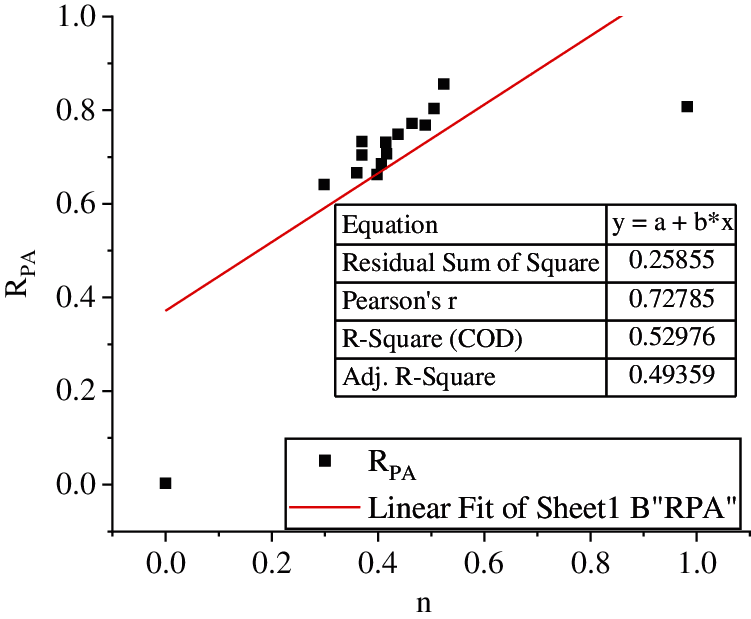
Figure 10: Results of regression analysis 1

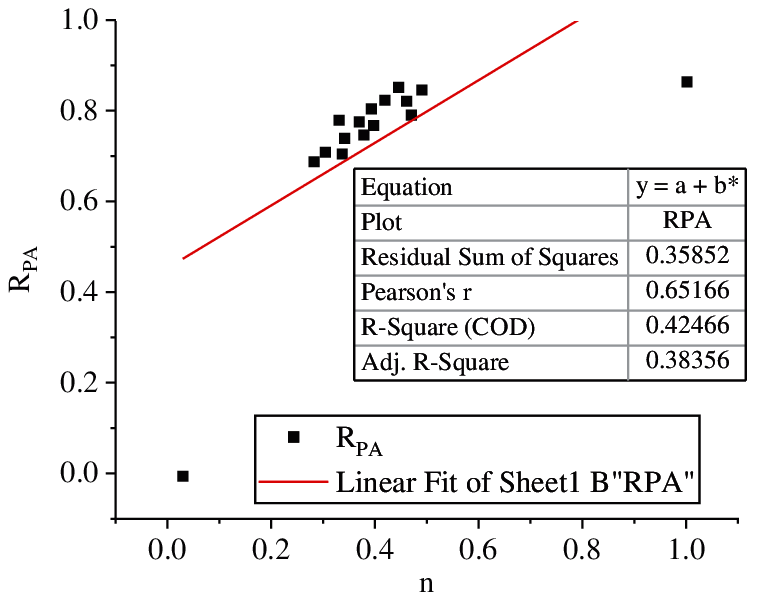
Figure 11: Results of regression analysis 2

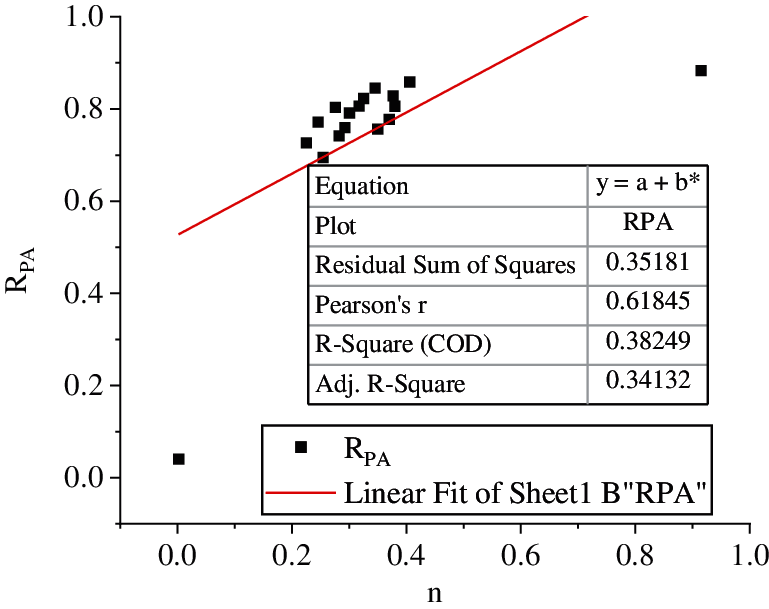
Figure 12: Results of regression analysis 3

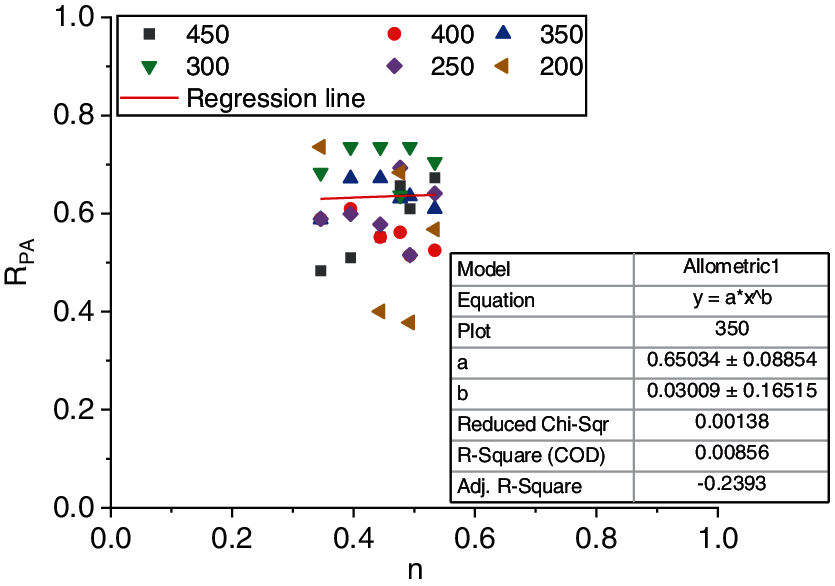
Figure 13: Results of regression analysis of the thickness of bound water film in Region 1

Figure 14: Results of regression analysis of the thickness of bound water film in Region 2

Figure 15: Results of regression analysis of the thickness of bound water film in Region 3

The figure shows that after the thickness of soil particles is combined with the bound water film, the basic trend of the relationship between the average pore area rate and porosity of soft soil is roughly the same, and the curtain function relationship between the two is well fitted. In the study area, the main components of soft soil are illite, montmorillonite, kaolinite, and chlorite. The results show that illite is the main mineral in the most of the soft soil, because illite can exist in alkaline, neutral, or weak acid environments, as well as in soft soil with various phases. For the soft soil in Area A, the main mineral is illite, with a small amount of kaolinite, chlorite, and illite montmorillonite mixed layer; The clay minerals of B and C are mainly illite, with little kaolinite and montmorillonite. Due to the different materials and soil quality, the thickness of the combined water film is set as 300 Å, and then the ranges of β and α of the sample soft soil are deduced. According to the fitting curve equation in Fig. 6, the value of coefficient β is very close to 1. If β is determined as l, the value of α is close to 0.6. When the thickness of the bound water film is 300 Å, the soil value α in each region of the bound water film is shown in Figs. 16–18.

Figure 16: Calculation results of soil values in Region 1 when the thickness of the bound water film is 300 Å

Figure 17: Calculation results of soil values in Region 2 when the thickness of the bound water film is 300 Å

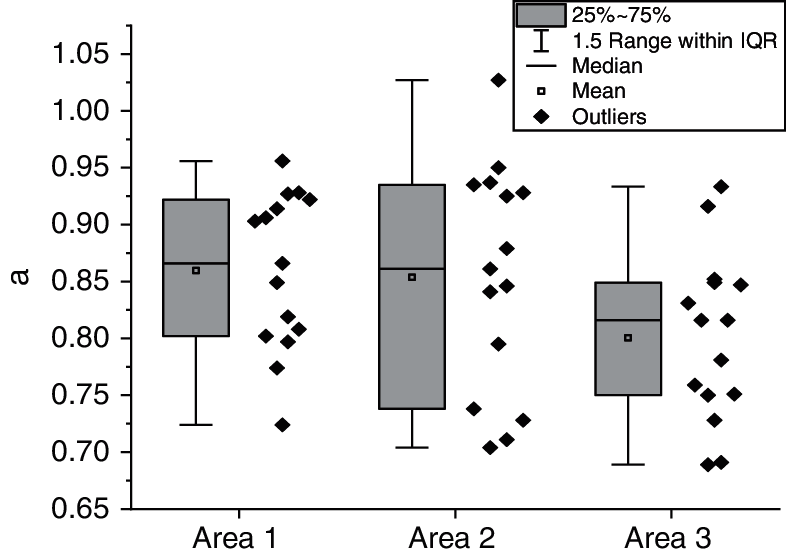
Figure 18: Calculation results of soil values in Region 3 when the thickness of the bound water film is 300 Å

The figure shows that the value of α in the same region does not change much, and sample deviations appear due to different sample preparation processes and human factors. For the soft soil samples taken from the same region, the corresponding value of α should follow the law of normal distribution. All the samples correspond to a normal population. The value of α of random variables can be characterized by mean and variance. The interval estimation is carried out by parameter estimation, and the confidence level is 0.95. The distribution of parameter estimation α is shown in Figs. 19, 20.

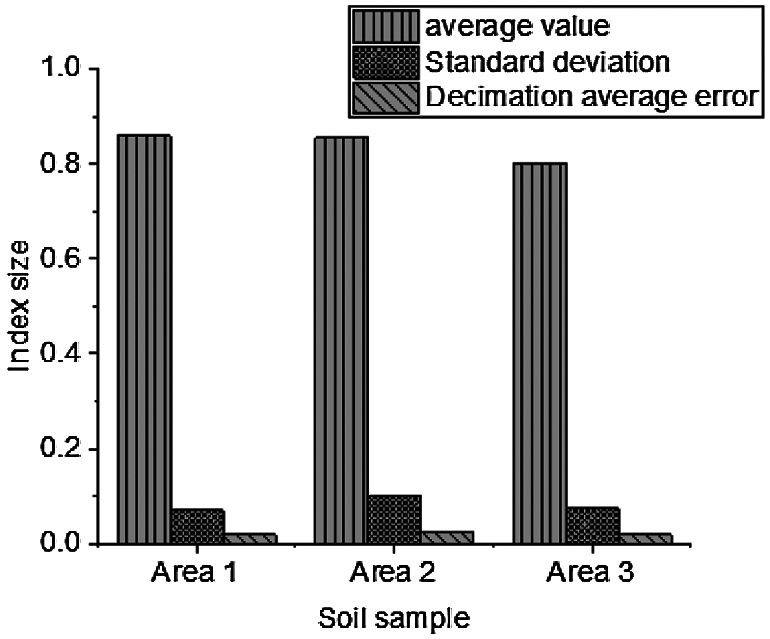
Figure 19: Distribution of parameter estimation (mean, standard deviation, sampling average error)

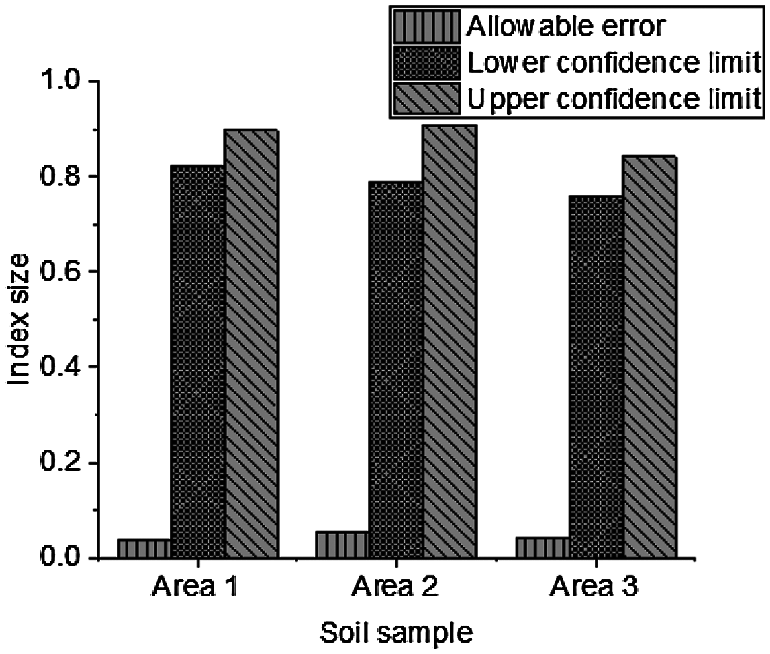
Figure 20: Distribution of parameter estimation (allowable error, upper and lower limits of the confidence)

The results of parameter estimation show that the range of α of soft soil in Regions 1 and 2 is between 0.8 and 0.9, while that of α is about 0.75–0.85 in Region 3. The range of α of soft soil in the three regions is not large. The value of α of soft soil in Regions 1 and 2 is 0.85, which is an average value, and that of the Fenghua soft soil is 0.8. The theoretical value curve of the average void area rate obtained from the obtained macro-porosity is plotted and compared with the average void area rate calculated by IPP to analyze the feasibility of the theoretical curve. Statistics RPA and theoretical analysis of soft soil in different regions are shown in Figs. 21–23.

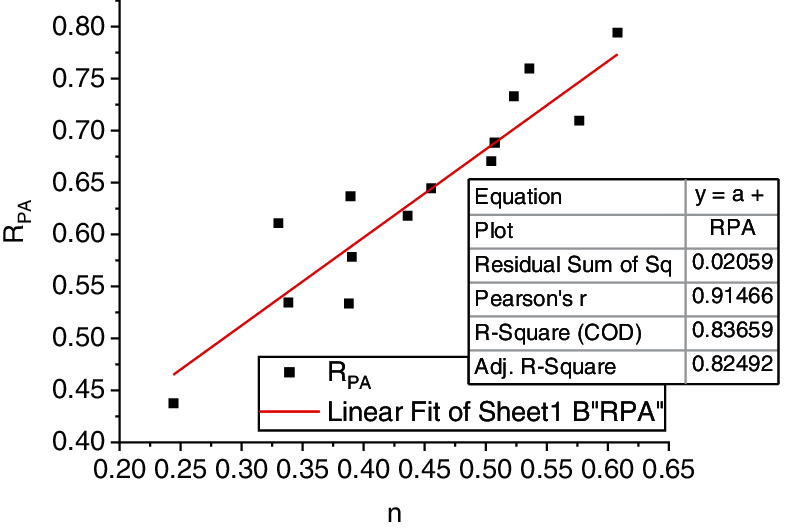
Figure 21: Results of statistics and theoretical analysis of soft soil in Region 1

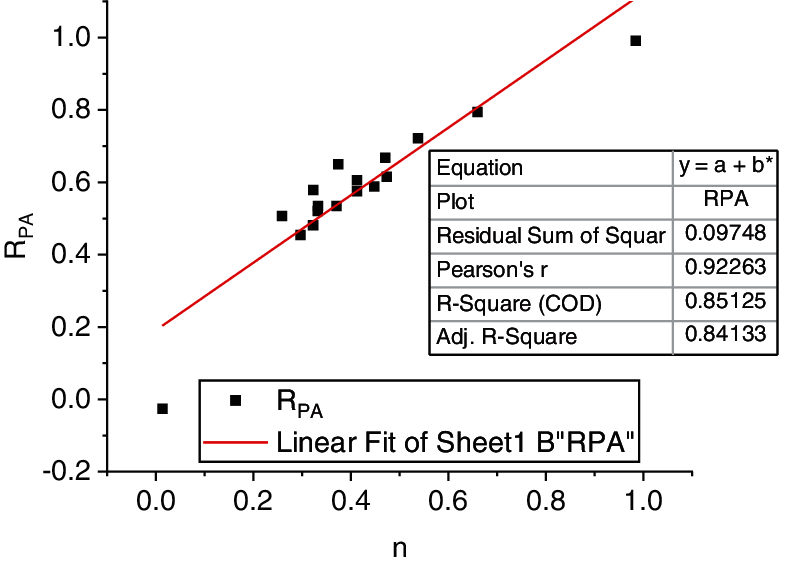
Figure 22: Results of statistics and theoretical analysis of soft soil in Region 2

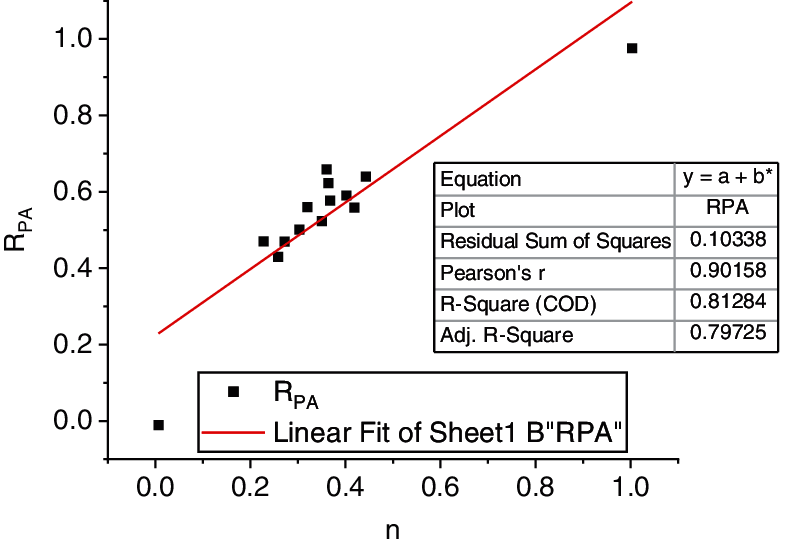
Figure 23: Results of statistics and theoretical analysis of soft soil in Region 3

The above figure shows that the statistical value is distributed in the vicinity of the theoretical curve. It is concluded that the fitting condition is better in Regions 1 and 2, and α of the soft soil 0.84. And α of the soft soil in Region 3 is 0.79. According to the equation, the relationship between the macro-porosity and the average contact area ratio of soil is:

RCA=1−RPA=1−n23α (24)

RCA, RpA are the average contact area ratio and average pore area ratio of soft soil, respectively. α is the undetermined parameter related to the component content and area of soft soil.

After the micro test results of soft soil in area A and surrounding areas under different porosity are analyzed, the data show that there is a certain relationship between the porosity of soft soil and the average contact area ratio, and the average contact area ratio decreases with the increase of the porosity of soil. With the help of the analysis software, the relationship between porosity and average pore area ratio is fitted, and the equation of the relationship is obtained.

4.2 Results of the Permeability Coefficient of Macroscopic Fluid

The physical indexes of the soft soil in the three regions obtained by indoor geotechnical tests are shown in Fig. 24.

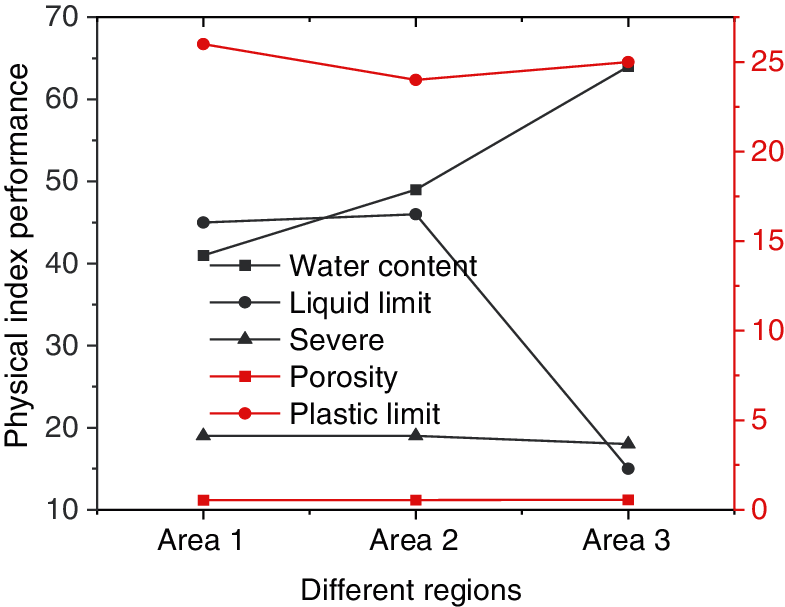
Figure 24: The performance of physical indexes of soft soil

The Figure shows that the soft soil in the three regions in the test is similar in weight and different in porosity. About α of the three kinds of soft soil, the value range of the soft soil in Regions 1 and 2 is 0.8~0.9. The value range of the soft soil in Region 3 is about 0.85~0.95, and the change is in the range of 0.1.

The permeability coefficients of the three kinds of soil are calculated, and the results are shown in Figs. 25–27.

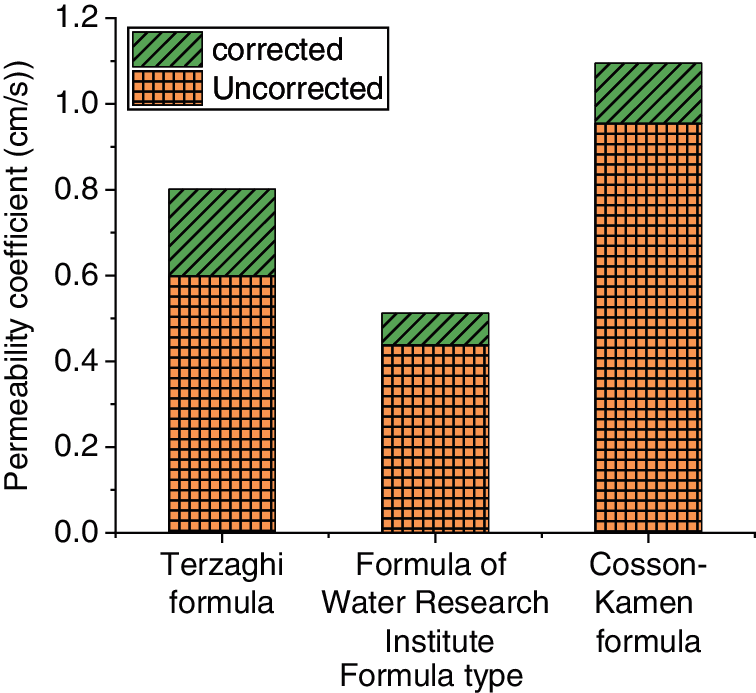
Figure 25: Results of the relationship between the equation and permeability coefficient in Region 1

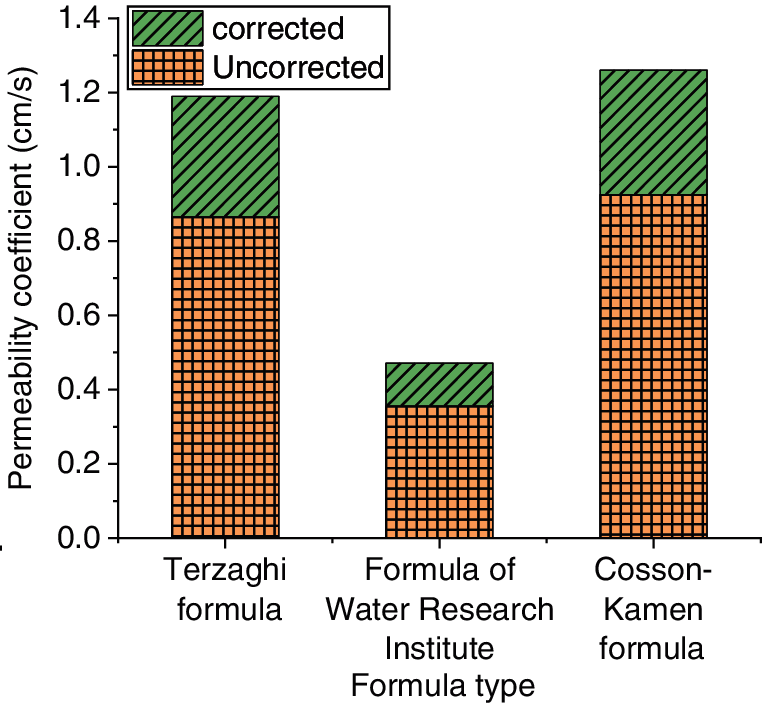
Figure 26: Results of the relationship between the equation and permeability coefficient in Region 2

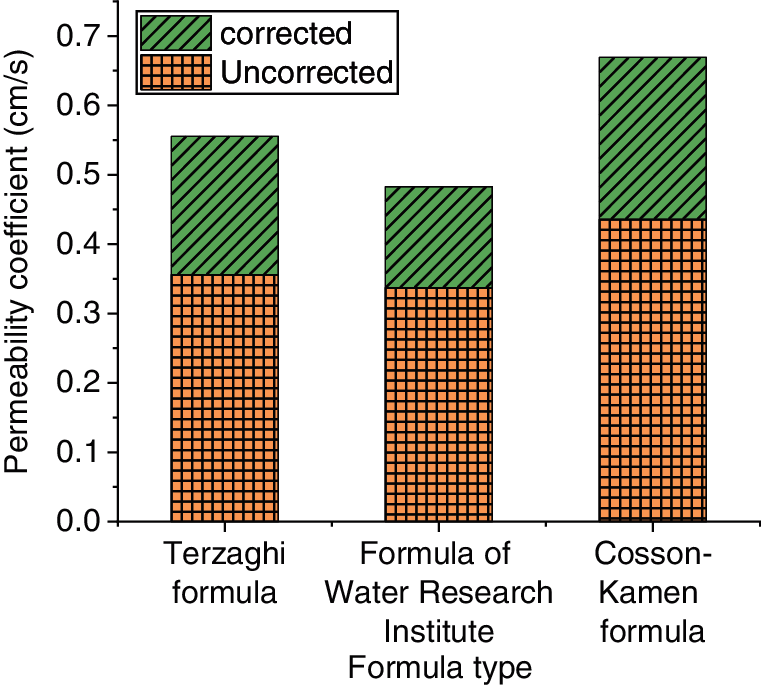
Figure 27: Results of the relationship between the equation and permeability coefficient in Region 3

According to the measured values and the calculated results, it is found that: 1. The natural void ratio is directly put into the three empirical equations without considering the influence of the microstructure of soil, and the calculated results of the permeability coefficient of soft soil in each region are 21.66, 16.51 and 31.23 times, 20.09, 8.79 and 21.12 times, and 13.21, 10.31 and 15.92 times of the experimental results. This proves that the empirical equation for calculating the permeability coefficient of coarse-grained soil without modification produces large errors. 2. After the empirical equation of the permeability coefficient of coarse-grained soil is modified into the empirical equation of the clay permeability coefficient by using the average contact area ratio theory, the calculated values of permeability coefficients of the three kinds of soil are not significantly different from the measured values in laboratory tests. This reduces the errors and the calculated results are closer to the measured values, and the applicability of the modified empirical equation to the permeability coefficient of clay soil is verified.

The microstructure of cohesive soil is analyzed by SEM. The results of microscopic research are used to analyze of the permeability of soil. Because of the influence of soil particle contact area on permeability, the permeability of cohesive soil is studied from the perspective of the microstructure of soft clay, and the permeability theory of cohesive soil with the contact area ratio is established. The empirical equation of the permeability coefficient of cohesive soil based on the particle contact area is given. Finally, the results of the unmodified, modified, and measured permeability coefficient are compared through calculation. The results show that the modified empirical equation of the permeability coefficient is also suitable for describing the seepage of cohesive soil.

5  Conclusion

The calculation method of the soil contact area ratio is obtained by comparing with that of macro-porosity. Through the analysis and calculation of specific data, the relationship between the soft soil contact area and porosity is further clarified, and the physical behavior characteristics of soil are explained from micro and macro perspectives. According to the particle shape of the clay image, the specific situation of porosity is quantitatively analyzed, and the calculation process of void in soft soil is described by using the binary gray method. This study provides an important reference for promoting the development of soil physics. Although the internal mechanism of soil is analyzed, there are still many shortcomings: (1) The scope of the samples is only in a single area, and the type of the soft soil in these areas is relatively single, so the research scope cannot be effectively extended. (2) In the analysis of the microstructure of soil, the relationship between the contact area and the macro-porosity is established, and the value is introduced. However, this mechanism does not only exist in soft soil, so it is necessary to expand the range of values. In the future, the calculation method should be constantly improved and the more critical internal mechanism should be analyzed.

Funding Statement: This work was supported by a key research projects of Henan higher schools (No. 21B560006).

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.