Fluid Dynamics & Materials Processing

DOI: 10.32604/fdmp.2022.017485

ARTICLE

Experimental Performance Evaluation and Artificial-Neural-Network Modeling of ZnO-CuO/EG-W Hybrid Nanofluids

Yuling Zhai*, Long Li, Zihao Xuan, Mingyan Ma and Hua Wang

Engineering Research Center of Metallurgical Energy Conversion and Emission Reduction, Ministry of Education, Kunming University of Science and Technology, Yunnan, 650093, China
*Corresponding Author: Yuling Zhai. Email: zhaiyuling00@126.com
Received: 13 May 2021; Accepted: 21 July 2021

1  Introduction

Active, passive, and combined methods are used for heat transfer enhancement. Among them, passive method is the best in increasing heat transfer. Many researchers have attempted to increase heat transfer of a fluid by dispersing nanoparticles into the fluid [1]. Hybrid nanofluids use two or more species of nanoparticles dispersed in the base fluid [2]. They are expected to have higher thermal conductivity than the corresponding single nanofluids, due to the synergistic effect [3]. The most important thermo-physical properties of hybrid nanofluids are the thermal conductivity and viscosity, which affect the pumping power and heat transfer coefficient in any thermal system. Base fluids account for the majority of any nanofluid, so their properties affect the thermal conductivity and viscosity of nanofluids. Water (W), oil-based fluids, ethylene glycol (EG), methylene glycol methanol, and several others are generally used as base fluids [4].

In the past few decades, the limited research on the base fluid has shown that is an important factor affecting the thermophysical properties for hybrid nanofluids. Most recent studies were focused on single nanofluids and there are contradictory research results on the enhancement effect of EG and W of thermal conductivity. Some studies have shown that the thermal conductivity enhancement of EG is larger than that observed when water is used as the base fluid. For example, Reddy et al. [5] found that the thermal conductivity of TiO2-based nanofluids could be increased by 5.01%, 4.38%, or 14.2% when in water, EG-W (40:60) and EG-W (50:50) at 1.0 vol.% TiO2 and 30°C. Babu et al. [6] found that relatively low thermal conductivity of base fluid exhibits high thermal conductivity enhancement of nanofluids. However, some contradictory results were observed in other studies. Chiam et al. [7] investigated Al2O3/W-EG nanofluids with W:EG ratios of 40:60, 50:50, and 60:40 from 30°C to 70°C. The results show that the viscosity can be increased up to 50% when W:EG = 60:40 and the thermal conductivity enhancement was found to increase by 2.6% to 12.8%. Similar results were found by Sonawane et al. [8] and Cabaleiro et al. [9], who investigated the addition of TiO2 nanoparticles in different base fluids (EG, W, and paraffin oil).

Whether these same results can be observed in hybrid nanofluids is not known yet. Das [10] reviewed the effect of the base fluid on the thermal conductivity of nanofluids published recently. Due to the contradictory results mentioned above, he mentioned that it is difficult to conclude the quantitative effect of the base fluid on changes in thermal conductivity enhancement. Hence, more experiments should be conducted at fixed particle concentration to demonstrate the effect of base fluids alone for all nanoparticles.

Recently, researchers have used reliable Artificial neural networks (ANN) to predict the thermos-physical properties of nanofluids [11,12]. It can model complex correlations with high speed and acceptable accuracy. Akhgar et al. [13] used ANN and curve fitting to study the change of thermal conductivity of MWCNT-TiO2/EG:W hybrid nanofluid at different temperatures and concentrations. After comparing with experimental data, they pointed out that accuracy of the ANN is much greater than the curve fitting method for hybrid nanofluid. Esfe et al. [14] obtained the same conclusion in the study of Al2O3/EG:W nanofluid. Shahsavar et al. [15] use GMDH type neural network optimization and data prediction. The proposed structure of the genetic algorithm with a single hidden layer is considered as the optimal network structure for predicting the thermal conductivity. Toghraie et al. [16] proposed an algorithm to generate the best architecture of ANN and use it to predict the dynamic viscosity of Silver/EG nanofluid, in the correlation method, MSE is 0.0012, SSE is 0.0512 and the maximum value of error is 0.0858.

Therefore, from the view point of the base fluid, the selection of the base fluid type and its mixture ratio is very important for preparing a nanofluids system that provides high heat transfer. Sajid et al. [17] pointed out that the most common base fluids for hybrid nanofluids are water, EG, water/EG mixtures, and various oils. Among them, water is the most widely available and has better thermal properties than other fluids. However, water can be frozen in cold areas, thus water is often used with EG to prevent freezing and improve the thermophysical property of water. EG has more a much a lower freezing point and a much higher boiling point than water (−12.9°C and 197.4°C, respectively). Therefore, the ratio of EG:W can be adjusted to design a suitable nanofluid. In the current limited studies, there are few studies on the influence of the ratio of EG:W on the thermos-physical properties of hybrid nanofluids.

Current research mainly focuses on the effects of nanoparticles, temperature and volume fraction on thermal properties of nanofluids [18,19]. However, the importance of the influence of the vast majority of base fluids on excellent thermal properties must be considered. In this paper, the stability, viscosity, thermal conductivity, and modeling of ZnO-CuO/EG-W hybrid nanofluids with different base fluids mixture ratios are studied.

This paper can be structured into three parts: first, the effects of sonication time and surfactant on the stability of ZnO-CuO (50:50)/EG-W hybrid nanofluids were investigated. Then, effect of base fluids ratio (EG:W) on viscosity and thermal conductivity was investigated. Finally, an artificial neural network (ANN) was used to model the thermophysical properties of ZnO-CuO/EG-W hybrid nanofluids. The experimental data obtained in the present work were compared with existing models available in the literature as well.

2  Experiments

2.1 Preparation and Characterization of Hybrid Nanofluids

Combinations of nanoparticles that do not interact with each other can be used to design a nanofluid with high thermal conductivity as they can produce the synergistic effect. In our previous study, we found that the synergistic mechanism is caused by dispersing different sizes of nanoparticles to form an ordered arrangement of liquid molecules around nanoparticles, and small size of nanoparticles fills into the space caused by large size of nanoparticles, which results in more compact solid-liquid interface and reasonable heat transfer network [20]. Metallic oxide nanoparticles have widely used as they are easy to prepare and tend to be chemically stable [21]. 30 nm ZnO and 50 nm CuO (99.9% purity, Beijing Deke Daojin Science and Technology Co., Ltd., China) were used in the hybrid nanofluid. The thermal conductivities of ZnO and CuO nanoparticles are 29 and 76.5 W/(m⋅K), respectively [22,23]. Fig. 1 shows transmission electron microscopy (TEM) images of ZnO and CuO nanoparticles. The nanoparticles have circular shapes, and large clusters of particles can be seen in the field of view. During transport and storage, the nanoparticles can become aggregated due to their high surface energy.

Figure 1: TEM images of CuO and ZnO nanoparticles

ZnO (50%) and CuO (50%) nanoparticles with combined mass fractions of 1.0, 2.0, 3.0, and 5.0 wt.% were prepared. EG and deionized water (W) were chosen as base fluid mixture with volume ratio ranging from 20:80 to 80:20. The mass fraction (w %) of nanofluids was calculated as following:

w%=mZnO+mCuOmZnO+mCuO+mEG+mW×100% (1)

where m is the mass of various materials, kg. The corresponding mass of nanoparticles and base fluid were weighed with a digital scale (ML304 T, China).

Single-step and two-step methods are commonly used to prepare nanofluids, although the two-step method is more popular. The main reason for this is its lower cost and the ability to produce nanofluids in large volume [24]. Fig. 2 shows a schematic of the two-step method for preparing homogenous and stable ZnO-CuO/EG-W hybrid nanofluids. A magnetic stirrer (JKI, 200–1500 rpm, China) and ultrasonicator (CP-2010GTS, 40 KHz, China) were used to disperse the nanoparticles. Nanoparticles are often hydrophobic and do not easily disperse into water or EG without surface treatment or surfactants [25]. Then, a surfactant is added to ensure uniform dispersion. Different surfactants exhibit different characteristics when used in the same fluid. Sodium dodecyl sulfate (SDS) and polyvinyl pyrrolidone (PVP) were chosen as surfactant in the present experiment.

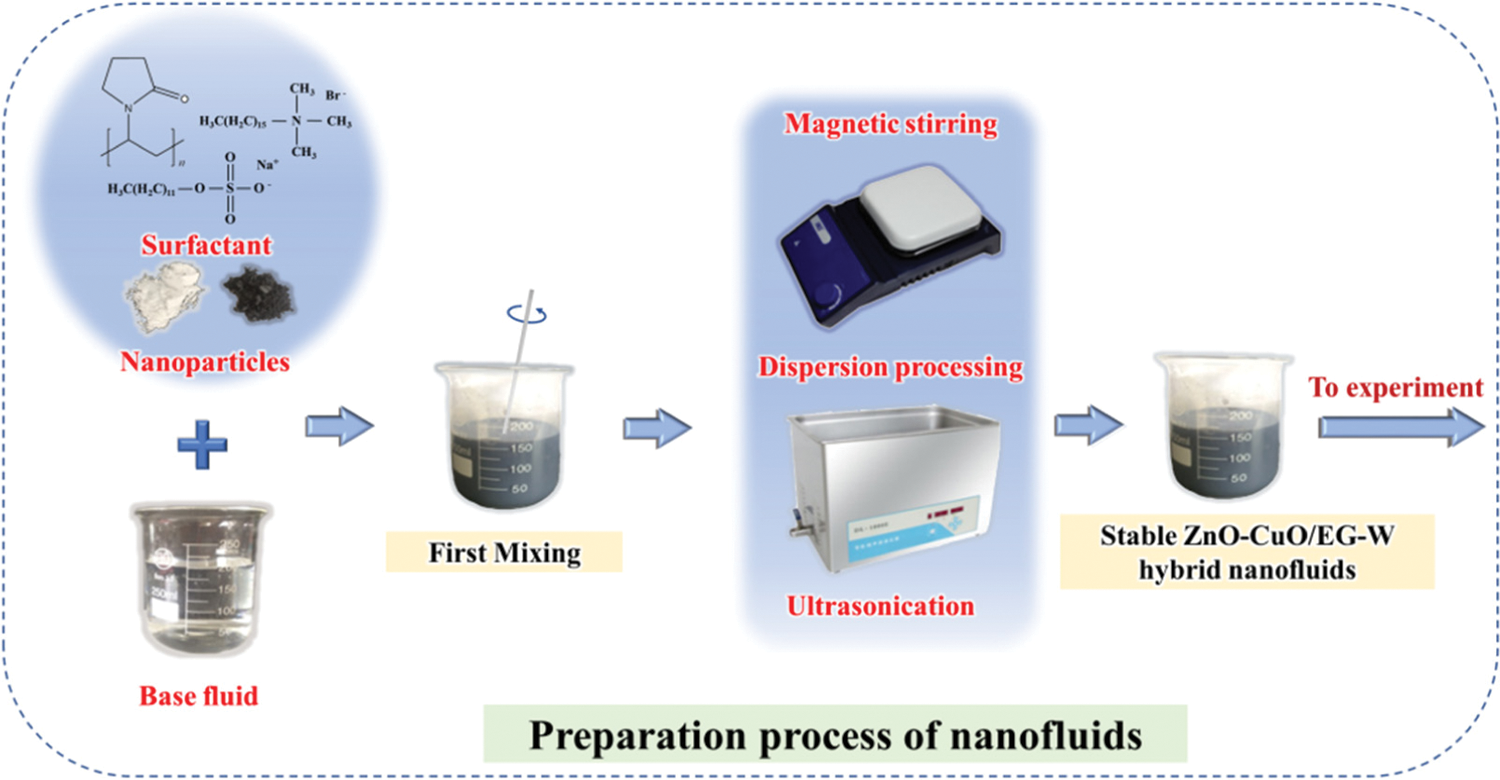
Figure 2: Preparation of ZnO-CuO/EG-W hybrid nanofluids with a two-step method

Apart from sonication power and surfactant type, the sonication time and the amount of surfactant will also influence the stability of nanofluids. Therefore, sonication time, appropriate surfactant type, and surfactant content should be optimized for the given nanofluids.

After preparing stable ZnO-CuO/EG-W hybrid nanofluids, X-ray diffraction (XRD) was used to analyze each component in the fluid and to determine the structure of each crystalline component. The hybrid nanofluids were dried in air, and the powder was removed for XRD analysis. XRD spectra were gathered at 5 °/min scanning rate from 5° to 90°. Fig. 3 shows the XRD pattern of the ZnO-CuO/EG-W hybrid nanofluid. The characteristic diffraction spectrum of the mixture is displayed in the upper right corner. It is worth mentioning that the diffraction peak of the mixture only arises due to mechanical superposition from each phase. Obviously, the composition of the ZnO-CuO/EG-W hybrid nanofluid coincides with the characteristic diffraction spectra of CuO and ZnO, revealing that the nanoparticles and base fluid are only physically mixed without chemical changes in the nanofluidic system. This shows that the resulting changes in the thermophysical properties of hybrid nanofluids can be explained in terms of physical movement and structure by mixing ZnO and CuO nanoparticles.

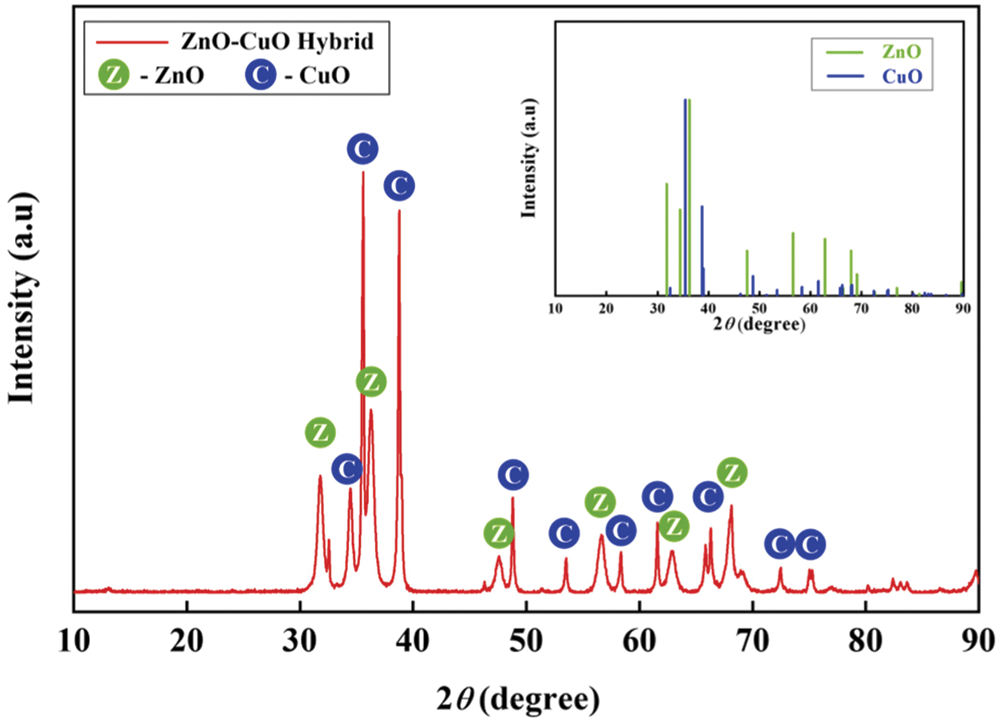
Figure 3: XRD pattern of the ZnO-CuO/EG-W hybrid nanofluid

2.2 Measurements of Thermophysical Properties

The viscosity and thermal conductivity were measured with a digital viscometer (Brookfield DV-3 T, USA) and thermal constant analyzer (Hotdisk TPS2500, Sweden). Viscometer works based on measuring the fluid resistance because of torque created by a spindle immersed in the fluid [26]. Transient plane sources (TPS) theory is used to calculate the thermal conductivity of nanofluids in the thermal constant analyzer (TCA) technique. The TCA technique enables measurement over a broad range of thermal conductivity values (0.02–200 W/(m⋅K)) without sample preparation and sample size requirements. All the experimental data were gathered with the sample placed in a temperature bath held from 25°C to 60°C in 5°C increments. At least three measurements were collected within 20 min and the average values were calculated for all samples. The uncertainties in the viscometer and thermal constant analyzer measurements were calculated as follows [27]:

Uμ=(δTT)2+(δμnfμnf)2 (2)

Uk=(δTT)2+(δknfknf)2 (3)

The maximum of δTT is 0.05 and 0.005 for the viscosity and thermal conductivity, respectively. Moreover, the accuracy of the Brookfield DV-3T viscometer and Hot Disk TPS2500S are ±1.0% and ±3.0%, respectively. According to Eqs. (2) and (3), the uncertainties were 1.11% and 3.04%, respectively.

Before conducting the nanofluid measurement, the equipment was validated by comparing measurements from the water/EG mixture with values from the ASHRAE handbook [28], as shown in Fig. 4. The thermal conductivity and viscosity data are found to be consistent from 25°C to 60°C, with deviations of less than 1.0%. Therefore, the viscosity and thermal conductivity of ZnO-CuO/EG-W hybrid nanofluids were measured by such two experimental setups.

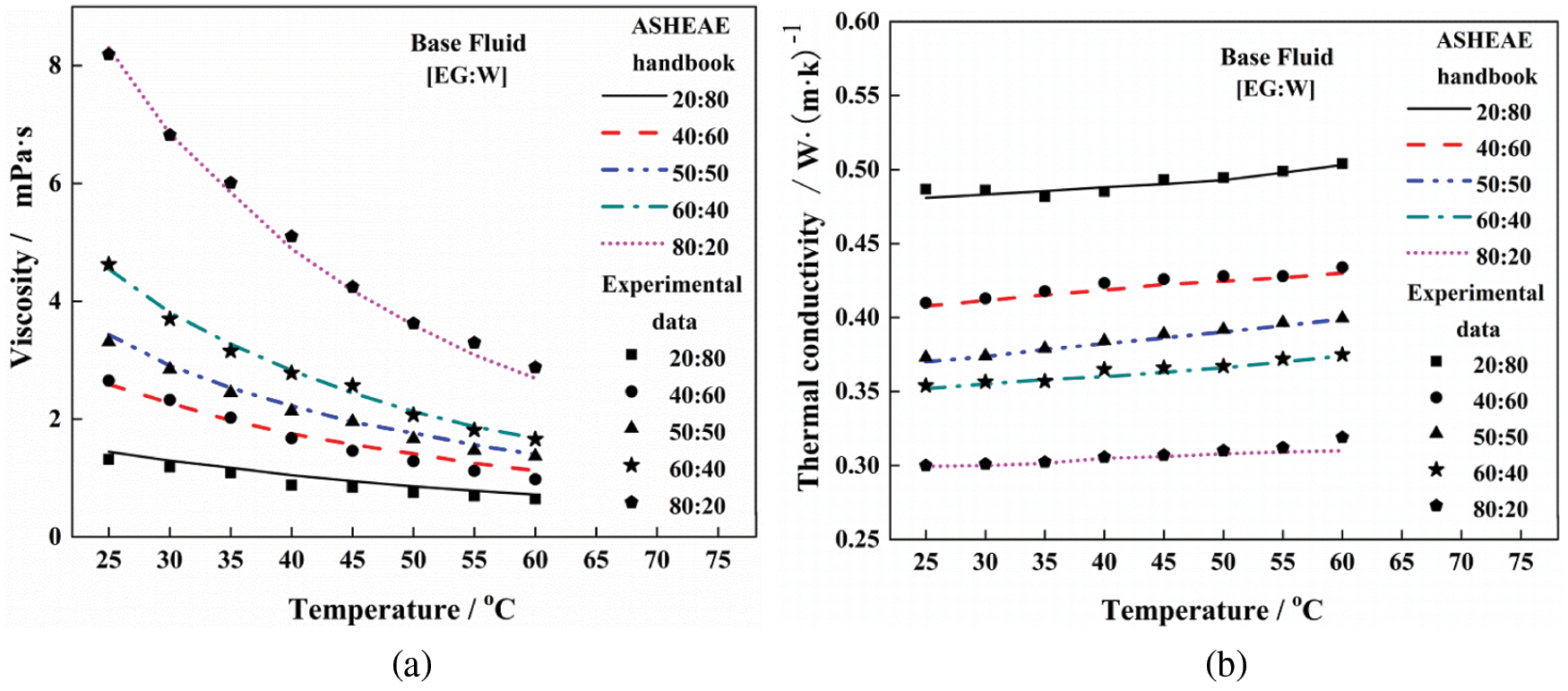
Figure 4: Validation of (a) viscosity and (b) thermal conductivity with literature

2.3 ANN Models

Many researchers have shown that an ANN can be used to predict thermophysical properties with up to 98% accuracy by using models. Among them, Esfe et al. [29–31] used ANN models to precisely predict the thermophysical properties based on the variable of base fluid ratio in Cu-TiO2/EG-W, MgO/EG-W, and ZnO-MWCNT/EG-W hybrid nanofluids. Therefore, we attempt to use an ANN model to describe the effectiveness of hybrid nanofluids as heat transfer fluids.

There were 240 experimental data for μ and λ, in which 168 values were used for training and 72 were used for testing. A feed-forward algorithm was used to model the viscosity and thermal conductivity of ZnO-CuO/EG-W hybrid nanofluids. Linear, Tan-Sig, and Log-Sig transfer functions were used to construct the ANN. More details on the ANN can be seen in our pervious publications [32,33]. The optimum number of layers and neurons was determined based on R-squared (R2) and the mean squared error (MSE). R2 and MSE are defined as follows [34,35]:

R2=1−∑i=1N(Kexp−Kpred)i2∑i=1N(Kexp)i2 (4)

MSE=1N∑i=1N(Kexp−Kpred)i2 (5)

where K is viscosity or thermal conductivity; the subscripts exp and pred indicate experimental data and modeled data, respectively.

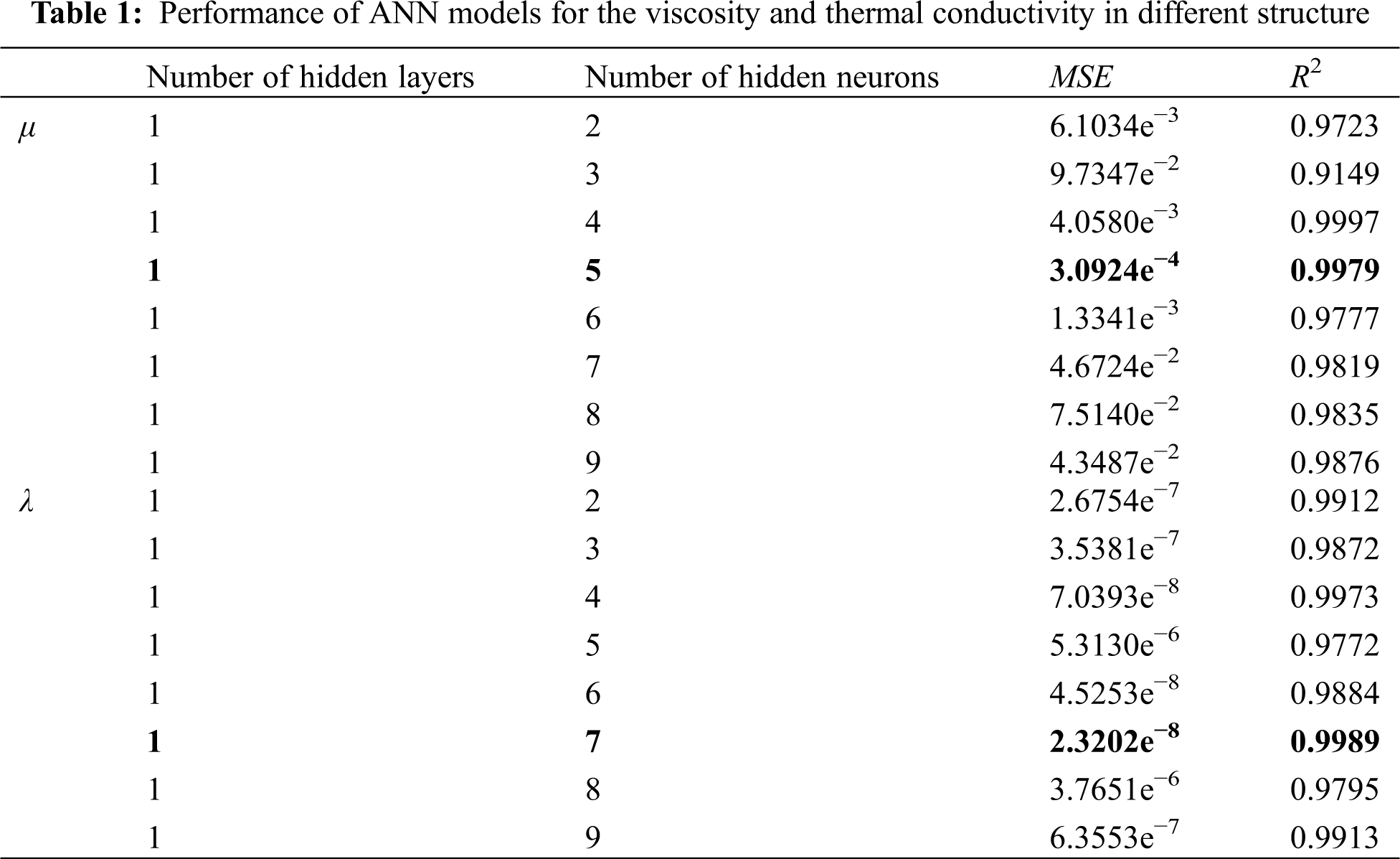
Different neural networks were designed to determine the optimum number of hidden layers and neurons. Table 1 shows the performance of these ANN models. As shown in Table 1, the optimum number of layers and neurons were 1 and 5 for viscosity, and 1 and 7 for thermal conductivity, respectively. Fig. 5 shows the optimum structure of the ANN models for describing viscosity and thermal conductivity. The input data for these present ANN models were weight fraction (w), base fluid ratio (R), and temperature (T), and the output data were the viscosity (μ) and thermal conductivity (λ).

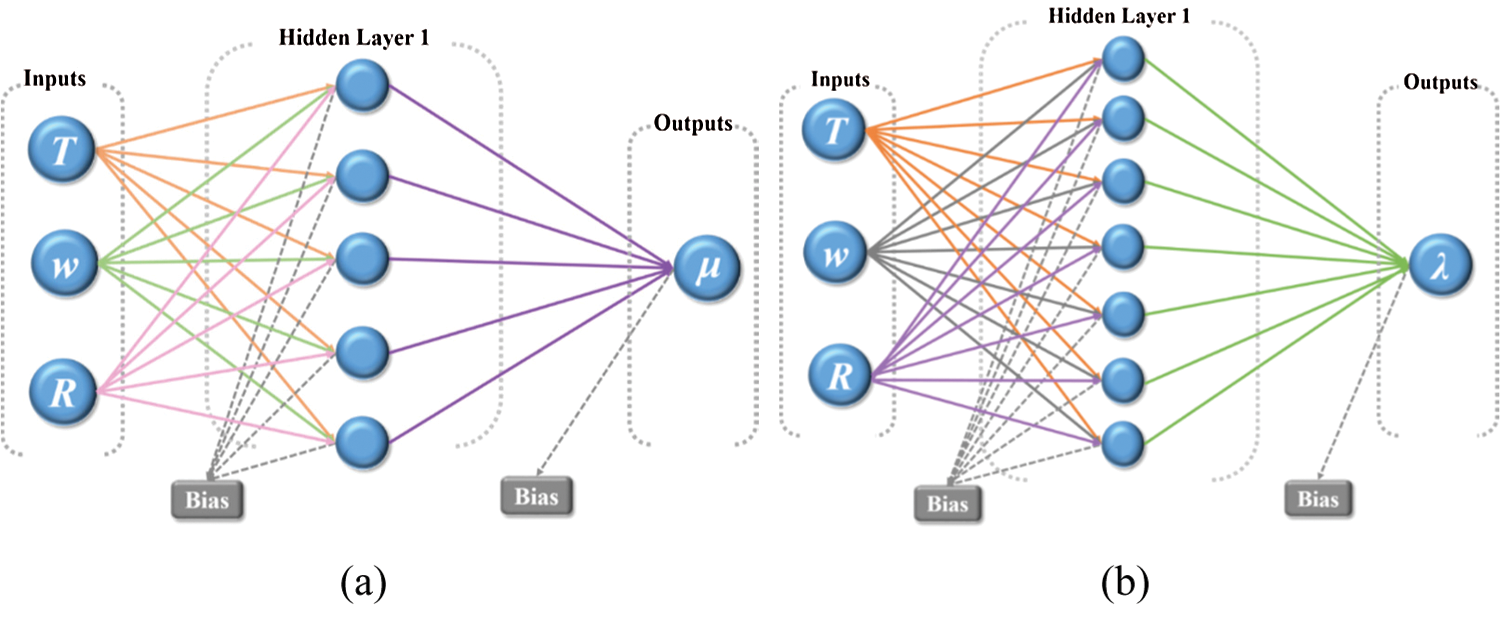
Figure 5: Optimum structure of the ANN models for (a) viscosity and (b) thermal conductivity

3  Equations and Mathematical Expressions

3.1 Stability of ZnO-CuO/EG-W Hybrid Nanofluids

The typical frequency used for ultrasonication ranges from 20 and 40 kHz. Apart from frequency and power, sonication time is the most crucial parameter that affects the stability of nanofluids. The effects of physical (ultrasonication) and chemical (adding surfactant) treatments on stability were examined. First, the optimum sonication time was determined without adding surfactant with a fixed sonication frequency of 40 kHz. Then, two different surfactants (SDS and PVP) were added to compare the stability for the given optimum sonication time. The stability of ZnO-CuO/EG-W hybrid nanofluids was observed using an ultraviolet-visible (UV-vis) spectrophotometer and by visually examining sedimentation. The absorbance measured with the UV-vis spectrophotometer was used to estimate the effect of sonication time on stability.

Fig. 6 shows the absorbance spectrum of various ZnO-CuO/EG-W hybrid nanofluids (1.0 wt.%) prepared with different sonication times. Higher absorbance values mean the nanoparticles are more evenly dispersed in the base fluid. The sonication period varies from 30 to 120 min for various base fluid ratios. It is found in Fig. 6 that the absorbance from 400 to 800 nm was greatest when the samples were sonicated for 120 min. This means the nanoparticles can be sufficiently dispersed into the EG/W mixture. Results from most studies are consistent in that it has been found that the thermal conductivity was maximized and the viscosity was kept sufficiently low when the nanofluid was stable and the nanoparticles were sufficiently dispersed [36,37]. Therefore, 120 min is considered as the optimum sonication time.

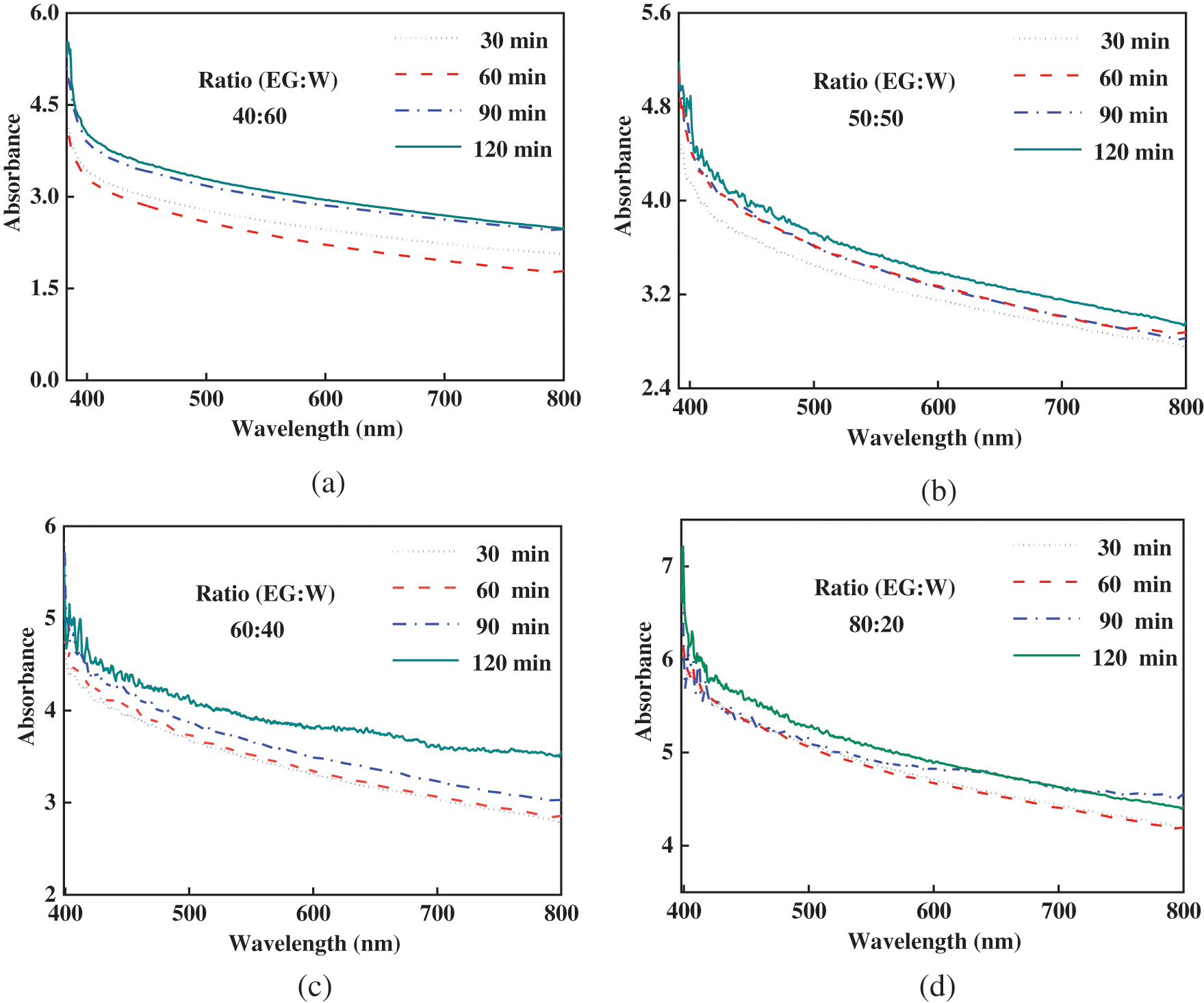
Figure 6: Absorbance of ZnO-CuO/EG-W hybrid nanofluids (1.0 wt.%) for different sonication time: (a) 40:60, (b) 50:50, (c) 60:40, and (d) 80:20

The effectiveness of the surfactant is linked to the chemical nature of the base fluid. To ensure the ZnO-CuO/EG-W hybrid nanofluids remain stable for a long period of time, a surfactant was added to the base fluid under the optimum sonication time of 120 min. A small amount of PVP and SDS surfactants (0.5 wt.%) were used to further ensure the fluid remained stable. Fig. 7 shows the absorbance spectrum from various ZnO-CuO/EG-W hybrid nanofluids with and without added surfactant. The absorbance of the fluid with added PVP is largest from 400 to 800 nm, indicating the fluid with added PVP is the most stable.

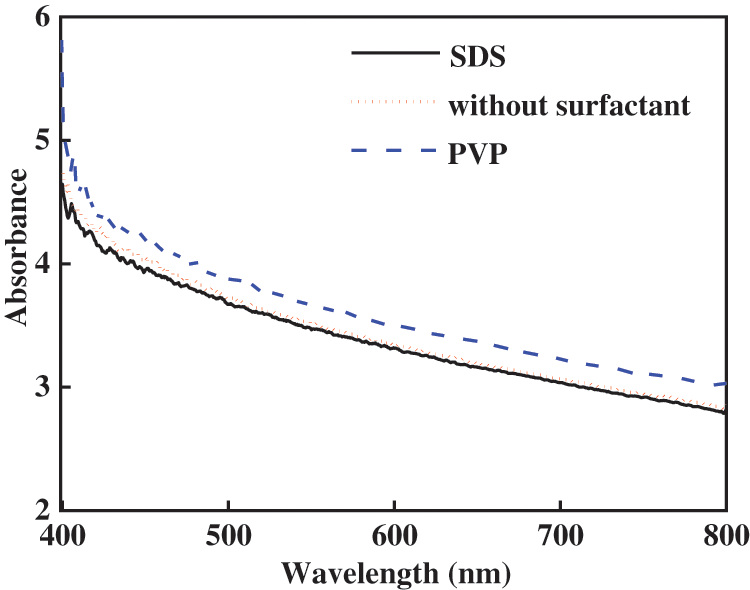
Figure 7: Absorbance of ZnO-CuO/EG-W hybrid nanofluids (1.0 wt.%) with and without added surfactants

Then, using the above nanofluids, the according visual sedimentation of ZnO-CuO/EG-W hybrid nanofluids (EG:W = 40:60) at various times is shown in Fig. 8. One can see that the nanofluids with added PVP surfactant can remain stable for the longest period of time, even exceeding 20 days without apparent sedimentation. 120 min of sonication time and adding PVP surfactant can significantly improve the stability. These two methods were used in other hybrid fluids with different mass concentration in the following experiment.

Figure 8: Stability of ZnO-CuO/EG-W hybrid nanofluids after (a) 0, (b) 3, (c) 10, and (d) 20 days (EG:W = 40:60)

3.2 Effects of Surfactant Ratio and Base Fluid Ratio

As mentioned in Section 3.1, PVP was found to be the appropriate surfactant for use in the present base fluid mixture. The influence of the amount of PVP on thermal conductivity and viscosity was also investigated by varying the mass concentration of PVP from 0.5 to 3 wt.%. Fig. 9 shows how the thermal conductivity and viscosity vary with surfactant mass concentration and temperature (EG:W = 60:40). The thermal conductivity tends to increase up to the maximum value and then starts to decrease when ωpvp = 1 wt.% at the same temperature. At 1 wt.% PVP, the ZnO-CuO/EG-W hybrid nanofluid exhibits the highest thermal conductivity and lowest viscosity. The main reason for this outcome is that the presence of a surfactant reduces the surface tension of the nanofluid. Thus, the nanoparticles can transfer more heat via Brownian motion. A similar result was observed by Hormozi et al. [38] and in our previous study [39]. In the following analysis, the experimental data were gathered from fluids prepared with 120 min sonication time and ωpvp = 1 wt.%.

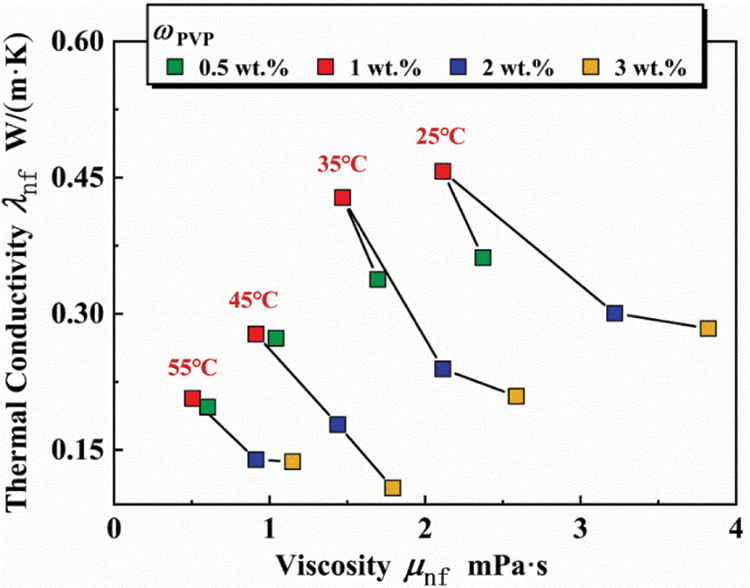
Figure 9: Thermal conductivity vs. viscosity for different surfactant ratios

The thermal conductivity of ZnO-CuO/EG-W hybrid nanofluids at different mass fractions (0 to 5.0 wt.%) and various temperatures (25°C to 60°C) is shown in Fig. 10. The thermal conductivity is an increasing nonlinear function of surfactant mass concentration and temperature. The highest thermal conductivity was found to be 0.6343, 0.5293, 0.4753, and 0.4346 W/(m⋅K) at a temperature of 60°C and 5.0 wt.%, for 20:80, 40:60, 50:50, and 80:20 (EG:W), which is higher than the corresponding base fluids. As the mass concentration and temperature increased, the greater surface area and more frequent Brownian motion between the nanoparticles and liquid molecules drive convective heat transfer inside the nanofluidic system.

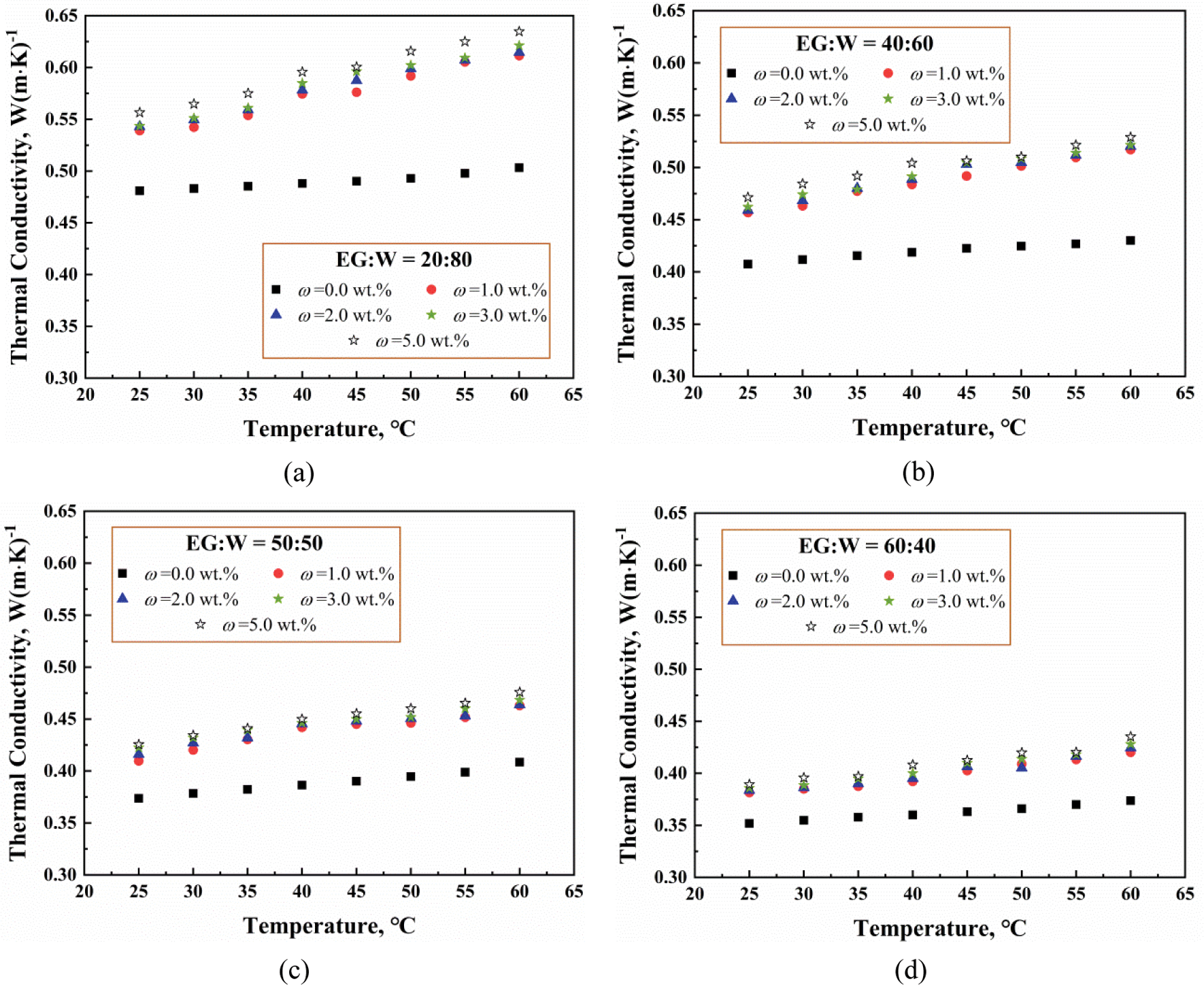
Figure 10: Thermal conductivity of ZnO-CuO/EG-W hybrid nanofluids with EG:W ratio of (a) 20:80, (b) 40:60, (c) 50:50, (d) EG:W = 60:40

Fig. 10 also shows that a fluid with a higher proportion of EG tends to have lower thermal conductivity. The thermal conductivity of EG is lower than that of water at the same temperature. Moreover, fluid molecules must overcome greater flow resistance when the fluid contains a higher proportion of EG, which inhibits Brownian motion. However, the decreasing trend does not depend nonlinearly on the ratio of EG:W due to the random motion of the nanoparticles. Therefore, the effects of mass concentration and temperature on the thermal conductivity of hybrid nanofluids are quite obvious.

The thermal conductivity enhancement (TCE) ratio can be defined as the change in thermal conductivity compared to the base fluid [40]:

TCE%=λnf−λbfλbf×100 (6)

where λnf and λbf are the thermal conductivities of the nanofluid and base fluid, respectively.

Fig. 11 shows the dependence of TCE on mixture ratio and temperature for a mass concentration of 1.0 wt.%. A similar trend is seen for other mass concentration values. A fluid with a smaller EG:W ratio has larger thermal conductivity. The highest TCE values were found to be 21.52%, 20%, 13.07%, 12.43% and 11.7% for mixture ratios of 20:80, 40:60, 50:50, 60:40, and 80:20 (EG:W) at a temperature of 60°C, respectively. This can be attributed to a lower base fluid viscosity, which would correspond to a larger thermal conductivity for a given nanoparticle weight fraction, as shown in Fig. 9 and as mentioned by Yang et al. [41].

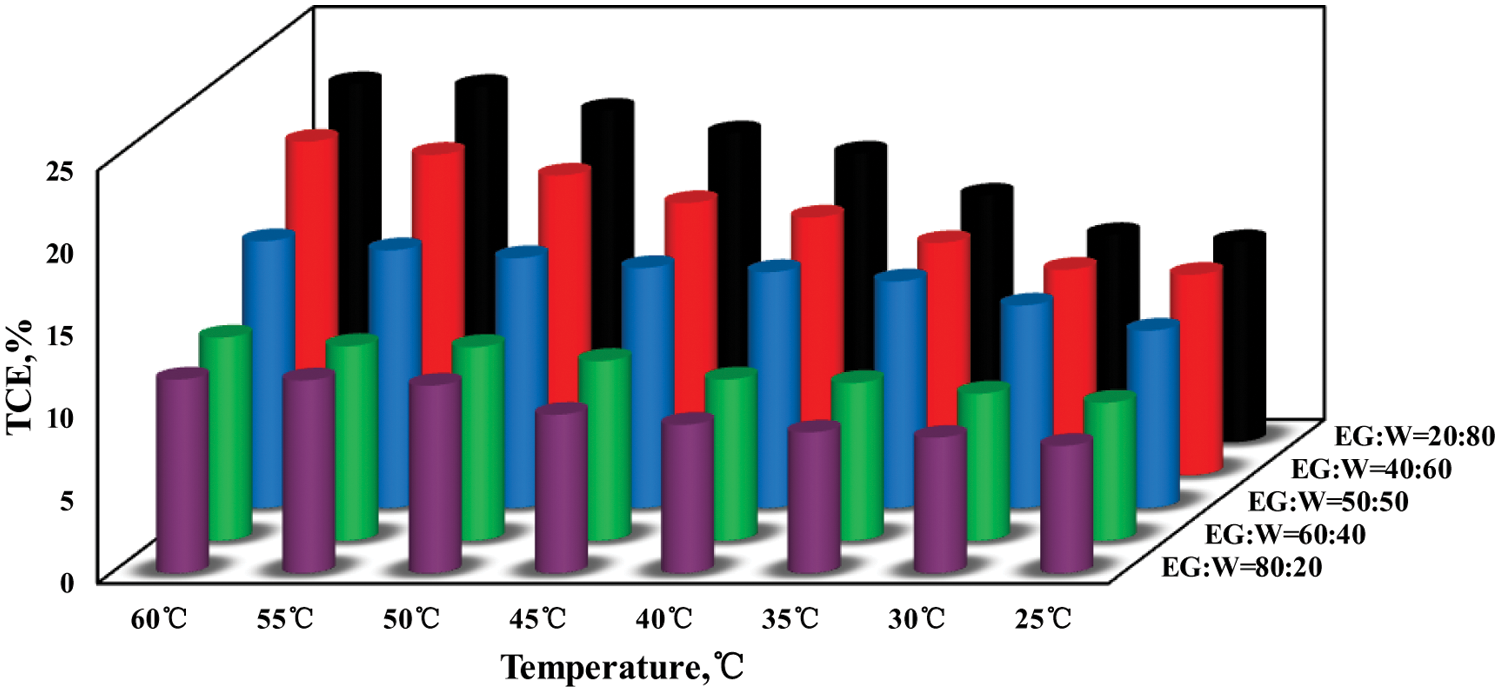
Figure 11: TCE as a function of temperature and mixture ratio (w = 1.0 wt.%)

Fig. 12 shows the viscosity of ZnO-CuO/EG-W hybrid nanofluids with mass concentration ranging from 1 to 5 wt.% for base fluid ratios (EG:W) of 20:80, 40:60, 50:50, and 60:40, respectively. A viscosity enhancement (VE) can be defined as follows:

VE(%)=μnf−μbfμbf×100 (7)

Fig. 12 shows VE for a 5 wt.% fluid; the VE value decreases from 62.78% to 32% when the EG:W ratio is varied from 20:80 to 80:20 at 25°C. In summary, nanofluids with a higher viscosity base fluid exhibit greater VE values compared to nanofluids with a low viscosity of base fluids. For each base fluid ratio, the same trend was observed when it varies with mass concentration and temperature. As the mass concentration and base fluid ratio increase, the viscosity increases nonlinearly. Similar effects of concentration and base fluid ratio on viscosity were found in other reports in the literature, such as Timofeeva et al. [42]. Adding more nanoparticles to the base fluid increases the flow resistance due to the presence of more internal friction. Moreover, a higher base fluid ratio has more EG, so it has higher viscosity. Fig. 12 shows that the viscosity decreases as the temperature increases for each base fluid ratio. As the temperature increases, the connection between liquid molecules and nanoparticles, and Van der Waals forces between particles, become weaker and the viscosity is lower.

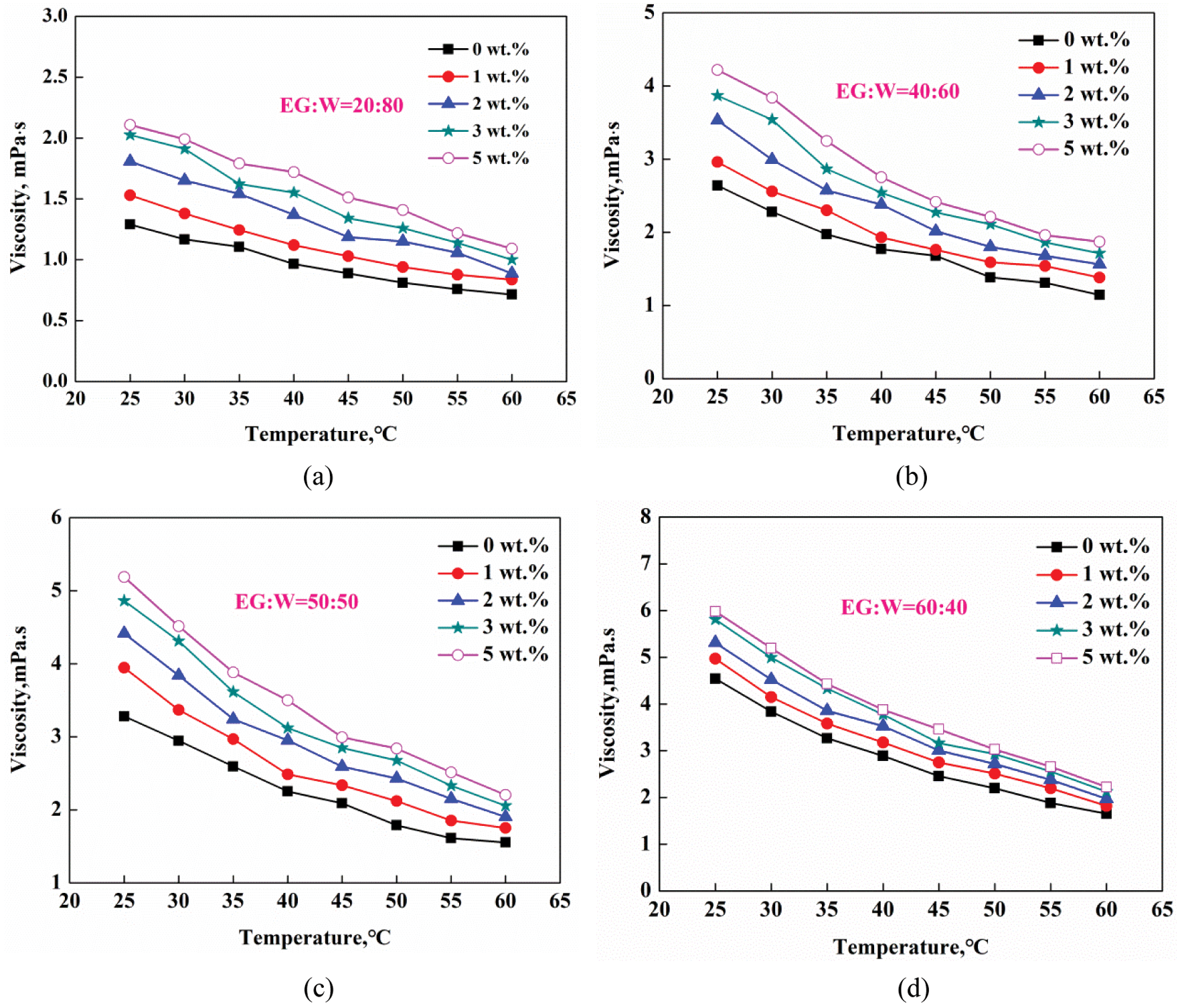
Figure 12: Viscosity as a function of temperature for various mass fractions and EG:W ratios of (a) 20:80, (b) 40:60, (c) 50:50, and (d) 60:40

The practical use of hybrid nanofluids is based on a trade-off between their high thermal conductivity and relatively low viscosity, which is related to the mass concentrations and base fluid ratio. Hence, the overall performance of nanofluids as working fluids in comparison with the base fluid can be estimated from the viscosity and thermal conductivity. The properties enhancement ratio (PER) presented by Hamid et al. [43] can be used to estimate the combined effect of thermal conductivity and viscosity:

PER=μnf/μbf−1λnf/λbf−1 (8)

If PER < 5, the nanofluid is suitable for heat transfer medium in a thermal management system. Fig. 13 shows the variation of PER in the ZnO-CuO/EG-W hybrid nanofluids. All data were distributed below the line PER = 5 for the given experimental conditions.

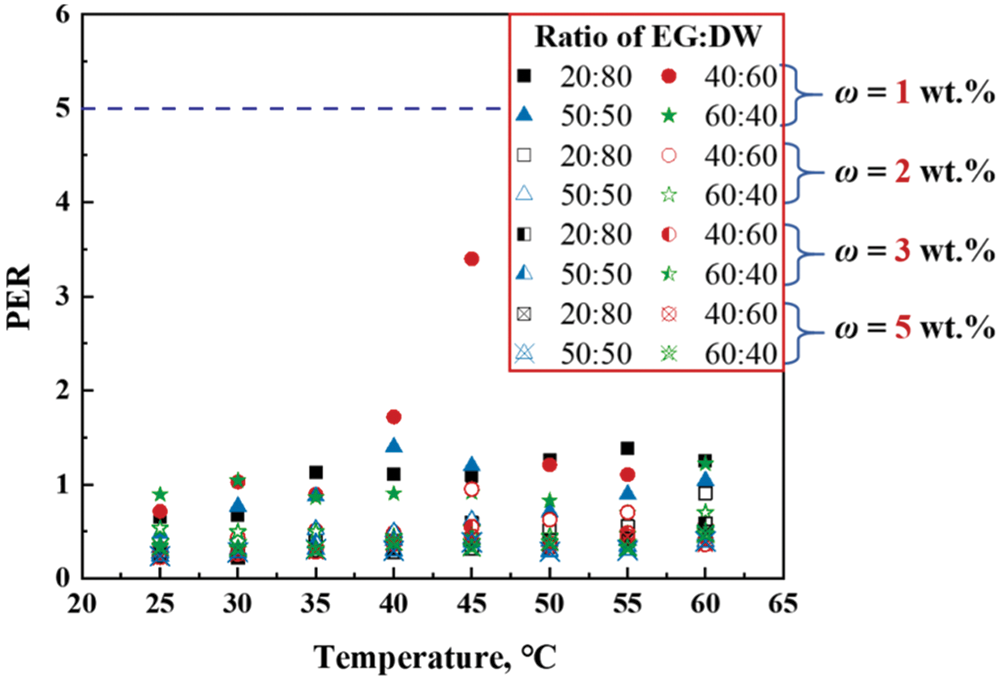
Figure 13: Variation of PER at different base fluid ratio and temperature

3.3 ANN Models for Viscosity and Thermal Conductivity

Fig. 14 shows a comparison of the viscosity and thermal conductivity with some other published data. A comparison against a 1 wt.% mass concentration and 40:60 (EG:W) in the experiment is also provided. Data presented in other studies is presented in Table 2. For viscosity, Nabila et al. [44] and Hamid et al.’s [43] models show excellent agreement with the present experimental data at all temperatures less than 35°C. However, there is a larger difference between the experimental values and data obtained predicted models, for thermal conductivity. Therefore, more accuracy of predicted models should be presented to reduce errors for the present thermal conductivity and viscosity.

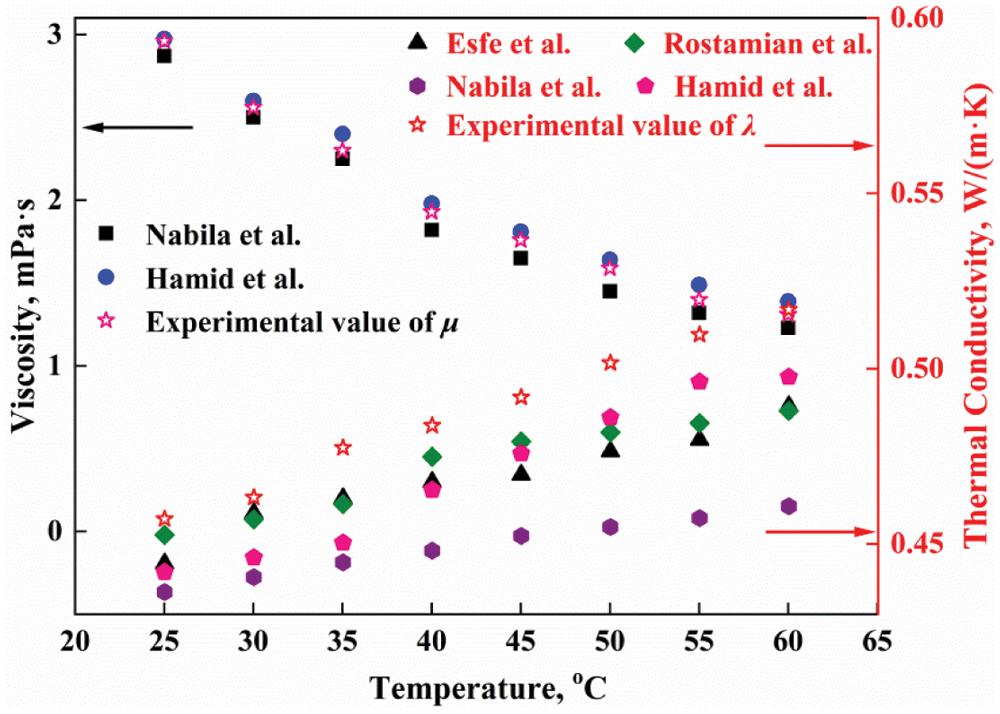
Figure 14: Comparison of μ and λ obtained from experimental data and results in the literature

Fig. 15 shows the margin of deviation (MOD) of the viscosity and thermal conductivity between the proposed ANN models and experimental data. MOD is defined as

MOD(%)=(Kexp−KpredKexp)×100 (9)

As shown in Fig. 15, the modeled values of μ and λ were accurate to within less than ±3% and ±2%, respectively. Moreover, Esfe et al. [47] mentioned that if the data is closer to the zero line, the accurate of predicted models increase. The deviation between the most of the modeled and experimental data is near 0%, showing good accuracy of ANN models.

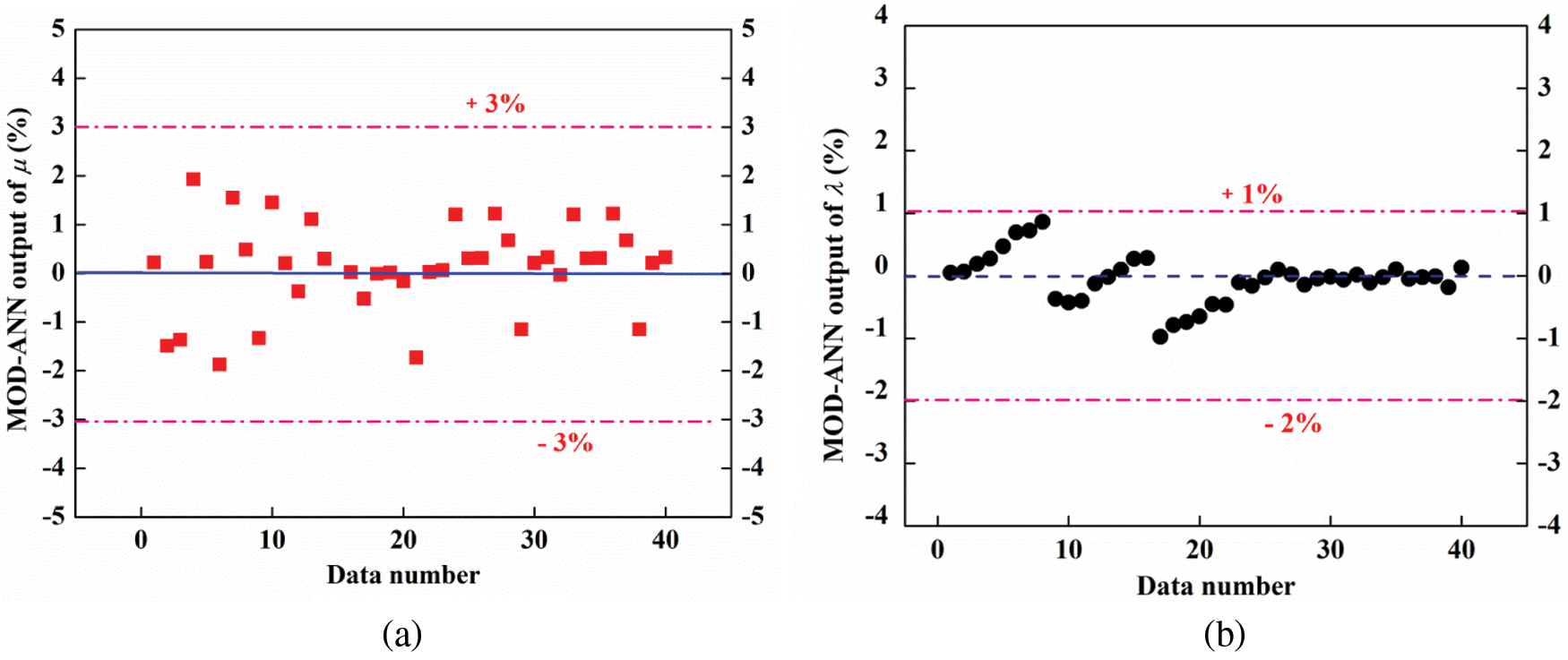
Figure 15: MOD of (a) μ and (b) λ determined from the proposed ANN model

Fig. 16 shows a comparison between the modeled and experimental data. It is found that all data were close in different mass concentration and base fluid ratio. This overlap indicates the ANN model can accurately describe the experimental data. The model has a coefficient of determination of R2 = 0.9979 for viscosity and R2 = 0.9989 for thermal conductivity. Therefore, these two ANN models can be used to sufficiently predict the viscosity and thermal conductivity of ZnO-CuO/EG-W hybrid nanofluids when temperature is 20°C–60°C, w: 0–5 wt.%, and EG:W = 20:80 to 80:20.

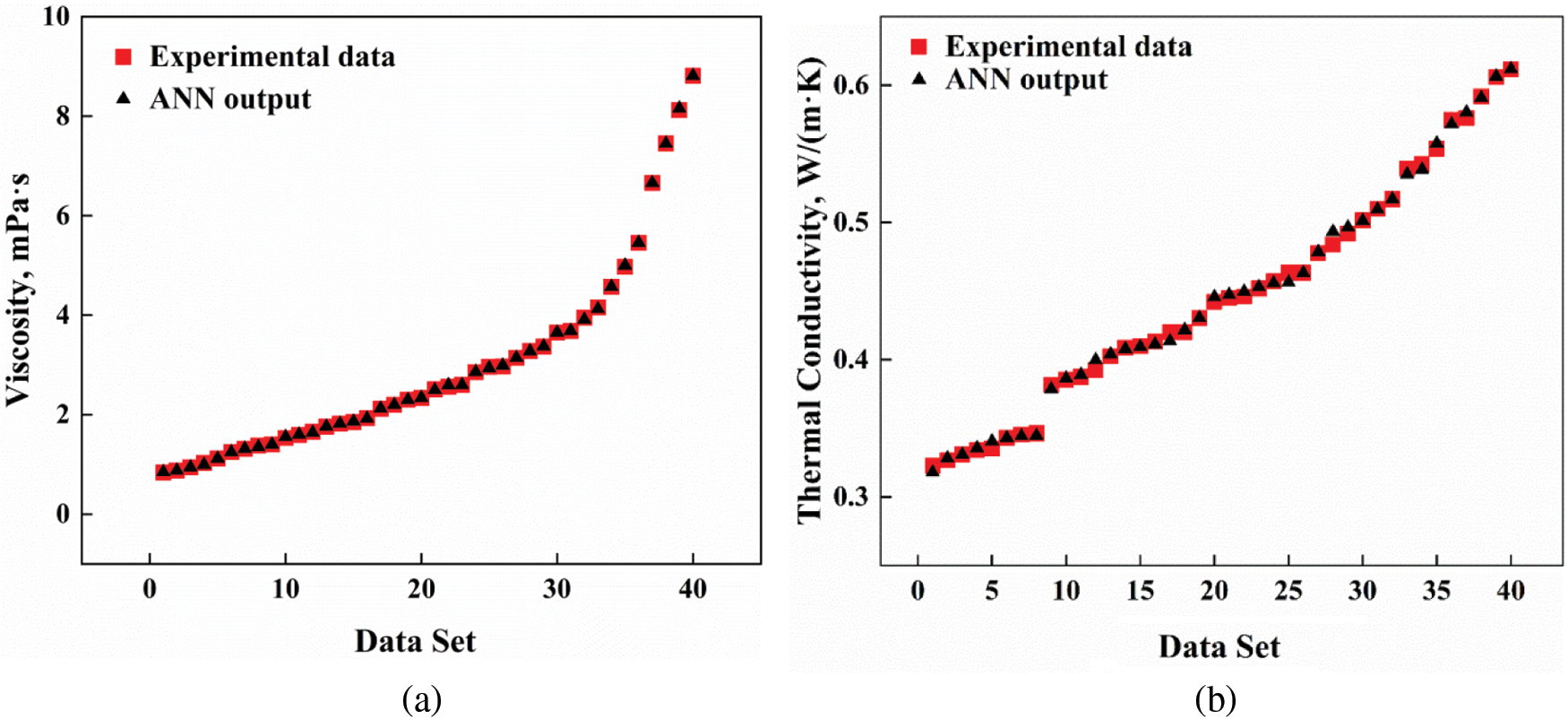
Figure 16: Comparison of ANN modeled data and experimental values of (a) μ and (b) λ

4  Conclusions

The effect of EG:W ratio in base fluids on the viscosity and thermal conductivity of ZnO-CuO/EG-W hybrid nanofluids was investigated in this study. Ultrasonication and added surfactant were used to prevent sedimentation. ANN models for describing viscosity and thermal conductivity were determined using measured data.

The hybrid nanofluid can be stabilized for at least 20 days after the optimal ultrasonic time of 120 min. Under the above conditions, adding 1 wt.% PVP surfactant showed the optimum thermal conductivity and viscosity for ZnO-CuO/EG-W (60:40), which were 0.428 and 1.476 at 35°C, respectively. A higher EG content results in lower thermal conductivity enhancement and higher viscosity enhancement of hybrid nanofluids. The choice of EG content in base fluids is conducive to obtaining lower viscosity and higher thermal conductivity. ANNs were used for regression, and the values of MOD between experimental and modeled data were ±3% and ±2% for describing viscosity and thermal conductivity.

The present work can enrich the data for different combination of nanoparticles and base fluids. It can provide engineers with the appropriate base fluid ratio under different requirements. The accurate and fast ANN model proposed can be used to estimate viscosity and thermal conductivity, which can effectively reduce the experimental cost.

Acknowledgement: This project is supported by the National Natural Science Foundation of China (No. 51806090), and the Basic Research Project of Yunnan Province (No. 202001AT070081).

Funding Statement: This project is supported by Yulingn Zhai and the National Natural Science Foundation of China (No. 51806090), and the Basic Research Project of Yunnan Province (No. 202001AT070081).

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  Al-Balushi, L. M., Rahman, M. M. (2020). Impacts of heat flux distribution, sloping magnetic field and magnetic nanoparticles on the natural convective flow contained in a square cavity. Fluid Dynamic & Materials Processing, 16, 441–463. DOI 10.32604/fdmp.2020.08551. [Google Scholar] [CrossRef]

 2.  Kazemi, I., Sefid, M., Afrand, M. (2020). A novel comparative experimental study on rheological behavior of mono & hybrid nanofluids concerned graphene and silicanano-powders: Characterization, stability and viscosity measurement. Powder Technology, 366, 216–229. DOI 10.1016/j.powtec.2020.02.010. [Google Scholar] [CrossRef]

 3.  Kumar, D. D., Arasu, A. V. (2018). A comprehensive review of preparation, characterization, properties and stability of hybrid nanofluids. Renewable & Sustainable Energy Reviews, 81, 1669–1689. DOI 10.1016/j.rser.2017.05.257. [Google Scholar] [CrossRef]

 4.  Gupta, M., Singh, V., Kumar, R., Said, Z. (2017). A review on thermophysical properties of nanofluids and heat transfer applications. Renewable & Sustainable Energy Reviews, 74, 638–670. DOI 10.1016/j.rser.2017.02.073. [Google Scholar] [CrossRef]

 5.  Reddy, M. C. S., Rao, W. (2013). Experimental studies on thermal conductivity of blends of ethylene glycol-water based TiO2 nanofluids. International Communications in Heat and Mass Transfer, 46, 31–36. DOI 10.1016/j.icheatmasstransfer.2013.05.009. [Google Scholar] [CrossRef]

 6.  Babu, J. A. R., Kumar, K. K., Rao, S. S. (2017). State-of-art review on hybrid nanofluids. Renewable & Sustainable Energy Reviews, 77, 551–565. DOI 10.1016/j.rser.2017.04.040. [Google Scholar] [CrossRef]

 7.  Chiam, H. W., Azmi, W. H., Usri, N. A., Mamat, R., Adam, N. M. (2017). Thermal conductivity and viscosity of Al2O3 nanofluids for different based ratio of water and ethylene glycol mixture. Experimental Thermal and Fluid Science, 81, 420–429. DOI 10.1016/j.expthermflusci.2016.09.013. [Google Scholar] [CrossRef]

 8.  Sonawane, S. S., Khedkar, R. S., Wasewar, K. L. (2015). Effect of sonication time on enhancement of effective thermal conductivity of nano TiO2–water, ethylene glycol, and paraffin oil nanofluids and models comparisons. Journal of Experimental Nanoscience, 10, 310–322. DOI 10.1080/17458080.2013.832421. [Google Scholar] [CrossRef]

 9.  Cabaleiro, D., Nimo, J., Pastoriza-Gallego, M. J., Legido, J. L., Lugo, L. et al. (2015). Thermal conductivity of dry anatase and rutile nano-powders and ethylene and propylene glycol-based TiO2 nanofluids. Journal of Chemical Thermodynamics, 83, 67–76. DOI 10.1016/j.jct.2014.12.001. [Google Scholar] [CrossRef]

10. Das, P. K. (2017). A review based on the effect and mechanism of thermal conductivity of normal nanofluids and hybrid nanofluids. Journal of Molecular Liquids, 240, 420–446. DOI 10.1016/j.molliq.2017.05.071. [Google Scholar] [CrossRef]

11. Esfe, M. H., Rostamian, H., Toghraie, D., Yan, W. M. (2016). Using artificial neural network to predict thermal conductivity of ethylene glycol with alumina nanoparticle. Journal of Thermal Analysis and Calorimetry, 126, 643–648. DOI 10.1007/s10973-016-5506-7. [Google Scholar] [CrossRef]

12. Maleki, A., Haghighi, A., Mahariq, I., (2021). Machine learning-based approaches for modeling thermophysical properties of hybrid nanofluids: A comprehensive review. Journal of Molecular Liquids, 322, 114843. DOI 10.1016/j.molliq.2020.114843. [Google Scholar] [CrossRef]

13. Akhgar, A., Toghraie, D., Sina, N. (2019). Developing dissimilar artificial neural networks (ANNs) to prediction the thermal conductivity of MWCNT-TiO2/Water-ethylene glycol hybrid nanofluid. Powder Technology, 355, 602–610. DOI 10.1016/j.powtec.2019.07.086. [Google Scholar] [CrossRef]

14. Esfe, M. H., Ahangar, M., Hajmohammad, M. H., Rostamian, H., Tourang, H. et al. (2016). Designing artificial neural network on thermal conductivity of Al2O3–water–EG (60–40%) nanofluid using experimental data. Journal of Thermal Analysis and Calorimetry, 126, 837–843. DOI 10.1007/s10973-016-5469-8. [Google Scholar] [CrossRef]

15. Shahsavar, A., Khanmohammadi, S., Toghraie, D., Salihepour, H. (2019). Experimental investigation and develop ANNs by introducing the suitable architectures and training algorithms supported by sensitivity analysis: Measure thermal conductivity and viscosity for liquid paraffin based nanofluid containing Al2O3 nanoparticles. Journal of Molecular Liquids, 276, 850–860. DOI 10.1016/j.molliq.2018.12.055. [Google Scholar] [CrossRef]

16. Toghraie, D., Sina, N., Jolfaei, N. A., Hajian, M., Afrand, M. (2019). Designing an artificial neural network (ANN) to predict the viscosity of silver/ethylene glycol nanofluid at different temperatures and volume fraction of nanoparticles. Physica A, 534, 122142. DOI 10.1016/j.physa.2019.122142. [Google Scholar] [CrossRef]

17. Sajid, M. U., Ali, H. M., (2018). Thermal conductivity of hybrid nanofluids: A critical review. International Journal of Heat and Mass Transfer, 126, 211234. DOI 10.1016/j.ijheatmasstransfer.2018.05.021. [Google Scholar] [CrossRef]

18. Esfe, M. H., Afrand, M., Yan, W. M. (2016). Effects of temperature and concentration on rheological behavior of MWCNTs/SiO2(20–80)-SAE40 hybrid nano-lubricant. International Communications in Heat and Mass Transfer, 76, 133–138. DOI 10.1016/j.icheatmasstransfer.2016.05.015. [Google Scholar] [CrossRef]

19. Ruhani, B., Toghraie, D., Hekmatifar, M., Hadian, M. (2019). Statistical investigation for developing a new model for rheological behavior of ZnO-Ag (50%–50%)/water hybrid newtonian nanofluid using experimental data. Physica A, 525, 741–751. DOI 10.1016/j.physa.2019.03.118. [Google Scholar] [CrossRef]

20. Ma, M. Y., Zhai, Y. L., Yao, P. T., Wang, H., Li, Y. (2020). Synergistic mechanism of thermal conductivity enhancement and economic analysis of hybrid nanofluids. Powder Technology, 373, 702–715. DOI 10.1016/j.powtec.2020.07.020. [Google Scholar] [CrossRef]

21. Amaa, C., Arca, B., Yy, C., Hv, C., Hjm, D. et al. (2020). Tailoring the viscosity of water and ethylene glycol based TiO2 nanofluids. Journal of Molecular Liquids, 297, 111982. DOI 10.1016/j.molliq.2019.111982. [Google Scholar] [CrossRef]

22. Hwang, Y., Lee, J. K., Lee, C. H., Jung, Y. M., Jang, S. P. (2007). Stability and thermal conductivity characteristics of nanofluids. Thermochimica Acta, 455, 70–74. DOI 10.1016/j.tca.2006.11.036. [Google Scholar] [CrossRef]

23. Kim, S. H., Choi, S. R., Kim, D. (2007). Thermal conductivity of metal-oxide nanofluids: Particle size dependence and effect of laser irradiation. Journal of Heat Transfer, 129, 298307. DOI 10.1115/1.2427071. [Google Scholar] [CrossRef]

24. Ali, H. M. (2020). Hybrid nanofluids for convection heat transfer. Academic Press. [Google Scholar]

25. Nabil, M. F., Azmi, W. H., Hamid, K. A., Zawawi, N., Priyandoko, G. et al. (2017). Thermo-physical properties of hybrid nanofluids and hybrid nanolubricants: A comprehensive review on performance. International Communications in Heat and Mass Transfer, 83, 30–39. DOI 10.1016/j.icheatmasstransfer.2017.03.008. [Google Scholar] [CrossRef]

26. Kazemi, I., Sefid, M., Afrand, M. (2020). A novel comparative experimental study on rheological behavior of mono & hybrid nanofluids concerned graphene and silica nano-powders: Characterization, stability and viscosity measurements. Powder Technology, 366, 216–229. DOI 10.1016/j.powtec.2020.02.010. [Google Scholar] [CrossRef]

27. Xuan, Z. H., Zhai, Y. L., Ma, M. Y., Wang, H. (2020). Thermo-economic performance and sensitivity analysis of ternary hybrid nanofluids. Journal of Molecular Liquids, 323, 114889. DOI 10.1016/j.molliq.2020.114889. [Google Scholar] [CrossRef]

28. Ashrae (2009). ASHRAE handbook–Fundamentals (SI Edition). Atlanta: American Society of Heating, Refrigerating and Air-Conditioning Engineers, Inc. [Google Scholar]

29. Esfe, M. H., Wongwises, S., Naderi, A. (2015). Thermal conductivity of Cu/TiO2-water/EG hybrid nanofluid: Experimental data and modeling using artificial neural network and correlation. International Communications in Heat and Mass Transfer, 66, 100–104. DOI 10.1016/j.icheatmasstransfer.2015.05.014. [Google Scholar] [CrossRef]

30. Esfe, M. H., Rostamian, H., Afrand, M. (2015). Modeling and estimation of thermal conductivity of MgO-water/EG (60:40) by artificial neural network and correlation. International Communications in Heat and Mass Transfer, 68, 98–103. DOI 10.1016/j.icheatmasstransfer.2015.08.015. [Google Scholar] [CrossRef]

31. Esfe, M. H., Esfandeh, S., Saedodin, S. (2017). Experimental evaluation, sensitivity analyzation and ANN modeling of thermal conduvtivity of ZnO-MWCNT/EG-water hybrid nanofluid for engineering applications. Applied Thermal Engineering, 125, 673–685. DOI 10.1016/j.applthermaleng.2017.06.077. [Google Scholar] [CrossRef]

32. Li, L., Zhai, Y., Wang, J., Ma, M. (2020). Stability, thermal performance and artificial neural network modeling of viscosity and thermal conductivity of Al2O3-ethylene glycol nanofluids. Powder Technology, 363, 360–368. DOI 10.1016/j.powtec.2020.01.006. [Google Scholar] [CrossRef]

33. Ma, M. Y., Zhai, Y. L., Wang, J. (2020). Statistical image analysis of uniformity of hybrid nanofluids and prediction models of thermophysical parameters based on artificial neural network (ANN). Powder Technology, 362, 257–266. DOI 10.1016/j.powtec.2019.11.098. [Google Scholar] [CrossRef]

34. Esfe, M. H., Esfandeh, S., Rejvani, M. (2018). Modeling of thermal conductivity of MWCNT-SiO2 (30:70%)/EG hybrid nanofluid, sensitivity analyzing and cost performance for industrial applications. Journal of Thermal Analysis and Calorimetry, 131, 1437–1447. DOI 10.1007/s10973-017-6680-y. [Google Scholar] [CrossRef]

35. Pare, A., Ghosh, S. K. (2021). A unique thermal conductivity model (ANN) for nanofluid based on experimental study. Powder Technology, 377, 429–438. DOI 10.1016/j.powtec.2020.09.011. [Google Scholar] [CrossRef]

36. Al-Hassani, K. A., Alam, M. S. (2021). Numerical simulations of hydromagnetic mixed convection flow of nanofluids inside a triangular cavity on the basis of a two-component nonhomogeneous mathematical model. Fluid Dynamic & Materials Processing, 17, 1–20. DOI 10.32604/fdmp.2021.013497. [Google Scholar] [CrossRef]

37. Zaydan, M., Riahi, M., Mebarek-Oudina, F., Sehaqui, R. (2021). Mixed convection in a two-sided lid-driven square cavity filled with different types of nanoparticles: A comparative study assuming nanoparticles with different shapes. Fluid Dynamic & Materials Processing, 17, 789–818. DOI 10.32604/fdmp.2021.015422. [Google Scholar] [CrossRef]

38. Hormozi, F., ZareNezhad, B., Allahyar, H. R. (2016). An experimental investigation on the effects of surfactants on the thermal performance of hybrid nanofluids in helical coil heat exchangers. International Communications in Heat and Mass Transfer, 78, 271276. DOI 10.1016/j.icheatmasstransfer.2016.09.022. [Google Scholar] [CrossRef]

39. Li, F. S., Li, L., Zhong, G. J. (2019). Effect of ultrasonic time, size of aggregates and temperature on the stability and viscosity of Cu-ethylene glycol (EG) nanofluids. International Journal of Heat and Mass Transfer, 129, 278–286. DOI 10.1016/j.ijheatmasstransfer.2018.09.104. [Google Scholar] [CrossRef]

40. Maji, N. C., Chakraborty, J. (2020). Explaining the disparity in nanofluid results: Role of morphology, material, and state of aggregation of colloidal particles. International Journal of Heat and Mass Transfer, 156, 119709. DOI 10.1016/j.ijheatmasstransfer.2020.119709. [Google Scholar] [CrossRef]

41. Yang, L., Hu, Y. H. (2017). Toward TiO2 nanofluids–Part 2: Applications and challenges. Nanoscale Research Letters, 12, 446. DOI 10.1186/s11671-017-2185-7. [Google Scholar] [CrossRef]

42. Timofeeva, E. V., Routbort, J. L., Singh, D. (2013). Particle shape effects on thermophysical properties of alumina nanofluids. Journal of Applied Physics, 106, 014304. DOI 10.1063/1.3155999. [Google Scholar] [CrossRef]

43. Hamid, K. A., Azmi, W. H., Nabil, M. F. (2018). Experimental investigation of thermal conductivity and dynamic viscosity on nanoparticle mixture ratios of TiO2-SiO2 nanofluids. International Journal of Heat and Mass Transfer, 116, 1143–1152. DOI 10.1016/j.ijheatmasstransfer.2017.09.087. [Google Scholar] [CrossRef]

44. Nabila, M. F., Azmia, W. H., Hamid, K. A. (2017). An experimental study on the thermal conductivity and dynamic viscosity of TiO2-SiO2 nanofluids in water: Ethylene glycol mixture. International Communications in Heat and Mass Transfer, 86, 181–189. DOI 10.1016/j.icheatmasstransfer.2017.05.024. [Google Scholar] [CrossRef]

45. Esfe, M. H., Arani, A. A. A., Firouzi, M. (2017). Empirical study and model development of thermal conductivity improvement and assessment of cost and sensitivity of EG-water based SWCNT-ZnO (30%:70%) hybrid nanofluid. Journal of Molecular Liquids, 244, 252–261. DOI 10.1016/j.molliq.2017.08.087. [Google Scholar] [CrossRef]

46. Rostamian, S. H., Saedodin, M. B. S. (2017). An inspection of thermal conductivity of CuO-SWCNTs hybrid nanofluid versus temperature and concentration using experimental data, ANN modeling and new correlation. Journal of Molecular Liquids, 231, 364–369. DOI 10.1016/j.molliq.2017.02.015. [Google Scholar] [CrossRef]

47. Esfe, M. H., Esfandeh, S. (2020). The statistical investigation of multi-grade oil based nanofluids: Enriched by MWCNT and ZnO nanoparticles. Physica A, 554, 122159. DOI 10.1016/j.physa.2019.122159. [Google Scholar] [CrossRef]

This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.