

 | Fluid Dynamics & Materials Processing |  |
DOI: 10.32604/fdmp.2022.020248
ARTICLE
An Investigation into the Behavior of Non-Isodense Particles in Chaotic Thermovibrational Flow
Department of Mechanical and Aerospace Engineering, University of Strathclyde, James Weir Building, Glasgow, G1 1XJ, UK
*Corresponding Author: Marcello Lappa. Email: marcello.lappa@strath.ac.uk
Received: 13 November 2021; Accepted: 16 December 2021
Abstract: The ability to control the distribution of particles in a fluid is generally regarded as a factor of great importance in a variety of fields (manufacturing processes, biomedical applications, materials engineering and various particle separation processes, to cite a few). The present study considers the hitherto not yet addressed situation in which solid spherical particles are dispersed in a non-isothermal fluid undergoing turbulent vibrationally-induced convection (chaotic thermovibrational flow in a square cavity due to vibrations perpendicular to the imposed temperature difference). Although the possibility to use laminar thermovibrational flows (in microgravity) and turbulent flows of various types (in normal gravity conditions) to induce the accumulation of solid mass dispersed in a non-isodense fluid is already known, the interplay of finite-size finite-mass particles with chaotic flow in weightlessness conditions has never been considered. In the present study this subject is tackled through direct numerical solution of the fluid and particle tracking equations in the framework of a one-way coupling approach. Results are presented for relatively wide ranges of vibrational amplitude, particle size and density.
Keywords: Thermovibrational flow; turbulence; particle accumulation; multiphase flow
Nomenclature
| b | Vibration amplitude |
| p | Pressure |
| Pr | Prandtl number |
| Ra | Rayleigh number |
| T | Temperature |
| t | Time |
| V | Velocity |
| x | Horizontal coordinate |
| y | Vertical coordinate |
| St | Particle Stokes Number |
| P | Vibrational period |
| Greek Symbols | |
| α | Thermal diffusivity |
| βT | Thermal expansion coefficient |
| ν | Kinematic viscosity |
| γ | Non-dimensional amplitude of vibrations |
| ρ | Density |
| ω | Angular frequency |
| Ω | Non-dimensional angular frequency |
| ΔT | Temperature difference |
| ξ | Fluid/particle density ratio |
| ζ | Non-dimensional Kolmogorov length scale |
| τ | Characteristic time scale |
| Subscripts | |
| Hot | Hot |
| Cold | Cold |
| Particle | Particle |
| Flow | Flow |
| Div | Divisions |
Many natural and industrial processes are known to depend on the delicate interplay of two or more phases. Such interactions, of a liquid-solid, gas-solid, gas-liquid and in some cases, gas-liquid-solid nature, typically result in multiphase flows [1]. These can occur in atmospheric and geological cycles and events [2] and in a variety of technological processes (including, but not limited to, those of the oil and gas industry, materials engineering, biotechnology and many other applications involving jets and sprays).
The mixing (or segregation) of the involved phases can depend on the type of fluid motion associated with the considered problem. As many natural and industrial processes are intrinsically turbulent, a vast literature exists where such phenomena have been investigated in these circumstances. In particular, most existing studies have focused on the preferential clustering of either isodense or non-neutrally buoyant solid particles in the case of isotropic turbulence [3,4] with the two-fold objective of describing the effect of turbulence on the dynamics of the discrete phase (including its sedimentation process) and elaborating strategies to modulate/attenuate turbulence [5–8]. In such analyses, particles have generally been observed to cluster and form irregular aggregates displaying fractal morphology.
More recently, other studies have been conducted considering turbulent natural (buoyancy) convection, which can no longer be considered isotropic. This type of flow can be further distinguished into two different variants according to the relative direction of gravity and the imposed temperature difference (a temperature gradient parallel [9] or perpendicular [10] to the gravity vector leading to the so-called Rayleigh-Bénard and Hadley convection, respectively). As an example of recent investigations for non-neutrally buoyant particles interacting with turbulence brought on by natural convection, it is worth citing Xu et al. [11], where the temperature gradient was set parallel to the gravity vector. In this work, (heavy) particles were observed to undergo accumulation into bands, with the strength of the bands depending on the inertial properties of the considered particles. For the companion problem represented by the Hadley flow, other authors, such as Gereltbyamba et al. [12], have found that the particle diameter can play a significant role in the resultant particle trajectories and their concentrations when relatively high value of the Rayleigh number are considered.
The present study focuses on the so-called thermovibrational convection, that is, a variant of standard buoyancy convection where steady gravity is replaced by, or superimposed onto, a sinusoidal displacement in time (i.e., vibrations). As shown by recent numerical efforts on this subject [13–16], specific configurations of multiphase (laminar) thermovibrational flow can be used to implement novel control mechanisms, by which a discrete phase can be forced to form very regular structures. The morphology of these aggregates depends on factors such as the shape and boundary conditions of the fluid container, the fluid properties, the amplitude and frequency of the vibrations, the temperature gradient and its direction with respect to vibrations, on the one hand, and the properties of the solid phase (shape, size, and density of the considered particles) on the other hand. In the near future, dedicated experiments will be executed onboard the International Space Station to shed some additional light on these phenomena and confirm the predictions of numerical studies (an example being the T-PAOLA project-Thermovibrationally-driven Particle Self-Assembly and Ordering mechanisms in Low gravity–also known as “Particle Vibration” experiment, set to be executed in 2023).
Despite these efforts and a few other relevant investigations [17–19], however, the problem related to particle behavior in microgravity conditions has received less attention than the corresponding case dealing with particles in terrestrial flows. For these reasons, in the present work we concentrate on the preferential clustering of non-isodense finite-mass finite-size particles induced in microgravity conditions by turbulent thermovibrational flow. This may be regarded as a new line of inquiry standing at the intersection of the previously segregated fields about the (terrestrial) dynamics of inertial particles in isotropic turbulence and the behavior of such particles in laminar thermovibrational flows.
A turbulent thermovibrational flow can be achieved when the amplitude of vibrations (or the related vibrational Rayleigh number) exceeds a given value and the fluid ‘response’ (in terms of induced velocity) becomes non-synchronous with the forcing of the system [20,21]. To clarify all these dynamics, the present short study is articulated into several sections as follows. In Section 2, a brief summary of the equations governing the response of a non-isothermal fluid under the effect of vibrations is presented. Section 3 briefly describes the numerical methods used to solve them, the effective resolution of such methods and the sensitivity of the results to the mesh size. Section 4 is finally used to describe some original results, where insights are sought from the critical comparison of representative cases selected ‘ad hoc’.
In line with many works cited in the introduction and owing to its simplicity, this work focuses on a classical differentially heated two-dimensional (2D) square cavity with length L. The vibrations are imposed perpendicularly to the temperature gradient and in a direction parallel to the adiabatic sidewalls of the cavity (see Fig. 1). Applying the Boussinesq approximation, the non-dimensional balance equations for mass, momentum and energy can be cast in condensed form as:
with
where ω = 2πf (f being the frequency of the vibrations (Hz), i.e., f = P−1, P being the related period in seconds), b is the amplitude of displacement (m), Pr is the fluid Prandtl number defined as Pr = ν/α, where ν is the kinematic viscosity (m2/s) and α is the thermal diffusivity (m2/s), βTis the coefficient of thermal expansion (K−1) and ΔT is the temperature difference across the fluid cell (K). The non-dimensional form of these equations follows by scaling the Cartesian coordinates (x, y), time (t), velocity (V), pressure (p) and temperature (T) by the reference quantities: L, L2/α, α/L, ρα2/L, and ΔT, respectively.
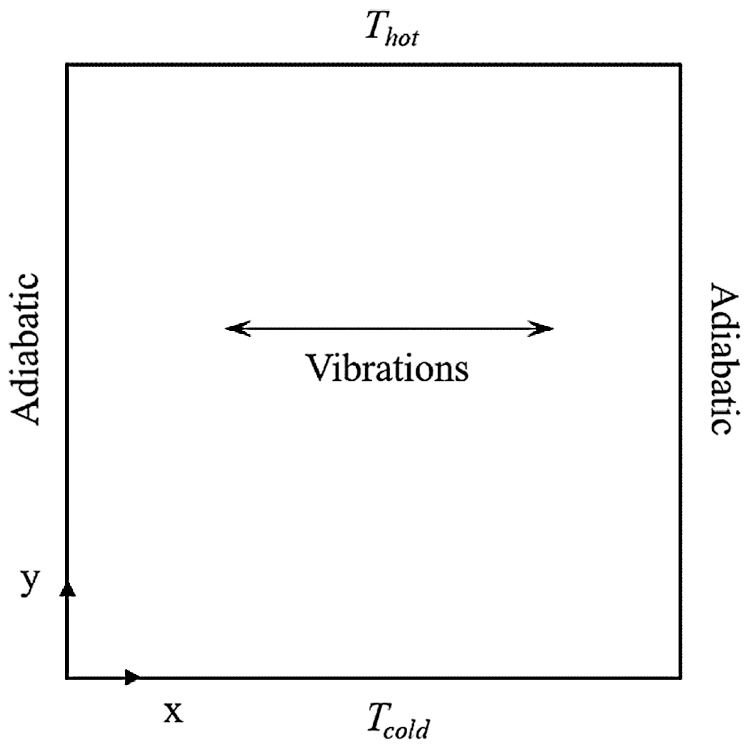
Figure 1: Square cavity, heated at the top and cooled at the bottom, with adiabatic walls and vibrations applied along the x-axis
In addition to solving the fluid flow itself, additional mathematical modeling is obviously required for the dispersed phase, which is accounted for through the solution of the Maxey-Riley equation, i.e., Eq. (4):
This may be regarded as an equation accounting for all the forces acting on the generic solid particle (with the exception of the Basset force, which can be considered negligible for the conditions considered in the present work) and the related balance in a Lagrangian frame of reference.
The additional non-dimensional parameters appearing in this equation are: ξ, i.e., the density ratio between the carrier fluid and the dispersed phase (ξ = ρparticle/ρfluid), St, namely, the well-known particle Stokes number defined as the ratio between the particle relaxation time and the time scale of the flow.
where Rparticle is the radius of the particle, and the non-dimensional vibrations amplitude γ:
The one-way coupling approach adopted in this work signifies that the dispersed phase has no effect on the fluid flow, which implicitly indicates that the present simulations refer (or are valid for) a dilute system.
3 Grid Refinement and Numerical Method
The present work has been carried out using the computational platform OpenFOAM on uniform grids. It is worth recalling that, for this type of grids and turbulent flows, according to well-known requirements based on arguments related to the so-called Kolmogorov length scale, the recommended number of divisions across the computational domain can be defined as:
Here, a maximum value of Raω = 109 is considered (along with Pr = 15), which according to this criterion would return a value of Ndiv = 96. As this, however, should be regarded only as a theoretical guideline, it has been deemed necessary to conduct a grid refinement study to verify the relevance of such a requirement.
The related outcomes shown in Fig. 2 reveal the difference in the results as the mesh density is increased and varied in a certain neighborhood of such a value. In particular, a difference of less than 0.1 K can be observed between 60 to 80, 80 to 96 and 96 to 110. As not to stray too far away from the original 96 divisions and keep the computational effort to a minimum, the 80 by 80 mesh has been chosen for this study.
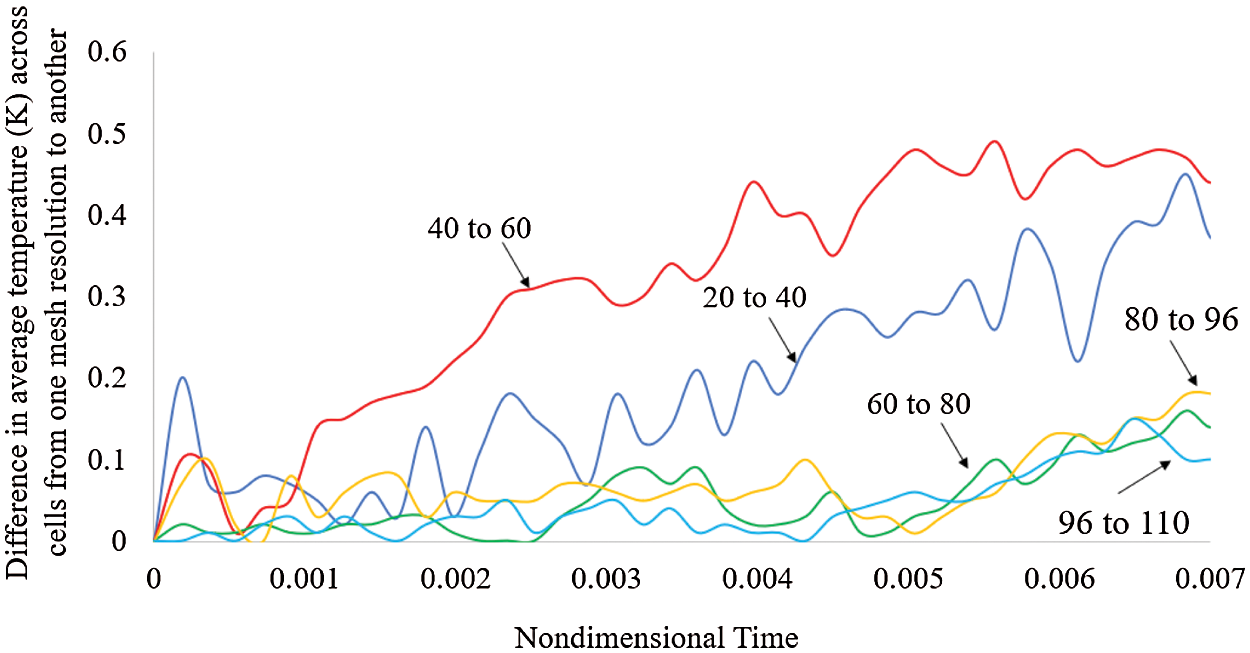
Figure 2: Difference in average temperature across cells from one mesh resolution to another, for Pr = 15, Raω = 1.00 × 109, Ω = 1.00 × 104, γ = 1.79 × 109
A backward differencing in time has been used together with upwind and central differencing schemes in space for the convective term and diffusion term appearing in Eqs. (2)–(3), respectively. The Maxey-Riley equation has been integrated at the same time with these equations (the interested reader being referred to [22,23] for additional information about the solution of this equation and particle-wall interaction model).
The results presented in this section can be used to identify the salient factors contributing to the behavior of particles under the effect of vibrations and related turbulent fluid flow. They have been obtained by changing the influential parameters in a segregated manner in order to reveal the influence of each of them (namely, St and ξ accounting for the inertial effects, and γ and Raω, accounting for the strength of vibrations and fluid motion induced accordingly). To reduce the (otherwise intractable) scale of the problem resulting from the consideration of so many parameters, without loss of generality, the vibrational frequency Ω has been fixed to 104.
We wish to start from an important premise. The accumulation of particles in turbulent flows comes primarily as a result of the inertial nature of the particles coupled with presence of eddies in the fluid. The investigation of Maxey et al. [4] into dispersed turbulent multiphase flow in the case of homogeneous, isotropic turbulence (for gas-particle and bubble-liquid mixtures), indeed, could show that the preferential concentration of bubbles/particles depends on the inertial properties of the dispersed phase and centrifugal effects.
Preferential accumulation is typically observed in regions of strong vorticity for bubbles and regions of strong strain-rate for particles, meaning that for cases where the dispersed phase is less dense than the continuous phase (ξ < 1) the particles will cluster in the center of the eddies/vortices and vice versa for the cases where the dispersed phase is denser than the continuous phase (ξ > 1).
The present results, however, reveal that, when subjected to vibrations, the displacement of the cavity gives rise to an external (‘additional’ with respect to the effects discussed before) force that influences the trajectory of the particles, whereby they are continuously pushed from one side of the cavity to another.
Notably, this causes the dispersed phase to accumulate periodically along the walls parallel to the y-axis (as the vibrations are imposed along the x-axis) and upon detachment from the wall, form filament type structures. As these filaments migrate periodically from wall to wall, they curve and bend around the eddies present in cavity (due to the chaotic nature of the flow). This delicate formation mechanism is illustrated in Fig. 3 where two filaments can be seen appearing and disappearing in the space of one vibrational period.
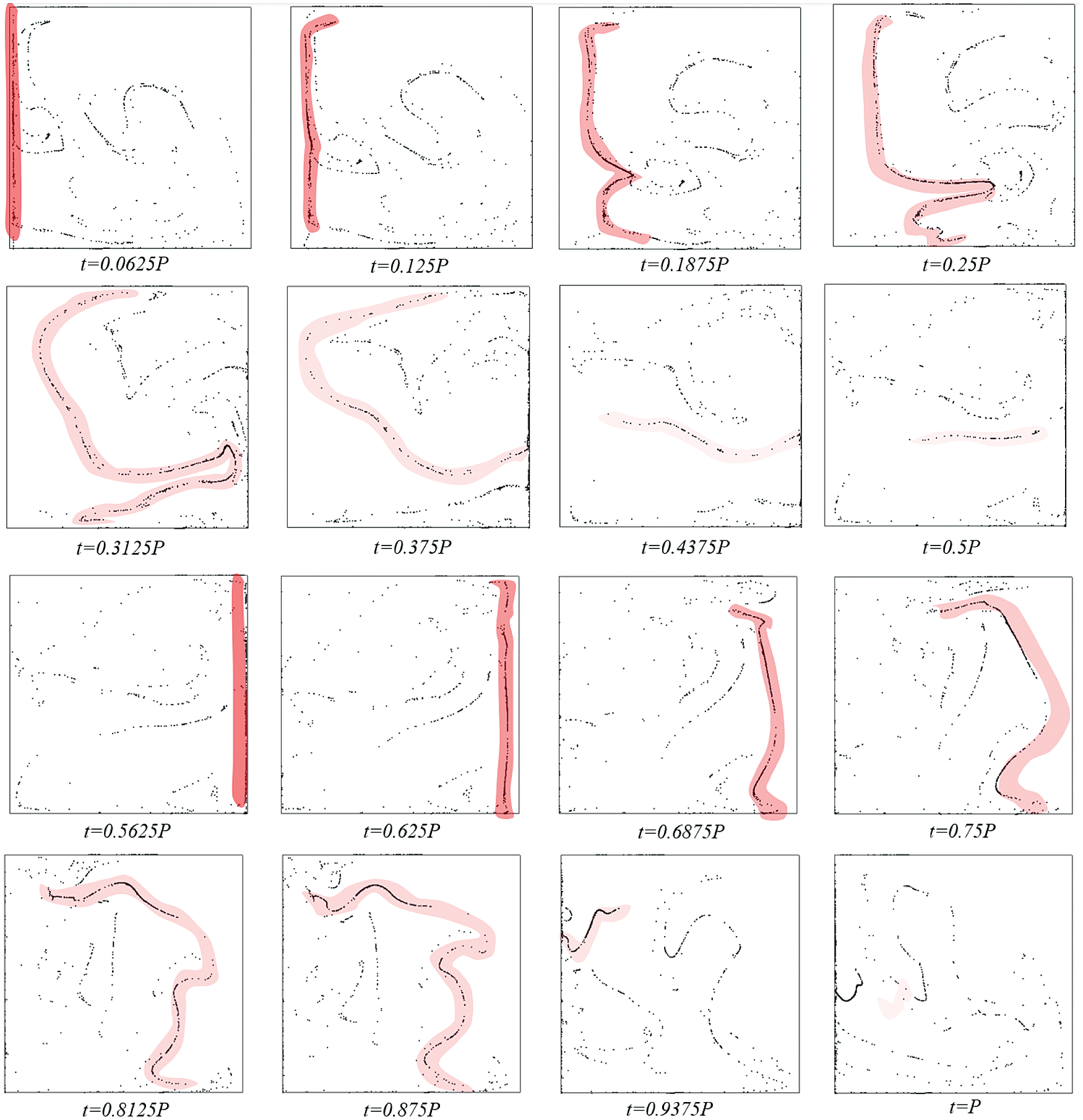
Figure 3: Sixteen equally spaced snapshots over one vibrational period P where P = 2π/ω, illustrating the formation mechanism on the filaments for Raω = 1.00 × 108, γ = 1.79 × 108, ξ = 0.3 and St = 9.39 × 10−4 (Ω = 104)
4.2 Influence of Vibrational Amplitude on Filament Survival
The formation and survival of the small structures described in Section 4.1 (simply referred to as ‘filaments’), occurs approximately twice per period depending on the amplitude of the vibrations. Indeed, as b is increased, the faster the particles accumulate on the opposite wall, hence reducing the filament survival time. This phenomenon is illustrated in Fig. 4, where the dashed lines delimit one vibrational period. In particular, these results represent three archetypal cases where an increase in b results in a simultaneous increase in Raωand γ. As qualitatively and quantitatively substantiated by this figure, for very high values of Raω and γ, the filaments survive approximately a quarter of the total period duration, due to the fact they are quickly absorbed by the opposing wall.
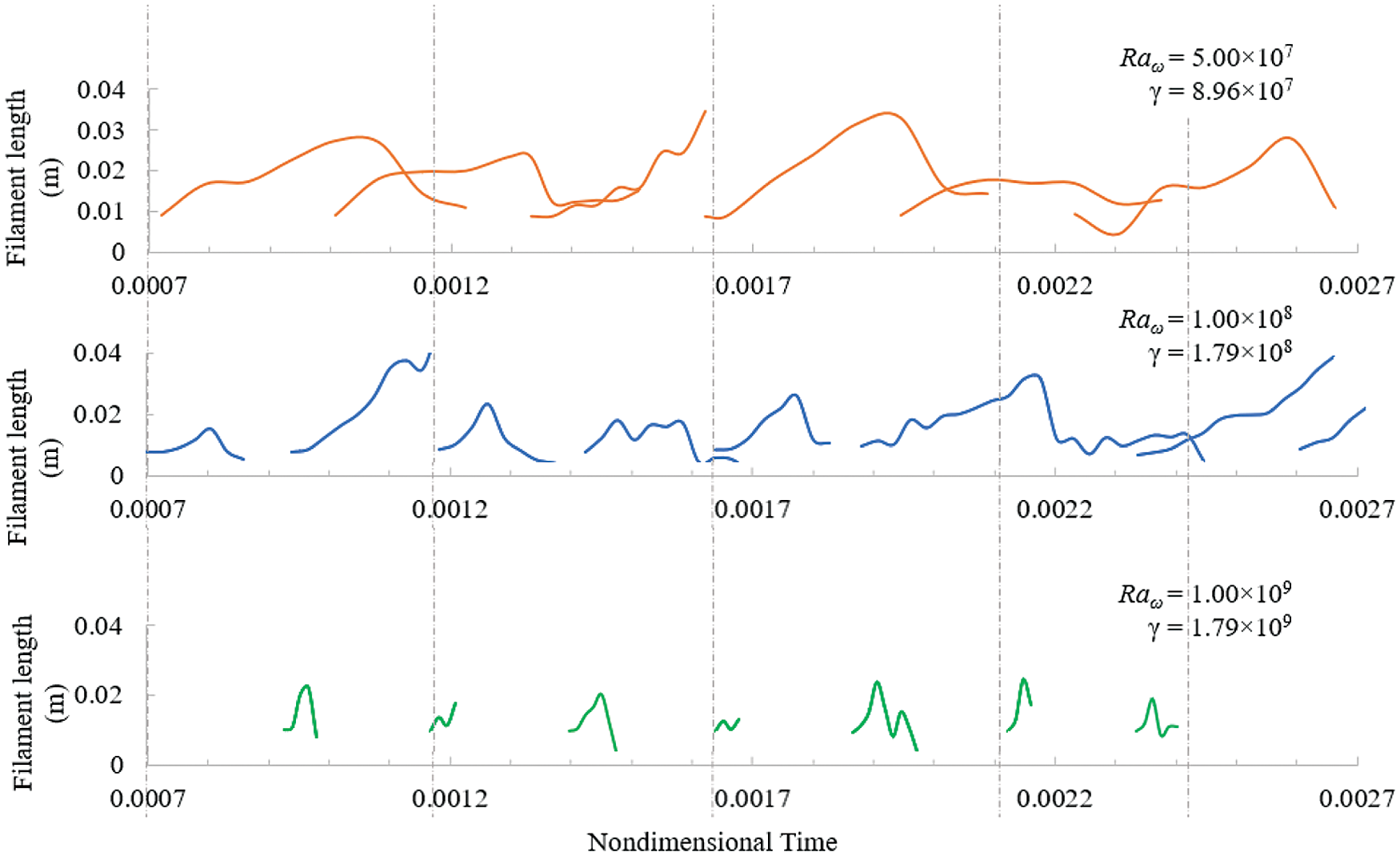
Figure 4: Filament length and survival time depending on Raω and γ, for ξ = 0.3 and St = 9.39 × 10−4 (Ω = 104)
This is also evident in Fig. 5. When comparing Columns 1 and 2 of this figure, the particles are pushed further way from the formation wall (indicated by the red arrow), following an increase in γ. However, for the same value of γ, and an increase in Raω,the filaments become less defined and appear more dispersed in the cavity.
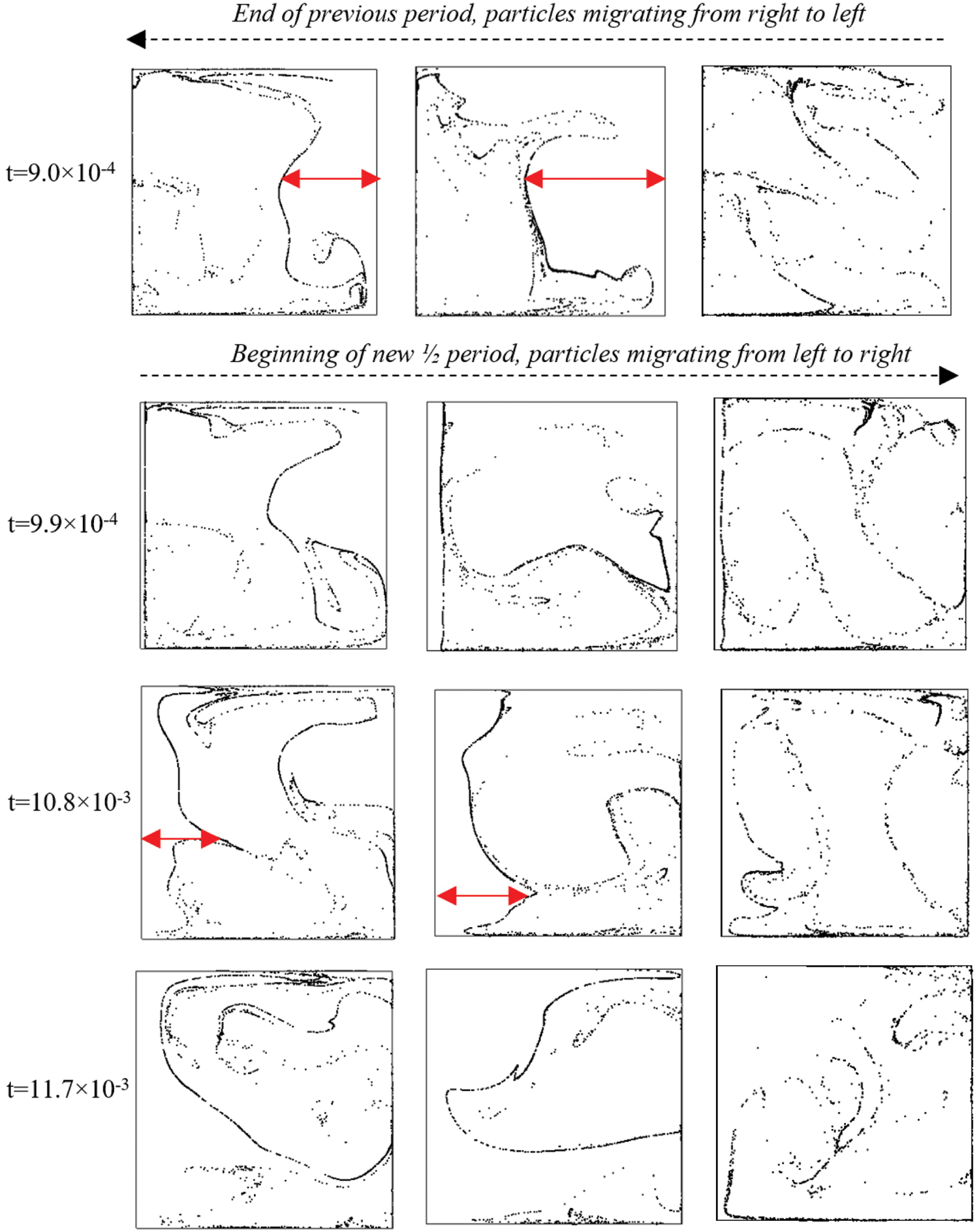
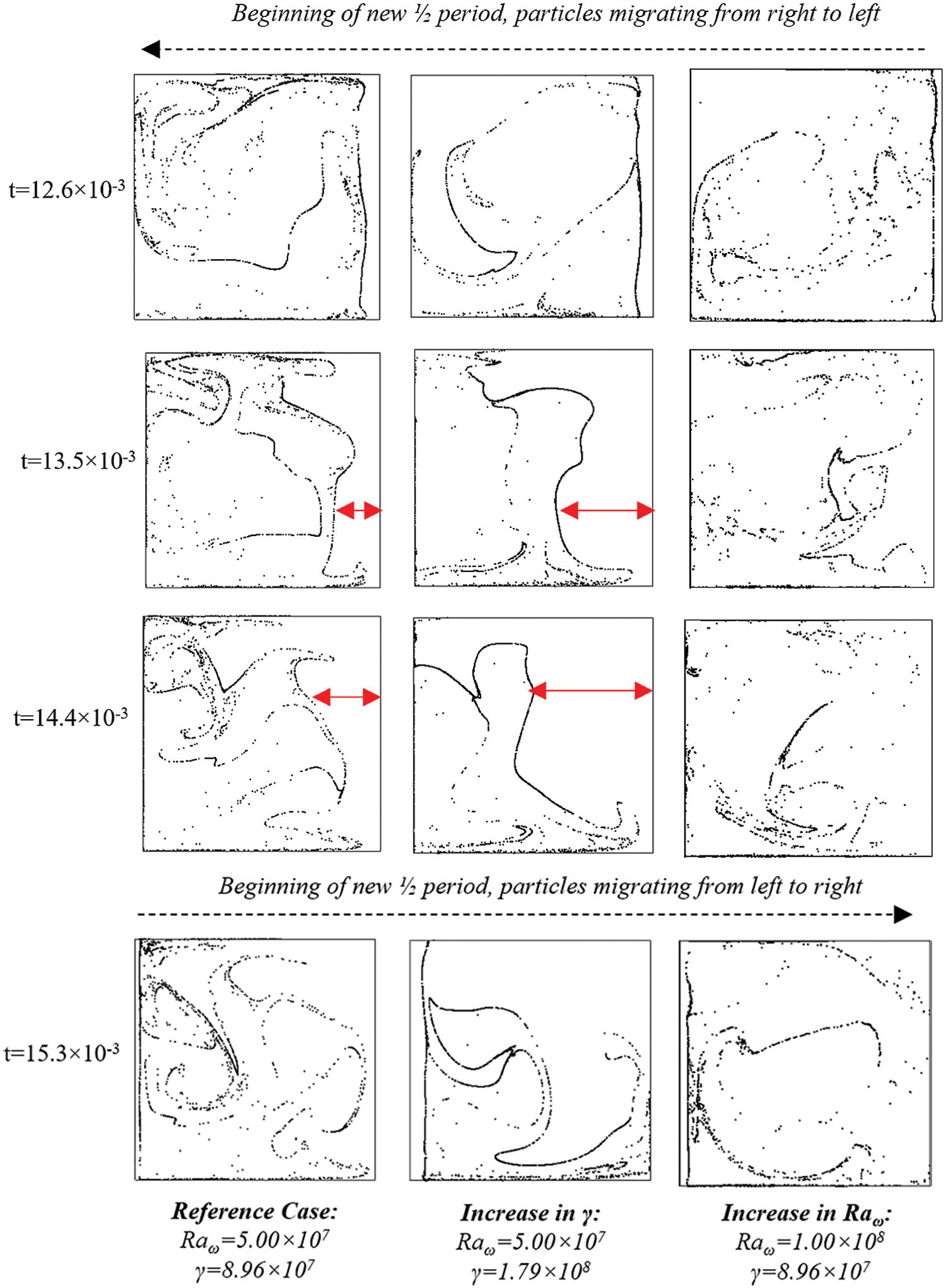
Figure 5: Isolated effects of on Raω and γ on filament behavior for ξ = 0.3 and St = 9.39 × 10−4 (Ω = 104)
4.3 Influence of the Particle Properties: ξ and St
The inertial properties of the particles can also influence greatly the formation (if any) of the structures. This is illustrated in Fig. 6, where the particle accumulations resulting from two different densities are superimposed over each-other at the same instantaneous points in time.
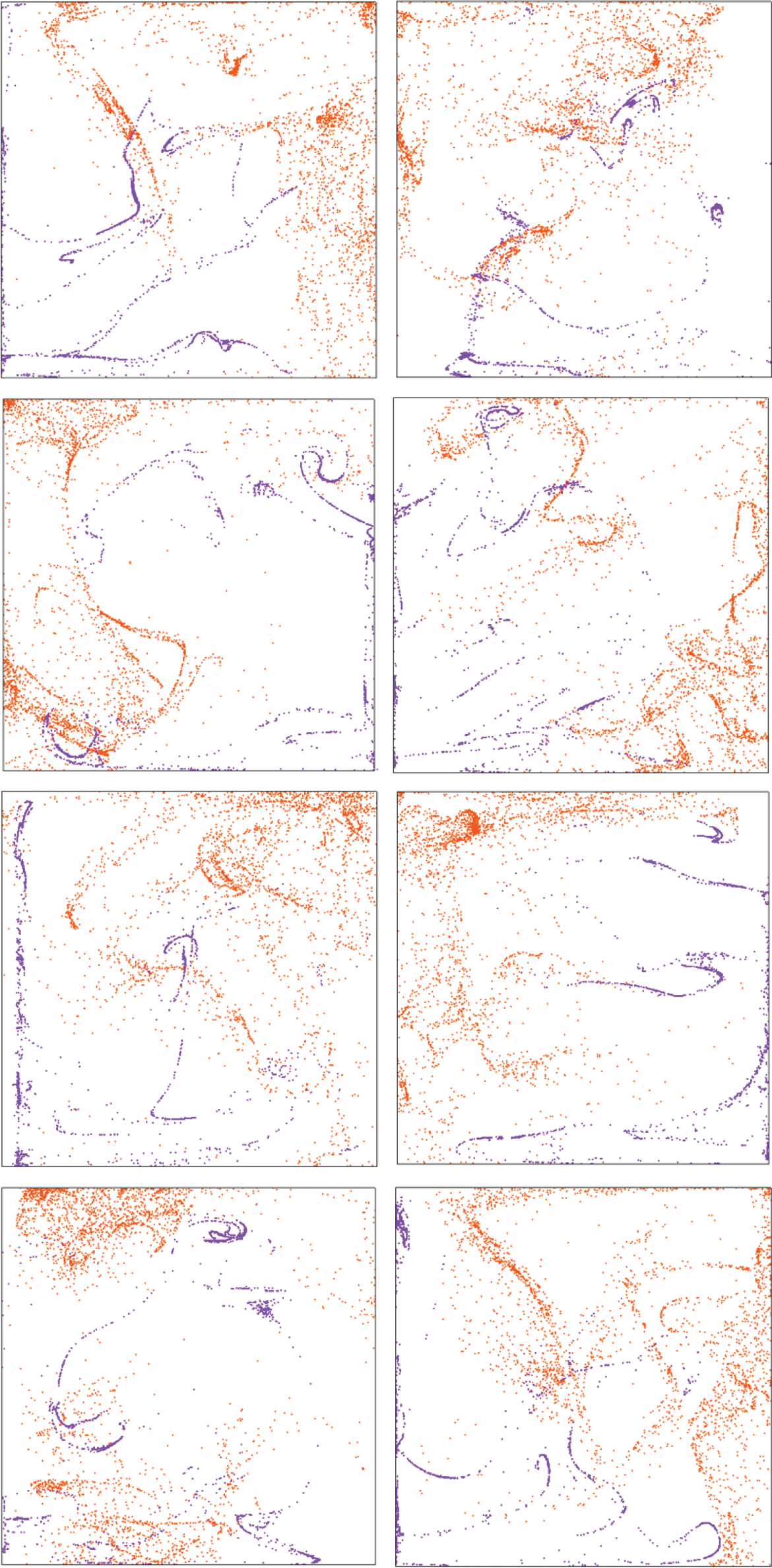
Figure 6: Eight snapshots equally spaced over two periods (2P) from left to right, where Raω = 1.00 × 108, γ = 1.79 × 108 and St = 9.39 × 10−4 (Ω = 104). The light particles (ξ = 0.3) are represented in purple and the heavy particles (ξ = 2), in orange
In particular, the light particles (ξ = 0.3) are represented in purple and the heavy particles (ξ = 2), in orange. Remarkably, it can be seen that the spaces occupied by the clouds formed for ξ = 0.3 and ξ = 2, are for the most part complimentary to each other; moreover, the light particles are prone to form stronger filaments than the heavy particles.
Another important influential factor, already identified in the earlier study by Lappa [13] (where however only laminar conditions were considered) is represented by the size of the particles, (the particle Stokes number St, from a non-dimensional standpoint). Along these lines, Figs. 7–10 show that a decrease in St, i.e., a decrease in particle size, can result in the inability of the dispersed phase to form any recognizable structure (under the specific considered operating conditions: Raωand γ).

Figure 7: Snapshots of particle behavior over one period (from left to right) for St = 9.41 × 10−4, Raω = 1.00 × 108, γ = 1.79 × 108 and ξ = 0.3 at time t = 6.28 × 10−3, 6.41 × 10−3, 6.53 × 10−3, 6.65 × 10−3 and 6.78 × 10−3 (Ω = 104)
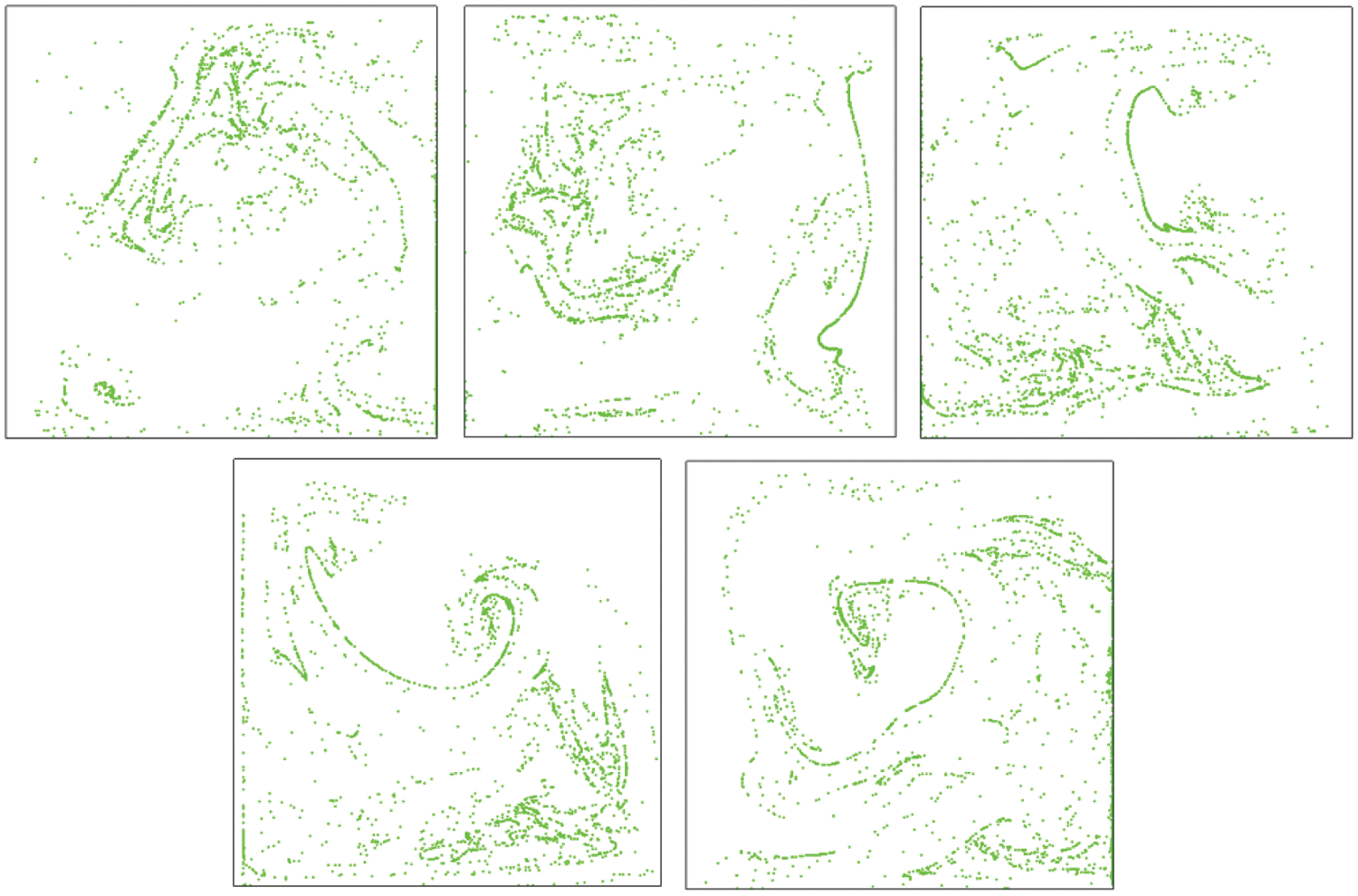
Figure 8: Snapshots of particle behavior over one period (from left to right) for St = 2.35 × 10−4, Raω = 1.00 × 108, γ = 1.79 × 108 and ξ = 0 at time t = 6.28 × 10−3, 6.41 × 10−3, 6.53 × 10−3, 6.65 × 10−3 and 6.78 × 10−3 (Ω = 104)

Figure 9: Snapshots of particle behavior over one period (from left to right) for St = 3.76 × 10−5, Raω = 1.00 × 108, γ = 1.79 × 108 and ξ = 0.3 at time t = 6.28 × 10−3, 6.41 × 10−3, 6.53 × 10−3, 6.65 × 10−3 and 6.78 × 10−3 (Ω = 104)
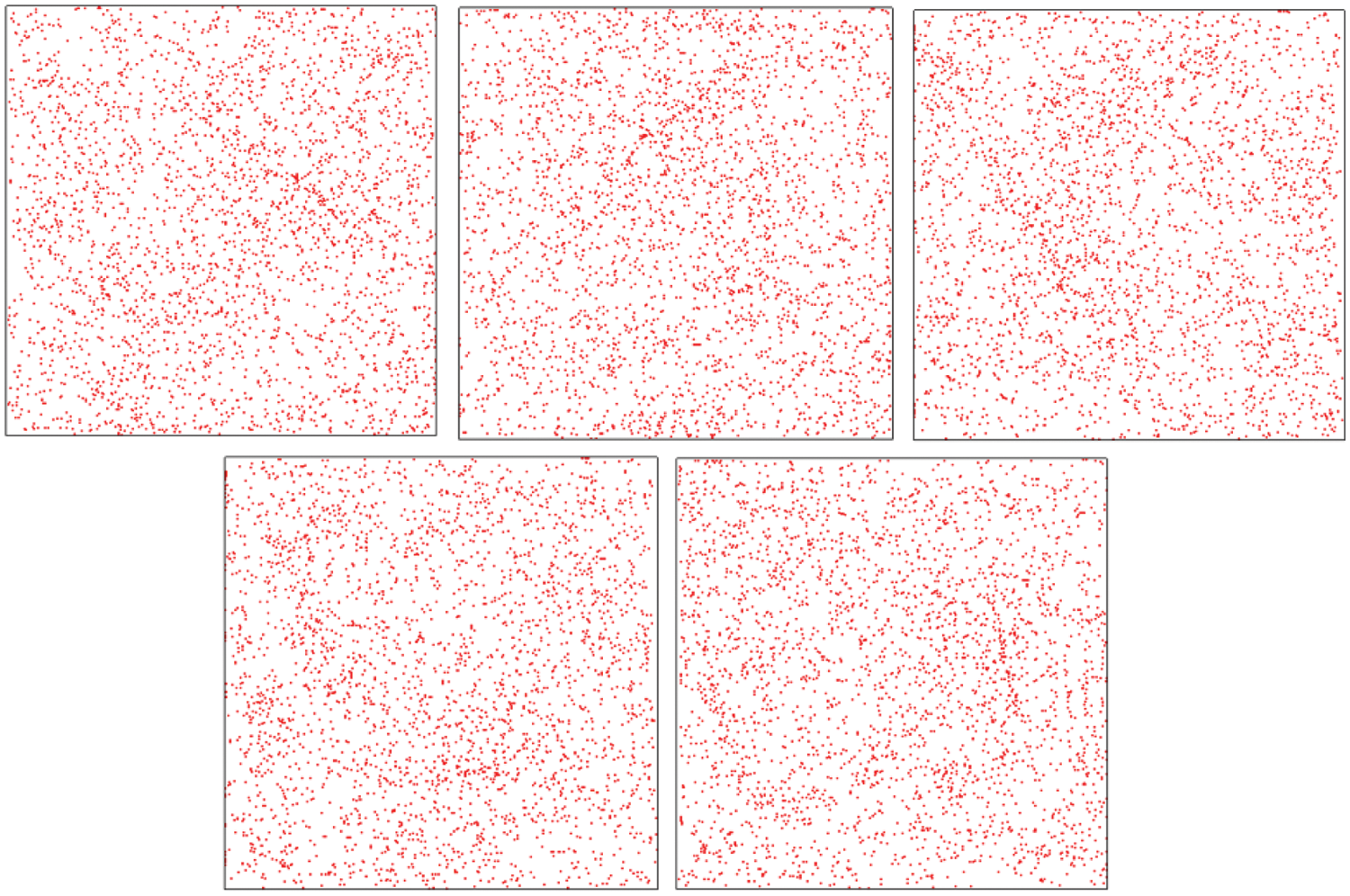
Figure 10: Snapshots of particle behavior over one period (from left to right) for St = 9.93 × 10−6, Raω = 1.00 × 108, γ = 1.79 × 108 and ξ = 0.3 at time t = 6.28 × 10−3, 6.41 × 10−3, 6.53 × 10−3, 6.65 × 10−3 and 6.78 × 10−3 (Ω = 104)
Towards the end of unifying the previously segregated fields represented by the study of particle behavior in terrestrial turbulent flows and that concerned with the high-regular aggregates formed by particles interacting with laminar vibrational flow in microgravity conditions, particle dynamics have been investigated in conjunction with chaotic (turbulent) thermovibrational flow.
It has been shown that circumstances still exist for which particles (initially uniformly distributed in the entire physical domain) de-mix from the fluid and form recognizable (well defined) structures. As opposed to the perfect morphology of clusters emerging in laminar flow, however, when thermovibrational flow is chaotic the topology of the structures is relatively irregular and time-dependent.
Nevertheless, precise trends and relationships can be established if specific problem ‘statistics’ are connected to the behavior of the temporally evolving structures. As an example, a lack of filament formation due to a decrease in St can be offset by an increase in the amplitude of vibration acceleration γ; in turn, however, this may decrease the filament survival time due to a faster absorption rate of the filaments by the opposing wall.
An exciting prospect for the future is to conduct an extensive analysis of these interdependences using the present relevant mathematical and numerical framework.
Data Availability Statement: Publicly available datasets were analyzed in this study. These data can be found in the pure repository of the University of Strathclyde. https://doi.org/10.15129/87679294-03e5-4e53-84ce-fcae7e63c597.
Funding Statement: This work has been supported by the UK Space Agency (STFC Grants ST/S006354/1, ST/V005588/1, ST/W002256/1 and ST/W007185/1) in the Framework of the PARTICLE VIBRATION (T-PAOLA) Project.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
1. Crowe, C. T., Tsuji, Y., Sommerfeld, M., Schwarzkopf, J. D. (2003). Introduction. In: Multiphase flows with droplets and particles (2nd editionpp. 1–3. Ukraine: CRC Press. DOI 10.1201/b11103. [Google Scholar] [CrossRef]
2. Lappa, M. (2016). On the nature, formation and diversity of particulate coherent structures in microgravity conditions and their relevance to materials science and problems of astrophysical interest. Geophysical and Astrophysical Fluid Dynamics, 110(4), 348–386. DOI 10.1080/03091929.2016.1194410. [Google Scholar] [CrossRef]
3. Squires, K. D., Eaton, J. K. (1991). Preferential concentration of particles by turbulence. Physics of Fluids A, 3, 1169–1178. DOI 10.1063/1.858045. [Google Scholar] [CrossRef]
4. Maxey, M. R., Patel, B. K., Chang, E. J., Wang, L. P. (1997). Simulations of dispersed turbulent multiphase flow. Fluid Dynamics Research, 20(1–6), 143–156. DOI 10.1016/S0169-5983(96)00042-1. [Google Scholar] [CrossRef]
5. Elghobashi, S., Truesdell, G. C. (1993). On the two-way interaction between homogeneous turbulence and dispersed solid particles I: Turbulence modification. Physics of Fluids A, 5, 1790–1801. DOI 10.1063/1.858854. [Google Scholar] [CrossRef]
6. Bhatnagar, A., Gupta, A., Mitra, D., Pandit, R. (2018). Heavy inertial particles in turbulent flows gain energy slowly but lose it rapidly. Physical Review E, 97, 033102. DOI 10.1103/PhysRevE.97.033102. [Google Scholar] [CrossRef]
7. Ireland, P. J., Bragg, A. D., Collins, L. R. (2016). The effect of Reynolds number on inertial particle dynamics in isotropic turbulence. Part 2. Simulations with gravitational effects. Journal of Fluid Mechanics, 796, 659–711. DOI 10.1017/jfm.2016.227. [Google Scholar] [CrossRef]
8. Petersen, A. J., Baker, L., Coletti, F. (2019). Experimental study of inertial particles clustering and settling in homogeneous turbulence. Journal of Fluid Mechanics, 864, 925–970. DOI 10.1017/jfm.2019.31. [Google Scholar] [CrossRef]
9. Lord Rayleigh, O. M. F. R. S. (1916). LIX. On convection currents in a horizontal layer of fluid, when the higher temperature is on the underside. The London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science, 32(192), 529–546. DOI 10.1080/14786441608635602. [Google Scholar] [CrossRef]
10. Hadley, G. (1735). Concerning the cause of the general trade winds. Philosophical Transactions of the Royal Society of London, 29, 58–62. DOI 10.1098/rstl.1735.0014. [Google Scholar] [CrossRef]
11. Xu, A., Tao, S., Shi, L., Xi, H. D. (2020). Transport and deposition of dilute microparticles in turbulent thermal convection. Physics of Fluids, 32(8), 083301. DOI 10.1063/5.0018804. [Google Scholar] [CrossRef]
12. Gereltbyamba, B., Lee, C. (2018). Behavior of settling inertial particles in a differentially heated cubic cavity at moderate Rayleigh number. Journal of Mechanical Science & Technology, 32, 3169–3182. DOI 10.1007/s12206-018-0620-z. [Google Scholar] [CrossRef]
13. Lappa, M. (2014). The patterning behavior and accumulation of spherical particles in a vibrated non-isothermal liquid. Physics of Fluids, 26(9), 093301. DOI 10.1063/1.4893078. [Google Scholar] [CrossRef]
14. Lappa, M. (2017). On the multiplicity and symmetry of particle attractors in confined non-isothermal fluids subjected to inclined vibrations. International Journal of Multiphase Flow, 93, 71–83. DOI 10.1016/j.ijmultiphaseflow.2017.03.015. [Google Scholar] [CrossRef]
15. Lappa, M. (2019). On the formation and morphology of coherent particulate structures in non-isothermal enclosures subjected to rotating g-jitters. Physics of Fluids, 31(7), 073303. DOI 10.1063/1.5098438. [Google Scholar] [CrossRef]
16. Lappa, M., Burel, T. (2020). Symmetry breaking phenomena in thermovibrationally driven particle accumulation structures. Physics of Fluids, 32(5), 053314. DOI 10.1063/5.0007472. [Google Scholar] [CrossRef]
17. Elghobashi, S., Truesdell, G. C., (1992). Direct simulation of particle dispersion in a decaying isotropic turbulence. Journal of Fluid Mechanics, 242, 655–700. DOI 10.1017/S0022112092002532. [Google Scholar] [CrossRef]
18. Fallon, T., Rogers, C. B. (2002). Turbulence-induced preferential concentration of solid particles in microgravity conditions. Experiments in Fluids, 33(2), 233–241. DOI 10.1007/s00348-001-0394-3. [Google Scholar] [CrossRef]
19. Love, S. G., Pettit, D. R., Messenger, S. R. (2014). Particle aggregation in microgravity: Informal experiments on the international space station. Meteoritics & Planetary Science, 49(5), 732–739. DOI 10.1111/maps.12286. [Google Scholar] [CrossRef]
20. Crewdson, G., Lappa, M. (2021). The zoo of modes of convection in liquids vibrated along the direction of the temperature gradient. Fluids, 6(1), 30. DOI 10.3390/fluids6010030. [Google Scholar] [CrossRef]
21. Crewdson, G., Lappa, M. (2021). Thermally-driven flows and turbulence in vibrated liquids. International Journal of Thermofluids, 11, 100102, DOI 10.1016/j.ijft.2021.100102. [Google Scholar] [CrossRef]
22. Capobianchi, P., Lappa, M. (2020). On the influence of gravity on particle accumulation structures in high aspect-ratio liquid bridges. Journal of Fluid Mechanics, 908, A29. DOI 10.1017/jfm.2020.882. [Google Scholar] [CrossRef]
23. Capobianchi, P., Lappa, M. (2020). Particle accumulation structures in noncylindrical liquid bridges under microgravity conditions. Physical Review Fluids, 5(8), 084304. DOI 10.1103/PhysRevFluids.5.084304. [Google Scholar] [CrossRef]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |