

 | Fluid Dynamics & Materials Processing |  |
DOI: 10.32604/fdmp.2022.018923
ARTICLE
A Novel Method for the Application of the ECMS (Equivalent Consumption Minimization Strategy) to Reduce Hydrogen Consumption in Fuel Cell Hybrid Electric Vehicles
School of Energy and Power Engineering, Shandong University, Jinan, 250061, China
*Corresponding Authors: Shuzhan Bai. Email: baishuzhan@sdu.edu.cn; Guoxiang Li. Email: liguox@sdu.edu.cn
Received: 24 August 2021; Accepted: 13 December 2021
Abstract: Fuel cell hybrid electric vehicles are currently being considered as ideal means to solve the energy crisis and global warming in today’s society. In this context, this paper proposes a method to solve the problem related to the dependence of the so-called optimal equivalent factor (determined in the framework of the equivalent consumption minimum strategy-ECMS) on the working conditions. The simulation results show that under typical conditions (some representative cities being considered), the proposed strategy can maintain the power balance; for different initial battery’s states of charge (SOC), after the SOC stabilizes, the fuel consumption is 5.25 L/100 km.
Keywords: Energy management; fuel cell hybrid electric vehicle; dynamic programming; adaptive equivalent consumption minimum strategy
Nomenclature
| Pdem: | vehicle demand power |
| m: | vehicle mass |
| v: | vehicle speed |
| g: | gravitational acceleration |
| f: | rolling resistance coefficient |
| | road slope |
| CD: | air drag coefficient |
| A: | vehicle front area |
| | ambient air density |
| TEM: | torque of electric motor |
| PEM: | power of electric motor |
| Tbrk: | fraction brake torque |
| | motor efficiency |
| | transmission efficiency |
| Pfc: | power of fuel cells |
| Pb: | battery power |
| Pa: | auxiliary power |
| E(H2,l): | the lower heating value of hydrogen |
| | hydrogen consumption |
| | fuel cell efficiency |
| Ibat: | battery current |
| Uocv: | open circuit voltage |
| R: | resistance |
| | battery discharge efficiency |
| | battery charge efficiency |
| SOC0: | initial value of battery |
| C: | battery capacity |
| | Instantaneous equivalent fuel consumption |
| Pbat: | battery power |
| HL: | the lower heating value of fuel |
| | average optimal equivalence factor |
| Abbreviation | |
| FCHEV: | Fuel cell hybrid electric vehicle |
| DP: | Dynamic programming |
| ECMS: | Equivalent consumption minimization strategy |
| AECMS: | Adaptive equivalent consumption minimization strategy |
As one of the most ideal means to solve the energy crisis and global warming in today’s society, electric vehicles have the characteristics of zero fossil fuel consumption and zero exhaust emissions [1]. On April 29, 2021, the “Global Electric Vehicle Outlook Report” released by the International Energy Agency (IEA) stated that the sales of electric vehicles began to explode around 2015, with cumulative sales exceeding 10 million as of 2020. By 2030, it is estimated that the number of electric vehicles on the global roads will reach 145 million. If governments speed up the achievement of climate goals, this number may soar to 230 million vehicles. Energy conservation and emission reduction is an important direction for future development. New energy vehicles are an important object of energy conservation and emission reduction. Countries around the world are rushing to study new energy vehicles. Fuel cells vehicles, as the most promising development direction of new energy vehicles, have been widely focused on.
As one of the most promising electric vehicles, fuel cell vehicles use fuel cells to generate electricity from hydrogen and air, which is used to drive the vehicle. Meanwhile, surplus power is stored in the energy storage system (ESS), such as batteries or super capacitors [2]. Fuel cell vehicles not only do not have any polluting gas emissions, but also have the potential to achieve extremely high thermal efficiency. Proton exchange membrane fuel cells have the advantages of high energy density, high thermal efficiency, reduced greenhouse gas emissions, relatively low working temperature and working pressure, and are used as one of the main alternatives for fuel cell hybrid vehicles [3]. However, engaging only proton exchange membrane fuel cells will cause their life to be shortened sharply, and the rapidly changing current will cause the fuel starvation and membrane damage of the proton exchange membrane fuel cell [4]. Therefore, in proton exchange membrane fuel cell vehicles, supercapacitors or power batteries are engaged as auxiliary equipment. The power source will improve the life and power of the proton exchange membrane fuel cell [5].
Thermal characteristics of batteries and fuel cells are one of the focuses of research. The high or low temperature will cause the change of the internal structure of the battery, that is, the internal resistance of the Li-ion battery will have different effects on electrode materials, thereby affecting the capacity, cycle life, safety, and reliability of the battery [6]. Energy management strategy is also the core of hybrid power system. Cheng et al. [7] analyzed the impact of different topologies and energy management strategies on the heating system from the perspective of heating. Chen et al. [8] used the sliding mode control method to effectively realize the prediction and fine-tuning of the braking system, which can achieve faster response. After in-depth research by scholars from various countries, the current energy management strategy can be roughly divided into the following categories: (1) Rule-based energy management strategy. This method optimizes the working time and state of the control components by setting the working threshold of the power source of the hybrid power system. However, this method does not consider the dynamic characteristics of the system and cannot achieve energy optimization to a large extent [9]; (2) Based on an optimized energy management strategy. This method uses planning algorithms (DP, MPC, etc.) to optimize the driving cycle globally, and can obtain a global optimal solution. It is very suitable for a mixture of strong dynamics, high degree of nonlinearity, and multiple control objectives power system, but this method requires prior knowledge of driving conditions. In engineering practice, control strategies are generally extracted from optimization results, and rule-based methods are used in engineering practice or used as criteria for other methods [10]; (3) Instantaneous optimization strategy. This method equates the electric energy released by the battery at the current stage to the fuel quality that the fuel cell will consume in the future. The optimal energy distribution ratio is determined by calculating the instantaneous equivalent fuel minimum (ECMS). This method has strong dynamic adaptability, no prior knowledge of driving conditions is required, and theoretical results similar to DP can be obtained, so extensive research has been obtained [11].
In the ECMS method, the acquisition of equivalent factors is the focus of research [12]. At present, the optimal equivalent factor is extracted by different methods based on the entire driving condition, and then the driving condition is identified in actual application to select the appropriate equivalent factor [13]. The main disadvantage of this method is that the equivalent factor has a high degree of correlation with the overall operating conditions, and it is often impossible to obtain the optimal value for the driving conditions with a higher degree of mixing, and the method heavily relies on the results of driving conditions recognition [14]. Xie et al. [15] created a table of multiple equivalent factors optimized by DP, and applied the equivalent factors of ECMS in real time through the look-up table method to achieve the goal of minimizing fuel consumption, which made the accuracy of ECMS higher. However, the corresponding calculation amount also became huge. Comparing the AECMS with the regular energy management strategy, Couch et al. [16] developed a control-oriented model to predict the behavior of the vehicle electrical system. The results show that the ECMS leads to a 100%–300% increase in the overall utilization of the battery, compared to the baseline controller, which may impact the durability. Zeng et al. [17] proposed optimization-based AECMS can quickly increase the SOC state without increasing the hydrogen consumption, and the error is only 0.3% after experimental verification. However, the hydrogen consumption change in the state of charge balance has not been studied. In order to reduce the correlation between the equivalent factor and the entire driving condition and improve the adaptability of the working condition, the article first starts from the point of view of the working condition, and obtains the relationship between the driving condition point and the optimal equivalent factor through dynamic programming backward, And finally find a more general relationship from the perspective of data statistics; Then, in order to maintain the power balance, an adaptive equivalent fuel consumption minimum strategy (A-ECMS) is designed according to the law between the obtained optimal equivalent factor and the operating point.
In order to solve the proposed optimization problem, it is necessary to model the vehicle longitudinally. The fuel cell hybrid vehicle used in this paper is shown in Fig. 1. It includes a proton exchange membrane fuel cell, a lithium-ion power battery, a DC/DC converter, a motor and its controller. The vehicle is driven by a motor. The main power source of the motor is a proton exchange membrane fuel cell, and the secondary power source is a lithium-ion power battery. As an energy storage system, it collects the excess energy produced by the proton exchange membrane fuel cell and the braking energy recovered by the motor. At the same time, it can play the role of peak shaving and valley filling during the operation of the vehicle.
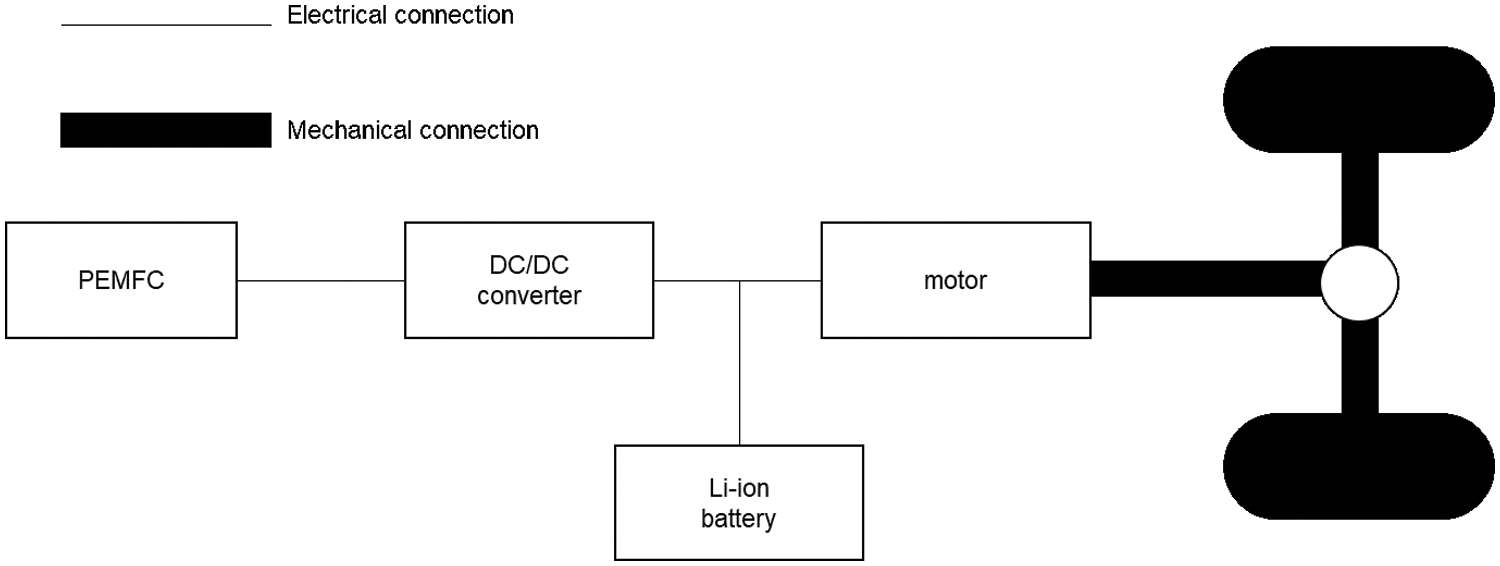
Figure 1: The FCHEVs configuration
2.1 Model of Vehicle Longitudinal Dynamics
Energy management strategies based on dynamic programming algorithms require a known mathematical model of the hybrid power system and its components. Since the hybrid vehicle is only a hybrid of power sources, the driving is completely performed by the electric motor, which is different from the traditional engine hybrid power system. The longitudinal dynamics equation of the vehicle in the normal driving state is [1]:
The required power of the motor is provided by the proton exchange membrane fuel cell and the lithium-ion power battery. When the required torque exceeds the limit that the motor can provide or exceeds the maximum current that the battery can provide, the motor will provide braking torque. The formula for motor torque and power demand is as follows:
The power provided by the electric motor outputs the power to the wheels of the vehicle through the transmission system. The relationship between the required power of the vehicle and the power of the electric motor is as follows:
The fuel cell is a power generation device that directly converts the chemical energy present in hydrogen and oxidant into electrical energy. Due to the characteristics of the fuel cell, its internal structure is extremely complex, so it is difficult to establish a complete FCS model. Therefore, the FCS model used in this study is a simplified model. The goal of EMS is to reduce hydrogen consumption, improve system efficiency, and keep the battery’s state of charge (SOC) within a reasonable range. The hydrogen consumption of FCS is determined by the power of FCS and the corresponding efficiency [18]:
Since the battery dynamic model is more complicated, the estimation algorithm of the battery state of charge (SOC) also has a certain complexity. For time cost considerations, the internal resistance-open circuit model shown in Fig. 2 is used in this article.
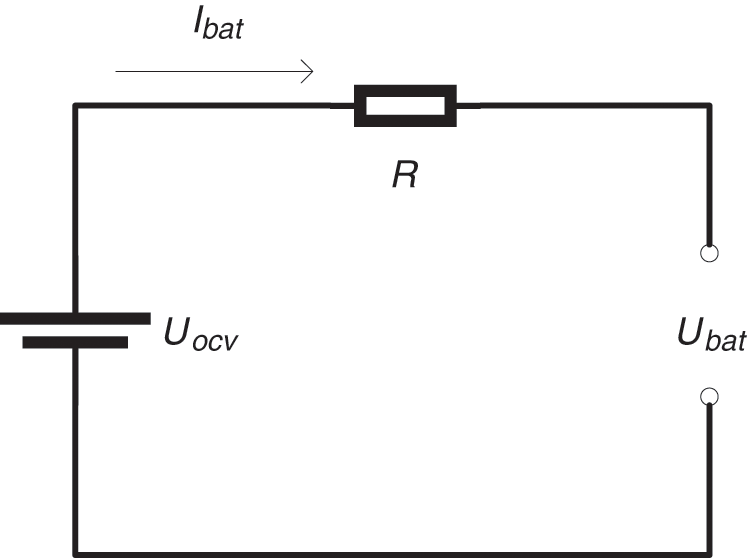
Figure 2: Internal resistance equivalent model of battery
From the circuit shown in the figure, it can be known from Kirchhoff’s voltage law [19]:
The battery charging and discharging efficiency is:
The relationship between battery power and motor demand power is:
The battery SOC is calculated using the ampere-hour method as:
Dynamic programming is an important method to solve the multi-stage decision-making process. Its core idea is to decompose the problem to be solved into several sub-problems, first solve the sub-problems, and then obtain the solution of the original problem from the sub-problems. For hybrid energy management strategy issues, dynamic programming requires that the system control requirements in the entire driving road be known in advance, and energy is allocated to meet the requirements of basic dynamics to achieve the optimal goal. The DP method can analyze the impact of operating conditions on the strategy in detail, and evaluate and screen the strategy. Therefore, it has become the most important reference method in the hybrid energy management strategy. The specific process of using DP for energy optimization can be divided into three stages: division stage, determination of decision-making and state transition equations, and determination of optimization equations [20–22].
1. Division stage. According to the time or space characteristics of the problem, the problem is divided into several stages in an orderly manner. State variables are the parameters of objective performance problems at each stage, and the choice of state variables needs to satisfy no aftereffect. For the energy management strategy problem, the battery state of charge SOC is one of the most important parameters that characterize the objective state of the hybrid system at a certain energy distribution ratio, so it can be used as the state variable of the problem.
2. Determination of decision-making and state transition equations. In the problem studied, the decision is the allocation ratio u of the total required power of the system at each stage between the power battery and the proton exchange membrane fuel cell. The state transition equation is the current stage k, the state x (and SOC) is under the action of the decision u, the stage k+1 system state, which can be expressed as:
3. Determination of optimization equations. According to the optimization requirements of the problem, the optimization equation can be directly written. Energy management strategy requires the system to consume the least fuel:
3.2 Equivalent Fuel Consumption Minimum Strategy
Regardless of external energy input (such as braking energy recovery), the energy consumption of the hybrid power system is ultimately provided by fuel. The minimum equivalent fuel consumption strategy, from the perspective of energy conservation, equates electrical energy to the hydrogen mass of the fuel cell, and provides theoretical support for the instantaneous optimization control of the hybrid power system. The calculation model of ECMS is [23,24]:
The purpose of the ECMS strategy is to obtain the most core parameter in the minimum equivalent fuel consumption value when the control variable u selects different values is the equivalent factor s. If the penalty factor added due to power maintenance is not considered, it is essentially a numerical embodiment of the conversion efficiency between energies. The reason why the equivalent factor is an uncertain value is that, in order to make the battery power consistent with the initial state in the future, the current consumption of electric energy is regarded as being compensated by the hydrogen consumption or recovered energy of the fuel cell engine in the future. Since the future working conditions are unknown, it is unknown under which working conditions this part of energy will be compensated, that is, the equivalent factor is an uncertain value. Therefore, the key of ECMS is to find the optimal equivalence factor, so that the current energy has the optimal conversion efficiency in the future compensation. Under this premise, the energy distribution at the current moment has the optimal conditions. Research shows that, for a given driving mode, the equivalent factor in Eq. (15) can be replaced by a constant value s0 (optimal equivalent factor), which is the optimal energy distribution. At present, the method of obtaining the optimal equivalent factor is generally exhaustive method. This method is simple and easy to implement, but it is impossible to clearly explain which factors and internal laws are affected by the optimal equivalent factor, and it is greatly affected by the overall driving cycle. In order to reveal the internal laws of the optimal equivalent factor in detail and improve the adaptability of the strategy, the optimal result obtained by the dynamic programming method is used to inversely obtain the optimal equivalent factor. By analyzing the simulation results, the change rule of the optimal equivalent factor with respect to the SOC maintenance value is obtained, and a new equivalent fuel consumption minimum strategy is designed on this basis.
3.3 Adaptive Minimum Equivalent Fuel Consumption Strategy Design
Use DP to obtain the best output power P of the power battery at time t, and the best SOC of the battery is
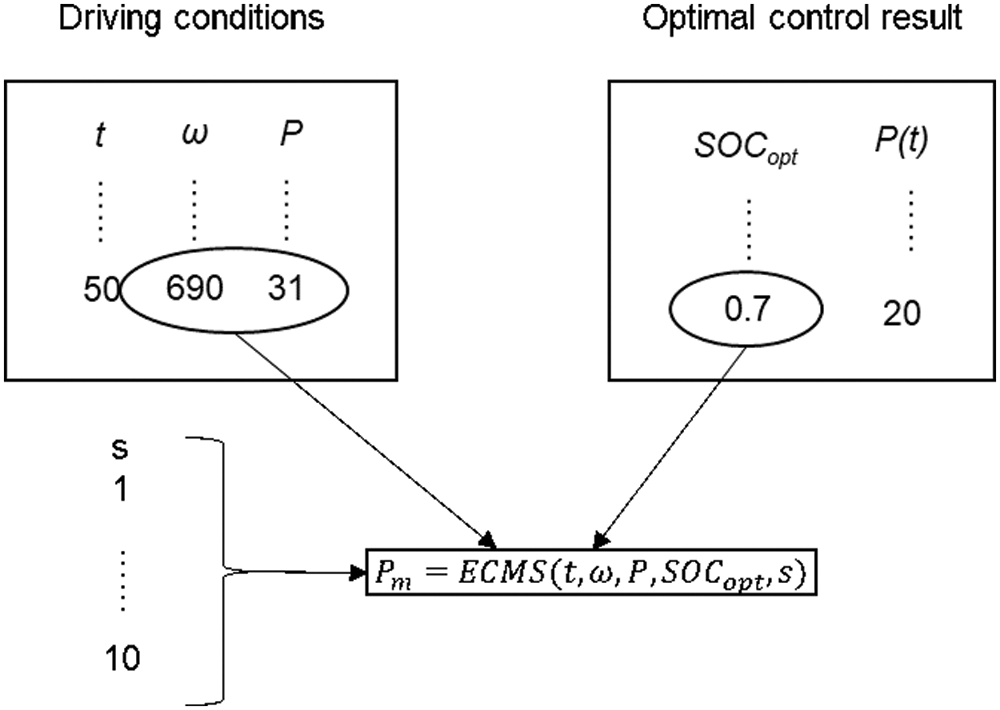
Figure 3: Optimal equivalent factor extraction method based on DP
The above methods are used to extract the optimal equivalent factors under several typical driving conditions. In order to ensure that the proposed A-ECMS has good adaptability to working conditions, the selected typical working conditions should cover most of the vehicle driving conditions and have good representativeness. Select the working conditions that cover the average vehicle speed from low to high and the relative idle time is long to short, and cover the urban and suburban working conditions, The sequence is: Japanese JN1015 cycle combined with urban and suburban working conditions, ECE_EUDC combined with steady-state high-speed driving conditions, NEDC steady-state working conditions with strict emissions, American UDDS working conditions with typical representative car commuting routes, and The U.S. Environmental Protection Agency’s EPA-designed urban road cycle FTP75, which has a high average vehicle speed and includes cold transition conditions, steady-state operating conditions, and hot transition conditions, and US06 that takes into account road changes. The optimal equivalent factor is extracted from the battery output power range of 0–35 kw, and the resulting equivalent factor distribution statistics are shown in Fig. 4.
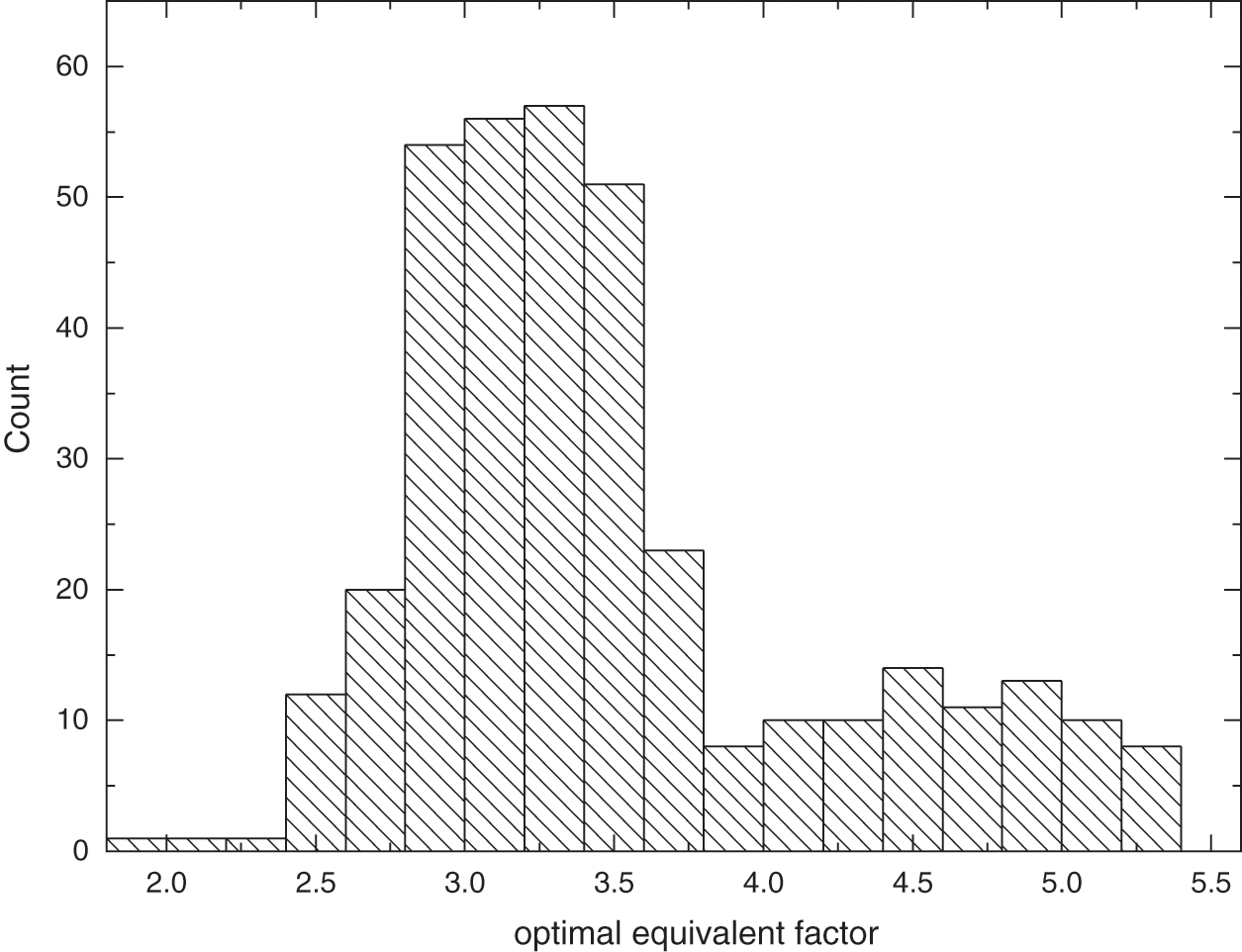
Figure 4: Relationship between optimal equivalent factor and demand power
It can be seen from Fig. 4 that the value of the optimal equivalent factor is distributed between 2–5.5, and as the power gradually increases, the optimal equivalent factor tends to gradually decrease. This is because the equivalent factor essentially reflects the conversion efficiency between energies and the degree of punishment adopted in order to maintain the power balance, and is affected by the inherent efficiency of the system, and the equivalent factor is maintained within a certain range. Generally speaking, the greater the power required by the system, the higher the possibility of higher system efficiency, the lower the equivalent fuel consumption, and the smaller the value of the equivalent factor. Among them, the relationship between the power maintenance level of the vehicle under the FTP-75 working condition (the initial SOC value is considered within the allowable error range) and the optimal equivalent factor is shown in Fig. 5.
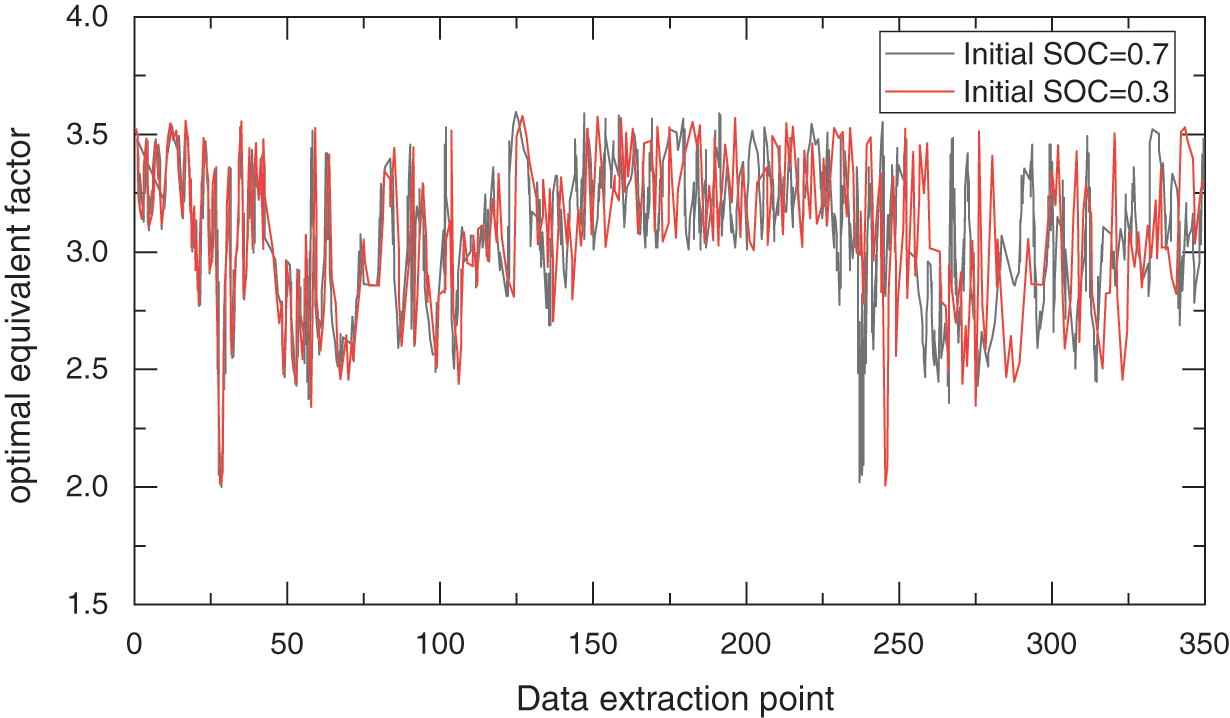
Figure 5: Relationship between optimal equivalent factor and charge sustaining
Because in the calculation process, the equivalent factor in some data points (such as the point where the speed is 0 and the demand torque is 0) is meaningless zero or non-number, so the abscissa no longer represents all the state points, but in the order from left to right, removing the status points remaining after the meaningless data points. In order to make the results clearer, only the optimal equivalent factor change trends when the initial SOC is 0.7 and 0.3 are selected in Fig. 5 for analysis and comparison. The results show that under different power maintenance levels, the trend of the optimal equivalent factor changes with the data points of driving conditions is the same, but the change range is different, which means that the power maintenance level has an important influence on the size of the equivalent factor. At the same time, because the optimal equivalent factor under the same power maintenance level changes with the change of the operating point, in order to focus on the impact of the power maintenance level on the optimal equivalent factor, it is necessary to average the optimal equivalent factors at all extraction points. The change law of the average optimal equivalent factor and the power maintenance level is extracted, and the relationship between the average optimal equivalent factor and the power maintenance level as shown in Fig. 6 is obtained.
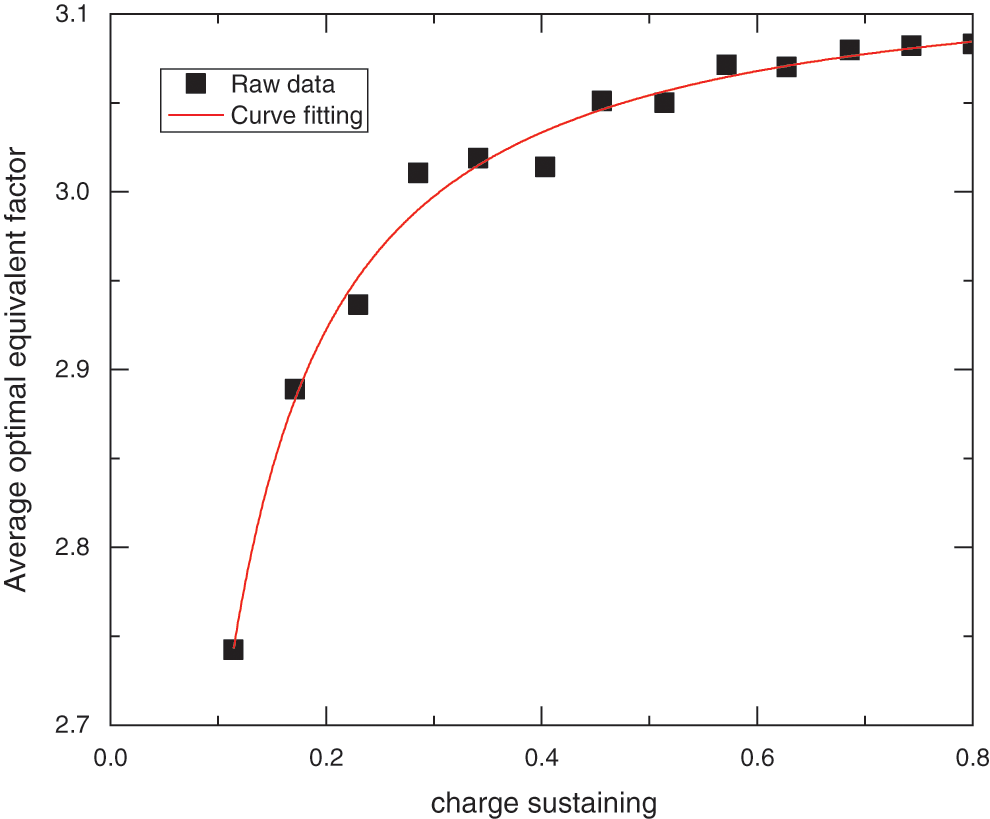
Figure 6: Relationship between average optimal equivalent factor and charge sustaining
The law of change obtained by fitting is:
The charging and discharging efficiency of the battery will have a large gap under different SOC maintenance levels. In order to further improve the system efficiency, it is necessary to explore the optimal SOC interval of the battery. Limited to the main content and length of the research in the article, the optimal power maintenance level interval is only determined by a relatively simple statistical screening method. In the case of keeping the initial SOC consistent with the end SOC, the DP algorithm is used to calculate from the minimum allowable SOC 0.3 at intervals of 0.001 to the maximum allowable SOC 0.9 to obtain each different SOC under each driving condition. Maintain different fuel consumption values per 100 kilometers at the same level. The lower 20%~30% continuous interval is selected as the optimal power maintenance interval for this working condition, and all the driving conditions used are combined, and the result is roughly the power maintenance level between 0.6 and 0.8, so that the used the driving condition reached is the lowest fuel consumption per hundred kilometers; Taking the average SOC = 0.7 as the power maintenance standard, the same initial conditions as the DP method can be guaranteed. At the same time, based on the foregoing analysis, the effective range of the equivalent factor is 2~6, so the following energy management strategy based on power balance is designed:
It can be seen from Eq. (15) that when the SOC is 0.6, the equivalent factor reaches the maximum value, which means that the equivalent fuel consumption is larger, and the proportion of fuel cell operation increases; when the SOC is 0.8, the equivalent factor reaches the minimum value, which means that at this time the power battery is the main power source, and the fuel cell consumes less fuel. At this time, the energy management strategy is inclined to the fuel cell working in a small working condition or not working.
The effectiveness of the method in this paper needs to be verified from two aspects: optimization effect (fuel economy, power maintenance) and adaptability to working conditions. Due to the large battery capacity used in the article, the battery capacity does not change significantly when a shorter driving cycle is used for simulation. Therefore, a superimposed typical driving cycle is used for long-distance simulation. The optimization process was performed in MATLAB R2020a environment using an AMD Ryzen 5600x processor.
4.1 Optimization Effect Verification
In order to verify the fuel economy of the method in this article, the superposition of 10 typical NEDC driving cycle is used to verify the power maintenance characteristics of the method used. Use DP and the method in the text to verify, and obtain the results shown in Fig. 7.
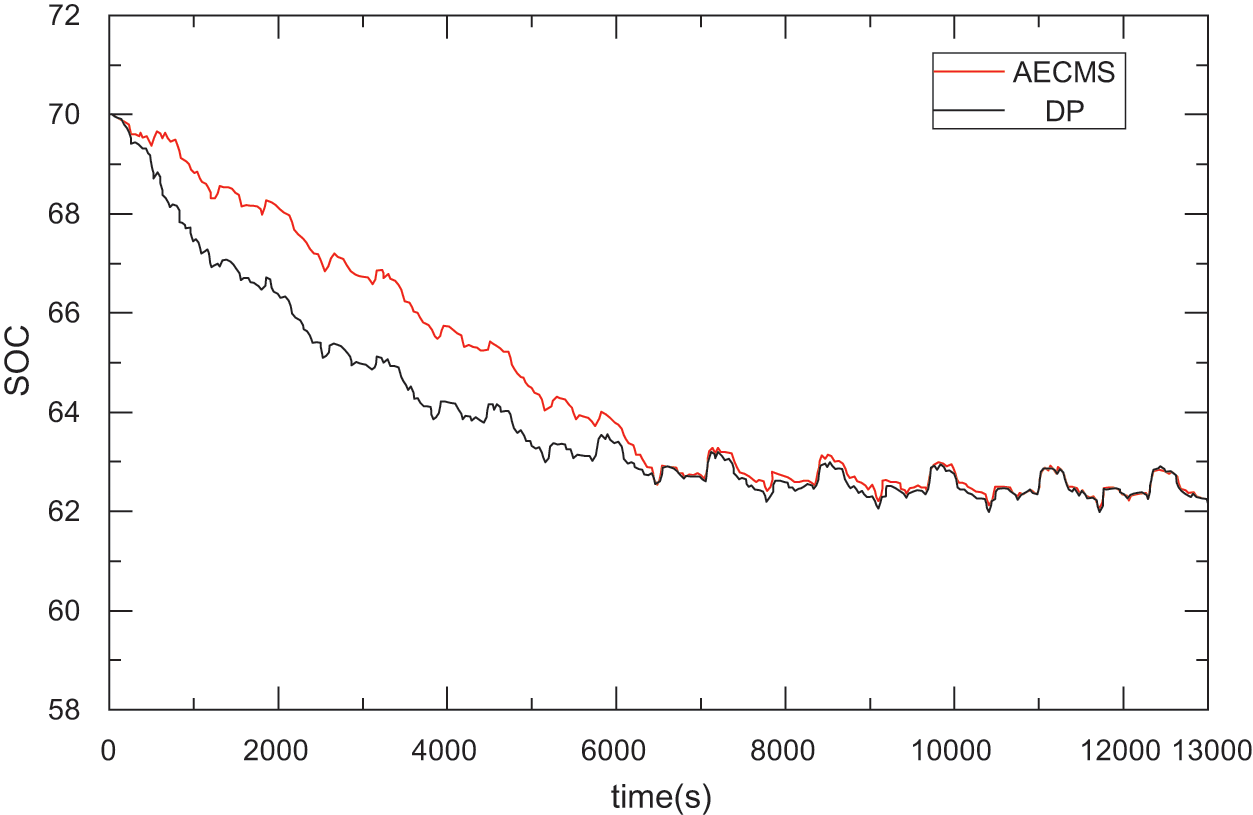
Figure 7: SOC results contrast between DP and the new method under the condition of superimposed cycle based on NEDC
It can be seen from Fig. 7 that the entire calculation process using the method in the text is clearly divided into two parts. After about 5 driving cycles, the battery SOC value tends to stabilize. This means that in the first 5 driving cycles, the control strategy is always looking for the optimal initial SOC value for the next stage. Once the value is determined, the system will enter a stable development stage. Due to the huge space and time cost of the DP algorithm in the simulation of stacked processing conditions, it cannot even run. Therefore, in order to compare the method in the paper with the DP algorithm, the whole process is divided into two parts: the transition phase and the stable phase. The simulation result is shown in Fig. 7. This method is not a global optimization in the whole process, but from the simulation results, under a fixed driving cycle, if the initial SOC value used by DP is the SOC value after the method in the text is stabilized, the result of the DP algorithm can be compared with the method in the text. The results of SOC coincide with each other (stabilization phase), thus treating the vehicle as an infinite process, ignoring the influence of the transition process on the entire driving cycle. It can be seen from the SOC change that for a fixed driving cycle, if a suitable initial SOC value can be selected, the error between the method in the transition phase and the DP will be reduced. The final fuel consumption comparison results of the two methods are shown in Table 1.
It can be seen from Table 1 that the comparison between the method in the article and DP only has a small gap in the transition phase, and the control result in the stable phase is almost the same as that of DP. The power maintenance characteristic is one of the important indicators of the A-ECMS strategy. Its purpose is to prevent overcharge and over discharge of the battery and increase the service life of the battery. The above-mentioned stacking conditions are also used to simulate with different initial SOC values. The results are as follows shown in Fig. 8.

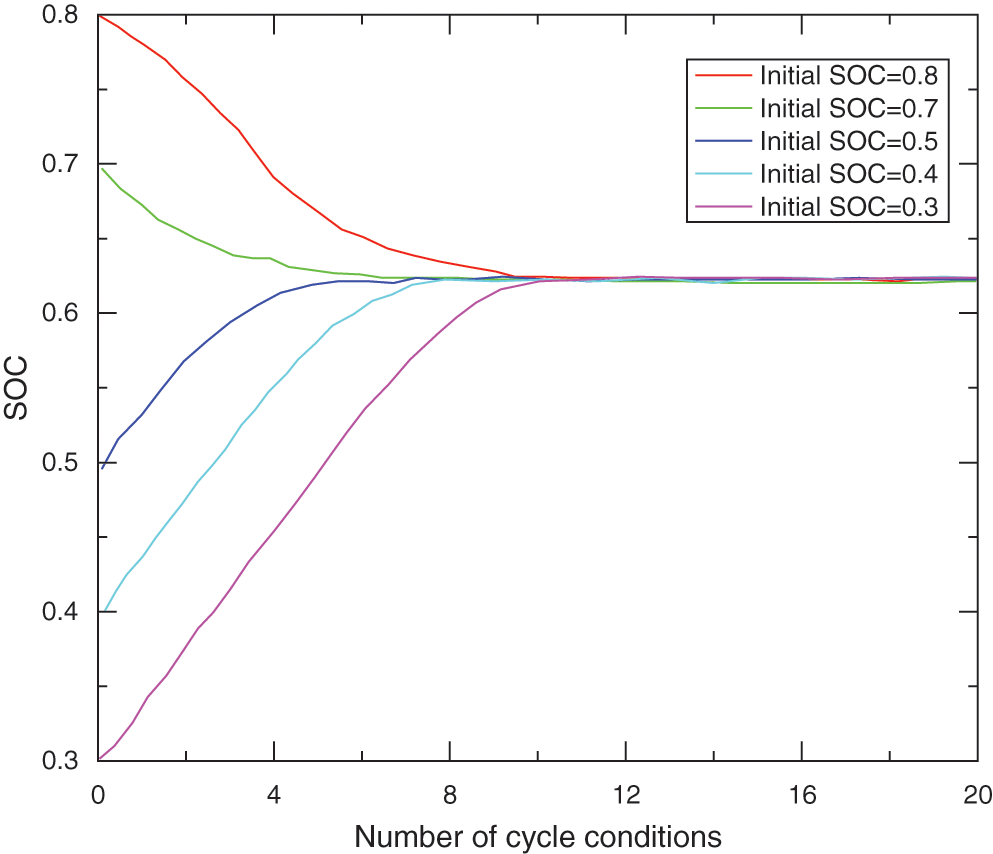
Figure 8: Charge-sustaining results in different initial SOC
It can be seen from Table 1 that the comparison between the method in the article and DP only has a small gap in the transition phase, and the control result in the stable phase is almost the same as that of DP. The power maintenance characteristic is one of the important indicators of the A-ECMS strategy. Its purpose is to prevent overcharge and over discharge of the battery and increase the service life of the battery. The above-mentioned stacking conditions are also used to simulate with different initial SOC values. The results are as follows shown in Fig. 8.
It can be seen from Fig. 8 that when the initial SOC is different, after about 10 cycles, the battery SOC can reach a stable value of 0.648 as the driving cycle increases, and then fluctuate around this value, which is consistent with the aforementioned phenomenon. It shows that the method in the article can better maintain the power balance. At the same time, it shows that the optimal SOC maintenance level for NEDC driving cycle should be around this value when the vehicle structure parameters are determined.
It can be seen from the figure and table that the ECMS method based on DP can obtain fuel consumption almost the same as the DP method. This strategy minimizes the total energy consumption of the vehicle per unit time by optimizing the power distribution of the fuel cell and the power battery under each instantaneous working condition, and at the same time achieves the maintenance of the battery state of charge. As a better method for global optimization, the DP method has strong credibility. As an instantaneous optimization strategy, ECMS can achieve the same results as DP through a smaller amount of calculation. It proved the feasibility of the proposed AECMS method
4.2 Working Condition Adaptability Test
In order to verify whether the method in this paper can be applied to different working conditions, a variety of typical driving conditions such as FTP75, NEDC, UDSS, etc., were selected, and simulations were also performed in the way of working conditions superimposed, and the results shown in Fig. 9 were obtained.
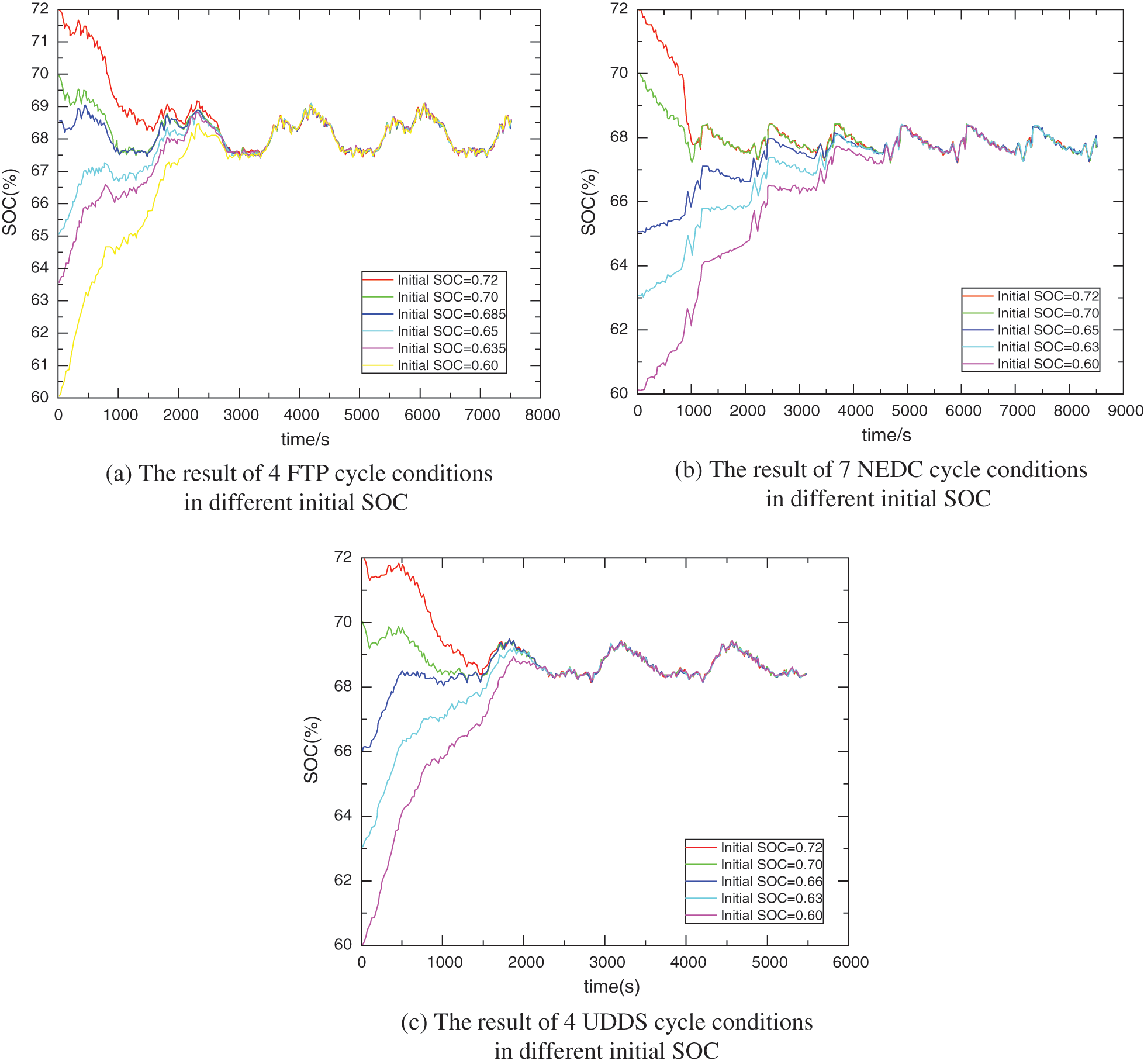
Figure 9: Results of charge sustaining in different driving cycle in different initial SOC
It can be seen from Fig. 9 that under different driving conditions and at different initial SOC values, as the driving cycle increases, the SOC can eventually stabilize. However, different driving conditions have different final SOC stable values, which means that due to different operating conditions, the selection of the optimal SOC interval is also different for different driving conditions, which ultimately leads to different optimal control results and lower fuel consumption. The comparison results are shown in Table 2.
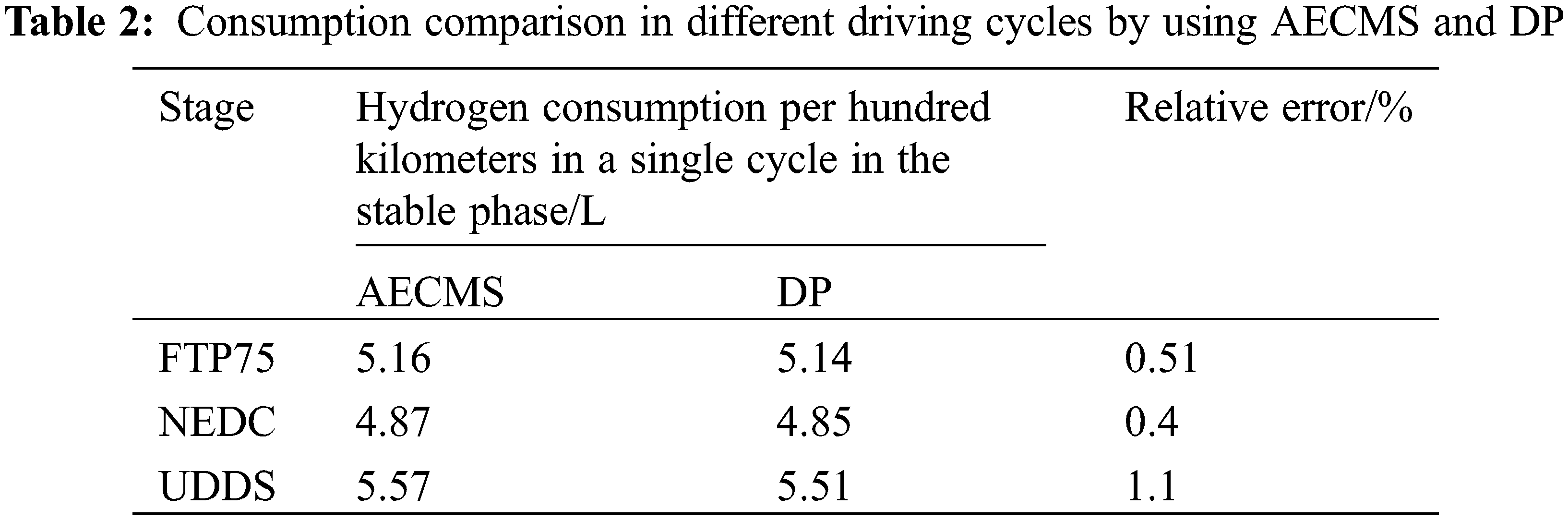
As analyzed in the previous article, if the appropriate initial SOC value is given, the DP method and the method in the text can obtain relatively consistent control results. Therefore, only the fuel consumption comparison in the stable phase is given in Table 2. It can be seen from Table 2 that the final fuel consumption of the typical driving conditions in 3 is only about 0.1%~0.2% compared with the DP, which further shows that the method in the article is more adaptable to the operating conditions.
In this paper, the dynamic programming algorithm is used to obtain the optimal control results of the hybrid power system under typical driving conditions. On this basis, the ECMS model is used to obtain the law between the average optimal equivalent factor and the power maintenance level, and the corresponding A-ECMS algorithm is designed according to the optimal initial SOC interval. The simulation results of working conditions in NEDC show that the method in this paper can finally maintain the level of electricity to stabilize, and the whole process is divided into two stages. In the transition stage, the fuel consumption difference with DP is only 1.6%, while it can be obtained in the stable stage. The control result is more consistent with the dynamic programming, and the error is only 0.4%. It fully shows that the method proposed in the article can reduce fuel consumption while maintaining power balance. At the same time, verified by multiple working conditions such as FTP-75, NEDC, UDDS, etc., the SOC change trend is consistent with the simulation results of NEDC driving cycle, and the error of the comparison result with the DP method in the stable phase is only 0.1%~1.1%, indicating that the paper proposed The method has strong adaptability to working conditions, and can provide a certain reference value for the optimal control of hybrid vehicles with regular driving.
Funding Statement: This work was supported by the Key Research and Development Program of Shandong Province (Grant No. 2019JZZY010912) and the Key Research and Development Program of Shandong Province (Grant No. 2020CXGC010406). And the authors would also acknowledge financial support from China Scholarship Council.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
1. Hou, S., Gao, J., Zhang, Y., Chen, M., Shi, J. et al. (2020). A comparison study of battery size optimization and an energy management strategy for FCHEVs based on dynamic programming and convex programming. International Journal of Hydrogen Energy, 45(41), 21858–21872. DOI 10.1016/j.ijhydene.2020.05.248. [Google Scholar] [CrossRef]
2. İnci, M., Büyük, M., Demir, M. H. (2021). A review and research on fuel cell electric vehicles: Topologies, power electronic converters, energy management methods, technical challenges, marketing and future aspects. Renewable and Sustainable Energy Reviews, 137(12), 110648. DOI 10.1016/j.rser.2020.110648. [Google Scholar] [CrossRef]
3. Zhou, Y., Obeid, H., Laghrouche, S., Hilairet, M., Djerdir, A. (2021). A novel second-order sliding mode control of hybrid fuel cell/super capacitors power system considering the degradation of the fuel cell. Energy Conversion and Management, 229(8), 113766. DOI 10.1016/j.enconman.2020.113766. [Google Scholar] [CrossRef]
4. Sulaiman, N., Hannan, M. A., Mohamed, A., Ker, P. J., Majlan, E. H. et al. (2018). Optimization of energy management system for fuel-cell hybrid electric vehicles: Issues and recommendations. Applied Energy, 228(2), 2061–2079. DOI 10.1016/j.apenergy.2018.07.087. [Google Scholar] [CrossRef]
5. Zhang, W., Li, J., Xu, L., Ouyang, M. (2017). Optimization for a fuel cell/battery/capacity tram with equivalent consumption minimization strategy. Energy Conversion and Management, 134(17), 59–69. DOI 10.1016/j.enconman.2016.11.007. [Google Scholar] [CrossRef]
6. Wang, Y., Ma, C. (2022). CFD-Based numerical analysis of the thermal characteristics of an electric vehicle power battery. Fluid Dynamics & Materials Processing, 18(1), 159–171. DOI 10.32604/fdmp.2022.017743. [Google Scholar] [CrossRef]
7. Cheng, L., Guo, B., Li, K. (2021). Design and optimization of a hybrid energy system for decentralized heating. Fluid Dynamics & Materials Processing, 17(1), 49–70. DOI 10.32604/fdmp.2021.011062. [Google Scholar] [CrossRef]
8. Chen, Q., Sun, H., Wang, N. (2020). Sliding mode control of hydraulic pressure in electro-hydraulic brake system-based on the linearization of higher-order model. Fluid Dynamics & Materials Processing, 16(3), 513–524. DOI 10.32604/fdmp.2020.09375. [Google Scholar] [CrossRef]
9. Fares, D., Chedid, R., Karaki, S., Jabr, R., Panik, F. et al. (2014). Optimal power allocation for a FCHV based on linear programming and PID controller. International Journal of Hydrogen Energy, 39(36), 21724–21738. DOI 10.1016/j.ijhydene.2014.09.020. [Google Scholar] [CrossRef]
10. Ahmadi, S., Bathaee, S. M. T., Hosseinpour, A. H. (2018). Improving fuel economy and performance of a fuel-cell hybrid electric vehicle (fuel-cell, battery, and ultra-capacitor) using optimized energy management strategy. Energy Conversion and Management, 160(6), 74–84. DOI 10.1016/j.enconman.2018.01.020. [Google Scholar] [CrossRef]
11. Zhou, D., Al-Durra, A., Matraji, I., Ravey, A., Gao, F. (2018). Online energy management strategy of fuel cell hybrid electric vehicles: A fractional-order extremum seeking method. IEEE Transactions on Industrial Electronics, 65(8), 6787–6799. DOI 10.1109/TIE.2018.2803723. [Google Scholar] [CrossRef]
12. Davis, K., Hayes, J. G. (2019). Fuel cell vehicle energy management strategy based on the cost of ownership. IET Electrical Systems in Transportation, 9(4), 226–236. DOI 10.1049/iet-est.2019.0021. [Google Scholar] [CrossRef]
13. Han, J., Park, Y., Kum, D. (2014). Optimal adaptation of equivalent factor of equivalent consumption minimization strategy for fuel cell hybrid electric vehicles under active state inequality constraints. Journal of Power Sources, 267(2), 491–502. DOI 10.1016/j.jpowsour.2014.05.067. [Google Scholar] [CrossRef]
14. Han, J., Park, Y., Park, Y. (2012). A novel updating method of equivalent factor in ECMS for prolonging the lifetime of battery in fuel cell hybrid electric vehicle. IFAC Proceedings, 45(30), 227–232. DOI 10.3182/20121023-3-FR-4025.00059. [Google Scholar] [CrossRef]
15. Xie, S., Chen, H., Liu, T., Wei, L. (2017). A research on energy management strategy for a plug-in hybrid electric bus based on DP-ECMS strategy. Automotive Engineering, 39(7), 736–747. DOI 10.19562/j.chinasae.qcgc.2017.07.002. [Google Scholar] [CrossRef]
16. Couch, J., Fiorentini, L., Canova, M. (2013). An ECMS-Based approach for the energy management of a vehicle electrical system. IFAC Proceedings, 46(21), 115–120. DOI 10.3182/20130904-4-JP-2042.00123. [Google Scholar] [CrossRef]
17. Zeng, T., Zhang, C., Zhang, Y., Deng, C., Hao, D. et al. (2021). Optimization-oriented adaptive equivalent consumption minimization strategy based on short-term demand power prediction for fuel cell hybrid vehicle. Energy, 227(2), 120305. DOI 10.1016/j.energy.2021.120305. [Google Scholar] [CrossRef]
18. Pivetta, D., Dall Armi, C., Taccani, R. (2021). Multi-objective optimization of hybrid PEMFC/Li-ion battery propulsion systems for small and medium size ferries. International Journal of Hydrogen Energy, 46(72), 35949–35960. DOI 10.1016/j.ijhydene.2021.02.124. [Google Scholar] [CrossRef]
19. Macias, A., El Ghossein, N., Trovão, J. (2021). Passive fuel cell/lithium-ion capacitor hybridization for vehicular applications. International Journal of Hydrogen Energy, 46(56), 28748–28759. DOI 10.1016/j.ijhydene.2021.06.126. [Google Scholar] [CrossRef]
20. Feroldi, D., Carignano, M. (2016). Sizing for fuel cell/supercapacitor hybrid vehicles based on stochastic driving cycles. Applied Energy, 183, 645–658. DOI 10.1016/j.apenergy.2016.09.008. [Google Scholar] [CrossRef]
21. Chen, S., Wu, C., Hung, Y., Chung, C. (2018). Optimal strategies of energy management integrated with transmission control for a hybrid electric vehicle using dynamic particle swarm optimization. Energy, 160(6), 154–170. DOI 10.1016/j.energy.2018.06.023. [Google Scholar] [CrossRef]
22. Ansarey, M., Shariat Panahi, M., Ziarati, H., Mahjoob, M. (2014). Optimal energy management in a dual-storage fuel-cell hybrid vehicle using multi-dimensional dynamic programming. Journal of Power Sources, 250(2), 359–371. DOI 10.1016/j.jpowsour.2013.10.145. [Google Scholar] [CrossRef]
23. Torreglosa, J. P., Jurado, F., García, P., Fernández, L. M. (2011). Hybrid fuel cell and battery tramway control based on an equivalent consumption minimization strategy. Control Engineering Practice, 19(10), 1182–1194. DOI 10.1016/j.conengprac.2011.06.008. [Google Scholar] [CrossRef]
24. Couch, J., Fiorentini, L., Canova, M. (2013). An ECMS-Based approach for the energy management of a vehicle electrical system. IFAC Proceedings, 46(21), 115–120. DOI 10.3182/20130904-4-JP-2042.00123. [Google Scholar] [CrossRef]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |