Fluid Dynamics & Materials Processing

DOI: 10.32604/fdmp.2022.019921

ARTICLE

On the Dynamics of a Viscoelastic Fluid-Conveying Nanotube

Ola Adil Ibrahim1, Gunawan Widjaja2, Abdulhussien N. Alattabi3, Krishanveer Singh4, Yasser Fakri Mustafa5, P. A. Krovopuskov6 and Mustafa M. Kadhim7,*

1General Directorate of Curricula-Ministry of Education-Iraq, Baghdad, 10020, Iraq
2Senior Lecturer Faculty of Public Health Universitas Indonesia/Faculty of Law Universitas Krisnadwipayana, Jakarta, 11440, Indonesia
3College of Petroleum Engineering, Al-Ayen University, Thi-Qar, 64005, Iraq
4GLA University Mathura-India, Mathura, Chaumuhan, Uttar Pradesh, 281406, India
5Department of Pharmaceutical Chemistry, College of Pharmacy, University of Mosul, Mosul, 41002, Iraq
6Lipetsk State Technical University, Lipetsk, 398600, Russia
7Department of Dentistry, Kut University College, Kut, Wasit, 52001, Iraq
*Corresponding Author: Mustafa M. Kadhim. Email: mohammad.ghani13spt@gmail.com
Received: 24 October 2021; Accepted: 04 January 2022

1  Introduction

Recently, nanotechnology has received widespread attention in many sciences, including engineering sciences [1–4]. Experiments show that carbon nanotubes (CNTs) have extraordinary properties compared to other materials. Among the wide applications of nanotubes, their use as fluid carriers is of great importance; because it includes features such as fluid storage and transfer. Therefore, the vibrational behavior of carbon nanotubes containing fluid has been studied in various studies and many aspects of it still need further research [5–9].

Because controlled nanoscale practical experiments as well as molecular dynamic simulations are very difficult and costly, modeling of elastic continuous environments is commonly used to study the mechanical behavior of nanotubes, including their vibrational characteristics. Recently, the use of elastic beam model and cylindrical plate model to study the dynamic behavior of CNTs, including buckling study [10–15] and vibration analysis [16–21] has been considered by many researchers. Among the existing theories, the Euler-Bernoulli beam theory has been widely used due to its simplicity and high power in studying the behavior of fluid conveying pipes [22–24]. Studies on this theory show that the results are in good agreement with the results obtained by the molecular dynamics method [25]. For example, Wang [26] investigated the vibrational behavior of fluid-containing nanotubes using the Euler-Bernoulli beam model. He used Newton’s second law to derive the equation of motion and then obtained the natural frequencies and critical velocities of carbon nanotubes using the DQM method. In another study, Wang [27] proposed a new model that considers the effects of the inner and outer layers of nanotubes, taking into account surface effects. Rezaee et al. [19,28] investigated the vibration behavior of single-walled carbon nanotubes conveying fluid and then investigated the effect of fluid velocity on the natural frequencies and stability of the system. Niyaraki et al. [29] considering the effects of fluid viscosity, extracted the equation of motion governing carbon nanotubes and then investigated the effect of fluid viscosity on the vibrational behavior of fluid-containing nanotubes. Their research results show that considering the viscosity of the fluid reduces the natural frequencies of the nanotubes and increases the effect of reducing the natural frequencies by increasing the velocity of the fluid. Lee et al. [30] studied the vibrational behavior of a multi-walled carbon nanotube. With the help of non-local theory of vibrations, Reddy also studied the buckling and bending of a nano-beam based on different beam theories [31]. Eltaher et al. [32] studied the vibrations of an Euler-Bernoulli nanowire using the finite element method and nonlocal theory for different boundary conditions. Lyu et al. [33] was studied the influence of nano-system uncertainties on the critical flow velocity of fluid-conveying carbon nanotubes (CNTs) under multi-physical fields. The nonlinear vibration and instability of a fluid-conveying nanopipe made of functionally graded (FG) materials with consideration of the initial geometric imperfection are investigated by [34]. Zhang et al. [35] investigated the dynamic behavior of functionally graded (FG) microbeams with different porosity distributions and acted by a moving harmonic load.

By review of literatures mentioned above, most of the analytical and theoretical studies, however, focus on the deterministic analysis of fluid-conveying CNTs, and the effect of the intermediate support on their vibration behaviors has aroused less attention. Accordingly, the main purpose of the present study is the vibration analysis of carbon nanotubes with intermediate support. For this purpose, using the analytical solution method based on power series method, and considering viscoelastic material behavior the vibration behavior of carbon nanotubes with intermediate support will be investigated. After verifying the proposed model, the effect of various parameters such as fluid flow velocity, geometric dimensions, position of the intermediate support as well as different types of intermediate supports on the natural frequency and critical velocity of the system are investigated.

2  Structure

2.1 Extraction of Equations of Motion

Fig. 1 shows the fluid-carrying carbon nanotube, which is considered to be a continuous beam, for the different abutment modes to be considered. To obtain the vibrational equation of the nanotube, an element of the nanotube is considered and equilibrium equations are written for that element. Fig. 2 shows a free diagram of a nanotube with a fluid. By writing the equations of dynamic equilibrium of forces and torques, the equation governing the transverse vibration behavior of carbon nanotubes can be extracted.

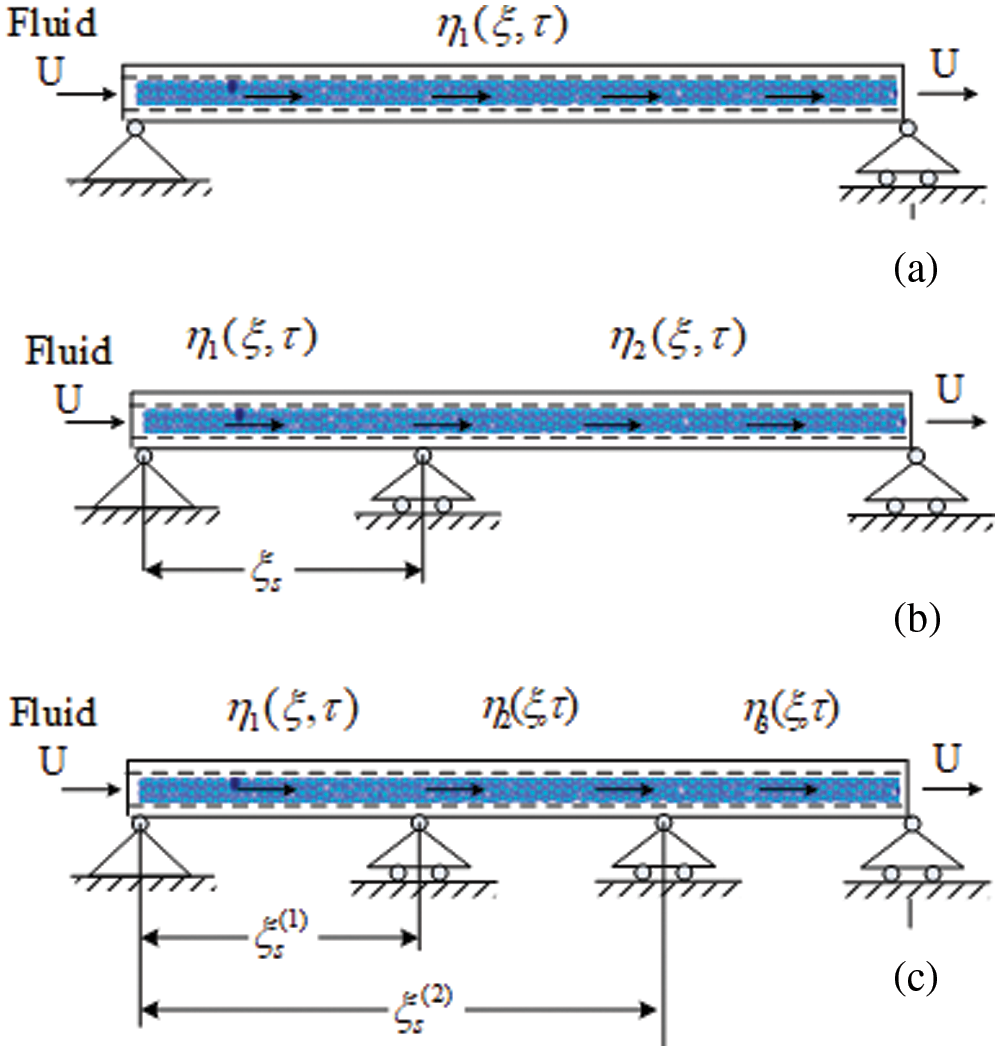
Figure 1: Different intermediate support for the fluid conveying nanotube

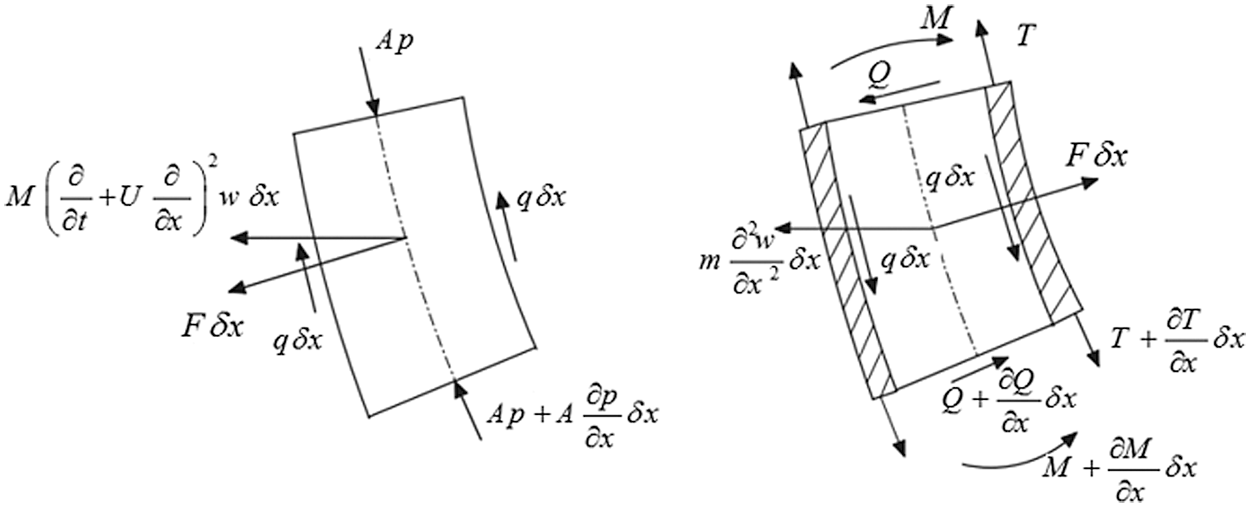
Figure 2: Free-body diagram of the fluid and nanotube

By writing the equations of dynamic equilibrium of forces in the w direction and torque around the center of mass of the nanotube and fluid element, assuming the angle of rotation is small, we have:

MU2∂2w(x,t)∂x2dx+2MU∂2w(x,t)∂x∂tdx+(m+M)dx∂2w(x,t)∂t2=−∂V∂xdx (1)

∂M∂x=V (2)

Given that M=EI∂2w(x,t)/∂x2 , considering the damping of Kelvin-Voight model and negating the axial force, the vibration equation of a carbon-carrying carbon nanotube is obtained by Eq. (3):

EI∗∂5y(x,t)∂x4∂t+EI∂4y(x,t)∂x4+MU2∂2y(x,t)∂x2+2MU∂2y(x,t)∂x∂t+(m+M)∂2y(x,t)∂t2=0 (3)

where EI is the flexural stiffness of the nanotube, U is the velocity of the fluid, EI* is the damping of the structures of the system, and m and M are the unit mass of the length of the nanotube and the fluid, respectively.

In order to study the parametric motion Eq. (3), it is rewritten in two-dimensional form. By defining dimensionless variables as follows:

η=yl,ξ=xl,β=Mm+M,u=MEIUl,τ=EI(m+M)l4t,γ=[IE(m+M)]12E∗l2 (4)

The equation of motion in terms of dimensionless parameters is obtained as follows:

γ∂5η∂ξ4∂τ+∂4η∂x4+u2∂2η∂ξ2+2β1/2u∂2η∂ξ∂τ+∂2η∂τ2=0 (5)

2.2 Boundary Conditions

As mentioned, the main purpose of this study is to investigate the effect of intermediate support on the vibrational behavior of fluid-carrying carbon nanotubes. Considering the boundary conditions of simple abutments at both ends, the equations for the different states of the intermediate abutment shown in Fig. 1 are as follows:

- Boundary conditions of simple supports at both ends

ξ=0:η(ξ.τ)=0.∂2η(ξ.τ)∂ξ2=0;ξ=1:η(ξ.τ)=0.∂2η(ξ.τ)∂ξ2=0 (6)

Compatibility conditions for the mode shown in Fig. 1b

ξ=ξs:η1(ξ.τ)=0.η2(ξ.τ)=0.

∂η1(ξ.τ)∂ξ=∂η2(ξ.τ)∂ξ=0.∂2η1(ξ.τ)∂ξ2=∂2η2(ξ.τ)∂ξ2=0 (7)

- Compatibility conditions for the mode shown in Fig. 1c

ξ=ξs(1):η1(ξ.τ)=0.η2(ξ.τ)=0.

∂η1(ξ.τ)∂ξ=∂η2(ξ.τ)∂ξ=0.∂2η1(ξ.τ)∂ξ2=∂2η2(ξ.τ)∂ξ2=0 (8)

ξ=ξs(2):η3(ξ.τ)=0.η2(ξ.τ)=0.

∂η3(ξ.τ)∂ξ=∂η2(ξ.τ)∂ξ=0.∂2η3(ξ.τ)∂ξ2=∂2η2(ξ.τ)∂ξ2=0 (9)

2.3 Solve the Governing Equation of Motion Using the Power Series Method

To solve the differential Eq. (5), we consider the time response of the system to be harmonic. Using the method of separating the variables, the response of the equation of motion is considered as η (ξ.τ) = W (ξ)e(−iΩτ) where W (ξ) is the shape of the vibration mode and Ω is the dimensionless natural frequency of the system. By placing the hypothetical answer in Eq. (5):

(iγΩ+1)d4Wdξ4+u2d2Wdξ2+2iβ12uΩd2Wdξ−Ω2W=0 (10)

The equation of motion is a fourth order linear differential equation with constant coefficients for which no analytical solution is provided. To solve the latter equation, a new analytical method based on power series is used. For this purpose, the solution of the equation is considered as follows:

W(ξ)=∑n=0Nanξn+R (11)

where R is the residual. It can be shown that the convergence radius of the above series is infinite, so as the number of sentences in the series increases, the remainder will tend to zero. By substituting Eq. (11) in Eq. (10), we have:

(iγΩ+1)∑n=0Nn(n−1)(n−2)(n−3)anξn−4+u2∑n=0Nn(n−1)anξn−2+2iβ12uΩ∑n=0Nnanξn−1−Ω2∑n=0Nanξn=0 (12)

To establish the above equation for all values of ξ, the different power coefficients ξ must be equal on both sides of the above equation. The above sets are rewritten so that the power of ξ is equal to n in all sentences. In this case we will have:

(iγΩ+1)∑n=0N−4(n+4)(n+3)(n+2)(n+1)an+4ξn+u2∑n=0N−2(n+2)(n+1)an+2ξn+2iβ12uΩ∑n=0N(n+1)an+1ξn−Ω2∑n=0Nanξn=0 (13)

By sorting the recent relationship can be shown:

∑n=0N−4{(iγΩ+1)(n+4)(n+3)(n+2)(n+1)an+4+u2(n+2)(n+1)an+2+2iβ12uΩ(n+1)an+1−Ω2an}ξn=0 (14)

With mathematical operations, the recursive relation for calculating the unknown coefficients an=4,5,…,N can be obtained as follows:

an+4=1(iγΩ+1)(n+4)(n+3)(n+2)(n+1)×{u2(n+2)(n+1)an+2+2iβ1/2uΩ(n+1)an+1−Ω2an}=0.n=0.….N (15)

The recent return relation provides a set of algebraic equations with the N-4 equation and the unknown N. Therefore, there are four additional unknowns that must be determined in such a way that, firstly, independent linear solutions are obtained and, secondly, the solutions obtained in Eq. (10) are valid and satisfy the prevailing boundary conditions. By solving the system of recent algebraic equations, all unknown coefficients an=4,5,…,N can be obtained in terms of four coefficients a0, a1, a2 and a3. By placing the coefficients obtained in Eq. (15) and after sorting according to the above five coefficients, the answer to Eq. (10) can be expressed as follows:

W(ξ)=a0W1(ξ)+a1W2(ξ)+a2W3(ξ)+a3W4(ξ) (16)

In the recent relation Wj(ξ),j=1,2,3,4 are the linear independent solutions of Eq. (10) and are constant coefficients obtained from the application of boundary conditions. By applying boundary conditions to Eq. (16), four algebraic equations in terms of unknowns an=0,1,2,3 is obtained as follows:

[Δ]{A}=0.{A}={a0.a1.a2.a3}T (17)

In the latter relation, [Δ] is a coefficient matrix that depends on the geometrical and mechanical properties of the nanotube, boundary conditions and fluid velocity. To have a non-obvious answer, the determinants of the coefficient matrix must be zero. Therefore, the frequency equation of the system is obtained by solving the following equation:

det([Δ])=0 (18)

From the solution of the latter equation, the natural frequencies of the fluid-carrying nanotubes with intermediate supports are obtained. From the equation of the above determinants, the frequency equation is obtained, the roots of which provide the dimensionless natural frequencies Ω. Given the damping sentences in Eq. (10), the roots of the latter equation will be complex. The real part of the roots represents the natural frequencies of the system and the imaginary part is related to the attenuation of the system.

After calculating the natural frequencies, by placing them in the relation of 16 unknown coefficients in each vibration mode is obtained. Using these coefficients and with the help of Eq. (16), the shape of the vibration mode can be determined analytically. In the following, using the above equation, the vibrational behavior and instability of the system will be investigated.

3  Results

After analyzing the extraction of natural frequencies and the shape of mixed modes in the previous section, in this section the vibrational behavior and instability of a carbon nanotube carrying a fluid with an intermediate support for different values of system parameters are studied. Geometric and mechanical characteristics of nanotubes are: l=2.14×10−8 m , M=3.22×10−16kg.m−1 and EI=1.425×10−25N.m [28]. In order to study the parameter, the two-dimensional parameters presented in Eq. (4) are used.

3.1 Validation of Results

Before studying the effect of different parameters on the vibrational behavior and instability of viscoelastic nanotubes carrying fluid with intermediate supports, the accuracy of the proposed model is investigated. Due to the fact that the vibration behavior of carbon nanotubes carrying fluid with intermediate supports and viscoelastic behavior has not been studied, so in order to evaluate the accuracy of the results, the intermediate support and viscoelastic behavior are omitted. In order to check the accuracy and precision of the proposed model, results of [1] have been used. Since in this reference only the changes of the first natural frequency of nanotubes have been studied, so only the first natural frequency is compared. Fig. 3 shows the changes in the first natural frequency vs. the dimensionless velocity obtained using the model presented in the present paper and the reference results [1]. As can be seen from Fig. 3, the results of the analytical method proposed to investigate the vibrational behavior of nanotubes containing fluid have an acceptable consistency with the results of reference [1].

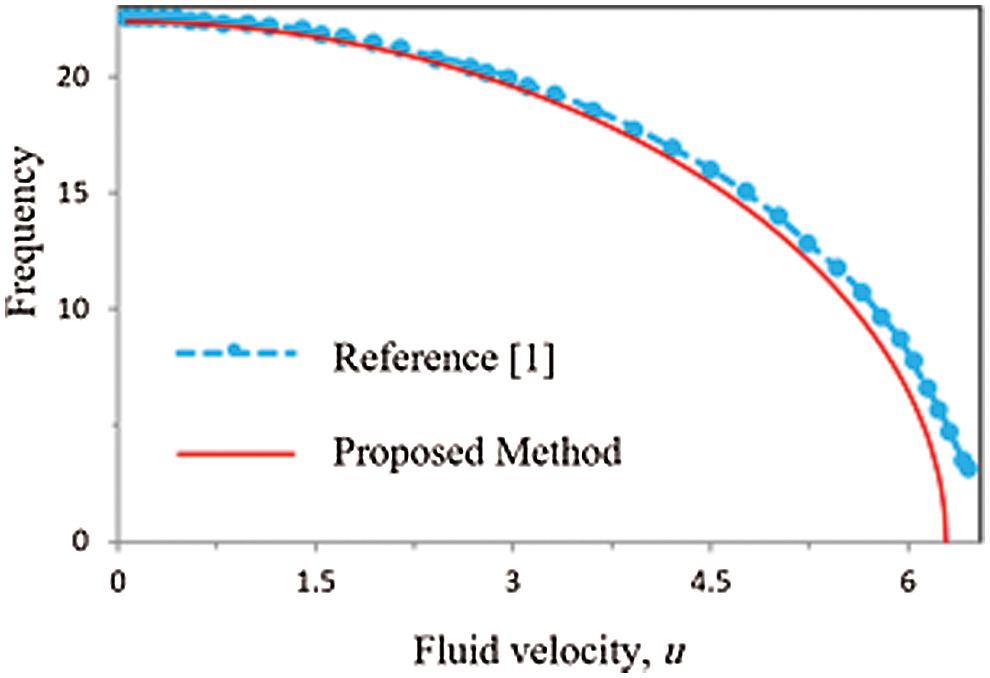
Figure 3: Variation of the first natural frequency of the simply-supported nanotube conveying fluid

3.2 Parametric Studies

The solution of eigenvalue problem (i.e., Eq. (18)) yields complex roots. The real part of these roots (Re(Ω)) represents the fundamental natural frequencies of damped system, i.e., when the fluid flows through the pipe, while the imaginary part (Im(Ω)) indicates the rate of decay of the free vibration. Figs. 4 and 5 show the effect of fluid velocity on the real and imaginary parts of the first and second dimensional natural frequencies of a fluid-carrying carbon nanotube with simple supports at both ends and without an intermediate support. As the results show, when the axial velocity is zero, the imaginary part of the mixed frequencies is zero. It is called critical speed. When the fluid velocity reaches the first critical velocity, ucr = 3.29, the real part of the natural frequency in the first mode becomes zero, Re(Ω_1) = 0, but the real part is bifurcated and has two values Im(Ω_1) > 0 and Im(Ω_1) < 0 becomes. In this case, due to the presence of a positive imaginary part, the time response of the system in the first mode increases over time and the first mode becomes unstable. Given that in this case the frequency of response fluctuations is zero, so the instability is static. Under these conditions, the second and third modes are still stable. With further increase of fluid velocity, for u = 6.37, the real part of the eigenvalues of the first and second modes is equalized and the corresponding imaginary part is also bifurcated, considering that in this case the real part has a non-zero value and the imaginary part is positive. So, the system will suffer from dynamic instability.

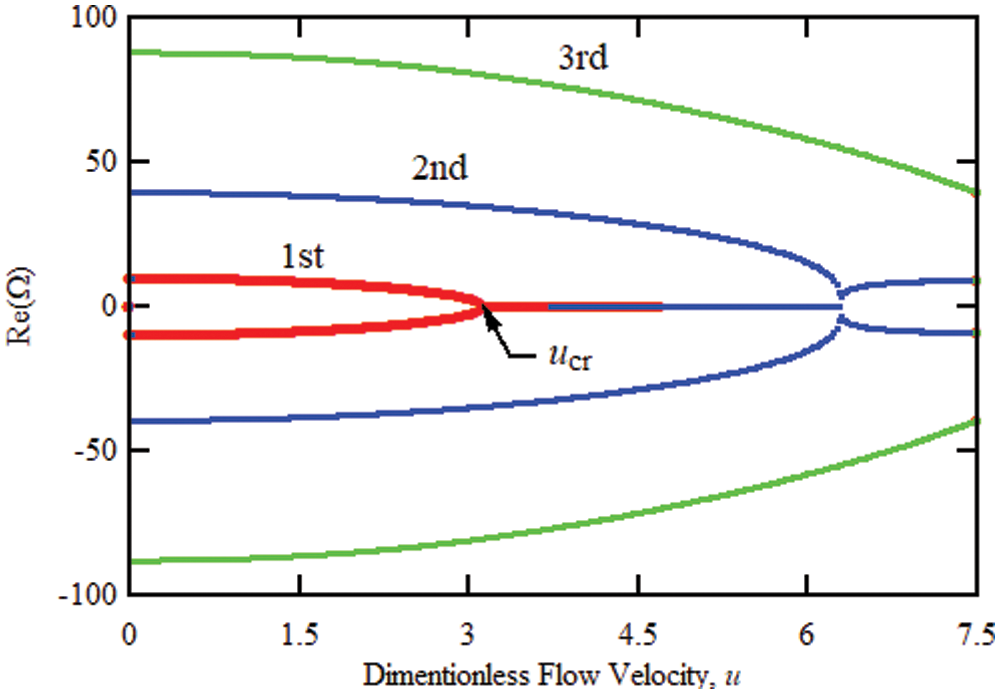
Figure 4: Variation of the real part of the first three eigenvalues of the simply-supported elastic carbon nanotube conveying fluid

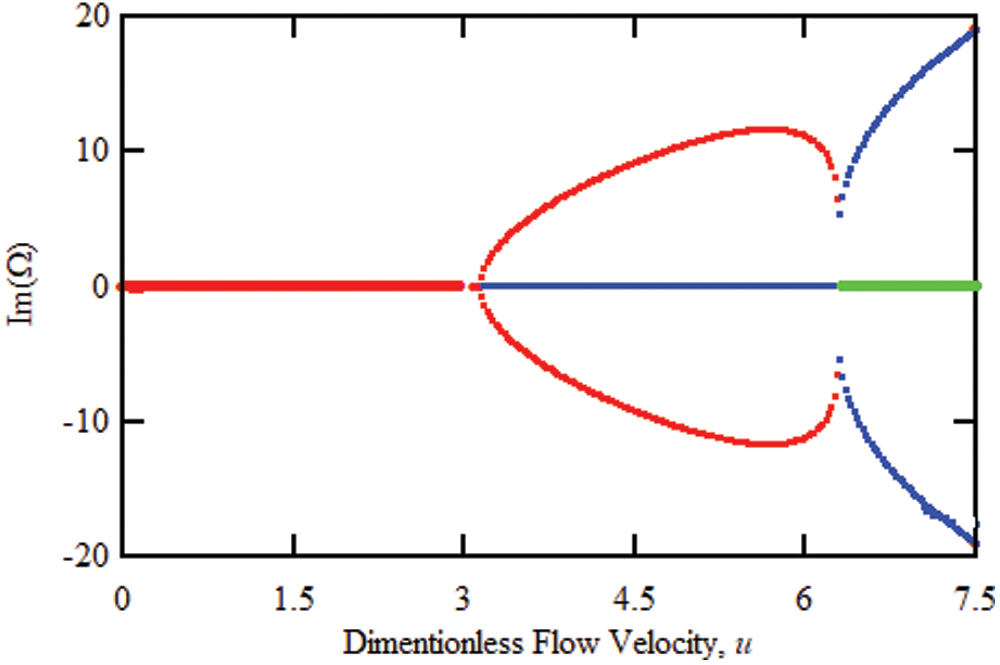
Figure 5: Variation of the imaginary part of the first three eigenvalues of the simply-supported elastic carbon nanotube conveying fluid

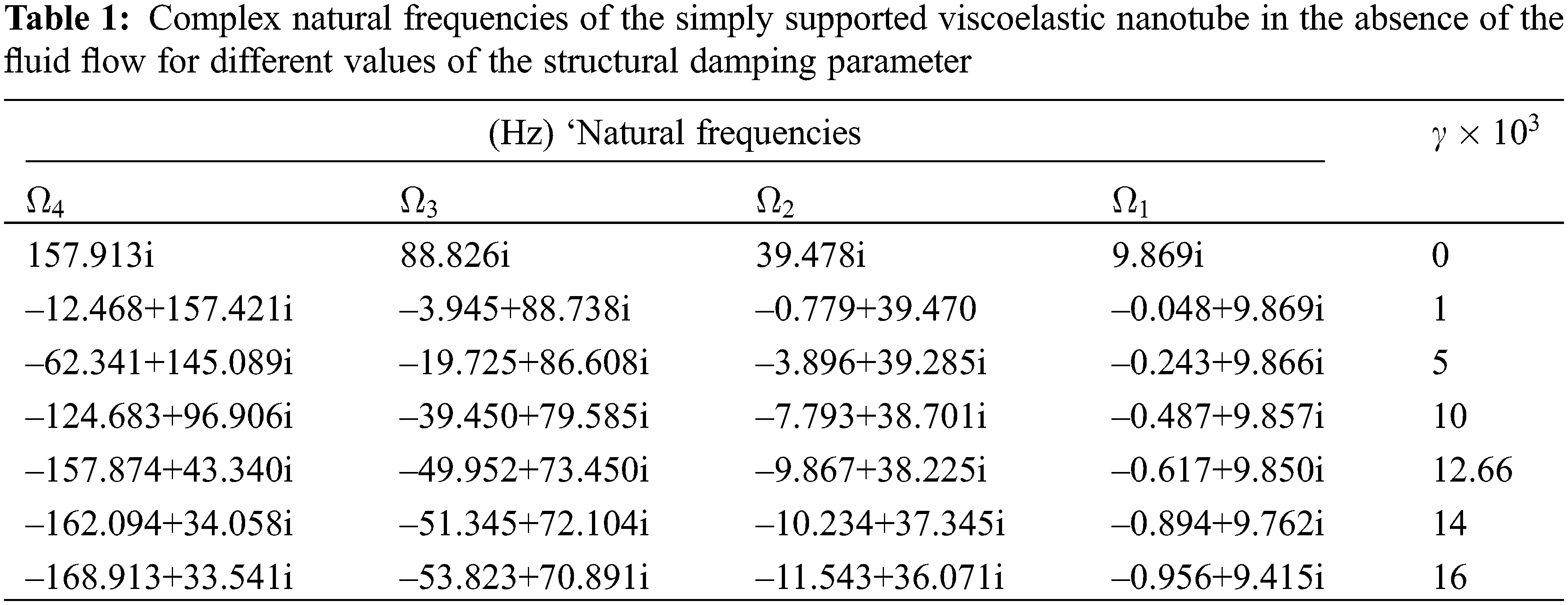
In order to investigate the damping effect of structures, first the static state of the flow, i.e., u = 0, is considered. If in this case the damping effects of the structure are ignored, then the eigenvalues will have only an imaginary part that represents the natural frequencies of the system. As the damping of the structure (parameter γ) increases, the eigenvalues will appear in a mixed form, with the real and imaginary parts representing the damping and the natural frequency of the system, respectively. Table 1 shows the first four special values of the pipe for different values of the dimensionless parameter γ in the absence of the intermediate abutment and fluid flow. As the results show, increasing the damping coefficient of structures causes the creation of a real part in special values which represents the damping of the system and the presence of structural damping has very little effect on the first and second natural frequencies but its effect on higher natural frequencies is very significant. As the γ damping parameter increases, the system damping and oscillation frequency decrease, so that for the dimensionless damping parameter of equal structures.

In Figs. 6 and 7, the real and imaginary sections show the specific values of the fluid-carrying nanotubes with simple supports at both ends for different damping values of the structure. The results show that considering the viscoelastic behavior or damping of the structure reduces the true part of the eigenvalues and the reduction of higher natural frequencies is much greater than the lower frequencies. For example, according to Fig. 6, for the damping of structures γ = 0.005 and at zero fluid velocity, the first natural frequency decreases from 9.87 to 9.86, the second natural frequency from 39.47 to 39.24 and the third natural frequency from 87.89 to 85.24, i.e., 3.18%. As can be seen, the effect of structural damping on lower frequencies is negligible and negligible, but in the form of higher modes, a significant reduction in natural frequencies is observed. The results show that the presence of structural attenuation reduces the real part and increases the imaginary part of eigenvalues and as a result the natural frequencies decrease and the system attenuation increases, which has a much greater effect on the shape of higher modes. In fact, for viscoelastic nanotubes carrying fluid, considering the structural damping model, the presence of damping reduces the natural frequencies and increases the damping of the system. Another effect of considering the viscoelastic behavior for fluid-carrying nanotubes is that the presence of structural damping increases the divergence instability rate at higher modes and secondly due to the lack of uniform effect of structural damping behavior on all vibrational modes. The behavior of hybrid modes does not appear. According to Fig. 6, it can be seen that for 6.27 < u < 7.27, although the first and second eigenvalues have the same real part, but due to the different imaginary parts of the eigenvalues, these two special values are different and the shape of the combination mode Will not be observed in system behavior. As can be seen in Fig. 5, considering the damping behavior of the structures, the instability of the system is of the first mode divergence, second mode divergence and combined mode flutter, respectively.

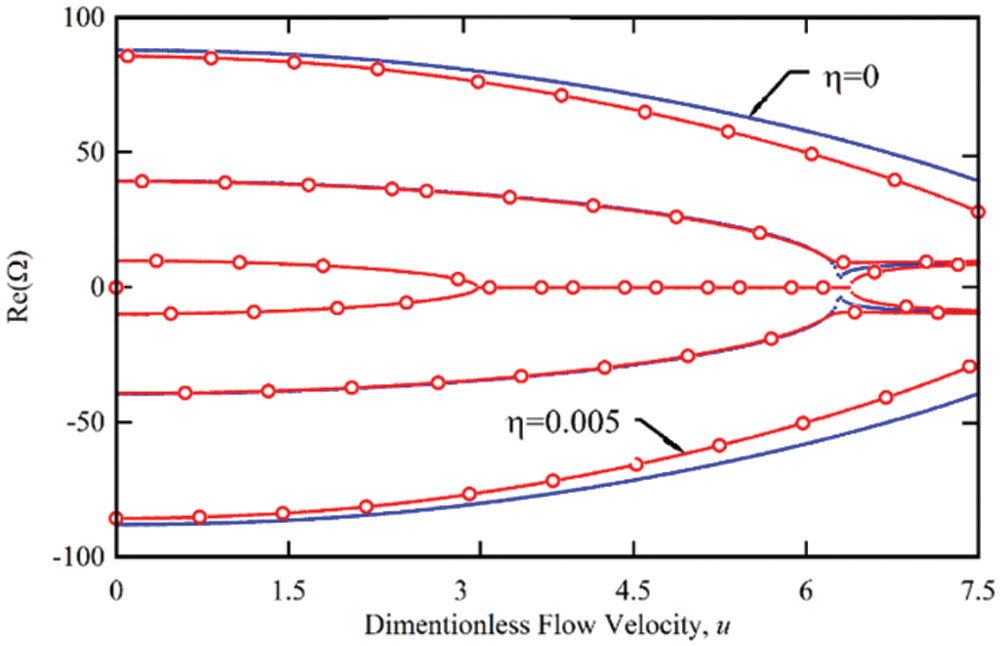
Figure 6: Variation of the real part of the first three eigenvalues of the simply-supported viscoelastic nanotube conveying fluid for different value of the γ

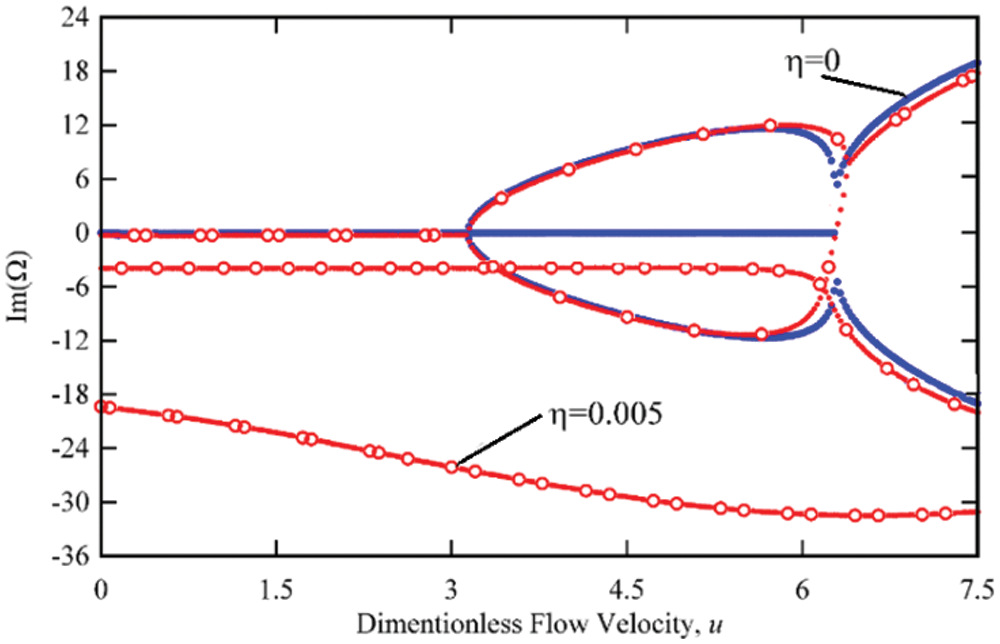
Figure 7: Variation of the imaginary part of the first three eigenvalues of the simply-supported viscoelastic nanotube conveying fluid for different value of the γ

The general sight is that; the natural frequency of the system was reduced with increase the fluid flow velocity. The natural frequency is mainly depending on the structural stiffness of the carbon nanotube. With growing the fluid flow velocity, the hydrodynamic stiffness resulted from increasing the fluid flow velocity is increased also due to the direct relationship between them. The hydrodynamic stiffness leads to weaken the structure stiffness of the nanotube. Then increasing the flow velocity means increasing in hydrodynamic stiffness and thereby decreasing in the nanotube stiffness which leads to decreasing in the frequency.

In the following, the effect of the intermediate support on the vibrational behavior of the carbon nanotube carrying the fluid is investigated. First, in front of Fig. 1b, the nano-tube with the middle support in the relative position of ξs from the left support is discussed. Figs. 8 and 9 show the changes of the real and imaginary parts of the fluid-carrying nanotube with the middle support located at ξs = 0.1. As can be seen, the presence of an intermediate support increases the natural frequencies and critical speed of the system.

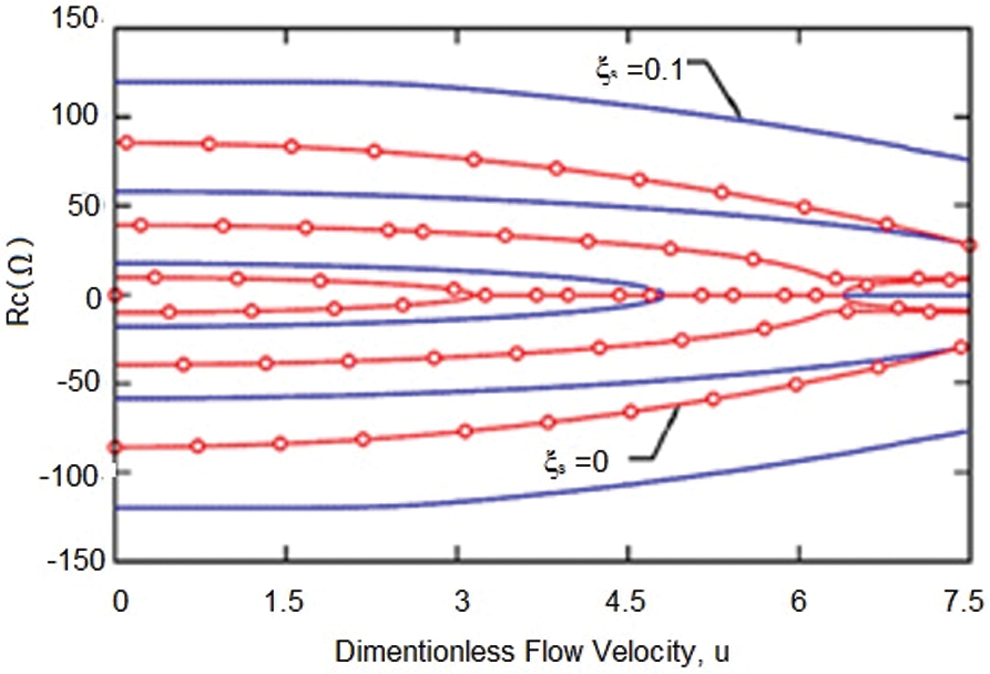
Figure 8: Variation of the real part of the first three eigenvalues of the simply-supported viscoelastic elastic nanotube conveying fluid for ξs = 0.1

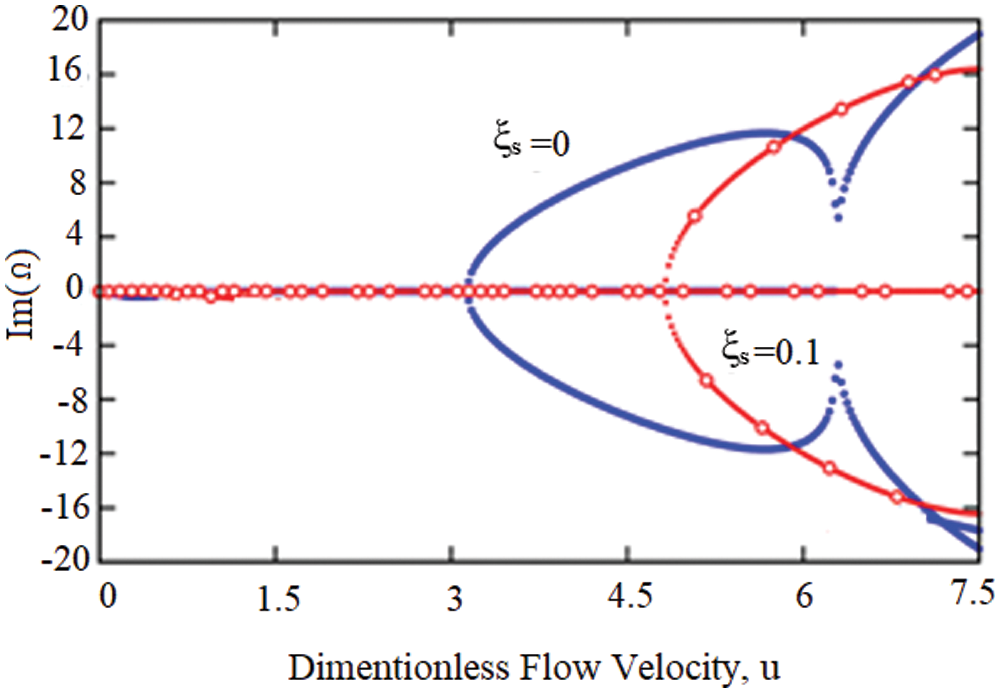
Figure 9: Variation of the imaginary part of the first three eigenvalues of the simply-supported viscoelastic elastic nanotube conveying fluid for ξs = 0.1

The results show that the presence of an intermediate support at the position ξs = 0.1 increases 43.53, 36.75 and 28.57% in the first, second and third frequencies, respectively. Also, the intermediate support increases the damping in higher modes. In addition, the presence of the abutment increases the critical speed of the system by 35% and the critical velocity is 4.83 for the intermediate abutment located at ξs = 0.1.

As the results show, the presence of an intermediate abutment has a significant effect on the vibrational behavior of fluid-carrying carbon nanotubes. Accordingly, the position of the intermediate support will also affect the vibrational characteristics. In order to investigate the effect of the position of the intermediate abutment on the natural frequencies of the system, Table 2 shows the first three natural frequencies of the carbon nanotube carrying the fluid for the different positions of the intermediate abutment.

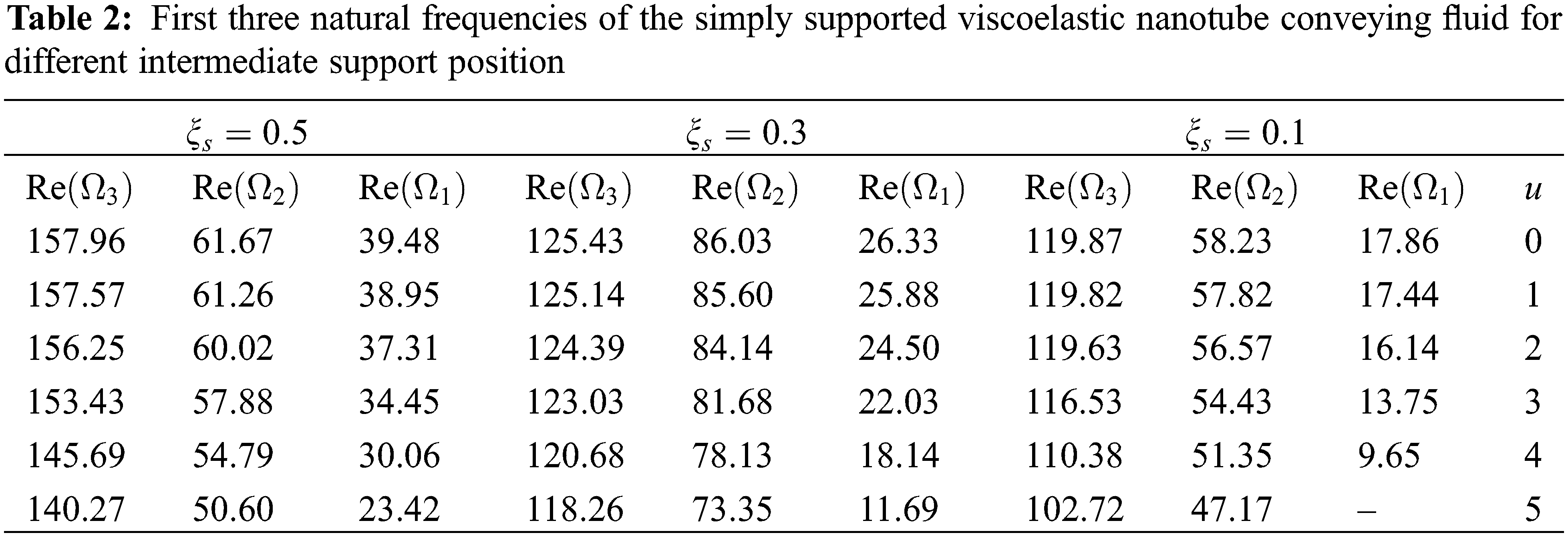
As the results show, the presence of the intermediate support increases the natural frequencies of the system and as the position of the intermediate support approaches the center of the nanotube, its effect on increasing the natural frequencies increases. Fig. 10 shows the effect of the position of the intermediate abutment on the first two natural frequencies of the fluid-carrying carbon nanotube per u = 1. As can be seen, the position of the intermediate abutment has a significant effect on the increase of the natural frequencies of the system and the position corresponding to the maximum increase of the frequency corresponding to each form of vibration mode is different. The middle abutment located at ξs = 0.5 causes the largest increase in the first natural frequency and the intermediate abutment located in ξs = 0.33 causes the largest increase in the second natural frequency.

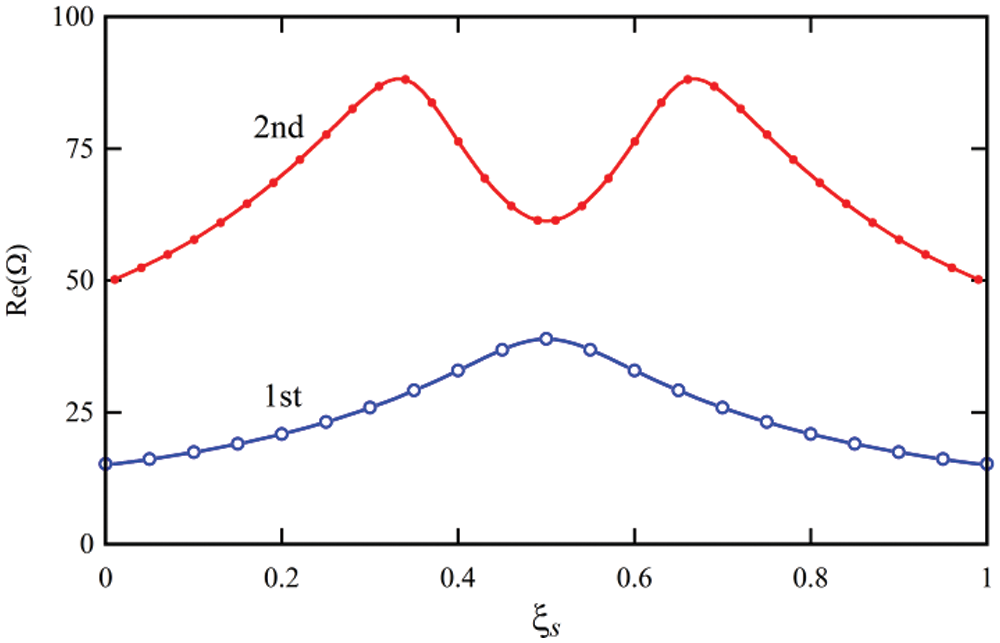
Figure 10: The effect of intermediate support on the first two natural frequencies of the simply supported viscoelastic nanotube conveying fluid for u = 1

A similar result is obtained for the critical speed of the system. Table 3 shows the effect of the position of the intermediate supports on the critical speed of the system shown in Fig. 1c. As can be seen, the proximity of the center support to the center of the pipe further increases the critical speed of the system.

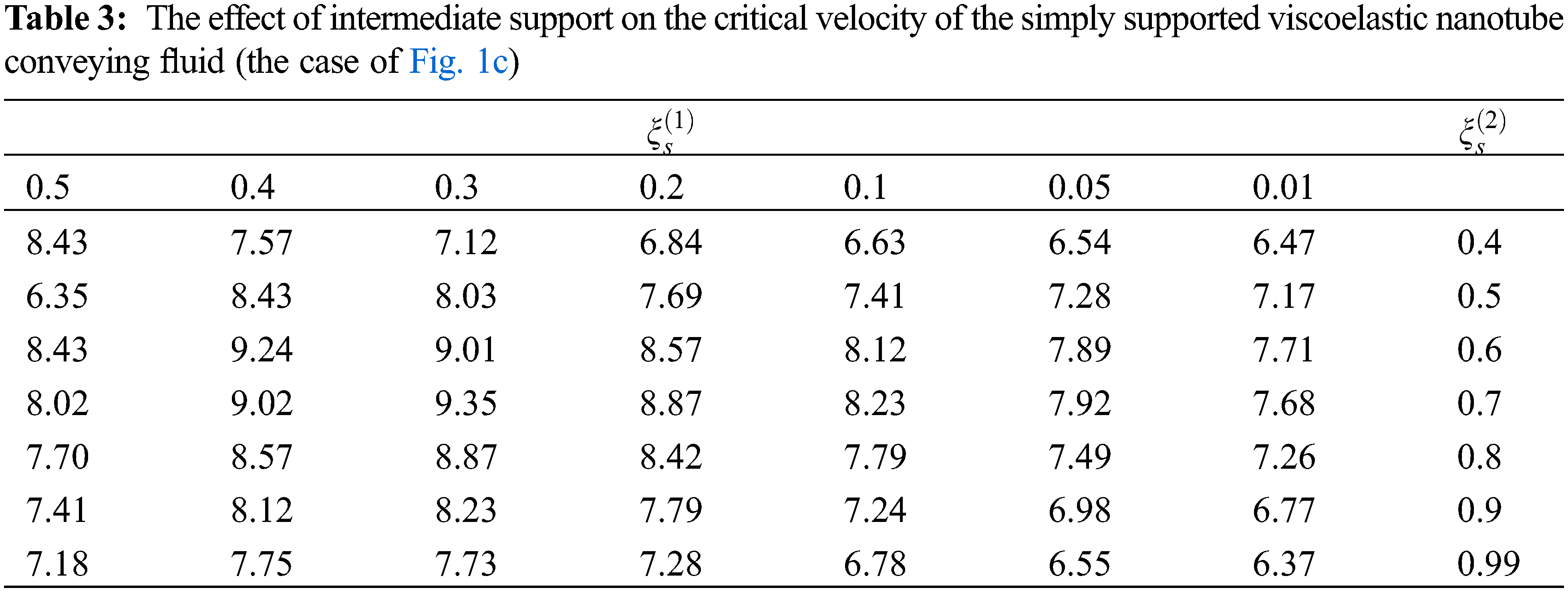
Fig. 11 shows the critical velocity changes of the system according to the position of the intermediate support. According to the figure, it can be seen that the presence of the abutment located in the position ξs = 0.5 causes a 50.16% increase in the critical speed of the carbon nanotube carrying the fluid with simple abutments at both ends.

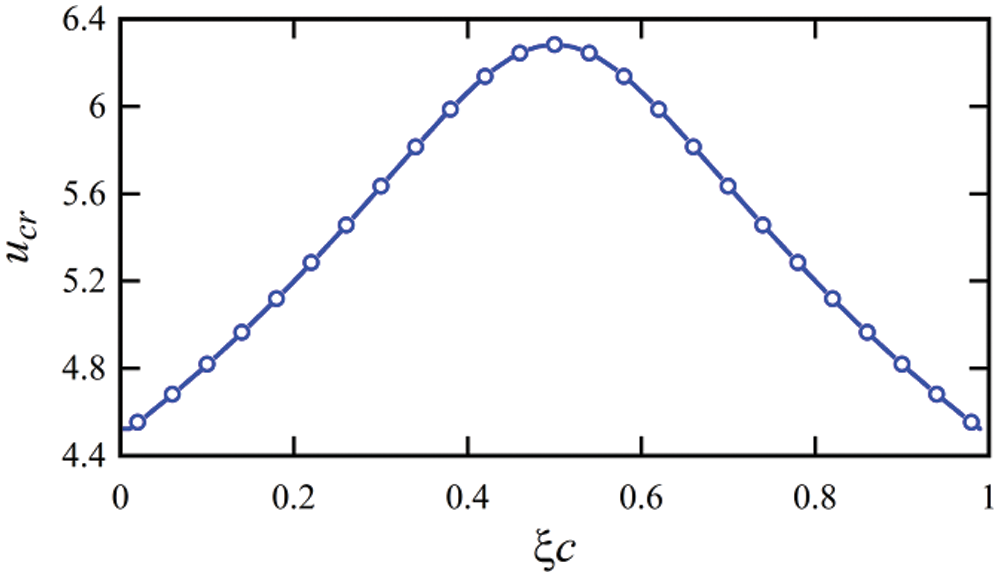
Figure 11: The effect of intermediate support on the critical velocity of the simply supported viscoelastic nanotube conveying fluid

4  Conclusion

In the present study, using Euler-Bernoulli’s theory, the behavior of transverse vibrations and the stability of viscoelastic nanotubes carrying fluid with intermediate supports were investigated. In order to consider more realistic hypotheses, the effect of structural damping was considered, and the governing differential equation was derived using the direct application of Newton’s second law. The governing equations of motion of the system were solved using the method of solving differential equations based on power series. After extracting the characteristic equation governing the system’s behavior, the effect of various parameters such as fluid velocity, type, and positions of intermediate supports on the vibrational characteristics and instability of the carbon nanotube bearing with simple supports at both ends having an intermediate support were investigated.

The results are presented and discussed using appropriate graphs. The results show that the presence of structural attenuation has very little effect on the first and second natural frequencies, but its effect on higher natural frequencies is very significant. As the γ damping parameter increases, the oscillation frequency decreases, so that for the dimensionless damping parameter of structures equal to γ = 12.66×10−3 , the fourth natural frequency becomes zero. Although in this case the imaginary part of the eigenvalue is equal to zero as in the case of divergence instability, but given that the real part of the eigenvalue is negative, the system will be stable. The results show that the presence of the intermediate abutment increases the natural frequencies and the critical speed of the system and as the position of the intermediate abutment approaches the center of the nanotube, its effect on increasing the natural frequencies increases. The presence of the support at the position ξs = 0.1 increases 43.53, 36.75 and 28.57% in the first, second and third frequencies, respectively. Also, the intermediate support increases the damping in higher modes.

Funding Statement: The authors received no specific funding for this study.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.