

 | Fluid Dynamics & Materials Processing |  |
DOI: 10.32604/fdmp.2022.021731
ARTICLE
CFD Analysis of Can Heating Process
1Mechanical and Industrial Manufacturing Department, Engineering Faculty of Mondragon Unibertsitatea, Mondragon, 20500, Spain
2Department of Food Engineering, Ankara University, Golbasi Kampusu, Golbasi, Ankara, 06830, Turkey
3Institute for Agricultural, Fisheries and Food Research ILVO, Merelbeke, 9820, Belgium
4NOFIMA Research Center, Stavanger, 4068, Norway
*Corresponding Author: David Alonso de Mezquia. Email: dalonso@mondragon.edu
Received: 31 January 2022; Accepted: 01 March 2022
Abstract: In this work, the thermal sterilization process in food cans has been analyzed using Computational Fluid Dynamics (CFD). STAR CCM+ software has been used in order to develop a numerical model to study the heating process of standard and the recently proposed toroidal shaped cans. The model has been validated comparing the results with the ones obtained experimentally and numerically that can be found in the literature. A good agreement between the obtained numerical results and the experimental ones has been obtained. The results also agree with other numerical models previously developed in the literature. Once the model has been validated, taking advance of the possibility to easily introduce movement in the simulations, new variables have been analyzed in the system using this model, such as rotational movement of the can. The model developed has been used to study the efficiency of the sterilization process with the two types of cans by means of calculating the temperature inside the systems and calculating the F0 parameter. It can be seen that the efficiency of the sterilization process is better in the toroidal cans. It has been also checked that CFD models can be very helpful in analyzing the temperature profiles inside the cans and making sure that the correct temperature has been obtained inside the can and the sterilization process has been correctly carried out.
Keywords: Toroidal can; heat transfer; CFD; retort
Nomenclature
| t | Time (s) |
| T | Temperature (°C) |
| F | F-value (min) |
| Z | Z-value (min) |
Sustainability is increasingly a global concern. This is evidenced by the goals for global sustainable development adopted by the United Nations [1,2]. Several of these objectives highlight the need to produce food more efficiently, increasing its lifespan and reducing the energy resources needed in this process. With regard to the use of food, one of the possible options is to increase the useful life of the products, thus avoiding their discarding due to expiration and making it possible to reach a greater number of people. There are different techniques to achieve this goal [3], being one of the most common food canning. In this process, the selected food is confined in a can, usually a metal can, and a sterilization process is carried out by means of a heat treatment. This heat treatment destroys as many pathogenic microorganisms, responsible for the food degradation, as possible while maintaining its nutritional and sensory characteristics.
For proper sterilization of the product, it is important to achieve a minimum temperature in all regions inside the can. If the right temperature conditions are not achieved throughout the can, there is a risk that the food will not be preserved as desired [4].
Depending on the pathogen to be eliminated, the minimum temperature to be reached and the time to maintain this temperature vary. Thus, for example, for Cl. Botulinum, one of the reference pathogens, 2.5 min at 121°C are necessary to obtain effective sterilization, while for Botulinum type E, the time required is 4.74 min at a temperature of 90°C. Additionally, these sterilization conditions also influence the sensorial quality of the final product obtained, so in some cases a different temperature is chosen and the time of process changes also [5].
There are methods to compare the effectiveness of heat treatment for each of the pathogens. One of the most used is the use of the parameter F0. This parameter makes it possible to compare the effectiveness of sterilization with respect to a pathogen by taking into account different temperature and time conditions in the process [5].
Food and its properties also have influence in the heating conditions obtained in the product being processed. Viscosity, for example, influences in which will be the main mechanism of heat transmission (conduction or convection). Other external parameters, such as movement (can rotation, agitation, etc.) can also have a profound impact on the rate of heat transfer [6].
The thermal process described above could be carried out in different devices, but they all have in common that a high amount of heat has to be applied for a certain time. The energy required for this process is generally high and the efficiency of the process is usually low. Achieving a reduction in process times would be a major step towards increasing the energy efficiency of the process.
One of the innovations made in these fields has been the toroidal can [7]. This toroidal can has a new design. It maintains the cylindrical shape but adds a hole from side to side in the center. The temperature distribution for the conduction and convection heated cases in this new can shape was studied both experimentally and numerically using Computational Fluid Dynamics (CFD) simulations, which have proven to be a powerful tool for the modelling and optimization of these processes. The results showed that the heating rate inside the can was improved, thus reducing the treatment time needed and the energy consumed in the process. However, the heating process inside the cans varies depending on the type of food inside it. One of the methods to available to analyse these processes and optimize their designs and process parameters, are the CFD tools. These tools allow different cases to be analyzed numerically, and the influence of each parameter on the process can be obtained.
In this work, this new canning system has been analyzed and compared with the standard canning geometry using the CFD methodology, through STAR CCM+ software. A numerical model has been developed and validated. This model has been used in order to analyze the thermal efficiency of these systems introducing new variables such as the rotational movement of the can. This work also demonstrates the ability of numerical analysis to identify the optimal conditions of the process.
The heating process of cans with different geometries has been analyzed. To do this, a computational model to simulate the heating process of a standard can of 73 × 110 mm has been used and of a toroidal can of the equivalent volume. In this case, the height of the can is maintained and the radius is changed to obtain the same volume. The radius of the hole of the can is of 9 mm. More detail of the dimensions of the cans can be seen in [6]. Both cases have been simulated with the cans in a vertical position and under static conditions. The simulations have been carried out using the STAR CCM+ software. These results have been compared with the previously published experimental and numerical results [6,7].
In the two numerical models used, an axisymmetric 2D geometry has been used. The use of this type of geometry makes it possible to greatly reduce the number of elements to be used and to reduce the time required for simulation. The selected mesh has been the trimmed type. The numerical models selected (laminar flow, VOF model, etc.) and the principal parameters (mesh size, time step, etc.) have been similar to those used in [6] and [7]. In order to be able to make a comparison between the results of this work and the ones published [6,7]. The meshes used for the numerical modeling are shown in Fig. 1.

Figure 1: Mesh used for the toroidal can (right) and the standard can (left)
The boundary conditions used for the simulations have been selected according to the experimental process used in [6]. In these experiments, the can was submerged in boiling water in a vertical retort. With this experimental procedure, it can be assumed that the temperature of the medium is constant. In all the numerical cases a can surface temperature equal to the temperature of the medium and an initial temperature of the can contents equal to the ambient temperature has been considered.
In order to make a comparison of the results obtained experimentally and numerically, in this work we have determined, in the case of the standard can, the temperature at two points inside the can, and in the case of the toroidal can, the temperature at one point inside the can. In the case of the standard can, these points are located in the middle of the radius of the cavity and at a height of 5.5 and 8.25 cm. In the case of the toroidal can, it is a point in the middle of the radius of the cavity and a height of 7.5 cm, as can be seen in Fig. 2. In toroidal can, as only one point is used, a point with a height between the ones of the other two has been selected.
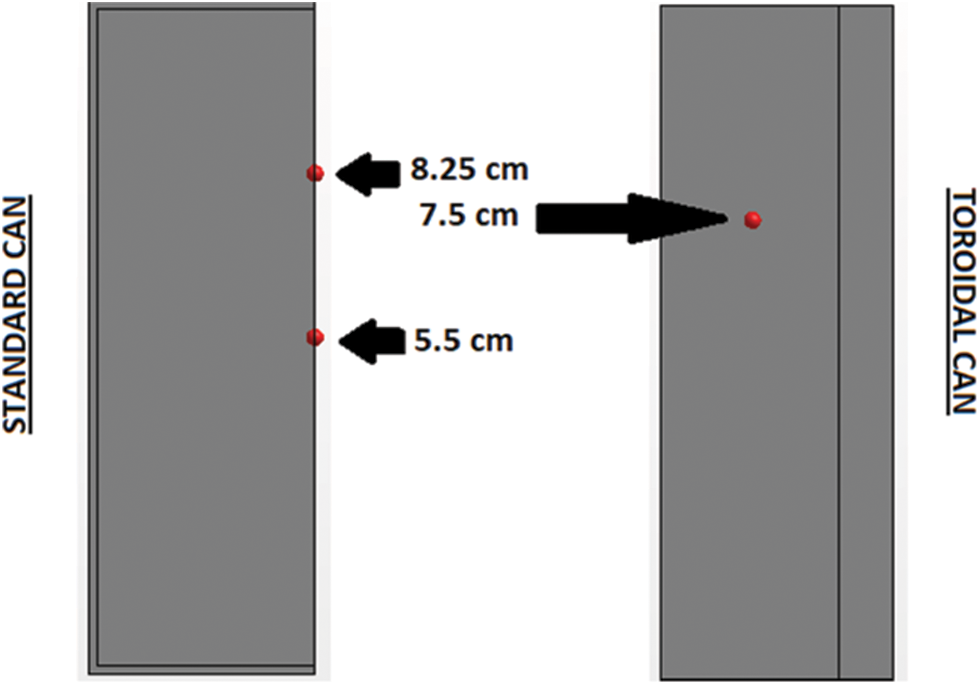
Figure 2: Position of the analyzed points in the standard can (left) and toroidal can (right)
As mentioned above, one of the main variables to consider is the lethality of the process. One of the ways to measure this parameter is through the F coefficient. This parameter allows comparing the effectiveness of the heat treatment for a specific pathogen and with different temperature and time conditions. When a reference temperature of 121.1°C and a z-value of 10°C is used, this parameter is called F0. There are different ways to calculate this parameter and with different expressions (general model, Ball method…) [8–11]. In this study the general method has been used, which is defined by the following expression:
This parameter has been calculated for the experimental values obtained for both toroidal and standard cans. This parameter has been obtained from the data of the temperature inside the can at the different points as a function of the process time. The results obtained for this parameter are shown in Section 3.
The data obtained for the temperature in the model developed has been analyzed. In the case of the toroidal can the data obtained for a can full of water has been compared with the one obtained experimentally and numerically with FLUENT that can be found in [5]. These data is shown in Fig. 3.
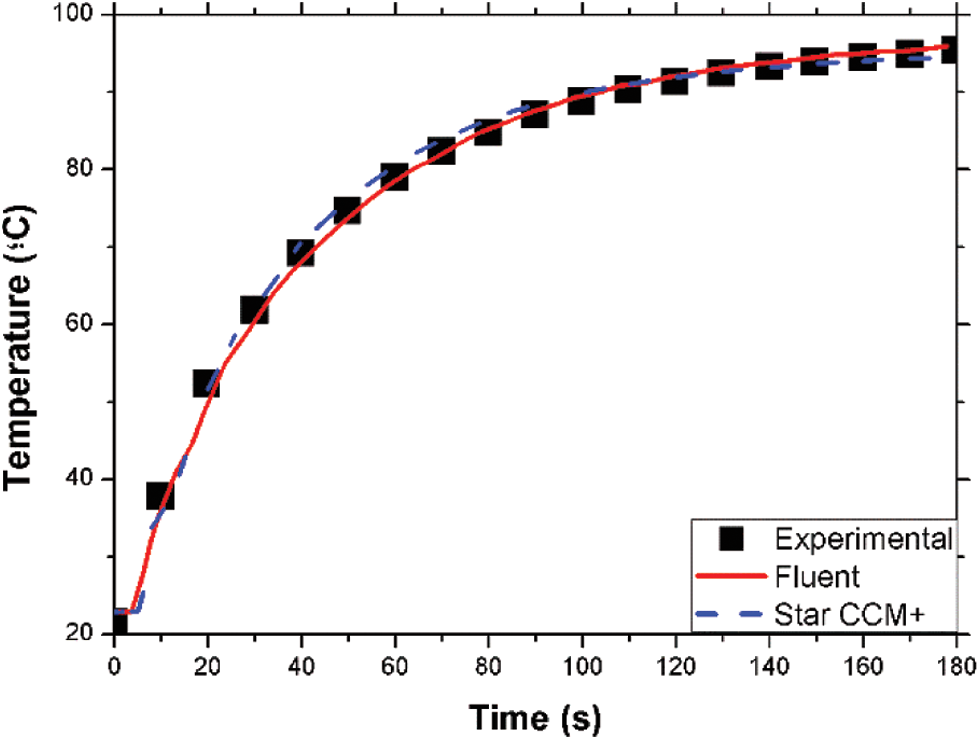
Figure 3: Temperature data on an internal point at 7.5 cm of the toroidal can obtained experimentally and numerically with ANSYS-FLUENT [5] and STAR CCM+
Fig. 4 shows the results obtained for the standard can at two different internal points. In this case, a standard can filled with water and a 10% of air headspace is studied.
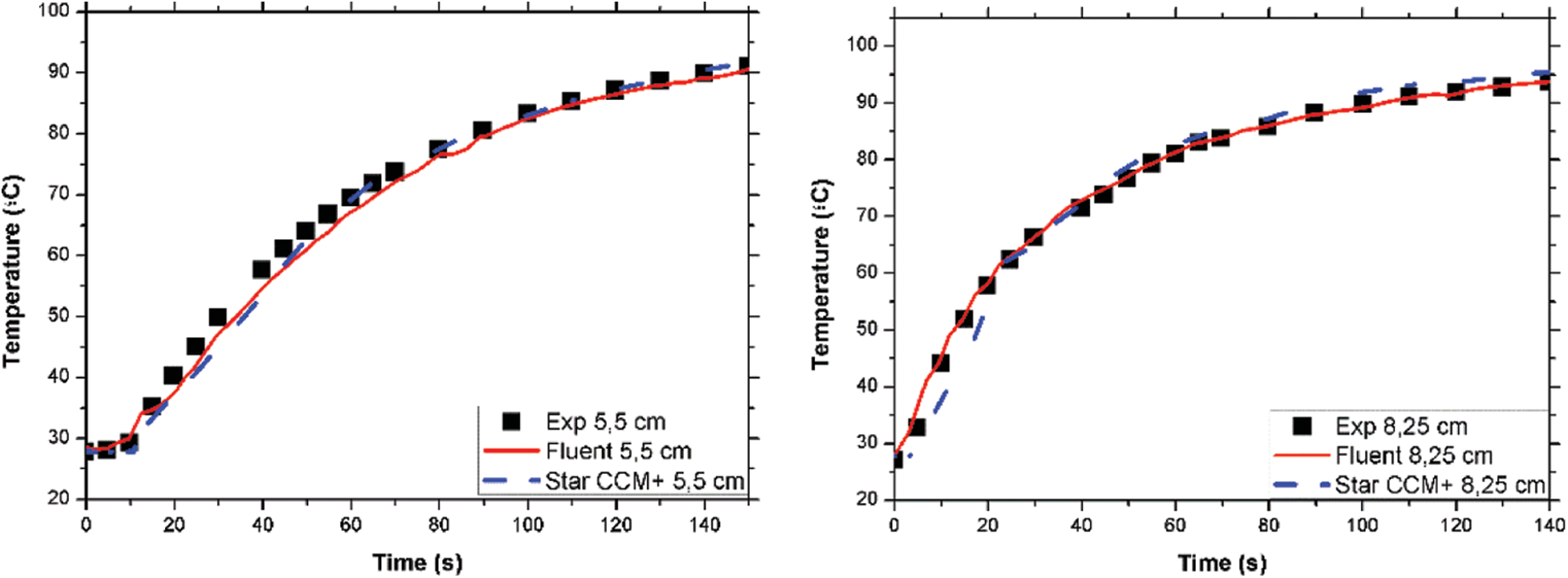
Figure 4: Temperature data on two internal points at 5.5 cm (left) and 8.25 cm (right) of the standard can obtained experimentally and numerically with ANSYS-FLUENT [7] and STAR CCM+
The results obtained show that the data calculated using the model developed in STAR CCM+ have a good agreement with the experimental ones both in the toroidal and the standard can. These results also agree with the ones obtained by other CFD software for these can geometries. This validates the numerical model developed for the case of both the standard and the toroidal can in the case when two phases (air and water) and present.
In the case of the cans analyzed in this study, no movement has been applied for the model development, but the movement of the cans (End Over End, rotation, etc.) improves the heating process and helps to homologize the temperature inside the cans. For this reason, once the model has been validated, additional simulations have been carried out in the toroidal can, introducing End Over End rotation. The results obtained can be seen in Fig. 5. Here the results obtained for the 7.5 cm height point in the can with no movement are compared with the ones for the 7.5 and 5.5 cm height points of the can with a 10 rpm EoE rotation. As can be seen, the temperature obtained in the case of the rotational can are slightly better. In this case, a higher temperature in the system is obtained in less time. This means that when introducing the movement of the can the pathogen suppressing process is started earlier so less total heating time is needed to obtain the same level of sterilization. One can also see that the temperature profile has more instabilities, but this should be because of the movement of the can that causes a more mass diffusion of the liquid inside the it. Another point that can be pointed out is that the temperature of the points at 7.5 and 5.5 cm is very similar. This confirms that the movement of the can helps to homologize the temperature of the fluid inside the can.
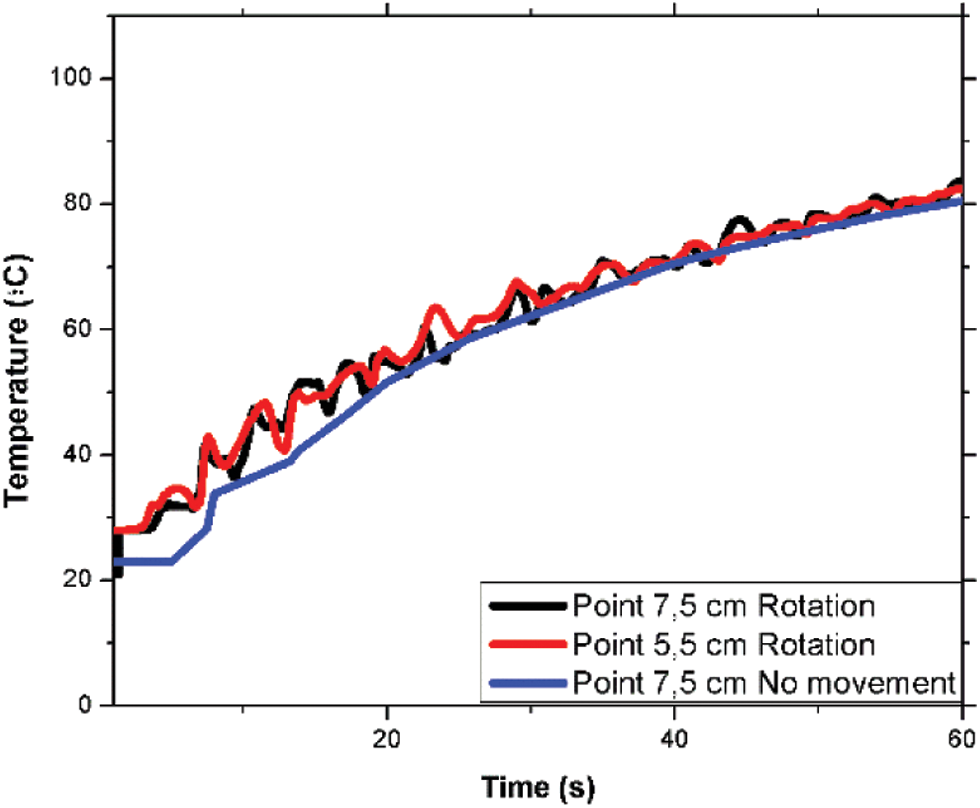
Figure 5: Comparison of the temperature of the points inside the toroidal can with no movement and rotation of the can
On the other hand, using the parameter F0, the efficiency of the thermal sterilization processes carried out on both cans with the same temperature of the external medium and same process time has been compared using the models developed. Only the heating part of the process, the one simulated previously, has been analyzed. In order to obtain a complete value of the F0, parameter the whole sterilization process should be analyzed, including the temperature maintaining and cooling parts, but this analysis of the heating part can give an idea behavior of the system. In this case, three points in the toroidal can and two points in the standard can have been studied. As the cans have no movement, a vertical gradient in the temperature is observed, Fig. 6 so the height is one of the most important parameters in this case. This is why points with the same height have been selected in the toroidal can in order to make a comparison with the standard one.
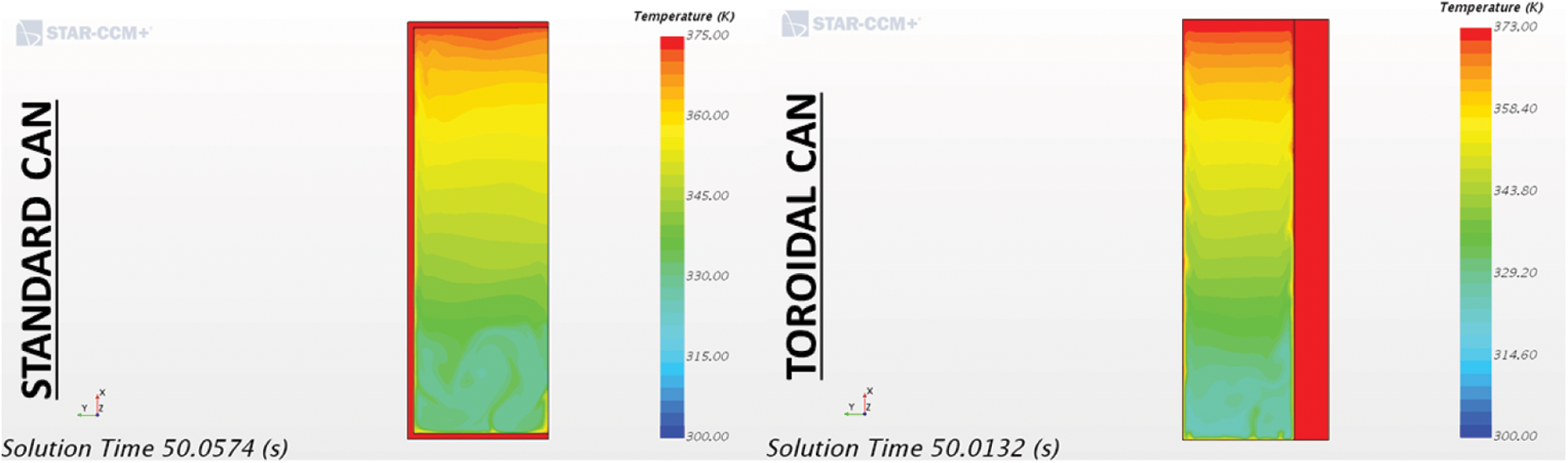
Figure 6: Temperature distribution inside the toroidal and standard can in function of time
Fig. 6 shows the data obtained for F0 parameter for the heating part of the process for both the standard and the toroidal can.
As can be seen in Fig. 7, in the standard can, at the point located at 5.5 cm, the lowest lethality factor is obtained, while for the point located at 8.25 cm for the toroidal can is the one, which has the higher sterilization value. As can be seen for the results obtained when comparing the equivalent points in both geometries, the toroidal can obtains better results. This confirms that the toroidal can could be a good option in order to improve the sterilization process in cans. However, one has to consider that the point to be taken as a reference is the most critical in terms of sterilization. If the minimum temperature has not been reached, the sterilization of the product inside the can cannot be assured. This remarks the importance of how to detect the lowest temperature point, and using this for sterilization calculations. Experimental data only allows data to be obtained from a limited number of points, whereas numerical models extend the range of points that can be analyzed. A correct numerical model would allow to obtain at any time which is the coldest point of the can and to use the temperature of the can to make the sterility calculations. This would be a more conservative method and would give greater assurance that the desired sterilization of the product has been achieved.
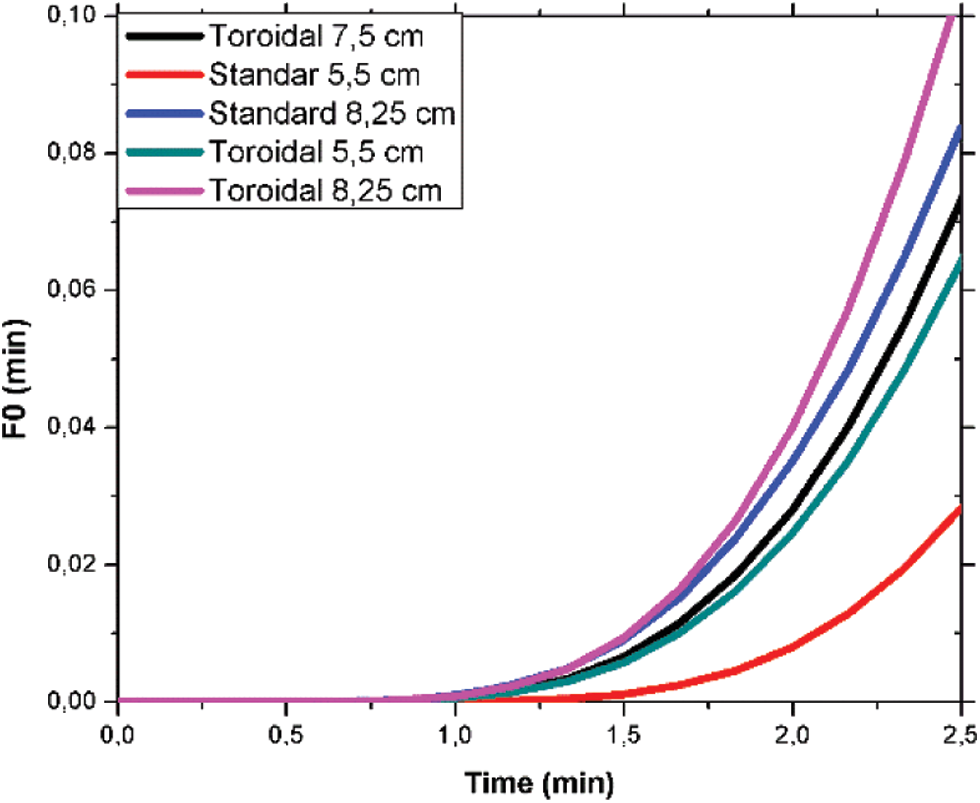
Figure 7: Lethality factor F0 calculated for each of the analysed can geometries
The results obtained show that to reach the same sterilization point, less time is needed in a toroidal can than in a standard can. This translates into a shorter treatment time and a reduction of the energy required in the process, and increases the energy efficiency of the process.
In this work, we have compared the results obtained in the simulation of the heating process of a standard can and the new proposed toroidal can geometry. The results obtained experimentally and numerically in the literature have been compared with the ones obtained by STAR CCM+ software. The results obtained show that there are no major differences between the two CFD programs, and there is a good agreement with the experimental data.
Additionally, the efficiency of both geometries has been compared in a sterilization process. For this purpose, the temperature data obtained inside the can as a function of time in equivalent points has been used to calculate the process parameter F0. The results obtained show that a higher level of sterility is achieved in the toroidal cans in less time at the same temperature of the medium, and therefore the treatment time needed with this type of can could be reduced. This would in turn reduce the energy required from the process and increase the energy efficiency of the process.
It has also been checked that it is important to compute the cooler point in the can. This point represents the point in which the sterilization level is smaller, and is the one that denotes the sterilization level achieved in the whole can. As this point changes position during the heating process, is not easy to measure it experimentally, but CFD simulations could help to track this point and determine its position to improve the sterilization process of the cans.
We have also checked that EOE rotation of the can also help to improve the temperature homogenization of the cans, improving also the efficiency of the process and the quality of the final product. A headspace of air is also a good option to improve the temperature homogenization in the cans. Adding this parameter to the simulation could also help to analyze its effect and to optimize the correct quantity of air that should be used in each case.
Funding Statement: This work was carried out in the framework of the SUSFOOD2 funded InProVe Project and the Project “Procesamiento Innovador de Verduras y Patatas” (PCI2018-093129) of the Spanish Government. It was also supported by the Research Group Program (IT1505-22) and μ4F (KK-2021/00082) from the Basque Government.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
1. UN General Assembly (2015). Transforming our world: The 2030 agenda for sustainable development. https://sdgs.un.org/goals. [Google Scholar]
2. Food and Agriculture Organization of the United Nations (2013). Food Wastage Footprint-Impacts on Natural Resources–Summary report, 2013. Food Wastage Footprint (Project). [Google Scholar]
3. Lee, S., Hoi, W., Jun, S. (2016). Conventional and emerging combination technologies for food processing. Food Engineering Reviews, 8, 414–434. DOI 10.1007/s12393-016-9145-3. [Google Scholar] [CrossRef]
4. Pflug, I. J. (1987). A textbook for introductory course in microbiology and engineering of sterilization. USA: University of Minneapolis, Environmental Sterilization Laboratory. [Google Scholar]
5. Holdsworth, D., Simpson, R. (2007). Thermal processing of packaged foods. USA: Springer. [Google Scholar]
6. Erdogdu, F., Tutar, M. (2010). Velocity and temperature field characteristics of water and air during natural convection heating in cans. Journal of Food Science, 76, E119–E129. DOI 10.1111/j.1750-3841.2010.01913.x. [Google Scholar] [CrossRef]
7. Karaduman, M., Uyar, R., Erdogdu, F. (2012). Toroid cans–an experimental and computational study for process innovation. Journal of Food Engineering, 111(1), 6–13. DOI 10.1016/j.jfoodeng.2012.02.009. [Google Scholar] [CrossRef]
8. Bigelow, W. D., Esty, J. R. (1920). The thermal death in relation to time of typical thermophilic organisms. Journal of Infectious Diseases, 27, 602–617. DOI 10.1093/infdis/27.6.602. [Google Scholar] [CrossRef]
9. Ball, C. O., Olson, F. C. W. (1957). Sterilization in food technology. Theory practice and calculation. USA: McGraw-Hill Book Company. [Google Scholar]
10. Teixeira, A. A., Dixon, J. R., Zahradnik, J. W., Zinsmeister, G. E. (1969). Computer determination of spore survival distributions in thermally-processed conduction-heated foods. Food Technology, 23(3), 78–80. [Google Scholar]
11. Teixeira, A. A., Dixon, J. R., Zahradnik, J. W., Zinsmeister, G. E. (1969). Computer optimization of nutrient retention in the thermal processing of conduction-heated foods. Food Technology, 23(3), 137–142. [Google Scholar]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |