

 | Fluid Dynamics & Materials Processing |  |
DOI: 10.32604/fdmp.2022.021500
ARTICLE
Numerical Analysis of the Influence of Buoyancy Ratio and Dufour Parameter on Thermosolutal Convection in a Square Salt Gradient Solar Pond
1Team of Heat Transfer and Energetic (UAE/U10FST), Faculty of Sciences and Techniques of Tangier, Abdelmalek Essaâdi University, Tangier, 90040, Morocco
2Mathematics and Physics Laboratory (LAMPS), Perpignan Via Domicia University, Perpignan, 66860, France
*Corresponding Author: Yassmine Rghif. Email: rghifyassmine@gmail.com
Received: 18 January 2022; Accepted: 20 February 2022
Abstract: This work aims to investigate numerically the influence of the buoyancy ratio and the Dufour parameter on thermosolutal convection in a square Salt Gradient Solar Pond (SGSP). The absorption of solar radiation by the saline water, the heat losses and the wind effects via the SGSP free surface are considered. The mathematical model is based on the Navier-Stokes equations used in synergy with the thermal energy equation. These equations are solved using the finite volume method and the Gauss algorithm. Velocity-pressure coupling is implemented through the SIMPLE algorithm. Simulations of the SGSP are performed for three values of buoyancy ratio (N = 1, 2 and 10), three values of Dufour parameter (Df = 0, 0.2 and 0.8) and some sample meteorological data (Tangier, Morocco). Results show that the highest dimensionless temperature of the storage zone is found for N = 10. In the same zone and for the same value of N, the dimensionless salt concentration decreases very slightly versus time (unlike for N = 1 or 2). Moreover, increasing Df from 0 to 0.8 causes a decrease in the dimensionless temperature of the SGSP storage zone and this decrease is more pronounced for N = 1 and N = 2.
Keywords: Buoyancy ratio; Dufour effect; numerical investigation; salt gradient solar pond; thermosolutal convection
Nomenclature
| C* | Dimensionless salt concentration |
| Df | Dufour parameter |
| g | Gravitational acceleration, m/s2 |
| H | Pond height, m |
| I0 | Incident solar radiation, W/m2 |
| Ir | Reflected solar radiation, W/m2 |
| L | Pond width, m |
| Le | Lewis number |
| N | Buoyancy ratio |
| P* | Dimensionless pressure |
| Pr | Prandtl number |
| T* | Dimensionless temperature |
| U | Wind velocity, m/s |
| (u*,v*) | Dimensionless velocity components |
| (x*,y*) | Dimensionless Cartesian coordinates |
| e.g. | |
| α | Thermal diffusivity, m2/s |
| κTC | Dufour coefficient, m5.K/kg.s |
| λ | Thermal conductivity, W/m.K |
| ν | Kinematic viscosity, m2/s |
| ρ | Density, kg/m3 |
| τ | Dimensionless time |
| φ | Heat flux density, W/m2 |
A Salt Gradient Solar Pond (SGSP) is considered as a simple device for solar energy collection and long term low-temperature heat storage [1,2]. It is a large pond composed by three water zones of different salt concentration [3], namely: the Lower Convective Zone (LCZ) at the pond bottom, the Upper Convective Zone (UCZ) at the pond top and the Non-Convective Zone (NCZ) located between these two convective zones. The highest salt concentration is in the LCZ whereas the lowest is in the UCZ. In the NCZ, the salt concentration increases linearly with the depth. Therefore, the heat and mass transfer between the LCZ and UCZ are by diffusion. The amount of solar heat stored in the LCZ can be extracted with heat exchangers [4] which are usually placed on the SGSP bottom [5,6]. However many works carried out on SGSP shown that heat extraction from both NCZ and LCZ improves the overall SGSP efficiency [7,8]. The amount of heat extracted can be used for many applications such as lower temperature industrial process [9], electricity generation [10] or to preheat the feed water for solar distillers [11].
The concept of a SGSP was introduced in 1902 by Kalecsinsky [12]. The latter noticed that the temperature of the natural lake Medve in Transylvania, Hangaria (42° 44’ N, 28° 45’ E) reached, at a depth of 1.32 m, 70°C [13]. Afterwards, several researchers reported the same notice in other lakes, such as Hot Lake in Washington-United States [14], Lake Mahega in Western Uganda [15] and Lake Vanda in Antarctica [16]. These lakes were characterized by high salt concentration in the lower part and low salt concentration in the upper part, leading to a vertical variation of the salt concentration [17]. In this sense, Kalecsinsky suggested that this high temperature is mainly due to the vertical variation of the salt concentration that prevents natural convection and traps solar radiation in the lower part of the lake [18].
The presence of both temperature and salt concentration gradients in the SGSPs leads to the development of thermosolutal convection [19]. The effects of this last one on the SGSP thermal performance and stability were evaluated for the first time by Suárez et al. [19]. The two-dimensional model developed is essentially based on Navier-Stokes, energy and mass transfer equations. They demonstrated that the LCZ temperature is over predicted if the thermosolutal convection is neglected. Thus, the SGSP efficiency can be overestimated, particularly in models that consider the UCZ temperature is the same of that of ambient air. Recently, in order to analyze Soret and Dufour effects on heat and mass transfer in a SGSP and its storage efficiency, Rghif et al. [20] were the pioneers to develop a two dimensional numerical model. This model is based on Navier-Stokes, thermal energy and diffusion equations. It was found, that the increase of Dufour parameter from 0 to 0.8 leads to an augmentation of the heat losses from the SGSP surface by about 8.53% and to a decrease of its storage efficiency by 5.56%. Following Rghif et al.’s study [20], it was recommended to integrate the phase change material in the SGSP, for the purpose to mitigate Dufour effect, if the value of the Dufour parameter is high [21].
In a previous work [20], it was shown that Dufour effect must be taken it account in order to avoid overestimation of the results. However, Rghif et al.’s [20] study was conducted for one value of buoyancy ratio (N = 10). Therefore, it is necessary to develop a model in order to analyze Dufour effect developed in a SGSP for different values of buoyancy ratio (N = 1, 2 and 10). Therefore, the present study aims to investigate numerically the thermosolutal buoyancies with Dufour effect developed in a square SGSP.
The physical model of the SGSP considered in this study is presented in Fig. 1. It consists of an open square enclosure (A = 1). Its vertical (x* = 0 or x* = 1 and 0 < y* < 1) and bottom (y* = 0 and 0 < x* < 1) walls are adiabatic and impermeable while its upper part (y* = 1) exchange heat (φtt) by convection (φconv), radiation (φrad) and evaporation (φevap) with its surrounding. Moreover, this SGSP has three zones (LCZ, NCZ and UCZ) of different salt concentration water and thickness as Fig. 1 illustrates. At the saline water free surface (y* = 1), a part of the solar radiation (I) is reflected back to the atmosphere (Ir), the rest is gradually absorbed by the saline water and undergoes a continuous attenuation (φy) before reaching the SGSP bottom (φy* = 0).
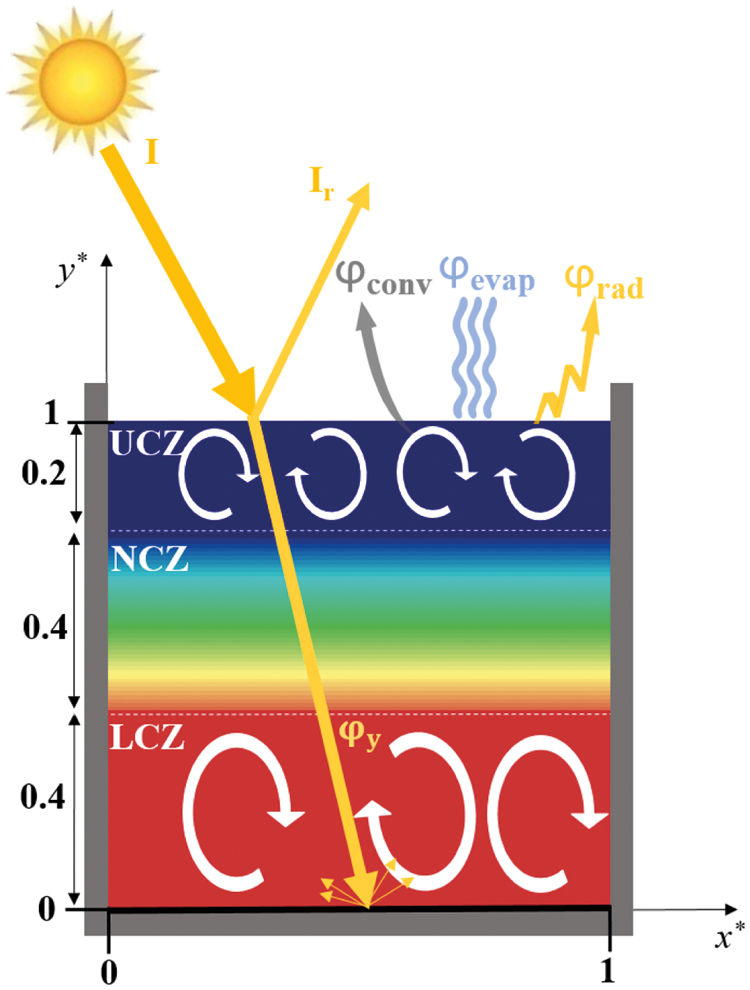
Figure 1: Physical model of the SGSP considered
In this study, it is assumed that: a) The saline water is an incompressible and Newtonian fluid; b) The flow is two-dimensional and the natural convection in the LCZ and UCZ is carried out in laminar mode; c) The thermal properties of the saline water are constants except the density in the buoyancy term, which obeys to the Boussinesq approximation [22,23].
Taking account of the above assumptions, the governing dimensionless equations describing the transfers that occur in the SGSP can be expressed in the referential (Oxy) as follows:
With the dimensionless quantities are:
The Prandtl number (Pr), the Rayleigh number (Ra), the buoyancy ratio (N), the Dufour parameter (Df), the dimensionless source term (S´) and the Lewis number (Le) are respectively defined as follows:
where S is the heat source term that represents the amount of the solar radiation absorbed by a layer of saline water. More calculation details of this term is presented elsewhere [21].
The dimensionless temperature profile, the dimensionless salt concentration in the LCZ and the UCZ are evaluated using the following expressions:
As initial conditions (τ = 0), the fluid is assumed to be motionless (u* = v* = 0) and the temperature of the saline water is equal to its initial temperature; so T* = 0. The salt dimensionless concentration is set equal to:
For τ > 0, on the walls, the two components of the velocity are null due to no slip boundary conditions. At the saline water free surface (y* = 1), the y-component velocity is set equal to 0 and its x-component is evaluated from the shear stress caused by the wind [24].
where Uy and Cf,y are the wind speed at a given height (y) above the SGSP and the drag coefficient, respectively. These parameters are calculated from the following expressions [24,25]:
K, y and z0 are respectively the Von Karman constant (K = 0.4 [25]), the height above the SGSP free surface and the roughness length (0.001 m for water [25]).
The evaluation of the heat losses (φtt) at y* = 1 by convection (φconv), radiation (φrad) and evaporation (φevap) are reported in our previous work [20]. Nevertheless, the vertical and bottom walls are adiabatic and impermeable. Thus, the dimensionless temperature and salt concentration boundary conditions are expressed as [20]:
3 Numerical Method and Validation
Eqs. (1)–(5) associated to initial and boundary conditions (11)–(15) are solved iteratively using the implicit finite volume method and Gauss elimination procedure. The pressure-velocity coupling is treated by SIMPLE algorithm [26]. The centered scheme is retained for the convective and diffusive terms. The iterative procedure is stopped when the following test is respected.
In order to accelerate the convergence of the iterative procedure, under relaxation coefficients 0.50 and 0.85 are used, respectively, for the momentum, the thermal energy and mass equations [26].
The numerical model developed in Fortran 95, was validated by applying it to three previous works reported in the literature (the numerical model validation is described in details elsewhere [20]). The first one is the problem of thermosolutal convection inside a rectangular enclosure with vertical temperature and salt concentration gradients (the upper and lower walls are adiabatic and impermeable). Computations were performed for A = 0.5, Pr = 1, Ra = 105, Le = 2 and for N = 0.8 and N = 1.3. The second one is about thermosolutal convection inside a rectangular cavity with Soret and Dufour effects. Calculations were conducted for A = 2, Pr = 1, Ra = 105, Le = 2 and for N = 2. The third one is about the solar radiation absorption model in Mirror Lake in Storrs, USA. Detailed validation steps are described in our previous work [20].
The effects of buoyancy ratio and Dufour parameter on the thermosolutal convection in the SGSP are investigated during ten days (midnight of July 03 to midnight of July 13) using meteorological data of Tangier [27,28], with Ra = 1012, Pr = 6, Le = 75, Δτ = 6 × 10–9, N = 1, 2 and 10, Df = 0, 0.2 and 0.8 and for a grid mesh of (50 × 100) [20].
The dimensionless temperature evolution versus time of the SGSP profiles during the simulation of the SGSP operation corresponding to a duration between τ = 0 and τ = 0.11 is presented in Fig. 2. As it can be seen in this figure, the dimensionless temperature profiles are similar from initial state (τ = 0) to τ = 0.008 and whatever the values of N and Df retained. As time increases, the LCZ and NCZ dimensionless temperatures increase due essentially to the augmentation of the amount of solar radiation absorbed by the saline water solution. Moreover, the heat losses via the SGSP free surface reduce the UCZ dimensionless temperature. At the end of the simulation duration (τ = 0.11), the lower values are located at the UCZ and the highest values of the LCZ dimensionless temperature are found for N = 10 and whatever the Df value (Fig. 2). For this value of N, the mass buoyancy forces are predominant compared to those of the thermal origins. Consequently, the mass convection is superior to the thermal convection leading to this highest temperature value in the LCZ. Hence, the diminution of the buoyancy ratio from 10 to 1 enhances the heat transfer in the SGSP more than the augmentation of Dufour parameter from 0 to 0.8.
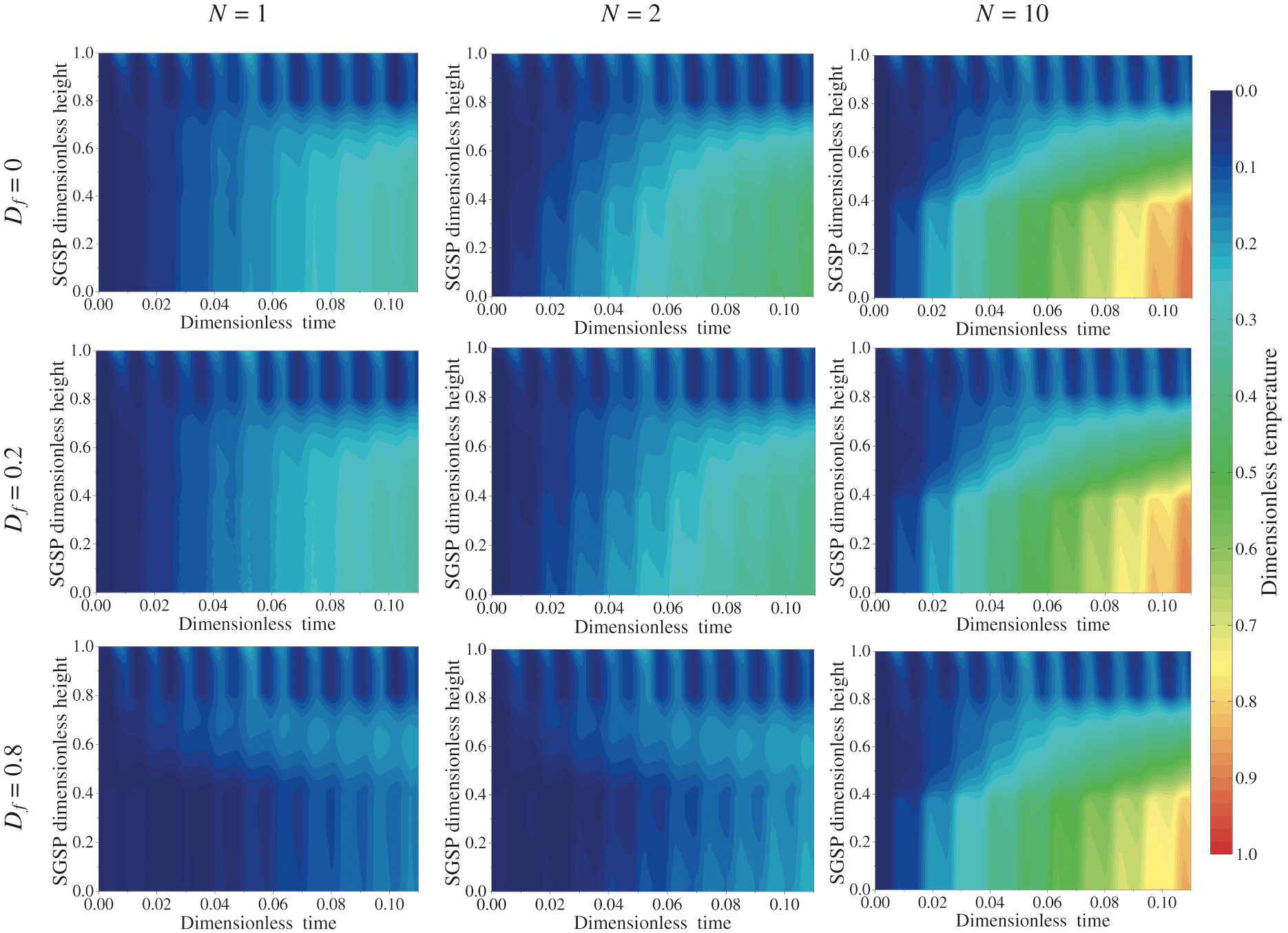
Figure 2: SGSP dimensionless temperature profiles during the simulation period
Fig. 3 shows the evolution over time of the dimensionless temperature at three positions in the LCZ: y* = 0 (bottom), y* = 0.2 (middle) and y* = 0.4 (top). It should be noted that when the thermal and mass buoyancy forces are equal (N = 1), the LCZ dimensionless temperature is the same. In addition, whatever the value of Df considered and for N = 2 or 10, the dimensionless temperature decreases linearly from the bottom to the top of this zone. It will be noted that this result cannot be obtained from the 1D model based on the assumption of a homogeneous temperature in the LCZ. Besides, the dimensionless temperature is depending on the value of the buoyancy ratio and Dufour parameter. For the three values of Df (0, 0.2 and 0.8), the highest temperature is found for N = 10 for which mass buoyancy forces are superior to those of thermal origins. Moreover, as buoyancy ratio decreases from 10 to 1, the Dufour effect on the LCZ dimensionless temperature is more pronounced. For example, in the LCZ bottom, the dimensionless temperature decreases as Df increases from 0 to 0.8 by about 0.23 for N = 2 and 0.08 for N = 10 (Fig. 3). Therefore, the Dufour effect is more relevant on the storage zone temperature as the buoyancy ratio is small. In this case, the thermal buoyancy forces are greater than to those of mass origins. Therefore, the thermal convection is predominant compared to the mass convection and consequently an augmentation of the Dufour effect.
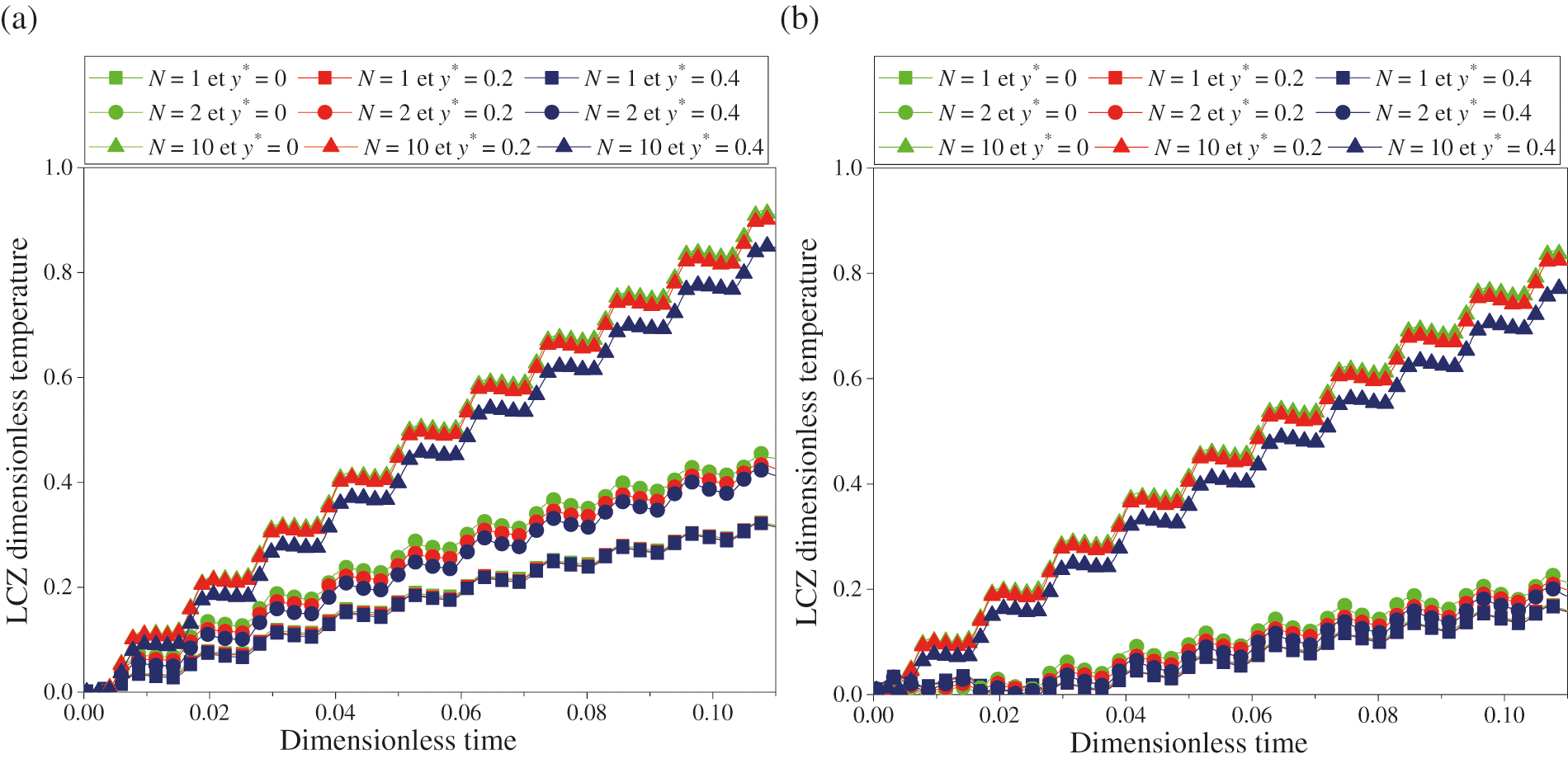
Figure 3: Dimensionless temperature variation over time of the LCZ for (a) Df = 0 and (b) Df = 0.8
4.2 SGSP Salt Concentration Fields
Controlling the salt concentration distribution in the SGSP is a key parameter for a long period operation of a SGSP. In this sense, the evolution over time of the dimensionless salt concentration in the LCZ and UCZ are presented, for the different values of Df and N retained in this study, in Figs. 4 and 5, respectively. As it can be seen in Fig. 4, the dimensionless salt concentration of the LCZ decreases quickly and continuously for N = 1 and N = 2 and very slightly for N = 10. The salt concentration of the upper convective zone increases over time as is presented in Fig. 5. Increasing Df from 0 to 0.8 leads to a decrease of the salt concentration in the LCZ and an increase in the UCZ for the three values of the buoyancy ratio considered. These results is in agreement with those reported in previously published work [20].
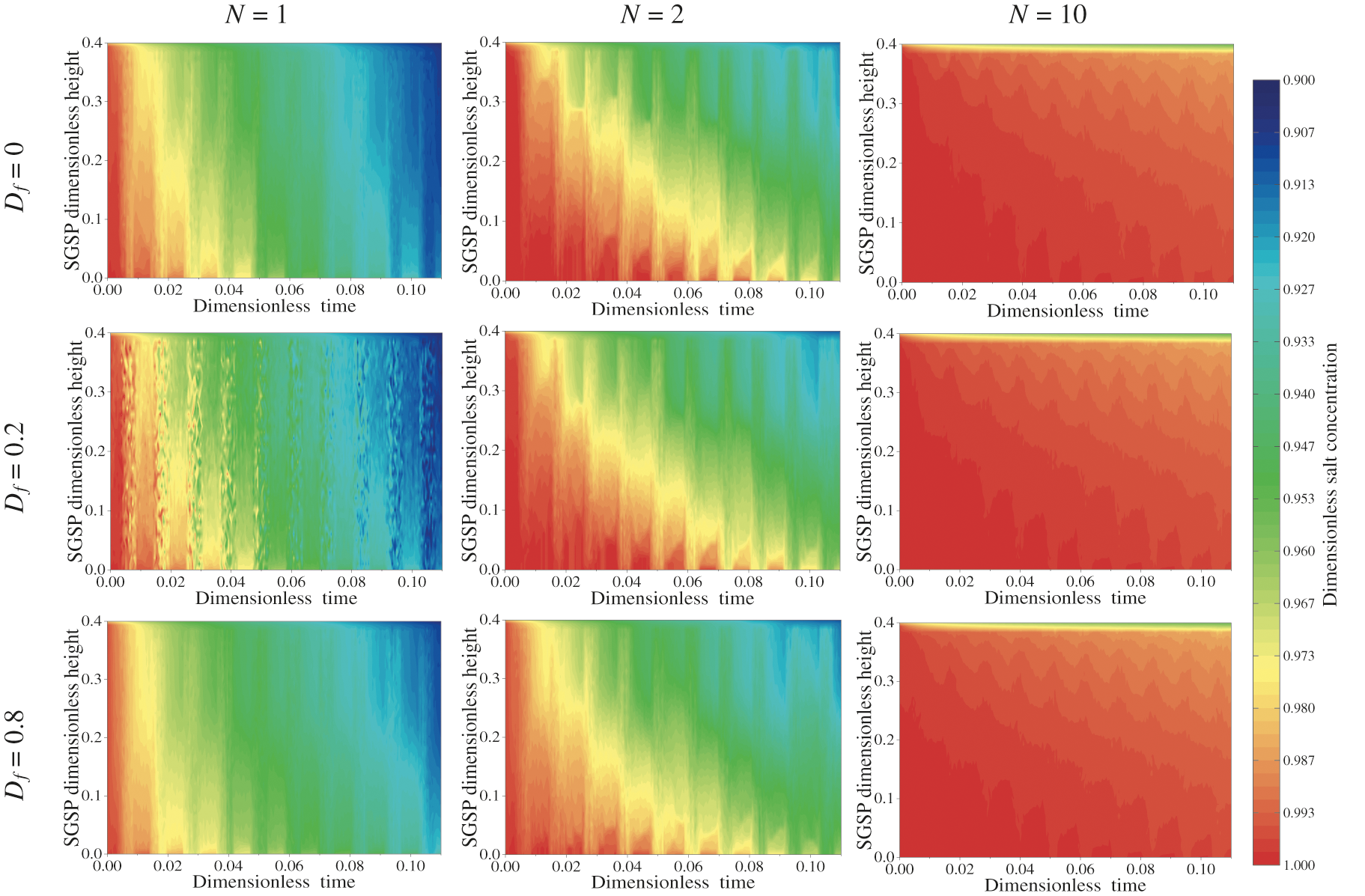
Figure 4: Variation of the LCZ salt concentration profiles during the simulation period

Figure 5: Variation of the UCZ salt concentration profiles during the simulation period
In this study, the influences of buoyancy ratio and Dufour parameter on thermosolutal convection in a square Salt Gradient Solar Pond (SGSP) are investigated numerically. The governing equations are solved using the implicit scheme and Gauss algorithm. The simulations are performed during ten days with the meteorological data of the Tangier city in Morocco, for three values of buoyancy ratio N = 1, 2 and 10 and three values of Dufour parameter Df = 0, 0.6 and 0.8. The main conclusions can be summarized as follows:
• Regardless the value of Dufour parameter, the higher LCZ temperatures are obtained for higher value of the buoyancy ratio (for N = 10);
• Increasing the value of the Dufour parameter decreases the storage zone dimensionless temperature;
• The Dufour effect on the LCZ dimensionless temperature is all the more relevant as the buoyancy ratio is low;
• The dimensionless salt concentration of the LCZ decreases quickly as time increases for N = 1, 2 and weakly for N = 10.
As future path of these current findings, an experimental analyze will be perform.
Acknowledgement: The authors are thankful to the National Center for Scientific and Technical Research of Morocco (CNRST) for providing us with the access to the HPC-MARWAN calculation service.
Funding Statement: The authors received no specific funding for this study.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
1. Rghif, Y., Zeghmati, B., Bahraoui, F. (2021). Numerical study of Soret and Dufour coefficients on heat and mass transfer in a salt gradient solar pond. AIP Conference Proceedings, 2345, 020003. DOI 10.1063/5.0049389. [Google Scholar] [CrossRef]
2. Colarossi, D., Principi, P. (2022). Experimental investigation and optical visualization of a salt gradient solar pond integrated with PCM. Solar Energy Materials and Solar Cells, 234(8), 111425. DOI 10.1016/j.solmat.2021.111425. [Google Scholar] [CrossRef]
3. Nait Brahim, A., Rghif, Y., Bahraoui, F. (2022). Numerical investigation of solar energy storage by a salt gradient solar pond in several Moroccan cities. E3S Web of Conferences, 336(2), 00020. DOI 10.1051/e3sconf/202233600020. [Google Scholar] [CrossRef]
4. Leblanc, J., Akbarzadeh, A., Andrews, J., Lu, H., Golding, P. (2011). Heat extraction methods from salinity-gradient solar ponds and introduction of a novel system of heat extraction for improved efficiency. Solar Energy, 85(12), 3103–3142. DOI 10.1016/j.solener.2010.06.005. [Google Scholar] [CrossRef]
5. Tabor, H. Z., Doron, B. (1990). The Beith Ha’Arava 5 MW(e) solar pond power plant (SPPP)—Progress report. Solar Energy, 45(4), 247–253. DOI 10.1016/0038-092X(90)90093-R. [Google Scholar] [CrossRef]
6. Jaefarzadeh, M. R. (2006). Heat extraction from a salinity-gradient solar pond using in pond heat exchanger. Applied Thermal Engineering, 26(16), 1858–1865. DOI 10.1016/j.applthermaleng.2006.01.022. [Google Scholar] [CrossRef]
7. Khalilian, M., Pourmokhtar, H., Roshan, A. (2018). Effect of heat extraction mode on the overall energy and exergy efficiencies of the solar ponds: A transient study. Energy, 154(4), 27–37. DOI 10.1016/j.energy.2018.04.120. [Google Scholar] [CrossRef]
8. Date, A., Yaakob, Y., Date, A., Krishnapillai, S. (2013). Heat extraction from non-convective and lower convective zones of the solar pond : A transient study. Solar Energy, 97(2), 517–528. DOI 10.1016/j.solener.2013.09.013. [Google Scholar] [CrossRef]
9. Ranjan, K. R., Kaushik, S. C. (2014). Thermodynamic and economic feasibility of solar ponds for various thermal applications: A comprehensive review. Renewable and Sustainable Energy Reviews, 32, 123–139. DOI 10.1016/j.rser.2014.01.020. [Google Scholar] [CrossRef]
10. Ding, L. C., Akbarzadeh, A., Tan, L. (2018). A review of power generation with thermoelectric system and its alternative with solar ponds. Renewable and Sustainable Energy Reviews, 81(7520), 799–812. DOI 10.1016/j.rser.2017.08.010. [Google Scholar] [CrossRef]
11. Suárez, F., Ruskowitz, J. A., Tyler, S. W., Childress, A. E. (2015). Renewable water: Direct contact membrane distillation coupled with solar ponds. Applied Energy, 158(1–2), 532–539. DOI 10.1016/j.apenergy.2015.08.110. [Google Scholar] [CrossRef]
12. Sayer, A. H., Al-Hussaini, H., Campbell, A. N. (2016). New theoretical modelling of heat transfer in solar ponds. Solar Energy, 125(3), 207–218. DOI 10.1016/j.solener.2015.12.015. [Google Scholar] [CrossRef]
13. Chiba, Y. (2005). Etude de l’utilisation d’un bassin d’eau comme capteur solaire. http://archives.umc.edu.dz/bitstream/handle/123456789/6585/CHI4455.pdf?sequence=1. [Google Scholar]
14. Anderson, G. C. (1958). Some limnological features of a Shallow Saline Meromictic Lake. Limnology and Oceanography, 3(3), 259–270. DOI 10.4319/lo.1958.3.3.0259. [Google Scholar] [CrossRef]
15. Melack, J. M., Kilham, P. (1972). Lake Mahega: A mesotrophic, sulphato-chloride lake in Western Uganda. African Journal of Tropical Hydrobiology and Fisheries, 2(2), 141–150. [Google Scholar]
16. Wilson, A. T., Wellman, H. W. (1962). Lake Vanda: An Antarctic lake. Nature, 196, 1048–1050. [Google Scholar]
17. Kaushika, N. D. (1984). Solar ponds: A review. Energy Conversion and Management, 24(4), 353–376. DOI 10.1016/0196-8904(84)90016-5. [Google Scholar] [CrossRef]
18. Hull, J. R. (1979). Physics of the solar pond. [Google Scholar]
19. Suárez, F., Tyler, S. W., Childress, A. E. (2010). A fully coupled, transient double-diffusive convective model for salt-gradient solar ponds. International Journal of Heat and Mass Transfer, 53(9–10), 1718–1730. DOI 10.1016/j.ijheatmasstransfer.2010.01.017. [Google Scholar] [CrossRef]
20. Rghif, Y., Zeghmati, B., Bahraoui, F. (2021). Soret and Dufour effects on thermosolutal convection developed in a salt gradient solar pond. International Journal of Thermal Sciences, 161(4), 106760. DOI 10.1016/j.ijthermalsci.2020.106760. [Google Scholar] [CrossRef]
21. Rghif, Y., Zeghmati, B., Bahraoui, F. (2021). Modeling the influences of a phase change material and the Dufour effect on thermal performance of a salt gradient solar pond. International Journal of Thermal Sciences, 166(8), 106979. DOI 10.1016/j.ijthermalsci.2021.106979. [Google Scholar] [CrossRef]
22. Ragui, K., Benkahla, Y. K., Labsi, N., Boutra, A. (2015). Natural convection heat transfer in a differentially heated enclosure with adiabatic partitions and filled with a bingham fluid. Heat Transfer Research, 46(8), 765–783. DOI 10.1615/HeatTransRes.2015007477. [Google Scholar] [CrossRef]
23. Ragui, K., Boutra, A., Benkahla, Y. K. (2016). On the validity of a numerical model predicting heat and mass transfer in porous square cavities with a bottom thermal and solute source: Case of pollutants spreading and fuel leaks. Mechanics and Industry, 17(3), 311. DOI 10.1051/meca/2015109. [Google Scholar] [CrossRef]
24. Atkinson, J. F., Harleman, D. R. F. (1983). A wind-mixed layer model for solar ponds. Solar Energy, 31(3), 243–259. DOI 10.1016/0038-092X(83)90012-9. [Google Scholar] [CrossRef]
25. Garratt, J. R. (1990). Boundary layer climates. Earth-Science Reviews, 27(3), 265. DOI 10.1016/0012-8252(90)90005-G. [Google Scholar] [CrossRef]
26. Patankar, S. V. (1980). Numerical heat transfer and fluid flow. Taylor and Francis, USA. [Google Scholar]
27. Rghif, Y., Zeghmati, B., Bahraoui, F. (2020). Modeling of a salt gradient solar pond under Moroccan climate taking into account double-diffusive convection. Materials Today: Proceedings, 30(4), 883–888. DOI 10.1016/j.matpr.2020.04.345. [Google Scholar] [CrossRef]
28. Rghif, Y., Zeghmati, B., Bahraoui, F. (2020). Soret and Dufour effects on thermal storage and storage efficiency of a salt gradient solar pond. IEEE Xplore, 5, 1–6. DOI 10.1109/REDEC49234.2020. [Google Scholar] [CrossRef]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |