[BACK]
images Fluid Dynamics & Materials Processing images

DOI: 10.32604/fdmp.2022.021917

ARTICLE

Simulation of the Hygrothermal Behavior of a Building Envelope Based on Phase Change Materials and a Bio-Based Concrete

Dongxia Wu1, Mourad Rahim1, Wendong Li1, Mohammed El Ganaoui1,* and Rachid Bennacer2

1University of Lorraine, LERMAB, IUT H Poincaré de Longwy, Longwy, 54400, France
2University of Paris-Saclay, ENS Paris-Saclay, CNRS, LMT, Gif-sur-Yvette, 91190, France
*Corresponding Author: Mohammed El Ganaoui. Email: mohammed.el-ganaoui@univ-lorraine.fr
Received: 12 February 2022; Accepted: 03 March 2022

Abstract: Phase Change Materials (PCMs) have high thermal inertia, and hemp concrete (HC), a bio-based concrete, has strong hygroscopic behavior. In previous studies, PCM has been extensively combined with many materials, however, most of these studies focused on thermal properties while neglecting hygroscopic aspects. In this study, the two materials have been combined into a building envelope and the related hygrothermal properties have been studied. In particular, numerical studies have been performed to investigate the temperature and relative humidity behavior inside the HC, and the effect of adding PCM on the hygrothermal behavior of the HC. The results show that there is a high coupling between temperature and relative humidity inside the HC, since the relative humidity changes on the second and third days are different, with values of 8% and 4%, respectively. Also, the variation of relative humidity with temperature indicates the dominant influence of temperature on relative humidity variation. With the presence of PCM, the temperature variation inside the HC is damped due to the high thermal inertia of the PCM, which also leads to suppression of moisture evaporation and thus damping of relative humidity variation. On the second and third days, the temperature changes at the central position are reduced by 4.6% and 5.1%, compared to the quarter position. For the relative humidity change, the reductions are 5.3% and 5.4% on the second and third days, respectively. Therefore, PCM, with high thermal inertia, acts as a temperature damper and has the potential to increase the moisture buffering capacity inside the HC. This makes it possible for such a combined envelope to have both thermal and hygric inertia.

Keywords: Phase change material (PCM); bio-based concrete; passive building envelope; heat and moisture transfer; hygrothermal performance

Nomenclature

Chc heat capacity of HC (J/(kg·K))
C∗ effective specific heat capacity of PCM (J/(kg·K))
Kw liquid water permeability (kg/(Pa·m·s))
Lv heat of vaporization (J/kg)
Mw molar mass of water (kg/mol)
pv,sat saturation pressure (Pa)
qst isosteric heat (J/kg)
R ideal gas constant (J/(mol·K))
T temperature (°C)
w volumetric moisture content (kg/m3)
δp water vapor permeability (kg/(Pa·m·s))
ξ sorption capacity
ρhc density of HC (kg/m3)
ρhc density of HC (kg/m3)
ρw density of water (kg/m3)
ρpcm density of PCM (kg/m3)
λ∗ effective thermal conductivity of PCM (W/(m·K))
λhc thermal conductivity of HC (W/(m·K))
λhc thermal conductivity of HC (W/(m·K))
φ relative humidity (%)

1  Introduction

Indoor temperature and relative humidity have a clear and direct impact on the comfort and health of occupants [1]. HVAC (heating, ventilation, and air conditioning) system is an active building method often used to manage indoor temperature and relative humidity, but it has the disadvantage of high energy consumption.

Bio-based materials are generally made from biologically renewable materials such as wood, hemp, cellulose wadding, straw, date palm fibers, etc. [2,3]. They have received a lot of attention in recent years based on their advantages. First, their raw materials come from natural plants and have low carbon emissions during manufacture, installation, utilization, maintenance, and demolition processes [4,5]. Besides, some bio-based materials have high porosity and low thermal conductivity and can be used as insulation for building envelopes to limit the heat transfer between indoor and outdoor environments [6]. Liu et al. [7] summarized four popular bio-based materials that can be used as building insulation materials: hemp, straw, flax, and wood. Moreover, the hygroscopic properties of bio-based materials can regulate the relative humidity in the surrounding environments, thus improving the indoor hygric environment, reducing the growth of mold, and saving energy [8,9]. The hygroscopic properties have been shown to be highly correlated with temperature properties. Poyet et al. [10] theoretically explained the relationship between vapor adsorption properties and temperature. Chennouf et al. [11], Rahim et al. [12], and Colinart et al. [13,14] experimentally and numerically investigated the relationship between temperature and hygroscopic properties; they concluded that hygroscopic properties are easily affected by temperature.

Several research projects on bio-based materials have been implemented by simulation and experimental methods [15,16]. In terms of simulation models, coupled heat and mass transfer has been studied for many years, and these models include single field [17,18], dual field [19], and triple field models [20], which were distinguished by different driving forces.

Similarly, combining phase change material (PCM) into a building envelope has proved to be an interesting technique due to its high thermal storage capacity [21]. PCM has been used as part of building compounds to regulate the thermal environment and save energy [22,23], such as wallboard, floor, roof, and window [24,25]. Moreover, PCM can be used in different seasons, countries, and climates by designing different thermal parameters, combination methods, and positions within the building envelope [26]. For the heat transfer model, the effective heat capacity model [27,28] and the enthalpy model [29] are often used to simulate the heat transfer of PCM.

The combination of PCM with other materials, such as cement mortar [30], bricks [31,32], concrete [33], diatomite [34], etc., has been extensively studied. However, these studies have only focused on the thermal performance of the combined envelope. As mentioned above, bio-based concrete has thermal properties and hygroscopic properties. The hygroscopic properties, meanwhile, are highly related to temperature properties. Therefore, it is necessary to investigate both the thermal and hygroscopic behavior of the combined envelope and the effect of the PCM on the hygrothermal behavior of HC.

The objectives of this study are to explore the feasibility of combining PCM and hemp concrete (HC), to investigate the hygrothermal behavior of HC, and to investigate the effect of PCM on the hygrothermal behavior of HC. Therefore, in this study, PCM and HC are combined as a new building envelope and the hygrothermal behavior of the combined envelope is investigated numerically. First, the mathematical models of PCM and HC are presented and validated, the structure of the combined envelope is described. Then, the temperature and relative humidity behavior inside the HC is studied and the effect of PCM on HC is analyzed. Finally, the conclusions are summarized.

2  Mathematical Model

Heat and mass transfer in HC can be treated as transfer activities in a porous medium. In the present study, the model is based on Kunzel’s model [35], which takes into account the moisture transport of liquid and vapor. The driving forces for the liquid and vapor phases are capillary pressure and partial water vapor pressure, respectively. To describe the relationship between the sorption characteristics and temperature, Poyet’s model [10] is used to link the relationship between two different moisture states. These models can be expressed as follows:

Mass conservation equation:

∂w∂φ|T∂φ∂t+∂w∂T|φ∂T∂t=∇((δppv,sat+KwρwRTφMw)∇φ+(δpφdpv,satdT+KwρwRln⁡(φ)Mw)∇T) (1)

Energy conservation equation:

ρhcChc∂T∂t=∇(λhc∇T)+Lv∇(δppv,sat∇φ+δpφdpv,satdT∇T) (2)

Sorption characteristics at two different states (T1, φ1) and (T2, φ2):

φ2(T2,w)=φ1(T1,w)Pv,sat(T1)Pv,sat(T2)eqst(w)MwR(T2−T1T1T2) (3)

Here, the latent heat of evaporation [36] and liquid water permeability [37] can be written as:

Lv=(2500−2.4T)×103 (4)

Kw=δpφMwpv,satRTρw (5)

For the model of PCM, the effective heat capacity model [27,28] is chosen. This model treats the phase change latent capacity as effective heat capacity under the phase transition range. The phase change problem can be transformed into a single-phase nonlinear problem, which simplifies the mathematical calculation. The energy conservation equation can be expressed by:

ρpcmC∗∂T∂t=▽(λ∗▽T) (6)

3  Simulation Procedure

Fig. 1 and Table 1 show the schematic diagram and dimensions of the single HC and the combined envelope. The combined envelope has a PCM layer arranged with four holes to ensure moisture migration through the HC. It should be noted that only the heat/mass transfer in the thickness direction is considered for both HC and PCM. Table 2 shows the physical properties of the two materials.

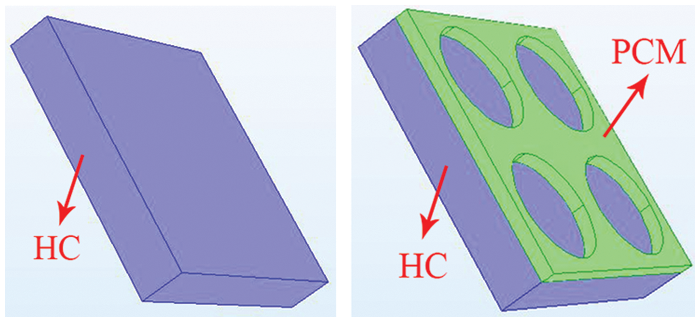
images

Figure 1: HC (left) and combined envelope (right)

images

images

The simulations were conducted with the commercial software COMSOL Multiphysics 5.3a, which uses finite element analysis to solve mathematical equations. The initial temperature of PCM and HC is 20°C and the initial relative humidity of HC is 50%. Fig. 2 shows the boundary conditions. For the external condition, the temperature increases from 10 to 20 and then 30°C; the relative humidity increases from 50% to 80% and then decreases back to 50%. Thus, there is an identical and an opposite trend in temperature and relative humidity over the three days variation, which helps to relate the hygrothermal behavior of the combined envelope to the obvious changes in temperature-relative humidity coupling.

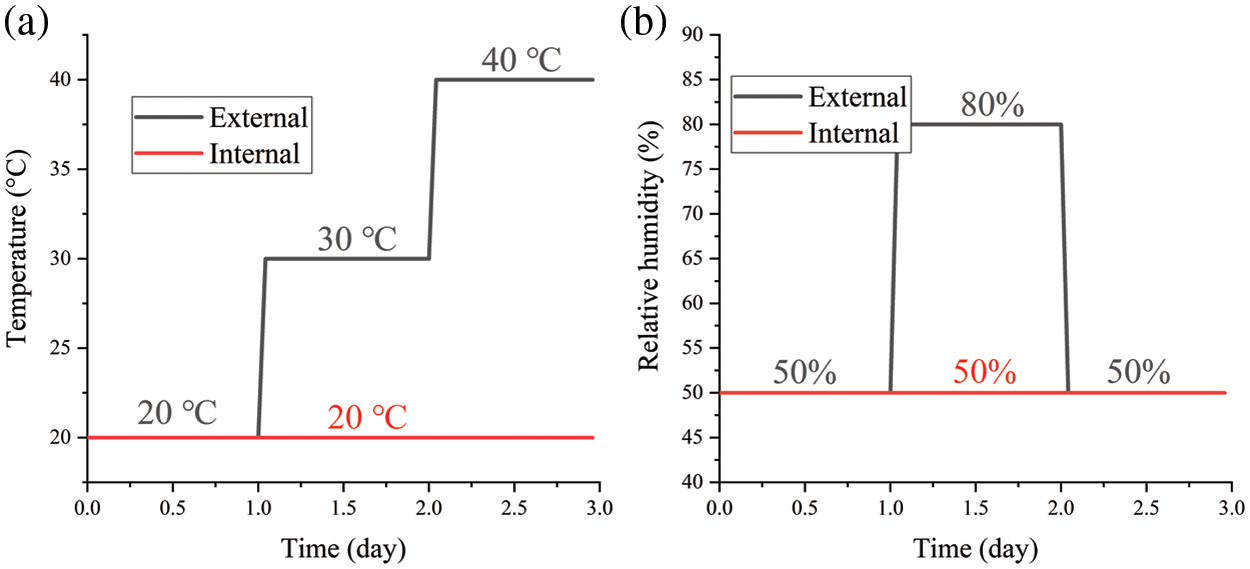
images

Figure 2: Internal and external boundary conditions of (a) Temperature and (b) Relative humidity

To investigate the effect of PCM on the hygrothermal behavior of HC, two positions were chosen as shown in Fig. 3:

•   Center position: in the geometric center of the HC layer;

•   Quarter position: at a position perpendicular to the center of the hole and in the middle of the HC layer.

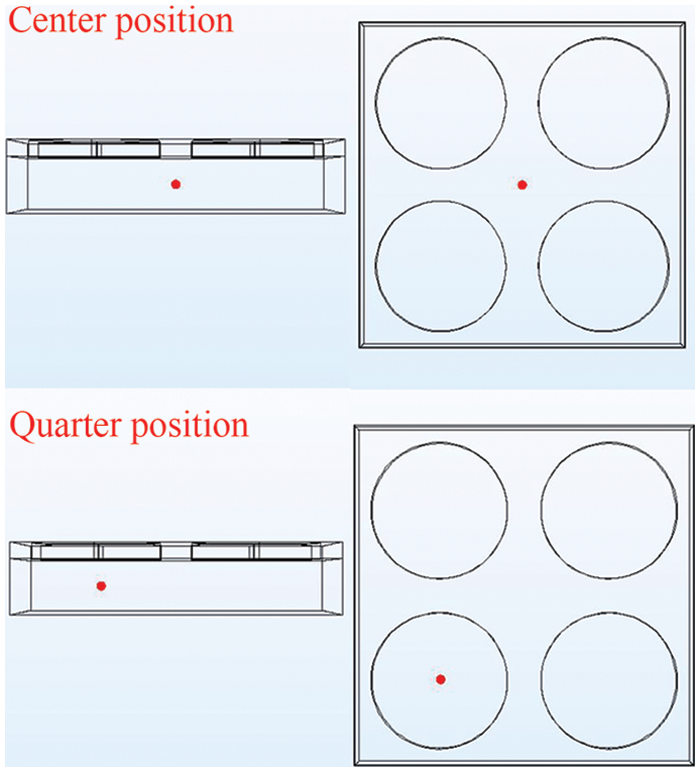
images

Figure 3: Center (above) and quarter (below) position of HC

Since only the heat/mass transfer along the thickness direction is considered, the two positions show the same hygrothermal behavior for single HC without PCM. In contrast, for the combined envelope, the transfer at the quarter position is not affected by the PCM, and the center position is affected by the PCM.

4  Results and Discussion

4.1 Model Validation

Experiments were performed to validate the mathematical model by placing an envelope between a climate chamber and a laboratory environment (Fig. 4). The experimented envelope consisted of one PCM layer and two HC layers. The PCM layer (50 × 50 × 2.12 cm3) was placed between the two HC layers (50 × 50 × 7 cm3) with a total dimension of 50 × 50 × 16.12 cm3. The physical properties of the HC and PCM were referenced to Table 2.

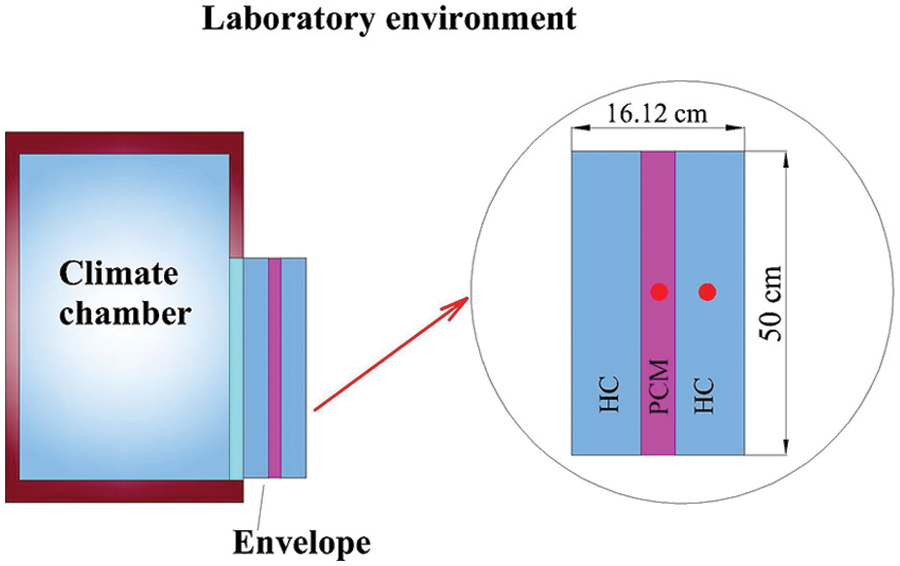
images

Figure 4: Experiment for model validation

The climate chamber provides variable temperature and relative humidity, which evolve according to a sinusoidal function with time (day) as the variables: T = 27.5 + 12.5 × sin (πt/12) and φ = 60% − 35% × sin (πt/12). In contrast, the temperature and relative humidity are relatively stable within the laboratory environment, with fluctuations of less than ±0.2°C and ±1.6%, respectively. The measurement point is in the middle of the PCM and the second HC. The experiment was carried out for 48 h, and the time step for recording the experimental data was 120 s.

Fig. 5 shows the comparison of simulation and experimental results. The simulation and experimental results agree well. By calculation, the relative error range for the two measurement points is from −3.2% to 2.4% for temperature and from −2.4% to 1.2% for relative humidity. These data show that the models exhibit high accuracy and can be used for further studies.

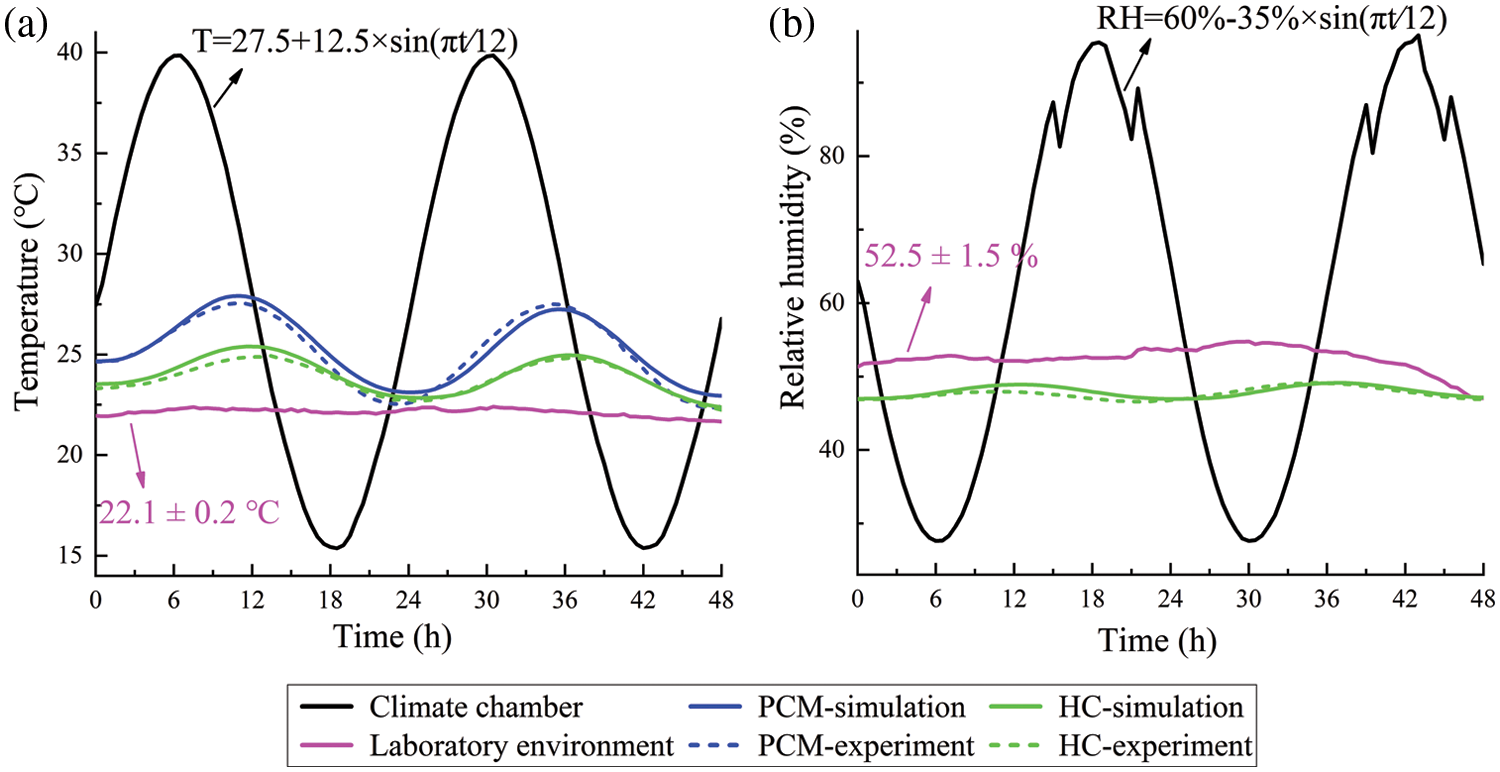
images

Figure 5: Comparison between the simulation and experimental results of (a) Temperature and (b) Relative humidity

4.2 Hygrothermal Behavior of HC Without PCM

Fig. 6 shows the temperature change of the HC at the center/quarter position without the PCM. Since the internal temperature remains constant, the temperature at the center/quarter position remains continuously increasing along with the external temperature.

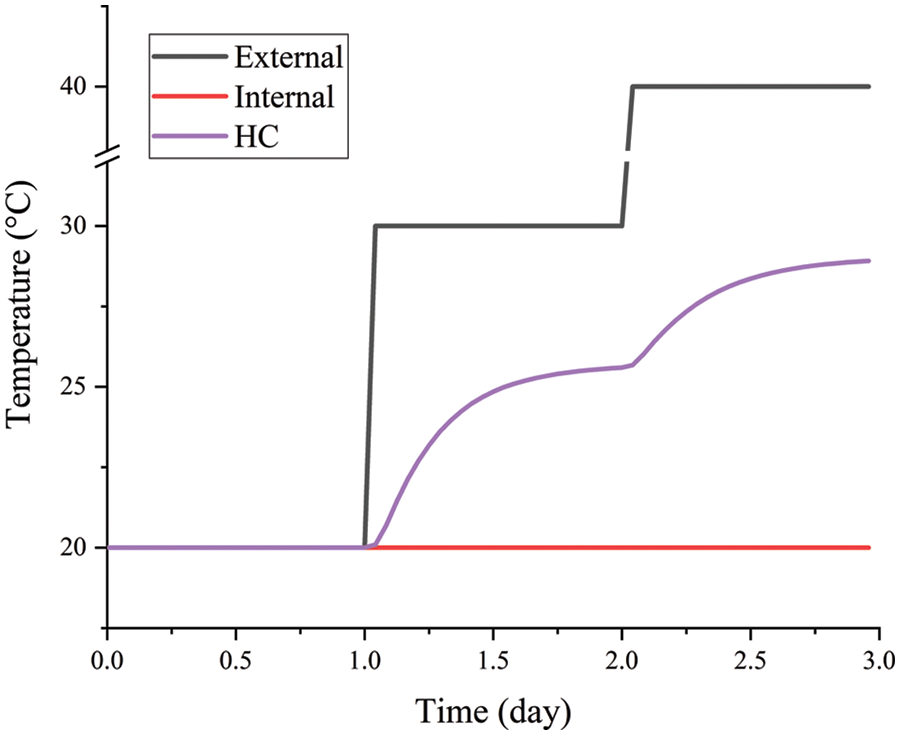
images

Figure 6: Temperature inside the HC without PCM

Fig. 7 shows the variation of relative humidity of HC at the center/quarter position. On the second day, the boundary temperature and relative humidity increase simultaneously, and the relative humidity inside the HC also increases. However, on the third day, when the external temperature increases and the relative humidity decreases, the relative humidity inside the HC still increases like the temperature inside the HC. That is, the trend of relative humidity inside the HC is not significantly affected by the boundary relative humidity, but remains consistent with the temperature. These phenomena can be explained by the moisture phase change caused by temperature. The increase in temperature leads to moisture evaporation inside the HC, which results in an increase in relative humidity. On the other hand, as temperature decreases, water vapor condensation occurs inside the HC and leads to a decrease in relative humidity. Thus, the successive increases in relative humidity on the second and third days are caused by the moisture evaporation.

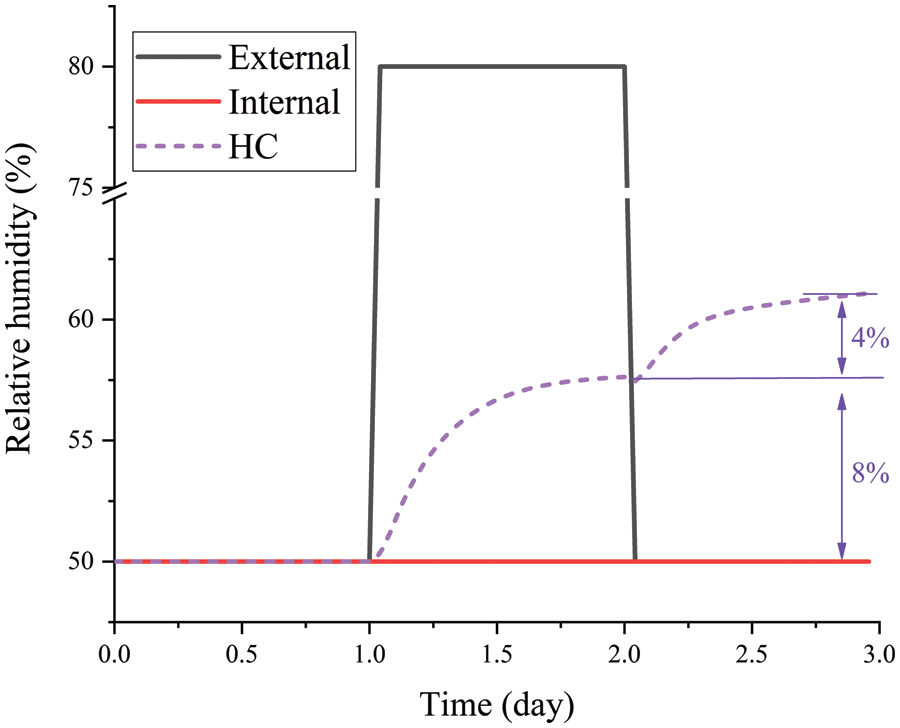
images

Figure 7: Relative humidity inside the HC without PCM

However, temperature is not the only factor guiding the relative humidity variation. The relative humidity change on the second and third day is not consistent with the values of 8.0% and 4.0%, respectively, because the relative humidity inside the HC is also affected by the boundary (external) relative humidity. As the external relative humidity increases, moisture diffuses from external to the HC and increases the relative humidity inside the HC. On the contrary, the decrease in external relative humidity causes the moisture vapor to evacuate from the HC to the external and decreases the relative humidity inside the HC. Therefore, both the boundary temperature and relative humidity promote the relative humidity increase inside HC on the second day. While on the third day, boundary temperature and relative humidity have opposite effects on relative humidity, with the former acting as a promoting effect to increase relative humidity and the latter acting as a suppressing effect to decrease relative humidity. The competition between the two effects indicates that the promoting effect is stronger and eventually leads to the increase of relative humidity, which is the reason that the relative humidity change on the third day is lower than that on the second day.

Consequently, the relative humidity change inside the HC highlights the coupling effect between temperature and relative humidity. Moreover, temperature plays a major role in determining the relative humidity variation.

4.3 Hygrothermal Behavior of HC with PCM

In this section, the hygrothermal behavior of HC is studied with the presence of PCM. Since only the heat and mass transfer in the thickness direction is considered, the temperature and relative humidity behavior at the quarter position is consistent with the results in Section 4.2 (without PCM). Thus, the comparison between the center and quarter positions reflects the effect of PCM on the hygrothermal properties of HC.

Figs. 8 and 9 show the temperature and relative humidity behavior at the center and quarter positions. Both positions show an increasing trend in temperature, but the increase is different. On the second and third day, the temperature increase at the quarter position is 5.60°C and 3.34°C, respectively. In contrast, at the central position, the temperature increases less with values of 5.34°C and 3.17°C, which are 4.6% and 5.1% reduced, respectively, compared to the quarter position. That is, the temperature at the central position changes more slowly than the quarter position during the same time period. Because PCM has a larger heat storage energy capacity (high thermal inertia) in the phase transition range due to the large specific heat capacity. As a result, a large amount of thermal energy is stored in the PCM layer, which dampens the temperature transfer and variation inside the combined envelope.

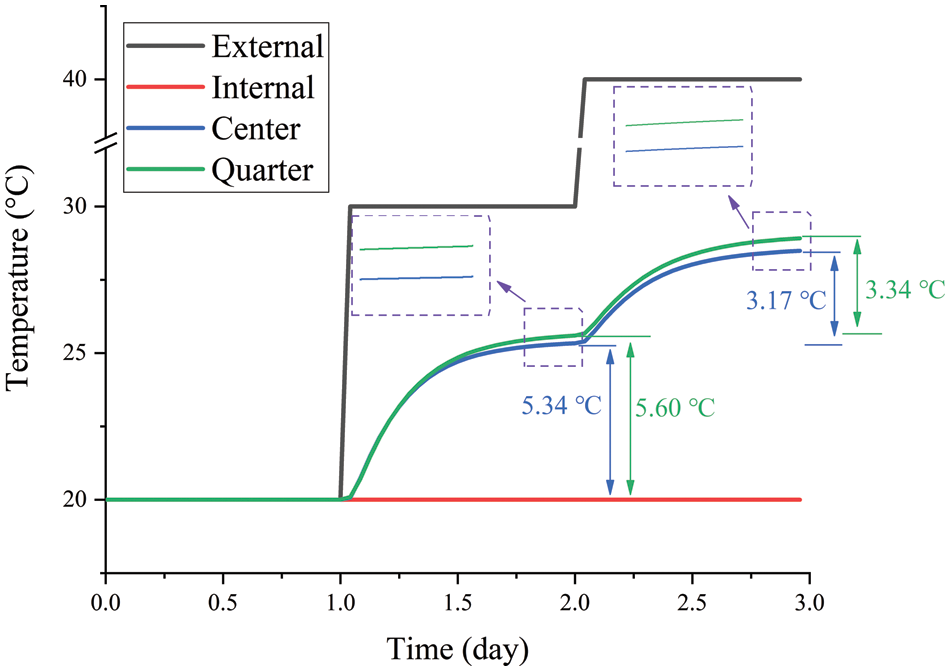
images

Figure 8: Temperature of HC at center and quarter with PCM

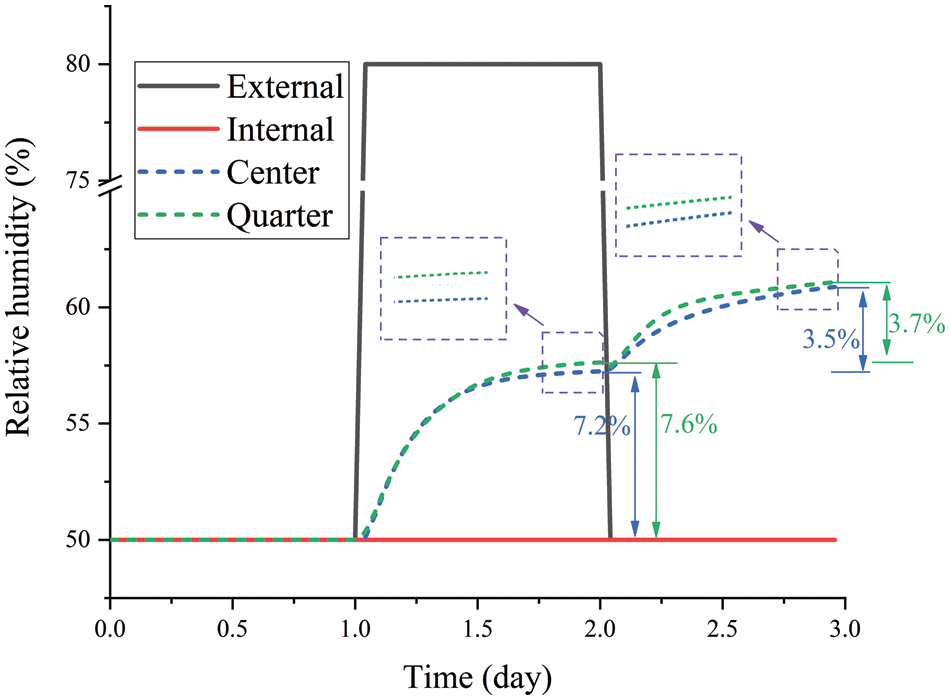
images

Figure 9: Relative humidity of HC at center and quarter with PCM

In terms of relative humidity in Fig. 9, an increasing trend is observed both on the second and third days at both positions due to the main effect of temperature. As for the relative humidity change, the values at the center position are 7.2% and 3.5% on the second and third day, respectively, which are 5.3% and 5.4% lower than those for the quarter position (7.6% and 3.7% on the second and third day, respectively). In other words, the relative humidity change is reduced at the center position during the same time period with the presence of PCM, meaning that the hygric inertia of HC is enhanced by PCM. This phenomenon can be explained from two aspects. On the one hand, the temperature has a major effect on the relative humidity inside the HC, and the relative humidity varies with temperature. As mentioned in Section 4.2, the increase in temperature increases the relative humidity by inducing moisture evaporation inside the HC. On the other hand, the center temperature is damped by the thermal inertia of the PCM and has a smaller temperature change than the quarter position. Therefore, the moisture evaporation phenomenon inside the HC is suppressed with the presence of PCM, leading to a decrease in relative humidity change compared to the quarter position.

Consequently, these results demonstrate the dual effect of PCM on heat and moisture transfer. The presence of PCM can improve the thermal inertia of the combined envelope by slowing down the temperature change inside the PCM and HC. In addition, PCM can also improve the hygric inertia of the combined envelope by slowing down the relative humidity change inside the HC.

5  Conclusions

In this study, PCM was combined with HC to explore the potential of combining thermal and hygric inertia. The hygrothermal behavior inside HC and the effect of PCM were studied numerically.

Temperature and relative humidity in the single HC show high coupling between heat and mass transfer. The changes of relative humidity on the second and third day are 8% and 4%, respectively, due to the dual effects of temperature and relative humidity (heat and mass transfer). Moreover, relative humidity variation is mainly influenced by temperature, caused by evaporation and condensation of moisture. Regardless of whether the trends of boundary temperature and relative humidity are the same, the relative humidity inside HC only shows the same variation trend as the temperature.

With the presence of PCM, the temperature variation within the HC is dampened. On the second and third day, the temperature changes at the center position are 5.34°C and 3.17°C, respectively, which are reduced by 4.6% and 5.1% compared to the quarter position (5.6°C and 3.34°C). Moreover, the relative humidity change at the central position is also dampened by PCM due to the damping of moisture evaporation caused by the damping of temperature. The relative humidity changes at the central position on the second and third day are 7.2% and 3.5%, which are 5.3% and 5.4% lower than those at the quarter position (7.6% and 3.7%).

Consequently, PCM can dampen not only the change of temperature, but also the change of relative humidity inside the HC. With the presence of PCM, it is possible to increase both the thermal and hygric inertia of the combined envelope. The current work is a start, and future research aims to explore the hygrothermal and energy performance of the combined envelope in real-climate applications.

Acknowledgement: We thank to the China Scholarship Council (CSC) for its financial support to the first author, No. 201808120084. CPER UL/Lorraine Region, PHC Maghreb, and EMPP Scientific Pole of the University of Lorraine are also acknowledged.

Funding Statement: The authors received no specific funding for this study.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

  1. Enescu, D. (2017). A review of thermal comfort models and indicators for indoor environments. Renewable and Sustainable Energy Reviews, 79, 1353–1379. DOI 10.1016/j.rser.2017.05.175. [CrossRef]
  2. Agoudjil, B., Benchabane, A., Boudenne, A., Ibos, L., & Fois, M. (2011). Renewable materials to reduce building heat loss: Characterization of date palm wood. Energy and Buildings, 43(2), 491-497. [Google Scholar] [CrossRef]
  3. Asdrubali, F., D’Alessandro, F., & Schiavoni, S. (2015). A review of unconventional sustainable building insulation materials. Sustainable Materials and Technologies, 4, 1-17. [Google Scholar] [CrossRef]
  4. Gustavsson, L., Joelsson, A., & Sathre, R. (2010). Life cycle primary energy use and carbon emission of an eight-storey wood-framed apartment building. Energy and Buildings, 42(2), 230-242. [Google Scholar] [CrossRef]
  5. Jami, T., Karade, S. R., & Singh, L. P. (2019). A review of the properties of hemp concrete for green building applications. Journal of Cleaner Production, 239, 117852. [Google Scholar] [CrossRef]
  6. Almalkawi, A. T., Soroushian, P., & Shrestha, S. S. (2019). Evaluation of the energy-efficiency of an aerated slurry-infiltrated mesh building system with biomass-based insulation. Renewable Energy, 133, 797-806. [Google Scholar] [CrossRef]
  7. Liu, L., Li, H., Lazzaretto, A., Manente, G., & Tong, C. (2017). The development history and prospects of biomass-based insulation materials for buildings. Renewable and Sustainable Energy Reviews, 69, 912-932. [Google Scholar] [CrossRef]
  8. Sinka, M., Bajare, D., Gendelis, S., & Jakovics, A. (2018). In-situ measurements of hemp-lime insulation materials for energy efficiency improvement. Energy Procedia, 147, 242-248. [Google Scholar] [CrossRef]
  9. Barbosa, R. M., Mendes, N. (2008). Combined simulation of central HVAC systems with a whole-building hygrothermal model. Energy and Buildings, 40(3), 276–288. DOI 10.1016/j.enbuild.2007.02.022. [CrossRef]
  10. Poyet, S., & Charles, S. (2009). Temperature dependence of the sorption isotherms of cement-based materials: Heat of sorption and clausius–Clapeyron formula. Cement and Concrete Research, 39(11), 1060-1067. [Google Scholar] [CrossRef]
  11. Chennouf, N., Agoudjil, B., Boudenne, A., Benzarti, K., & Bouras, F. (2018). Hygrothermal characterization of a new bio-based construction material: Concrete reinforced with date palm fibers. Construction and Building Materials, 192, 348-356. [Google Scholar] [CrossRef]
  12. Rahim, M., Tran Le, A. D., Douzane, O., Promis, G., & Langlet, T. (2016). Numerical investigation of the effect of non-isotherme sorption characteristics on hygrothermal behavior of two bio-based building walls. Journal of Building Engineering, 7, 263-272. [Google Scholar] [CrossRef]
  13. Colinart, T., & Glouannec, P. (2017). Temperature dependence of sorption isotherm of hygroscopic building materials. Part 1: Experimental evidence and modeling. Energy and Buildings, 139, 360-370. [Google Scholar] [CrossRef]
  14. Colinart, T., Glouannec, P., Bendouma, M., & Chauvelon, P. (2017). Temperature dependence of sorption isotherm of hygroscopic building materials. Part 2: Influence on hygrothermal behavior of hemp concrete. Energy and Buildings, 152, 42-51. [Google Scholar] [CrossRef]
  15. Kong, F., & Zhang, Q. (2013). Effect of heat and mass coupled transfer combined with freezing process on building exterior envelope. Energy and Buildings, 62, 486-495. [Google Scholar] [CrossRef]
  16. Zhang, H., Yoshino, H., & Hasegawa, K. (2012). Assessing the moisture buffering performance of hygroscopic material by using experimental method. Building and Environment, 48, 27-34. [Google Scholar] [CrossRef]
  17. Henry, P. S. H. (1939). Diffusion in absorbing media. Royal Society, 171, 215–241. DOI 10.1098/rspa.1939.0062. [CrossRef]
  18. Lewis, W. K. (1921). The rate of drying of solid materials. Journal of Industrial & Engineering Chemistry, 13(5), 427-432. [Google Scholar] [CrossRef]
  19. de Vries, D. A. (1987). The theory of heat and moisture transfer in porous media revisited. International Journal of Heat and Mass Transfer, 30(7), 1343-1350. [Google Scholar] [CrossRef]
  20. Luikov, A. V. (1975). Systems of differential equations of heat and mass transfer in capillary-porous bodies (review). International Journal of Heat and Mass Transfer, 18(1), 1-14. [Google Scholar] [CrossRef]
  21. Saxena, R., Rakshit, D., & Kaushik, S. C. (2020). Experimental assessment of phase change material (PCM) embedded bricks for passive conditioning in buildings. Renewable Energy, 149, 587-599. [Google Scholar] [CrossRef]
  22. Kong, X., Wang, L., Li, H., Yuan, G., & Yao, C. (2020). Experimental study on a novel hybrid system of active composite PCM wall and solar thermal system for clean heating supply in winter. Solar Energy, 195, 259-270. [Google Scholar] [CrossRef]
  23. Abden, M. J., Tao, Z., Pan, Z., George, L., & Wuhrer, R. (2020). Inclusion of methyl stearate/diatomite composite in gypsum board ceiling for building energy conservation. Applied Energy, 259, 114113. [Google Scholar] [CrossRef]
  24. Larwa, B., Cesari, S., & Bottarelli, M. (2021). Study on thermal performance of a PCM enhanced hydronic radiant floor heating system. Energy, 225, 120245. [Google Scholar] [CrossRef]
  25. Zhang, S., Hu, W., Li, D., Zhang, C., & Arıcı, M. (2021). Energy efficiency optimization of PCM and aerogel-filled multiple glazing windows. Energy, 222, 119916. [Google Scholar] [CrossRef]
  26. Ahangari, M., & Maerefat, M. (2019). An innovative PCM system for thermal comfort improvement and energy demand reduction in building under different climate conditions. Sustainable Cities and Society, 44, 120-129. [Google Scholar] [CrossRef]
  27. Wijesuriya, S., Tabares-Velasco, P. C., Biswas, K., & Heim, D. (2020). Empirical validation and comparison of PCM modeling algorithms commonly used in building energy and hygrothermal software. Building and Environment, 173, 106750. [Google Scholar] [CrossRef]
  28. Liu, L., Zhang, X., Xu, X., Zhao, Y., & Zhang, S. (2020). The research progress on phase change hysteresis affecting the thermal characteristics of PCMs: A review. Journal of Molecular Liquids, 317, 113760. [Google Scholar] [CrossRef]
  29. Iten, M., Liu, S., & Shukla, A. (2018). Experimental validation of an air-PCM storage unit comparing the effective heat capacity and enthalpy methods through CFD simulations. Energy, 155, 495-503. [Google Scholar] [CrossRef]
  30. Kontoleon, K. J., Stefanidou, M., Saboor, S., Mazzeo, D., & Karaoulis, A. (2021). Defensive behaviour of building envelopes in terms of mechanical and thermal responsiveness by incorporating PCMs in cement mortar layers. Sustainable Energy Technologies and Assessments, 47, 101349. [Google Scholar] [CrossRef]
  31. Hamidi, Y., Malha, M., & Bah, A. (2021). Analysis of the thermal behavior of hollow bricks walls filled with PCM: Effect of PCM location. Energy Reports, 7, 105-115. [Google Scholar] [CrossRef]
  32. Mahdaoui, M., Hamdaoui, S., Ait Msaad, A., Kousksou, T., & El Rhafiki, T. (2021). Building bricks with phase change material (PCM): Thermal performances. Construction and Building Materials, 269, 121315. [Google Scholar] [CrossRef]
  33. Shen, Y., Liu, S., Zeng, C., Zhang, Y., & Li, Y. (2021). Experimental thermal study of a new PCM-concrete thermal storage block (PCM-CTSB). Construction and Building Materials, 293, 123540. [Google Scholar] [CrossRef]
  34. Yu, H., Li, C., Zhang, K., Tang, Y., & Song, Y. (2020). Preparation and thermophysical performance of diatomite-based composite PCM wallboard for thermal energy storage in buildings. Journal of Building Engineering, 32, 101753. [Google Scholar] [CrossRef]
  35. Künzel, H. (1995). Simultaneous heat and moisture transport in building components.
  36. Zhou, S., Zhang, R., Zhang, Z. (2002). Climatology and meteorology.
  37. Wang, Y., Fan, Y., Wang, D., Liu, Y., & Liu, J. (2021). The effect of moisture transfer on the inner surface thermal performance and the thermal transmittance of the roof-wall corner building node in high-temperature and high-humidity areas. Journal of Building Engineering, 44, 102949. [Google Scholar] [CrossRef]
  38. Energain®, Dupont (2010). Hydrocarbon-based PCM applications. https://cdn2.hubspot.net/hub/55819/file-14755587-pdf/docs/buildings-xi/dupont_energain.pdf.
images This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.