

 | Fluid Dynamics & Materials Processing |  |
DOI: 10.32604/fdmp.2022.021619
ARTICLE
Numerical Study of Natural Convection in an Inclined Porous Cavity
1Laboratoire des Transports Polyphasiques et Milieux Poreux, LTPMP, ALGER, 16111, ALGERIE
2Laboratoire des Mathématiques et Physique des Systèmes, LAMPS, Perpignan, 66860, France
*Corresponding Author: Saad Adjal. Email: sadjaldz@gmail.com
Received: 24 January 2022; Accepted: 23 February 2022
Abstract: Two-dimensional transient laminar natural convection in a square cavity containing a porous medium and inclined at an angle of 30∘ is investigated numerically. The vertical walls are differentially heated, and the horizontal walls are adiabatic. The effect of Rayleigh number on heat transfer and on the road to chaos is analyzed. The natural heat transfer and the Darcy Brinkman equations are solved by using a finite volume method and a Tri Diagonal Matrix Algorithm (TDMA). The results are obtained for a porosity equal to 0.45, a Darcy number and a Prandtl respectively equal to 10−3 and 0.71; they are analyzed in terms of streamlines, isotherms, phase portrait, attractors, and spectra amplitude as a function of the Rayleigh number. It is found that, as Rayleigh number increases, the natural convection changes from a steady state to a time-periodic state and finally to a chaotic condition.
Keywords: Natural convection; porous medium; finite volumes; chaos; attractors
This work is part of a recent branch of nonlinear physics devoted to dissipative dynamical systems. The heat transfer in porous medium is found in various applications, cooling of electronics components, oil recovery, applications related to geothermal energy extraction, thermal insulation and safety issues in the cores of nuclear reactors.
Scientists have long sought to geometrically represent order hidden in chaos by a trajectory the trajectory represented by an attractor in a phase space called (phase space) which describes the whole evolution of the system, this trajectory converges towards a particular region of phase space, it is called (attraction pool).
In 1987, Moya et al. [1] analyzed numerically two-dimensional natural convection in an inclined rectangular cavity containing a porous medium, using the Darcy model and the Boussinesq approximation. The external parameters considered are the tilt angle, the aspect ratio and the Darcy-Rayleigh number. They presented the local and global Nusselt number according to these parameters, a multiplicity of solution is explored for a form ratio equal to unity.
In recent years, the appearance of more powerful computers has made it possible to simulate numerically the phenomena responsible for the appearance of unsteady natural convection and their interpretation in a concrete way.
Ragui et al. [2] highlighted a numerical model predicting the heat transfers in the porous media, in a case of spreading of pollutants and fuel leaks. The work refers to the study of natural convection in a confined porous medium, the side walls are maintained at a uniform temperature, lower than that of a heat source located in the center of the lower wall, the rest of the horizontal walls are kept isolated. The physical model of the conservation of momentum equation uses the Brinkman extension of the classical Darcy equation, the set of coupled equations is solved using the finite volume method and the SIMPLER algorithm. To account for the effects of key parameters such as the porous thermal Rayleigh number, as well as the source length, the heat transfer characteristics was extensively inspected and then new powerful correlations are proposed that predict the numerical results. The validity of the code used was checked by comparing the results obtained with experimental and numerical data already available in the literature.
Aklouche-Benouaguef et al. [3] presented a numerical study on the road to chaos for a transient natural convection in a square enclosure with horizontal adiabatic walls. The other walls were assumed to be insulated. The transfer equations were solved using the formulation of the current function-vorticity. The effects of Rayleigh’s number on heat transfer were also analyzed, and the road to chaos taken by the convective flow. The first Hopf bifurcation was observed and quasi-periodic flows appeared before the onset of chaos. In 2017, another digital study was carried out by the same authors on natural convection in a square cavity containing air and inclined at an angle of 45° [4]. This study showed that the flow undergoes bifurcation sequences from the steady state to an oscillating convective state. In the vicinity of the critical point, the study made it possible to characterize the nature of the first bifurcation (Hopf bifurcation). They found that stationary and periodic solutions are early compared to a horizontal cavity.
Oztop et al. [5] used Darcy’s model and Boussinesq’s approximation to perform a numerical analysis of permanent laminar natural convection. The flow and transfer of heat takes place in an inclined and partially cooled porous cavity. The transfer equations are solved using the finite volumes and the Tri-Diagonal Matrix algorithm with the SIMPLE algorithm. They analyzed the effects of Rayleigh number, tilt angle for a Prandtl equal to 1 on flow rate, and heat transfer. The results presented show that the heat transfer decreases as the aspect ratio increases. The maximum heat transfer is obtained at an inclination angle equal to 30°.
Subhash et al. [6] carried out a numerical study of natural convection in a square enclosure filled with a porous medium. The cavity has a pair of vertical rigid and thin partition of length equal to half of that of the wall. They are investigating the effects of the vertical diathermal baffle on decreasing the rate of heat transfer through the fluid-saturated porous medium. The transfer equations based on the Darcy model and the Boussinesq approximation are solved using a finite difference scheme. They analyzed the effects of Rayleigh number and partition ratio on flux and heat transfer. The partition has been shown to significantly reduce the rate of heat transfer. The decrease in the Nusselt number is, whatever the modified Ra, all the more important when the aspect ratio is less than 0.3 or 0.4.
An experimental study of laminar mixing in several types of two-dimensional cavity flows by means of material line and drop deformation in an experimental system composed of two sets of roller pairs connected by belts is presented by Chien et al. [7]. Their apparatus can be tuned to produce a range of aspect ratios, Reynolds numbers, and various types of flow fields with one or two moving boundaries. The alternating periodic motion of two bands in a cavity flow is an example of laminar flow that could lead to chaotic mixing. The determining parameter is the dimensionless oscillation frequency of the walls, which, under the right conditions, is capable of producing horseshoe functions of various types. They found that the mixing efficiency strongly depends on the frequency value and that there is an optimal frequency value that produces the best mixing in a given time.
A two-dimensional numerical simulation is performed for natural convection in a V-shaped cavity heated from below and cooled from above using a finite volume method [8]. A wide range of Rayleigh numbers for the aspect ratio of A = 0.5 and the Prandtl number of Pr = 0.71 is considered. A set of supercritical bifurcations in a transition to chaotic flow is described, which includes a Pitchfork bifurcation from a symmetric to asymmetric state and a Hopf bifurcation from a stable to unstable state. The Pitchfork bifurcation occurs between Ra = 7.5 103 and 7.6 103 and the Hopf bifurcation occurs between Ra = 1.5 107 and 1.6 107. Additionally, another periodic state bifurcation to chaotic occurs between Ra = 5 107 and 6 107. The power spectral density, the phase space trajectory and the largest Lyapunov exponent of the unstable flows during the transition to a chaotic state have been described. In addition, the heat transfer in the cavity is calculated and the corresponding dependence on the Rayleigh number is discussed and quantified.
Finally, Adjal et al. [9] presented a numerical study of a periodic and chaotic behavior of natural convection in a square cavity, with a porous layer. The studied cavity is made up of two opposite vertical walls, the lower half-walls of which are warm and the upper half-walls of which are cold, while the horizontal walls are adiabatic. The porous medium is located in the lower part of the cavity. Natural heat transfer and Darcy Brinkman’s equations are solved using the finite volume method. The results show that natural thermal convection evolves into deterministic chaos following the Curry and Yorke scenario.
The present work is an exploration of the routes towards the chaos of a natural thermal convection in a porous medium.
Fig. 1 shows the totally porous inclined cavity, the lower half-walls and the upper half-walls are brought respectively to a warm and a cold temperature, the horizontal walls are adiabatic.
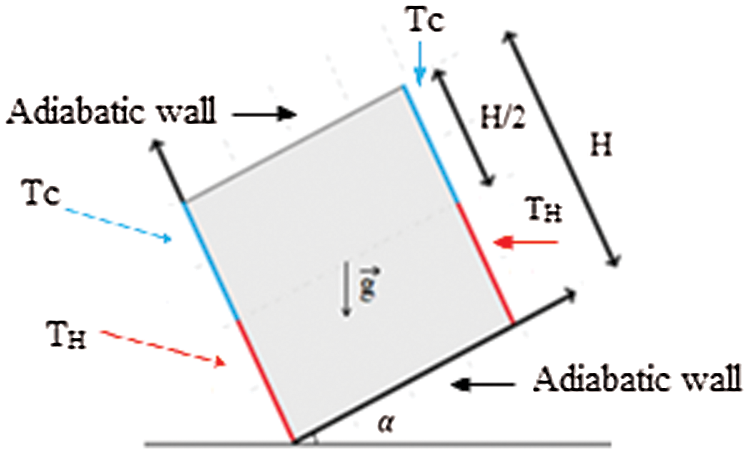
Figure 1: Physical model
2.2 System and Governing Equations
The phenomena of natural convection are described by the general equations of fluid dynamics complemented by the energy conservation equation deduced from the first principle of thermodynamics.
2.2.1 Assumptions and Dimensionless Form of Equations
We consider Newtonian and incompressible fluid and two-dimensional flow. All the physical properties of fluid are constant except the density (approximation of Boussinesq). The medium is considered isotropic, no chemical reaction in the porous medium, thermo-physical properties are considered constant and the local thermal equilibrium is assumed. The Darcy-Brinkman model while neglecting the radiation, the viscous dissipation and the work of the pressure forces in the heat equation governs the motion of the fluid in the porous medium.
The governing equations of natural convection are written in non-dimensional form as follows:
3.1 Numerical Method and Validation of the Numerical Simulation
The governing equations are solved by the finite volume technique. The semi-implicit ADI method was applied. The algebraic equations systems are solved, for each time step, by Tri Diagonal Matrix Algorithm.
In order to validate our results a comparison was made with those obtained by LAURIAT and PRASAD. The parameters chosen are ε = 0.4, Ra = 107 and 105, Da = 10−1 and 10−6, Pr = 1 and 10−2. The results are summarized in in Tables 1 and 2. We observe a good agreement between the obtained results and reference.


We carried out several mesh and time step sensitivity tests to obtain an optimal mesh and time step for the calculation of the stationary and periodic solutions.
The calculation of the relative error for different dynamic parameters considering the influence of the mesh and the time step led us to determine the stationary solution (Fig. 2), this one is defined for a Rayleigh number Ra = 8 106, a time step dτ = 9 10−5 and a mesh of (111 × 111).
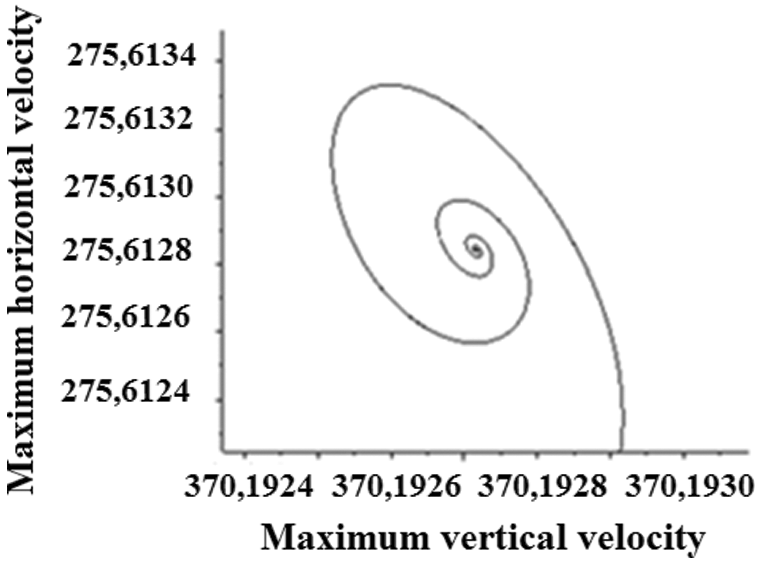
Figure 2: Phase portrait stationary solution (Ra = 8 106)
The phase portrait is a spiral, which tends towards a fixed limit point. It is an attractor for which all the values of a parameter tend to a constant value when the time tends to infinity. The effects of non-linearity diminishes and the trajectories of the points of the system tend towards a basin of attraction in the form of a spiral, which ends by point. This explains the stationary state of the system.
The evolution as a function of time of a dynamic parameter such as the Nusselt number, the function of the current and the speeds shows that the dynamic system undergoes oscillations having large amplitudes then they attenuate after some dimensionless time until stability is achieved (Fig. 3).
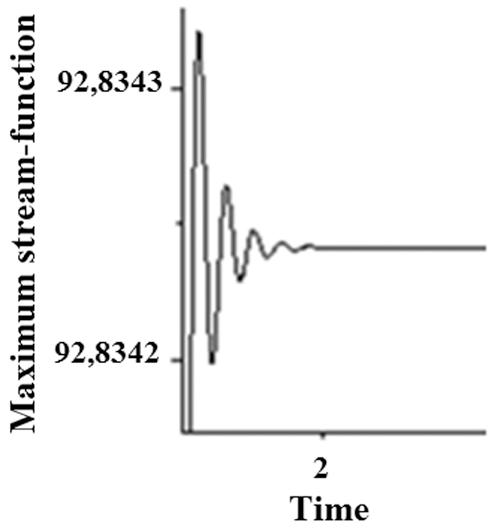
Figure 3: Temporal evolution (Ra = 8 106)
The temporal evolution of maximal stream-function begins with a transient regime and then tends towards the steady state. This stationary state is characterized by the damping of the oscillations having zero amplitude.
To confirm the stationarity of the dynamic system, it is necessary to have recourse to the spectral analysis (Fig. 4), which consists in using the fast Fourier transform (FFT). This makes it possible to transform the temporal evolution into a sinusoidal signal. Since the representation of amplitude as a function of frequency does not show energy peaks, we conclude that the solution is stationary.
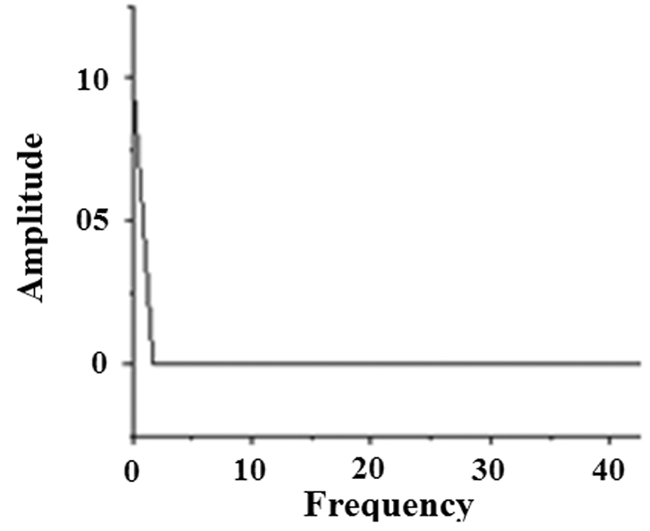
Figure 4: Amplitude spectrum (Ra = 8 106)
We increase the Rayleigh number while keeping the mesh and the time step that we have previously designated and we plot the phase portraits (Fig. 5). A new attractor appears in the form of a cycle sign of a periodic solution, this one is confirmed by the appearance of a peak by the FFT (Fig. 6).
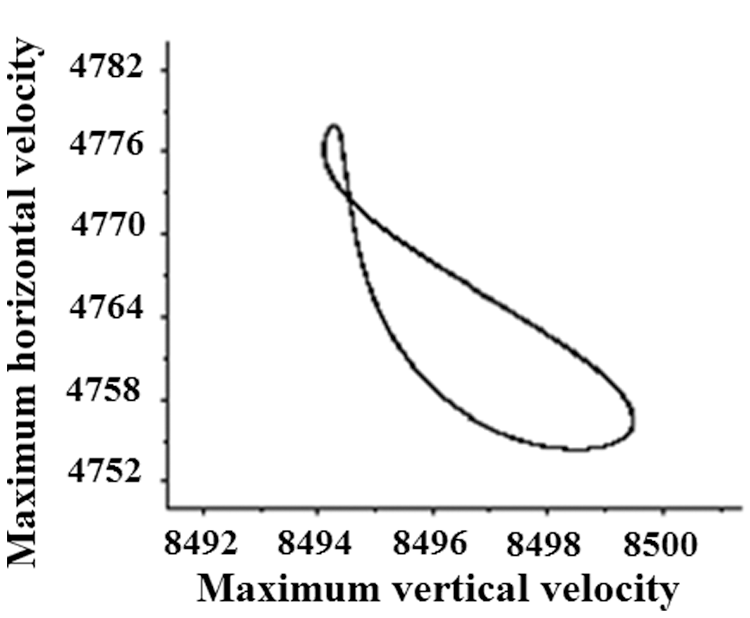
Figure 5: Phase portrait stationary solution (Ra = 1.5 108)
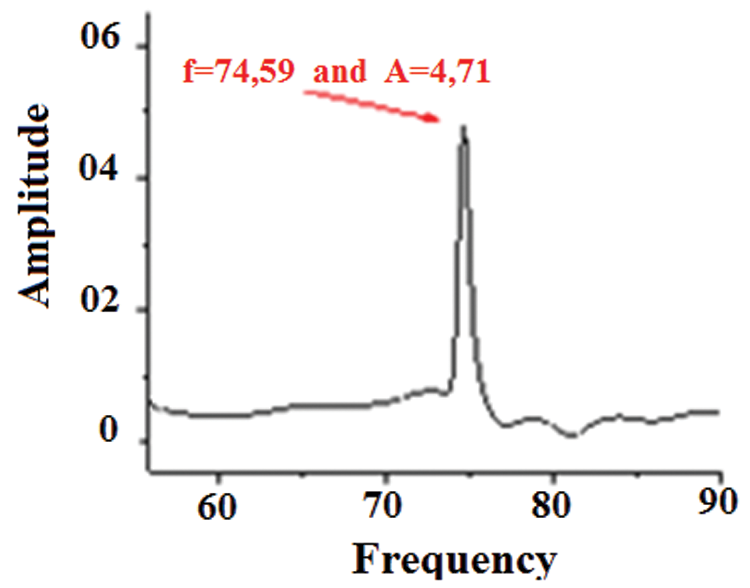
Figure 6: Amplitude spectrum (Ra = 1.5 108)
We keep increasing the Rayleigh number while keeping the mesh and the time step and we plot the phase portraits. We notice the appearance of strange geometry of attractor, sign of the progressive change in the state of our system as a function of the Rayleigh number, up to get a persistent chaos for a Rayleigh number equal to 1011 (Fig. 7).
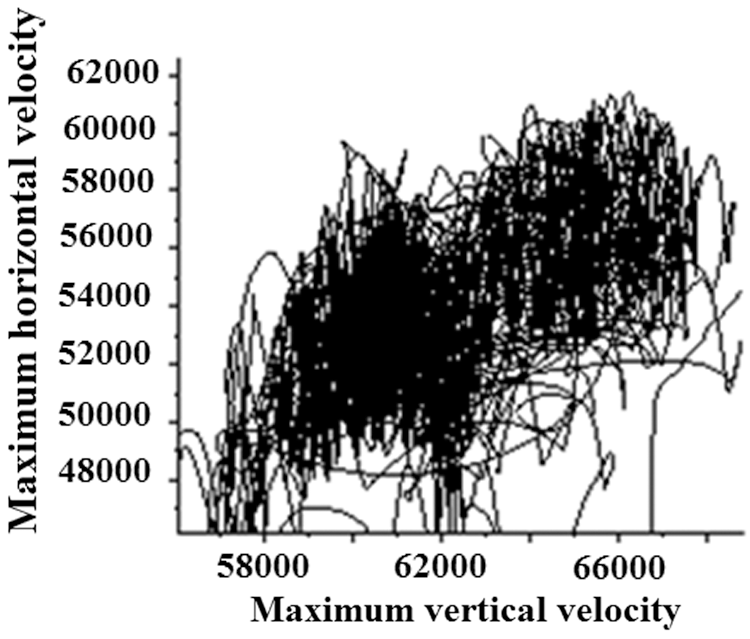
Figure 7: Phase portrait chaotic solution (Ra = 1011)
The appearance of strange shape of attractors in the phase space (Fig. 7), the corresponding amplitude spectrum (Fig. 8) includes peaks whose ratios are irrational. The identification of the first bifurcation as that of Hopf and the results obtained in Figs. 7 and 8 lead us to conclude that our system evolves towards chaos.
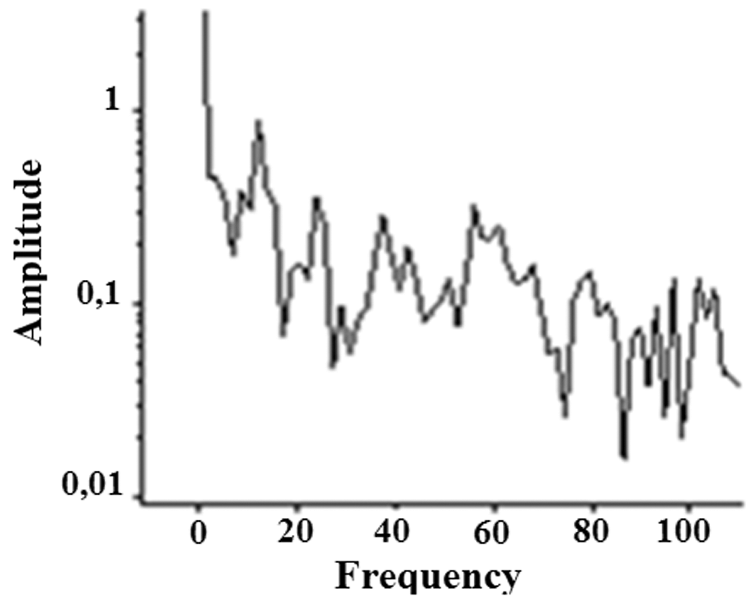
Figure 8: Amplitude spectrum (Ra = 1011)
In Figs. 9 and 10, the plot of the evolutions of the stream function and the temperatures within the cavity for the stationary case displays a flow structure described by three cells, the largest cell occupies along the diagonal of the cavity. The isotherms are perpendicular to the adiabatic horizontal walls. Near the vertical walls, the shape of the isotherms are characteristic of a boundary layer type flow.

Figure 9: Stream function of Ra = 8 106
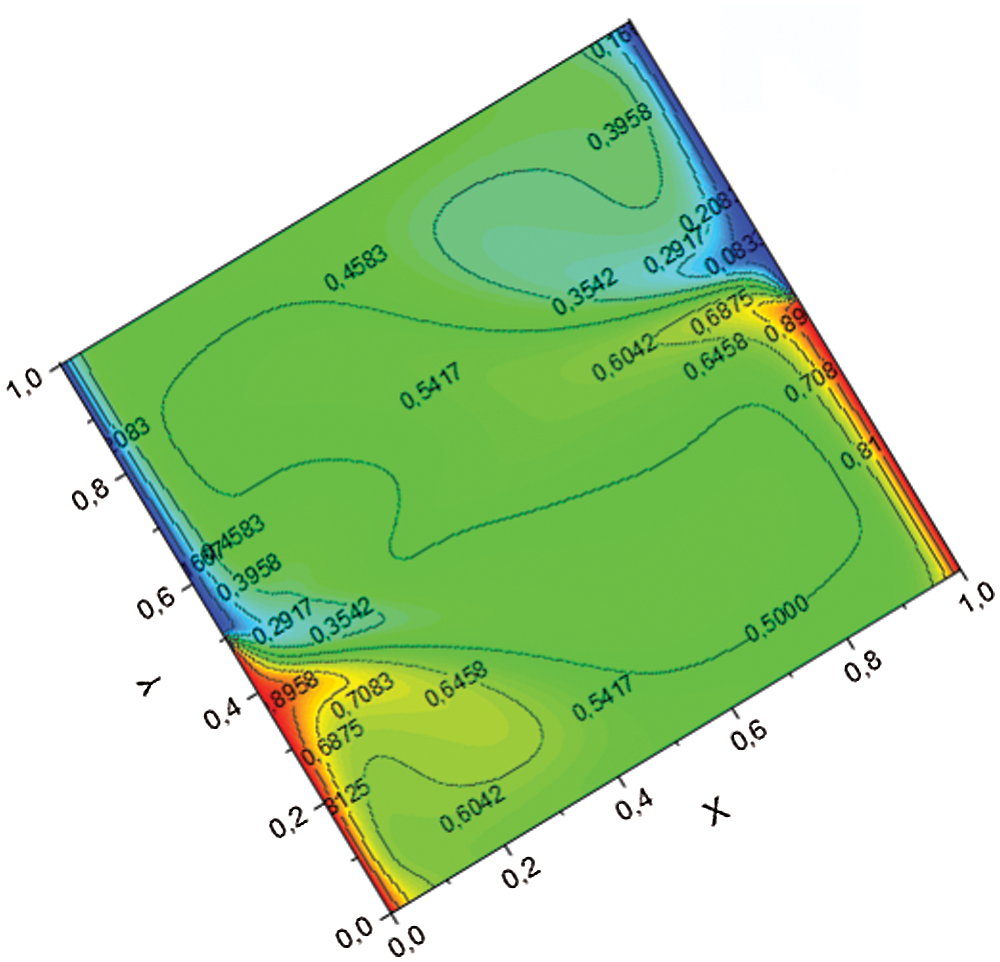
Figure 10: Isotherm of Ra = 8 106
The cell who occupies the diagonal is very intense which means that the transfer is high in this part of the cavity.
The cellular, which occupy the right side of the upper part of the cavity as well as the left side of the lower part of the cavity, rotate in the same direction. This phenomenon is manifested in the trace of the Fig. 10, which shows that the isotherms propagate from the down right side of the cavity to the cold side at the top of the cavity.
The boundary layer formed on the hot and cold sides of the cavity is very important this shows that the heat transfer is ensured by convection.
For the periodic solution (Figs. 11 and 12), the flow structure is described by a tricellular configuration. The isotherms are thin in the in the upper part of the cavity and perpendicular to the horizontal walls. We can explain this by a better heat transfer for a very high Rayleigh number.
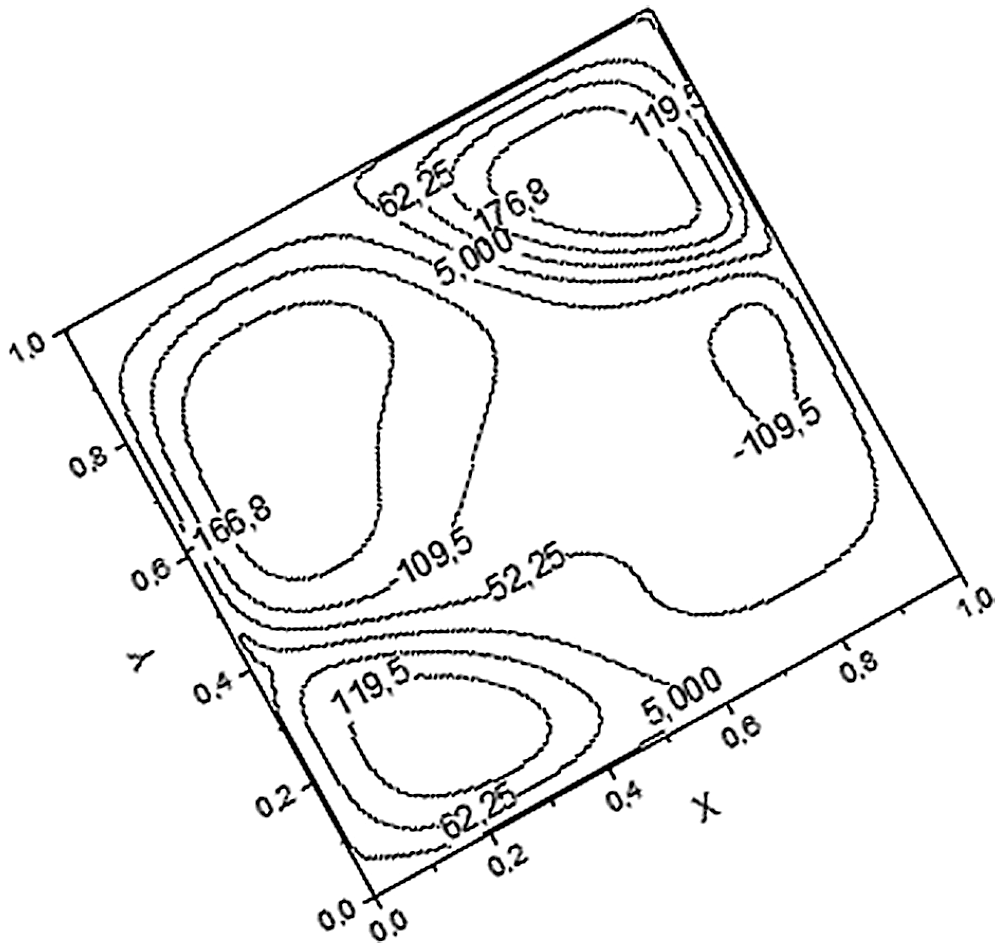
Figure 11: Stream function of Ra = 1011
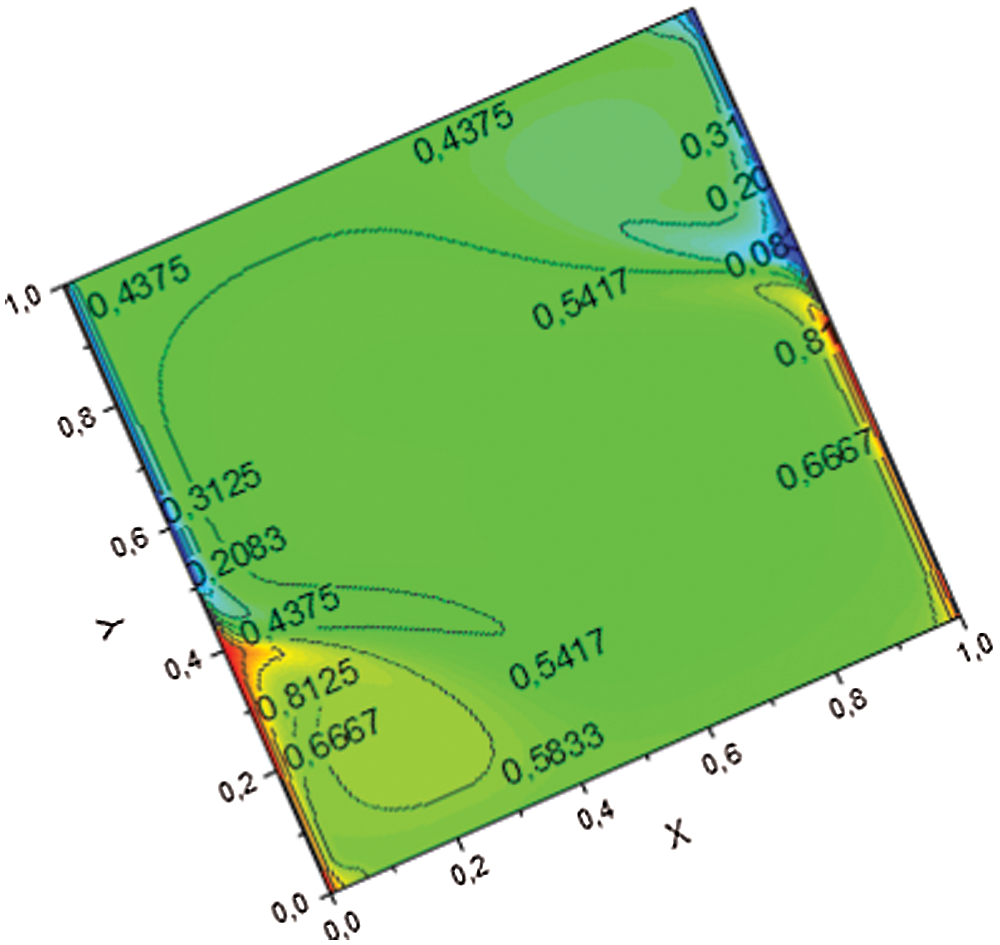
Figure 12: Isotherm of Ra = 1011
We presented in this work a numerical study on the unstationary natural convection in an inclined square, closed and totally porous enclosure. We used the Darcy-Brinkman model and the Boussinesq approximation to establish our equations. The SIMPLE algorithm solves the governing equations governing the phenomenon.
To determine the states of the system, we have used the representation of the attractors in a phase space and the representation of the temporal evolution of dynamics parameters.
The study was carried out for a porous medium having porosity equal to 0.45 and Darcy number equal to 10−3.
The numerical study allowed us to obtain the following results:
− The fixed-point attractor corresponding to the stationary solution is obtained for a Rayleigh number equal to 8.106, a time step equal to 9 × 10−6, and a mesh equal to 111 × 111. The tilt promotes thermal transfer into the cavity due to the buoyant forces.
− The chaos occurs when the number of Rayleigh reaches the value of 1011. The structure of current lines is a disorder causing disorder in the cavity characterized by an excess of energy which is localized throughout the cavity.
Acknowledgement: This work was done at the LTPMP Laboratory, USTHB, Algeria.
Funding Statement: The authors received no specific funding for this study.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
1. Moya, S. I., Ramos, E., Sent, M. (1987). Numerical study of naturel convection in a tilted rectangular porous material. Heat Transfer, 30(4), 741–756. DOI 10.1016/0017-9310(87)90204-3. [Google Scholar] [CrossRef]
2. Ragui, K., Boutra, A., Benkahla, Y. A. (2016). On the validity of a numerical model predicting heat and mass transfer in porous squares with a bottom thermal and solute source: Case of pollutants spreading and fuel leaks. Mechanics and Industry, 17, 311. DOI 10.1051/meca/2015109. [Google Scholar] [CrossRef]
3. Aklouche-Benouaguef, S., Zeghmati, B., Bouhadef, K. (2014). Numerical simulation of chaotic natural convection in a differentiated closed square cavity. Numerical Heat Transfer, Part A: Applications, 65, 229–246. DOI 10.1080/10407782.2013.826113. [Google Scholar] [CrossRef]
4. Aklouche, S., Zeghmati, B. (2017). Bifurcations in two-dimensional differentially heated cavity. Journal of Applied Engineering Science & Technology, 3(1), 7–11. [Google Scholar]
5. Oztop, H. F. (2007). Natural convection in partially cooled and inclined porous rectangular enclosures. International Journal of Thermal Sciences, 46, 149–146. DOI 10.1016/j.ijthermalsci.2006.04.009. [Google Scholar] [CrossRef]
6. Subhash, J. C. (2019). Numerical analysis on the effect of wavy partitions on natural convection in porous enclosure. International Journal of Thermal Sciences, 144(42), DOI 10.1115/1.4047502. [Google Scholar] [CrossRef]
7. Chien, W., Rising, H., Ottino, J. (1986). Laminar mixing and chaotic mixing in several cavity flows. Journal of Fluid Mechanics, 170, 355–377. DOI 10.1017/S0022112086000927. [Google Scholar] [CrossRef]
8. Bhowmick, S., Saha, S. C., Qiao, M., Xu, F. (2019). Transition to a chaotic flow in a V-shaped triangular cavity heated from below. International Journal of Heat and Mass Transfer, 128, 76–86. DOI 10.1016/j.ijheatmasstransfer.2018.08.126. [Google Scholar] [CrossRef]
9. Adjal, S., Aklouche-Benouaguef, S., Zeghmati, B. (2018). Natural convection in a partially porous cavity: Roads to chaos. Numerical Heat Transfer, Part A: Applications, 74(8), 1443–1467. DOI 10.1080/10407782.2018.1525158. [Google Scholar] [CrossRef]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |