

 | Fluid Dynamics & Materials Processing |  |
DOI: 10.32604/fdmp.2022.021760
ARTICLE
Coupled Conductive-Convective-Radiative Heat Transfer in Hollow Blocks with Two Air Cells in the Vertical Direction Subjected to an Incident Solar Flux
1Polydiscilinary Faculty of Ouarzazate, Ibn Zohr University, Ouarzazate, Morocco
2Faculty of Sciences Semlalia, Cadi Ayyad University, Marrakesh, Morocco
*Corresponding Author: Mourad Najjaoui. Email: mourad.najjaoui@edu.uiz.ac.ma
Received: 02 February 2022; Accepted: 24 February 2022
Abstract: This work presents the results of a set of steady-state numerical simulations about heat transfer in hollow blocks in the presence of coupled natural convection, conduction and radiation. Blocks with two air cells deep in the vertical direction and three identical cavities in the horizontal direction are considered (typically used for building ceilings). Moreover, their outside horizontal surface is subjected to an incident solar flux and outdoor environment temperature while the inside surface is exposed to typical indoor environment conditions. The flows are considered laminar and two-dimensional over the whole range of parameters examined. The conservation equations are solved by means of a finite difference method based on the control volumes approach, relying on the SIMPLE algorithm for what concerns the coupling of pressure and velocity. The effects of the number of cells in the horizontal direction and the thermal conductivity on the heat transfer through the alveolar structure have been investigated. The results show that the number of holes has a significant impact on the value of the overall heat flux through the considered structure.
Keywords: Numerical simulation; heat transfer coupled; hollow concrete block; control volumes approach
Nomenclature
| H | structure height (m) |
| h | cavity height (m) |
| dF | view factor between finite surfaces |
| dS | finite area (m2) |
| ei | horizontal partition thickness (m) |
| e’j | vertical partition thickness (m) |
| G | incident solar flux (W.m−2) |
| g | gravity (m.s−2) |
| J | radiosity (W.m−2) |
| k | thermal conductivity (W.m−1.K−1) |
| L | structure depth (m) |
| l | cavity width (m) |
| Nr | radiation to conduction number, σ |
| Nk | thermal conductivity ratio, kf/ks |
| P | dimensionless pressure, (p+0gy)/(0(αf/H) 2) |
| p | pressure (Pa) |
| Q | average heat flux, Q = (ksxQaxΔT)/H |
| Qa | dimensionless average heat flux |
| qr, k | net radiative heat flux at surface k (W.m−2) |
| Qr, k | dimensionless net radiative heat flux at surface k, |
| E | incident radiative heat flux (W.m−2) |
| r | position on the cavity surface |
| r’ | dimensionless position associated with r |
| Pr | Prandtl number, νf /αf |
| Ra | Rayleigh number, gβΔTH4/(νf αf) |
| T | temperature (K) |
| U, V | dimensionless velocity components in x and y directions, (u, v)/(αf/H) |
| X, Y | dimensionless Cartesian coordinates in x and y directions, (x, y)/H |
| Greek symbols | |
| β | thermal expansion coefficient (K−1) |
| α | thermal diffusivity (m2.s−1) |
| ε | cavity surface emissivity |
| ρ | fluid density, (kg.m−3) |
| σ | Stephan-Boltzman constant (W.m−2.K−4) |
| η | dimensionless coordinate normal to a cavity surface |
| ν | kinematics viscosity (m2.s−1) |
| θ | dimensionless temperature, (T-Ti)/ΔT |
| Ψ | dimensionless streamline function |
| Subscripts | |
| f | fluid |
| i | inside |
| e | outside |
| s | solid |
The hollow blocks are generally the main component of the construction of building roofs in Morocco. These hollow blocks were designed to increase the thermal resistance of the roofs construction and for then help reduce the energy consumption requirements for heating or cooling. In general, each hollow block is formed by empty cavities surrounded by concrete partitions, and the heat transfer within these types of structures is complex and done by conduction, natural convection and radiation. Therefore, obvious non-linear characteristics exist within the heat transfer process of these perforations. So, the problems of coupling between the three modes of heat transfer are of great importance in recent years. Citing here some examples: Balaji et al. [1] Ramesh et al. [2], Wang et al. [3], Alvarado et al. [4], Vivek et al. [5], Martyushev et al. [6]. Certain exceptions are nevertheless to be found. numerically investigated coupled heat transfers by conduction, natural convection and radiation in hollow structures heated from below or above are discussed for example, in studies by Ait-Taleb et al. [7,8]. Antar et al. [9] examined conjugate heat transfer across a hollow block. Results show that increasing the number of cavities while keeping the block width constant decreases the heat loss (increases the R-value) significantly. A maximum number of six cavities can fit the building block without compromising the strength. Del Coz Díaz et al. [10] observed that heat flux through walls depended upon the thermal conductivity of block and the size and distribution of cavities.
Sambou et al. [11] studied the conjugate heat transfer across partitioned enclosures with thick conductive partitions and walls. They evaluated the impacts of the thermal conductivity ratio, the partitions number and the enclosure void fraction on the heat transfer.
Recently, a detailed numerical study that takes into account the coupling between the three modes of heat transfer in a three-cavity hollow block used in the construction of building roofs was presented by Najjaoui et al. [12].
This literature review shows that most studies concerning the coupling between the three modes of heat transfer (conduction, convection and/or radiation) are devoted to simple configurations consisting in rectangular cavities with or without conducting walls, subjected to a vertical temperature gradient. where the hallow block are heated from below or from above. The objective of this work is to study numerically in steady state, the heat transfer coupled by natural convection, conduction and radiation in an hallow block has two cells in the vertical direction but subject to real boundary conditions: such as incident solar flux, and heat exchange with the ambient environment via internal exchange coefficients hi and external exchange coefficients he. The results will be presented in terms of streamlines and isotherms, temperature profiles and global heat transfer. moreover, the effect of thermal conductivity, the incident solar flux and the number of cells in the horizontal direction will be presented and examined.
2.1 Studied Structure and Mathematical Equations
Fig. 1 below shows the physical model of the studied configuration. It is a hollow concrete block which Consisting of six cavities each of width l and height h and having vertical conducting walls of thickness ei and horizontal ones of thickness e’j. The upper horizontal surface is exposed to an incident solar flux (G) and to an external ambient temperature Te with a surface exchange coefficient he. The inside surface is submitted to indoor environment temperature, Ti and with a surface exchange coefficient hi. The vertical faces are considered adiabatic.
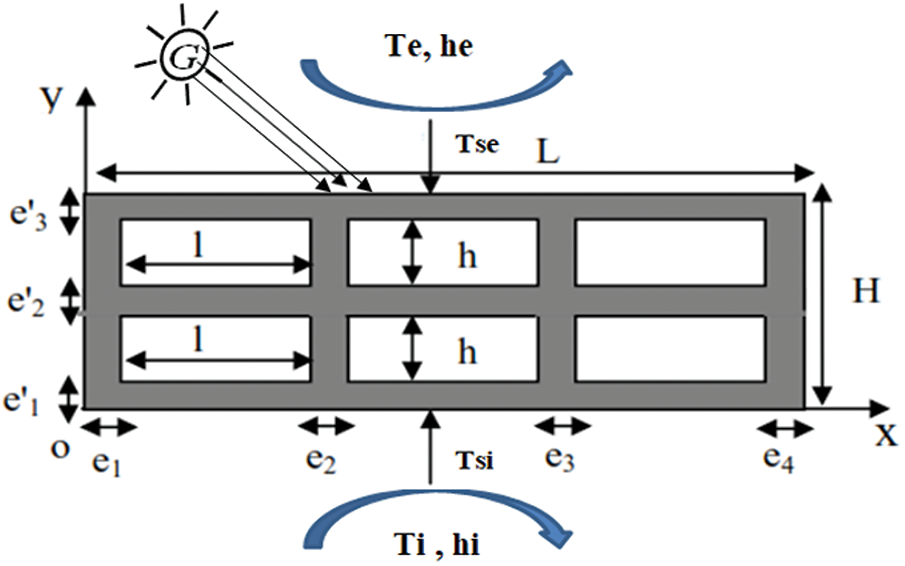
Figure 1: Studied configuration
By using the Boussinesq approximation, the obtained dimensionless governing equations are [13,14]:
The dimensionless equation for heat conduction in solid walls is:
where θs is the dimensionless solid temperature and αf and αs are the fluid and the solid thermal diffusivities, respectively.
The boundary conditions are expressed as follows:
• Adiabaticity condition on the vertical sides:
• For the external horizontal face:
• For the inner horizontal face:
• The continuity of the temperature and the heat flux at the fluid–solid interfaces gives:
The dimensionless radiative heat flux can be expressed as [15]:
The dimensionless average heat flux across the structure is given by:
2.2 Validation of the Numerical Procedure
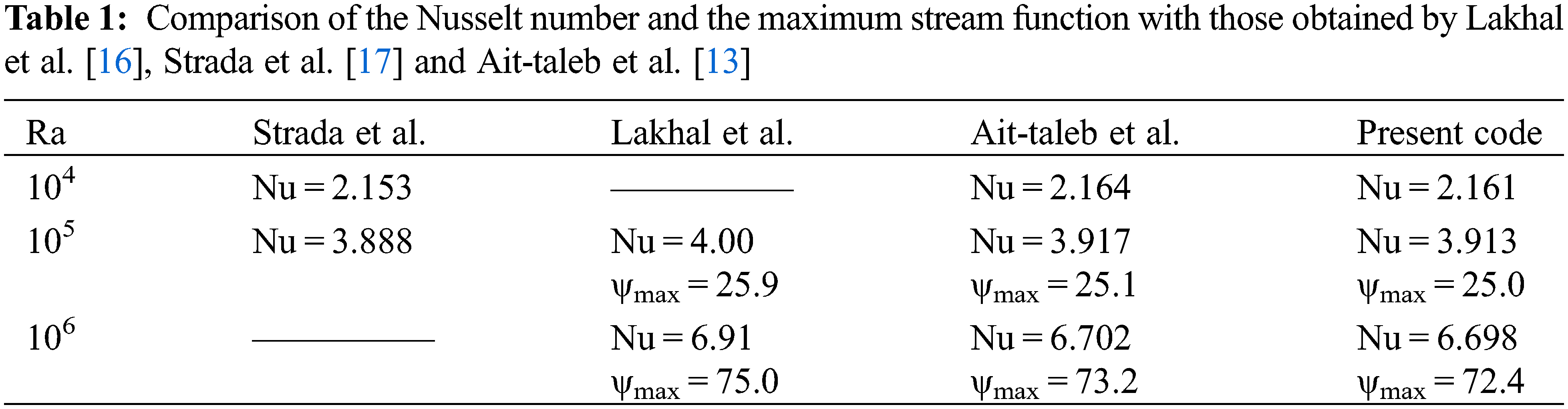
The numerical code performed using FORTRAN software was validated by comparing the results with those of Lakhal et al. [16], Strada et al. [17] and Ait-taleb et al. [7], who studied the natural convection in a heated from below square cavity. Results given in Table 1 show that the Nusselt number and the maximum stream function obtained for different Rayleigh numbers in good agreement.
The results presented in this study are obtained for hollow block charactezied by the geometric dimensions given in Table 2. The thermal conductivity of solid partitions ks varies between 0.5 and 1 W/mK. The incident solar flux G on the outside face of the structure is fixed at the value 1000 W/m2, the fluid that reigns in the cavities is the air with the thermal conductivity ka = 0.0262 W/mK and the Prandtl number Pr = 0.71, The emissivity of the internal surfaces of the cavities is ε = 0.9.

3.1 Effect of Heat Conductivity
3.1.1 Isotherms and Streamlines
Fig. 2. gives the streamlines contours (top) and the isotherms (bottom) obtained for a hollow block with two cells in the direction (oy) Ny = 2, The results in the figure show that the flow structures in each cavity are characterized by four cells and flow in opposite directions testifying to the two-dimensional flow. These small recirculation cells (at the level of the current lines) are due to low intensity flows. It should be noted that this type of flow is similar to that which has been observed in the case of an hollow block with a single cell in the vertical direction [12], but having the same geometric dimensions, for the internal cavities and the solid partitions, than the one studied here. for ks = 0.5 and ks = 0.8 W/mK there is an appearance of small vortices at the corners. This behavior indicates that the fluid heated from above or cooled from below tends to circulate just in the vicinity of the active walls. for ks = 1 and ks = 0.8 W/mK the isotherms are linear in the solid and in the fluid. And for ks = 1 W/mK the distortion of the isotherms in the solid walls separating the different cavities indicates a two-dimensional character of the heat transfer, whereas there are almost parallel lines in the cavities indicating a state of thermal stratification of the fluid.
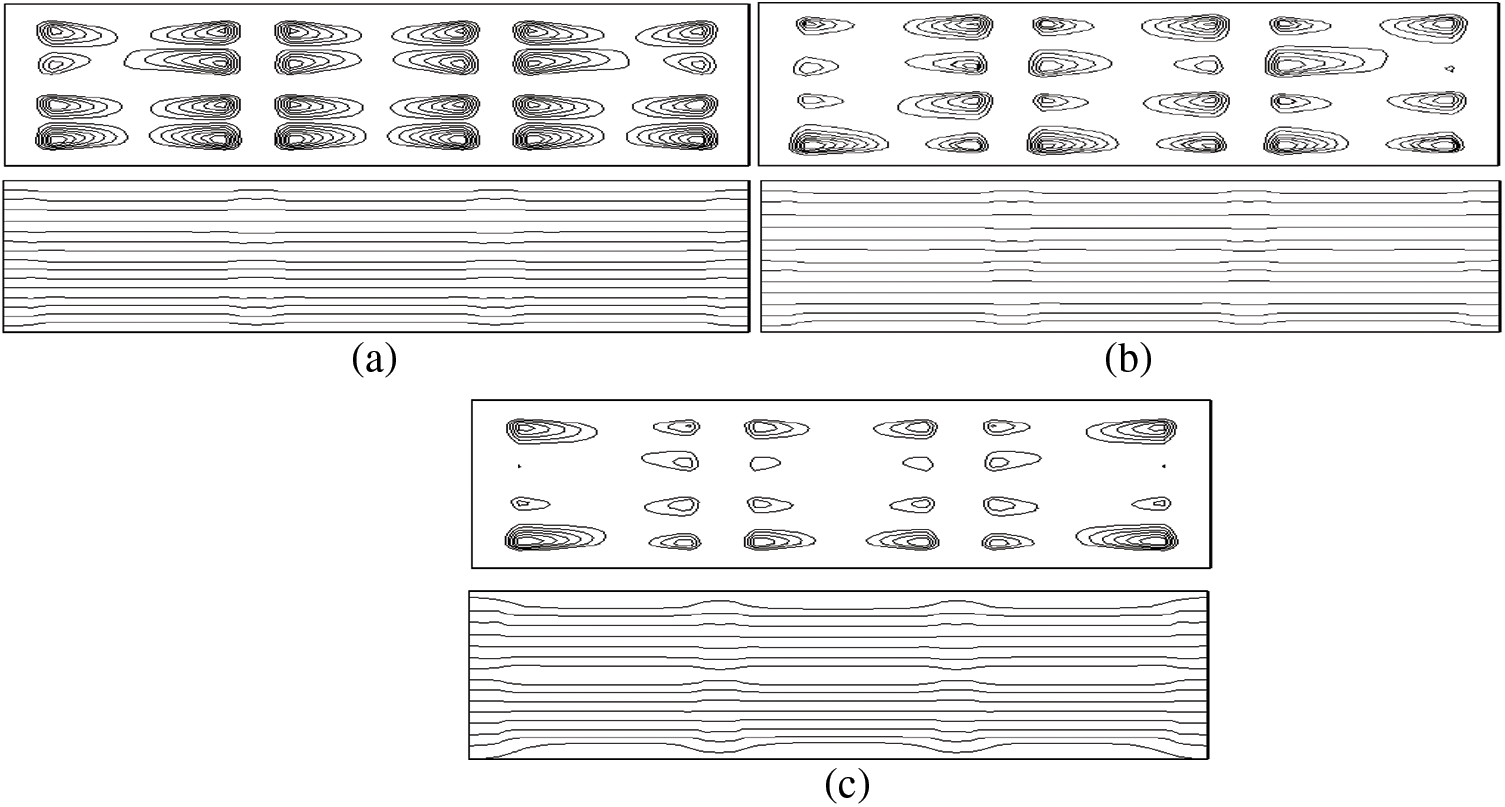
Figure 2: Streamlines and isotherms obtained for (a) ks = 0.5 W/m.K, (b) ks = 0.8 W/m.K and (c) ks = 1 W/m.K
Fig. 3 shows the distribution of the overall heat flux crossing the hot upper surface as a function of the width X. In general, the heat flux passing through the block increases as the thermal conductivity ks increases, Indeed, the average value of the total flux increases from value 132.59 W/m² for ks = 0.5 W/m.K to 217.75 W/m² for ks = 1 W/m.K. This corresponds to an increase of approximately 64%. This can be explained by the conductive transfer rate which increases with increasing thermal conductivity according to Fourier’s law. The profile of this behavior remains the same for the three values of ks considered. the heat flow presents a maximum at the level of the solid walls and inside the cavities there is a moderation of the heat transfer marking the absence of the convective transfer for the three values of ks (heating from above).
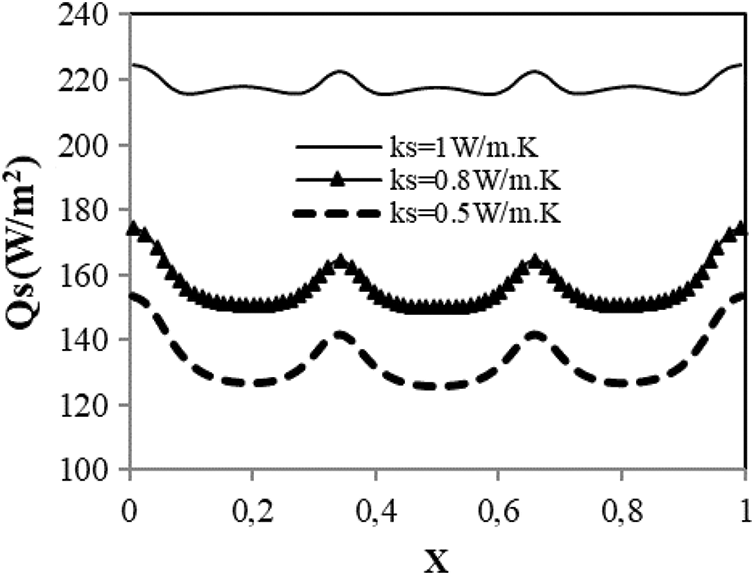
Figure 3: Variation of the heat flux Qs
3.2 Effect of Incident Solar Flux on Thermal Field
In order to examine the effect of incident solar flux G on the temperatures of the upper and lower surfaces of the studied system. we represent on Fig. 4 the variation of the temperature for G = 0 W/m² and G = 1000 W/m². The figure shows that that the increase of the incident solar flux G leads to an increase in the temperature of both external (upper) and internal (lower) surfaces of the hollow block. Indeed, when the flux G pass from 0 W/m² to 1000 W/m² the upper temperature face Tse increases by 13% while that of the lower face Tsi increases by 4%. We also note that the temperature differences between the upper (hot) and lower (cold) surfaces increases significantly as the incident solar flux increases. As an indication, the temperature difference between the hot and cold horizontal faces of the hollow block varies from 13.36°C for G = 0 W/m² to 42.75°C for G = 1000 W/m². We also note that the temperature profile of the top and bottom surfaces of the structure is nearly constant as a function of X.
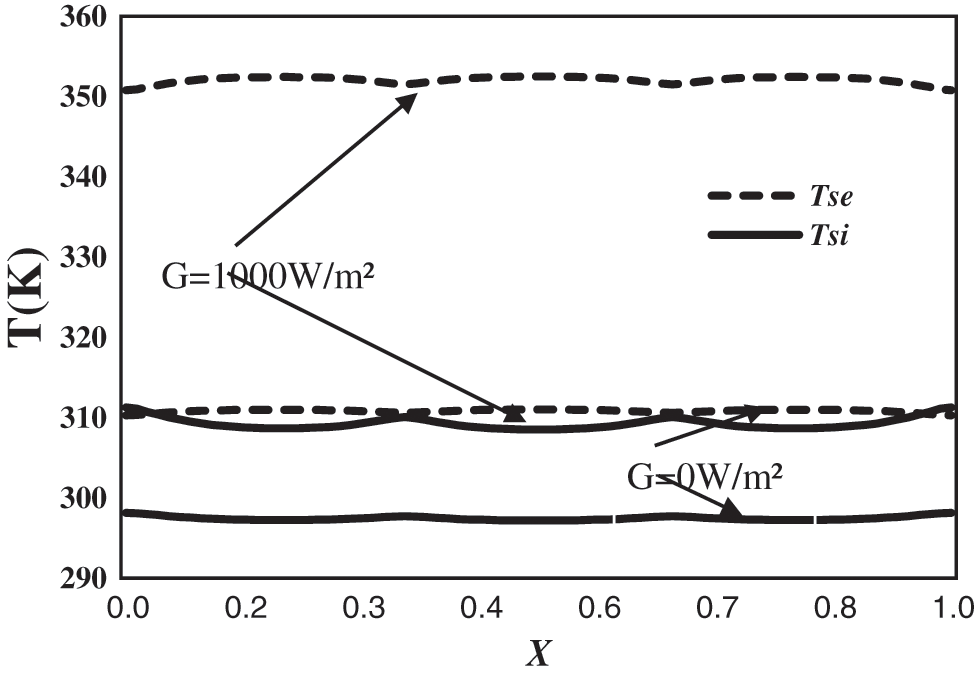
Figure 4: Temperature variation of horizontal faces of the studied system
3.3 Effect of the Number of Cells in the Vertical Direction
The objective of this paragraph is to study the effect of the number of holes in a horizontal row on the heat flow through the hollow block. the Fig. 5. presents he variation of the mean heat flow Q (in W/m2) crossing the alveolar structure as a function of the incident solar flux G, for thermal conductivity ks = 1 W/m.K. The results of this figure show that this flux increases when the incident flux G increases, and varies almost linearly as a function of G especially for (Ny = 1). It can be noticed that the heat flux crossing the structure with one air cell deep in direction vertical (Ny = 1) is distinctly upper to the one found for (Ny = 2). Indeed, The structure having 2 holes in a vertical row decreases the heat transfer by about 35% with respect to the type with 1 hole. Indicating that this structure contributes to the improvement of the thermal performance of the roof of the building.
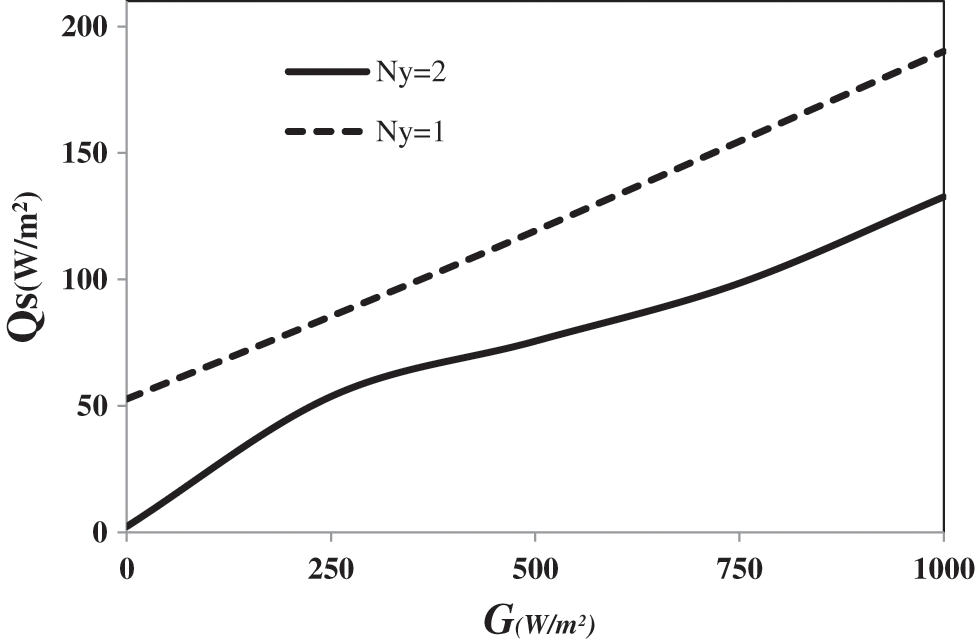
Figure 5: Variation of the global heat flux as a function of the incident solar flux G for Ny = 1 and Ny = 2
This work was given to the investigation of coupled heat transfer by conduction, natural convection and radiation through a structure with two air cells deep in direction oy submitted to an incident heat flux G. We examined the effect of thermal conductivity ks, the incident solar flux and the number of cells in a hollow concrete block.
Based on the findings of the present work, the following conclusions are drawn:
• The number of holes has a significant impact on the value of the overall heat flux through the structure studied, the heat transfer through the system could be considerably reduced by using a structure with two cells. This is increasing thermal resistance of the envelope and hence, reducing transmission loads.
• The incident solar flux alters significantly the thermal fields through the studied structure. Indeed, the studied system has decreased the temperature by about 42°C between the outside and the inside of the roof of the building, which helps to ensure the reduction of thermal loads.
• It has also been found that the effect of conductivity is important on the structure of the flow and the temperature field, Thus the heat transfer through the hollow block strongly depends on the thermal conductivity of the solid partitions ks, This corresponds to an increase of about 64% passing from ks = 0.5 W/m.K to ks = 1.0 W/m.K.
These results can contribute to the future building envelope design in terms of insulation capacity and fill the gaps for research in the area of insulation systems.
Funding Statement: This research has not received any funding from any fellowship program.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study
1. Balaji, C. S., Venkateshan, P. (1993). Interaction of surface radiation with free convection in a square cavity-sciencedirect. International Journal of Heat and Fluid Flow, 14(3), 260–267. DOI 10.1016/0142-727X(93)90057-T. [Google Scholar] [CrossRef]
2. Ramesh, N., Venkateshan, S. P. (2012). Effect of surface radiation on natural convection in a square enclosure. Journal of Thermophysics & Heat Transfer, 13(3), 299–301. DOI 10.2514/2.6458. [Google Scholar] [CrossRef]
3. Wang, H., Xin, S., Le Quéré, P. (2006). Numerical study of natural convection-surface radiation coupling in air-filled square cavities. Comptes Rendus-Mecanique, 334, 48–57. DOI 10.1016/j.crme.2005.10.011. [Google Scholar] [CrossRef]
4. Alvarado, R., Xamán, J., Hinojosa, J., Alvareza, G. (2008). Interaction between natural convection and surface thermal radiation in tilted slender cavities. International Journal of Thermal Sciences, 47, 355–368. DOI 10.1016/j.ijthermalsci.2007.03.007. [Google Scholar] [CrossRef]
5. Vivek, V., Sharma, A. K., Balaji, C. (2012). Interaction effects between laminar natural convection and surface radiation in tilted square and shallow enclosures. International Journal of Thermal Sciences, 60, 70–84. DOI 10.1016/j.ijthermalsci.2012.04.021. [Google Scholar] [CrossRef]
6. Martyushev, S. G., Sheremet, M. A. (2015). Numerical simulation of 3D regimes of natural convection and surface radiation in a differentially heated enclosure. Journal of Engineering Thermophysics, 24, 22–32. DOI 10.1134/S1810232815010038. [Google Scholar] [CrossRef]
7. Ait-Taleb, T., Abdelbaki, A., Zrikem, Z. (2008a). Numerical simulation of coupled heat transfers by conduction, natural convection and radiation in hollow structures heated from below or above. International Journal of Thermal Sciences, 47(4), 378–387. DOI 10.1016/j.ijthermalsci.2007.01.035. [Google Scholar] [CrossRef]
8. Ait-Taleb, T., Abdelbaki, A., Zrikem, Z. (2008b). Transfer function coefficients for time varying coupled heat transfers. application to hollow concrete brick. Building Simulation Journal, 1, 303–310. DOI 10.1007/s12273-008-8131-y. [Google Scholar] [CrossRef]
9. Antar, M. A., Baig, H. (2009). Conjugate conduction–natural convection heat transfer in a hollow building block. Applied Thermal Engineering, 29, 3716–3720. DOI 10.1016/j.applthermaleng.2009.04.033. [Google Scholar] [CrossRef]
10. Del Coz Díaz, J. J., García Nieto, P. J., Alvarez Rabanal, F. P., Hernández Domínguez, J. (2012). Non-linear thermal analysis of the efficiency of light concrete multi-holed bricks with large recesses by FEM. Applied Mathematics and Computation, 218, 10040–10049. DOI 10.1016/j.amc.2012.03.096. [Google Scholar] [CrossRef]
11. Sambou, V., Lartigue, B., Monchoux, F., Adj, M. (2014). Modeling of the thermal performance of air-filled partitioned enclosures: Effects of the geometry and thermal properties. Journal of Building Physics, 39, 321–341. DOI 10.1177/1744259114561578. [Google Scholar] [CrossRef]
12. Najjaoui, M., Ait-Taleb, T., Abdelbaki, A., Zrikem, Z., Chaib, H. (2018). Coupled heat transfers in a three cavities hollow block subjected to an incident solar flux: Effect of heat conductivity. IOP Conference Series: Earth and Environmental Science, 161(1), 012002. DOI 10.1088/1755-1315/161/1/012002. [Google Scholar] [CrossRef]
13. Ragui, K., Benkahla, Y. K., Labsi, N., Boutra, A. (2015). Natural convection heat transfer in a differentially heated encloseure with adiabatic partitions and filled with a bingham fluid. Journal Heat Transfer Research, 46(8), 765–783. DOI 10.1615/HeatTransRes.2015007477. [Google Scholar] [CrossRef]
14. Ragui, K., Boutra, A., Benkahla, Y. K. (2016). On the validity of a numerical model predicting heat and mass transfer in porous squares with a bottom thermal and solute source: Case of pollutants spreading and fuel leaks. Mechanics & Industry, 17, 311. DOI 10.1051/meca/2015109. [Google Scholar] [CrossRef]
15. Siegel, R., Howell, J. R. (1981). Thermal Radiation Heat Transfer, 2nd ed. New York: McGraw-Hill. [Google Scholar]
16. Lakhal, E. K., Hasnaoui, M., Bilgen, E., Vasseur, P. (1994). Convection naturelle dans une cellule carrée chauffée périodiquement par le bas: Etude numérique. Revue Générale de Thermique, 392, 480–485. [Google Scholar]
17. Strada, M., Heinrich, J. C. (1982). Heat transfer rates in natural convection at high Rayleigh numbers in rectangular enclosures: A numerical study. Numerical Heat Transfer, 5, 81–93. DOI 10.1080/10407788208913436. [Google Scholar] [CrossRef]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |