

 | Fluid Dynamics & Materials Processing |  |
DOI: 10.32604/fdmp.2022.021949
ARTICLE
Navier Slip and Heat Transfer in a Nanofluid Due to a Stretching/Shrinking Sheet: An Analytical Study
1Department of Mathematics, Shivagangotri, Davangere University, Davangere, 577007, India
2Institut Universitaire de Technologie de Longwy, Université de Lorraine 186 rue de Lorraine, Cosnes et Romain, 54400, France
3LMT/ENS-Cachan/CNRS/Université Paris Saclay, Cachan, 94235, France
*Corresponding Author: U. S. Mahabaleshwar. Email: u.s.m@davangereuniversity.ac.in
Received: 15 February 2022; Accepted: 07 March 2022
Abstract: This paper is devoted to the analysis of the heat transfer and Navier’s slip effects in a non-Newtonian Jeffrey fluid flowing past a stretching/shrinking sheet. The nanoparticles, namely, Cu and Al2O3 are used with a water-based fluid with Prandtl number 6.272. Velocity slip flow is assumed to occur when the characteristic size of the flow system is small or the flow pressure is very small. By using the similarity transformations, the governing nonlinear PDEs are turned into ordinary differential equations (ODE’s). Analytical results are presented and analyzed for various values of physical parameters: Prandtl number, Radiation parameter, stretching/shrinking parameter and mass transpiration for the flow and heat transfer. The considered problem is relevant to various physical applications in the field of engineering, e.g., the production of certain materials, the preparation of plastic and rubber sheets and glass blowing. It is shown that the considered nanofluid increases the thermal efficiency. The nanoparticles act as a heater by increasing the solid volume fraction and thermal radiation. Vice versa, they can act as a cooler if the strength of magnetic field is increased. The flow strength decreases by increasing the values of Deborah number.
Keywords: Nanofluid; navier’s slip; radiation; ordinary differential equations
Nomenclature
| A and B | coefficients of first and second order slip, respectively |
| a and b | constants |
| B0 | uniform magnetic field (Tesla) |
| CP | specific heat at constant pressure (JKg−1K−1) |
| c | constant |
| Erfc | complementary error function |
| k | solution domain |
| | mean absorption coefficient |
| l1 and l2 | first and second order slip, respectively |
| Pr | Prandtl number |
| Q | Chandrasekhar’s number |
| qr | radiative heat flux |
| qw | local heat flux (wm−2) |
| R | thermal radiation |
| T∞ | ambient temperature (K) |
| Tw | temperature at wall (K) |
| T | temperature (K) |
| uw(x) | velocity at wall |
| ue(x) | potential velocity |
| vw | mass flux (ms−1) |
| VC | mass transpiration |
| (u, v) | components of velocity (ms−1) |
| (x, y) | Cartesian coordinate (m) |
| Greek symbols | |
| σ | electrical conductivity (Sm−1) |
| | Stefan-Boltzmann constant (Wm−2K−4) |
| λ | stretching/shrinking parameter |
| ξ1 and ξ2 | related to relaxation parameter |
| β | Deborah number (cξ2) |
| Λ | strength parameter |
| η | similarity variable |
| νnf | kinematic viscosity of nanofluid (m2s−1) |
| νf | kinematic viscosity of base fluid (m2s−1) |
| ρnf | density of nanofluid (kgm−3) |
| ρf | density of base fluid (kgm−3) |
| | thermal diffusivity of nanofluid. |
| μnf | dynamic viscosity of nanofluid (kgm−1S−1) |
| μf | dynamic viscosity of base fluid (kgm−1S−1) |
| κ | thermal conductivity (W/mK) |
| K | temperature jump |
| τw | skin friction |
| τ | inclined angle |
| Subscripts | |
| w | quantities at wall |
| ∞ | quantities at freestream |
| f | fluid |
| nf | snanofluid |
| Abbeviations | |
| MHD | magnetohydrodynamics |
| ODE | ordinary differential equation |
| PDE | partial differential equation |
In the recent few eras the researchers show much interest on the flow of non-Newtonian fluids. This interest is growing like a stem of a tree because of its huge technological and industrial applications in many fields such as engineering applications, exchanger of heat, extrusion of metal and polymer process, manufacturing of paper, cable coating and so on. Numerous investigations take place on the flow of a fluid through a stretching/shrinking surface. Most of them agreed that Sakiadis [1] conducted the first investigation on the flow of a fluid induced by a moving surface. The flow of a fluid due to a stretching sheet is analyzed by Crane [2]. In this he studied the flow due to a sheet with constant speed from a slit into a fluid at rest. Motivated by Crane’s work, many researchers conducted an experiment on the flow caused by the stretching/shrinking sheet. See the examples of Mahabaleshwar et al. [3,4] and Amkadni et al. [5]. Further, many more investigations take place on the flow of a stretching/shrinking sheet in the presence of MHD. Pavlov [6,7] primarily examined the stretching wall problem in the presence of MHD, this study describes the flow of a conducting fluid through a deformation of a plane elastic surface in a transverse magnetic field and it is analyzed in the approximation of boundary layer theory. Later Mahabaleshwar et al. [8,9] investigated the flow problem in the presence of MHD, this study describes the characteristics of heat and MHD imposed on the stretching sheet and it is solved analytically. Fang et al. [10] examined the magnetohydrodynamic flow in the presence of slip condition through a permeable stretching surface and the solution is solved analytically by inclusion of MHD and radiation. Smith [11] 1st work on the effect of radiation in a boundary layer flow, this work describes the radiation in the boundary layer on aerodynamic heat transfer. After this huge research was conducted on radiation. Siddheshwar et al. [12], worked on MHD flow and heat transfer in a viscoelastic liquid past a stretching sheet in the presence of radiation. Later Mahabaleshwar et al. [13] various methods have been conducted to improve the thermal conductivity of flow fluid by adding nano sized particles inside the liquids: then these liquids are called nanofluids. see the two examples of research on nanofluids [14,15]. Recently many works have been conducted on nanofluids, hybrid nanofluids and carbon nanotubes with a variety of boundary conditions under many situations such as MHD and thermal radiation, mass transpiration and so on. Mahabaleshwar et al. [16–18] and Anusha et al. [19] worked on role of brinkmann model with non-Newtonian fluid flow in the presence of porous medium with heat transfer and the effect of hybrid nanofluid flow with superlinear stretching sheet and Navier’s slip effects on flow of a fluid with thermal radiation and mass transpiration.
Apart from these research some of the researchers conducted an experiment on Jeffrey fluid. The magnetohydrodynamics effects and other physical mechanisms show huge significance in many Jeffrey fluid applications. Jeffrey fluid past a Narrow tube with a Magnetic field is examined in [20]. Peristaltic flow of chyme in the small intestine with magnetic field and their characteristics explained in [21]. Kumar et al. [22] described incompressible Jeffrey fluid flow in the presence of a magnetic field with the annulus of rotating concentric.
Inspired by the above research papers the present work is to extend the articles [23,24], this work fulfills the impact of inclined MHD and second order slip in the presence of nanofluid. The governing PDEs of the problems are transformed into ODEs with the help of similarity variables; the whole investigation takes place on Cu-water nanofluid. The flow is caused due to stretching/shrinking sheets, with the help of suitable similarity transformation. The resulting ODEs are solved analytically to get the solution domain, this solution domain is used in heat equation and solved direct integration technique to obtain exact solution. The results of Cf and Nu can be attained with the help of graphs.
2 Physical Modeling and Governing Equations
In the current work Jeffrey nanofluid flow is taken into account. This flow is a laminar steady state and it is emerging towards the x-axis near the stagnation point in the presence of Cu-water nanofluid. The flow is caused through a permeable stretching/shrinking surface lying at y = 0, the flow configuration is physically explained in Fig. 1. Also the nanofluids quantities are represented at Table 1. The uniform magnetic field B0 is inserted at the deforming velocity of the wall uw(x). Along with potential velocity ue(x), assume the uniform ambient temperature T∞ at the for field. The governing Navier’s stokes equations are given below:
the applied boundary conditions (see [25,26])
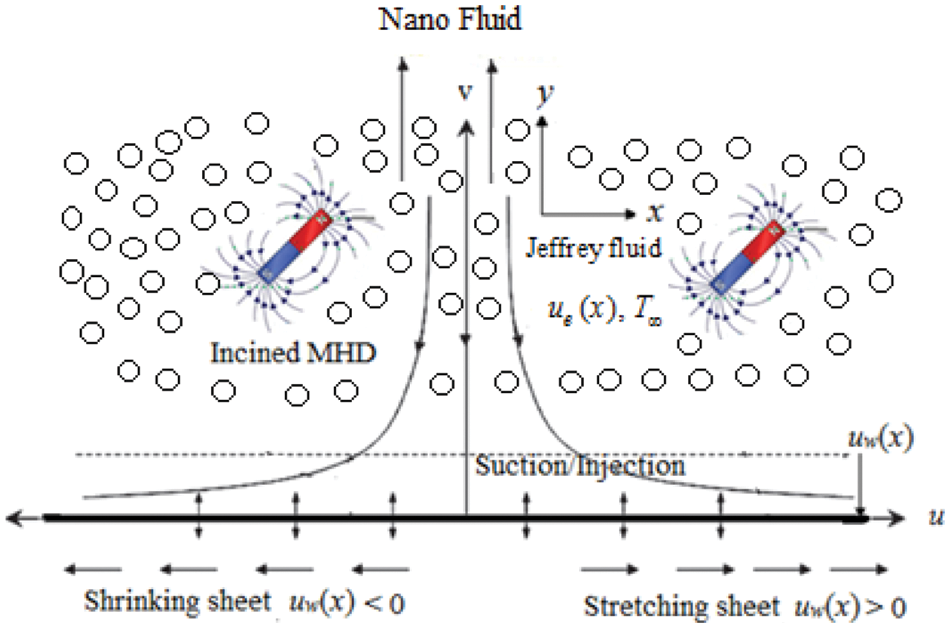
Figure 1: Physical representation of jeffrey fluid flow
It is mentioned that there are two boundary conditions exist for wall temperature Tw(x), either it is constant or evolving with x linearly via Tw(x) = Tw + bx. T denotes the temperature of the fluid, and vw denotes the mass flux velocity with vw < 0 represents suction and vw < 0 represents injection. For the purpose of obtaining exact solutions the fluid properties are assumed to be constant, ξ1 and ξ2 are associated to relaxation parameters., at lastly stretching case is represented by λ = 1 and shrinking case by λ = −1.
The Rosseland’s formulation for the radiative heat flux can be simplified for radiation as (see [27–32])
where, T4 is expressed in the form of linear function of the temperature. Increasing the term T4 in the form of Taylor series and also some terms are ignored.
Substituting Eqs. (5a) and (5b) in Eq. (3) and the following suitable transformation applied to get the ordinary differential equations:
on applying these similarity transformations to the Eqs. (1) to (4), then these equations are simplified to
the constant parameters inserted in the Eqs. (5) to (7), can be defined as
The BC’s transformed to
Here
3 Physical Quantities of Interest
The skin friction coefficient Cf and Local Nusselt number Nux is given by
where
Substituting, Eq. (11) in Eq. (10), after some manipulation the Cf and Nux are given by
4 An Analytical Solution for Momentum and Energy Equations
Let us assume the solution of the Eq. (6)
in order to get the algebraic formula connecting with the physical parameters by equating Eqs. (13) into (6). The constraint k must be positive to achieve the solution.
For limiting case Λ = 0, then Eqs. (13) and (14) reduce to
Further, we assuming the solution of temperature equation
Substituting (13) and (17), in (8), then we found the solution as
After some manipulation on equating (16) and (18), we get the root of the equation as
where, k > 0 is independent of λ, l1 and l2, and also the Parameter VC will change with these parameters, the Cf and Nu are then becomes
Therefore, the Cf will decreases by increasing first and second order slip
Next we take particular case Λ = 1, and λ = 1, then Eq. (13) becomes
Substituting this in Eq. (7), the solution obtained as
where
The Jeffrey nanofluid flow is considered in the current investigation, the impact of inclined MHD and second order slip is taken into account with this flow in the presence of Cu-water nanofluid. The flow is conducted due to a stretching/shrinking sheet. The governing PDEs are mapped into ODEs with the help of similarity transfromations, the momentum equation of this problem is verified exactly to get solution domain. By using direct integration technique to verify the energy equation and also the solution domain connected with heat equation through f(η). To understand the problem tharougly skin friction and Nusselt number can be verified. The results of this investigation can be conducted with the help of graphs on varying the different parameters.
Figs. 2 and 3 demonstrate that the impact of f(η) on similarity variable η for stretching and shrinking case. In Fig. 2a it is observed that the stretching case condition, i.e., λ = 1, in this the flow of a fluid increases with increase of Radiation parameter R, and also the boundary layer thickness is away from the x-axis. Here the flow fluid increases with increase of β value. Whereas Fig. 2b indicates the shrinking case λ = −1, in this also in this the flow of a fluid increases with increase of Radiation parameter R, and also the boundary layer thickness is away from the x-axis. But the flow fluid decreases with increase of β value. Thermal radiation is much impact on fields it increases the flow velocity and heat transfer rate.
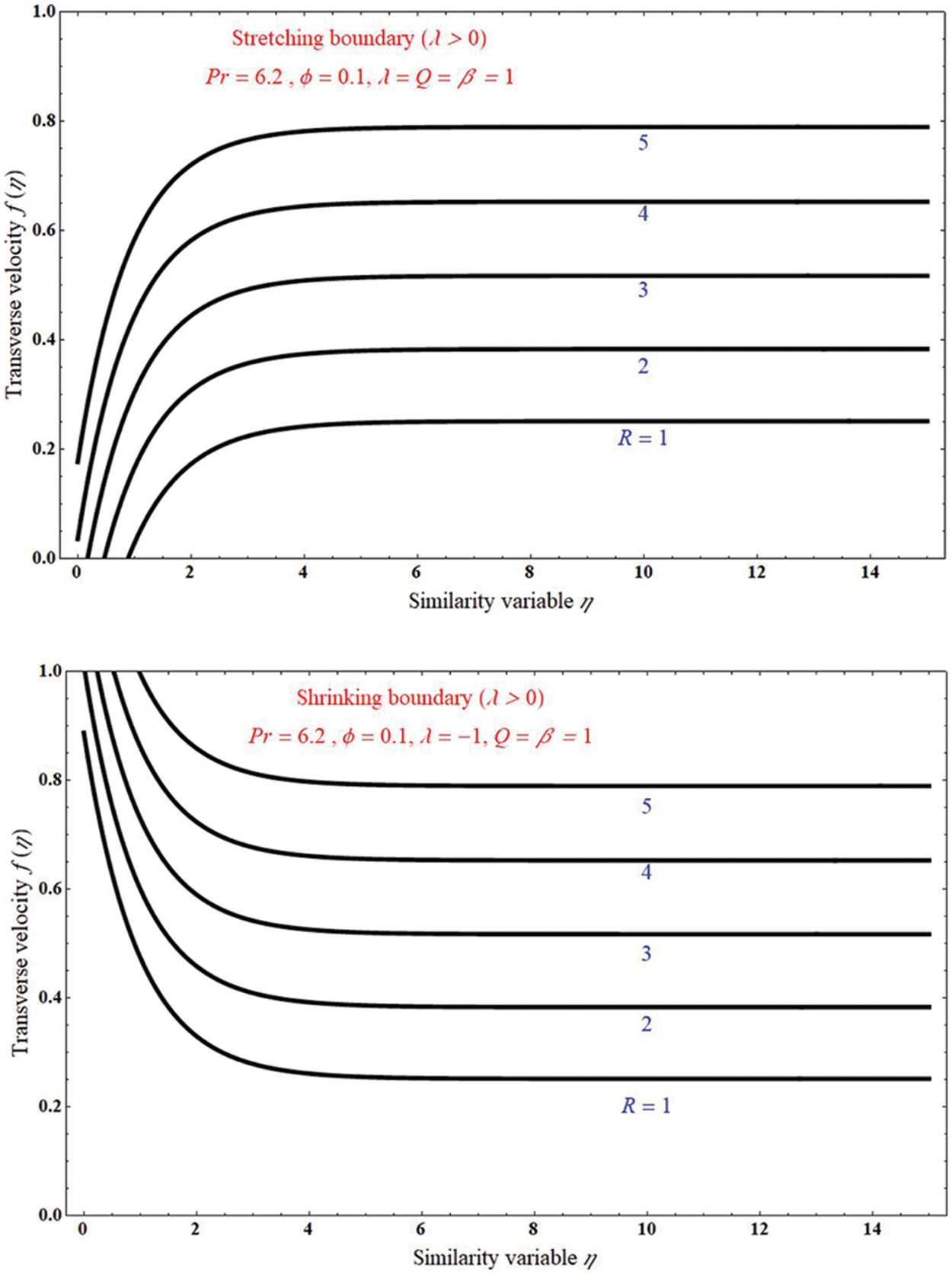
Figure 2: The impact of transverse velocity on similarity variable η for unlike values of radiation parameter R, at (a) stretching case λ = 1, and (b) shrinking case λ = −1
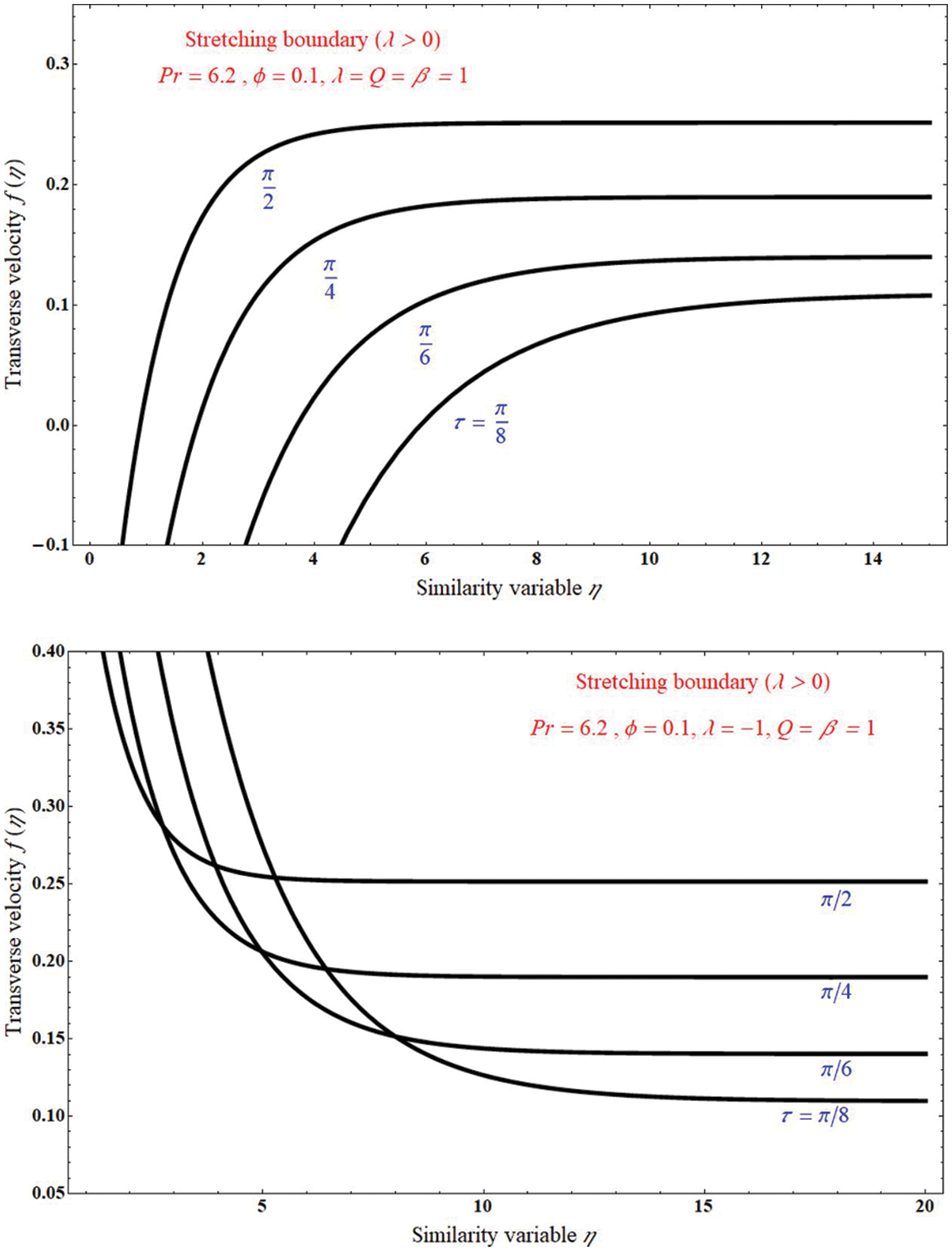
Figure 3: The impact of transverse velocity on similarity variable η for unlike values of inclined angle τ, at (a) stretching case λ = 1, and (b) shrinking case λ = −1
Figs. 3a and 3b analyse the flow of a fluid with unlike values of inclined angle τ for stretching and shrinking case, respectively. In both stretching and shrinking case the transverse velocity decreases with increase of inclined angle τ, and boundary value thickness is towards the x-axis.
The effect of tangential velocity on similarity variable η can be represented by Figs. 4 and 5. In Figs. 5a and 5b it is indicating that the tangential velocity decreases for stretching case and it is increased for shrinking case when we varying the Chandrasekhar’s number Q, respectively, boundary layer thickness is away from the x-axis in stretching case, and boundary layer thickness is towards the x-axis in shrinking case. Figs. 6a and 6b represent the stretching case and shrinking case, respectively. In Fig. 6a it is observed that the tangential velocity increases with increases of inclined angle τ and this effect is reversed in Fig. 6b, also boundary layer thickness is away and towards the x-axis, respectively.
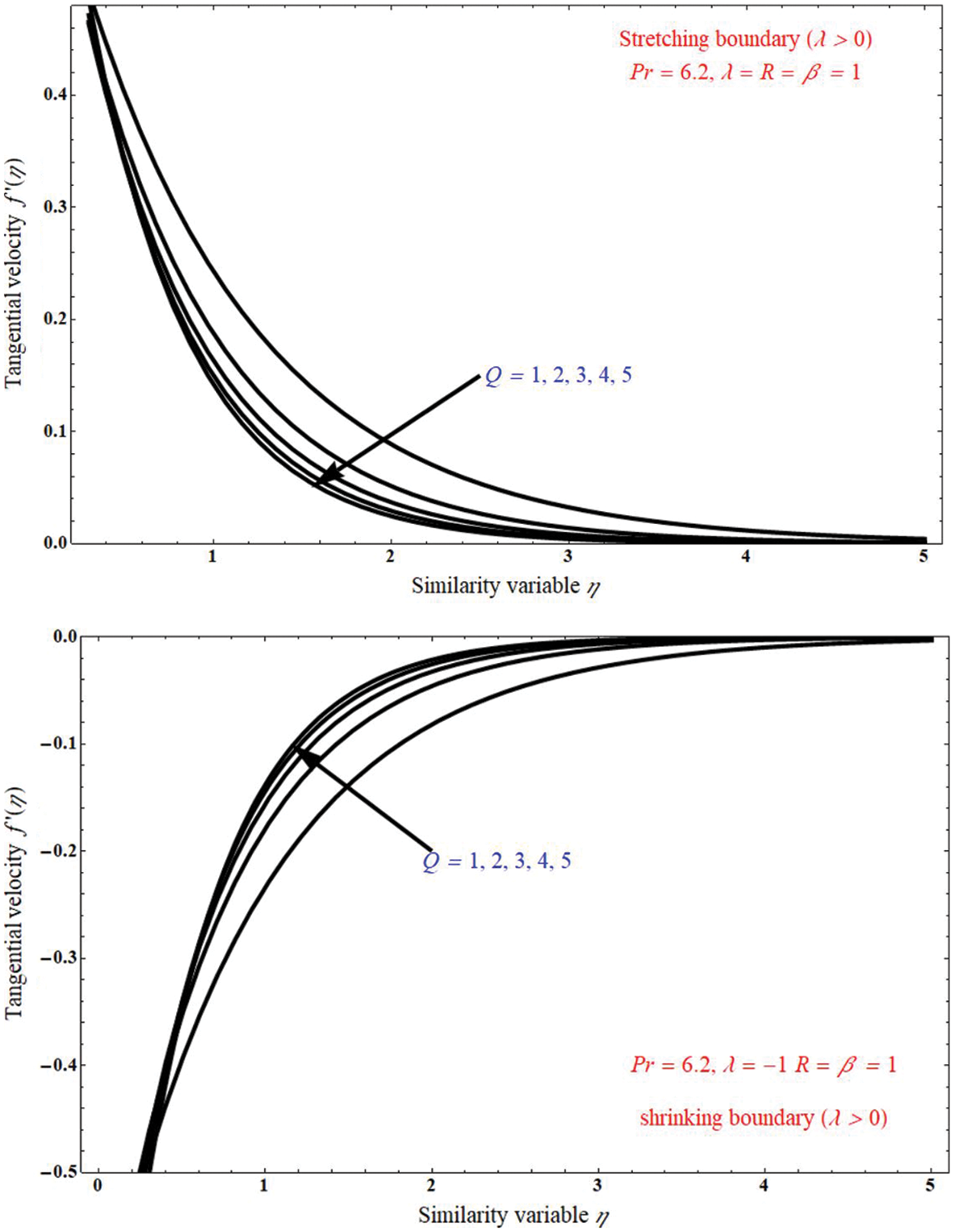
Figure 4: The impact of tangential velocity on similarity variable η for unlike values of Chandrasekhar’s number Q, at (a) stretching case λ = 1, and (b) shrinking case λ = −1
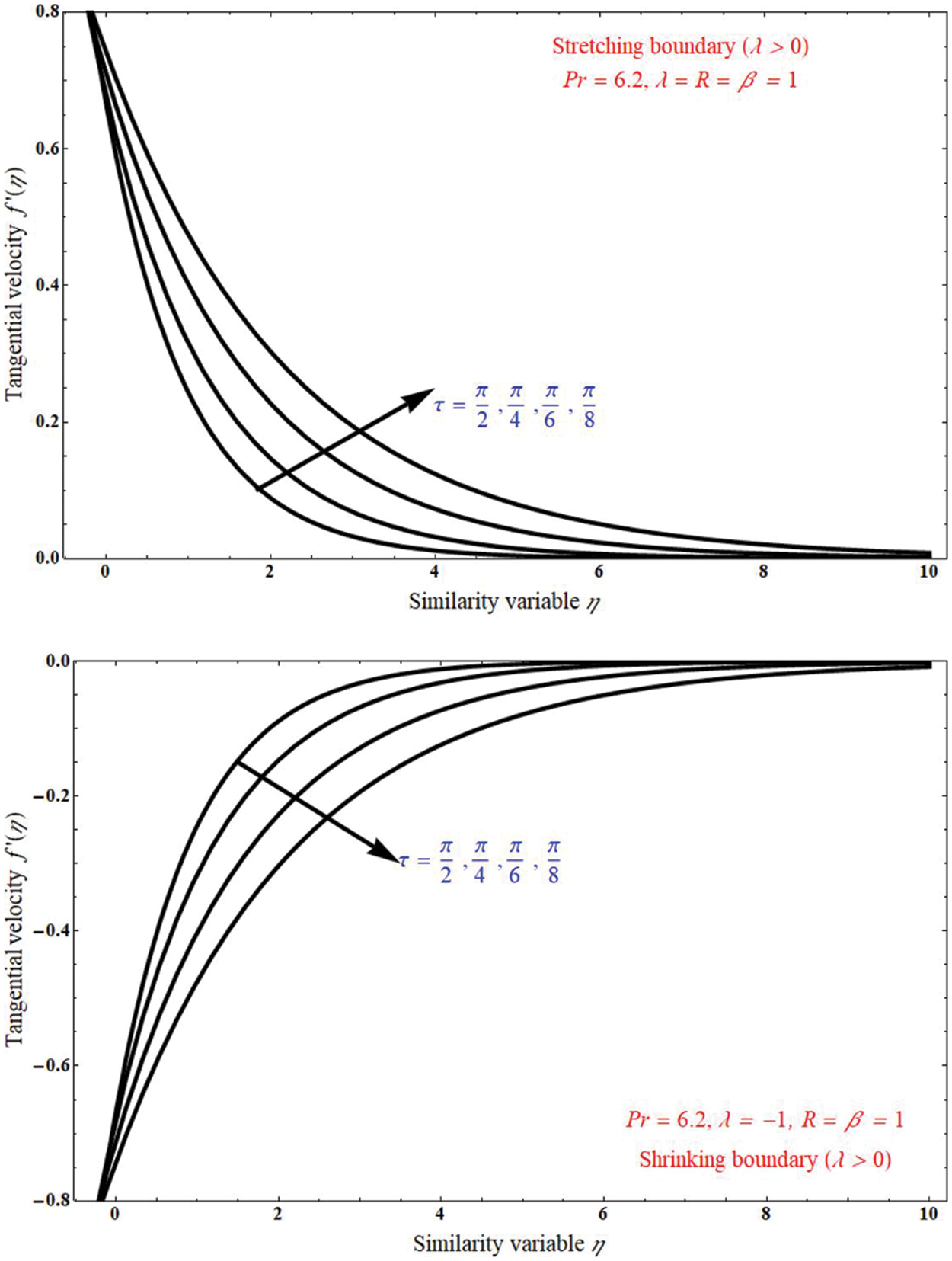
Figure 5: The impact of tangential velocity on similarity variable η for unlike values of inclined angle τ, at (a) stretching case λ = 1, and (b) shrinking case λ = −1
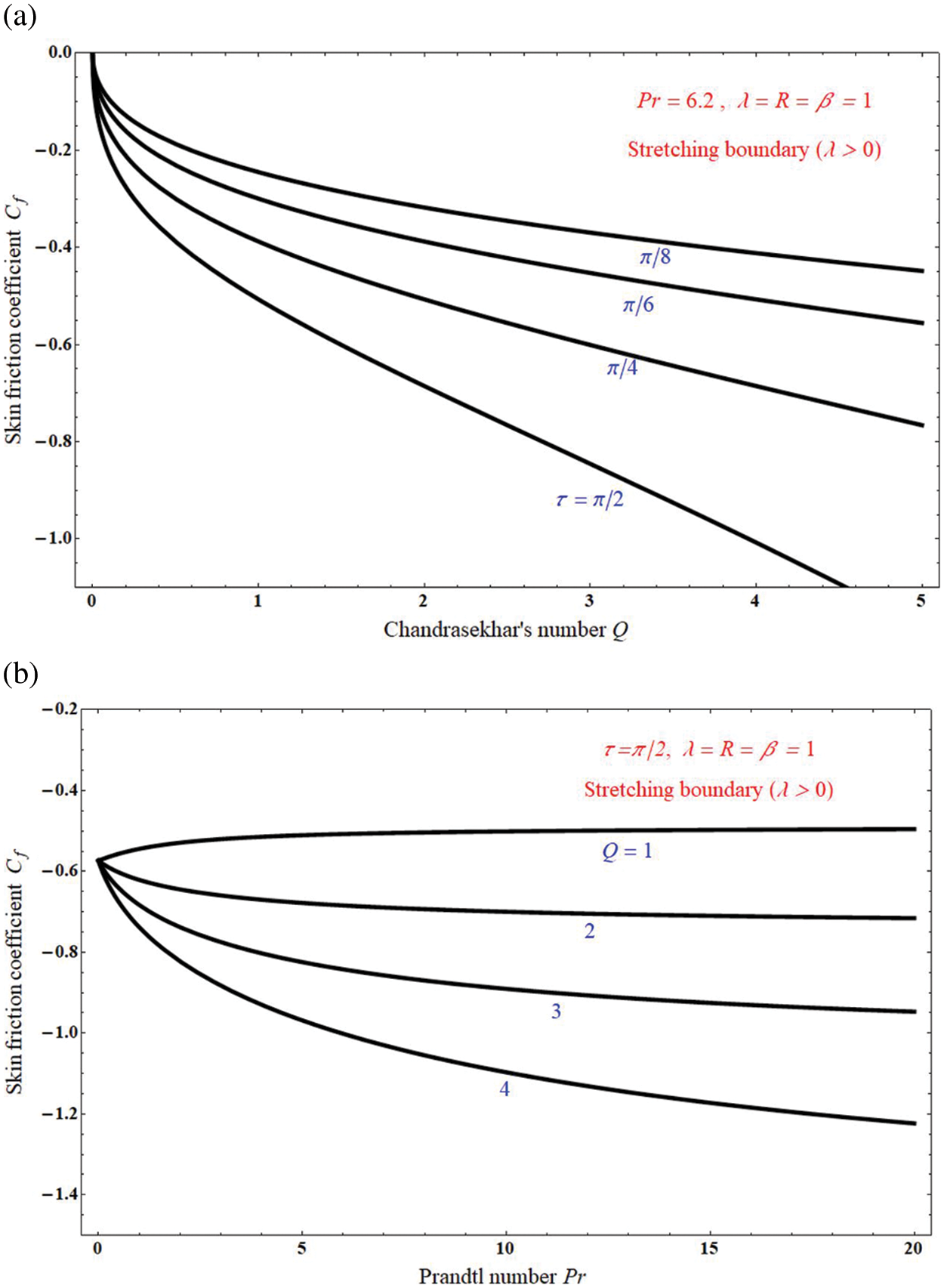
Figure 6: a) The effect of skin friction coefficient Cf on Chandrasekhar’s number Q for unlike values of inclined angle τ; b) The effect of skin friction coefficient Cf on Prandtl number
The impact of skin friction coefficient Cf on the functions Chandrasekhar’s number Q and Prandtl number Pr can be represented from the Figs. 7a and 7b, respectively. In Fig. 7a it is clear that the Cf is increases with increasing the inclined angle τ, and also from Fig. 7b it is conclude that the Cf is decreases with increasing the Chandrasekhar’s number Q. Furthermore, from both of the figure we observed that the Cf will decreases by increasing the slip parameters l1 and l2. The large values of Q causes the lesser skin friction and lesser heat transfer rate.
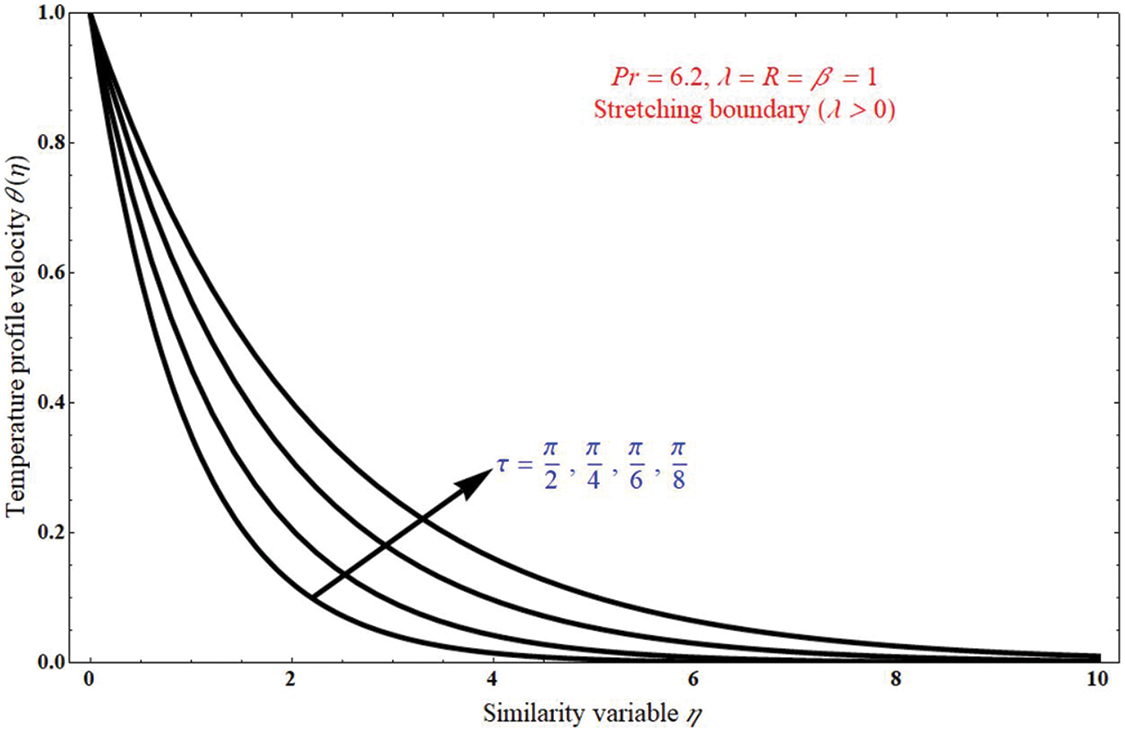
Figure 7: The impact of temperature profile velocity θ(η) on similarity variable η for unlike values of inclined angle τ
Fig. 8 represents the impact of temperature profile θ(η) expressed in Eq. (17), on the similarity variable η, in this it is analysed that the θ(η) increases with inclined angle τ, and the boundary value thickness is away from the x-axis. Similarly, Figs. 8a and 8b represent the effect of temperature profile θ(η) derived in Eq. (23), on the similarity variable η, θ(η) decreases with increase of mass transpiration VC and increases with increase of Radiation parameter R, it is observed graphically in Figs. 8a and 8b, respectively.
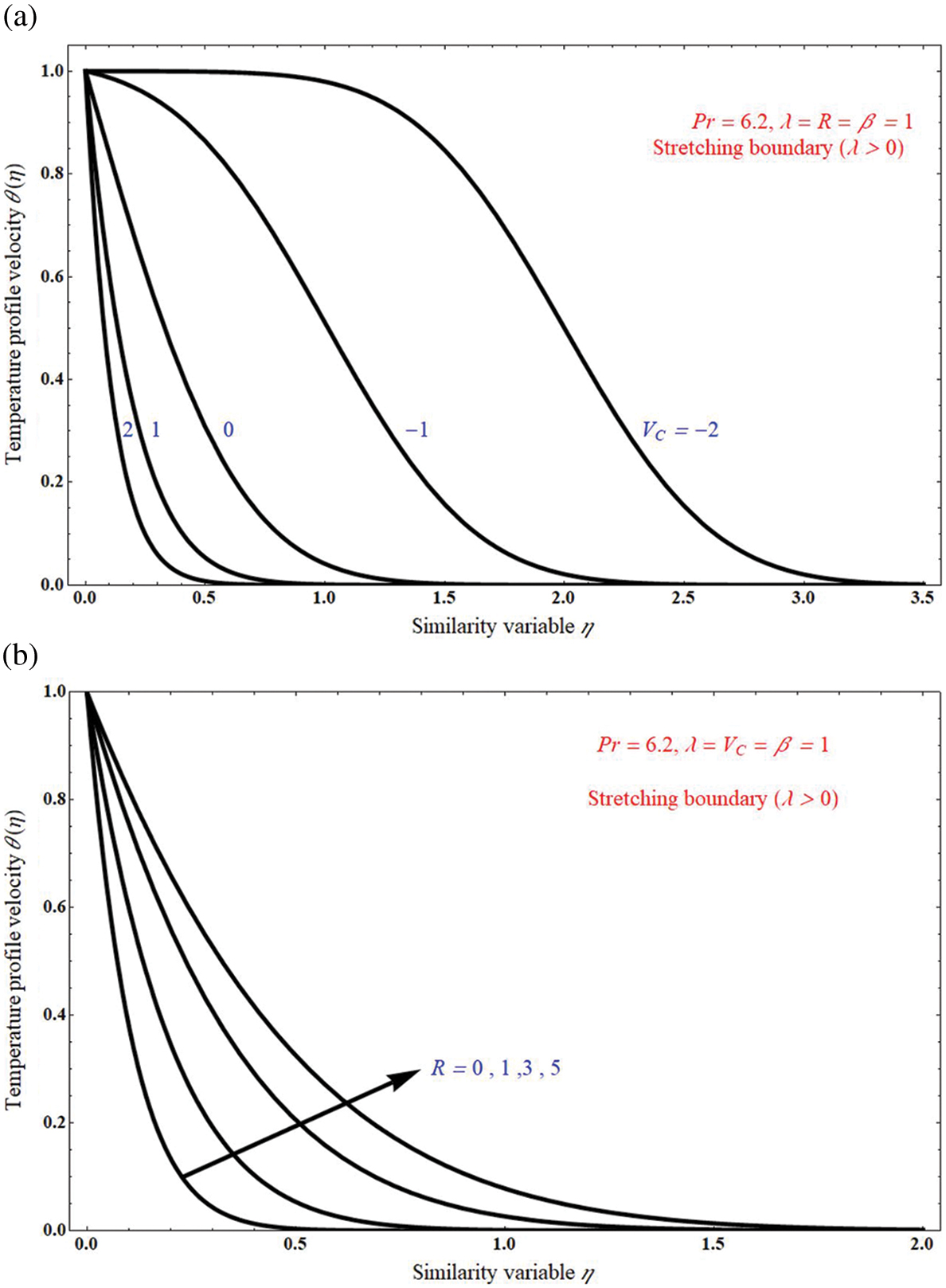
Figure 8: a) The impact of temperature profile velocity θ(η) on similarity variable η for unlike values of mass transpiration VC; b) The impact of temperature profile velocity θ(η) on similarity variable η for unlike values of radiation parameter R
Figs. 9a and 9b demonstrated that the impact of Nusselt number Nu derived from (12) and (21), on the inclined angle τ and Radiation parameter R in the presence of a function Chandrasekhar’s number Q, and Mass transpiration VC. In both figures the Nusselt number Nu decreases with increase of inclined angle τ and Radiation parameter R.
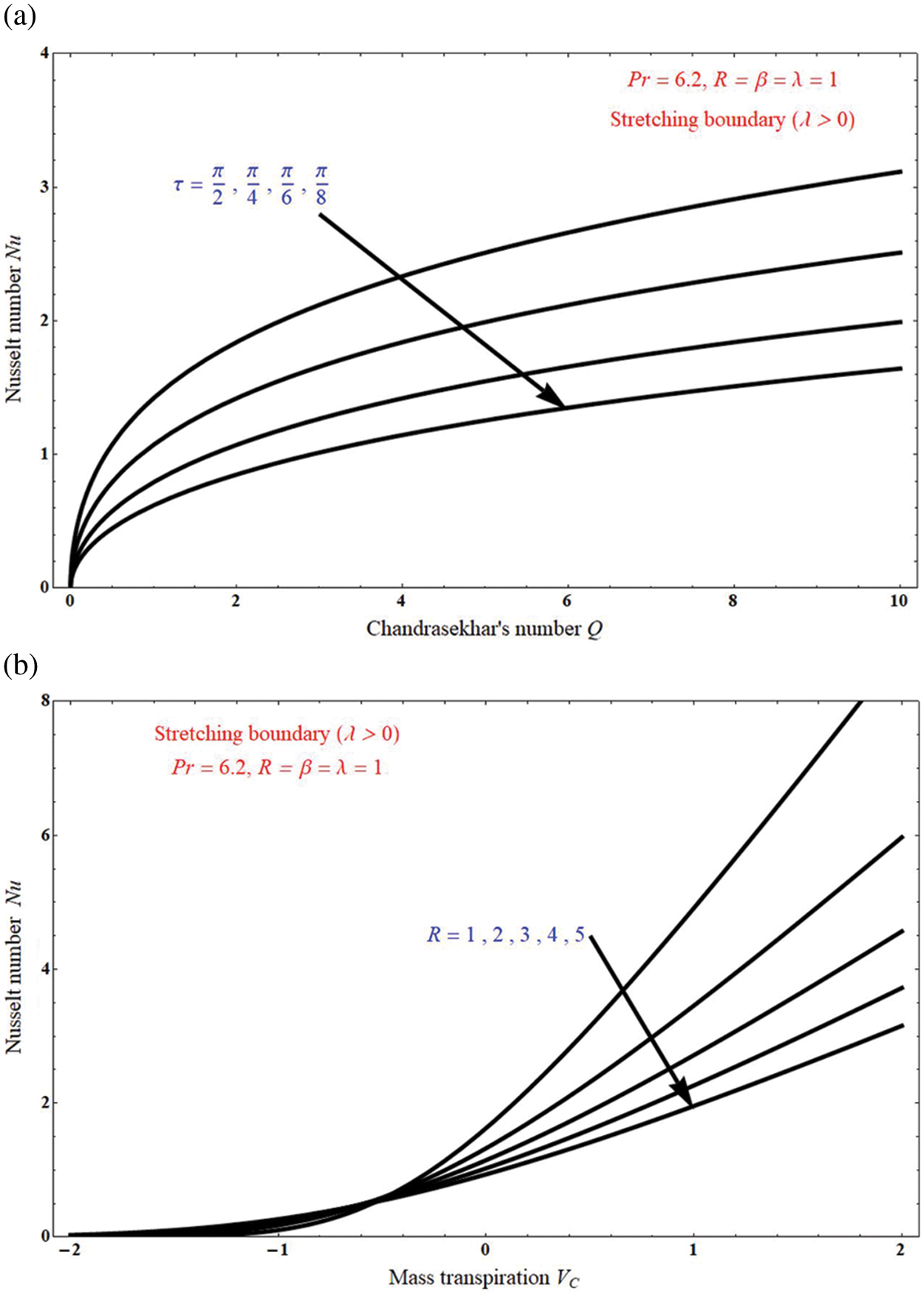
Figure 9: a) The effect of Nusselt number Nu on Chandrasekhar’s number Q for unlike values of inclined angle τ; b) The effect of Nusselt number Nu on mass transpiration VC for unlike values of radiation parameter R
Similarly, the same investigation carried out for Al2O3-water nanoparticle, it also shows the approximately same effect when we compared with Cu-water nanoparticle. The present investigation helps to conduct new research on nanofluids with stretching sheet problems and also direct integration technique helps to solve heat transfer equation easily.
The current article investigates the Jeffrey nanofluid flow in the presence of Cu-water nanofluid. The nonlinear PDE’s are changed into ODEs with the help of suitable similarity transformations. Later the momentum equation solved analytically to get the solution domain, this domain is linked with heat equation through f(η). Then the heat equation is solved under direct integration technique to get the solution. Additionally, inclined magnetic field and radiation term is taken into account in the whole calculation. The foremost findings of this analysis are given below:
• Flow fluid decreases with increase of Deborah number β value.
• The skin friction coefficient Cf will decreases by increasing the slip parameters l1 and l2.
• The rate of heat transfer increases by adding nanofluid.
• Temperature T is not influenced by parameters λ, l1, and l2.
• The classical Crane [2] problem is obtained from Eq. (6) if Q = τ = β = Λ = 0, and C1 = C2 = C3 = 1.
• The classical Pavlov [6] problem is obtained from Eq. (6) if β = Λ = 0, τ = 90° and C1 = C2 = C3 = Q = 1.
• The Turkyilmazoglu [24] problem is obtained from Eqs. (6)–(8) if R = 0, τ = 90° and C1 = C2 = C3 = 1, Q = M.
• The present work is help to conduct future research on nanofluid flows, and also direct integration technique is one of the easy ways to solve the energy equation, it helps to many reasearchers.
Funding Statement: The authors received no specific funding for this study.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
1. Sakiadis, B. C. (1961). Boundary layer behavior on continuous solid surfaces: I boundary layer equations for two dimensional and axisymmetric flow. American Institute of Chemical Engineers, 7(1), 26–28. DOI 10.1002/(ISSN)1547-5905. [Google Scholar] [CrossRef]
2. Crane, L. J. (1970). Flow past a stretching plate. Journal of Applied Mathematics and Physics, 21, 645–647. DOI 10.1007/BF01587695. [Google Scholar] [CrossRef]
3. Mahabaleshwar, U. S., Nagaraju, K. R., Sheremet, M. A., Baleanu, D., Lorenzini, E. (2019). Mass transpiration on newtonian flow over a porous stretching/shrinking sheet with slip. Chinese Journal of Physics, 63, 130–137. DOI 10.1016/j.cjph.2019.11.016. [Google Scholar] [CrossRef]
4. Mahabaleshwar, U. S. (2013). Linear stretching sheet problem with suction in porous medium. Open Journal of Heat, Mass and Momentum Transfer, 1(1), 13–18. DOI 10.12966/hmmt.07.02.2013. [Google Scholar] [CrossRef]
5. Amkadni M., Azzouzi A., Hammouch, Z. (2008). On the exact solutions of laminar MHD flow over a stretching flat plate. Communications in Nonlinear Science and Numerical Simulation, 13(2), 359–368. DOI 10.1016/j.cnsns.2006.04.002. [Google Scholar] [CrossRef]
6. Pavlov, K. B. (1973). Oscillatory magnetohydrodynamic flows of viscoelastic media in plane ducts. Magnetohydrodynamics, 9(2), 197–199. [Google Scholar]
7. Pavlov, K. B. (1974). Magnetohydrodynamic flow of an incompressible viscous fluid caused by deformation of a plane surface. Magnetohydrodynamics, 10(4), 507–510. [Google Scholar]
8. Mahabaleshwar, U. S., Nagaraju, K. R., Vinay kumar, P. N., Nadagoud, M. N., Bennacer, R. et al. (2020). An MHD viscous stagnation point flow and heat transfer with thermal radiation and transpiration. Thermal Science and Engineering Progress, 16, 100379. DOI 10.1016/j.tsep.2019.100379. [Google Scholar] [CrossRef]
9. Mahabaleshwar, U. S., Nagaraju, K. R., Vinay Kumar, P. N., Nadagoud, M. N., Bennacer, R. et al. (2020). Effects of dufour and soret mechanisms on MHD mixed convective-radiative non-newtonian liquid flow and heat transfer over a porous sheet. Thermal Science and Engineering Progress, 16, 100459. DOI 10.1016/j.tsep.2019.100459. [Google Scholar] [CrossRef]
10. Fang, T., Zhang, J., Yao, S. S. (2009). Slip MHD viscous flow over a stretching sheet–An exact solution. Communications in Nonlinear Science and Numerical Simulation, 14(11), 3731–3737. DOI 10.1016/j.cnsns.2009.02.012. [Google Scholar] [CrossRef]
11. Smith, W. J. (1952). Effect of gas radiation in the boundary layer on aerodynamic heat transfer. Journal of the Aeronautical Science, 20(8), 579–580. DOI 10.2514/8.2740. [Google Scholar] [CrossRef]
12. Siddheshwar, P. G., Mahabaleshwar, U. S. (2005). Effects of radiation and heat source on MHD flow of a viscoelastic liquid and heat transfer over a stretching sheet. International Journal of Non-Linear Mechanics, 40(6), 807–820. DOI 10.1016/j.ijnonlinmec.2004.04.006. [Google Scholar] [CrossRef]
13. Mahabaleshwar, U. S., Pazanin, I., Radulovic, M., Suarez-Grau, F. J. (2017). Effects of small boundary perturbation on the MHD duct flow. Theoretical and Applied Mechanics, 44(1), 83–101. DOI 10.2298/TAM170511004M. [Google Scholar] [CrossRef]
14. Hamad, M. A. A., Pop, I. (2011). Scaling transformations for boundary layer flow near the stagnation-point on a heated permeable stretching surface in a porous medium saturated with a nanofluid and heat generation/absorption effects. Transport in Porous Media, 87, 25–39. DOI 10.1007/s11242-010-9683-8. [Google Scholar] [CrossRef]
15. Mahabaleshwar, U. S., Vinay Kumar, P. N. (2016). Mikhail sheeremet, magnetohydrodynamics flow of a nanofluid driven by a stretching/shrinking sheet with suction. Springer Plus, 5(1), 1–9. DOI 10.1186/s40064-016-3588-0. [Google Scholar] [CrossRef]
16. Mahabaleshwar, U. S., Vishalakshi, A. B., Azese, M. N. (2022). The role of brinkmann ratio on non-newtonia fluid flow due to a porous stretching/shrinking sheet with heat transfer. European Journal of Mechanics-B/Fluids, 92, 153–165. DOI 10.1016/j.euromechflu.2021.12.003. [Google Scholar] [CrossRef]
17. Mahabaleshwar, U. S., Vishalakshi, A. B., Andersson, H. I. (2022). Hybrid nanofluid flow past a stretching/shrinking sheet with thermal radiation and mass transpiration. Chinese Journal of Physics, 75, 152–168. DOI 10.1016/j.cjph.2021.12.014. [Google Scholar] [CrossRef]
18. Mahabaleshwar, U. S., Anusha, T., Hatami, M. (2021). The MHD newtonian hybrid nanofluid flow and mass transfer analysis due to super-linear stretching sheet embedded in porous medium. Scientific Reports, 11(1), 1–17. DOI 10.1038/s41598-021-01902-2. [Google Scholar] [CrossRef]
19. Anusha, T., Mahabaleshwar, U. S., Hatami, M. (2021). Navier slip effect on the thermal-flow of walter’s liquid B flow due to porousstretching/shrinking with heat and mass transfer. Case Studies of Thermal Engineering, 28, 101691. DOI 10.1016/j.csite.2021.101691. [Google Scholar] [CrossRef]
20. Santhosh, N., Radhakrishnamcharya, G. (2015). Jeffrey fluid flow through a narrow tube in the presence of a magnetic field. Proceedia Engineering, 127, 185–192. DOI 10.1016/j.proeng.2015.11.325. [Google Scholar] [CrossRef]
21. Akbar, S. A., Nadeem, S., Changhoon, L. (2013). Characteristics of jeffrey fluid model for peristalic flow of chyme in small intestine with magnetic field. Results in Physics, 3, 152–160. DOI 10.1016/j.rinp.2013.08.006. [Google Scholar] [CrossRef]
22. Kumar, D., Ramesh, K., Sumith, C. (2018). Effectiveness of magnetic field on the flow of jeffrey fluid in an annulus with rotating concentric cylinders. Journal of the Brazilian Society of Mechanical Sciences and Engineering, 40(6), 305. DOI 10.1007/s40430-018-1232-3. [Google Scholar] [CrossRef]
23. Turkyilmazoglu, M., Pop, I. (2013). Exact analytical solutions for the flow and heat transfer near the stagnation point on a stretching/shrinking sheet in a jeffrey fluid. International Journal of Heat and Mass Transfer, 57(1), 82–88. DOI 10.1016/j.ijheatmasstransfer.2012.10.006. [Google Scholar] [CrossRef]
24. Turkyilmazoglu, M. (2016). Magnetic field and slip effects on the flow and heat transfer of stagnation point jeffrey fluid over deformable surfaces. Zeitschrift fur Naturforschung A, 71(6), 549–556. DOI 10.1515/zna-2016-0047. [Google Scholar] [CrossRef]
25. Mahabaleshwar, U. S., Sarris, I. E., Lorenzini, G. (2018). Effect of radiation and navier slip boundary of walters’ liquid B flow over a stretching sheet in a porous media. International Journal of Heat and Mass Transfer, 127, 1327–1337. DOI 10.1016/j.ijheatmasstransfer.2018.02.084. [Google Scholar] [CrossRef]
26. Mahabaleshwar, U. S., Anusha, T., Sakanaka, P. H., Suvanjan, B. (2021). Impact of inclined lorentz force and schmidt number on chemically reactive newtonian fluid flow on a stretchable surface when stefan blowing and thermal radiation are significant. Arabian Journal of Science and Engineering, 46(12), 12427–12443. DOI 10.1007/s13369-021-05976-y. [Google Scholar] [CrossRef]
27. Mahabaleshwar, U. S., Nagaraju, K. R., Vinay Kumar, P. N., Azese, M. N. (2020). Effect of radiation on thermosolutal marangoni convection in a porous medium with chemical reaction and heat source/sink. Physics of Fluids, 32(11), 113602. DOI 10.1063/5.0023084. [Google Scholar] [CrossRef]
28. Mahabaleshwar, U. S., Sneha, K. N., Huang-Nan, H. (2021). An effect of MHD and radiation on CNTS-water based nanofluid due to a stretching sheet in a newtonian fluid. Case Studies in Thermal Engineering, 28, 101462. DOI 10.1016/j.csite.2021.101462. [Google Scholar] [CrossRef]
29. Xenos, M. A., Petropoulou, E. N., Siokis, A., Mahabaleshwar, U. S. (2020). Solving the nonlinear boundary layer flow equations with pressure gradient and radiation. Symmetry, 12(5), 710. DOI 10.3390/sym12050710. [Google Scholar] [CrossRef]
30. Anusha, T., Huang-Nan, H., Mahabaleshwar, U. S. (2021). Two dimensional unsteady stagnation point flow of casson hybrid nanofluid over a permeable flat surface and heat transfer analysis with radiation. Journal of the Taiwan Institute of Chemical Engineers, 127, 79–91. DOI 10.1016/j.jtice.2021.08.014. [Google Scholar] [CrossRef]
31. Anusha, T., Mahabaleshwar, U. S., Yahya, S. (2021). An MHD of nanofluid flow over a porous stretching/shrinking plate with mass transpiration and brinkman ratio. Transport in Porous Media, 154, 1–20. DOI 10.1007/s11242-021-01695-y. [Google Scholar] [CrossRef]
32. Sneha, K. N., Mahabaleshwar, U. S., Bennacer, R., Ganaoui, M. E. L. (2021). Darcy brinkman equations for hybrid dusty nanofluid flow with heat transfer and mass transpiration. Computation, 9(11), 118. DOI 10.3390/computation9110118. [Google Scholar] [CrossRef]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |