Fluid Dynamics & Materials Processing

DOI: 10.32604/fdmp.2022.019741

ARTICLE

A Mathematical Model and a Method for the Calculation of the Downhole Pressure in Composite-Perforation Technological Processes

Xufeng Li1,2,3 and Yantao Bi1,2,3,*

1Shengli Petroleum Engineering Co., Ltd. of Sinopec, Dongying, 257100, China
2Key Laboratory of Ultra-Deep Well Drilling Engineering Technology of Sinopec, Dongying, 257100, China
3Key Laboratory of Unconventional Drilling and Completion Technology of China Petroleum and Chemical Corporation, Dongying, 257100, China
*Corresponding Author: Yantao Bi. Email: biyantaobyt@163.com
Received: 12 October 2021; Accepted: 21 December 2021

1  Introduction

The development of oil and gas well perforation technology has a long history of more than 100 years and has been a key technology in oil exploration and development. Researchers have come to realize the importance of studying the dynamic pressure of perforation in recent years, and from their findings, the enhancement of perforation technology directly affects the productivity of oil and gas wells and the protection of reservoirs [1–3]. As the gun body, charge quantity, and hole-density limit the perforating charge, it is therefore difficult to design the desired shape and size of cartridge case in the design process due to fluctuation of pressure rate. Nevertheless, it is necessary to consider the explosion height of the perforating charge in the gun, and whether there is an interference between them. Simultaneously, the optimization of perforation design and the improvement of perforation check are both conditioned by the improvement of penetration depth of the perforating charge in order to enhance the safety and success of downhole perforation [4,5].

High-energy gas fracturing technology (HEGP) is an important stimulation measure that creates fractures in all radial directions at short distances. HEGP is a propellant-based technology initially developed for enhancing production in natural gas wells. The pressure rise interval of this technology is measured in milliseconds, the energy transfer is fast, the peak pressure is moderate, and the gas pressure entering the channels extends the fracture to the depth of the formation [6–8]. Composite perforation is an efficient perforation completion technology, which integrates conventional perforation and high-energy gas fracturing. Composite perforation technology is also called ‘‘propellant perforation technology’’ or ‘‘propellant assisted perforation technology’’. It can simultaneously combine both perforation and high-energy gas fracturing through a single construction operation, which can greatly improve the efficiency of perforation and the productivity of wells [9,10]. The process of perforation involves lowering a perforating gun into a wellbore to a precise depth and energizing the gun to be safely fired. The perforation process is simulated using the finite element software, and a prediction model is obtained based on the simulation data, which have been promoted the research progress [10]. However, the dynamic perforation pressure system on the packer under realistic deep-water conditions is unsettled.

It is well known that, the load output of perforating explosion in wellbore is very complex, as it includes detonation wave, shock wave, interaction between detonation gas and perforation fluid, fluid solid coupling, etc. Moreover, the reflection and transmission of shock waves at the interfaces of the packers are almost impossible to be predicted using theoretical formulae. Therefore, the difficulty to analyze such dynamic pulsation by theoretical and experimental methods is an existential issue in drilling engineering. Thanks to the development of modern science and technology, numerical simulations are conducive for the study of downhole perforation as they reveal the pulsation of perforation pressure in the wellbore. Meanwhile, their conductivity and flexibility to acquire dynamic data at distinct positions in the wellbore during the simulation convey a basis for in-depth study of the packer safety under distinct perforating conditions.

At present, the perforation process is simulated by using the finite element software, and a prediction model is obtained based on the simulation data where the outer sheath type of the composite perforator sets the fracturing agent outside the perforator. In the perforation process, the fracturing agent is triggered by the jet to form perforations and fracturing maybe completed instantly [11–14]. Hence, the fracturing agent is wrapped outside the gun body of the perforating gun as a result to enable the energy to be directly released into the wellbore, thereby efficiently conquering the issue connected to gun blasting in drilling operations [15]. The ultimate objective here is to allow oil and gas to flow from the formation to the surface in a safe and secure manner. However, due to the lack of research on external casing composite perforation, the development of related technology is scanty within the published literature. Therefore, this work proposes in-depth knowledge by implementing a combination of two techniques including, the gunpowder combustion model of outer-sheath type of composite perforator and the pressure distribution model of high-energy gas in the fracture. Thus, providing a theoretical guidance for the construction design of outer-sheath type of composite perforation.

2  Geometric Model of Gunpowder Combustion

The combustion of fracturing gunpowder in outer sheath type of composite perforator is a complex process. In order to simulate the operation of various gun systems, the mathematical models are constantly modified with the development of gun propellant. During perforating charge explosion, high-energy gas rapidly invades the fracturing propellant to form a hole and ignite the fracturing propellant. At the same time, under high temperature and high-pressure conditions, the fracturing propellant also starts to burn from the outer layer. Therefore, the combustion process of the outer fracturing propellant is a combination of two combustion processes including, combustion along the hole and internal combustion from the outer layer of the sleeve. Therefore, the above model can be simplified into two combustion forms, named as single-sided combustion along the outer side of the sleeve and annular combustion from the perforation to the surrounding (see Fig. 1). The outer radius of the fracturing powder sleeve is R, m; the inner radius is r, m; the length of the fracturing powder sleeve is h, m; the perforation density is n; the perforation radius is R1, m; and the burning core thickness is e, m.

Figure 1: Schematic diagram of fracturing agent combustion

2.1 Single Side Combustion

In the process of perforation explosion, the periphery of the fracturing gunpowder is ignited and burned under high-temperature and high-pressure. During the combustion process, the core thickness of the tubular gunpowder burning outside is denoted by e at specific time interval.

The volume burned is denoted by the mathematical expression:

A1=π[R2−(R−e)2]−nπr12e (1)

The total volume of fracturing powder after perforation is described as:

A=π(R2−r2)h−nπr12(R−r) (2)

The ratio of the volume of burnt fracturing propellant to the volume of fracturing propellant after perforation is given by dividing Eqs. (1) and (2):

ψ1=π[R2−(R−e)2]h−nπr12eπ(R2−r2)h−nπr12(R−r) (3)

2.2 Toroidal Combustion

The fracturing agent expands and burns around the perforating hole in a ring simultaneously with the explosion of the perforating charge. The time is set as t, and the core thickness of the tubular gunpowder burned outside during the combustion process is represented by e.

The volume burned is given by the mathematical relationship:

A2=nπ[(r1+e)2−r12](R−r−e) (4)

Then, the ratio of burned fracturing powder volume to fracturing powder volume after perforation is given by Eqs. (4) and (2):

ψ2=nπ[(r1+e)2−r12](R−r−e)π(R2−r2)h−nπr12(R−r) (5)

Since the combustion is completed instantly with the combustion along the hole and internal combustion from the outer layer of the sleeve, the general combustion model of gunpowder is derived from the combination of the two combustion processes:

ψ=π[R2−(R−e)2]h−nπr12e+nπ[(r1+e)2−r12](R−r−e)π(R2−r2)h−nπr12(R−r) (6)

3  Downhole Pressure-Time Calculation Model

For an unclogged combustion chamber (with an open pressure relief hole at one end), generally referred to a semi closed combustion chamber, the fracturing bomb which is essentially perceived to a semi closed combustion chamber, is based on the following equations.

3.1 Mass Balance Equation

According to the principle of mass conservation, the mass of gas retained in the combustion chamber should be equal to the mass of the burned part of the gunpowder from which the mass of gas flowing out from the nozzle at a certain moment is subtracted during the combustion stage of the charge.

Vψρg=ωYR−∫0tqdt (7)

where, Vψ: Free volume of fracturing bomb, also known as the space where gas molecules can move freely, m3; ρg: Gas density, Kg/m3; ωYR: Mass of ignited powder at a certain moment, Kg; ∫0tqdt : Total outflow of fracturing bomb gas at a specific interval, Kg; q: Second mass flow of gas, Kg/s.

Since the combustion in the fracturing bomb is a semi-closed system, the total free volume of gas includes the sum of the initial gas volume, the volume of gas entering the channels and the volume occupied by gas due to the combustion part of the gunpowder. If the upper-end of the perforated section is kill fluid, then:

Vψ=V0+ωYRγ+Sx+V (8)

V0: Represents the initial free volume of the hollow part of the inner diameter of the fracturing cartridge when the gunpowder is unburned, m3; S: Casing sectional area, m2; Sx: Volume occupied by gas due to upward movement of kill fluid, m3; V: Volume of gas and kill fluid entering the channels, m3.

3.2 Gas Equation of State

If the gas is considered ideal, the equation of state can be written as:

p=ρgRT1 (9)

where, p represents pressure of deflagration gas, Pa; T1 is the temperature of deflagration gas, K; and R represents the molar gas constant, J/(mol.K).

Using Eq. (7), the derivative with respect to time can be obtained as:

Vψdρgdt+ρgdVψdt=ωdψdt−q (10)

Using Eq. (8), the derivative relative to time can be written as:

dVψdt=1γdωYRdt+Sdxdt+dVdt=ωγdψdt+Sv+dVdt (11)

Using Eq. (9), the derivative as a function of time can be expressed as:

dρgdt=1RTdpdt (12)

By simultaneous derivation of Eqs. (10), (11) and (12) the general formula is obtained:

dpdt=ωdψdt(RT−RTρgγ)−RT(Sv+dVdt)ρgVψ=ωdψdt(fTT1−pγ)−(Sv+dVdt)pVψ (13)

4  Crack Propagation Model

4.1 Pressure Distribution Model of High-Energy Gas in Fracture

The outer sheath type of composite perforator sets the fracturing agent outside the perforator, which is characterized by a high gas production. Therefore, the variation in downhole pressure and the pressure distribution of high-energy gas in fracture zone has a great impact on the extension of the fracture. In this investigation, it is assumed that high-energy gas is ideal. Considering the short execution time, the heat conduction and leakage of high-energy gas are not considered.

On this basis, the mass conservation equation and momentum conservation equation of gas deflagration can be implemented according to Nilson’s model [16]:

∂∂t(ρw)+∂∂x(ρwu)+2ρv=0 (14)

∂∂t(ρwu)+1r∂∂x(rρwu2)=−ρw(1ρ∂p∂x+λ) (15)

ρ: The gas density of the flow section, Kg/m3; u: The longitudinal velocity of the flow section, m/s; p: Gas pressure, Pa; w: Crack opening displacement, m; λ=12μwv2q : Friction coefficients.

q = ρwu, then, Eqs. (14) and (15) are converted into:

∂∂t(ρw)+∂q∂x=0 (16)

∂q∂t+1rw+x∂∂x[(rw+x)q2ρw]=−ρw(1ρ∂p∂x+λ) (17)

q: Gas mass flow per unit crack height, Kg/s; rw= well diameter, m; when x = 0, q = q0, p = p0, T = T0.

Substituting λ=12μwv2q in Eq. (14) and integrate Eqs. (16) and (17) to obtain:

q=rwrw+xq0−1rw+x∫0L(rw+x)∂(ρw)∂tdx (18)

p=p0+∫0L[12μqρw3dx−∫0L1w∂q∂t+q2ρw2(rw+x)+1w∂∂x(q2ρw)]dx (19)

Assuming that the gas density and crack width change slightly with time, the second derivative of Eq. (18) can be overlooked. Therefore, Eq. (18) can be inserted into Eq. (19), and the resulting partial derivative of x is obtained as:

∂p∂x[1−rw2q0w2ρ2(rw+x)2RT0]=12μrwq0w31ρ(rw+x)−rww∂q0∂t1rw+x+rw2q02w21ρ(rw+x) (20)

4.2 Calculation Model of Crack Length and Width

According to the theory of elasticity, the crack width can be calculated based on Paris formula [17]:

Wf(x)= 4(1−νr)πGr∫xl[∫0η(Pf(x,t)−σ0)η2−ξ2dξ]ηdηη2−x2 (21)

Herein, the crack propagation is controlled by the fracture-breaking criterion of linear elastic fracture mechanics occurring during the crack propagation and, the stress intensity factor at the top of fracture, K, is greater than the critical stress intensity factor of the rock Kic [18].

K=(πLf(t))12∫0L[p(x,t)−σ(x)]Lf(t)+xLf(t)−xdx (22)

Taking as a reference the theory of fracture mechanics, when K ≥ Kic, the fracture initiation is observed and when K ≤ Kic, the fracture extension ceases.

The speed of fracture extension can be calculated according to the following formula:

VS=0.38Cp (23)

Vs = Extension speed, m/s, Cp = Longitudinal wave velocity in rock, m/s.

5  Kill Fluid Motion Model

In composite perforation process, the high-temperature and high-pressure gas influence the properties of kill fluid. On the one hand, the kill fluid would promote the upward movement. On the other hand, the kill fluid plays a key role in maintaining the pressure of the gas produced by combustion. Usually, water is used as kill fluid in the process of compound perforation due to its low compressibility, and the motion of kill fluid column is regarded as a rigid body motion (see Fig. 2).

Figure 2: Force diagram of the upper control fluid in the wellbore

The kill fluid flows from the top as a whole under the action of high-energy gas, and the velocity of kill fluid can be obtained according to Newton’s second law.

d(Mv)dt=[P(t)−P0]A−Mg−f (24)

M: Mass of displacing liquid, Kg; A: Casing sectional area, m3; ρ: Density of kill fluid, Kg/m3; H: Kill fluid height, m; P0: Local atmospheric pressure, Pa; f: Viscous resistance, N.

f=λHDρv22πD24=λπDHρv28 (25)

By substituting Eq. (25) into Eq. (24), the following expression is obtained:

dvdt=P(t)−PaρH−g−λv22D (26)

v: Movement speed, m/s; D: Casing inner diameter, m; λ: Friction coefficient.

6  Solution Method and Application Example

6.1 Influence of Flow Variation Rate

In this subsection, the influence of variation rates of inlet flow is analyzed using the parameters listed in Table 1 and the results are indicated in Fig. 3.

Figure 3: Relationship between pressure distribution and variation rate of flow in fracture

As shown in Fig. 4, the pressure in the channel gradually reduced along the direction of crack extension. This is mainly due to the fact that, after the high-energy invaded the channels, the crack length not only increased but also the frictional effect expansion induced gradual drop of high-energy gas pressure. In addition to the aforementioned phenomenon, the pressure distribution in the channels controlled the flow variation rate at the cracks inlet. When the variation rate of gas flow is less than 1 × 105 kg/ms2, the variation of deflagration pressure along the crack length is ambiguous, and the rate change of deflagration gas flow had little effect on the pressure distribution of deflagration gas. However, when the variation rate of gas is greater than 5 × 105 kg/ms2, the pressure of deflagration gas varied remarkably along the cracks length. This phenomenon was ascribed to flow limitation effect of perforations. Furthermore, when the variation rate of flow at the cracks inlet (i.e., hole) became faster, a large amount of high-energy gas prevented the smooth invasion of the facture. This resulted in a diminution of the energy of high-energy gas transmitted to the cracks within a time interval driving rapid drop in pressure along the direction of fracture extension.

Figure 4: Calculation process of downhole pressure of outer sheath type of composite perforator

Taking together, during the process design of outer sheath type of composite perforation, one should select the gunpowder with a slow burning rate, so as to control the variation rate of gunpowder deflagration gas flow which would enable the transfer of more energy from the high-energy gas to the fracture resulting in favoring the fracture extension.

6.2 Solution Method and Verification

Based on the aforementioned mathematical models, the entire combustion processes of the outer sheath type of composite perforator could be described. The representative curve of the downhole pressure variation of the outer sheath type of composite perforator was obtained via programming, and the established calculation process is shown in Fig. 4.

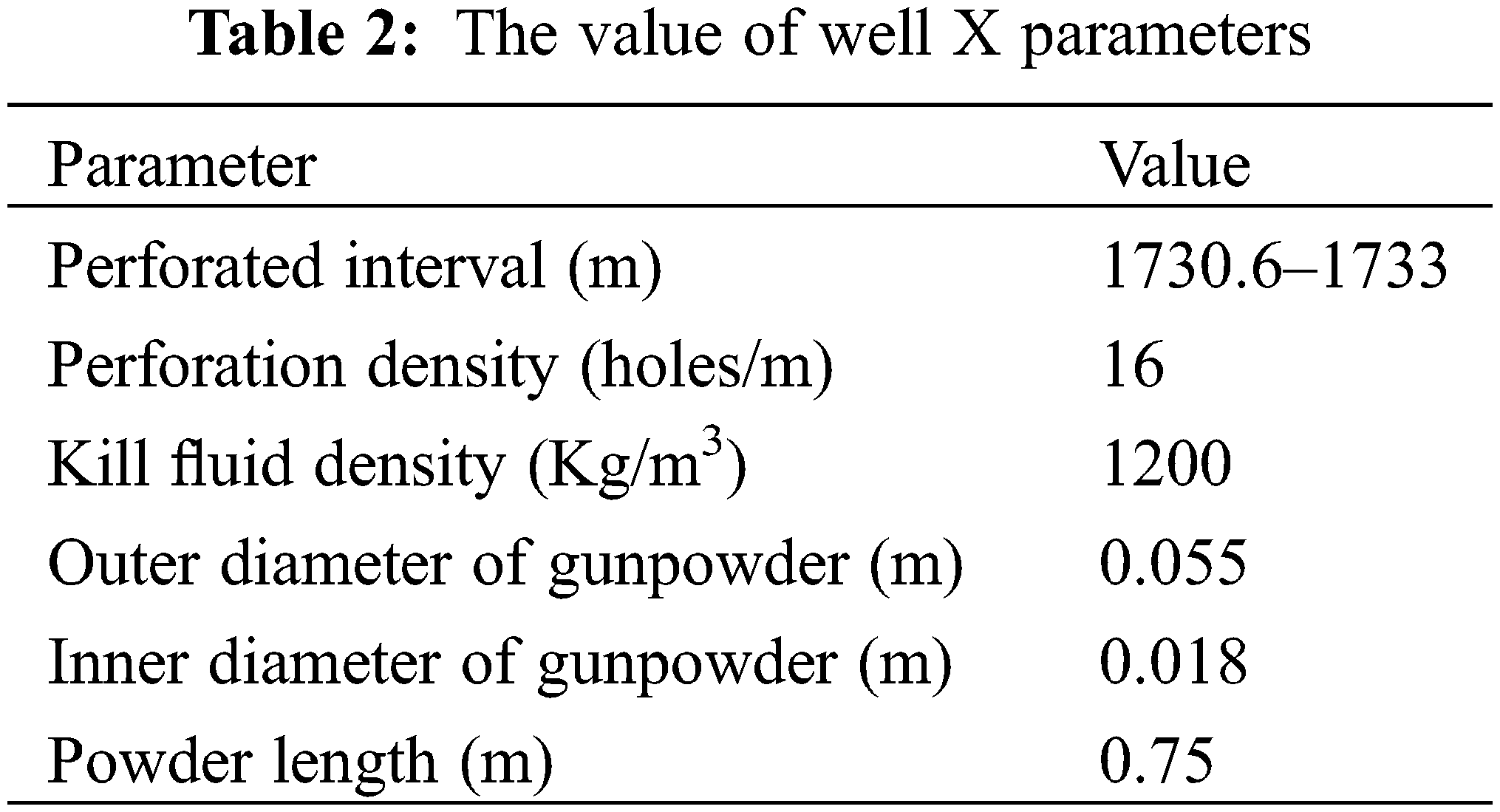
Case-study: The composite perforation technology was applied for field construction in the well named Shu X. The considered parameters are listed in Table 2.

In this construction, in order to detect the variation law of downhole pressure of the well, a P-T tester was inserted. Subsequently, the field P-T simulation curve of well Shu X was obtained after data analysis, as indicated in Fig. 5.

Figure 5: Field P-T simulation curve of well Shu X

After the construction, the curve of the downhole pressure variation was obtained by the measuring P-T tester as indicated in Fig. 6.

Figure 6: Field P-T test curve of well Shu X

When comparing the aforementioned Figures, it could be noticed that the pressure and duration exerted a tremendous influence on peak pressure induced by composite perforation technology in the drilling well. Moreover, the curve of the deflagration pressure increased sharply the crack length with increasing time and reached a maximum value. Interestingly, two obvious peaks could be observed as the pressure smoothly dropped to constant value. The predicted peak pressure was 47 MPa, while the actual measured one was obtained as 46 MPa, translating an error of approximately 2%. Subsequently, the corresponding value for predicted pressure rise rate was 47 × 104 MPa/s, while that of the actual measured one had a rise rate of 45.5 × 104 MPa/s, inferring an error of 3.3%. In addition, the predicted pressure with duration greater than 30 MPa had a time of 155 ms, while the measured one had time interval of 175 ms, with an error of 12.9%. Furthermore, for the predicted pressure with duration greater than 25 MPa, the time was 250 ms, meanwhile it could be found that the actual pressure under identical condition was 270 ms, with an error of 7.4%. The results indicate that the data obtained using the proposed model agrees well with the field measurement.

7  Conclusions

In this work, a mathematical model based on conservation equations for mass, momentum was developed to calculate downhole pressure in perforated-composite technological processes. A user-friendly computer program was employed for the optimization of the perforation operation using finite element software. The investigation revealed the following findings:

•   Through the analysis of Nilson model, the pressure distribution in the crack depends not only on the length of the crack, but also on the variation of flow rate at the crack inlet.

•   During the construction design of outer sheath type of composite perforation, the propellant with slow burning rate should be selected, so as to control the variation rate of explosive gas flow, transfer more energy of high-energy gas to the fracture and promote the fracture extension.

•   By comparing the predicted results and the field measurement (case-study) results, it is observed that the predicted results are reasonable and reliable.

Funding Statement: The authors received no specific funding for this study.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  Liu, H., Wang, F., Wang, Y. C., Gao, Y., Cheng, J. L. (2014). Oil well perforation technology: Status and prospects. Petroleum Exploration and Development, 41(6), 731–737. DOI 10.1016/S1876-3804(14)60096-3. [Google Scholar] [CrossRef]

 2.  Hunt, W. C., Shu, W. R. (1989). Controlled pulse fracturing for well stimulation. Low Permeability Reservoirs Symposium, Denver, Colorado. [Google Scholar]

 3.  Li, D. C., Zhu, G. B., Yu, H. Y. (2008). Analysis of penetration performance for shaped perforator in concrete target. Technology Supervision in Petroleum Industry, 24(6), 8–11. DOI 10.3969/j.issn.1004-1346.2008.06.002. [Google Scholar] [CrossRef]

 4.  Wang, C. S., Feng, G. F., Wang, B. X. (2006). Combustion mechanism and experimental analysis of multistage powder charging technology in super positive pressure composite perforation. Well Logging & Perforation, 9(4), 74–77. [Google Scholar]

 5.  Qin, F. D. (1992). Research on the application of accumulated energy effect of high-energy gas fracturing. Journal of Xi’an Petroleum Institute, 7(3), 17–22. [Google Scholar]

 6.  Wang, S. S., Zheng, C. J., Zhao, C. H. (2005). Application of combined perforating technology in x53-ping 37 horizontal well. Well Logging Technology, 29, 49–51. DOI 10.16489/j.issn.1004-1338.2005.s1.017. [Google Scholar] [CrossRef]

 7.  Miller, K. K., Prosceno, R. J., Woodroof Jr, R. A., Haney, R. L. (1998). Permian basin field-tests of propellant-assisted perforating. SPE Permian Basin Oil and Gas Recovery Conference, Midland, Texas. [Google Scholar]

 8.  Smith, K. T., Schmid, J. C. (1984). Application of an alternate stimulation method for the ferguson sandstone in the powder river basin. SPE Rocky Mountain Regional Meeting, Casper, Wyoming. [Google Scholar]

 9.  Boscan, J., Almanza, E., Folse, K., Bortot, M. (2003). Propellant perforation breakdown technique: Eastern Venezuela field applications. SPE International Improved Oil Recovery Conference in Asia Pacific, Kuala Lumpur, Malaysia. [Google Scholar]

10. Hollabaugh, G. S., Dees, J. M. (1993). Propellant gas fracture stimulation of a horizontal Austin chalk wellbore. SPE Annual Technical Conference and Exhibition, Houston, Texas. [Google Scholar]

11. Yang, B. J., Guo, W. (1997). Development and application of combined perforation technology. Oil Drilling & Production Technology, 19(6), 58–62. DOI 10.13639/j.odpt.1997.06.013. [Google Scholar] [CrossRef]

12. Wu, J. J., Ma, R. H. (2000). Study and application of the combined perforation fracturing technique. Oil Field Equipment, 29(2), 31–33. DOI 10.3969/j.issn.1001-3482.2000.02.009. [Google Scholar] [CrossRef]

13. Zou, L. Z. (2013). Analysis of compound perforation technology in oil and gas wells. World Well Logging Technology, 1, 63–66. [Google Scholar]

14. Administration, N. E. (2011). SY/T 6824−2011 combined perforator general technical specification and detection method for oil and gas wells. Beijing: Petroleum Industry Press. [Google Scholar]

15. Zhang, F., Jia, J. H., Cai, W. (2016). Calculation model for detonation gas pressure in compound perforation. Ordnance Industry Automation, 35(12), 41–44. DOI 10.7690/bgzdh.2016.12.012. [Google Scholar] [CrossRef]

16. Nilson, R. H., Proffer, W. J., Duff, R. E. (1985). Modelling of gas-driven fracture induced by propellant combustion within a borehole. International Journal of Rock Mechanics and Mining Sciences & Geomechanics Abstracts, 22(1), 3–19. DOI 10.1016/0148-9062(85)92589-6. [Google Scholar] [CrossRef]

17. Tada, H., Paris, P. C., Irwin, G. R. (1973). The stress analysis of crack handbook. Hellertown: Del Res, Corp. [Google Scholar]

18. Whittaker, B. N., Singh, R. N., Sun, G. (1992). Rock fracture mechanics. Principles, design and applications. Elsevier, Amsterdam. [Google Scholar]

This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.