Fluid Dynamics & Materials Processing

DOI: 10.32604/fdmp.2022.021975

ARTICLE

Numerical Simulation of a Granular Flow on a Smooth Inclined Plane

Rida Tazi1, Adil Echchelh1, Mohammed El Ganaoui2 and Aouatif Saad3,*

1Laboratory of Materials and Energy, Faculty of Sciences, Ibn Tofail University, Kenitra, Morocco
2LERMAB/IUT Longwy, Institut Carnot, Nancy, France
3ASELab Advanced Systems Engineering Laboratory, National School of Applied Sciences, Ibn Tofail University, Kenitra, Morocco
*Corresponding Author: Aouatif Saad. Email: saad.aouatif@uit.ac.ma
Received: 15 February 2022; Accepted: 21 March 2022

1  Introduction

Granular materials have a multiphase behavior as they can behave like solids, fluids or gases. They appear in many industrial applications such as food processing or pharmaceutics and also in geotechnical and physical phenomena like avalanches.

Despite a large amount of dedicated research [1–9], modeling and predicting granular flows remains a challenging goal. Granular flows are characterized by a very large diversity of behaviors. For example, the simple controlled experiment of a granular layer flowing on an inclined plane reveals more intriguing features than one would expect. Many researches [10–12] were based on the Saint-Venant equations to model the granular flow, this restrictive model consider a dry granular flow taking into consideration only the interaction between substances-substrat and neglecting the cohesion between grains themselves.

In our numerical study and in order to enlarge the specter of parameters and factors that intervenes in the flow, we have opted for the Savage-Hatter model [13]. Many macroscopic models have been proposed to describe granular flows, including this model for simulating the motion of granular flows on a gentle slope [13]. The main assumptions in the Savage–Hutter model are: (1) the density of the granular flow is constant; (2) the effects of side wall and erosion are ignored; (3) the granular material remains shallow during flow. In our numerical study, we furthermore, studied the effect of thickness variation, compactness, density, roughness and temperature on the flow velocity. We have found that these parameters often neglected by previous researches [14,15] mainly influence the granular flow behavior.

2  Mathematical Model

We consider the flow of a granular mass (we denote “m” and “d” for the average mass and the diameter of the grains) along a slope of inclination θ, under the effect of gravity g.

For simplicity, we describe the two-dimensional situation, where the position along the slope is marked by the direction ‘x’. We denote ‘y’ the direction perpendicular to the slope (y = 0 corresponds to substance-substrate contact surface), and u(y) the velocity profile (Fig. 1). We denote H the thickness of the flowing layer and V¯=1H∫0H⁡u(y)dy the mean velocity of the layer.

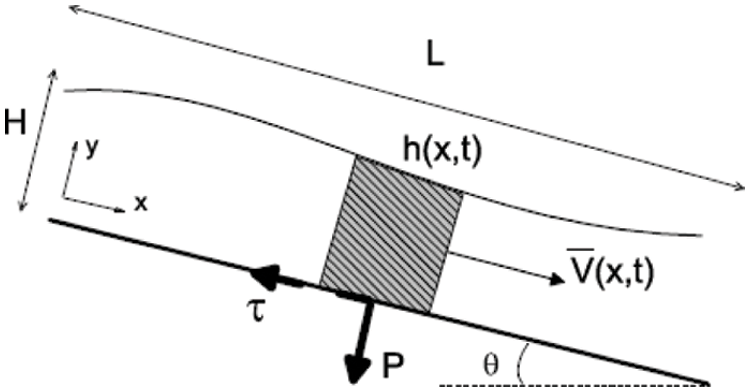
Figure 1: Principle of the saint-venant formalism to simulate a flow along a slope

At the base of the flow, there is a pressure P and a shear stress τ in the material. We call μ∗=τ/P the effective coefficient of friction of the material on the slope.

The effective description of the flow, known as of Saint-Venant model, is obtained by integrating the mass conservation equations (Eq. (1)) and the momentum equation (Eq. (2)) along the thickness of the material, we thus obtain two derivative partial equations for the two quantities H and V¯ :

∂H∂t+∂HV¯∂x=0 (1)

∂(HV¯)∂t+∂(HV¯2)∂x=gHcos⁡θ(tanθ−μ∗−K∂H∂x) (2)

The K parameter determined by the ratio of the normal stresses within the flow. We can see in the second equation the crucial importance of the effective coefficient of friction μ∗ and the average speed V¯ , the knowledge of these quantities is essential for the description of granular flows.

The granular flow is similar to the dense flow regime; thus, we have the following friction law [16]:

μ∗(I)≈μmin∗+bI  (3)

With:

I: Inertial Nombrer I=γ˙dρgP ,

γ˙ : Shear rate,

ρg: Surface mass,

P: Pressure,

b: Parameter of grain type.

Hypothesis:

For a uniform stationary flow, the inclination θ is equal to the effective coefficient of friction μ∗ (we will systematically make the approximation

μ∗=tanθ≈θ, μmin∗=tan∅=∅ and cosθ=1 within the considered tilt range).

We then used the friction law just identified in homogeneous shear to discuss the shear rate profile in dense stationary flow on a rough inclined plane. The shear rate allowed to determine the variation of the speed ux(y) which will be integrated along the thickness (H) of the layer to have the average speed V¯ .

To determine the shear rate, we consider the density ρ=ρgϑ ( ϑ is the compactness) as constant within the layer, the pressure is hydrostatic P(y) = ρgcosθ(H − y), neglecting the increase of ‘I’ near the free surface and near the base, we will consider that I is a constant within the flowing layer:

I=γ˙dρgP (4)

γ˙(y)≈ϑg(θ−∅)bdH−y  (5)

The latter (shear rate) is used to determine the speed profile:

ux(y)=∫y=0y⁡γ˙(y)dy

ux(y)=23ϑ.gb.d.(θ−∅).(H32−(H−y)32  (6)

We thus find the law of flow:

V¯=1H∫0H⁡u(y)dy

V¯(H,θ)≈25ϑ.gb.d.(θ−∅).H32 (7)

The combined measurement of the thickness H of the flowing layer, the inclination θ and the average speed V¯ revealed the following flow law:

V¯∝ H32(θ−∅)

where ∅︀ appears as the threshold flow angle (stop angle).

3  Treatment Cycle

We have developed a computational program that aims to visualize the velocity profile and the effect of substrate roughness on flow blockage.

A study is carried out on an elementary volume of a rectangular substance 10 m long and 6 m thick placed on a rough substrate. The substance is characterized by a density of 1600 kg.m−3 , a compactness of 0.78 and a stop angle of 12°.

Our first simulation consists in visualizing the profile of the speed along the thickness ux(y=0→H,θ) for different inclination angle. The implemented algorithm is reported in the following Fig. 2.

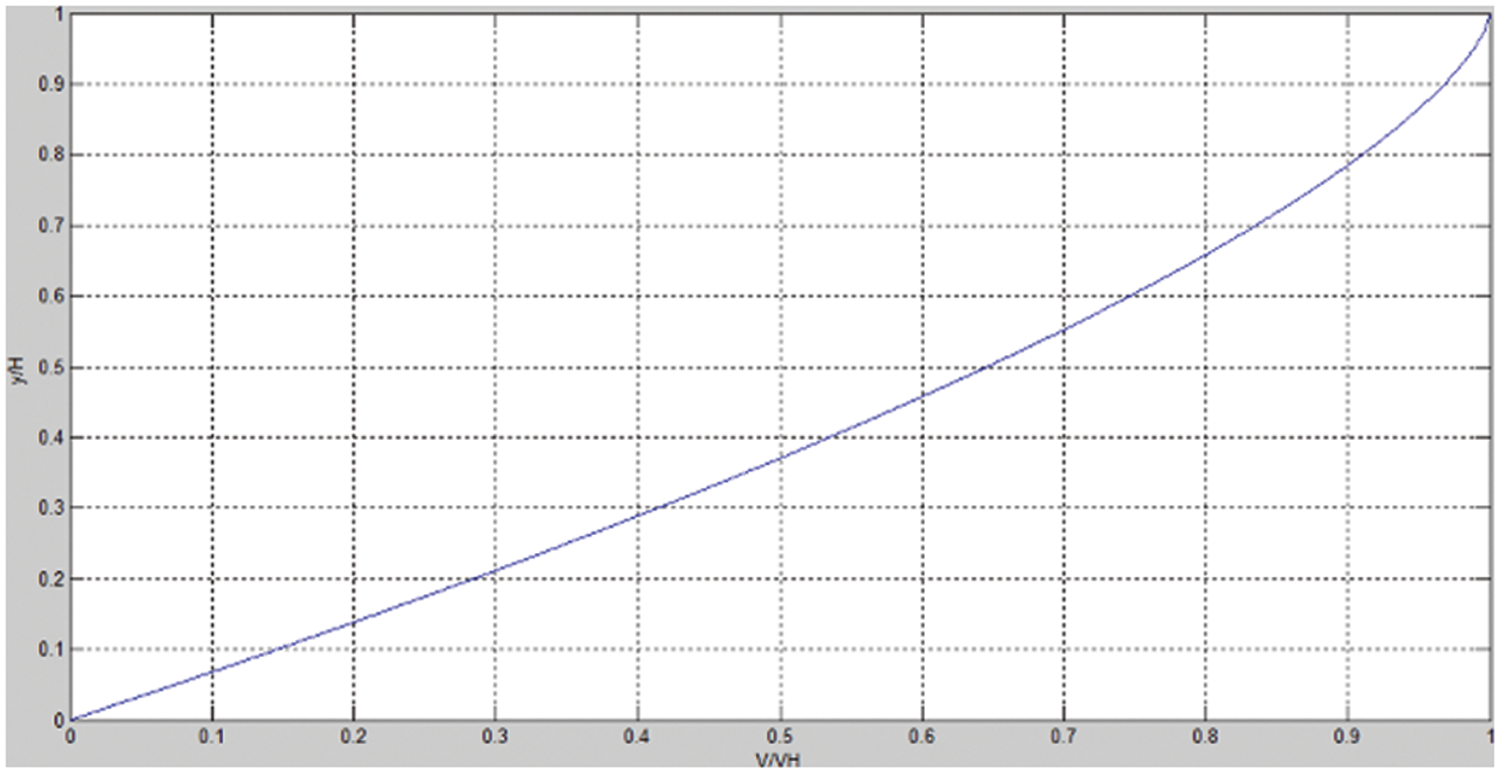
Figure 2: The variation of speed as a function of substance thickness

In our second simulation, we have used the effective description of Saint-Venant flow, Eq. (2) will be simplified since H = cst→ ∂(V¯)∂t=gcos⁡θ(tanθ−μ∗) , to visualize the effect of the substrate roughness μ∗ on the average speed profile of the layer over time (variation of θ (t)) (Fig. 5). The algorithm implemented is as follows:

4  Results and Discussion

Several simulations were performed to visualize the effect of height, density, compactness and temperature of the substance on the flow velocity. From Fig. 2, we see that for a fixed angle of inclination the speed profile ux(yi,θfixe) increases, going from the substrate to the free surface (y = 0 to H). This result can be explained by the fact that the substance near the substrate is more influenced by friction, so, it is more attached to the substrate and consequently its velocity is low. Contrarily to the substance near the free surface where the velocity is higher.

Density and compactness are crucial parameters that affect the speed of the flow. In order to visualize the effect of density, we have considered three different values as (ρ1 = 1000, ρ2 = 1600, ρ3 = 2000 kg/m3). It can be seen from Fig. 3 that the more the density increases, the more the flow speed increases. The compactness follows the same analogy as the density, we have chosen 3 different compactness values for each simulation (c1 = 0.78, c2 = 0.88 and c3 = 0.98) (see Fig. 4).

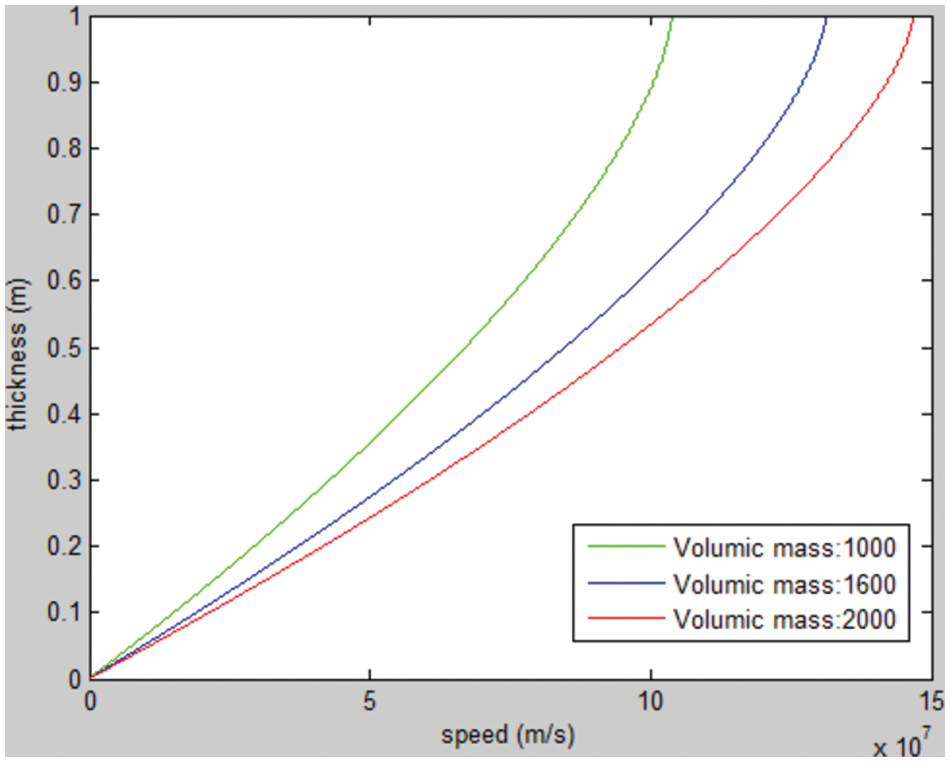
Figure 3: Effect of density on speed, with compactness = 0.78, H = 4 and the angle of inclination = 45°

Figure 4: Effect of compactness on speed, with density ρ = 1600, H = 4 and the angle of inclination = 45°

Furthermore, to study the variation of the flow velocity as a function of the substance temperature, it was necessary to add to the momentum (Eq. (2)), a viscosity term. This results to the following equation after solving with the finite-difference method:

uin+1=uin−ΔtΔxuin(ui+1n−uin)+Δt.g.cosθ(tanθ−μ)+η.ΔtΔx2.(ui+1n−2uin+ui−1n) (8)

η: viscosity (η = cste T)

In our simulation, we have chosen the water viscosity for three different temperatures η1 = 1, 787e − 3 at T = 0°-C, η2 = 1, 002e − 3 at T = 20°-C and η3 = 0.2818e − 3 at T = 100°-C).

The results presented in Fig. 5 show that the temperature increases, the more the flow speed decreases.

Figure 5: The variation of the speed as a function of time for 3 different substance temperatures

In this second part, we have studied the effect of roughness on the blocking of the flow. We mean by blocking the flow when the grains are trapped in the roughness and can only start rolling from an inclination θstart.

Accelerated by gravity and slowed down by dissipative shocks on the substrate, the grains reach a stationary speed V¯(θ,H).  If we then decrease the inclination, the grains feel more and more the influence of roughness, and stop abruptly when its speed becomes less than the speed of “release” of the traps, for an inclination θstop. A simulation was performed in order to show the effect of roughness.

For a coefficient of friction μ∗=0.5774  equivalent θ = 30°, one notes (see Fig. 6):

–   The average layer speed will be slowed down to blockage for all θi < 30°-.

–   The mean velocity of the layer will be uniform for θi = 30°-.

–   The average speed of the layer will be accelerated for all θi > 30°-.

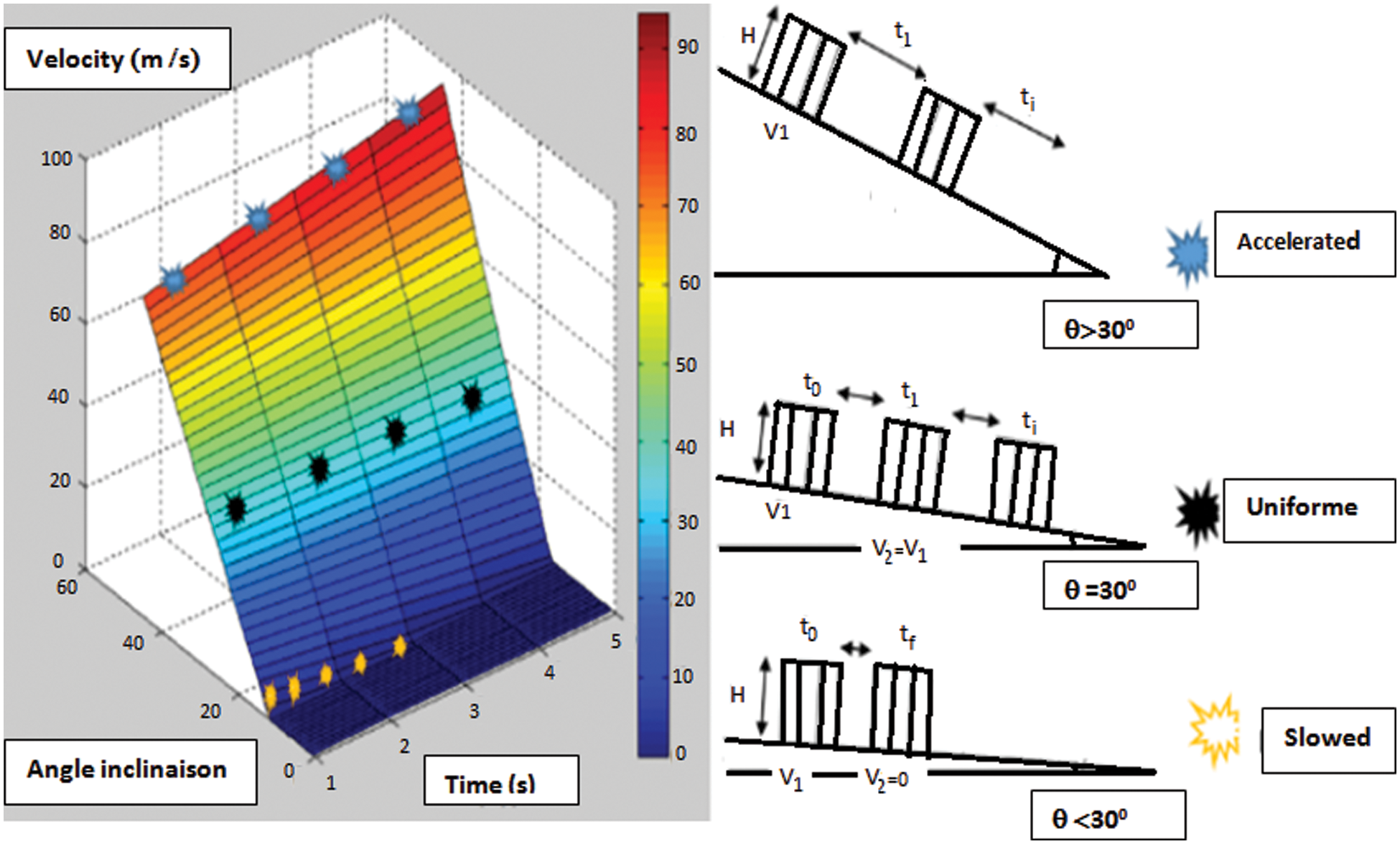
Figure 6: The variation of speed as a function of time with coefficient of friction 0.54774

This simulation proves that in order that our substance does not block, it is necessary that ( μ∗<tanθ ).

5  Conclusion

In this work we have opted for the Savage-Hatter model to study a granular flow in an inclined plane. We have provided new numerical results that highlight the effect of substrate temperature, the roughness, the compactness, the density of the substance on the flow behavior, which was neglected in previous models. We demonstrated that, the more the density and the compactness are important and the temperature of the substance is low, the more we will have a significant flow velocity. Furthermore, the inclination angle plays an important role in the speed of the granular flow, to have a flow; the angle of inclination must be greater than the start angle. Despite, the advantages of the Savage-Hatter model, but this latter, do not take into account the effects of forces that appear between particles during the flow. For this purpose, we aimed in the future work to highlight the effect of these forces (Forces of Hertz, Visco-elastic force…) on the flow velocity of particles on a plane with variable angles of inclination.

Funding Statement: The authors received no specific funding for this study.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  Brown, R. L., et Richards, J. C. (1970). Principles of Powder Mechanics. The Boulevard, Langford Lane, Kidlington, OX51GB, Oxford, UK: Pergamon Press. [Google Scholar]

 2.  Duran Sables, J. (1997). Poudres et grains. Paris : Eyrolles Sciences. [Google Scholar]

 3.  Savage, S. B. (1989). Flow of granular materials in theoretical and applied mechanics, pp. 241–266. North Holland, Amsterdam. [Google Scholar]

 4.  Hutter, K., Rajagopal, K. R. (1994). On flows of granular materials. Continuum Mechanics andThermodynamics, 6, 81–139. DOI 10.1007/BF01140894. [Google Scholar] [CrossRef]

 5.  Desrues, J., Chambon, R., Mokni, F., Mazeroll, M. (1996). Void ratio evolution inside shear bands intriaxial sand specimens studied by computed tomography. Géotechnique, 46, (3), 529–546. DOI 10.1680/geot.1996.46.3.529. [Google Scholar] [CrossRef]

 6.  Michaél, P. (2002). Ecoulements denses de grains secs (Ph.D. Thesis). Ecole desPonts ET CHAUSSÉESParisTech. [Google Scholar]

 7.  Nicolas, T. (2005). Ecoulements gravitaires de materiaux granulaires (Ph.D. Thesisvol. 1. Université Rennes. [Google Scholar]

 8.  Pierre, R. (2006). Rhéologie des matériaux granulaires cohésifs. Application aux avalanches de neige dense (Ph.D. Thesis). Ecole des Ponts ParisTech. [Google Scholar]

 9.  Christelle, L. (2013). Modélisation numérique des écoulements gravitaires viscoplastiques avec transition fluide/solide (Ph.D. Thesis). Ecole Nationale des Ponts et Chaussées. [Google Scholar]

10. Bell, J. B., Colella, P., Glaz, H. M. (1989). A Second-order projection method for the incompressible navier–Stokes equations. Journal of Computational Physics, 85, 257–283. DOI 10.1016/0021-9991(89)90151-4. [Google Scholar] [CrossRef]

11. Saingier, G., Deboeuf, S., Lagrée, P. Y. (2015). On the front shape of an inertial granular flow down a rough incline. Physics of Fluids, 28(5). DOI 10.1063/1.4948401. [Google Scholar] [CrossRef]

12. Mangeney-Castelnau, A., Bouchut, F., Vilotte, J. P., Lajeunesse, E., Aubertin, A. et al. (2005). On the use of saint venant equations to simulate the spreading of a granular mass. Journal of Geophysical Research, 110, B09103, DOI 10.1029/2004JB003161. [Google Scholar] [CrossRef]

13. Minglong, F., Qicheng, S., Deyu, Z., Gordon G. D. Z. (2012). Simulations of granular flow along an inclined plane using the savage–Hutter model. Particuology, 10(2), 236–241. DOI 10.1016/j.partic.2011.11.007. [Google Scholar] [CrossRef]

14. Pudasaini, S. P., Hutter, K. (2007). Avalanche dynamics—Dynamics of rapid flows of dense granular avalanches. Berlin: Springer. [Google Scholar]

15. Savage, S. B., Hutter, K. (1989). The motion of a finite mass of granular material down a rough incline. Journal of Fluid Mechanics, 199, 177–215. DOI 10.1017/S0022112089000340. [Google Scholar] [CrossRef]

16. Pierre, R., Jean-Noël, R., Mohamed, N., François, C. (2007). Bidisperse granular flows on an inclined plane: Friction law and two-layer model. Bulletin de Liaison des Laboratoires des Ponts et Chaussees. [Google Scholar]

This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.