

 | Fluid Dynamics & Materials Processing |  |
DOI: 10.32604/fdmp.2022.022220
ARTICLE
Turbulent Double-Diffusive Natural Convection and Entropy Generation within an Inclined Square Cavity
Laboratoire des Sciences et Ingénierie Maritimes, Faculté de Génie Mécanique, Université des Sciences et de la Technologie Mohamed BOUDIAF d’Oran, Oran El-Mnouar, Algérie
*Corresponding Author: Khaled Said. Email: khalednabil2016@yahoo.com
Received: 27 February 2022; Accepted: 30 March 2022
Abstract: The present study deals with double-diffusive convection within a two-dimensional inclined cavity filled with an air-CO2 binary gas mixture. The left and the right vertical walls are differentially heated and subjected to different locations of (CO2) contaminants to allow for the variation of the buoyancy strength (N). However, the horizontal walls are assumed adiabatic. The simulations are conducted using the finite volume method to solve the conservation equations of continuity, momentum, energy, and species transport. Good agreement with other numerical results in the literature is obtained. The effect of multiple parameters, namely, buoyancy ratio (N), thermal Rayleigh number (Ra), and inclination angle (α) on entropy generation rate is analyzed and discussed in the postprocessing stage, while considering both laminar and turbulent flow regimes. The computations reveal that these parameters considerably affect both the heat and mass transfer performances of the system.
Keywords: CFD; entropy generation; double diffusive convection; inclination angle; CO2; turbulent regime
Nomenclature
| As | Aspect ratio |
| Be | Bejan number |
| C | Concentration, kg m–3 |
| C* | Dimensionless concentration |
| D | Mass diffusivity, m2 s–1 |
| Le | Lewis number |
| N | Buoyancy ratio |
| NS | Entropy number |
| Pr | Prandtl number |
| R | Gas constant, J kg–1 K–1 |
| RaT, RaS | Thermal, solutal Rayleigh numbers |
| Sgen | Entropy generation, W m–3 K–1 |
| T | Temperature, K |
| u, v | Horizontal, vertical velocity component, m s–1 |
| U, V | Horizontal, vertical dimensionless velocity component |
| X, Y | Dimensionless coordinates |
| Greek symbols | |
| α | Inclination angle |
| | Thermal diffusivity, m2 s–1 |
| βs | Solutal expansion coefficient, m3 kg–1 |
| βT | Thermal expansion coefficient, K–1 |
| θ | Dimensionless temperature |
| λ | Thermal conductivity, W m–1 K–1 |
| μ | Dynamic viscosity, kg m–1 s–1 |
| δ | Error |
| Subscripts | |
| T | Thermal entropy |
| D | Viscous entropy |
| M | Diffusive entropy |
Conjugate heat and mass transfer, widely referred to as double-diffusive convection or thermosolutal convection, is a buoyancy-driven flow governed by two components with different molecular diffusivities and opposing contributions to the vertical density gradient. Owing to its engineering and industrial applications, including the design of chemical processing equipment, formation, and dispersion of fog, environmental pollution, oceanography, etc., double-diffusive convection received great interest among researchers. Beghein et al. [1] were one of the foremost researchers who studied natural thermosolutal convection inside cavities. Particular attention was devoted to the effect of non-dimensional parameters, i.e., Le, RaS, and N. A significant effect was noted on fluid motion inside the cavity core. The problem of double-diffusive convection under the turbulent regime was handled by Arellano et al. [2] as well as Arellano et al. [3]. The enhancement of heat and mass transfer is continuously accompanied by entropy generation. Several publications have appeared in recent years documenting the second law of thermodynamic and in particular entropy minimization due to its ability to optimize heat and mass transfer. One of the first examples is Magherbi et al. [4]. The influence of three different inclination angles besides thermal Grashof number and buoyancy ratio was explored numerically under the laminar regime. The numerical results have shown a significant effect of the inclination angle on entropy generation in addition to heat and mass transfer rates. Quite recently, Oueslati et al. [5] reported a numerical study of double-diffusive natural convection and entropy generation inside a three-dimensional inclined cavity. The study aimed to explore the effect of various parameters such as aspect ratio, buoyancy ratio, and enclosure inclination angle. It was reported that as the buoyancy ratio increases, the total entropy generation decreases regardless of aspect ratio variation. The authors have also found that the average Nusselt and Sherwood numbers profiles reach a minimum at the buoyancy ratio value of N = –1.0. Similar papers were found in the literature [6,7]. An important rise in entropy generation under high Rayleigh numbers was noted by Chen et al. [8] and Chen et al. [9]. These authors studied the effects of Rayleigh numbers and buoyancy ratios besides aspect ratios by way of CFD computations for aiding flow (N > 0). Meanwhile, the entropy production rates due to thermal, viscous, and diffusive effects were calculated due to turbulent double-diffusive convection by Said et al. [10]. Multiple Rayleigh numbers ranging from 103 to 1010 and various buoyancy ratios varying from –5.0 to +5.0 were investigated.
In spite of the turbulence’s huge effect and according to the extensive bibliographic research examined so far, previous studies’ attention was mostly devoted to entropy production under the laminar regime. The turbulent flow was widely neglected. Accordingly, the present work aims to solve numerically double-diffusive convection and entropy generation under turbulent flow regime. Entropy production under opposing flow i.e., N < 0 was also investigated and presented in this paper.
2.1 Physical Problem and Boundary Conditions
Fig. 1 depicts a schematic illustration of the physical domain and the boundary conditions considered in the present paper. An inclined square cavity of a perfect air and carbon dioxide mixture was studied. Temperature and species gradients were imposed on the vertical walls, while the horizontal ones were fully insulated. In this study, the maximum and the minimum contaminant concentrations were alternatively localized either along the right or the left perpendicular walls to allow for variance in the buoyancy strength. For all boundaries, zero velocity at the wall was assumed (no-slip condition).

Figure 1: Physical model and boundary conditions
The governing partial differential equations of a mathematical model that describes heat and mass transfer are continuity, momentum, energy, and species diffusion equations. From a simplification point of view, the working fluid is assumed as a Newtonian and incompressible perfect binary gas mixture. Soret and Dufour effects are also neglected in addition to the radiative exchanges between surfaces. On the other hand, all the fluid physical properties were constant except density in the buoyancy force term. Therefore, the Boussinesq approximation is satisfied. In view of these considerations, the governing equations could be written as [2]:
where,
The total entropy generation due to conjugate heat and mass transfer is the sum of three different irreversibilities, i.e., friction, heat, and species diffusion. For a Newtonian and incompressible perfect binary gas mixture over a two-dimensional domain it takes the following form [1]:
Using the following dimensionless variables:
The dimensionless form of entropy production is obtained as follows:
Therefore:
where,
The discretization of the governing equations described above was ensured by way of the finite volume method technique. To couple pressure and velocity, the SEMPLEC algorithm was employed in this work. The standard k-ε turbulence model has been adopted to deal with high Rayleigh numbers. A third-order accurate scheme (QUICK) was employed for the continuity discretization. Meanwhile, a central second-order scheme was selected for all remaining equations.
Entropy generation due to laminar and turbulent double-diffusive natural convection process inside a square cavity for different inclination angles and multiple buoyancy ratios is analyzed in this section. The Prandtl number, as well as the Lewis number, were taken to be constant: Pr = 0.71 and Le = 1.0.
Multiple quadratic grids were tested in order to satisfy an optimum balance between computational time and results accuracy. The Mean, the minimum, and the maximum values of the Nusselt number at the hot wall beside the dimensionless components of the vertical and horizontal velocities at the cavity mid-section were calculated and verified for Ra = 105 and N = 0. It is observed that the mesh density has an insignificant effect between the third and fourth meshes. Accordingly, the mesh 175 × 175 has been used for the remaining computations. The obtained results are summarized in Table 1.
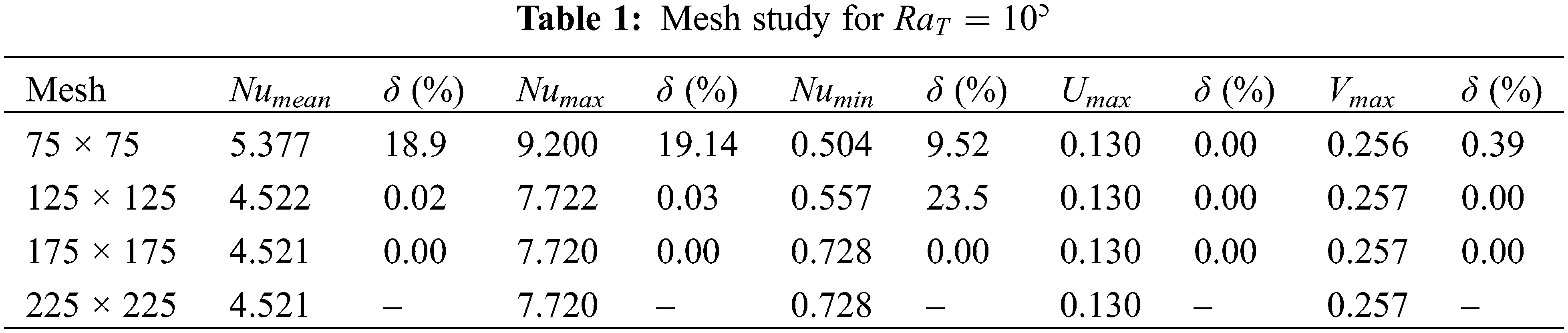
Once the optimum mesh was indicated, it is preceded to the numerical code validation. Every simulation must undergo this process to verify the accuracy of its numerical outputs. The numerical results were confronted quantitively and qualitatively with various data found in the literature.
First, the issue of double-diffusive convection under the laminar regime was simulated and evaluated against various authors for multiple buoyancy ratios (N) within a square cavity. Later on, the simulation of natural convection was conducted and validated with the experimental data gathered by Ampofo et al. [11] in order to validate our model under a turbulent regime. This was mainly due to the deficiency of turbulent double-diffusive data in the body of the literature
Fig. 2 shows the evolution of the local Nusselt number along the hot wall caused by the laminar double-diffusive natural convection. An excellent agreement was found with Beghein et al. [1] numerical results with a maximum error of less than 1%.

Figure 2: Local Nusselt number evolution at the hot wall vs. Beghein et al. [1] data for Ra = 104 and Le = 1.0
Table 2 shows an excellent agreement in terms of mean Nusselt number for a wide range of buoyancy ratios –0.01 ≤ N ≤ –5.0. The results were confronted with different authors where the maximum error was estimated by 1% compared to reference [1].
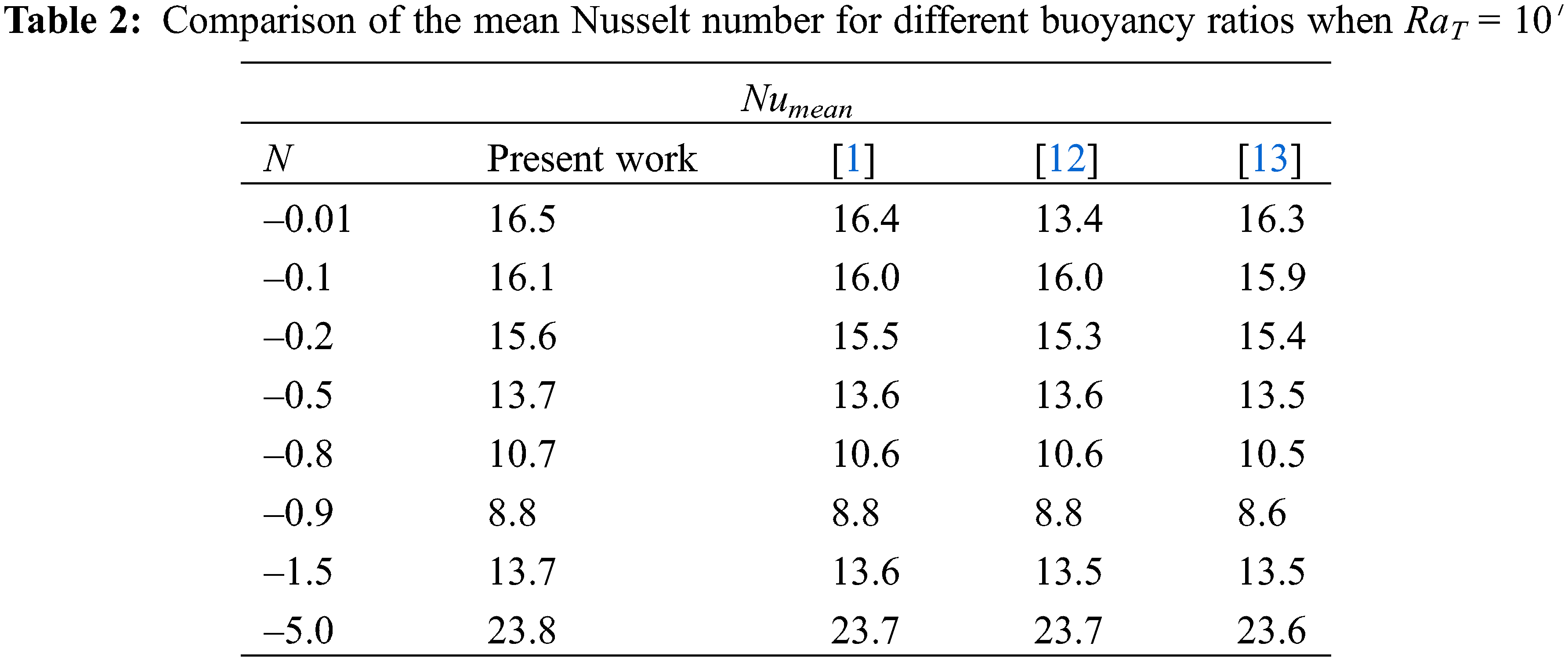
Fig. 3 depicts graphically dimensionless temperature and vertical velocity components at the cavity mid-section. A good match between the obtained results and those of Ampofo et al. [11] was noted.

Figure 3: Dimensionless temperature (a) Velocity (b) Profiles, at the cavity center
3.3 Flow Characteristics and Heat Transfer
Figs. 4 and 5 exhibit streamlines and dimensionless temperature contours respectively. From a similarity viewpoint, the results were only presented for an inclination angle of α = 30° (a) and α = 0° (b). The effect of the buoyancy ratio (N) inside a square sloped cavity was the main focus of the present section. Five different flow natures were detected. Table 3 summarizes the most conspicuous results.

Figure 4: Streamlines contours for α = 30° under turbulent flow regime with various buoyancy ratios

Figure 5: Heat results contours for α = 0° under turbulent flow regime with various buoyancy ratios

Fig. 6 outlines the variation of dimensionless entropy numbers for different buoyancy ratios under the laminar regime (left) and turbulent flows (right). As can be seen from this figure a huge growth in entropy production was noted for high Rayleigh numbers except for N = –1.0 owing to the convection non-existence phenomena. Therefore, under a turbulent regime, the minimum entropy was monitored when N = –1.0. Concerning laminar flow, N = 0 presents minimum as a result of relatively low thermal entropy as well as slight friction entropy production and the absence of mass diffusive irreversibility.

Figure 6: Dimensionless entropy number evolution under the laminar regime (left) and turbulent flow (right) for three different tilt angles
The inclination effect was more significant on entropy generation for low and large buoyancy ratios, i.e., N ≥ +1.5 and N ≤ –1.5 particularly for high Rayleigh numbers (RaT = 109). It is observed that for opposing flow (N < 0) the entropy peaks at α = 0° (non-inclined cavities) on the other hand, it reduces as α augment. In contrast, for aiding flow it was noted that the entropy reaches a maximum at α = 45°. It can be clearly seen that the inclination effect on entropy production depends primarily on the flow’s nature, i.e., aiding or opposing flow.
Therefore, the inclination angle should be taken into account in order to define the optimum design of any apparatus due to its important implication.
For the assessment of the dominant irreversibility of the entropy components, i.e., thermal, viscous, and diffusion, the Bejan number was investigated using the following formula:
where if Be < 0.5 then fluid friction entropy dominates, else it indicates the dominance of heat and mass transfer entropy.
Fig. 7 illustrates the variation of the Bejan number as a function of the buoyancy ratio for three different inclination angles under the laminar regime (left) and turbulent flow (right). From this figure, it can be seen that under the laminar regime the entropy is mostly dominated by heat and mass diffusive due mainly to the negligibility of viscous entropy. On the other hand, as the buoyancy ratio increases or decreases far from N = –1.0, the flow accelerates and therefore the viscous effect becomes more significant. In contrast, under high Rayleigh numbers, the flow was amplified significantly, and consequently, the friction was dominating both heat and mass diffusive entropy. This situation was valid for all buoyancy ratios except N = –1.0. Therefore, the Bejan number was maximum at this point.

Figure 7: Bejan number evolution under the laminar regime (left) and turbulent flow (right) for three different tilt angles
In the present study, double-diffusive convection under the laminar and turbulent regimes inside an inclined cavity was explored numerically. The effects of three different inclination angles and various buoyancy forces (N) were studied. Constant Prandtl and Lewis numbers were considered in this work of Le = 1.0 and Pr = 0.71, respectively. In order to define the optimum design of the double-diffusive process, further studies on entropy production should be conducted with different inclination angles other than those investigated in this study. Future studies should also target more realistic settings and different geometries such as rectangular, wavy walled, and complex enclosures to examine the effect of inclinations under turbulent regimes. The cardinal findings of the present paper can be summarized as follows:
• The buoyancy ratio (N) and the inclination angles are the key parameters that control entropy production inside the systems.
• Due to convection non-existence when N = –1.0, the flow was driven only by heat and mass diffusion.
• The influence of inclination angle is more significant under the turbulent regime, especially at small and high buoyancy ratios (N).
• Except N = –1.0, the entropy production was highly intensified under turbulent regimes.
Funding Statement: The authors received no specific funding for this study.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
1. Beghein, C., Haghighat, F., Allard, F. (1992). Numerical study of double-diffusive natural convection in a square cavity. International Journal of Heat and Mass Transfer, 35(4), 833–846. [Google Scholar]
2. Serrano-Arellano, J., Gijón-Rivera, M. (2014). Conjugate heat and mass transfer by natural convection in a square cavity filled with a mixture of Air-CO2. International Journal of Heat and Mass Transfer, 70, 103–113. [Google Scholar]
3. Alvarado-Juárez, R., Álvarez, G., Aman, J., Hernández-López, I. (2013). Numerical study of conjugate heat and mass transfer in solar still device. Desalination, 325, 84–94. [Google Scholar]
4. Magherbi, M., Abbassi, H., Hidouri, N., Ben Brahim, A. (2006). Second law analysis in convective heat and mass transfer. Entropy, 8(1), 1–17. [Google Scholar]
5. Oueslati, F., Ben Beya, B. (2017). Analysis of thermosolutal natural convection and entropy generation within a three-dimensional inclined cavity with various aspect ratios. Journal of Thermal Science and Technology, 12(2), JTST0017. [Google Scholar]
6. Mchirgui, A., Hidouri, N., Magherbi, M., Ben Brahim, A. (2014). Second law analysis in double diffusive convection through an inclined porous cavity. Computers & Fluids, 96(7), 105–115. DOI 10.1016/j.compfluid.2014.03.008. [Google Scholar] [CrossRef]
7. Zhu, Q. Y., Zhuang, Y. J., Yu, H. Z. (2017). Entropy generation due to three-dimensional double diffusive convection of power-law fluids in heterogeneous porous media. International Journal of Heat and Mass Transfer, 106(3), 61–82. DOI 10.1016/j.ijheatmasstransfer.2016.10.050. [Google Scholar] [CrossRef]
8. Chen, S., Du, R. (2011). Entropy generation of turbulent double-diffusive natural convection in a rectangle cavity. Energy, 36(3), 1721–1734. DOI 10.1016/j.energy.2010.12.056. [Google Scholar] [CrossRef]
9. Chen, S., Yang, B., Xiao, X., Zheng, C. (2015). Analysis of entropy generation in double-diffusive natural convection of nanofluid. International Journal of Heat and Mass Transfer, 87, 447–463. DOI 10.1016/j.ijheatmasstransfer.2015.04.023. [Google Scholar] [CrossRef]
10. Said, K., Ouadha, A., Sabeur, A. (2020). CFD-based analysis of entropy generation in turbulent double diffusive natural convection flow in square cavity. MATEC Web of Conferences, 330(15), 01023. DOI 10.1051/matecconf/202033001023. [Google Scholar] [CrossRef]
11. Ampofo, F., Karayiannis, T. G. (2003). Experimental benchmark data for turbulent natural convection in an air filled square cavity. International Journal of Heat and Mass Transfer, 46(19), 3551–3572. [Google Scholar]
12. Koufi, L., Cherif, L., Younsi, Z., Naji, H. (2018). Double-diffusive natural convection in a mixture filled cavity with Walls’ opposite temperatures and concentrations. Heat Transfer Engineering, 42(12), 1059–1066. [Google Scholar]
13. Xamán, J., Ortiz, A., Álvarez, G., Chávez, Y. (2011). Effect of a contaminant source (CO2) on the air quality in a ventilated room. Energy, 36(5), 3302–3318. [Google Scholar]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |