DOI:10.32604/iasc.2020.011617
| Intelligent Automation & Soft Computing DOI:10.32604/iasc.2020.011617 | |
| Article |
An Improved Range Doppler Algorithm Based on Squint FMCW SAR Imaging
Changchun University of Science and Technology, Changchun, China
*Corresponding Author’s Email: Wei Cui. Email: cuiwei7805@126.com
Received: 19 May 2020; Accepted: 16 June 2020
Abstract: The existing range-Doppler algorithms for SAR imaging are affected by a fast-time Doppler effect so they cannot be directly applied to FMCW SAR. Moreover, range migration is more evident in squint mode. To reveal the influence of the continuous motion of FMCW SAR in the squint mode on the echo signal and optimize the imaging process, an improved range-Doppler algorithm is based on squint FMCW SAR imaging is proposed in this paper. Firstly, the imaging geometry model and echo signal model of FMCW SAR are analyzed and deduced. The problem of Doppler center offset under squint mode is eliminated by linearly correcting the echo signal. By dealing with the range migration in the frequency domain, the processing process can be simplified. Finally, the effectiveness and feasibility of the algorithm are verified by simulation. The results are as follows: (1) The image quality is improved by correcting the linear motion in squint mode. (2) The peak sidelobe ratio (PSLR) and the integral sidelobe ratio (ISLR) of the imaging index of the improved algorithm are close to the theoretical values. Therefore, the improved range-Doppler algorithm can effectively perform high-efficiency imaging in the case of squint.
Keywords: Frequency modulated continuous wave; synthetic aperture radar; range doppler algorithm; range migration; squint imaging
The airborne platform for earth observation and imaging system, based on Synthetic Aperture Radar (SAR), is widely used in search and rescue, regional monitoring, disaster monitoring, and control, small unmanned aerial vehicles (UAV) ground reconnaissance and other aspects [1–3]. Traditional SAR equipment is characterized by a complex structure, large size, high cost, and limited application scenarios so that researchers combine FMCW with SAR technology to make it lightweight, low cost and small size, which makes SAR convenient to use in small UAVs or model aircraft with strict load requirements [4,5]. The application demand for FMCW SAR is gradually increasing, and the relevant research has also made significant progress. More and more units are involved in the research, design, production, and application of FMCW SAR. The University of Brigham Young has successfully developed the Micro SAR and applied it to small UAVs, which can operate in the 4–12 GHz signal band [6].
Due to the pulse width of the FMCW reaches the millisecond level, the position change of the radar in the period of the transmitting pulse cannot be neglected, so that the working mode suitable for the pulse-type SAR “stop-and-stop” is no longer applicable, and the load, cost, and power consumption are limited on the micro-platform. Therefore, it is necessary to improve the processing efficiency and reduce the amount of calculation under the premise of ensuring image quality.
Based on this, the researchers have conducted much research on the imaging processing methods applicable to FMCW SAR [7–11] by improving the processing speed of the onboard system and simplifying the imaging algorithm process, etc. However, it is still difficult to effectively deal with the problems of range migration and intra-pulse instantaneous slant range in the squint mode. In FMCW SAR real-time imaging of unmanned equipment, people hope to transmit high-quality radar imaging images in real time, which strictly requires the real-time processing of FMCW SAR system. We need to ensure the imaging quality of the radar while maintaining the low cost and low power consumption of the FMCW SAR system, and also better improve the processing power of related algorithms and minimize the system operation overhead. Therefore, how to establish the signal echo model accurately, correct the linear migration problem effectively, and analyze the effect of range migration on imaging accurately is an urgent problem to be solved.
Thus, an echo signal model is derived by analyzing the imaging geometry of FMCW SAR in squint mode. In order to efficiently process the influence of intra-pulse instantaneous slant range on imaging and optimize the range-Doppler algorithm step, which will provide a reference for high efficiency and high-quality imaging of FMCW SAR in squint mode, the characteristics of demodulation signal, the influence of instantaneous slant range on imaging quality and the effect of matching filtering on computational efficiency are analyzed.
Researchers have done a lot of research on imaging algorithms applicable to FMCW SAR. Tebaldini et al. [12] proposed the signal model of FMCW SAR in-band (cluster) mode, analyzed the effect of the intra-pulse aircraft motion on imaging. Wang et al. [13] analyzed the influence of intra-pulse motion on imaging and proposed an improved wavenumber domain algorithm, which used Stolt variable substitution for range migration correction. However, in actual data acquisition, the instability of aircraft will lead to a severe error of platform motion and further leads to image defocusing. Ribalta et al. [14] proposed an improved Back Projection Algorithm (BPA), which can be suitable for FMCW SAR imaging, but the computational complexity is too high because the algorithm completes focusing in the time domain. Palm et al. [15] proposed the real-time imaging processing process of FMCW SAR by combining with the MIRANDA 35 system of FHR, which can get SAR images in real-time. However, the obtained image resolution is not high, and the algorithm flow needs to be further improved. Liu et al. [16] analyzed the influence of the intra-pulse motion of the aircraft on the range migration and proposed the range-Doppler algorithm applicable to FMCW SAR. Gu et al. [17] proposed a parallel processing strategy in the process of SAR data processing, which significantly reduced the processing time of SAR imaging. However, this method has many limitations, such as two-dimensional rate mismatch and complex phase function generation method, which reduce the utilization rate of hardware resources. Cai et al. [18] conducted an in-depth study on the residual video phase and range migration of FMCW SAR, but did not consider the signal processing of the aircraft in squint mode. According to previous research [19] a miniature synthetic aperture experimental system is designed, mainly composed of signal modulation and processing module, circular horn antenna, and x-band transmitting module. However, it can only imagine a simple environment, and the system’s real-time performance is poor. Aiming at the fact that FMCW SAR transmits and receives signals during high-speed motion, Chen et al. [20] used a precise Doppler echo model to illustrates that the spectral peaks directly compressed by Fourier transform have not only Doppler offset but also have the phenomenon of broadening and peak dropping. Therefore, the compensation function was given to improve the range resolution, but the compensation function was inconveniently determined and needed real-time correction. Liu et al. [21] analyzed the basic principle of high-resolution imaging of the FMCW radar, elaborated the design idea and critical technology of the radar system in detail, and designed and realized a miniaturized FMCW SAR system. However, it has high requirements on the processing speed of the onboard system. In order to achieve high-resolution imaging of airborne FMCW SAR, Wang et al. [22] combined the wavenumber domain algorithm with two-step motion compensation through improved Stlot transform azimuth focusing can adequately compensate the error after second motion compensation and obtain good imaging effect. However, the Stolt transform needs interpolation processing in the two-dimensional frequency domain. The accuracy of frequency domain interpolation has a severe impact on image quality, and interpolation accuracy is not easy to grasp. Fu et al. [23] proposed to construct a uniform compensation function to compensate for the echo signal, to make full use of the bandwidth, and ensure that the range resolution is not affected by the echo time delay, but the characteristics of the de-chirp signal are not fully utilized. Wang et al. [24] proposed a new FMCW SAR imaging algorithm. In addition to using range resolution, it can also use intra-pulse Doppler frequency, which can provide a proper range resolution. However, the algorithm has a large amount of computation, which cannot meet the real-time requirements of a small airborne SAR system.
The above research results are mainly aimed at the imaging geometry and signal echo characteristics of FMCW SAR in positive and side view mode, but few studies on the imaging of FMCW SAR in the squint mode, especially the correlation research of high-efficiency real-time imaging. In this paper, the first established geometric model of FMCW SAR in squint mode and the instantaneous slant range on echo signals is analyzed. Then the echo signal model in squint mode is derived from analyzing the Doppler characteristics of echo signals and the computational complexity of range migration in the frequency domain, which provides a theoretical basis for the optimization of algorithm flow.
The rest of the article is organized as follows. In the third section, the geometric model in strip mode is established, and the signal echo model and detailed algorithm flow are derived. In the fourth section, the algorithm is analyzed and compared with the classical algorithm. Simulation experiments verify the effectiveness of the algorithm. The final section summarizes the paper and gives relevant conclusions.
In this section, FMCW SAR operating in squint mode is analyzed. Taking the squint geometry model in the strip mode as an example, the geometric model of the radar imaging and its geometric oblique plane with the imaging target are shown in Fig. 1.
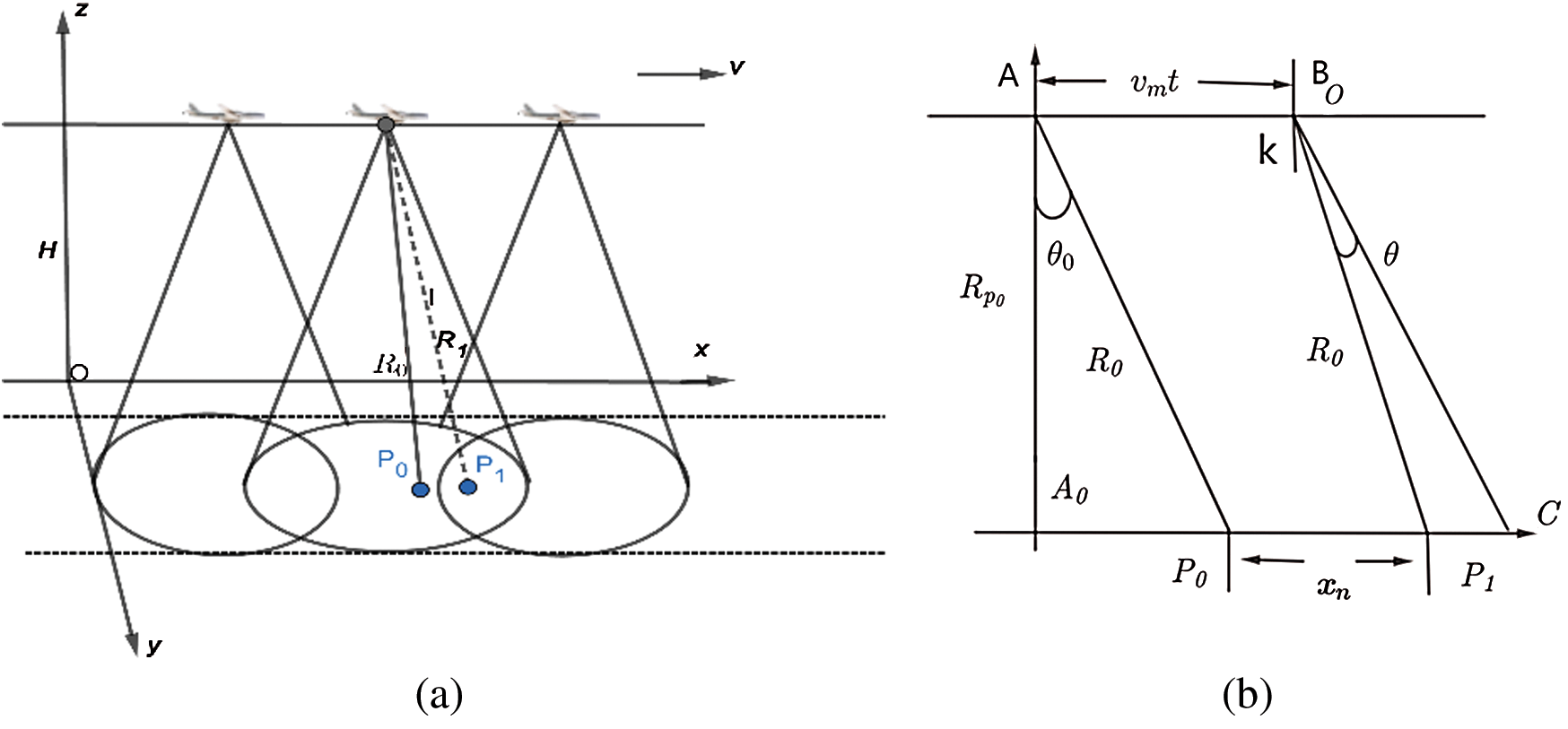
Figure 1: The observation geometry of FMCW SAR
In Fig. 1(a), the aircraft radar operates in strip mode. The height of the small-size aircraft radar is H from the ground, its flight speed is vm, and the shortest instantaneous slant range from the center of the radar beam to the target P1 is R1. In Fig. 1(b), assuming that the starting time of radar in slow azimuth time is calculated when the aircraft passes the point A, and the aircraft reaches the point B from the point A at the speed vm after the full time t(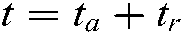
). During this motion, the radar beam center sweeps through the target center point P1 and intersects with the starting point P0 of slow time in the scanning band. The distance between point A and point B is 
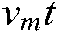, and the distance between the mapping band P0 and P1 is Xn.
According to the analysis, since FMCW SAR has been moving at a uniform speed during the transmission of signals during the whole radar working period, the instantaneous slant range between the aircraft and the target to be measured is not only related to the slow time ta, but also to the fast time tr and the slant angle. Whose expression is as Eq. (1):
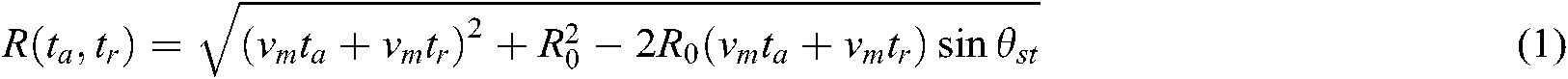
The instantaneous slant range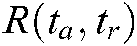 
is expanded at Taylor at fast time tr = 0, and the influence of the second order and higher order terms are ignored, which can be approximated as Eq. (2):
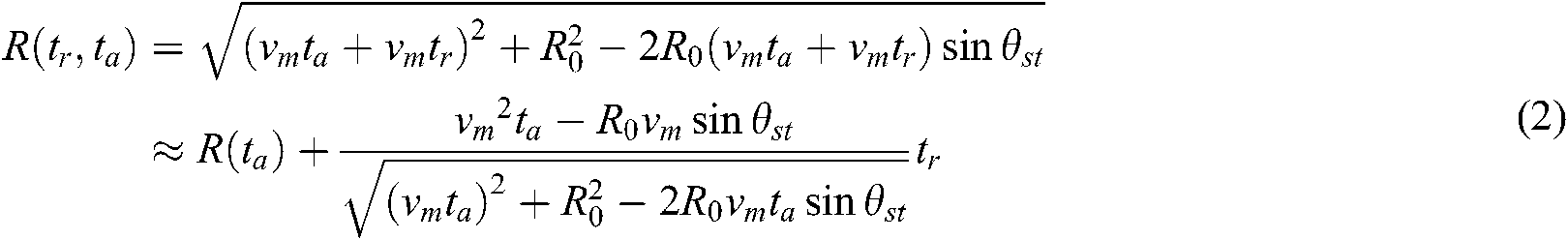
where
Describing the echo range variation in radar imaging scene is related to Eq. (3). Taylor expansion of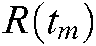 
at tm = 0 can be obtained as follows:
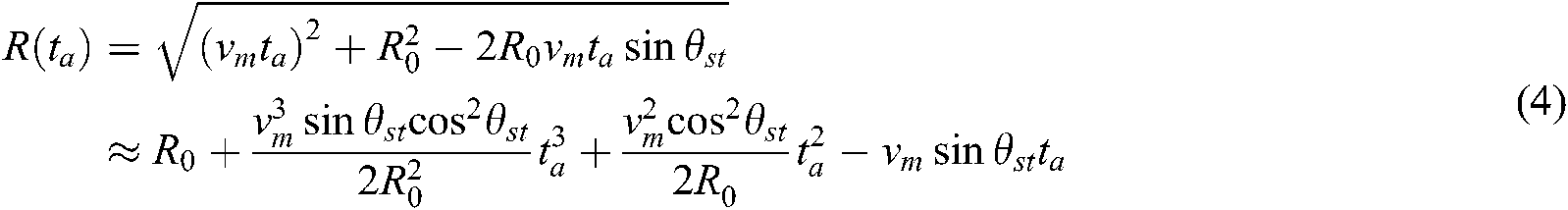
where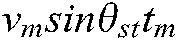 
is the range travelled by the airplane relative to the target in unit slow time, and the influence of this parameter on imaging cannot be ignored.
This section derives the signal echo model based on the imaging geometry model in Section 3.1. Let the transmitted signal be the LFM signal and the amplitude of the transmitted signal be constant. The mathematical expression of the transmitted signal is
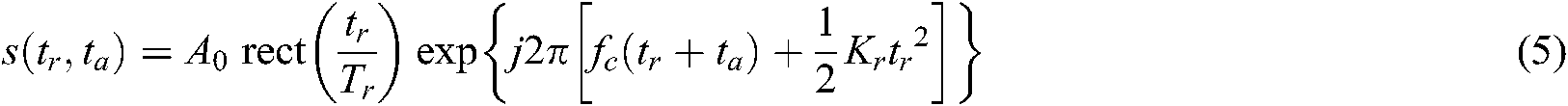
where fc is the signal center frequency,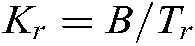 
is the linear modulation frequency, and Tr is the signal frequency scanning period.
After the radar receives the reflection of the signal, the delay signal is:
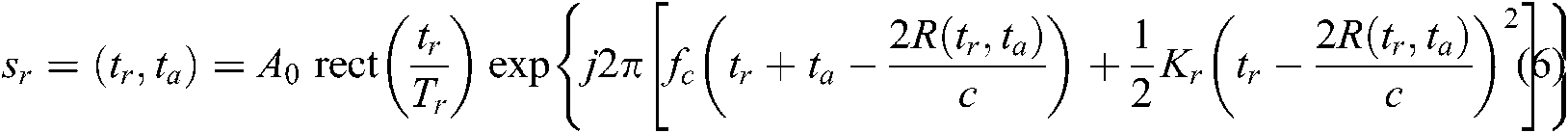
De chirp of echo signal is processed. Assuming that the reference slant range is Rref, then the reference signal expression is:
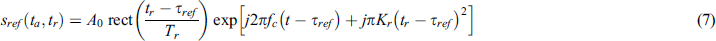
where 
. After de-chirp being processed, the echo signal is expressed as:
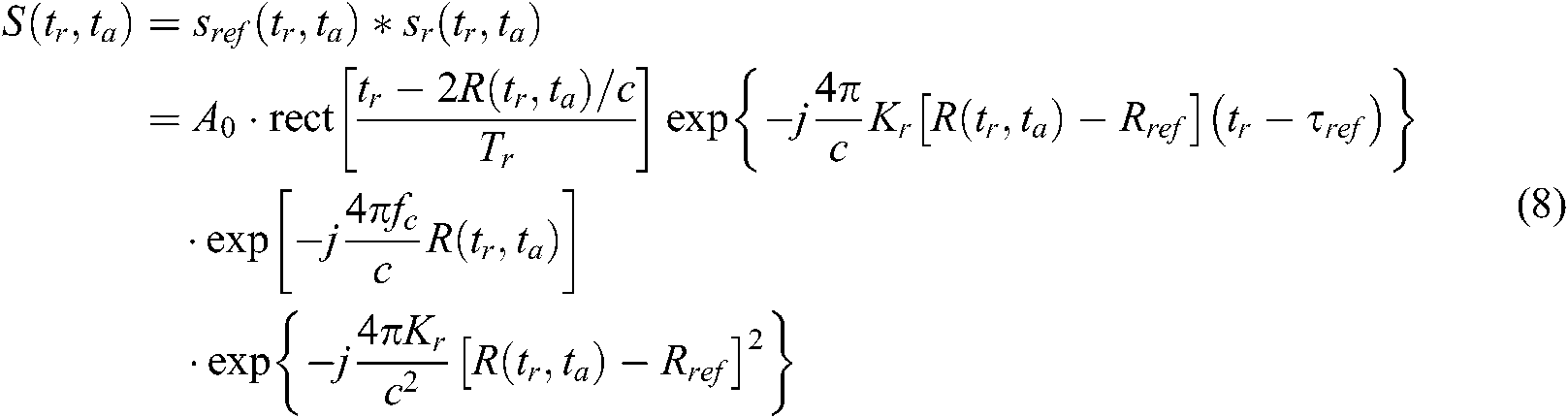
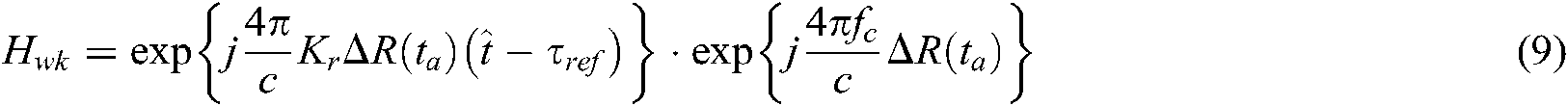
where A0 is the backscattering coefficient of the imaging point target; the first exponential term is the phase information in the range direction of the target; the second exponential term is the Doppler phase in the azimuthal direction, which can be used for the azimuth direction focusing, and the third exponential term is the Remain Video Phase (RVP), which can be ignored in the imaging process [25].
3.3 R–D Algorithm in Squint Mode
3.3.1 Linear Motion Morrection
Based on the analysis in Section 3.2, it is known that each exponential term in the de-chirp difference frequency signal contains the linear walking component. We need to correct the linear walking component in the echo signal. The corresponding linear walking component correction function is:
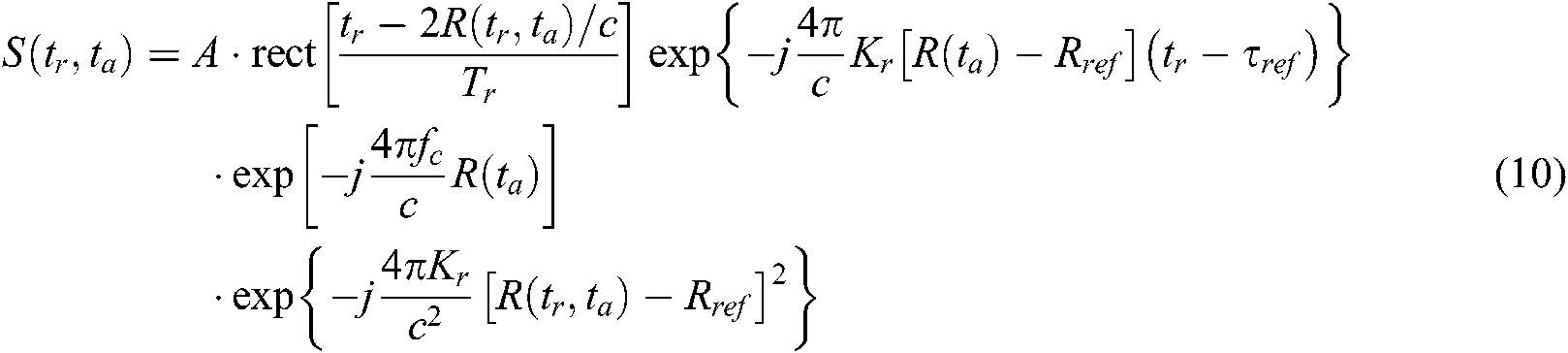
where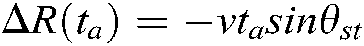 
. After compensation, the linear walking component in the range migration is eliminated, only the range bending term is included, and the Doppler center fc offset of the radar imaging is also compensated. At this time, the working mode of radar imaging is equivalent from the squint mode to positive and side view mode, and its echo function is:
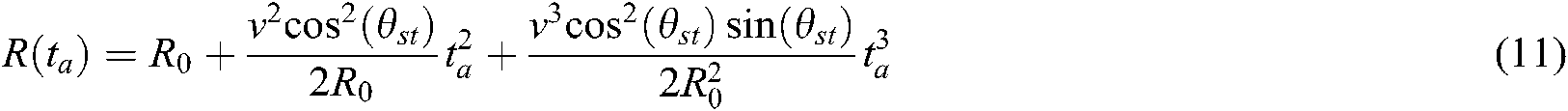
where
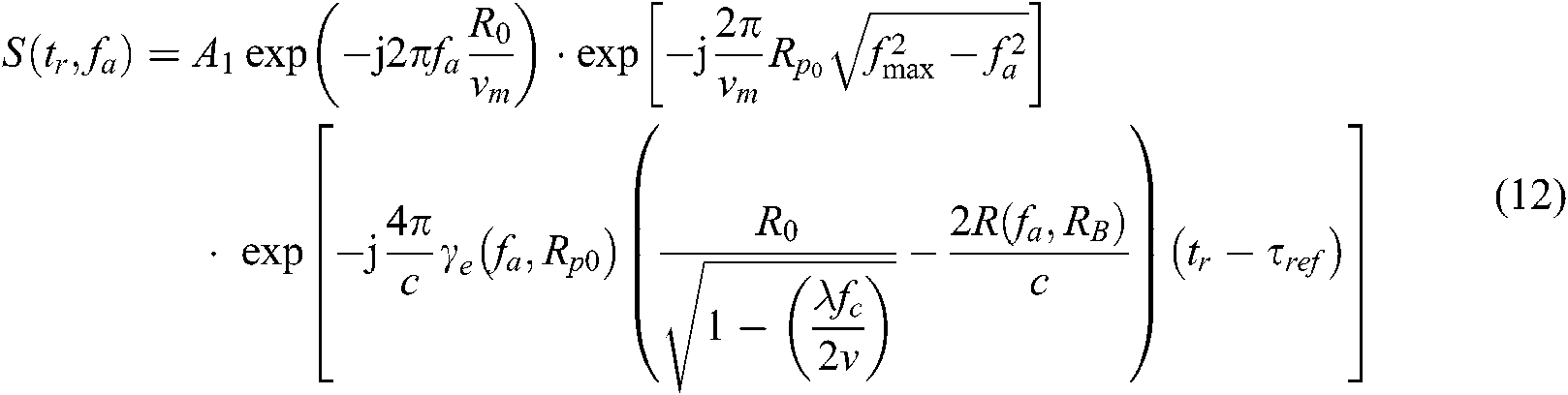
Because the subsequent signal processing ignores the impact on the RVP term, the RVP term is no longer processed during the correction linear walk.
3.3.2 Matching Filter Processing
In this section, the process of optimizing range Doppler algorithm is deduced in detail. Eq. (10) performs Fourier transform in azimuth direction according to the stationary phase theorem, and completes the range compression of the echo signal at the same time. Therefore, Eq. (10) becomes:
where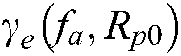 
is the linear modulation frequency, and its size changes with the change of radar Doppler fa. We can analyze its relationship from Fig. 2.
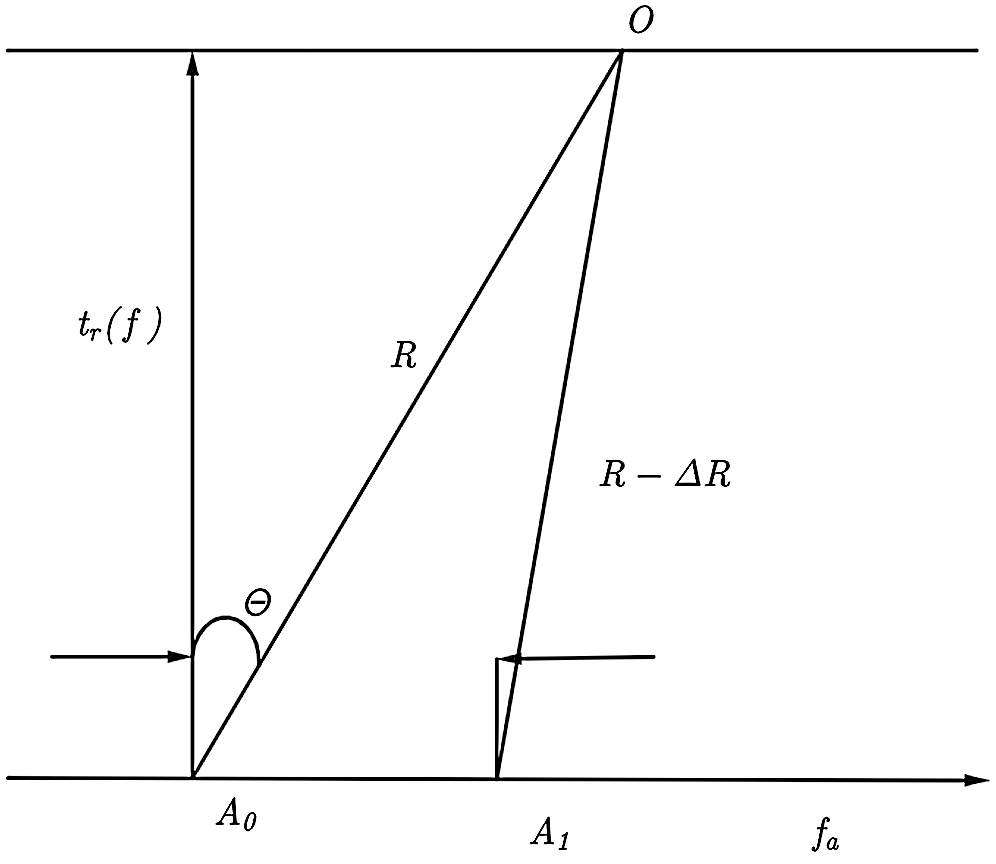
Figure 2: Doppler frequency shift
As shown in Fig. 2, we assume that at point A, the signal frequency is fc, and the angle of point O relative to point A is θ. Its Doppler is
When the signal frequency is converted from fc to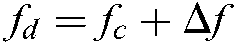 
, its Doppler is
Therefore, at the point fa in the Fig. 2, the frequency of point A1 is the frequency of point fa, and then fa is
Then the instantaneous slant range difference in the Fig. 2 is ΔR, ignoring the high-order term. From the geometric relationship of the Fig. 2, the expression is given by
Therefore, the frequency of the fast time along the range in the Doppler domain is
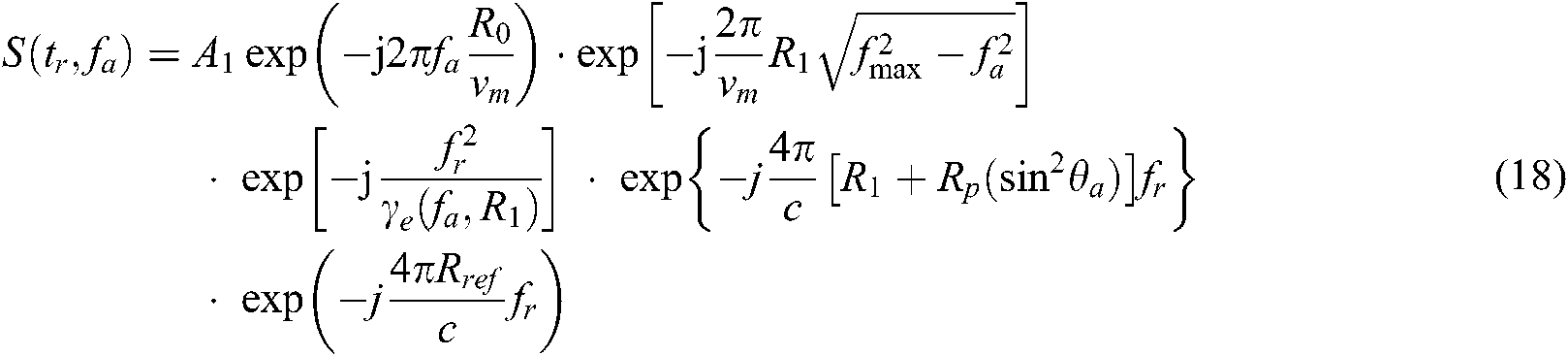
The distance Fourier transform is performed on Eq. (12) and the expression is
Since the reference distance is introduced, the reference distance needs to be compensated, and the compensation phase function is
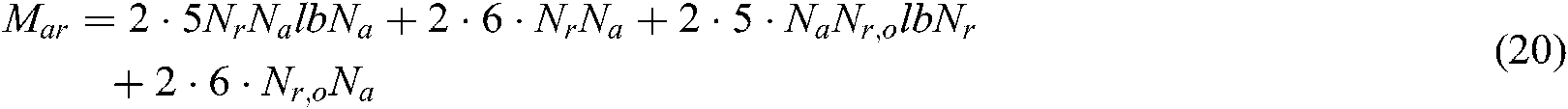
The fourth exponential term in Eq. (12) is generated by the delay of the echo signal in the fast time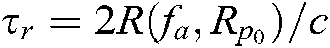 
in the range direction. The range bending at different distances in the imaging scene can be unified into the range bending at the center of the imaging scene. In other words, the spatial variability of the range bending can be ignored. Then, the influence on range migration in the squint mode is
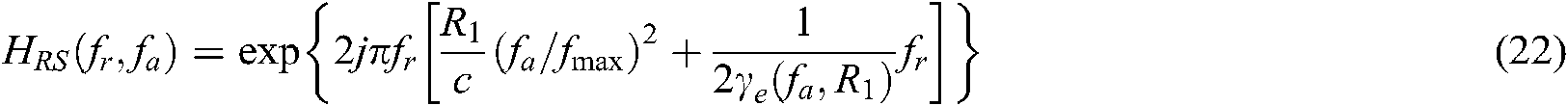
According to Eq. (21), range migration increases with the increase of Angle. The range migration term is calibrated in the range Doppler frequency domain, and the fa value is moved forward by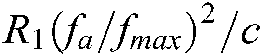 
in the direction of azimuth fast time in the frequency domain. The second pulse compression and two-dimensional decoupling are performed on Eq. (12), and the correction function is
The correction function of Eq. (22) is multiplied by Eq. (18) to complete the second pulse compression and two-dimensional decoupling of the signal. Then the processed signal is processed by inverse Fourier transform in the range direction and pulse compression in the azimuth range. The corresponding matched filtering function is
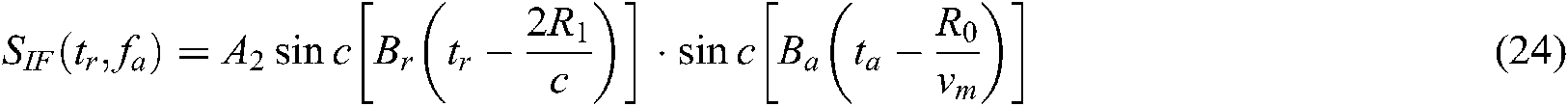
Multiply this function by the decoupled signal and then perform the azimuthal inverse Fourier transform, so that the azimuthal compression is completed. The scene image at this time is
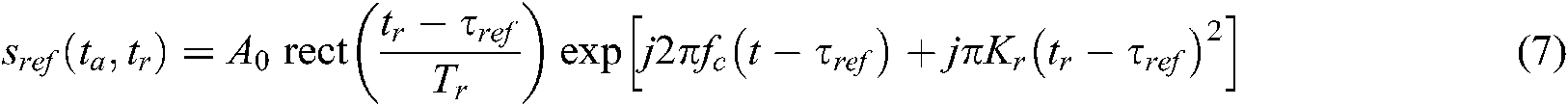
where Br and Ba are azimuth doppler bandwidth and range doppler bandwidth respectively. The complete flow chart of squint FMCW SAR processing is shown as follows:
4 Result Analysis and Discussion
4.1 Calculation Efficiency Analysis
In this section, the computational complexity of the improved algorithm in Section 3.3 is analyzed. The computational cost of a N-point FFT or IFFT is 5 NlbN times of floating-point operation (FLOP), while a reset multiplication is 6 times of FLOP without optimization. As can be seen from Fig. 3, the improved algorithm in this paper has no complex interpolation operation, and all the operations are FFT or phase multiplication, so the total computation amount of this algorithm is where Nr and Na are respectively the range and azimuth sampling points. According to document [26], this algorithm is 40% more efficient than classical R–D algorithm, especially suitable for real-time imaging processing in miniature unmanned equipment.
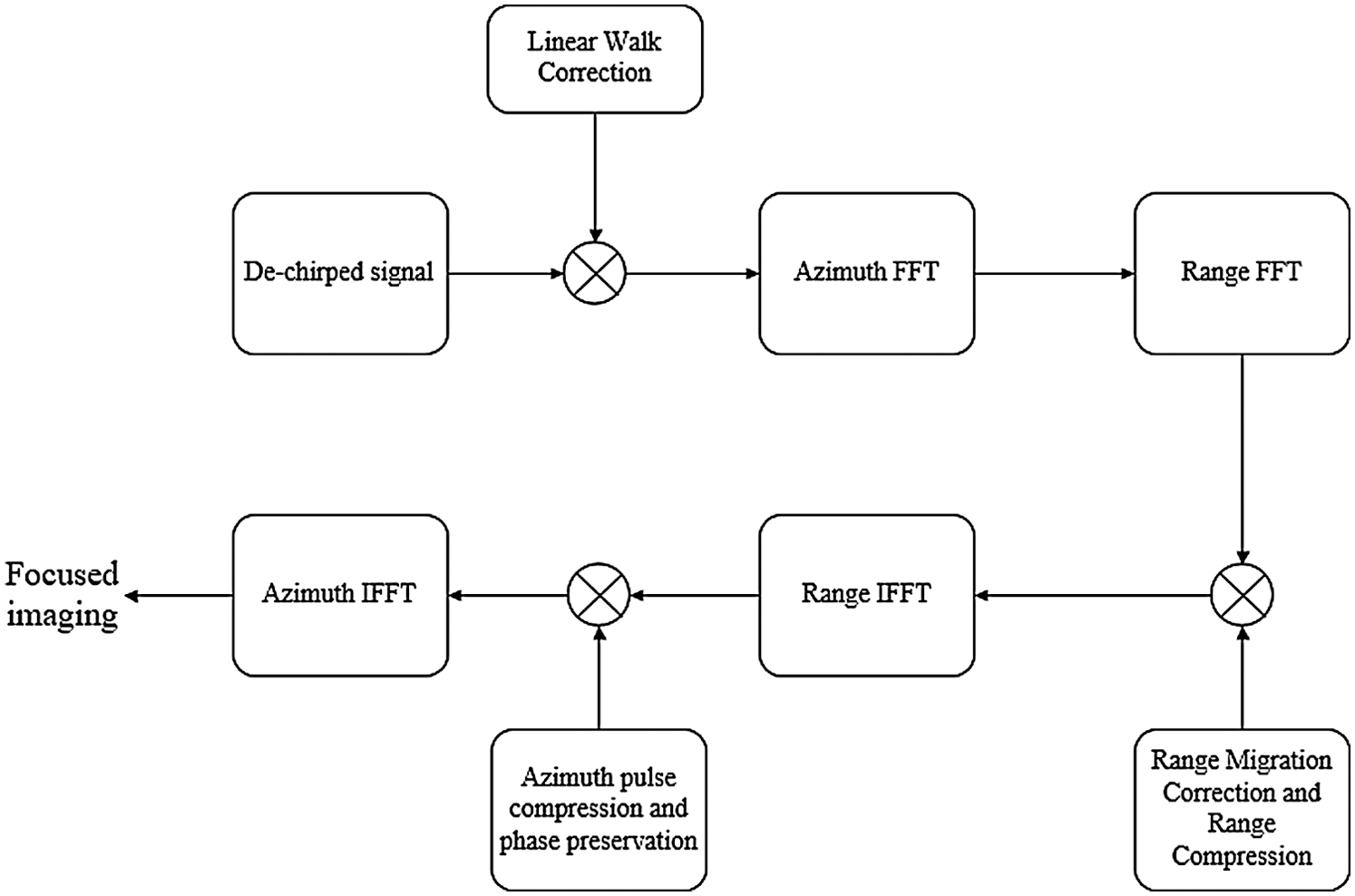
Figure 3: Flow chart of R–D algorithm in squint mode
In order to verify the effectiveness of the proposed improved algorithm, Matlab software is used to simulate the echo signal. The parameters of FMCW SAR system are shown in Tab. 1. The system operates in side-view and strip-mode, with the platform moving in parallel along a line.
Table 1: FMCW SAR system simulation parameters
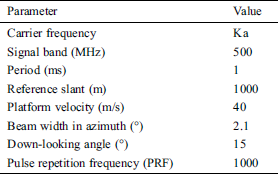
The specific simulation parameters are shown in Tab. 1.
Using the data in Tab. 1, FMCW SAR is simulated when the squint angle is 15 degrees. The simulation results are as follows:
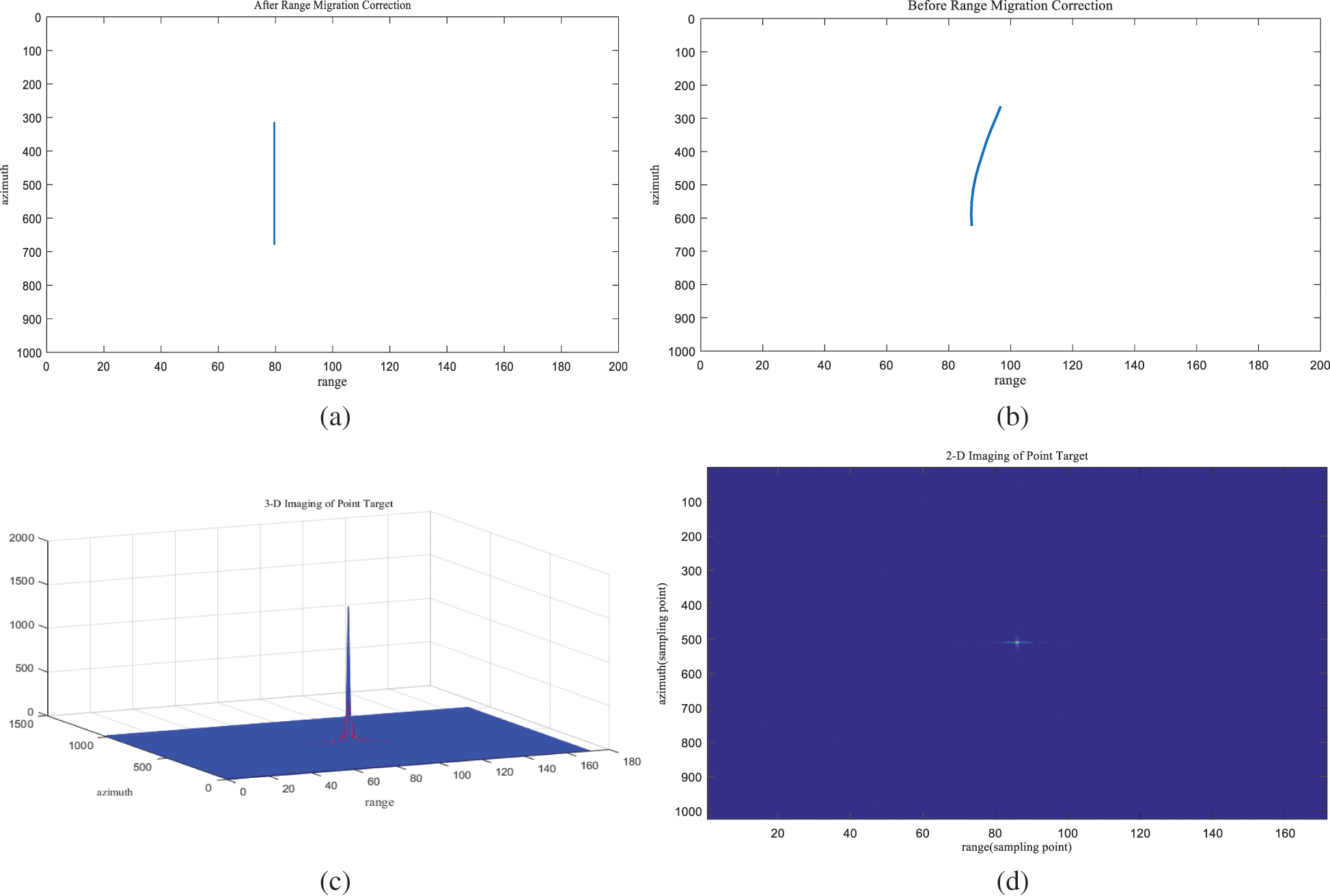
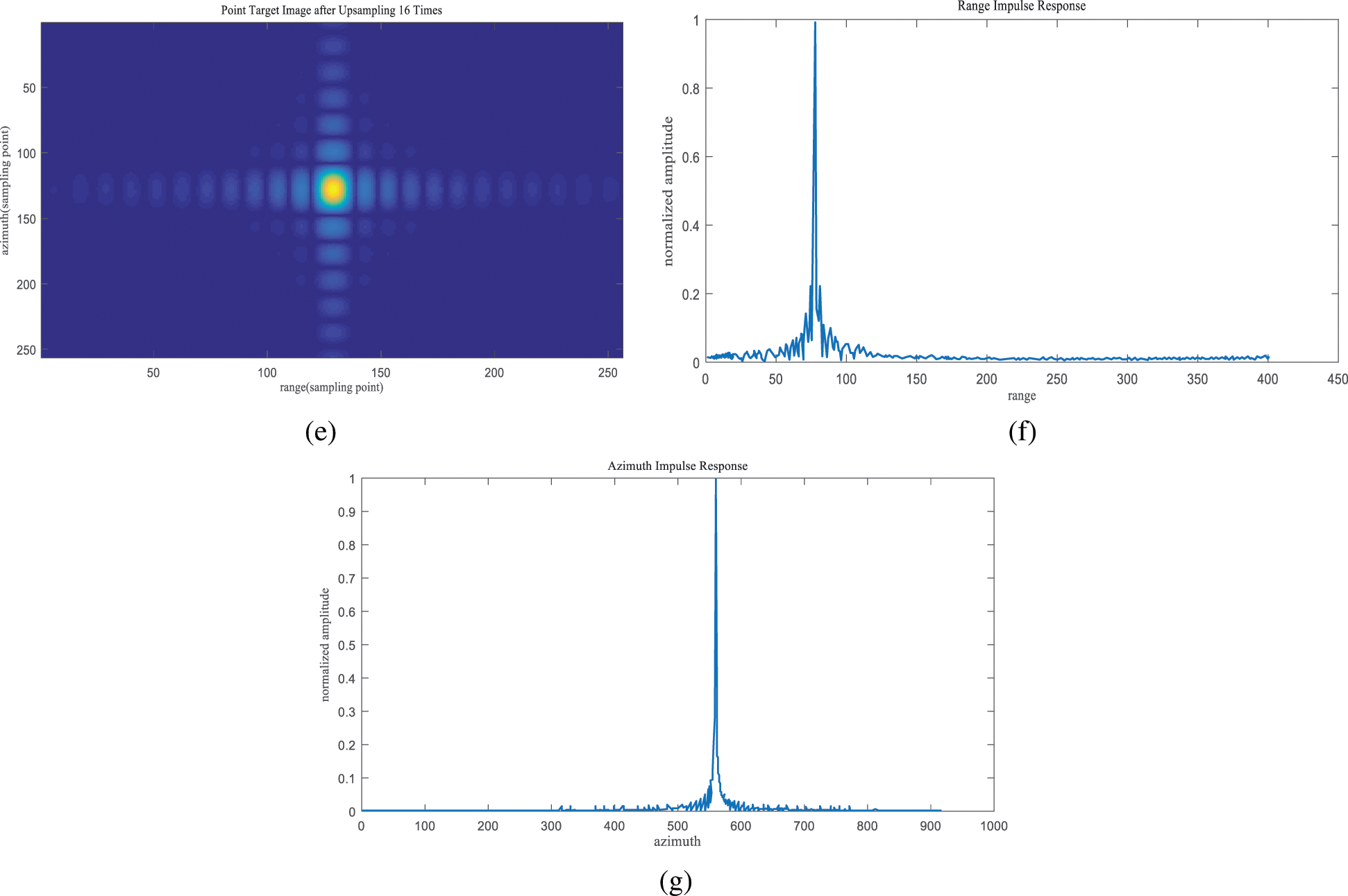
Figure 4: Improved R–D algorithm for point-target imaging results. (a) After range migration correction. (b) Before range migration correction. (c) 3-D imaging of point target. (d) 2-D imaging of point target. (e) Point target image after upsampling 16 times. (f) Normalization amplitude of Range signal. (g) Normalized amplitude of azimuth signal
The simulation results of the above simulation experiments under the condition of 15 degree squint angle prove that the improved algorithm achieves good simulation results. Fig. 4(b) is the corrected point of range migration. It can be seen that the range migration curve has been well compressed and ‘leveled.’ The elevation pattern of point target in Fig. 4(e) has clear main lobes and symmetrical side lobes, and presents an ideal “cross” shape, which can be reliably distinguished. Tab. 2 gives the evaluation of point target imaging results.
Table 2: Evaluation of imaging results of point targets
As can be seen from Tab. 2, both the peak sidelobe ratio (PSLR) and the integral sidelobe ratio (ISLR) of the imaging indicators are in line with the actual situation. The above results indicate that the point target can be well focused under the improved algorithm.
In order to explore the squint imaging characteristics of FMCW SAR, the relationship between echo signal and instantaneous slant range is analyzed, and the range Doppler algorithm flow is optimized. Starting from the squint geometric model of FMCW SAR, the echo signal model, the Doppler characteristics of the echo signal and the operational efficiency of the algorithm are analyzed by mathematical deduction and analysis. Finally, the following conclusions are drawn:
First, the influence of linear walk in squint mode on FMCW SAR imaging quality cannot be neglected. As the squint angle increases, the azimuth spectrum is no longer centered symmetrical with respect to Doppler.
Second, the range curvature term in range migration is inversely proportional to the squint angle and directly proportional to the range walk.
Third, when range migration is corrected in the frequency domain, the interpolation operation of the algorithm can be replaced by FFT transform and phase multiplication, which can effectively improve the operation efficiency.
By analyzing the geometric model of FMCW SAR imaging and establishing the signal echo model, an improved range Doppler algorithm in squint mode is proposed, which provides an effective and feasible solution to meet the real-time imaging needs of small airborne radar. Due to the lack of measured data, the motion of the aircraft has a certain impact on the imaging. Therefore, in the future research, the combination of the motion compensation of the aircraft and the echo signal model will be revised, and the recognition of the imaging characteristics of FMCW SAR in squint mode will be more accurate.
Funding Statement: The author(s) received no specific funding for this study.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
1. J. Ting, D. Oloumi and K. Rambabu. (2018). “FMCW SAR system for near-distance imaging applications—practical considerations and calibrations,” IEEE Transactions on Microwave Theory and Techniques, vol. 66, no. 1, pp. 450–461, . DOI 10.1109/TMTT.2017.2706693. [Google Scholar]
2. K. A. C. de Macedo, S. Placidi and A. Meta. (2019). “Bistatic and monostatic InSAR results with the metasensing airborne SAR system,” in 2019 6th Asia–Pacific Conf. on Synthetic Aperture Radar (APSARXiamen, China, pp. 1–5. [Google Scholar]
3. X. Hu, C. Ma, R. Hu and T. S. Yeo. (2018). “Imaging for small UAV-borne FMCW SAR,” Sensors (Basel), vol. 19, no. 1, pp. pp.–87. [Google Scholar]
4. G. Jia, M. Buchroithner, W. Chang and X. Li. (2015). “Simplified real-time imaging flow for high-resolution FMCW SAR,” IEEE Geoscience and Remote Sensing Letters, vol. 12, no. 5, pp. 973–977, . DOI 10.1109/LGRS.2014.2370733. [Google Scholar]
5. C. Gu, W. Chang, X. Li, G. Jia and X. Luan. (2017). “A new distortion correction method for FMCW SAR real-time imaging,” IEEE Geoscience and Remote Sensing Letters, vol. 14, no. 3, pp. 429–433, . DOI 10.1109/LGRS.2017.2647962. [Google Scholar]
6. Y. A. Su, W. Liu, H. Feng and B. P. Ng. (2017). “Study of multi-rotor UAV SAR processing,” in 2017 IEEE Radar Conf. (RadarConfSeattle, WA, pp. 226–232. [Google Scholar]
7. Z. Wang, Y. Li, S. Shao, S. Li and J. Xiao,. (2018). et al., “Improved range doppler algorithm based on squint FMCW-SAR,” in 2018 12th Int. Conf. on Signal Processing and Communication Systems (ICSPCSCairns, Australia, pp. 1–5. [Google Scholar]
8. V. Gowrishankar and K. Venkatachalam. (2019). “High precision SAR ADC using CNTFET for internet of thing,” Computers Materials & Continua, vol. 60, no. 3, pp. 947–957, . DOI 10.32604/cmc.2019.07749. [Google Scholar]
9. Z. Abidin and A. Munir. (2016). “Development of FMCW SAR on L-band frequency for UAV payload,” in 2016 10th Int. Conf. on Telecommunication Systems Services and Applications (TSSADenpasar, pp. 1–5. [Google Scholar]
10. H. Bi, J. Wang and G. Bi. (2019). “Wavenumber domain algorithm-based FMCW SAR sparse imaging,” IEEE Transactions on Geoscience and Remote Sensing, vol. 57, no. 10, pp. 7466–7475, . DOI 10.1109/TGRS.2019.2913761. [Google Scholar]
11. Y. Li and S. OuYoung. (2015). “Focusing bistatic FMCW SAR signal by range migration algorithm based on fresnel approximation,” Sensors, vol. 15, no. 12, pp. 32123–32137, . DOI 10.3390/s151229910. [Google Scholar]
12. S. Tebaldini, F. Rocca, A. Meta and A. Coccia. (2015). “A processing driven approach to airborne multi-baseline SAR tomography,” in 2015 IEEE Int. Geoscience and Remote Sensing Sym. (IGARSSMilan, pp. 2935–2938. [Google Scholar]
13. R. Wang, O. Loffeld, H. Nies, S. Knedlik and M. Hagelen,. (2010). et al., “Focus FMCW SAR data using the wavenumber domain algorithm,” IEEE Transactions on Geoscience and Remote Sensing, vol. 48, no. 4, pp. 2109–2118, . DOI 10.1109/TGRS.2009.2034368. [Google Scholar]
14. A. Ribalta. (2011). “Time-domain reconstruction algorithms for FMCW-SAR,” IEEE Geoscience and Remote Sensing Letters, vol. 8, no. 3, pp. 396–400, . DOI 10.1109/LGRS.2010.2078486. [Google Scholar]
15. S. Palm, A. Wahlen, S. Stanko, N. Pohl and P. Wellig,. (2014). et al., “Real-time onboard processing and ground based monitoring of FMCW-SAR videos,” in EUSAR 2014 10th European Conf. on Synthetic Aperture Radar, pp. 1–4. [Google Scholar]
16. X. Liu, W. Chang and Y. Guan. (2016). “Study of the squint imaging algorithm for FMCW SAR,” in 2016 Progress in Electromagnetic Research Sym. (PIERSShanghai, pp. 1384–1388. [Google Scholar]
17. C. F. Gu, W. G. Chang, X. Y. Li and Z. H. Liu. (2015). “Multi-core DSP based parallel architecture for FMCW SAR real-time Imaging,” Radioengineering, vol. 24, no. 4, pp. 1084–1090, . DOI 10.13164/re.2015.1084. [Google Scholar]
18. Y. J. Cai, X. K. Zhang and J. S. Jiang. (2016). “A study on system design and imaging of millimeter wave, FMCW SAR,” Modern Radar (China), vol. 38, no. 2, pp. 1–5. [Google Scholar]
19. C. W. Qu, Y. Wang, Y. Huang and B. Deng. (2010). “FMCW SAR imaging based on fractional fourier transformation,” Fire Control & Command Control (China), vol. 35, no. 6, pp. 43–45. [Google Scholar]
20. L. Y. Chen, Y. Qu, J. Zhang and J. Lu. (2015). “Range resolution improvement of FMCW SAR range doppler algorithm on high-speed motion platform,” Modern Radar (China), vol. 37, no. 11, pp. 32–36. [Google Scholar]
21. Y. L. Liu, Y. J. Cai, X. K. Zhang and J. S. Jiang. (2016). “Design and realization of LFMCW SAR system,” Remote Sensing Technology and Application (China), vol. 31, no. 2, pp. 255–259. [Google Scholar]
22. L. Y. Wang, H. J. Zhao and C. H. Du. (2015). “Motion compensation based on wavenumber domain algorithm for FMCW SAR,” Journal of Projectiles, Rockets, Missiles and Guidance (China), vol. 35, no. 4, pp. 162–166. [Google Scholar]
23. K. C. Fu, Z. X. Zhang, Y. H. Xie and Y. Qu. (2016). “A compensation method for improving range resolution of FMCW SAR,” Electronics Optics & Control (China), vol. 23, no. 12, pp. 23–26. [Google Scholar]
24. L. Wang, Y. R. Yue and Q. Xiong. (2017). “A FMCW SAR imaging algorithm capable of exploiting doppler resolution,” Journal of Signal Processing (China), vol. 33, no. 7, pp. 961–969. [Google Scholar]
25. B. Wang, Z. Hu, W. Guan, Q. Liu and J. Guo. (2015). “Study on the echo signal model and R–D imaging algorithm for FMCW SAR,” in IET Int. Radar Conf. 2015, Hangzhou, pp. 1–6. [Google Scholar]
26. G. Cumming and F. H. Wong. (2005). Digital processing of synthetic aperture radar data: Algorithms and implementation. Norwood, MA: Artech House, pp. 315–316. [Google Scholar]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |