DOI:10.32604/iasc.2021.01008
| Intelligent Automation & Soft Computing DOI:10.32604/iasc.2021.01008 | |
| Article |
A Fuzzy-Based Bio-Inspired Neural Network Approach for Target Search by Multiple Autonomous Underwater Vehicles in Underwater Environments
School of Physics and Electronic Electrical Engineering, Huaiyin Normal University, Huaian, 223300, China
*Corresponding Author: Xiang Cao. Email: cxeffort@126.com
Received: 14 October 2020; Accepted: 06 November 2020
Abstract: An essential issue in a target search is safe navigation while quickly finding targets. In order to improve the efficiency of a target search and the smoothness of AUV’s (Autonomous Underwater Vehicle) trajectory, a fuzzy-based bio-inspired neural network approach is proposed in this paper. A bio-inspired neural network is applied to a multi-AUV target search, which can effectively plan search paths. In the meantime, a fuzzy algorithm is introduced into the bio-inspired neural network to make the trajectory of AUV obstacle avoidance smoother. Unlike other algorithms that need repeated training in the parameters selection, the proposed approach obtains all the required parameters that do not require learning and training. And the model parameters are not sensitive. The simulation and experiment results show that the proposed algorithm can quickly and security search targets in the complex obstacle environments. Compared with the PSO (Particle Swarm Optimization) algorithm, the simulation results show that the proposed algorithm can control a multi-AUV to complete multi-target search tasks with higher search efficiency and adaptability. At the same time, the fuzzy obstacle-avoidance improves the search trajectory smoothness.
Keywords: Target search; multi-AUV; fuzzy approach; bio-inspired neural network
Multi-AUV (multiple autonomous underwater vehicle) systems have many advantages over a single AUV: 1) By appropriately decomposing tasks, multi-AUVs can accomplish different sub-tasks in parallel, thereby increasing work efficiency [1–2]; 2) The members of the system can be designed to “experts” who complete a task, not “generalists” [3–4]; 3) Through the cooperation between members, the algorithm can increase the redundancy and robustness of the scheme [5–6]. It can provide more solutions and reduce system cost and complexity. Because of these advantages, many scholars have used multi-AUV systems for target search tasks. A large number of multi-AUV target search strategies are proposed.
The target search based on a behavioral strategy is a standard method in early studies. The behavioral approach is a heuristic method that endows a robot with simple behavior sets, such as searching along boundaries, and avoiding obstacles. Target search tasks in complex environments can be accomplished through a hierarchical combination of these simple behaviors [7–8]. Balch et al. [9] adopted a behavior-based heuristic approach to multi-robot target search tasks to solve map coverage problems. Magid et al. [10] analyzed the advantages of behavioral strategy from the perspective of cost and benefit. The robots based on this strategy do not need expensive positioning sensors, do not need to use limited computing resources to calculate the precise positions of robots, so the cost of the robot is reduced. This behavior-based search strategy does not require the advance selection of the search path. Instead, it focuses on the overall behavior of multiple robots by randomly selecting directions. However, the algorithm does not guarantee the integrity of the map search, nor does it ensure no duplication, resulting in an inefficient search. And there is no collaboration between the robots, which violates the original purpose of using multiple robots for a target search [11–12].
To increase cooperation among multiple robots, Yamauchi [13] proposed a boundary-based distributed multi-robot target search strategy. The algorithm defines the boundary as that between the known open area and the unsearched area. During the search process, each robot continuously selects the nearest boundary point for environmental search until all reachable areas are searched, and the task is completed. Due to the limited coordination of information between robots in this strategy, some robots may move to the same boundary, causing collisions and repeated searches, which is inefficient. To further enhance the collaboration of multi-AUVs, Yoon et al. [14] proposed a synchronous search algorithm that can achieve large-scale target search. AUVs exchange data through regular rendezvous to perform a collaborative search of targets. The algorithm has redundancy error capability, and after some AUV failures, the search task can be completed. However, this algorithm only studies the ideal two-dimensional environment without considering current and obstacles, which reduces its practicability [15].
To improve the efficiency of the target search, Zolt et al. [16] proposed a multi-robot target search algorithm based on a market economy mechanism. A robot shares target information and calculates the cost of reaching the target based on the local map. The algorithm is distributed, robust, and efficient. The cooperation of robots is realized by explicit communication, which increases resource consumption. The performance of the target search is significantly diminished when transmission is interrupted. Ferranti et al. [17] proposed a method based on multi-robot self-search in an unknown environment. This algorithm constructs indirect communication between multiple robots. The method avoids disadvantages such as unreliability. The process does not require a robot to have advance environmental knowledge, and can coordinate the movement of multiple robots in terrain with different topological features. Cai et al. [18] and Hashemi et al. [19] proposed a distributed self-organizing multi-robot target search algorithm based on particle swarm optimization (PSO). The method transforms the process of searching for the optimal solution in the abstract solution space to the search of the unsearched area in the new map to realize the target search for unknown environments [20]. These three methods are not suitable for a large-scale target search.
To improve the efficiency of a multi-AUV target search in complex environments, Cao et al. [21] combined a bio-inspired neurodynamic model and velocity vector synthesis algorithm for multi-AUV target search in current settings. This method can not only complete the search task but can automatically avoid obstacles and overcome the influence of current on AUV navigation [22]. However, the algorithm does not consider security when avoiding obstacles and does not apply to environments with multiple barriers.
This paper studies the safety navigation problem of multi-AUV target searching. To improve the safety of an AUV in obstacle avoidance, a fuzzy-based bio-inspired neural network approach (FBNN) is proposed. The bio-inspired neural network (BNN) algorithm plans an effective search path for an AUV. When the AUV meets obstacles, the fuzzy algorithm improves its navigation path. The improved trajectory is more reasonable and secure. A fuzzy algorithm makes the trajectory of AUV obstacle avoidance smoother. Simulation results show that the proposed approach can control multi-AUVs to achieve the search of multiple targets with higher efficiency and adaptability compared to PSO. At the same time, fuzzy obstacle-avoidance improve the security of the AUV trajectory. Experimental results show that the proposed algorithm can be applied in real underwater environments.
The advantages of the algorithm can be summarized as follows: 1) The method’s parameters do not require learning and training, and they are not sensitive; 2) Fuzzy obstacle-avoidance improves track smoothness; and 3) a real-time, safety-aware navigation paradigm guides the AUV locally to plan more reasonable and safer trajectories.
The rest of this paper is organized as follows. The principles of the proposed algorithm are given in Section II. Simulations of various situations are described in Section III. A pool experiment is outlined in Section IV. Section V provides our conclusions.
This paper proposes a fuzzy-based bio-inspired neural network approach to realize a real-time multi-AUV target search task in an underwater environment with obstacles. A bio-inspired neural network topologically organized is constructed to represent the dynamic environments. Through the model’s dynamic neural activity landscape, the target globally attracts the AUV, while the obstacles locally push the AUV away to avoid a collision. The AUV generates its search path to the targets autonomously by a steepest gradient descent rule. When encountering obstacles, AUVs move using the fuzzy obstacle-avoidance method. The flowchart of the approach is shown in Fig. 1.
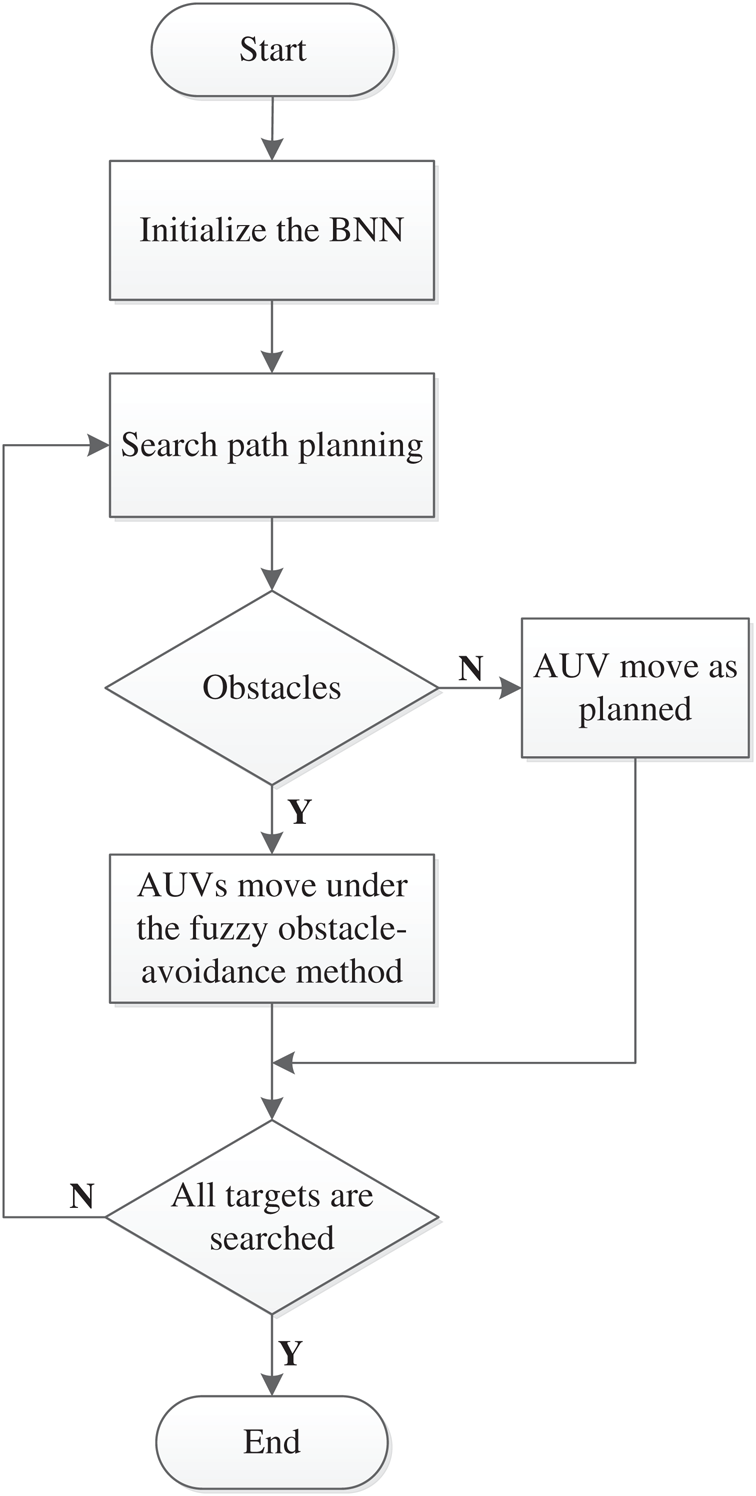
Figure 1: Flowchart of multi-AUV target search
2.1 Bio-Inspired Neural Network
A bio-inspired neural network in underwater environments is established (as shown in Fig. 2), in which a neuron represents a grid cell. The information of the grid cell is described by neural activities. Each neuron is connected to adjacent ones to form a network for their transmission of activity (for simplicity, only connections of the central neuron are shown, and those of other neurons are omitted).
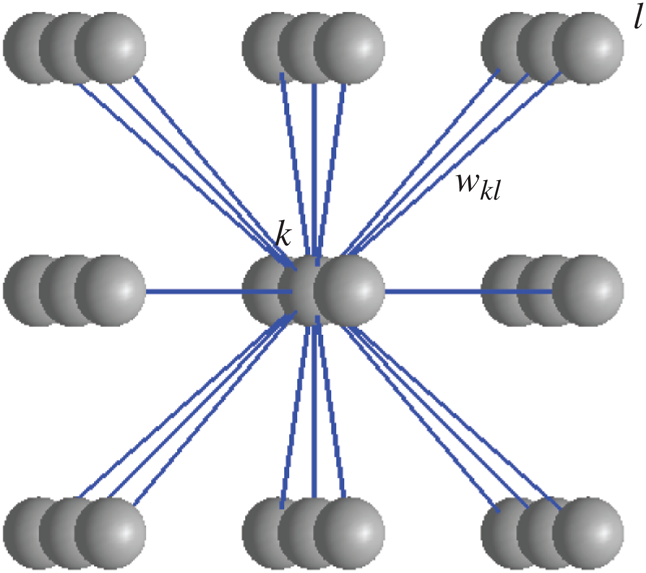
Figure 2: Diagram of neural network
The change rule of neuronal activity in the neural network is expressed as [23]:
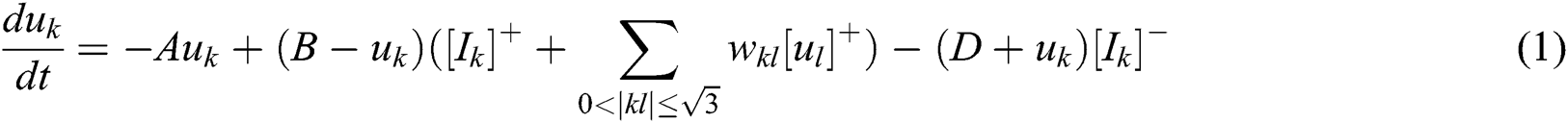
where uk represents the activity value of the k-th neuron, ul represents the activity value of other neurons connected to the k-th neuron, and Ik represents the grid cell signal’s input defined as [24]:
A, B, and D are positive constants; A reflects the passive decay rate of neuron k’s activity; B and D are upper and lower limits of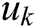 
, i.e., 
. 
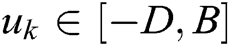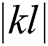is the Euclidean distance between neuron k and its neighbor l on the 3D space,
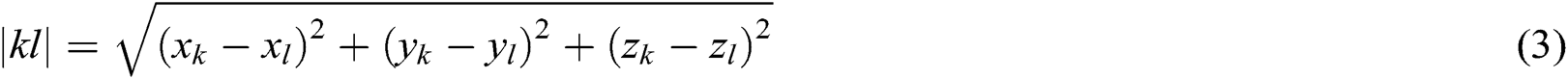
where (xk, yk, zk) and (xl, yl, zl) are the coordinates of the k-th and l-th neurons, respectively, in the 3D coordinate system.
In Eq. (1), wkl is the connection weights between neuron k and its neighbor l, which can be defined as [25]:
where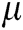 
is a positive constant, and generally, 
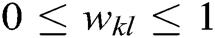. As the connections between neurons are not directional, the connection weight coefficients are symmetric, i.e., 
.
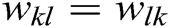It can be seen from Eq. (1) that the activity values of the target neurons are positive, and those of the obstacle neurons are negative. That means that some excitation signals come from external inputs, and others from internal incremental gains of interconnecting neurons. If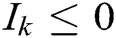 
, then 
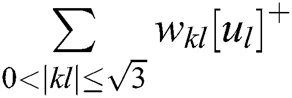, which means there is no external input for neuron k, and all its excitation signals are transmitted through the neuronal network. In contrast, 
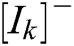means that all the inhibitory inputs for signals k are external. Therefore, the excitation signals are transmitted between neurons. The value of the positive activity of neurons in a neural network has a global effect while the inhibitory signals do not transmit and the negative activity of neurons has only a local effect.
2.2 3D Search Path Planning Model
We transform the search path planning problem of an AUV to one of finding its next navigation position. Only by accurately finding the position can an AUV quickly find unknown targets and avoid collisions with obstacles. In this regard, the next navigation position of an AUV must be determined in conjunction with the specific dynamic environment and the previous position and current position of the AUV. Hence, the research of AUV search path planning is transformed to the study of neuron activity output values in the neural network structure. The navigation position of an AUV at the next moment is determined by the distribution of neuron activity output values. In the target search mission, all of an AUVs movements are guided by the dynamic activity landscape of the neural network. The activity of each neuron is obtained by a shunting Eq. (1). The influence of the targets and obstacles, the state workspace varies according to the dynamics of the neural network. The motion of the AUV is determined by the landscape of the dynamic activity of the topologically organized neural network. An AUV's search path selection strategy can be written as [26]:
where M represents the number of neurons adjacent to the k-th neuron, Pn represents the AUV’s location at the next moment in the map, and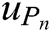 
is the highest activity value of the k-th neuron’s neighbors. When an AUV selects a path, it compares the activity value of the neuron of its current location with its neighbors and chooses the one with the largest value as the next step. Repeating this performance, the AUV keeps moving towards the targets.
Fuzzy obstacle-avoidance rules can provide different line speeds and angular velocities for a single AUV when facing obstacles. These rules can improve the smoothness of the AUV trajectory.
The structure of the fuzzy control module embedded in the control system is shown in Fig. 3. It has four main parts [27]:
(1) The fuzzification interface converts input to membership and compares it to rules in the rule library.
(2) The rule base contains rules based on common knowledge and experience.
(3) Decision logic evaluates the current situation, selects the appropriate fuzzy rules, and converts the fuzzy input to fuzzy output.
(4) The defuzzification interface converts the fuzzy output to a non-fuzzy instruction that the AUV recognizes.
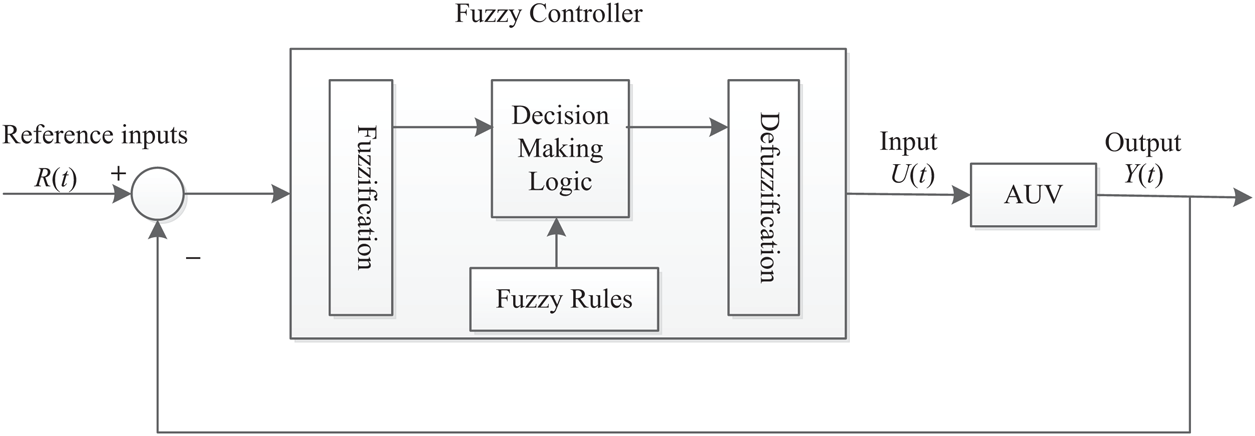
Figure 3: Fuzzy controller architecture
The fuzzy controller has the characteristics of intelligence and real-time performance. The output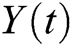 
of the system is fed back to the fuzzy controller and compared to the reference input 
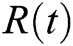. The input 
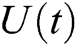is extracted by the fuzzy controller to meet the requirements of the underwater robot. The inputs and outputs of the fuzzy controller are shown in Fig. 4.
Figure 4: Fuzzy controller
There are two fuzzy inputs,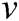 
and 
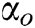in the fuzzy controller, where 
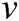is the linear degree of freedom of the AUV, and 
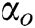is the angle of attack between the AUV and the obstacle. This design represents line velocity fuzzy terms as VS (velocity small), VM (velocity middle), and VL (velocity large). The angular fuzzy terms are expressed as ANS (angle negative small), ANL (angle negative large), APS (angle positive small), and APL (angle positive large). The membership functions of the above three fuzzy inputs are shown in Fig. 5 [28].
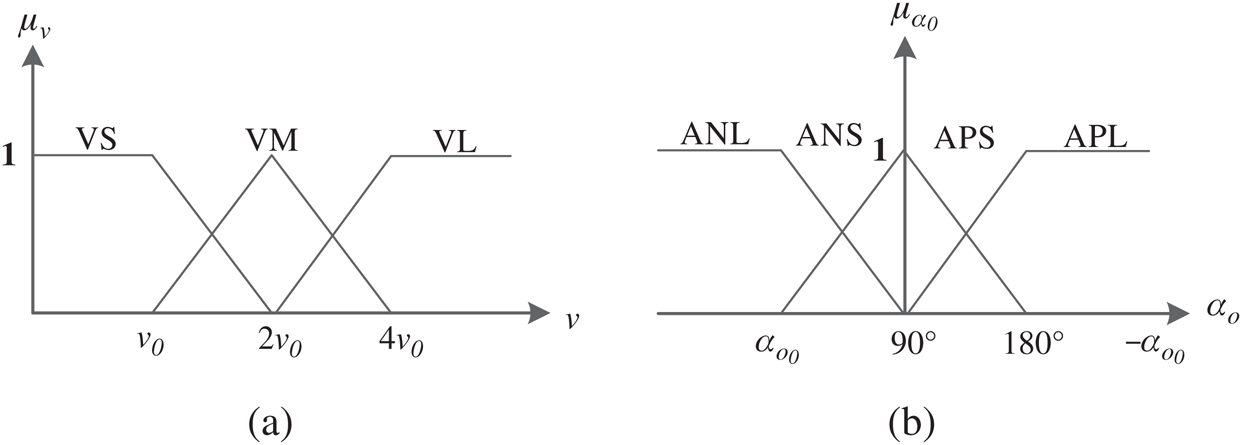
Figure 5: Membership functions of inputs (a) Membership function of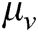 
(b) Membership function of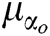 
The AUV’s motion is adjusted by the output command of the fuzzy controller, which has two fuzzy outputs:,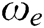 
is the desired curve speed of the AUV, and 
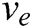is its desired line speed. To effectively avoid obstacles, 
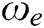has five fuzzy items, represented as NL (negative large), NS (negative small), Z (zero), PS (positive small), and PL (positive large). The fuzzy terms of 
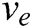are similarly represented as VS (velocity small), VM (velocity middle), and VL (velocity large), as shown in Fig. 6. For example, if the AUV is required to turn right, then 
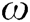would has the fuzzy term PS or PL, depending on the input [29].
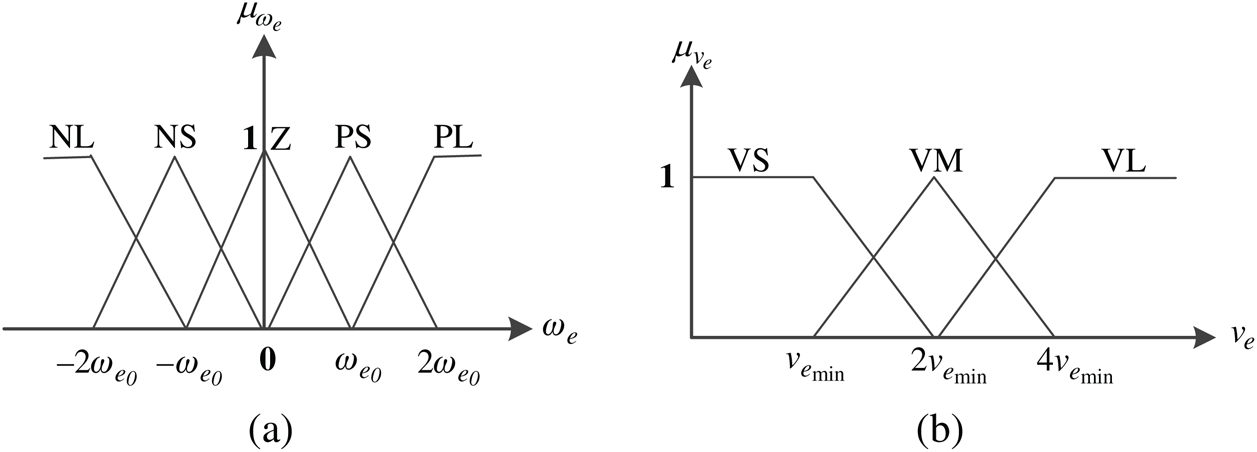
Figure 6: Membership functions of outputs (a) Membership function of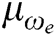 
(b) Membership function of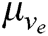 
The center of gravity algorithm is used for defuzzification, and the fuzzy output is converted to a motion command output to control the motion of the AUV. The fuzzy controller can effectively guide the AUV to avoid obstacles and improve the motion track [30].
The main task of the rule is to make the system have a reasonable output. The rules in Tab. 1 apply to all possible AUV obstacle avoidance scenarios. Each “IF” condition contains sub-conditions of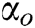 
and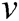 
, and all fuzzy sets basically come from experience and common knowledge.
Table 1: Rulebase for obstacle-avoidance
The practicability of the algorithm was verified by simulating the 3D multi-AUV target search under static and dynamic conditions on MATLAB R2011a. The underwater search space in the simulation experiment was set to 100 × 100 × 100. AUVs, targets, and obstacles were randomly distributed in the search space before the search task began. An AUV only knew the number of targets and environmental boundaries. AUVs and targets could move within the search space. AUVs moved according to the proposed algorithm, and the target moved randomly before discovery by the AUV. When all the targets were found, the multi-AUV target search ended.
To test the performance of the proposed algorithm, the search for static targets by multiple AUVs was simulated. The simulation consisted of three targets, three AUVs, and several obstacles in underwater environments. The targets had initial positions (41, 88, 76), (74, 72, 18), and (94, 58, 82), and three AUVs had initial positions (98, 34, 25), (32, 11, 97), and (38, 94, 27), as shown in Fig. 7. At the beginning of the search task, since the target affected the entire search area through neural transmission, the activity of each neuron could be derived from the shunt Eq. (1). When the AUV selected its path, it compared the activity value of the neuron at its current location to its neighbors and selected the neuron with the largest value as the next step. In the proposed algorithm, the target and obstacles respectively are the excitation and suppression of the neural network. Repeating the path selection, the AUV moved toward the target, and could bypass obstacles to avoid collisions. At the same time, through fuzzy obstacle-avoidance, the AUV search path became smoother, and the AUV made no sharp turns when the avoiding obstacles. As shown in Fig. 8, the static targets T1, T2, and T3 were found by AUVs R3, R1, and R2, respectively, which showed that the proposed algorithm could realize the joint search of multiple static targets.
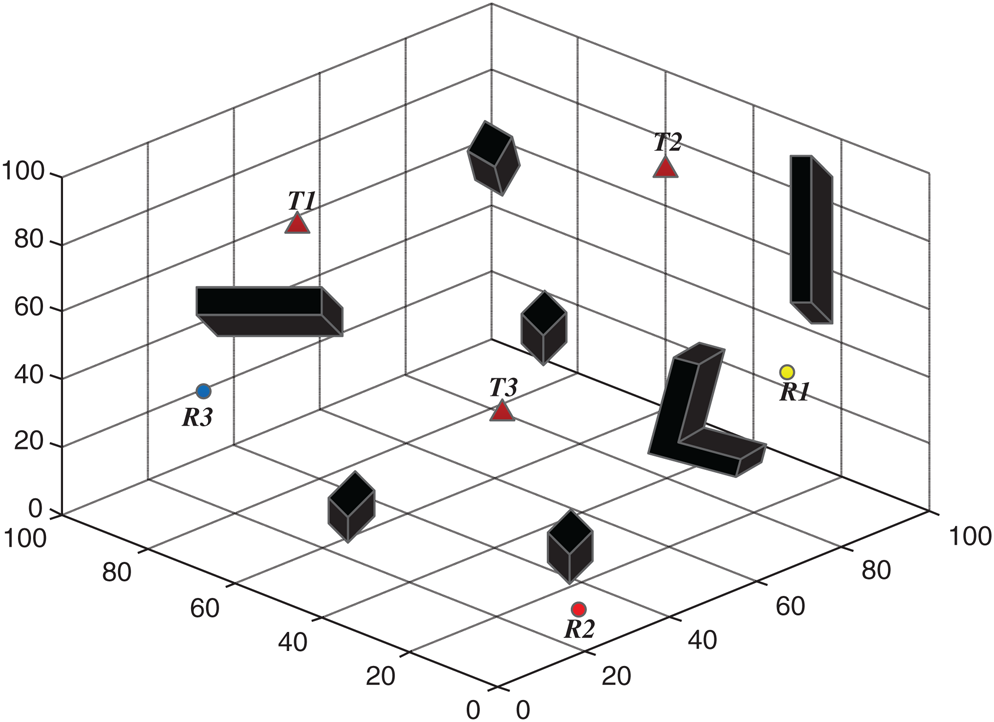
Figure 7: Initial state of static targets
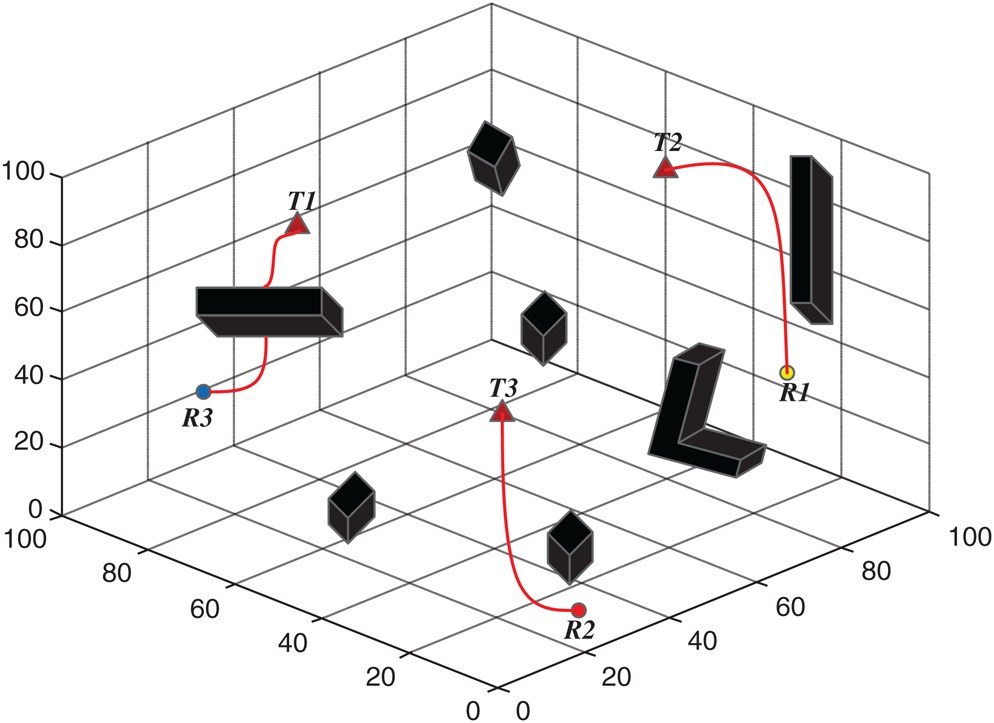
Figure 8: Search process with static targets
Multiple AUVs searched for multiple dynamic targets in the second simulation. Dynamic targets undoubtedly bring more difficulties to the search task. But the proposed algorithm solved the problem. Due to pre-definition, the activity values of the neurons in the target were positive, and the target globally attracted AUVs through the dynamic neural activity landscape of the model. It can be known from Eq. (1) that when a target’s position changes, the activity values of the adjacent neurons of the AUV will change accordingly. By changing the activity values of neighboring neurons, each AUV can obtain real-time information on the change in the position of a moving target. The algorithm can continuously adjust the search path according to the evolution of adjacent neural activity values.
Figs. 9 and 10 show the process of three AUVs searching for three dynamic targets. A target moves randomly, and an AUV moves according to the proposed algorithm. Fig. 9 shows the initial positions of AUVs, targets, and obstacles. Fig. 10 shows the trajectory of the search targets, where the dotted and solid lines respectively indicate the moving track of the target and the moving trajectory of the AUV. The simulation results showed that the algorithm realized the joint search for multiple dynamic targets.
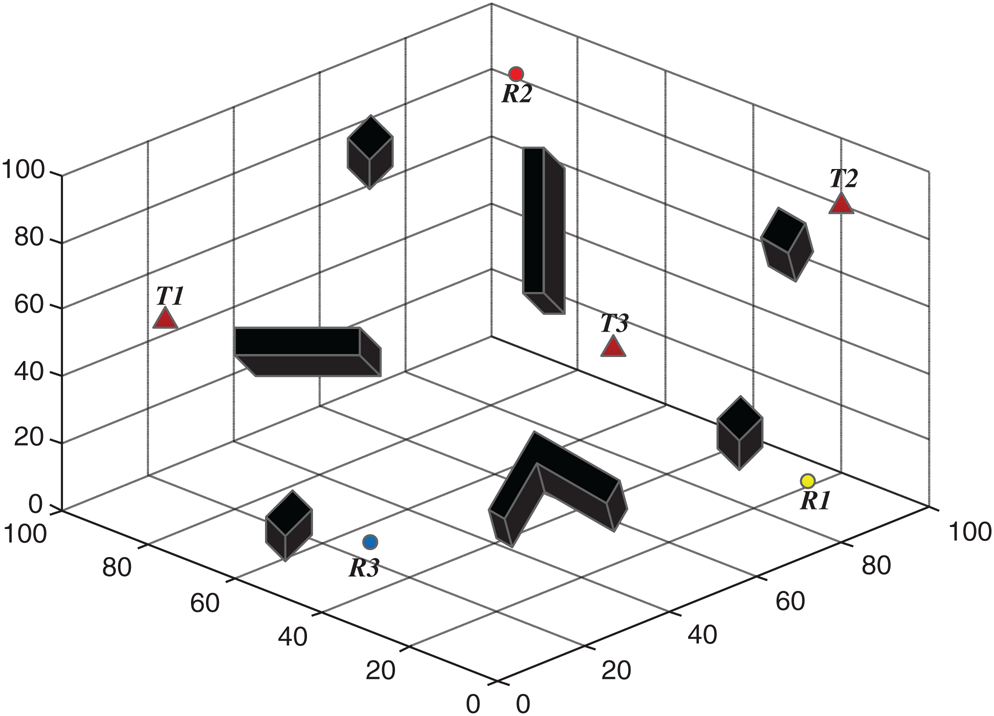
Figure 9: Initial state of dynamic targets
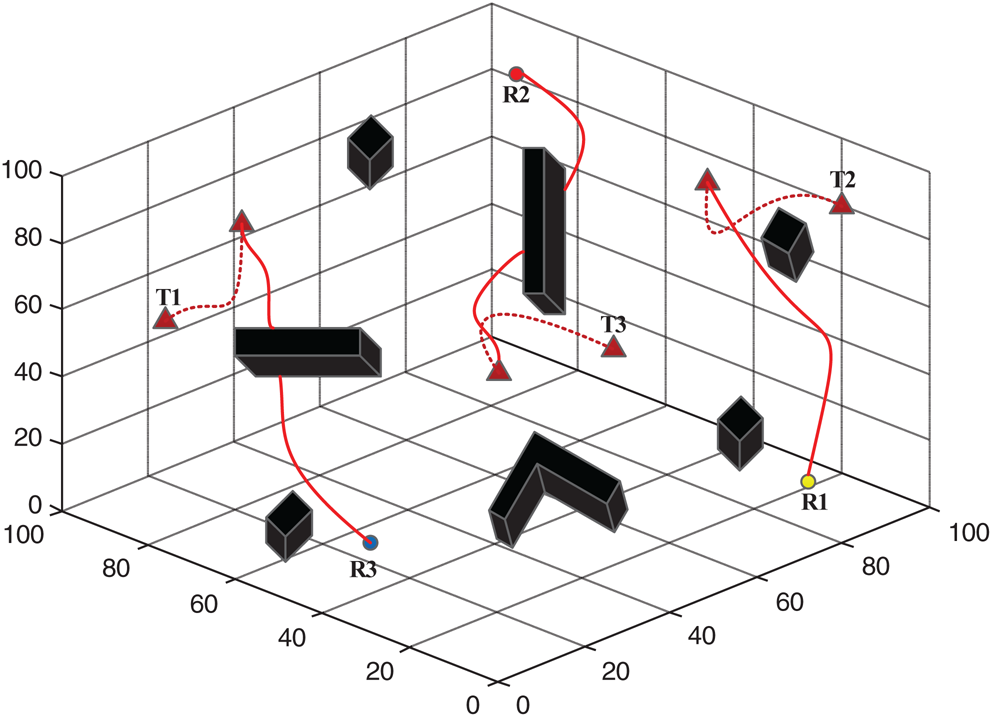
Figure 10: Search process with dynamic targets
An AUV may experience mechanical failure when searching in real 3D underwater environments. In the case of partial AUV failure, whether the target search can be completed is an important indicator to measure the fault tolerance of the algorithm. We simulated a target search in the event of an AUV failure. In the simulation environments, four AUVs were to search for three dynamic targets. Initially, the four AUVs searched for targets. After a while, an AUV failed and other AUVs were still working, as shown in Fig. 11a. Although R1 failed, the team continued to search. After target T1 was detected, its activity value was set to 0. Since target T4 was not found, its activity value was 1. R2, R3, and R4 continued to search in its direction. As shown in Fig. 11b, R3 detected target T4. The AUVs found all the targets in the given space, and the search task ended. The simulation showed that the algorithm could complete a search task under the condition of AUV mechanical failure, the algorithm’s good fault-tolerant performance.
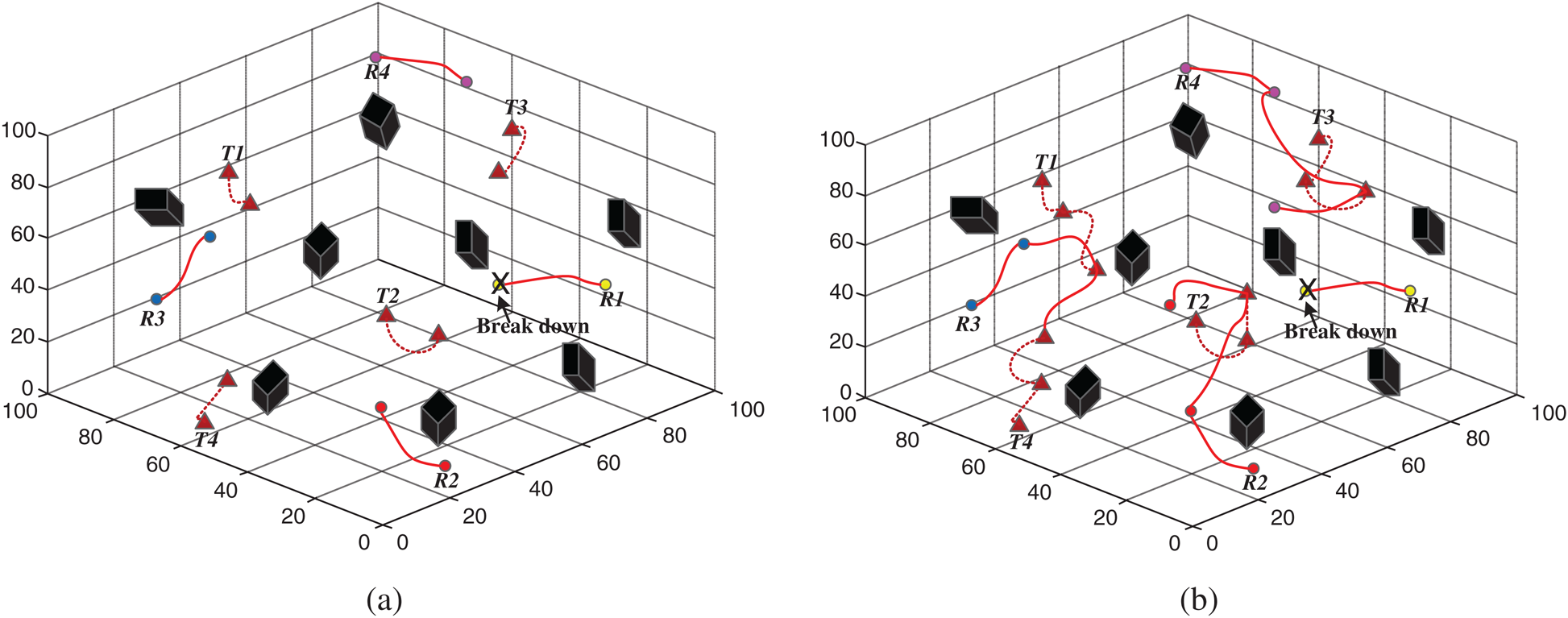
Figure 11: Search process when one AUV breaks down (a) One AUV breaks down (b) Final trajectories of entire search process
3.4 Performance Comparison of Different Algorithms
Compared to commonly used algorithms such as PSO, the proposed algorithm is expected to improve the efficiency of multi-AUV collaborative search. The PSO algorithm optimizes the solution by improving candidate solutions based on given iterations. The algorithm randomly generates particles, evaluates their fitness, and finds the individual and optimal global positions of the group.
The comparative simulation was of three AUVs searching for three targets in underwater environments with obstacles. The targets had initial positions (41, 88, 76), (78, 78, 6), and (80, 37, 58), and AUVs were randomly distributed, with positions (38, 94, 27), (58, 21, 12) and (93, 55, 83). Figs. 12a, 12b show the search process for two algorithms. Fig. 12 shows that the search path of the algorithm was shorter than that of the PSO algorithm for each AUV member. This is because the solution to the fitness function of PSO is only related to the distance between targets. In complex situations, the PSO algorithm does not adequately guide the AUV to avoid obstacles. The simulation results showed the proposed algorithm’s greater efficiency and adaptability compared to the PSO algorithm.
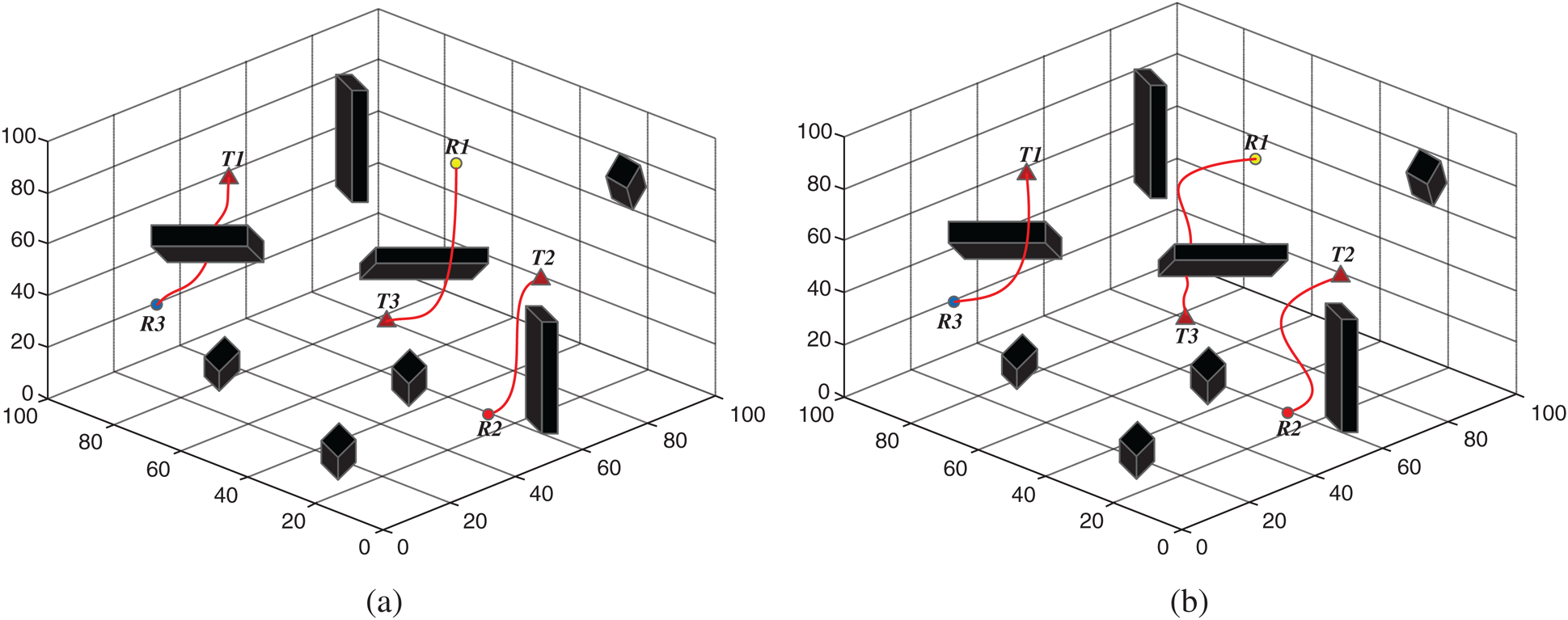
Figure 12: Searching process with different algorithms (a) Proposed algorithm (b) PSO algorithm
To compare the trajectory smoothness of the proposed algorithm and the PSO algorithm, Fig. 13 shows the trajectories of the two algorithms to avoid obstacles. Fig. 13a, 13b show the obstacle avoidance result of the proposed algorithm and PSO algorithm, respectively. The fuzzy obstacle avoidance of the proposed algorithm can provide better trajectory smoothness than the PSO control method. An AUV avoids sharp turns when it detects obstacles.
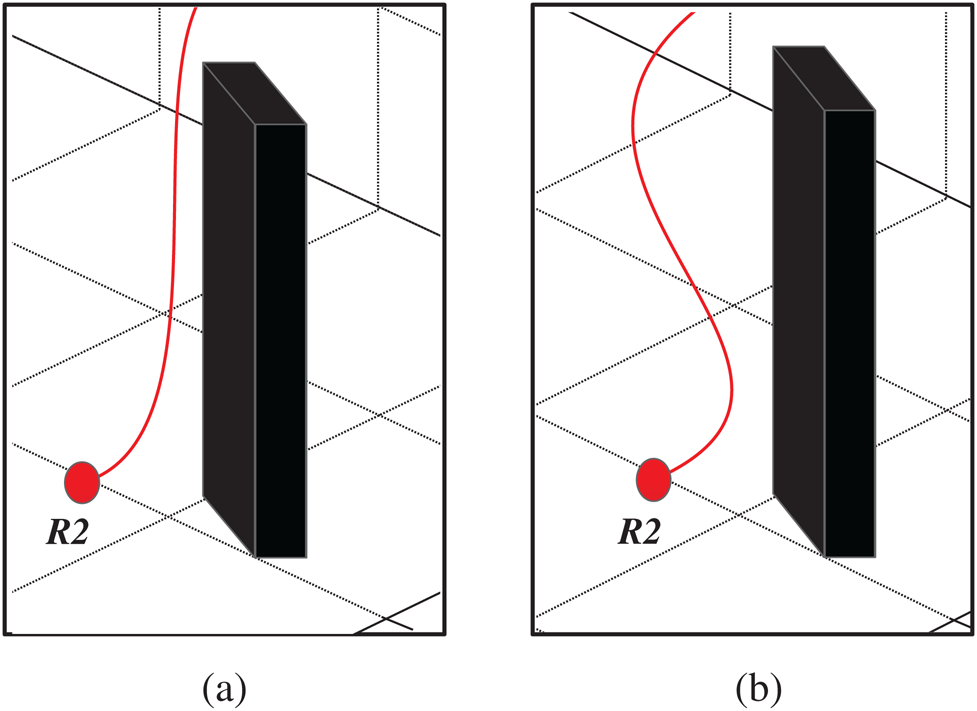
Figure 13: Trajectory comparison of avoiding obstacle (a) Proposed algorithm (b) PSO algorithm
We used the Neptune-1 AUV model to test the performance of the proposed algorithm in a real pool environment (see Fig. 14). The model was based on a remote submarine produced by Thunder-Tiger. We made it an AUV by adding a positioning module and rebuilding the remote-control system. The AUV thruster had a speed of 2 knots (1.08kN). Since underwater acoustic communication is not yet mature, this experiment was carried out on the water’s surface. The AUVs communicated using WiFi.
Figure 14: AUV model
The AUV position information was obtained through a water surface control platform, and the search track of the AUV was plotted. Fig. 15 shows the target search experiment of the AUV in the pool with an obstacle. We placed an ROV (remotely operated vehicle) in the pool as an obstacle. At the beginning of the experiment, the two AUVs searched in different directions to avoid overlapping search areas. Next, an AUV searched for the target according to the proposed algorithm. When encountering obstacles, AUVs moved using the fuzzy obstacle-avoidance method, which improved the smoothness and safety of the trajectory. Finally, two AUVs completed a search for a target, and the search path was similar to that obtained in our simulations. Experiments showed that the proposed algorithm was useful for target search in an obstacle pool.
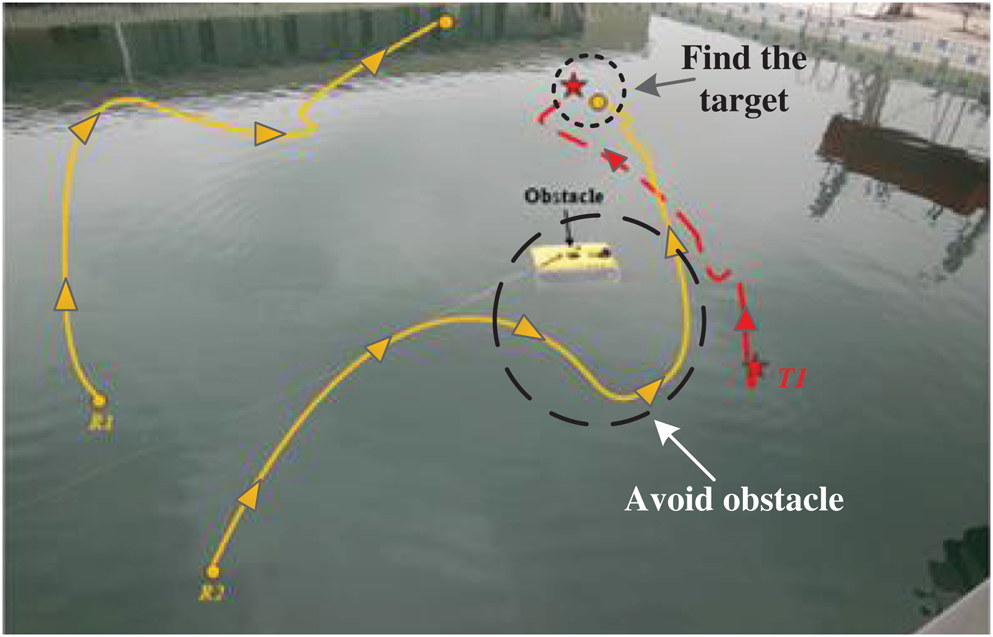
Figure 15: Pool experiment with an obstacle
Fig. 16 shows the target search experiment with two AUVs in the pool with multiple obstacles. Although obstacles were added to the environment, an AUV could safely avoid them under the guidance of the proposed algorithm. Finally, R1 searched for the target. It can be seen that the proposed algorithm could still complete the target search task in a complex environment, and the search path was smooth.
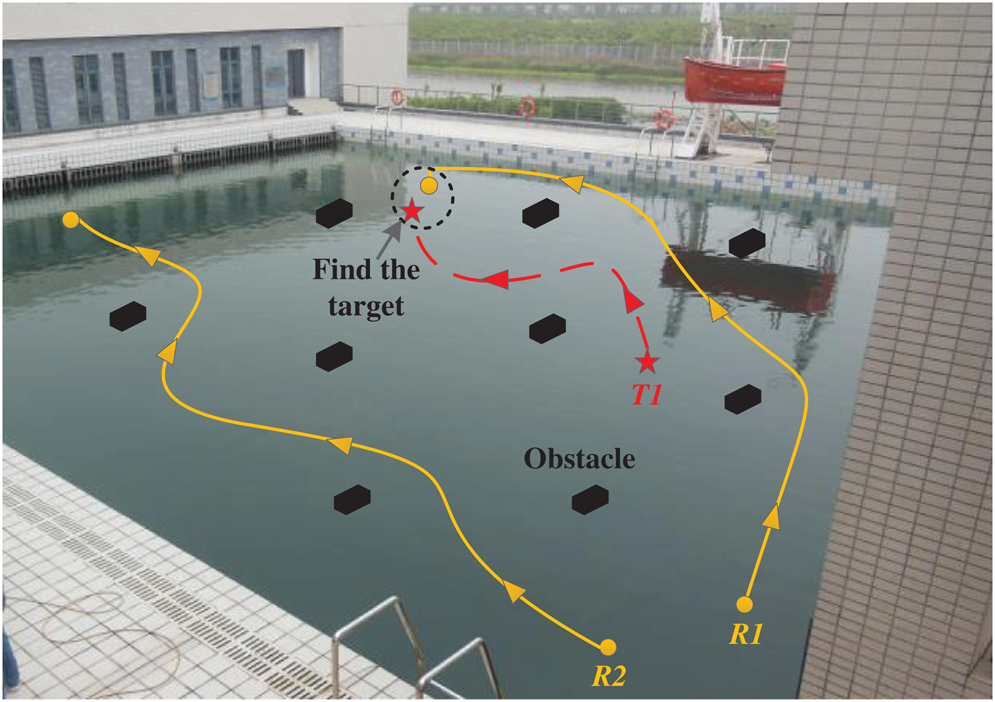
Figure 16: Pool experiment with multi-ple obstacles
A bio-inspired neural network and fuzzy obstacle-avoidance method were combined to realize the collaborative search for targets in underwater environments with obstacles. A bio-inspired neural network algorithm with certain cooperation rules could accomplish handle the target search tasks. It did not require an explicit environment model, nor trial and error to select parameters. Due to obstacles in underwater environments, a fuzzy obstacle-avoidance algorithm was introduced to optimize the search path. Simulations and experiments showed that the integrated algorithm enabled complete search tasks of multiple AUV teams and performed better than other algorithms. Although the algorithm has certain advantages, some problems have not been fully considered, such as ocean currents and the shape of an AUV. Further research is needed to obtain better algorithms that are consistent with real underwater environments.
Funding Statement: This project is supported by the National Natural Science Foundation of China (61773177), the Natural Science Foundation of Jiangsu Province (BK20171270), Jiangsu Undergraduate Training Program for Innovation and Entrepreneurship (201810323001Z, 201910323054Y).
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
1. Q. Li, Y. Y. Ben, S. M. Naqvi, J. A. Neasham and J. A. Chambers. (2018). “Robust student’s t-based cooperative navigation for autonomous underwater vehicles,” IEEE Transactions on Instrumentation and Measurement, vol. 67, no. 8, pp. 1762–1777. [Google Scholar]
2. X. Cao and D. Q. Zhu. (2017). “Multi-AUV task assignment and path planning with ocean current based on biological inspired self-organizing map and velocity synthesis algorithm,” Intelligent Automation & Soft Computing, vol. 23, no. 1, pp. 31–39. [Google Scholar]
3. X. Li and D. Q. Zhu. (2018). “An adaptive SOM neural network method for distributed formation control of a group of AUVs,” IEEE Transactions on Industrial Electronics, vol. 65, no. 10, pp. 8260–8270. [Google Scholar]
4. X. Cao, H. C. Yu and H. B. Sun. (2019). “Dynamic task assignment for multi-AUV cooperative hunting,” Intelligent Automation & Soft Computing, vol. 25, no. 1, pp. 25–34. [Google Scholar]
5. X. Xiang, C. Yu, L. Lapierre, J. Zhang and Q. Zhang. (2018). “Survey on fuzzy-logic-based guidance and control of marine surface vehicles and underwater vehicles,” International Journal of Fuzzy Systems, vol. 20, no. 2, pp. 572–586. [Google Scholar]
6. S. MahmoudZadeh, A. M. Yazdani, K. Sammut and D. M. W. Powers. (2018). “Online path planning for AUV rendezvous in dynamic cluttered undersea environment using evolutionary algorithms,” Applied Soft Computing, vol. 70, pp. 929–945. [Google Scholar]
7. W. Y. Gan and D. Q. Zhu. (2018). “Complete coverage belief function path planning algorithm of autonomous underwater vehicle based on behavior strategy,” Journal of System Simulation, vol. 30, no. 5, pp. 1857–1868. [Google Scholar]
8. C. Y. Wei, K. V. Hindriks and C. M. Jonker. (2016). “Dynamic task allocation for multi-robot search and retrieval tasks,” Applied Intelligence, vol. 45, no. 2, pp. 383–401. [Google Scholar]
9. T. Balch and R. C. Arkin. (1994). “Communication in reactive multiagent robotic systems,” Autonomous Robots, vol. 1, no. 1, pp. 27–52. [Google Scholar]
10. E. Magid, T. Tsubouchi and E. Koyanagi. (2011). “Building a search tree for a pilot system of a rescue search robot in a discretized random step environment,” Journal of Robotics and Mechatronics, vol. 23, no. 4, pp. 567–581. [Google Scholar]
11. J. Melo and A. Matos. (2017). “Survey on advances on terrain based navigation for autonomous underwater vehicles,” Ocean Engineering, vol. 139, pp. 250–264. [Google Scholar]
12. S. Y. Chien, Y. L. Lin, P. J. Lee, S. Han, M. Lewis et al. (2018). , “Attention allocation for human multi-robot control: cognitive analysis based on behavior data and hidden states,” International Journal of Human-Computer Studies, vol. 117, pp. 30–44. [Google Scholar]
13. H. Yamaguchi. (2003). “A distributed motion coordination strategy for multiple nonholonomic mobile robots in cooperative hunting operations,” Robotics and Autonomous Systems, vol. 43, no. 4, pp. 257–282. [Google Scholar]
14. S. Yoon and C. Qiao. (2011). “Cooperative search and survey using autonomous underwater vehicles (AUVs),” IEEE Transactions on Parallel and Distributed Systems, vol. 22, no. 3, pp. 364–379. [Google Scholar]
15. S. Uttendorf, B. Eilert and L. Overmeyer. (2017). “Combining a fuzzy inference system with an A* algorithm for the automated generation of roadmaps for automated guided vehicles. At-Automatisierungstechnik, vol. 65, no. 3, pp. 189–197. [Google Scholar]
16. R. Zlot and A. Stentz. (2016). “Market-based multirobot coordination for complex tasks,” International Journal of Robotics Research, vol. 25, no. 1, pp. 73–101. [Google Scholar]
17. E. Ferranti and N. Trigoni. (2011). “Practical issues in deploying mobile agents to explore a sensor-instrumented environment,” Computer Journal, vol. 54, no. 3, pp. 309–320. [Google Scholar]
18. Y. F. Cai and S. X. Yang. (2013). “An improved PSO-based approach with dynamic parameter tuning for cooperative multi-robot target searching in complex unknown environments,” International Journal of Control, vol. 86, no. 10, pp. 1720–1732. [Google Scholar]
19. A. B. Hashemi and M. R. Meybodi. (2011). “A note on the learning automata based algorithms for adaptive parameter selection in PSO,” Applied Soft Computing Journal, vol. 11, no. 1, pp. 689–705. [Google Scholar]
20. J. Kim and M. Jin. (2016). “Synchronization of chaotic systems using particle swarm optimization and time-delay estimation,” Nonlinear Dynamics, vol. 86, no. 3, pp. 2003–2015. [Google Scholar]
21. X. Cao and D. Q. Zhu. (2015). “Multi-AUV underwater cooperative search algorithm based on biological inspired neurodynamics model and velocity synthesis,” Journal of Navigation, vol. 68, no. 6, pp. 1075–1087. [Google Scholar]
22. X. Cao, H. Sun and G. E. Jan. (2018). “Multi-AUV cooperative target search and tracking in unknown underwater environment,” Ocean Engineering, vol. 150, pp. 1–11. [Google Scholar]
23. H. Ögmen and S. Gagné. (1990). “Neural network architectures for motion perception and elementary motion detection in the fly visual system,” Neural Networks, vol. 3, no. 5, pp. 487–505. [Google Scholar]
24. C. M. Luo and S. X. Yang. (2008). “A bioinspired neural network for real-time concurrent map building and complete coverage robot navigation in unknown environments,” IEEE Transactions on Neural Networks, vol. 19, no. 7, pp. 1279–1298. [Google Scholar]
25. M. A. Haque, A. R. Rahmani and M. B. Egerstedt. (2011). “Biologically inspired confinement of multi-robot systems,” International Journal of Bio-Inspired Computation, vol. 3, no. 4, pp. 213–224. [Google Scholar]
26. X. Cao, D. Q. Zhu and S. X. Yang. (2016). “Multi-AUV cooperative target search based on biological inspired neurodynamics model in three-dimensional underwater environments,” IEEE Transactions on Neural Networks and Learning Systems, vol. 27, no. 11, pp. 2364–2374. [Google Scholar]
27. Xia M., Zhang C., Weng L., Liu J., Wang Y., Tiwari S., Trivedi M. and Kohle M. L. (2018). “Robot path planning based on multi-objective optimization with local search,” Journal of Intelligent & Fuzzy Systems, vol. 35, no. 2, pp. 1755–1764. [Google Scholar]
28. M. Elhoseny, A. Shehab and X. H. Yuan. (2017). “Optimizing robot path in dynamic environments using Genetic Algorithm and Bezier Curve,” Journal of Intelligent & Fuzzy Systems, vol. 33, no. 4, pp. 2305–2316. [Google Scholar]
29. B. Sun, D. Q. Zhu and S. X. Yang. (2018). “An optimized fuzzy control algorithm for three-dimensional AUV path planning,” International Journal of Fuzzy Systems, vol. 20, no. 2, pp. 597–610. [Google Scholar]
30. T. Y. Abdalla, A. A. Abed and A. A. Ahmed. (2017). “Mobile robot navigation using PSO-optimized fuzzy artificial potential field with fuzzy control,” Journal of Intelligent & Fuzzy Systems, vol. 32, no. 6, pp. 3893–3908. [Google Scholar]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |