DOI:10.32604/iasc.2021.015285

| Intelligent Automation & Soft Computing DOI:10.32604/iasc.2021.015285 |  |
| Article |
Optimal Eighth-Order Solver for Nonlinear Equations with Applications in Chemical Engineering
Department of Mathematical Sciences, Universiti Kebangsaan Malaysia, Bangi Selangor, 43600, Malaysia
*Corresponding Author: Ishak Hashim. Email: ishak_h@ukm.edu.my
Received: 13 November 2020; Accepted: 01 December 2020
Abstract: A new iterative technique for nonlinear equations is proposed in this work. The new scheme is of three steps, of which the first two steps are based on the sixth-order modified Halley’s method presented by the authors, and the last is a Newton step, with suitable approximations for the first derivatives appeared in the new scheme. The eighth-order of convergence of the new method is proved via Mathematica code. Every iteration of the presented scheme needs the evaluation of three functions and one first derivative. Therefore, the scheme is optimal in the sense of Kung-Traub conjecture. Several test nonlinear problems are considered to compare the performance of the proposed method according to other optimal methods of the same order. As an application, we apply the new scheme to some nonlinear problems from the field of chemical engineering, such as a chemical equilibrium problem (conversion in a chemical reactor), azeotropic point of a binary solution, and volume from van der Waals equation. Comparisons and examples show that the presented method is efficient and comparable to the existing techniques of the same order.
Keywords: Nonlinear equations; root finding method; iterative methods; Halley’s method; optimal order of convergence
Searching for a solution of 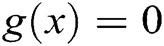 , when
, when 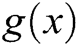 is nonlinear is highly significant in mathematics. Newton’s iterative technique for solving such equations is defined as
is nonlinear is highly significant in mathematics. Newton’s iterative technique for solving such equations is defined as

It was shown by Traub [1] that the scheme given by (1) has the second-order of convergence. Many researchers have improved the method of Newton to attain better results and to increase the convergence order, for instance see [2–5] and the references therein. Petković [6] has presented a general class of multipoint root finding methods of arbitrary order 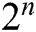 . Because of the huge number of iterative techniques that appear in the literature, Petković et al. [7] have presented a review for the most efficient iterative methods and developed techniques in a general sense. Also, Cordero et al. [8] have presented a general survey on optimal iterative schemes and how to design optimal methods of different orders.
. Because of the huge number of iterative techniques that appear in the literature, Petković et al. [7] have presented a review for the most efficient iterative methods and developed techniques in a general sense. Also, Cordero et al. [8] have presented a general survey on optimal iterative schemes and how to design optimal methods of different orders.
One of the most famous improvements of Newton’s scheme is the technique of order three given by Halley [9]:

Halley’s method has been studied widely and improved in different ways. For example, a two-step Halley’s scheme with order of convergence equals six was implemented by Noors et al. [10] using a predictor-corrector technique. But finding the second derivative is not always an easy task. Because of that Noor et al. [11] have improved the previous technique with the help of the finite difference and implemented a new second derivative-free scheme of order five. Very recently, Said Solaiman et al. [12] have established two sixth-order modifications of Halley’s method, with one of them without second derivative.
One of the most common ways to compare the efficiency of iterative methods is the efficiency index which can be determined by 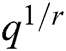 , where
, where 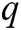 is convergence order of the iterative scheme and
is convergence order of the iterative scheme and 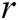 represents number of functions needed to be found at each iteration. Kung et al. [13] mentioned in a conjecture that the iterative scheme with the number of functional evaluations equals
represents number of functions needed to be found at each iteration. Kung et al. [13] mentioned in a conjecture that the iterative scheme with the number of functional evaluations equals 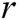 is optimal if its order of convergence equals
is optimal if its order of convergence equals 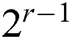 . Many authors have constructed optimal iterative methods of different orders. The default way for constructing optimal method is the composition technique together with the usage of some interpolations and approximations to minimize the number of functional evaluations. Different optimal fourth-order iterative methods have been constructed, see for examples [14–16]. Optimal eighth-order of convergence methods have been presented by many authors, see [2,17,18–22]. A comparison using the dynamics of different families of optimal eighth-order of convergence methods was proposed by Chun et al. [23].
. Many authors have constructed optimal iterative methods of different orders. The default way for constructing optimal method is the composition technique together with the usage of some interpolations and approximations to minimize the number of functional evaluations. Different optimal fourth-order iterative methods have been constructed, see for examples [14–16]. Optimal eighth-order of convergence methods have been presented by many authors, see [2,17,18–22]. A comparison using the dynamics of different families of optimal eighth-order of convergence methods was proposed by Chun et al. [23].
We propose in this work a new optimal eighth-order iterative technique for nonlinear equations. The new method is a modification of the modified Halley method (MH2) introduced by Said Solaiman et al. [12]. We use the composition technique with Hermite’s interpolation for the first derivative to reach the eighth-order of convergence with optimality, which can be considered as the major motivation of this research. The work in this paper is distributed as follows. In Section 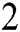 , below the new scheme is illustrated. In Section
, below the new scheme is illustrated. In Section 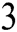 , the order of convergence of the new scheme is determined. In Section
, the order of convergence of the new scheme is determined. In Section 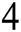 , four chemical engineering problems in addition to six nonlinear examples are used to demonstrate the efficiency of the proposed scheme, and tables are used to illustrate the comparison between our optimal method with other techniques having equal order. Lastly, in Section
, four chemical engineering problems in addition to six nonlinear examples are used to demonstrate the efficiency of the proposed scheme, and tables are used to illustrate the comparison between our optimal method with other techniques having equal order. Lastly, in Section 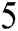 the conclusion is given.
the conclusion is given.
Let 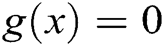 be an equation such that
be an equation such that 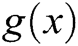 is a nonlinear function defined on some open interval
is a nonlinear function defined on some open interval 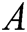 and sufficiently differentiable. Let
and sufficiently differentiable. Let 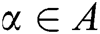 be a simple root of
be a simple root of 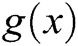 , and consider
, and consider 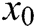 as an initial guess which is sufficiently close to
as an initial guess which is sufficiently close to 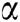 . Said Solaiman and Hashim [12] obtained the following iterative scheme using Taylor’s expansion of
. Said Solaiman and Hashim [12] obtained the following iterative scheme using Taylor’s expansion of 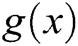 with Newton’s and Halley’s methods.
with Newton’s and Halley’s methods.
Algorithm 1: Let 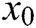 be an initial guess of the solution of
be an initial guess of the solution of 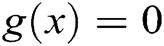 . Then we can approximate
. Then we can approximate 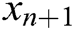 by the iterative method defined by:
by the iterative method defined by:
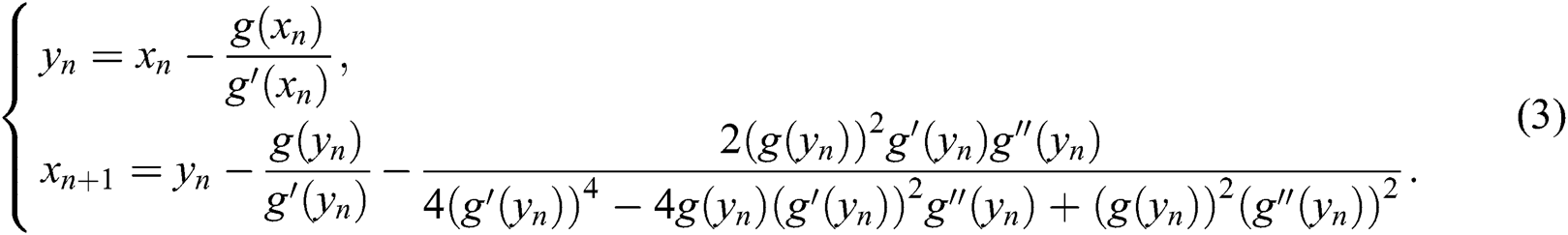
Said Solaiman et al. [12] named Algorithm 1 as MH1. They proved that MH1 is of order of convergence equals six. MH1 needs at each iteration the evaluation of two functions, two first derivatives, and one second derivative evaluation. So, the efficiency index of MH1 is 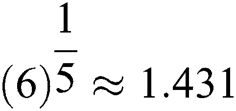 , which is not as good as Halley’s method.
, which is not as good as Halley’s method.
To make the efficiency index of Algorithm 1 better, Hermite’s approximation of the second derivative is used to produce a second derivative-free method given by:
Algorithm 2: Let 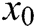 be an initial guess of the solution of
be an initial guess of the solution of 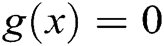 . Then we can approximate
. Then we can approximate 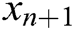 by the iterative method defined by:
by the iterative method defined by:
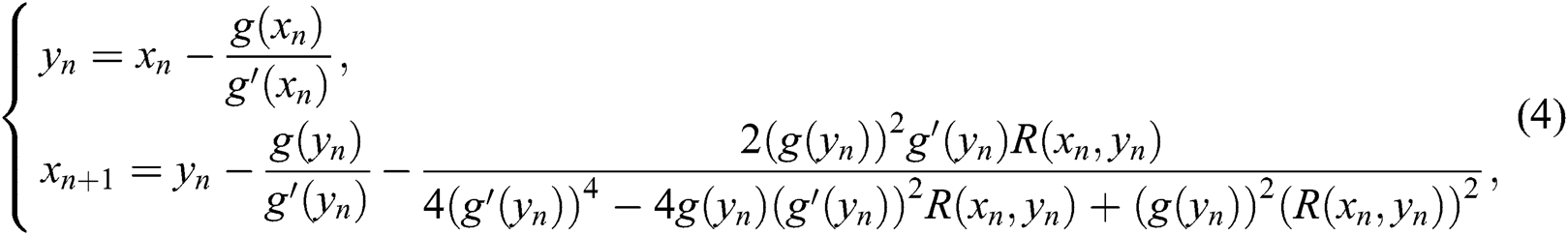
where the second derivative 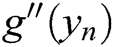 is approximated by
is approximated by
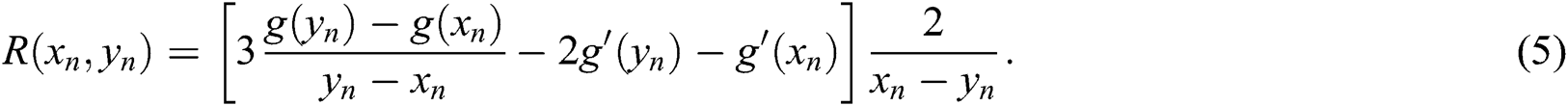
Algorithm 2 is called MH2. Said Solaiman et al. [12] proved that it is of order six. MH2 needs at each iteration the computation of two functions, and two first derivatives only. So, MH2 has efficiency index equals 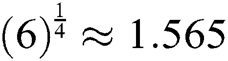 , which is better than
, which is better than 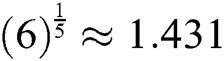 of MH1 and
of MH1 and 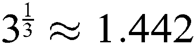 of Halley’s method.
of Halley’s method.
In order to reach the optimality, we reduce the number of functions needed to be evaluated at each iteration by using divided differences, Hermite’s interpolation, and the composition of Algorithm 2 with Newton’s method. Now, by using Algorithm 2 as a predictor, and Newton’s technique as a corrector one obtains the following algorithm:
Algorithm 3: Let 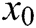 be an initial guess of the solution of
be an initial guess of the solution of 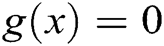 . Then we can approximate
. Then we can approximate 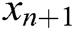 by the iterative method defined by:
by the iterative method defined by:
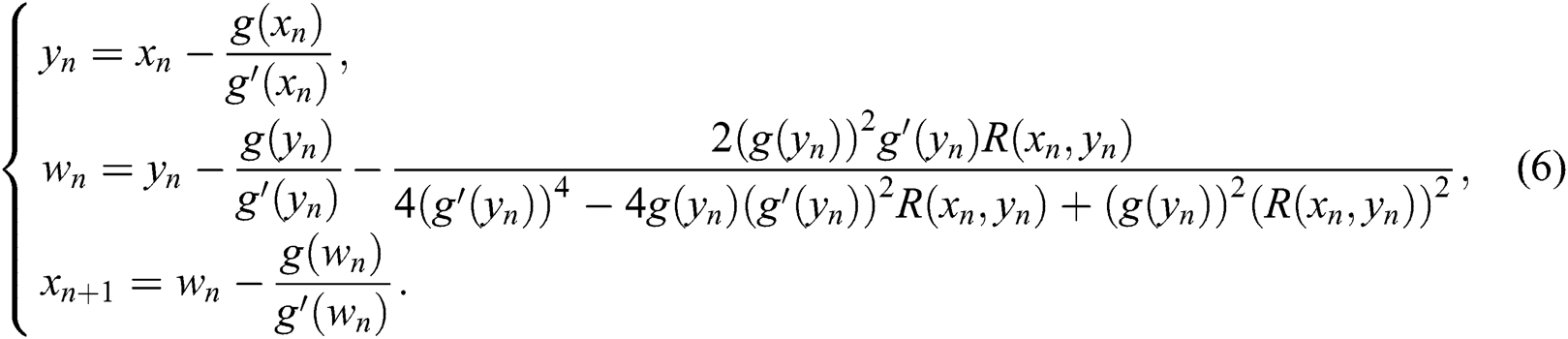
Algorithm 3 has order of convergence equals twelve with error term 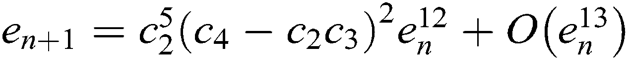 . At each iteration, Algorithm 3 requires three function evaluations and needs three first derivatives. Our goal is to rewrite
. At each iteration, Algorithm 3 requires three function evaluations and needs three first derivatives. Our goal is to rewrite 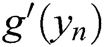 and
and 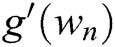 by using a combination of already evaluated functions.
by using a combination of already evaluated functions.
Using the second-order polynomial interpolation of the function 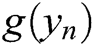 one simply obtains
one simply obtains

where 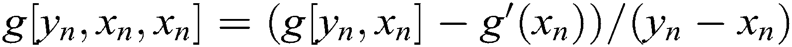 . Simplifying (7) and using
. Simplifying (7) and using 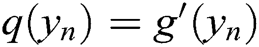 gives
gives

Now, we will use the technique which proposed before by Petković [6] and Petković et al [7] to approximate 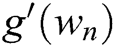 , consider Hermite’s interpolating polynomial of order 3
, consider Hermite’s interpolating polynomial of order 3
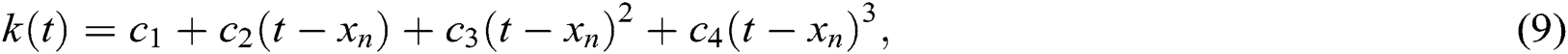
where 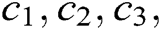 and
and 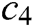 need to be found. With the conditions
need to be found. With the conditions
 and by solving the system of linear equations resulted from the above conditions, we get
and by solving the system of linear equations resulted from the above conditions, we get
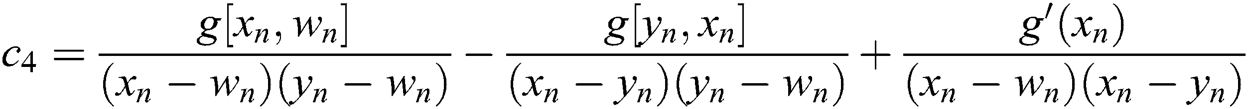 . Substituting these into Eq. (9) and using the approximation
. Substituting these into Eq. (9) and using the approximation 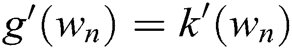 , one can write
, one can write
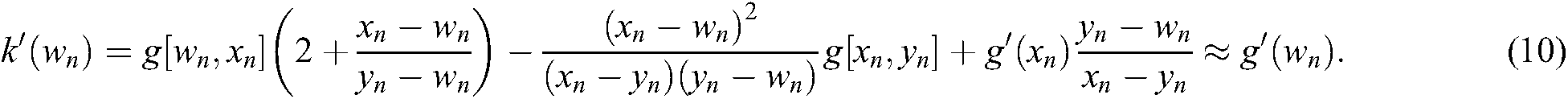
Replacing 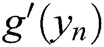 and
and 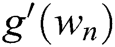 in Algorithm 3 and in Eq. (5) with the approximations (8) and (10) respectively, the following algorithm is obtained.
in Algorithm 3 and in Eq. (5) with the approximations (8) and (10) respectively, the following algorithm is obtained.
Algorithm 4: Let 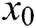 be an initial guess of the solution of
be an initial guess of the solution of 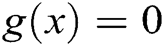 . Then we can approximate
. Then we can approximate 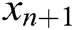 by the iterative method defined by:
by the iterative method defined by:
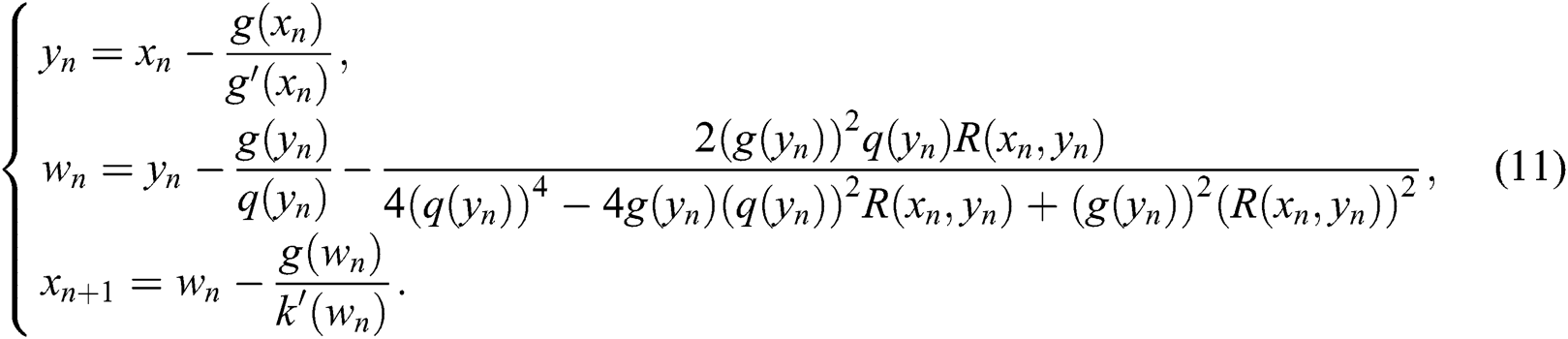
We call the above scheme the third modified Halley’s method MH3, which has convergence order equals eight as we will see in the next section. Each iteration in Algorithm 4 requires the evaluation of three functions, and one first derivative only. Based on the conjecture of Kung et al. [13], MH3 attains optimality and has efficiency index 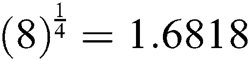 .
.
In this section we establish the order of convergence of the presented method MH3 given by Algorithm 4 by using Mathematica codes to prove the order of convergence. Consider for the next theorem that 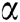 is a root of
is a root of 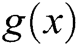 , and let
, and let 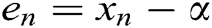 be the error at the
be the error at the 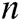 -th iteration. Using Taylor’s series expansion of
-th iteration. Using Taylor’s series expansion of 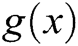 about
about  :
: 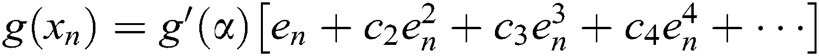 , where
, where 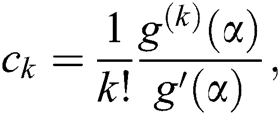
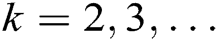 we have the following:
we have the following:
Theorem 1 Let 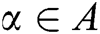 be a simple root of the function
be a simple root of the function 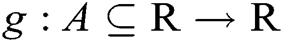 , where
, where 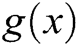 is sufficiently differentiable in an open interval
is sufficiently differentiable in an open interval 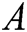 . Let
. Let 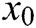 be an initial guess close enough to the root
be an initial guess close enough to the root 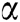 . The proposed scheme given by (11) has at least eighth-order of convergence.
. The proposed scheme given by (11) has at least eighth-order of convergence.
Proof. The following Mathematica code proves the theorem
In [1]:= g[e_]:= dg[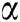 ] (e+c
] (e+c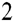 e
e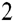 +c
+c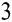 e
e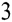 +c
+c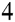 e
e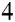 ); (*g(x) series with dg[
); (*g(x) series with dg[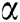 ]=
]=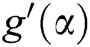 *).
*).
In [2]:= g[x_,y_]:= 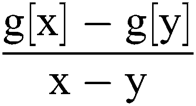 ; (*This is the finite difference*).
; (*This is the finite difference*).
In [3]:= q[x_,y_]:= 2 g[x,y]-g [x]; (*
[x]; (*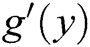 approximation *).
approximation *).
In [4]:= R[x_,y_]:= (3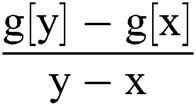 -2q[x,y]-g
-2q[x,y]-g [y])
[y])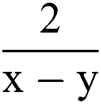 ; (*Second derivative approximation*).
; (*Second derivative approximation*).
In [5]:= k[x_,y_,w_]:= g[w,x] (2+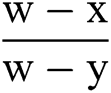 )-
)-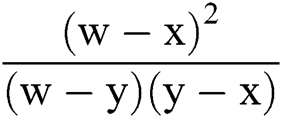 g[x,y]+g’[x]
g[x,y]+g’[x] 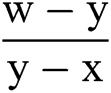 ;(*
;(*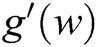 approximation*).
approximation*).
In [6]:= y =e-Series[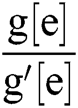 ,{e,0,8}]; (*First step of Alg. 4 *).
,{e,0,8}]; (*First step of Alg. 4 *).
In [7]:= w =y-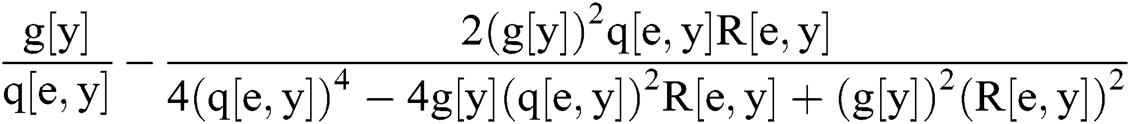 ;(*Second step of Alg. 4 *).
;(*Second step of Alg. 4 *).
In [8]:= e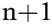 = w-
= w-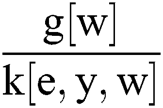 // FullSimplify (* Third step of Alg. 4 *).
// FullSimplify (* Third step of Alg. 4 *).
Out [8]:= c c
c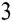 (c
(c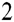 c
c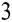 -c
-c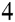 )e
)e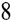 +O[e
+O[e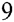 ]
]
Hence, MH3 technique given by Algorithm 4 is of eighth-order of convergence.
4 Applications and Numerical Examples
To show the efficiency of the new optimal eighth-order method MH3, several examples will be tested including some chemical engineering problems. Comparison will be done against the following schemes of optimal eighth-order of convergence: the method proposed by Kung et al. [13], the method presented by Cordero et al. [2] with 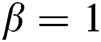 , the second case of the first family with
, the second case of the first family with 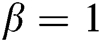 proposed by Sharma et al. [19], the method presented by Behl et al. [21] with
proposed by Sharma et al. [19], the method presented by Behl et al. [21] with 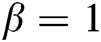 , and the special case
, and the special case 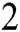 with
with 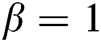 from the method presented by Behl et al. [18]. We denote the methods by the following abbreviations respectively: KT, CLMT, SA, BGMM, and BAM.
from the method presented by Behl et al. [18]. We denote the methods by the following abbreviations respectively: KT, CLMT, SA, BGMM, and BAM.
We consider 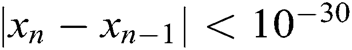 and
and 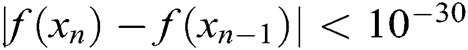 at the same time as a stopping criterion of the computer programs. Mathematica 9 was used to carry out all computations with 10000 significant digits.
at the same time as a stopping criterion of the computer programs. Mathematica 9 was used to carry out all computations with 10000 significant digits.
Tabs. 1–5illustrate the comparisons between the iterative methods, where 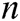 indicates number of the iterations such that the stopping criterion is affirmed,
indicates number of the iterations such that the stopping criterion is affirmed, 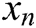 is the approximate root,
is the approximate root, 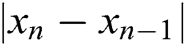 is the absolute difference between two successive approximations of the root such that
is the absolute difference between two successive approximations of the root such that 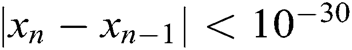 and
and 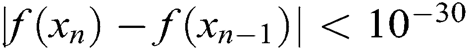 ,
, 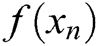 is the value of the approximate root, the approximated computational order of convergence (ACOC) given by Cordero et al. [24], which can be estimated as follows
is the value of the approximate root, the approximated computational order of convergence (ACOC) given by Cordero et al. [24], which can be estimated as follows
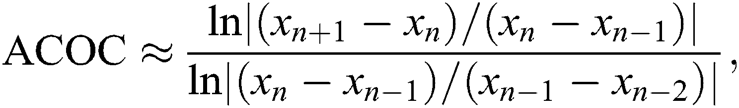 and finally, the time in seconds required to satisfy the stopping criterion using the built-in function “TimeUsed” in Mathematica 9 software. All calculations have been performed under the same conditions on Intel Core i7-3770 CPU @3.40 GHz with 4GB RAM, with Microsoft Windows 10, 64 bit based on X64-based processor.
and finally, the time in seconds required to satisfy the stopping criterion using the built-in function “TimeUsed” in Mathematica 9 software. All calculations have been performed under the same conditions on Intel Core i7-3770 CPU @3.40 GHz with 4GB RAM, with Microsoft Windows 10, 64 bit based on X64-based processor.
Consider the following test examples:
Example 1 (A chemical equilibrium problem) Consider the equation from [25] which describes the fraction of the nitrogen-hydrogen feed that gets converted to ammonia (this fraction is called fractional conversion). Also, consider that we have pressure of 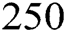 atm and temperature of
atm and temperature of 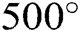 C, the original problem consists of finding the root of the function
C, the original problem consists of finding the root of the function
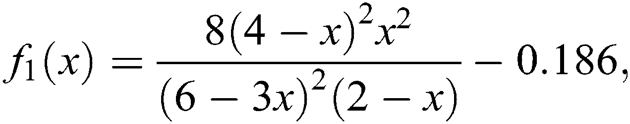 which can be reduced in polynomial form as:
which can be reduced in polynomial form as:
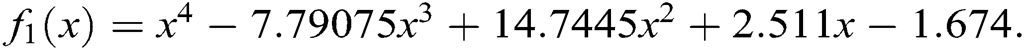
The four roots of this function are: 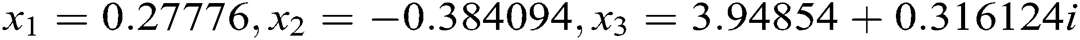 and
and 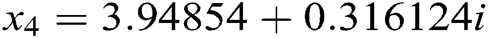 . By the definition, the factional conversion must be between
. By the definition, the factional conversion must be between 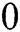 and
and 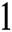 . So, only the first real root
. So, only the first real root 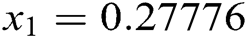 is acceptable and physically meaningful. We started by
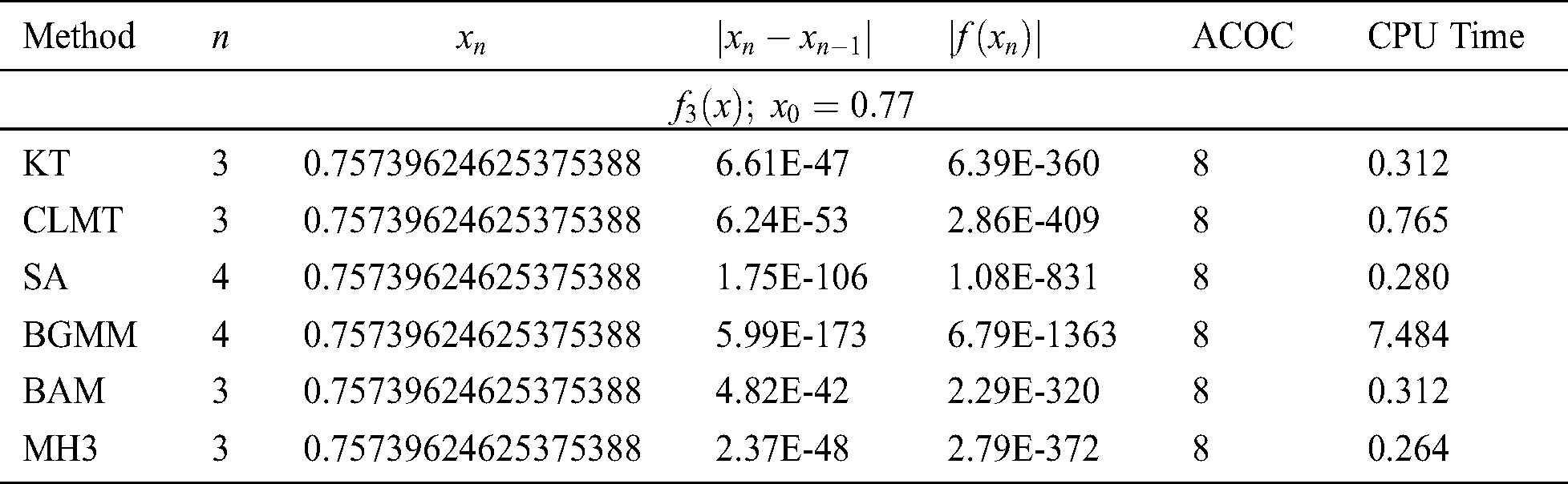
is acceptable and physically meaningful. We started by 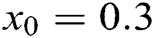 as an initial guess. The results are concluded in Tab. 1.
as an initial guess. The results are concluded in Tab. 1.
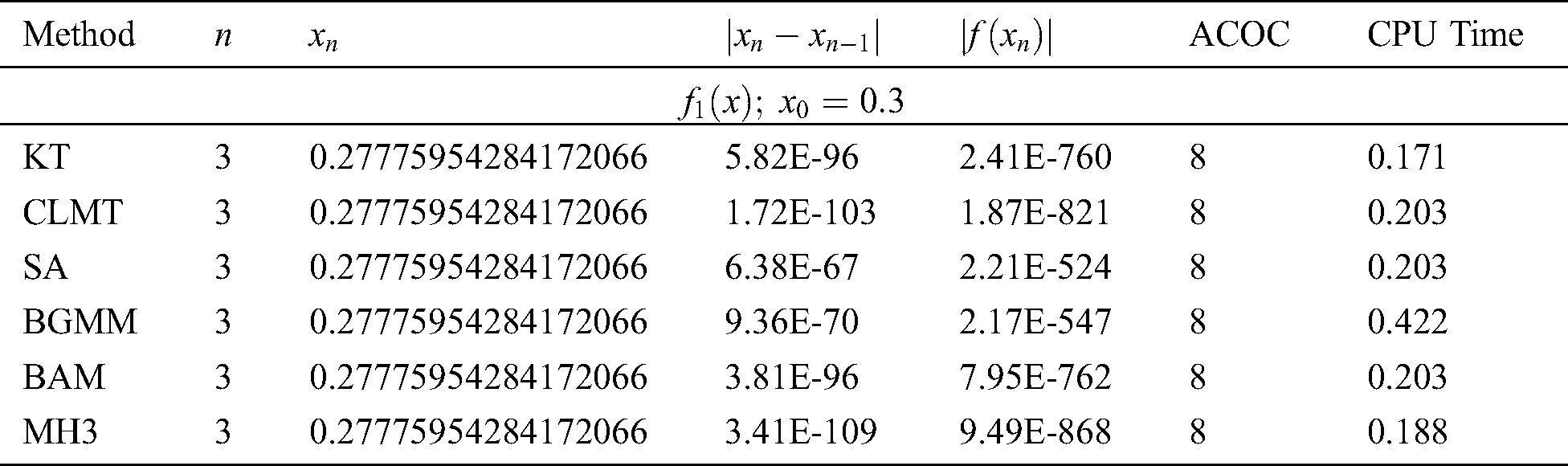
Table 1: Comparisons between different methods on test function 
Example 2 (Azeotropic point of a binary solution) Consider the problem obtained by Shacham et al. [26] to determine the azeotropic point of a binary solution:
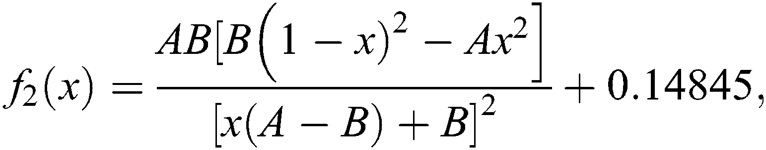 where A and B are coefficients in the Van Laar equation which describes phase equilibria of liquid solutions. Consider for this problem that
where A and B are coefficients in the Van Laar equation which describes phase equilibria of liquid solutions. Consider for this problem that 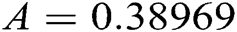 and
and 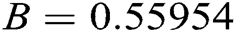 .
.
The root of this equation is 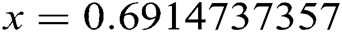 . We took the initial approximation
. We took the initial approximation 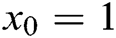 . See Tab. 2 for the results and comparisons.
. See Tab. 2 for the results and comparisons.
Table 2: Comparisons between different methods on test function 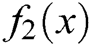
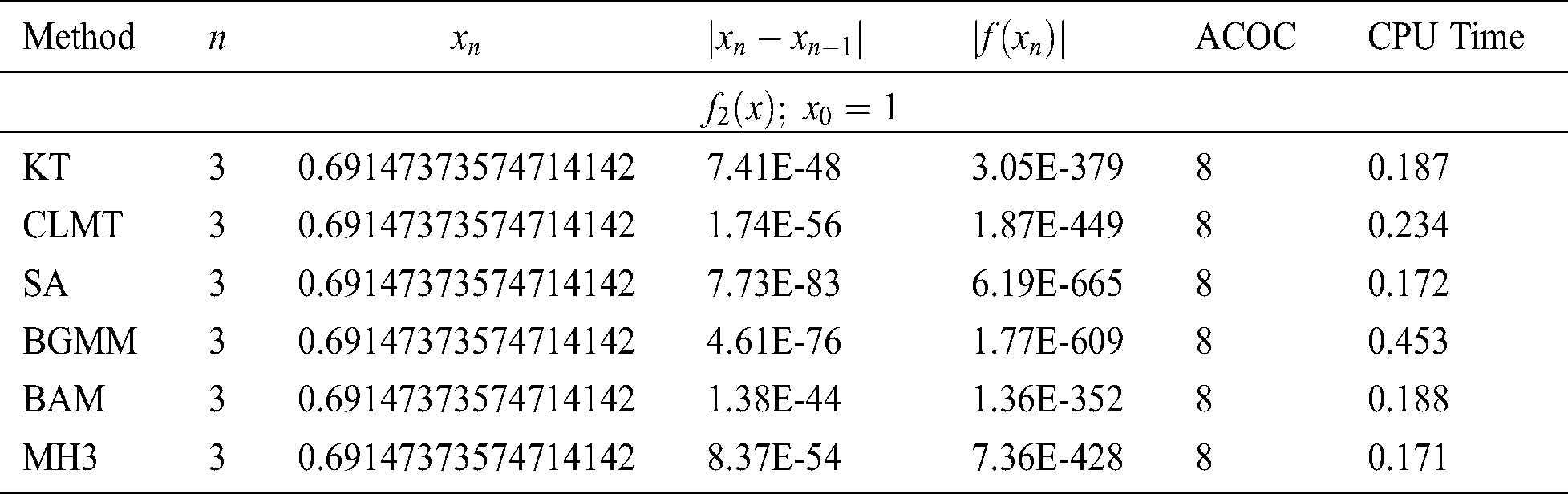
Example 3 (Conversion in a chemical reactor) In this example from [27], the following nonlinear equation is to be solved
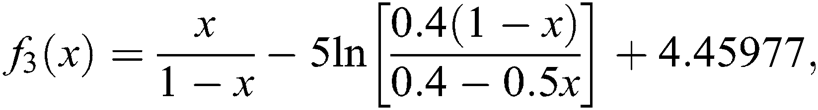 where
where 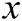 is the fractional conversion of species in a chemical reactor. Therefore,
is the fractional conversion of species in a chemical reactor. Therefore, 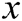 should be bounded between
should be bounded between 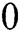 and
and 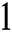 .
.
The solution of this equation is 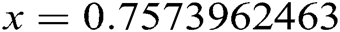 . As an initial solution, we selected
. As an initial solution, we selected 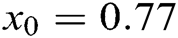 . Check the results in Tab. 3.
. Check the results in Tab. 3.
Table 3: Comparisons between different methods on test function 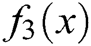
Example 4 (Volume from Van Der Waals equation) Van Der Waals’ equation is given by
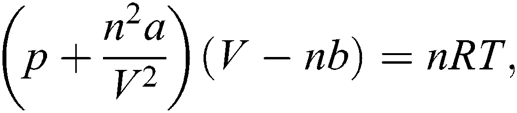
where 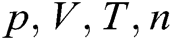 are the pressure, volume, temperature in Kelvin and number of moles of the gas.
are the pressure, volume, temperature in Kelvin and number of moles of the gas. 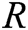 is the gas constant equals
is the gas constant equals 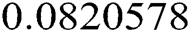 . Finally, a and b are called Van Der Waals constants and they depend on the gas type. Its clear that the above equation is nonlinear in
. Finally, a and b are called Van Der Waals constants and they depend on the gas type. Its clear that the above equation is nonlinear in 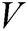 . It can be reduced to the following function of
. It can be reduced to the following function of 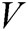 .
.
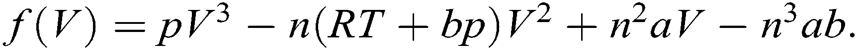 For instance, if one has to find the volume of
For instance, if one has to find the volume of 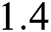 moles of benzene vapor under pressure of
moles of benzene vapor under pressure of 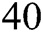 atm and temperature of
atm and temperature of 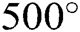 C, given that Van Der Waals constants for benzene are
C, given that Van Der Waals constants for benzene are 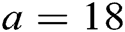 and
and 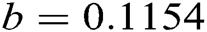 , then the problem arises is to find roots of this polynomial
, then the problem arises is to find roots of this polynomial
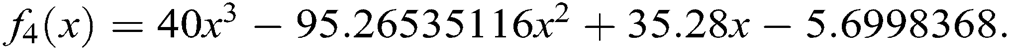 The above equation has three roots:
The above equation has three roots: 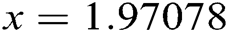 and
and 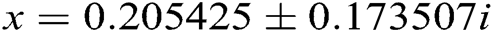 . As
. As 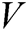 is a volume, therefore only the positive real roots are physically meaningful, that is the first root. We considered the initial approximation
is a volume, therefore only the positive real roots are physically meaningful, that is the first root. We considered the initial approximation 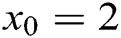 for this problem. The results and comparisons are concluded in Tab. 4.
for this problem. The results and comparisons are concluded in Tab. 4.
Table 4: Comparisons between different methods on test function 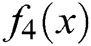
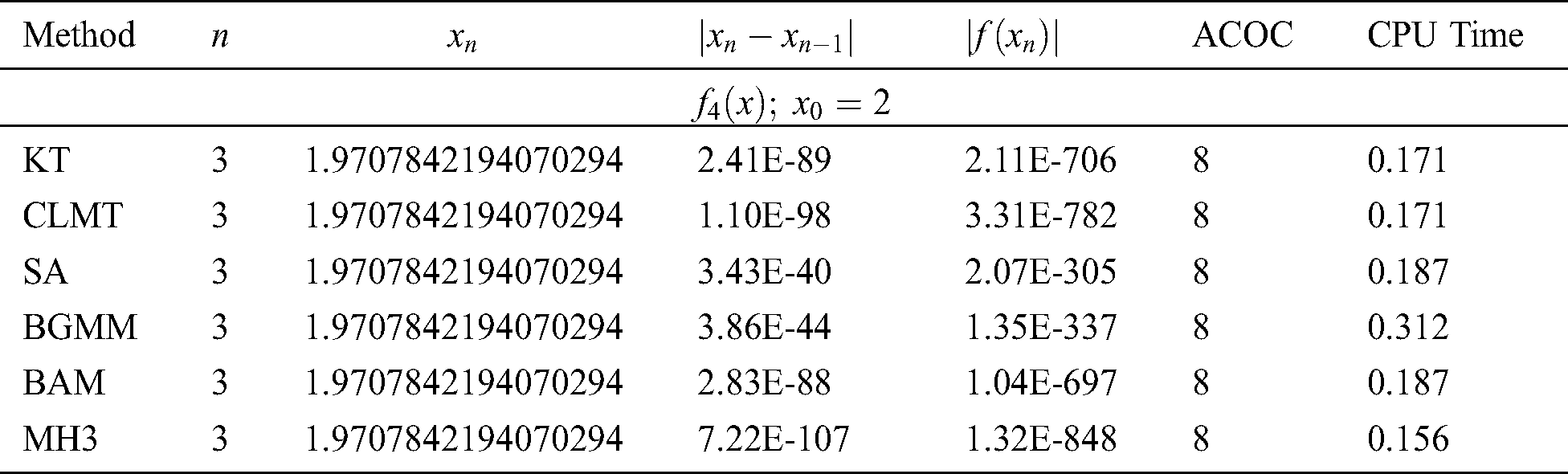
Example 5 To study the proposed method on some nonlinear functions, consider the following six test functions:
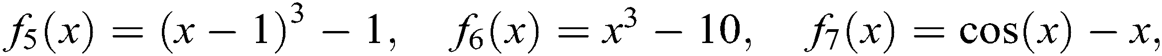
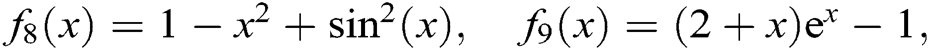
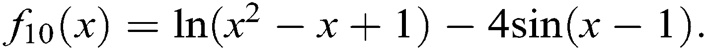
Comparisons’ results of Example 5 are presented in Tab. 5.
Table 5: Comparisons between different methods on test functions 
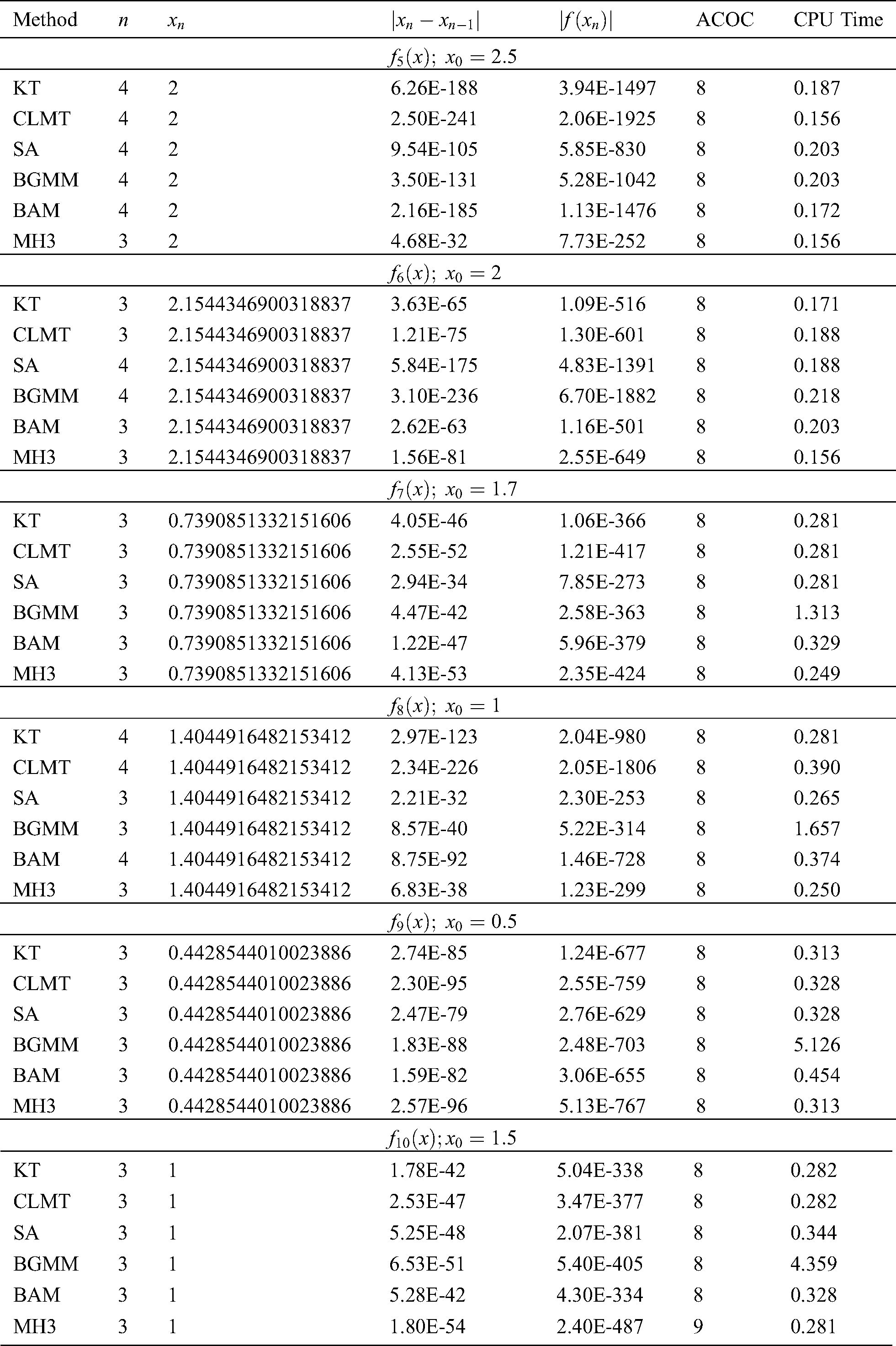
It is clear from Tabs. 1–5 that MH3 needs less iterations to satisfy the stopping criterion than the other tested methods, or in some cases it needs the same number of iterations. Based on the numerical experiments, the iterative scheme given by MH3 is comparable to the tested schemes of equal order. Note that even if MH3 has the same number of iterations needed to satisfy the convergence criterion, it is still superior to the other schemes considered in this study since 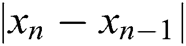 and
and 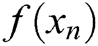 are less for MH3 than the other tested methods of the same order. Also, in the last column of Tabs. 1–5, the CPU time required to satisfy the convergence condition of MH3 is less in nine out of 10 functions than that of the other tested methods. Overall, based on either the number of iterations or CPU time needed to satisfy the convergence criterion, the new method would be preferable as compared to the tested methods.
are less for MH3 than the other tested methods of the same order. Also, in the last column of Tabs. 1–5, the CPU time required to satisfy the convergence condition of MH3 is less in nine out of 10 functions than that of the other tested methods. Overall, based on either the number of iterations or CPU time needed to satisfy the convergence criterion, the new method would be preferable as compared to the tested methods.
For the test functions in Example 5, we test another convergence condition, that is number of required iterations such that 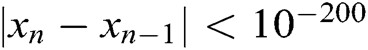 . It is obvious from Tab. 6 that MH3 requires number of iterations which is fewer or equal to the number needed by the tested methods of equal order of convergence to satisfy the convergence criterion. Overall, MH3 is comparable to the other tested methods if we want to take in account the accuracy of the approximate zero with the CPU time needed to satisfy the stopping criterion.
. It is obvious from Tab. 6 that MH3 requires number of iterations which is fewer or equal to the number needed by the tested methods of equal order of convergence to satisfy the convergence criterion. Overall, MH3 is comparable to the other tested methods if we want to take in account the accuracy of the approximate zero with the CPU time needed to satisfy the stopping criterion.
Table 6: Comparisons between different methods such that 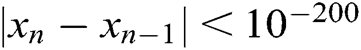

A new optimal root finding scheme for nonlinear equations has been established in this work. The optimality of the proposed method was reached by using composition technique with Hermite’s polynomial and finite differences. The software Mathematica has been used to show that the optimal technique is convergent with convergence order equals eight. Several numerical examples with four real life problems from the field of chemical engineering were examined, demonstrating the strength of the proposed method. Overall, the implemented method is comparable to the tested iterative schemes of equal order of convergence.
Funding Statement: We are grateful for the financial support from UKM’s research Grant GUP-2019-033.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
1. J. F. Traub. (1964). Iterative Methods for the Solution of Equations. Englewood Cliffs, NJ, USA: Prentice-Hall. [Google Scholar]
2. A. Cordero, T. Lotfi, K. Mahdiani and J. R. Torregrosa. (2015). “A stable family with high order of convergence for solving nonlinear equations,” Applied Mathematics and Computation, vol. 254, pp. 240–251. [Google Scholar]
3. A. Kumar, P. Maroju, R. Behl, D. K. Gupta and S. S. Motsa. (2018). “A family of higher order iterations free from second derivative for nonlinear equations in R,” Journal of Computational and Applied Mathematics, vol. 330, pp. 676–694. [Google Scholar]
4. O. S. Solaiman and I. Hashim. (2019). “Efficacy of optimal methods for nonlinear equations with chemical engineering applications,” Mathematical Problems in Engineering, vol. 2019, pp. 11. [Google Scholar]
5. S. Sharifi, M. Salimi, S. Siegmund and T. Lotfi. (2016). “A new class of optimal four-point methods with convergence order 16 for solving nonlinear equations,” Mathematics and Computers in Simulation, vol. 119, pp. 69–90. [Google Scholar]
6. M. S. Petković. (2010). “On a general class of multipoint root-finding methods of high computational efficiency,” SIAM Journal on Numerical Analysis, vol. 47, no. 6, pp. 4402–4414. [Google Scholar]
7. M. S. Petković, B. Neta, L. D. Petković and J. Džunić. (2014). “Multipoint methods for solving nonlinear equations: a survey, ” in Applied Mathematics and Computation, vol. 226, Elsevier Inc., pp. 635–660. [Google Scholar]
8. A. Cordero and J. R. Torregrosa. (2016). “On the design of optimal iterative methods for solving nonlinear equations, ” in Advances in Iterative Methods for Nonlinear Equations, SEMA SIMAI Springer Series, S. Amat, S. Busquier, 10. New York City, NY: Springer International Publishing, pp. 79–111. [Google Scholar]
9. E. Halley. (1694). “A new; exact and easy method of finding the roots of equations generally and that without any previous reduction,” Philosophical Transactions of the Royal Society, vol. 18, no. 210, pp. 136–148. [Google Scholar]
10. K. I. Noor and M. A. Noor. (2007). “Predictor-corrector Halley method for nonlinear equations,” Applied Mathematics and Computation, vol. 188, no. 2, pp. 1587–1591. [Google Scholar]
11. M. A. Noor, W. A. Khan and A. Hussain. (2007). “A new modified Halley method without second derivatives for nonlinear equation,” Applied Mathematics and Computation, vol. 189, no. 2, pp. 1268–1273. [Google Scholar]
12. O. S. Solaiman and I. Hashim. (2019). “Two new efficient sixth order iterative methods for solving nonlinear equations,” Journal of King Saud University—Science, vol. 31, no. 4, pp. 701–705. [Google Scholar]
13. H. T. Kung and J. F. Traub. (1974). “Optimal order of one-point and multipoint iteration,” Journal of the ACM, vol. 21, no. 4, pp. 643–651. [Google Scholar]
14. C. Chun. (2008). “Some fourth-order iterative methods for solving nonlinear equations,” Applied Mathematics and Computation, vol. 195, no. 2, pp. 454–459. [Google Scholar]
15. R. Sharma and A. Bahl. (2015). “An optimal fourth order iterative method for solving nonlinear equations and its dynamics,” Journal of Complex Analysis, vol. 2015, no. 8, pp. 1–9. [Google Scholar]
16. R. Behl, P. Maroju and S. S. Motsa. (2017). “A family of second derivative free fourth order continuation method for solving nonlinear equations,” Journal of Computational and Applied Mathematics, vol. 318, pp. 38–46. [Google Scholar]
17. O. S. Solaiman, S. A. A. Karim and I. Hashim. (2019). “Optimal fourth- and eighth-order of convergence derivative-free modifications of King’s method,” Journal of King Saud University—Science, vol. 31, no. 4, pp. 1499–1504. [Google Scholar]
18. R. Behl, I. K. Argyros and S. S. Motsa. (2016). “A new highly efficient and optimal family of eighth-order methods for solving nonlinear equations,” Applied Mathematics and Computation, vol. 282, pp. 175–186. [Google Scholar]
19. J. R. Sharma and H. Arora. (2016). “Some novel optimal eighth order derivative-free root solvers and their basins of attraction,” Applied Mathematics and Computation, vol. 284, pp. 149–161. [Google Scholar]
20. G. Matthies, M. Salimi, S. Sharifi and J. L. Varona. (2016). “An optimal three-point eighth-order iterative method without memory for solving nonlinear equations with its dynamics,” Japan Journal of Industrial and Applied Mathematics, vol. 33, no. 3, pp. 751–766. [Google Scholar]
21. R. Behl, D. González, P. Maroju and S. S. Motsa. (2018). “An optimal and efficient general eighth-order derivative free scheme for simple roots,” Journal of Computational and Applied Mathematics, vol. 330, pp. 666–675. [Google Scholar]
22. Y. H. Geum, Y. I. Kim and B. Neta. (2018). “Constructing a family of optimal eighth-order modified Newton-type multiple-zero finders along with the dynamics behind their purely imaginary extraneous fixed points,” Journal of Computational and Applied Mathematics, vol. 333, pp. 131–156. [Google Scholar]
23. C. Chun and B. Neta. (2016). “Comparison of several families of optimal eighth order methods,” Applied Mathematics and Computation, vol. 274, pp. 762–773. [Google Scholar]
24. A. Cordero and J. R. Torregrosa. (2007). “Variants of Newton’s method using fifth-order quadrature formulas,” Applied Mathematics and Computation, vol. 190, no. 1, pp. 686–698. [Google Scholar]
25. G. V. Balaji and J. D. Seader. (1995). “Application of interval Newton’s method to chemical engineering problems,” Reliable Computing, vol. 1, no. 3, pp. 215–223. [Google Scholar]
26. M. Shacham and E. Kehat. (1972). “An iteration method with memory for the solution of a non-linear equation,” Chemical Engineering Science, vol. 27, no. 11, pp. 2099–2101. [Google Scholar]
27. M. Shacham. (1986). “Numerical solution of constrained non-linear algebraic equations,” International Journal for Numerical Methods in Engineering, vol. 23, no. 8, pp. 1455–1481. [Google Scholar]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |